Transport dynamics of sediment-laden jet: A review
Abstract
Wastewater disposal through the dumping of spoil and sludge into the river, lake, or ocean is typically in the form of a sediment-laden jet. The inorganic and organic solids from the effluent settling close to the source often result in the formation of sludge banks which can have a damaging effect on the marine ecosystem. Therefore, predicting the transport and deposition of sediment-laden wastewater jet flows has been a focus of intense research for decades. In this paper, we discussed the fundamental understanding of sediment-laden jets and the progress made in their predictions. We also highlighted some of the pertinent research challenges revealed by the previous studies and identified some key research issues that need to be addressed to achieve sustainable marine wastewater disposal in the face of increasing river, lake, and marine pollution.
1 INTRODUCTION
Sediment-laden jet is a two-phase flow that is commonly found in nature or in engineering works. Examples in a natural environment include hydrothermal vents (black smokers), silt or sediment-laden river plumes, and volcanic eruption. In engineering, submarine wastewater disposal through dumping of spoil and sludge into the river, lake, or ocean are often in the form of a sediment-laden jet. Figure 1a shows an image of hydrothermal vents (black smokers) which are commonly found in ocean basins. A venting black smoker emits jets of particle-laden fluids. The particles are predominantly very fine-grained sulfide minerals. Research has shown that deep-sea mud contains high concentrations of rare-earth elements, possibly sourced from hydrothermal plumes (Kato et al., 2011). Figure 1b shows an image of a volcanic eruption that begins with an accumulation of gas-rich magma in reservoirs near the earth's surface which is preceded by emissions of steam and gas from small vents in the ground forming a sediment-laden plume. In the deep ocean, oceanographers have reported many large submarine volcanoes (Figure 1c) which rise to over 1000 m above the seafloor. The peaks are often found hundreds to thousands of meters below the sea surface (Nybakken & Bertness, 2005).

Figure 1e shows an image of a Costa Rican river discharging silt-laden waters (caused by erosion) into the ocean. The result of this phenomenon is a massive amount of silt or sediment being accumulated in the estuary as well as in the ocean. Benthic organisms such as coral, oysters, shrimps, and mussels are greatly affected by the silt, as they are filter feeders and may literally become “choked up” by silt-laden discharges. Other harmful impacts include pollution and degradation of aquatic resources. Dumping (Figure 1d) of sediment or waste materials into the ocean as sediment-laden flow also affects aquatic resources. Additionally, the balance and stability of human health and the ecosystem can be gravely threatened by pollutants from submarine wastewater discharges (Figure 1f) as such pollutants are a potential threat to the local marine environmental and ecological systems (Roberts et al., 2010; Xu et al., 2017).
The dumping operations of waste materials, therefore, need to be carefully controlled to minimize the negative effects of discharged contaminants into the marine environment, together with regular monitoring of water quality. As an environmentally friendly approach, submarine wastewater discharges undergo some treatment to reduce the toxicity, heavy metal content, nutrient content, and so forth, before being discharged (Binelli et al., 2015; Mennaa et al., 2015; Metcalf & Eddy, 1991; G. Zhou et al., 2016). Nevertheless, partially treated wastewater is often discharged in the form of sediment-laden buoyant jets with suspended solids concentrations ranging from 20 mg/L after secondary treatment to 220 mg/L in untreated sewage. These inorganic and organic solids may settle close to the source, giving rise to the formation of sludge banks. The water environment and water ecology near the outfall nozzles hence experience a continuing negative impact from these sludges (Chan, 2013; Gomes & Lester, 2003; Lee, 2010; Minh et al., 2009). In addition, these bottom sediments serve as a source of oxygen demand and a reservoir for microorganisms, nutrients, and toxic substances, thus adversely affecting the aquatic environment and benthic fauna (Maldonado et al., 2000; Pritchard, 1997; Santschi et al., 2001).
Due to the importance of sediment-laden jet flows in both natural environments and engineering works, predicting the transport and deposition of such flows has been a subject of active research for decades. This article will review the fundamental understanding and research progress of sediment-laden jets. It will be mainly restricted to low-concentration sediment-laden jets and their applications for wastewater disposal and dredging/dumping of spoil and sludge into the ocean which are predominantly dominated by the wave-current environment. Some key challenges are highlighted and major research questions that are yet to be answered are discussed.
2 SEDIMENT-LADEN JETS
Sediment-laden jets are a challenging flow problem due to the complicated water–particles interaction between the suspended particles and the surrounding fluid (Thacher et al., 2021). Researchers, therefore, usually start by making some assumptions according to the characteristics of the specific flow to simplify the problem. The research is either conducted through experimental studies or theoretical/numerical models with different jet orientations submerged in the hydrostatic or hydrokinetic environment (Bouvard & Petkovie, 1973; Chan, 2013; Cuthbertson & Davies, 2008; Hino, 1963; Jiang et al., 2005; J. H. W. Lee & Cheung, 1990; Liu & Lam, 2015; Vanoni & Nomicos, 1960).
2.1 Sediment-laden jets in hydrostatic environment
2.1.1 Vertical downward sediment-laden jets
Under a hydrostatic water environment, sediment-laden jets have been studied considering different nozzle orientations, such as vertical downward, vertical upward, horizontal, and inclined (Huai et al., 2012; Jiang et al., 2005; Mazurek et al., 2002; L. Zhang et al., 2018). The simplest form is the vertical downwards jet as the fluid flow moves in the same direction as the sediment's natural gravitational settling. The diffusion rate of both the solid phase and fluid phase is determined by the particle size, turbulence intensity, and volumetric concentration (Brush, 1962; Mazurek et al., 2002; Muste et al., 1998; Parthasarathy & Faeth, 1987). The fluid turbulence is not the only factor controlling the diffusion rate, instead, the effect of particle turbulence is also significant (Shi et al., 2022; L. Zhang et al., 2018). The mean sediment velocity is taken as the sum of fluid velocity and the settling velocity (Jiang et al., 2005). Model predictions on the movement of sediment particles in turbulent flows have shown that the computationally demanding Basset force term can be neglected in turbulent conditions (Chan, 2013).
2.1.2 Vertical upward sediment-laden jets
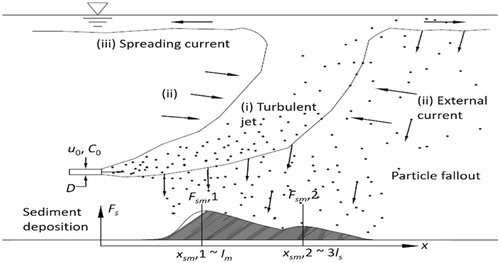
For vertical upward sediment-laden jets, the initial momentum of the jet and the gravity effects on the sediments are both in the vertical direction. Impingement of the jet at the free surface leads to the development of a hydraulic jump which generates spreading gravity currents responsible for sedimentation and re-entrainment (Figure 2). The spreading gravity current is commonly found to be in Gaussian distribution (Cardoso & Zarrebini, 2002; Lippert & Woods, 2020; Sparks et al., 1991). Re-entrainment of sediment results in increased particle flux along the plume. Thus, entrainment and re-entrainment processes are important to describe the final sediment deposition distribution (Carey et al., 1988; Ernst et al., 1996; Mingotti & Woods, 2019, 2020; Rafati et al., 2022). The particle–water interaction determines the sedimentation patterns on the bottom layer and the deposition rate decreases in radial distance due to the velocity decay. The velocity decay rate of the sediment is found to be higher than that of the fluid. At high initial velocity, the jet distribution is higher and spreads further in the radial direction (Huai et al., 2012; M. J. Neves & Fernando, 1995; Zarrebini & Cardoso, 2000). Within the jet core, two regions have been identified, the suspension region where the sediment particles are in suspension by the jet flow, and the settling region where the settling velocity exceeds the fluid velocity (Jiang et al., 2005).
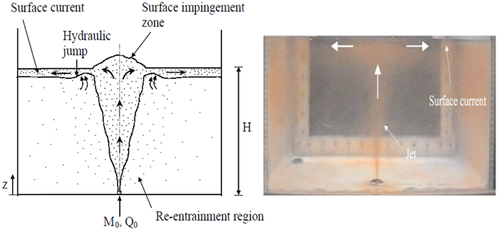
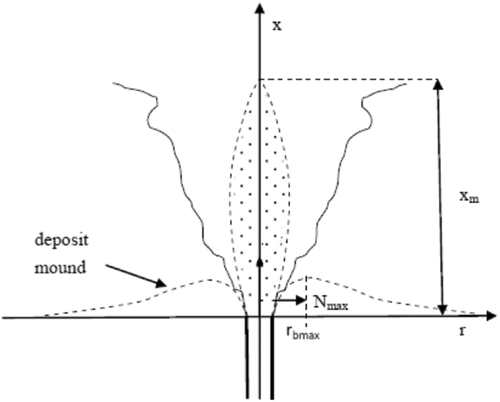
Hall et al. (2010) suggested that the exit densimetric Froude number is the main factor affecting the distributions of the fluid and sediment. The nozzle densimetric Froude number F, which gives an estimate of the intensity of the sediment-laden jet was then defined in the study of Huai et al. (2012). On the basis of the intensity of the sediment-laden jets caused by the densimetric Froude number different deposition patterns were observed for weaker jet intensity and stronger jet intensity. The parameters used in defining the deposition pattern include the radius of the deposition (r), the deposition depth (N), the maximum deposition depth (Nmax), the distance at which the deposition depth is maximum (rbmax) and the maximum rise height of the sediment particles (xm), (see Figure 3).
2.1.3 Horizontal momentum sediment-laden jet
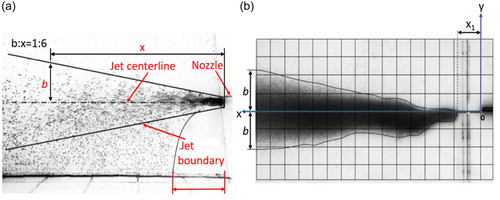
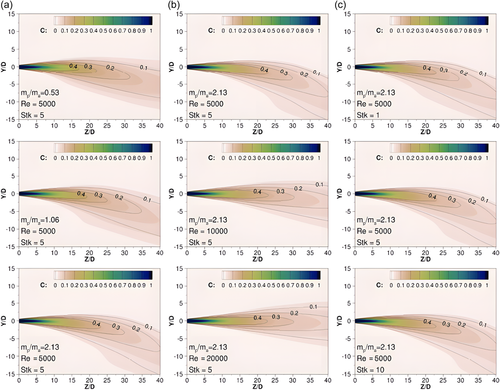
The initial momentum of the horizontal momentum particle-laden jet mainly acts in the horizontal direction, while the gravity of the sediment is vertically downwards (Figure 4a). With the decrease in momentum, the sediments begin to settle soon after leaving the nozzle, exhibiting the “sand cloud” phenomenon, and settle in a zig-zag trajectory (Figure 4b) (Lee et al., 2013; A. C. Y. Li, 2006). From experiments or a three-dimensional (3D) stochastic particle tracking model, the bottom deposition pattern is found to be in Gaussian distribution (Bleninger et al., 2002; Chan & Lee, 2014; Lee, 2010; A. C. Y. Li, 2006; M. Neves et al., 2002). The mean jet flow is dragged downwards when initial sediment concentration C0 > 0.1% of volumetric concentration. With an initial sediment concentration of C0 ≤ 0.1% of volumetric concentration, there are no significant changes in the general properties of the jet flow. Intensive particle–flow interaction is predominant in jets of high sediment concentrations (Liu & Lam, 2010, 2013, 2015). The increase in sediment concentration results in an increase in the gravitational force on the jet and its downward deflection (Figure 5). Additionally, increasing the Stokes number (defined as the characteristic time of Lagrangian to the characteristic time of the flow) causes sediment to fallout at a higher speed thus resulting in lower deviation of the jet. Nevertheless, an increase in Reynolds number results in the jet rise and lower capability of the gravitational force to cause jet deviation (Tavangar et al., 2019, 2020).
2.1.4 Horizontal buoyant sediment-laden jet
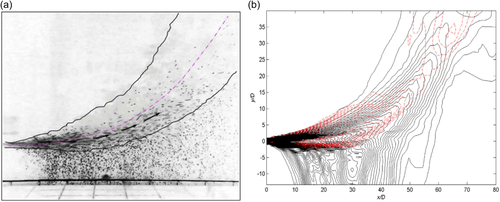
A horizontal buoyant sediment-laden jet (see Figure 6) is characterized by a horizontal momentum jet, with rising plume, bending trajectory, and a horizontal surface gravity current (Chan & Lee, 2016; James et al., 2022). Two-modes of settling mechanism and two modes of bottom deposition exist, those are, settling from the jet edge which causes deposition close to the jet nozzle, and settling from spreading current which causes deposition at a distance from the nozzle (McLarnon & Davies, 1999; Cuthbertson et al., 2008; Liu & Lam, 2015). The buoyancy generated from the density difference between the jet and the ambient water leads to a deflected jet trajectory, with a highly nonuniform distribution of the laden particles (Figure 7a), thus the buoyancy effect has a greater impact on the sediment movement (Chan & Lee, 2016; A. C. Y. Li, 2006; Mingotti & Woods, 2022). The nonuniform distribution of the laden particles is due to high turbulence intensities at the lower outer layer of the jet flow (Figure 7b) (Liu & Lam, 2015). The apparent settling velocity can be reduced by as much as 30% of the hydrostatic water settling velocity (Chan, 2013; Chan et al., 2014).
2.2 Sediment-laden jets in hydrokinetic environment
In the hydrokinetic water environment, the diffusion and dilution processes of the jet fluid undergo significant changes, and the sediment transport and sedimentation characteristics will also be adjusted accordingly (Figure 8). Reliable prediction for the initial mixing with numerical models has been achieved (Frick, 1984; J. H. W. Lee & Cheung, 1990). Similar to sediment-laden jet in a hydrostatic environment, the volumetric source sediment concentrations C0 ≤ 0.1% had no significant influence on the jet trajectory (Jiang et al., 2005; H. Wang & Wing-Keung law, 2002; M. Zhou et al., 2022). Nevertheless, the deposition rate for sediment-laden jets under hydrokinetic ambient fluid is significantly reduced than that under hydrostatic ambient fluid (Figure 9). The main factors in determining the sediment deposition trajectories are the relative magnitudes of the ambient flow and particle fall velocity (Cuthbertson & Davies, 2008).
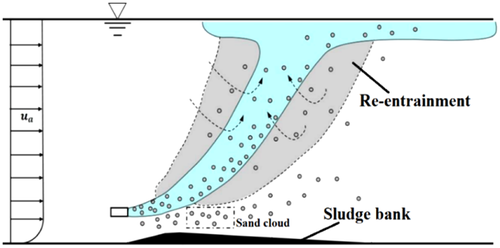
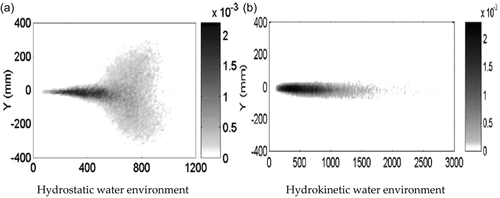
The deposition of the sediments begins when the vertical component of the entrainment velocity becomes smaller than the settling velocity. Also, the deposition is controlled by the settling velocity, entrainment velocity, volume flux, and sediment concentration (Terfous et al., 2016). Sediments are “blown” out of the rising plume by the ambient current, leaving very little sediment reaching the spreading surface layer and the sediment deposition profile is shifted downstream by the ambient current (Chan, 2013).
3 PARTICLE TRANSPORT AND DEPOSITION
To successfully predict the transport and deposition of particles from the outfall system, the most important processes to consider is the turbulent flow, particle coagulation, and flocculation. These processes control the particle settling velocity and rate of deposition in any environment (Jiang et al., 2019; Spearman et al., 2020; Tousi et al., 2022; J. J. Zhang & Li, 2006). Previous studies on particle settling velocity were conducted either in hydrostatic or turbulence ambient environments.
3.1 Particle settling velocity in a hydrostatic environment
Particle settling velocity in a hydrostatic environment is widely used in environmental flow modeling, such as sediment transport modeling in rivers. The settling velocity of a particle in a hydrostatic environment is controlled by the force of gravity and drag force. The drag force depends on particle diameter, particle and fluid densities, and fluid kinematic viscosity (Bleninger & Carmer, 2000). The relationship between the drag coefficient and particle Reynolds number of natural sediments or irregular particles depends on the particle shape. Comparing the settling velocity of an irregularly shaped particle to a sphere, the former would settle at the most stable orientation with the maximum cross-sectional area perpendicular to the direction of motion, therefore resulting in a smaller settling velocity than the sphere of the same nominal diameter. There are several empirical formulae for estimating the settling velocity of irregular particles or natural sediments (e.g. Cheng, 1997; Hallermeier, 1981; Van Rijn, 1984; Soulsby, 1997).
In a hydrostatic water environment, particles settle with the same velocity as the hydrostatic water settling velocity (Bühler and Papantoniou, 2001). Weak discharge velocity with large particles causes fast deposition; the gravity and buoyancy forces are the predominant factors that determine the particle settling velocity in this case. Particles those are closely spaced to each other can fall in a group with higher settling velocity than that of a particle falling alone. The previously settled particles generate additionally a counter-current that reduces the settling velocity (Bleninger & Carmer, 2000). Comparing the second row of snapshots in Figure 10, it is evident that there is a clear formation of a spherical cluster that increases in size. Particles in the center of a sediment cluster fall faster and further than those on the peripheries of the cluster, before being recirculated up and moving along the edges of the cluster. This implies that particles with higher local concentrations move faster than those with lower local concentrations (D. Wang et al., 2016). The dispersion process is significantly controlled by the particle size and the general homogeneity of the particle mixture (Tan & Ng, 2016).

3.2 Particle settling velocity in a turbulent environment
Understanding the physical mechanisms responsible for particle settling velocity helps to predict sediment transport and deposition in a turbulent environment (Haghshenas & Groll, 2022; Huang et al., 2019; Shao & Lima, 2022). Many previous studies showed that particles settle more slowly in a turbulent flow, reducing to as much as 40% of the settling velocity in still water for homogeneous vertically oscillating fluid (Ho, 1964). In turbulent flow generated by oscillating gird with different frequencies, the sediment settling velocity is substantially regulated by the turbulence causing a reduction of settling velocity up to 30% (Murray, 1970; Nielsen, 1993). Similarly, Doroodchi et al. (2008) and Q. Zhou and Cheng (2009) also observed a 25% reduction in settling velocity under grid-generated turbulence. The experimental results of Ho (1964) and Murray (1970) were explained through analytical solutions derived by Hwang (1985). Another effect of turbulence on sediment settling velocity is that some of the sediment is kept inside the jet flow by turbulence (Koh & Chang, 1973).
The settling velocity reduction is also due to nonlinear drag (Mei, 1991). The existing studies on the effect of the nonlinear drag on settling velocity show that the settling velocity reduction depends on the frequency of oscillation, the ratio of turbulent fluctuation to settling velocity (σ/ωs), and particle Reynolds number (Stout et al.,1995). For high relative turbulence intensity, the settling velocity is enhanced while for intermediate relative turbulence intensity, the effect of turbulence on settling velocity depends on the size of the sediment and the Stokes number (Cuthbertson & Ervine, 2007; Jobson & Sayre, 1970; Kawanisi & Shiozaki, 2008). Very heavy or big particles do not follow the turbulent motion of the fluid. Thus, sediment with a larger settling velocity is less affected by the turbulent diffusion and entrainment of the jet flow (Jazi & Wells, 2020). The turbulence intensity decreases if the particle concentration in the liquid is very high (Bleninger & Carmer, 2000).
The sediment inertia force responsible for sediment settling and dispersion has been accurately modeled with a two-phase flow model that considers the main features of sediment-laden flows: the horizontal velocity difference between particles and fluid, the dispersion of particles by fluid turbulent motion, and the damping of fluid turbulent kinetic energy (Chauchat & Guillou, 2008).
4 PATHWAYS FORWARD TO IMPROVE THE STUDY OF SEDIMENT-LADEN WASTEWATER DISPOSAL
Industrial and domestic wastewater laden with sediments disposed into the ocean, river, and lake is feasible because the effluent decay duration is of the order of days. The concentration of the effluent is initially reduced very rapidly after discharge (Koh & Brooks, 1975). The wastewater carries sediment of various sizes but the sediment concentration depends on the effluent treatment level. For primary treatment, solids with the size >200 μm are removed while smaller solids are discharged through outfalls. These sediments deposit close to the outfall and negatively impact the benthic ecology (Maldonado et al., 2000; Miller et al., 2018; Pritchard, 1997; Roberts et al., 2010; Santschi et al., 2001; Xu et al., 2017).
Many numerical and experimental studies have been conducted to predict the transport and deposition for instantaneous and continuous dumping from thermal waste (Bühler & Papantoniou, 2001; Bush et al., 2003; Gensheimer et al., 2013; Koh & Chang, 1973; C. W. Li, 1997). The results show three sediment transport phases including the convective jet or thermal phase influenced by initial momentum and buoyancy, the collapse phase as sediment falls out from the jet or thermal, and the far field advective diffusion phase.
Farley (1990) developed a two-layer model for predicting the sediment deposition from an ocean outfall in a stratified environment. The model incorporates tidal transport and mixing, fine sediment coagulation, and sediment-nutrient dynamics. The model was validated with field data and found to be in good agreement. Cromey et al. (1998) developed a model for predicting sediment deposition from sewage discharge and its biological impact. The model used stochastic particle tracking to simulate sediment transport and settling. It incorporated models of sediment resuspension, organic carbon chemistry, and benthic biology. Subsequently, J. J. Zhang and Li (2006) used both laboratory experiments and numerical simulations to study coagulation in the transport and sedimentation of sediment from sediment-laden wastewater which occurs after discharge. Both laboratory and numerical simulation results demonstrated that coagulation played an important role in regulating the transport of solid pollutants, especially in the early phase of outfall discharge (J. J. Zhang & Li, 2006).
Although researchers have already achieved a fairly good understanding of the characteristics of the sediment-laden jet motion, as for particle transport in sediment-laden wastewater discharges, and the impact of the bottom sludge, there were some limitations in conducting such studies and their research results still cannot fully reflect the movement characteristics of the sediment-laden wastewater discharge into the sea. Therefore, some of these research challenges in addition to research questions needing to be explored to help fully reflect the movement characteristics of sediment-laden wastewater disposal are highlighted in the subsequent paragraphs.
4.1 Research challenges on sediment-laden jet
As already elaborated in the above literature, it is obvious that the studies on sediment-laden wastewater jets are indeed a very complicated research problem. The initial stages of such studies were carried out through physical experiments. In recent years, with the development of numerical simulation methods, researches on modelling the sediment-laden jet has also been carried out. The challenges and possible solutions are introduced separately for physical experiments and numerical simulation methods for sediment-laden jet studies.
4.1.1 Challenges in physical experimental methods
At present, the research on the sediment-laden jet mainly focuses on four aspects, that is, the jet trajectory, velocity field, sediment concentration field, and deposition rate of bottom sludge. The main technical difficulty is the simultaneous observation of the fluid-particle velocity field and concentration field for the two phases during the experiment.
For the sediment-laden jet velocity field, noncontact measuring instruments based on optical principles, such as laser Doppler anemometer and particle image velocimetry (PIV), are commonly used for the measurement. Since the experiment needs to measure the velocity field data of the fluid phase and the solid phase at the same time, the difficulty in phase separation is mainly related to the following two methods: (1) use of physical hardware (filter) for phase separation (Jiang et al., 2005; Liu & Lam, 2013; Simiano et al., 2009), and (2) use of image postprocessing techniques for phase separation (Bryant et al., 2009). The first method marks the fluid phase and the solid phase separately and measures the velocity of the fluid phase and the solid phase separately by installing a suitable filter according to the wavelength of the reflected laser light (Figure 11). The fluid and solid phases are distinguished by the difference in the brightness and size of the trace particles in the jet fluid and solid particles from the original image. However, the image postprocessing calculation in this method is cumbersome, and there is a large “blind area” in the processed image (i.e., there may be not enough particles), which affects the measurement accuracy and is, therefore, less used.

For the sediment-laden jet concentration field, most of the experiments are measured by planar laser-induced fluorescence (PLIF) (Jiang et al., 2005; Webster et al., 2001). But the intensity of the laser is significantly attenuated with increasing distance, hence affecting the size of the shooting range. In addition, the fluorescent agent (rhodamine B) is susceptible to chemical reactions with chlorine in the water, which may cause the measured concentration to be systematically small. Thus, difficult in producing sufficiently strong fluorescence signals on the camera for small sediment sizes over a large jet flow area. There is also a difficulty in the calibration of PLIF levels against jet effluent concentration (Liu & Lam, 2013). Another drawback is the high cost of a fluorescent agent. Recently, Lee et al. (2013) proposed a new method for concentration measurement using traditional PLIF technology, that is, the number of particles in a certain area is counted according to the original image obtained by PLIF. The sediment concentration is then calculated by averaging the total number of particles for all the images and multiplying by the mass of each particle within the measuring area. The comparison with the data measured by the suction sampling technique shows that the method has high reliability.
Moreover, during previous experimental works, the sediment was usually premixed with the stored source fluid using mechanical mixers. This poses great difficulty in providing constant initial sediment concentration for the jet, especially for heavier particles. A. C. Y. Li (2006) developed a sediment supply method that greatly alleviate this difficulty and improved the experimental accuracy.
4.1.2 Limitations in numerical simulation methods
For the numerical simulation methods of sediment-laden jet studies, there are mainly three types of models: (1) integral model based on the Lagrangian field, (2) two-phase flow model based on the Euler field, and (3) particle tracking model based on the Lagrangian–Eulerian field. In order to overcome certain research difficulties, researchers usually gave reasonable assumptions for simplicity. The integral model based on the Lagrangian field is based on the empirical rule of experimental research, and the integral assumption is given. Ernst et al. (1996) established an integrated numerical model for simulating a sediment-laden jet by assuming that the relationship between the rate of change in sediment mass and the total mass of sediment in the body is controlled to close the equation. A momentum integral model that can simulate the sediment deposition of the sand was established by Lane-Serff and Moran (2005) with the assumption that the sedimentation velocity of the solid particles is greater than the local entrainment velocity. Terfous et al. (2016, 2012) used the entrainment coefficient to close the fluid motion equation. The relationship between the particle settling velocity and the entrainment velocity closes the solid-state equation of motion, and the integral model of the sediment flow in the hydrodynamic conditions was established. The above method is simple in numerical solution, and the required calculation time is short. But multiple hypothetical conditions need to be introduced in the simplified process, and these conditions maybe not fit in the study of wave-current environment.
The numerical model based on Euler fields assumes that both fluid and solid phases are continuous media filled in the whole space. According to the mass conservation law, the continuous flow of fluid and solid two-phase flow was derived through the Reynolds time average equations and momentum equations (Huai et al., 2012). In recent years, the two-phase flow numerical model based on the Euler field, including the fluid-solid turbulence model (Chauchat & Guillou, 2008), the fluid-solid particle interaction model (Yu et al., 2012) and the interaction model between sediment particles (Maurin et al., 2018) have been greatly improved, and have been well applied to the simulation of large-scale water and sediment movement under tidal current (Dong & Zhang, 2002; Hsu et al., 2003; Maurin et al., 2018). Since this type of model assumes that the sediment particles are in continuous operation, the state of motion is, therefore, suitable for the sediment-laden jets with large sediment concentrations such as high-concentration river discharge into the ocean (e.g. Figure 1e), but it is not suitable for the discharge of sediments with low sediment concentration (Liu & Lam, 2015).
The particle tracking model based on the Euler–Lagrangian field calculates the fluid phase and the solid phase separately. For the fluid phase, the fluid flow is regarded as a continuous medium, and the k–ε turbulence equation is used (Chan & Lee, 2014) or the large eddy turbulence equation (Liu & Lam, 2015) or the momentum integral equation (Chan & Lee, 2016) as the governing equation, using the traditional discrete method for numerical solution to calculate the background flow field. For the solid phase, the particles are regarded as a dispersion medium, and the particle motion equation is established according to the force of the dispersed particles in the water body (e.g., mass force, drag force, differential pressure force, lift force, and interaction force between particles) and capturing each motion of a particle to obtain the statistical average motion characteristics of the sediment particles, so the distribution of the entire sediment field can be obtained. Chan and Lee (2016) used the particle tracking model to successfully simulate the transport and sedimentation process of sediment in low-concentration sediment-laden buoyancy jets under a hydrostatic environment. Thus, the particle tracking model based on the Euler–Lagrange field can realistically simulate the sediment transport and sedimentation problems in low-concentration sediment-laden jets but its successful simulation under more complex dynamic environments such as wave current is yet to be known.
4.2 Research questions and possible ways forward
Considering the ambient conditions for previous studies on sediment-laden jets, they were either carried out in a hydrostatic environment or under a constant cross-flow environment. For practical application in ocean disposal of sediment-laden wastewater, these studies cannot fully reflect the hydrodynamics of discharge effluent into the sea. The main reason for this limitation is the existence of nonconstant coexisting dynamic factors such as waves and currents in the marine environment. In other words, the time scale of the tidal current is much larger than the time scale of the initial dilution of the jet. Therefore, the tidal current can be regarded as a “quasi-constant” flow to analyze its influence on the near field diffusion and dilution process (S. S. Li & Hodgins, 2010); but the time scale of the wave is comparable to the time scale of the jet, and the short-cyclic wave motion plays a significant role in the jet behavior characteristics.
According to previous studies on pure jet streams (Figure 12), the movement and diffusion laws of jet streams under a wavy current environment are quite different from those in still water or in a constant cross-flow environment (Chen et al., 2008, 2012; Fang et al., 2019; Otoo et al., 2019, 2022; Y. Wang et al., 2015; Xu et al., 2016, 2017, 2018, 2019, 2020), which will inevitably have a significant impact on the movement of sediment particles in the sediment-laden jet. Therefore, to fully capture the true movement of the sediment-laden jet under the marine dynamic environment, the interaction between sediment-laden jet flow with wave and current needs to be tackled. Up until now, even the effects of wave and current on the zoning characteristics of sediment-laden jet flow are yet to be addressed.

The concentration distribution of the effluent determines the rate of dilution, therefore the influence mechanism of multidynamic coupling on the concentration distribution of the sediment is also an important topic to be addressed. Among the numerical simulation methods for sediment-laden jet studies, the particle tracking model based on the Euler–Lagrange field can realistically simulate the sediment transport and sedimentation problems in low-concentration sediment-laden jets but its successful simulation under more complex dynamic background environments needs to be addressed for future 3D spatial and temporal distribution characteristics of sediment-laden sediment concentration in the wave environment. Sediment transport and its influence on sedimentation under the action of wave and current remains an unsolved problem. The water environment and water ecology near the outfall nozzle experience a continuing negative impact from the sludge banks. Hence, the deposition process of sludge along the bottom and the quantitative calculation model of sludge deposition rate at the bottom, predicting the growth rate and impact range of sludge deposits in the wave and current environment are of foremost importance to control their adverse effects.
With the advancements in experimental and numerical techniques, the above-mentioned research questions can be addressed and overcome the limitations of the previous research methods. For sediment-laden jets under a wavy current environment, the use of a filter and PIV/PLIF system (Jiang et al., 2005; Liu & Lam, 2013; Pedocchi et al., 2008; Simiano et al., 2009) to perform optical phase separation have encountered difficulties as laser scattering occurs when the laser beam touches the free surface of the wave. Thus, the stability of the intensity of the laser cannot meet the requirements of the measurement. When conventional PIV/PLIF systems are used for the test, the number of samples per second is greatly limited by the laser frequency, so there are deviations in the capture of wave peak, wave trough, and other characteristic phases in a wave cycle. These deviations are unfavorable for further analysis of the movement pattern of a sediment-laden jet under each characteristic phase. As a solution to these problems, the authors propose the use of two cameras to observe the fluid and sediment phases separately. Coordinated and synchronous acquisition of data from the cameras is a key factor to ensure the quality of data. The two cameras should be calibrated simultaneously with a calibration plate to ensure the shooting range is consistent. Surface added light guide plate (Y. Wang et al., 2015) may solve the problem of wave surface reflection; a new PIV and PLIF acquisition system using continuous wave laser and the high-speed camera can increase the sampling frequency and enhance the capture of the turbulent characteristics of a sediment-laden jet.
For numerical simulation of a sediment-laden jet under a wavy current environment, the two-phase flow particle tracking method based on the Euler-Lagrangian field can track the movement of solid particles in the sediment-laden jet, and obtain the microscopic movement behavior of individual sediment particles under different external environments compared to the integral model based on Lagrangian field and numerical model based on Euler field. However, the Euler Lagrangian method is more expensive than the Lagrangian integration method and the Euler method. In addition to the time cost and calculation accuracy problems of different simulation methods, numerical simulation of a sediment-laden jet under wave-current action may be faced with certain challenges such as the buoyant sediment-laden jet will carry sediment to the free surface to form surface flow; therefore, the accuracy of water surface flow simulation needs to be improved. In view of these problems, the level set method could be introduced into the numerical model to capture the free surface movement of waves; in the integral model, the physical model test results can be referred to; the distribution pattern of sediment concentration in sediment-laden jet under wave-current environment can be corrected; so as to improve the simulation accuracy of the integral model.
5 CONCLUSION
Although a good understanding of the motion characteristics of the sediment-laden jet, its particle transport in sediment-laden wastewater discharges, and the impact of the bottom sludge has been achieved, there are still some difficulties that prevent the research results from fully reflecting the movement characteristics of the sediment-laden wastewater discharge into the sea. To fully reflect the true movement of the sediment-laden jet under the marine dynamic environment, the details of sediment-laden jet flow interaction with a wave and current need to be addressed. This paper has highlighted some of the pertinent research difficulties and questions that can lead to positive decisions and actions for sustainable marine wastewater disposal in the face of increasing marine pollution.
It is suggested that the study of the sediment-laden jet in a wave-current environment can be carried out by combining physical experiments with numerical simulation in an integrated approach. Based on physical experiments, we observed the shape of sediment-laden jets, obtained intuitive knowledge, and qualitatively described the interaction mechanism of waves, currents, jets, and sediment; the PIV, PLIF, and image recognition technologies are used to synchronously measure the velocity field and concentration field of fluid and sediment phases in the sediment-laden jet. The quantitative statistics of the total sediment deposition is carried out to provide the necessary verification data for the numerical models. In terms of numerical simulation, the large eddy turbulence model is used to accurately simulate the flow eddy structure of jet discharge at different angles under the wave-current environment; the sediment movement module is constructed based on the particle tracking method to calculate sediment concentration distribution, sediment deposition rate at the bottom and influence range of sludge deposition. At the same time, considering the efficient calculation, a set of the Lagrangian integral model is established to solve the problem of predicting the bottom deposition rate of sediment laden-jet under the combined action of wave and current. Finally, compare and verify the experimental measurement results with the numerical model. On this basis, carry out more sets of numerical experiments. Deeply study the 3D fluid and sediment movement characteristics of sediment-laden jets in the wave-current environment. Studying the velocity field, the concentration of vertical and horizontal jets in the wave-current environment, and the quantitative distribution law of solid particle deposition can be used to realize the quantitative prediction of sludge deposition rate and influence range at the bottom of a sediment-laden jet under the combined action of wave and current.
ACKNOWLEDGMENTS
This work was partly funded by the National Natural Science Foundation of China (Grant Nos. 51979076, 52211530103), the Research Funds for the Central Universities (Grant No. B200204017), and the Belt and Road Special Foundation of the State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering (Grant No. 2021491911).
ETHICS STATEMENT
None declared.
Open Research
DATA AVAILABILITY STATEMENT
The data that support the findings of this study are available from the corresponding author upon reasonable request.




