International Journal of Robust and Nonlinear Control

Volume 31, Issue 18 pp. 9008-9025

RESEARCH ARTICLE

Time-varying formation control of linear multiagent systems with time delays and multiplicative noises

Ruru Jia,

Ruru Jia

orcid.org/0000-0002-7408-7765

School of Automation, China University of Geosciences, Wuhan, China

Hubei Key Laboratory of Advanced Control and Intelligent Automation for Complex Systems, Wuhan, China

Engineering Research Center of Intelligent Technology for Geo-Exploration, Ministry of Education, Wuhan, China

Search for more papers by this author

Xiaofeng Zong,

Corresponding Author

Xiaofeng Zong

[email protected]

orcid.org/0000-0001-9486-5264

School of Automation, China University of Geosciences, Wuhan, China

Hubei Key Laboratory of Advanced Control and Intelligent Automation for Complex Systems, Wuhan, China

Engineering Research Center of Intelligent Technology for Geo-Exploration, Ministry of Education, Wuhan, China

Correspondence Xiaofeng Zong, School of Automation, China University of Geosciences, Wuhan 430074, China.

Email: [email protected]

Search for more papers by this author

Ruru Jia,

Ruru Jia

orcid.org/0000-0002-7408-7765

School of Automation, China University of Geosciences, Wuhan, China

Hubei Key Laboratory of Advanced Control and Intelligent Automation for Complex Systems, Wuhan, China

Engineering Research Center of Intelligent Technology for Geo-Exploration, Ministry of Education, Wuhan, China

Search for more papers by this author

Xiaofeng Zong,

Corresponding Author

Xiaofeng Zong

[email protected]

orcid.org/0000-0001-9486-5264

School of Automation, China University of Geosciences, Wuhan, China

Hubei Key Laboratory of Advanced Control and Intelligent Automation for Complex Systems, Wuhan, China

Engineering Research Center of Intelligent Technology for Geo-Exploration, Ministry of Education, Wuhan, China

Correspondence Xiaofeng Zong, School of Automation, China University of Geosciences, Wuhan 430074, China.

Email: [email protected]

Search for more papers by this author

First published: 23 September 2021

https://doi.org/10.1002/rnc.5754

Citations: 9

Funding information: National Natural Science Foundation of China, 62073305

Share a link

Email
Wechat
Bluesky

Abstract

This article investigates time-varying formation control problems of linear multiagent systems with time delays and multiplicative noises under the undirected interactive topology. First, the time-varying formation control problem under time delays and multiplicative noises is transformed into the asymptotic stability problem of a closed-loop stochastic system. Then, sufficient conditions for formation feasibility under the unstable and stable formation centers are provided by constructing the Lyapunov functional and the Lyapunov function, respectively. For the case of an unstable formation center, we give the formation feasibility conditions and the explicit formation control design. For the case of a stable formation center, it is proved that the formation can be achieved for any given time delay and noise intensity. Finally, numerical simulations on a group of unmanned aerial vehicles are provided to illustrate the effectiveness of the theoretical results.

CONFLICT OF INTEREST

The authors declare no potential conflict of interest.

Open Research

DATA AVAILABILITY STATEMENT

Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.

REFERENCES

1Beard RW, Lawton J, Hadaegh FY. A coordination architecture for spacecraft formation control. IEEE Trans Control Syst Technol. 2001; 9(6): 777-790.
10.1109/87.960341
Web of Science® Google Scholar
2Rahimi R, Abdollahi F, Naqshi K. Time-varying formation control of a collaborative heterogeneous multi agent system. Robot Auton Syst. 2014; 62(12): 1799-1805.
10.1016/j.robot.2014.07.005
Web of Science® Google Scholar
3He X, Geng Z. Leader-follower formation control of underactuated surface vessels. Sci China Inf Sci. 2022; 65:209201.
10.1007/s11432-020-2948-y
Web of Science® Google Scholar
4Pack DJ, DeLima P, Toussaint GT, York G. Cooperative control of UAVs for localization of intermittently emitting mobile targets. IEEE Trans Syst Man Cybern. 2009; 39(4): 959-970.
10.1109/TSMCB.2008.2010865
PubMed Web of Science® Google Scholar
5Dong X, Yu B, Shi Z, Zhong Y. Time-varying formation control for unmanned aerial vehicles: theories and applications. IEEE Trans Control Syst Technol. 2014; 23(1): 340-348.
10.1109/TCST.2014.2314460
Web of Science® Google Scholar
6 Nuño E, Loría A, Hernández T, Maghenem M, Panteley E. Distributed consensus-formation of force-controlled nonholonomic robots with time-varying delays. Automatica. 2020; 120. https://doi.org/10.1016/j.automatica.2020.109114
10.1016/j.automatica.2020.109114
Web of Science® Google Scholar
7Ren W, Sorensen N. Distributed coordination architecture for multi-robot formation control. Robot Auton Syst. 2008; 56(4): 324-333.
10.1016/j.robot.2007.08.005
Web of Science® Google Scholar
8Wang C, Zuo Z, Gong Q, Ding Z. Formation control with disturbance rejection for a class of Lipschitz nonlinear systems. Sci China Inf Sci. 2017; 60(7):070202.
10.1007/s11432-016-9125-2
Web of Science® Google Scholar
9Lewis MA, Tan K-H. High precision formation control of mobile robots using virtual structures. Auton Robot. 1997; 4(4): 387-403.
10.1023/A:1008814708459
Web of Science® Google Scholar
10Zhang Q, Lapierre L, Xiang X. Distributed control of coordinated path tracking for networked nonholonomic mobile vehicles. IEEE Trans Ind Inform. 2013; 9(1): 472-484.
10.1109/TII.2012.2219541
Web of Science® Google Scholar
11Balch T, Arkin RC. Behavior-based formation control for multirobot teams. IEEE Trans Robot Autom. 1998; 14(6): 926-939.
10.1109/70.736776
Web of Science® Google Scholar
12Oh K-K, Park M-C, Ahn H-S. A survey of multi-agent formation control. Automatica. 2015; 53: 424-440.
10.1016/j.automatica.2014.10.022
Web of Science® Google Scholar
13 Xiao F, Wang L, Chen J, Gao Y. Finite-time formation control for multi-agent systems. Automatica. 2009; 45(11): 2605-2611.
10.1016/j.automatica.2009.07.012
Web of Science® Google Scholar
14Ge X, Han Q-L. Distributed formation control of networked multi-agent systems using a dynamic event-triggered communication mechanism. IEEE Trans Ind Electron. 2017; 64(10): 8118-8127.
10.1109/TIE.2017.2701778
Web of Science® Google Scholar
15 Dong X, Li Q, Wang R, Ren Z. Time-varying formation control for second-order swarm systems with switching directed topologies. Inf Sci. 2016; 369: 1-13.
10.1016/j.ins.2016.05.043
Web of Science® Google Scholar
16 Dong X, Hu G. Time-varying formation control for general linear multi-agent systems with switching directed topologies. Automatica. 2016; 73: 47-55.
10.1016/j.automatica.2016.06.024
Web of Science® Google Scholar
17Wang R, Dong X, Li Q, Ren Z. Distributed time-varying output formation control for general linear multiagent systems with directed topology. IEEE Trans Control Netw Syst. 2019; 6(2): 609-620.
10.1109/TCNS.2018.2863047
Web of Science® Google Scholar
18Mastellone S, Stipanović DM, Graunke CR, Intlekofer KA, Spong MW. Formation control and collision avoidance for multi-agent non-holonomic systems: theory and experiments. Int J Robot Res. 2008; 27(1): 107-126.
10.1177/0278364907084441
Web of Science® Google Scholar
19Dong X, Hu G. Time-varying formation tracking for linear multiagent systems with multiple leaders. IEEE Trans Automat Contr. 2017; 62(7): 3658-3664.
10.1109/TAC.2017.2673411
Web of Science® Google Scholar
20Zong X, Li T, Zhang J-F. Consensus control of second-order delayed multiagent systems with intrinsic dynamics and measurement noises. Int J Robust Nonlinear Control. 2018; 28(16): 5050-5070.
10.1002/rnc.4301
Web of Science® Google Scholar
21Shahab MA, Mozafari B, Soleymani S, Dehkordi NM, Shourkaei HM, Guerrero JM. Stochastic consensus-based control of 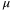$urn:x-wiley:10498923:media:rnc5754:rnc5754-math-0481$ Gs with communication delays and noises. IEEE Trans Power Syst. 2019; 34(5): 3573-3581.
10.1109/TPWRS.2019.2905433
Web of Science® Google Scholar
22 Liu C-L, Tian Y-P. Formation control of multi-agent systems with heterogeneous communication delays. Int J Syst Sci. 2009; 40(6): 627-636.
10.1080/00207720902755762
Web of Science® Google Scholar
23Dong X, Xi J, Lu G, Zhong Y. Formation control for high-order linear time-invariant multiagent systems with time delays. IEEE Trans Control Netw Syst. 2014; 1(3): 232-240.
10.1109/TCNS.2014.2337972
Google Scholar
24Wang J, Han L, Li X, Dong X, Li Q, Ren Z. Time-varying formation of second-order discrete-time multi-agent systems under non-uniform communication delays and switching topology with application to UAV formation flying. IET Control Theory Appl. 2020; 14(14): 1947-1956.
10.1049/iet-cta.2020.0183
Web of Science® Google Scholar
25 Ge X, Han Q-L, Zhang X-M. Achieving cluster formation of multi-agent systems under aperiodic sampling and communication delays. IEEE Trans Ind Electron. 2018; 65(4): 3417-3426.
10.1109/TIE.2017.2752148
Web of Science® Google Scholar
26Qin L, He X, Zhou D. Distributed proportion-integration-derivation formation control for second-order multi-agent systems with communication time delays. Neurocomputing. 2017; 267: 271-282.
10.1016/j.neucom.2017.05.088
Web of Science® Google Scholar
27 Han L, Xie Y, Li X, Dong X, Li Q, Ren Z. Time-varying group formation tracking control for second-order multi-agent systems with communication delays and multiple leaders. J Frankl Inst-Eng Appl Math. 2020; 357(14): 9761-9780.
10.1016/j.jfranklin.2020.07.048
Web of Science® Google Scholar
28 Lu X, Austin F, Chen S. Formation control for second-order multi-agent systems with time-varying delays under directed topology. Commun Nonlinear Sci Numer Simul. 2012; 17(3): 1382-1391.
10.1016/j.cnsns.2011.07.029
Web of Science® Google Scholar
29 Bai J, Wen G, Song Y, Rahmani A, Yu Y. Distributed formation control of fractional-order multi-agent systems with relative damping and communication delay. Int J Control Autom Syst. 2017; 15(1): 85-94.
10.1007/s12555-015-0132-x
Web of Science® Google Scholar
30Ni Y-H, Li X. Consensus seeking in multi-agent systems with multiplicative measurement noises. Syst Control Lett. 2013; 62(5): 430-437.
10.1016/j.sysconle.2013.01.011
Web of Science® Google Scholar
31Cheng L, Hou Z-G, Tan M, Wang X. Necessary and sufficient conditions for consensus of double-integrator multi-agent systems with measurement noises. IEEE Trans Automat Contr. 2011; 56(8): 1958-1963.
10.1109/TAC.2011.2139450
Web of Science® Google Scholar
32Zong X, Li T, Zhang J-F. Consensus conditions for continuous-time multi-agent systems with additive and multiplicative measurement noises. SIAM J Control Optim. 2018; 56(1): 19-52.
10.1137/15M1019775
Web of Science® Google Scholar
33Liu S, Xie L, Zhang H. Mean square formation and containment control of multi-agent systems under noisy measurements. Proceedings of the 2013 52th IEEE Conference on Decision and Control (CDC); 2013; Florence, Italy.
Google Scholar
34 Wang B, Tian Y-P. Distributed formation control: asymptotic stabilization results under local noisy information. IEEE Trans Cybern. 2021; 51(1): 16-27.
10.1109/TCYB.2019.2897605
PubMed Web of Science® Google Scholar
35 Li Z, Huang T, Tang Y, Zhang W. Formation control of multiagent systems with communication noise: a convex analysis approach. IEEE Trans Cybern. 2021; 51(4): 2253-2264. https://doi.org/10.1109/TCYB.2019.2936347
10.1109/TCYB.2019.2936347
PubMed Web of Science® Google Scholar
36 Mo L, Guo S, Yu Y. Mean-square $urn:x-wiley:10498923:media:rnc5754:rnc5754-math-0482$ antagonistic formations of second-order multi-agent systems with multiplicative noises and external disturbances. ISA Trans. 2020; 97: 36-43.
10.1016/j.isatra.2019.07.019
PubMed Web of Science® Google Scholar
37 Lai L, Chen S, Lu X, Zhou H. Formation tracking for nonlinear multi-agent systems with delays and noise disturbance. Asian J Control. 2015; 17(3): 879-891.
10.1002/asjc.937
Web of Science® Google Scholar
38Zong X, Li T, Yin G, Wang LY, Zhang J-F. Stochastic consentability of linear systems with time delays and multiplicative noises. IEEE Trans Automat Contr. 2018; 63(4): 1059-1074.
10.1109/TAC.2017.2732823
Web of Science® Google Scholar
39Zong X, Li T, Yin G, Zhang J-F. Delay Tolerance for Stable Stochastic Systems and Extensions. IEEE Trans Automat Contr. 2021; 66(6): 2604-2619.
10.1109/TAC.2020.3012525
Web of Science® Google Scholar
40Gu K. An integral inequality in the stability problem of time-delay systems. Proceedings of the 2000 39th IEEE Conference on Decision and Control (CDC); 2000; Sydney, Australia.
Google Scholar