Stability of nonlinear distributed delay system with parameter uncertainties: Integral-based event-triggered impulsive control strategy
Hongfei Li
State Key Laboratory for Turbulence and Complex Systems, Department of Advanced Manufacturing and Robotics, BIC-ESAT, College of Engineering, Peking University, Beijing, China
Search for more papers by this authorLiruo Zhang
Department of Electrical and Computer Engineering, The University of Auckland, Auckland, New Zealand
Search for more papers by this authorXiaoyu Zhang
Chongqing Key Laboratory of Nonlinear Circuits and Intelligent Information Processing, College of Electronic and Information Engineering, Southwest University, Chongqing, China
Search for more papers by this authorCorresponding Author
Junzhi Yu
State Key Laboratory for Turbulence and Complex Systems, Department of Advanced Manufacturing and Robotics, BIC-ESAT, College of Engineering, Peking University, Beijing, China
Correspondence Junzhi Yu, State Key Laboratory for Turbulence and Complex Systems, Department of Advanced Manufacturing and Robotics, BIC-ESAT, College of Engineering, Peking University, Beijing 100871, China.
Email: [email protected]
Search for more papers by this authorHongfei Li
State Key Laboratory for Turbulence and Complex Systems, Department of Advanced Manufacturing and Robotics, BIC-ESAT, College of Engineering, Peking University, Beijing, China
Search for more papers by this authorLiruo Zhang
Department of Electrical and Computer Engineering, The University of Auckland, Auckland, New Zealand
Search for more papers by this authorXiaoyu Zhang
Chongqing Key Laboratory of Nonlinear Circuits and Intelligent Information Processing, College of Electronic and Information Engineering, Southwest University, Chongqing, China
Search for more papers by this authorCorresponding Author
Junzhi Yu
State Key Laboratory for Turbulence and Complex Systems, Department of Advanced Manufacturing and Robotics, BIC-ESAT, College of Engineering, Peking University, Beijing, China
Correspondence Junzhi Yu, State Key Laboratory for Turbulence and Complex Systems, Department of Advanced Manufacturing and Robotics, BIC-ESAT, College of Engineering, Peking University, Beijing 100871, China.
Email: [email protected]
Search for more papers by this authorFunding information: Chongqing Natural Science Foundation Project, cstc2019jcyjmsxm2068; National Natural Science Foundation of China, 61903007; 61903052; 61906023; 62003008; U1909206; Post-Doctoral Science Foundation of China, 2021M690226
Abstract
This article investigates the stability of nonlinear uncertain distributed delay system via integral-based event-triggered impulsive control (IETIC) strategy. First, a IETIC mechanism is presented to reduce the redundant data transmission over the system, in which the integral-based event-triggered mechanism uses the integration of system states over a time period in the past. Second, a new lemma is proposed to eliminate the Zeno behavior of the established model through the IETIC mechanism. Third, a novel Lyapunov–Krasovskii functional (LKF) method related to probability density function is constructed to guarantee the stability of the established model based on LMI conditions, where a probability density function is introduced as a distributed delay kernel. Compared with existing methods, the constructed novel LKF method is less conservative or requiring less number of decision variables. Numerical examples are further provided to confirm the effectiveness and advantages of the proposed approach.
CONFLICT OF INTEREST
The authors declare no potential conflict of interests.
Open Research
DATA AVAILABILITY STATEMENT
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
REFERENCES
- 1Xie K, Lyu Z, Liu Z, Zhang Y, Chen CLP. Adaptive neural quantized control for a class of MIMO switched nonlinear systems with asymmetric actuator dead-zone. IEEE Trans Neural Netw Learn Syst. 2020; 31(6): 1927-1941.
- 2Zhang Z, He Y, Wu M, Wang Q. Exponential synchronization of neural networks with time-varying delays via dynamic intermittent output feedback control. IEEE Trans Syst Man Cybern Syst. 2019; 49(3): 612-622.
- 3 Li H, Li C, Ouyang D, Nguang SK. Impulsive stabilization of nonlinear time-delay system with input saturation via delay-dependent polytopic approach. IEEE Trans Syst Man Cybern Syst. 2020; 1-12. https://doi.org/10.1109/TSMC.2019.2963398
- 4Li X, Cao J, Ho DWC. Impulsive control of nonlinear systems with time-varying delay and applications. IEEE Trans Cybern. 2020; 50(6): 2661-2673.
- 5 Li H, Li C, Ouyang D, Nguang SK, He Z. Observer-based dissipativity control for T-S fuzzy neural networks with distributed time-varying delays. IEEE Trans Cybern. 2020. https://doi.org/10.1109/TCYB.2020.2977682
- 6Li X, Yang X, Cao J. Event-triggered impulsive control for nonlinear delay systems. Automatica. 2020; 117: 108981.
- 7 Guo Z, Yao D, Bai W, Li H, Lu R. Event-triggered guaranteed cost fault-tolerant optimal tracking control for uncertain nonlinear system via adaptive dynamic programming. Int J Robust Nonlinear Control. 2021. https://doi.org/10.1002/rnc.5403
- 8
Wu Y, Xie X, Hou Z. Adaptive fuzzy asymptotic tracking control of state-constrained high-order nonlinear time-delay systems and its applications. IEEE Trans Cybern. 2020. https://doi.org/10.1109/TCYB.2020.2985707
10.1109/TCYB.2020.2985707 Google Scholar
- 9 Li H, Li C, Ouyang D, Nguang SK. Impulsive synchronization of unbounded delayed inertial neural networks with actuator saturation and sampled-data control and its application to image encryption. IEEE Trans Neural Netw Learn Syst. 2021; 32(4): 1460-1473. https://doi.org/10.1109/TNNLS.2020.2984770
- 10Yu J, Liu J, Wu Z, Fang H. Depth control of a bioinspired robotic dolphin based on sliding-mode fuzzy control method. IEEE Trans Ind Electron. 2018; 65(3): 2429-2438.
- 11Goebel G, Münz U, Allgöwer F. Stabilization of linear systems with distributed input delay. Proceedings of the 2010 American Control Conference; Baltimore, MD; 2010:5800-5805.
- 12Huang Y, He Y, An J, Wu M. Polynomial-type Lyapunov-Krasovskii functional and Jacobi-Bessel inequality: further results on stability analysis of time-delay systems. IEEE Trans Automat Contr. 2021; 66(6): 2905-2912.
- 13Qian F, Nguang SK. Stabilization of uncertain linear distributed delay systems with dissipativity constraints. Syst Control Lett. 2016; 96: 60-71.
- 14Chen J, Xu S, Zhang B. Single/multiple integral inequalities with applications to stability analysis of time-delay systems. IEEE Trans Automat Contr. 2017; 62(7): 3488-3493.
- 15Chen W, Zheng W. Input-to-state stability for networked control systems via an improved impulsive system approach. Automatica. 2011; 47(4): 789-796.
- 16Nguyen K. An adaptive controller for uncertain nonlinear systems with multiple time delays. Automatica. 2020; 117: 108976.
- 17Wang C, Wu Y, Zhao Y, Yu J. Asymptotic tracking control for time-delay nonlinear systems with parametric uncertainties and full state constraints. ISA Trans. 2020; 98: 101-109.
- 18Luo Y, Xiao X, Cao J, Li A. Event-triggered guaranteed cost consensus for uncertain nonlinear multi-agent systems with time delay. Neurocomputing. 2020; 394: 13-26.
- 19Liu Q, Long L. State-dependent switching law design with guaranteed dwell time for switched nonlinear systems. Int J Robust Nonlinear Control. 2020; 30(8): 3314-3331.
- 20Wang M, Xie Y, Li W. Exponential bipartite synchronization of random signed networks with Markovian switching via impulsive control. Int J Robust Nonlinear Control. 2020; 30(17): 7496-7516.
- 21 Li X, Zhu H, Song S. Input-to-state stability of nonlinear systems using observer-based event-triggered impulsive control. IEEE Trans Syst Man Cybern Syst. 2020. https://doi.org/10.1109/TSMC.2020.2964172
- 22Li H, Li C, Huang T. Periodicity and stability for variable-time impulsive neural networks. Neural Netw. 2017; 94: 24-33.
- 23 Li X, Peng D, Cao J. Lyapunov stability for impulsive systems via event-triggered impulsive control. IEEE Trans Automat Contr. 2020. https://doi.org/10.1109/TAC.2020.2964558
- 24Zhai X, Wen G, Peng Z, Zhang X. Leaderless and leader-following fixed-time consensus for multiagent systems via impulsive control. Int J Robust Nonlinear Control. 2020; 30(13): 5253-5266.
- 25Nie L, Peng J, Teng Z, Hu L. Existence and stability of periodic solution of a Lotka-Volterra predator-prey model with state dependent impulsive effects. Math Meth Appl Sci. 2011; 224(2): 544-555.
- 26Nie L, Teng Z, Hu L, Peng J. Existence and stability of periodic solution of a predator-prey model with state-dependent impulsive effects. Math Comput Simul. 2009; 79(7): 2122-2134.
- 27Li H, Li C, Huang T, Zhang W. Fixed-time stabilization of impulsive Cohen-Grossberg BAM neural networks. Neural Netw. 2018; 98: 203-211.
- 28Wang Z, Wu H. Fuzzy impulsive control for uncertain nonlinear systems with guaranteed cost. Fuzzy Sets Syst. 2016; 302: 143-162.
- 29Zong G, Xu S, Wu Y. Robust
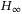stabilization for uncertain switched impulsive control systems with state delay: an LMI approach. Nonlinear Anal Hybrid Syst. 2008; 2(4): 1287-1300.
- 30Liu C, Liu X, Wang H, Zhou Y, Lu S, Xu B. Event-triggered adaptive tracking control for uncertain nonlinear systems based on a new funnel function. ISA Trans. 2020; 99: 130-138.
- 31Zhang X, Han Q, Zhang B. An overview and deep investigation on sampled-data-based event-triggered control and filtering for networked systems. IEEE Trans Ind Informat. 2017; 13(1): 4-16.
- 32 Shangguan X, He Y, Zhang C, Jin L, Wu M. Control performance standards-oriented event-triggered load frequency control for power systems under limited communication bandwidth. IEEE Trans Control Syst Technol. 2021. https://doi.org/10.1109/TCST.2021.3070861
- 33Ding S, Wang Z, Zhang H. Event-triggered stabilization of neural networks with time-varying switching gains and input saturation. IEEE Trans Neural Netw Learn Syst. 2018; 29(10): 5045-5056.
- 34Li Y, Yang G. Observer-based fuzzy adaptive event-triggered control codesign for a class of uncertain nonlinear systems. IEEE Trans Fuzzy Syst. 2018; 26(3): 1589-1599.
- 35Fan Q, Yang G. Event-based fuzzy adaptive fault-tolerant control for a class of nonlinear systems. IEEE Trans Fuzzy Syst. 2018; 26: 2686-2698.
- 36Li Y, Yang G, Tong S. Fuzzy adaptive distributed event-triggered consensus control of uncertain nonlinear multiagent systems. IEEE Trans Syst Man Cybern Syst. 2019; 49(9): 1777-1786.
- 37 Fan X, Wang Z. Event-triggered integral sliding mode control for fractional order T-S fuzzy systems via a fuzzy error function. Int J Robust Nonlinear Control. 2021. https://doi.org/10.1002/rnc.5400
- 38 Zhang T, Hua Y, Xia X, Yi Y. Unified adaptive event-triggered control of uncertain multi-input multi-output nonlinear systems with dynamic and static constraints. Int J Robust Nonlinear Control. 2021. https://doi.org/10.1002/rnc.5401
- 39 Zhang Z, Peng S, Liu D, Wang Y, Chen T. Leader-following mean-square consensus of stochastic multiagent systems with ROUs and RONs via distributed event-triggered impulsive control. IEEE Trans Cybern. 2020. https://doi.org/10.1109/TCYB.2020.2999359
- 40
Sun W, Zheng H, Guo W, et al. Quasisynchronization of heterogeneous dynamical networks via event-triggered impulsive controls. IEEE Trans Cybern. 2020. https://doi.org/10.1109/TCYB.2020.2975234
10.1109/TCYB.2020.3012707 Google Scholar
- 41Tan X, Cao J, Li X. Consensus of leader-following multiagent systems: a distributed event-triggered impulsive control strategy. IEEE Trans Cybern. 2019; 49(3): 792-801.
- 42 Wang X, Fei Z, Gao H, Yu J. Integral-based event-triggered fault detection filter design for unmanned surface vehicles. IEEE Trans Ind Inform. 2019; 15(10): 5626-5636. https://doi.org/10.1109/TII.2019.2900230
- 43Mousavi S, Marquez H. Integral-based event triggering controller design for stochastic LTI systems via convex optimisation. Int J Control. 2016; 89(7): 1416-1427.
- 44 Singh B, Kumar N, Panigrahi BK. Steepest descent laplacian regression based neural network approach for optimal operation of grid supportive solar PV generation. IEEE Trans Circuits Syst II-Express Briefs. 2020. https://doi.org/10.1109/TCSII.2020.2967106
- 45Seuret A, Gouaisbaut F. Stability of linear systems with time-varying delays using Bessel-Legendre inequalities. IEEE Trans Automat Contr. 2018; 63(1): 225-232.
- 46
Boyd S, Ghaoui LE, Feron E, Balakrishnan V. Linear Matrix Inequalities in System and Control Theory. SIAM; 1994.
10.1137/1.9781611970777 Google Scholar
- 47Xie L, Fu M, De Souza CE. H∞ control and quadratic stabilization of systems with parameter uncertainty via output feedback. IEEE Trans Automat Contr. 1992; 37(8): 1253-1256.
- 48Seuret A, Gouaisbaut F. Hierarchy of LMI conditions for the stability analysis of time-delay systems. Syst Control Lett. 2015; 81: 1-7.
- 49 Zhang L, Nguang SK, Ouyang D, Yan S. Synchronization of delayed neural networks via integral-based event-triggered scheme. IEEE Trans Neural Netw Learn Syst. 2020; 31(12): 5092-5102. https://doi.org/10.1109/TNNLS.2019.2963146
- 50Seuret A, Gouaisbaut F, Ariba Y. Complete quadratic Lyapunov functionals for distributed delay systems. Automatica. 2015; 62: 168-176.
- 51Roesch O, Roth H. Remote control of mechatronic systems over communication networks. Proceedings of the IEEE International Conference Mechatronics and Automation (ICMA); Vol. 3; 2005:1648-1653; Niagara Falls, Canada
