On the robustness of distributed proportional-integral consensus protocols under channel uncertainties

This article studies the robust consensus problem for uncertain multiagent systems under distributed proportional-integral (PI) protocols. For both continuous-time and discrete-time multiagent systems, we allow additive channel uncertainties that are stable and bounded in 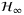norm. By exploiting the generalized network complementary sensitivity function (GNCSF), necessary and sufficient conditions under which the robust consensus with distributed PI protocols can be guaranteed are derived. For the continuous-time case, it is shown that the robust consensus can be reached if and only if the uncertainty radius and the 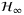norm of the GNCSF satisfy certain constraint. For the discrete-time case, it is shown that the robust consensus can be preserved under both the constraints on the parameters of the PI protocols and the relationship of the uncertainty radius and the 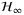norm of the GNCSF. Finally, numerical examples are provided to show the effectiveness of the theoretical results.