Robust adaptive model predictive control: Performance and parameter estimation
Summary
For systems with uncertain linear models, bounded additive disturbances and state and control constraints, a robust model predictive control (MPC) algorithm incorporating online model adaptation is proposed. Sets of model parameters are identified online and employed in a robust tube MPC strategy with a nominal cost. The algorithm is shown to be recursively feasible and input-to-state stable. Computational tractability is ensured by using polytopic sets of fixed complexity to bound parameter sets and predicted states. Convex conditions for persistence of excitation are derived and are related to probabilistic rates of convergence and asymptotic bounds on parameter set estimates. We discuss how to balance conflicting requirements on control signals for achieving good tracking performance and parameter set estimate accuracy. Conditions for convergence of the estimated parameter set are discussed for the case of fixed complexity parameter set estimates, inexact disturbance bounds, and noisy measurements.
1 INTRODUCTION
Model predictive control (MPC) repeatedly solves a finite-horizon optimal control problem subject to input and state constraints. At each sampling instant a model of the plant is used to optimize predicted behavior and the first element of the optimal predicted control sequence is applied to the plant.1 Any mismatch between model and plant causes degradation of controller performance.2 As a result, the amount of model uncertainty strongly affects the bounds of the achievable performance of a robust MPC algorithm.3
To avoid the disruption caused by intrusive plant tests,2 adaptive MPC attempts to improve model accuracy online while satisfying operating constraints and providing stability guarantees. Although the literature on adaptive control has long acknowledged the need for persistently exciting (PE) inputs for system identification,4 few articles have explored how to incorporate PE conditions with feasibility guarantees within adaptive MPC.5 In addition, adaptive MPC algorithms must balance conflicting requirements for system identification accuracy and computational complexity.5, 6
Various methods for estimating system parameters and meeting operating constraints are described in the adaptive MPC literature. Depending on the assumptions on model parameters, parameter identification methods such as recursive least squares (RLS)7, comparison sets,8 set membership identification,9, 10 and neural networks11, 12 have been proposed. Heirung et al13 propose an algorithm where the unknown parameters are estimated using RLS and system outputs are predicted using the resulting parameter estimates. The use of RLS introduces nonlinear equality constraints into the optimization. On the other hand, the comparison model approach described in Aswani et al8 addresses the trade-off between probing for information and output regulation by decoupling these two tasks; a nominal model is used to impose operating constraints whereas performance is evaluated via a model learned online using statistical identification tools. However, the use of a nominal model implies that the comparison model approach cannot guarantee robust constraint satisfaction.
Tanaskovic et al9 consider a linear finite impulse response (FIR) model with measurement noise and constraints. This approach updates a model parameter set using online set membership identification; constraints are enforced for the entire parameter set and performance is optimized for a nominal prediction model. The article proves recursive feasibility but does not show convergence of the identified parameter set to the true parameters. To avoid the restriction to FIR models, Lorenzen et al10 consider a linear state space model with additive disturbance. An online-identified set of possible model parameters is used to robustly stabilize the system. However, the approach suffers from a lack of flexibility in its robust MPC formulation, which is based on homothetic tubes,14 allowing only the centers and scalings of tube cross-sections to be optimized online, and it does not provide convex and recursively feasible conditions to ensure PE control inputs.
In this article, we also consider linear systems with parameter uncertainty, additive disturbances, and constraints on system states and control inputs. Compared with Reference 10, the proposed algorithm reduces the conservativeness in approximating predicted state tubes by adopting more flexible cross-section representations. Building on Reference 15, we take advantage of fixed complexity polytopic tube representations and use hyperplane and vertex representations interchangeably to further simplify computation. We use, similarly to Reference 13, a nominal performance objective, but we impose constraints robustly on all possible models within the identified model set. We prove that the closed-loop system is input-to-state stable (ISS). In comparison with the min-max approach of Reference 15, the resulting performance bound takes the form of an asymptotic bound on the 2-norm of the sequence of closed-loop states in terms of the 2-norms of the additive disturbance and parameter estimate error sequences. In addition, we convexify the persistence of excitation (PE) condition around a reference trajectory and include a penalty term in the cost function to promote convergence of the parameter set. The convexification method is somewhat analogous to that proposed in References 16, 17, where the uncertainty information of the parameter set is approximated using a nominal gain. Here, however, the convexification is obtained by direct linearization of PE constraints on predicted trajectories. The cost function modification proposed here allows the relative importance of the two objectives, namely, controller performance and convergence of model parameters, to be specified.
Bai et al18 consider a particular set membership identification algorithm and show that the parameter set estimate converges with probability 1 to the actual parameter vector (assumed constant) if: (a) a tight bound on disturbances is known; (b) the input sequence is persistent exciting; and (c) the minimal parameter set estimate is employed. However, the minimal set estimate can be arbitrarily complex, and to provide computational tractability various nonminimal parameter set approximations have been proposed, such as n-dimensional balls19 and bounded complexity polytopes.9 The current article allows the use of parameter set estimates with fixed complexity and proves that, despite their approximate nature, such parameter sets converge with probability 1 to the true parameter values. We also derive lower bounds on convergence rates for the case of inexact knowledge of the disturbance bounding set and for the case that model states are estimated in the presence of measurement noise.
This article has five main parts. Section 2 defines the problem and basic assumptions. Section 3 gives details of the parameter estimation, robust constraint satisfaction, nominal cost function, convexified PE conditions, and the MPC algorithm. Section 4 proves recursive feasibility and ISS of the proposed algorithm. Section 5 proves the convergence of the parameter set in various conditions and Section 6 illustrates the approach with numerical examples.
Notation: 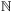 and
and 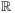 denote the sets of integers and reals, and
denote the sets of integers and reals, and 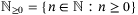 ,
, 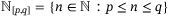 . The ith row of a matrix A and ith element of a vector a are denoted [A]i and [a]i. Vectors and matrices of 1s are denoted 1, and
. The ith row of a matrix A and ith element of a vector a are denoted [A]i and [a]i. Vectors and matrices of 1s are denoted 1, and 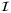 is the identity matrix. For a vector a, ‖a‖ is the Euclidean norm and
is the identity matrix. For a vector a, ‖a‖ is the Euclidean norm and 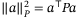 ; the largest element of a is
; the largest element of a is 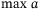 and
and 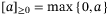 . The absolute value of a scalar s is
. The absolute value of a scalar s is 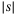 and the floor value is ⌊s⌋.
and the floor value is ⌊s⌋. 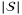 is the number of elements in a set
is the number of elements in a set 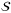 .
. 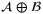 is Minkowski addition for sets
is Minkowski addition for sets  and
and  , and
, and 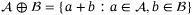 . The matrix inequality A ≽ 0 (or A ≻ 0) indicates that A is positive semidefinite (positive definite) matrix. The k steps ahead predicted value of a variable x is denoted xk, and the more complete notation xk|t indicates the k steps ahead prediction at time t. A continuous function
. The matrix inequality A ≽ 0 (or A ≻ 0) indicates that A is positive semidefinite (positive definite) matrix. The k steps ahead predicted value of a variable x is denoted xk, and the more complete notation xk|t indicates the k steps ahead prediction at time t. A continuous function 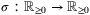 is a
is a 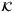 -function if it is strictly increasing with
-function if it is strictly increasing with 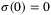 , and is a
, and is a 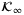 -function if in addition
-function if in addition 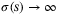 as s → ∞. A continuous function
as s → ∞. A continuous function 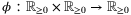 is a
is a 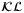 -function if, for all t ≥ 0,
-function if, for all t ≥ 0, 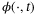 is a
is a 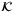 -function, and, for all s ≥ 0,
-function, and, for all s ≥ 0, 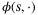 is decreasing with
is decreasing with 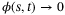 as t → ∞. For functions
as t → ∞. For functions 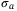 and
and 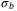 we denote
we denote 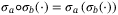 , and
, and 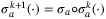 with
with 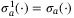 .
.
2 PROBLEM FORMULATION AND PRELIMINARIES
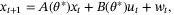 (1)
(1) is the system state,
is the system state, 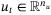 is the control input,
is the control input, 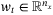 is an unknown disturbance input, and t is the discrete time index. The system matrices
is an unknown disturbance input, and t is the discrete time index. The system matrices 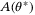 and
and 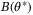 depend on an unknown but constant parameter
depend on an unknown but constant parameter 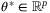 . The disturbance sequence {w0,w1, …} is stochastic and (wi,wj) is independent for all i ≠ j. States and control inputs are subject to linear constraints, defined for
. The disturbance sequence {w0,w1, …} is stochastic and (wi,wj) is independent for all i ≠ j. States and control inputs are subject to linear constraints, defined for  ,
, 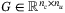 by
by
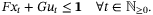 (2)
(2)
Assumption 1. (Additive disturbance)The disturbance wt lies in a convex and compact polytope 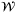 , where
, where
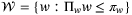 (3)
(3)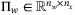 ,
, 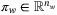 and
and  .
.
Assumption 2. (Parameter uncertainty)The system matrices A and B are affine functions of the parameter vector 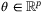 :
:
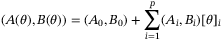 (4)
(4)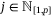 , and
, and  lies in a known, bounded, convex polytope
lies in a known, bounded, convex polytope 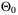 given by
given by
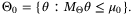
Assumption 3. (State and control constraints)The set
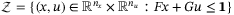
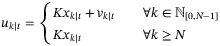 (5)
(5)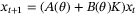 ,
, 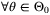 in the absence of constraints. This assumption can be stated as follows.
in the absence of constraints. This assumption can be stated as follows.
Assumption 4. (Feedback gain and contractive set)There exists a polytopic set 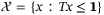 and feedback gain K such that
and feedback gain K such that 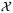 is
is 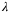 -contractive for some
-contractive for some 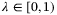 , that is
, that is
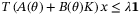 (6)
(6)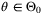 . The representation
. The representation 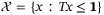 is assumed to be minimal in the sense that it contains no redundant inequalities.
is assumed to be minimal in the sense that it contains no redundant inequalities.
3 ADAPTIVE ROBUST MPC
In this section, a parameter estimation scheme based on References 20, 21 is introduced. We then discuss the construction of tubes to bound predicted model states and associated constraints.
3.1 Set-based parameter estimation
At time t we use observations of the system state xt to determine a set 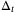 of unfalsified model parameters. The set
of unfalsified model parameters. The set 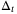 is then combined with the parameter set estimate
is then combined with the parameter set estimate 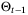 to construct a new parameter set estimate
to construct a new parameter set estimate 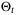 .
.
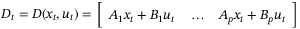 (7)
(7)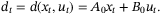 (8)
(8)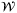 in (3), the unfalsified parameter set at time t is given by
in (3), the unfalsified parameter set at time t is given by
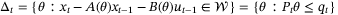 (9)
(9)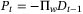 and
and 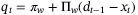 .
. be an a priori chosen matrix. The estimated parameter set
be an a priori chosen matrix. The estimated parameter set 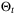 is defined by
is defined by
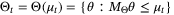 (10)
(10)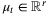 is updated online at times
is updated online at times 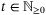 . The complexity of
. The complexity of 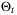 is controlled by fixing
is controlled by fixing 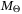 , which fixes the directions of the half-spaces defining the parameter set. We assume that
, which fixes the directions of the half-spaces defining the parameter set. We assume that 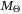 is chosen so that
is chosen so that 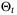 is compact for all
is compact for all 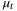 such that
such that 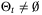 . Using a block recursive polytopic update method,20
. Using a block recursive polytopic update method,20 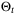 is defined as the smallest set (10) containing the intersection of
is defined as the smallest set (10) containing the intersection of 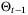 and unfalsified sets
and unfalsified sets 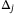 over a window of length Nu:
over a window of length Nu:
 (11)
(11)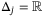 for all j ≤ 0). We refer to Nu as the PE window. Note that Nu is independent of the MPC prediction horizon N. Using linear conditions for polyhedral set inclusion22
for all j ≤ 0). We refer to Nu as the PE window. Note that Nu is independent of the MPC prediction horizon N. Using linear conditions for polyhedral set inclusion22 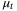 in (11) can be obtained by solving a linear program for each
in (11) can be obtained by solving a linear program for each 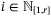 :
:

3.2 Polytopic tubes for robust constraint satisfaction
 satisfying, for all
satisfying, for all 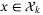 ,
, 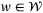 ,
, 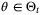 ,
,
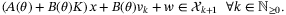 (12)
(12)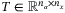 satisfying Assumption 4 and
satisfying Assumption 4 and 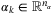 , let
, let 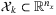 denote the k steps ahead cross-section of the predicted state tube:
denote the k steps ahead cross-section of the predicted state tube:
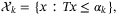 (13)
(13)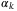 to be an optimization variable. If, for a given
to be an optimization variable. If, for a given 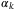 , the constraint
, the constraint 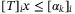 is redundant for some
is redundant for some 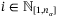 in the hyperplane description (13) (ie, if the set
in the hyperplane description (13) (ie, if the set 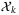 is unchanged by removing this constraint), we define (without loss of generality)
is unchanged by removing this constraint), we define (without loss of generality) 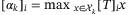 . Thus, for each
. Thus, for each 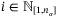 ,
, 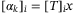 necessarily holds for some
necessarily holds for some 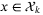 . Then (12) is equivalent to, for all
. Then (12) is equivalent to, for all 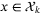 and
and 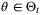 ,
,
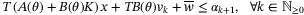
 is the vector with ith element
is the vector with ith element 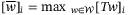 for all
for all 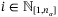 . Substituting D(x,u) and d(x,u) from (7), (8), this implies linear conditions on
. Substituting D(x,u) and d(x,u) from (7), (8), this implies linear conditions on 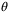 , for all
, for all 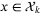 ,
, 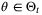 :
:
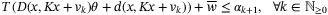
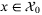 requires
requires
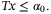 (14)
(14)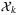 has an equivalent representation in terms of its vertices, which we denote as
has an equivalent representation in terms of its vertices, which we denote as 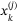 ,
, 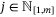 :
:
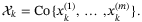 (15)
(15)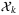 , is fixed, and for given
, is fixed, and for given 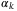 in (13), we may have
in (13), we may have 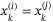 for some
for some 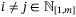 in (15) (ie, the vertex description may contain repeated vertices). The presence of repeated vertices does not affect the formulation. For each
in (15) (ie, the vertex description may contain repeated vertices). The presence of repeated vertices does not affect the formulation. For each 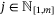 , define an index set
, define an index set 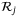 (with
(with  ), such that the ith row of T and ith element of
), such that the ith row of T and ith element of  satisfy
satisfy
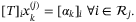
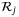 associated with active inequalities at the vertex x(j) is independent of
associated with active inequalities at the vertex x(j) is independent of 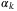 and can be computed offline. Therefore, for each
and can be computed offline. Therefore, for each 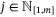 , we have
, we have
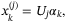 (16)
(16)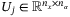 can be computed offline given knowledge of
can be computed offline given knowledge of 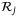 using the property that
using the property that
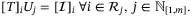 (17)
(17)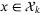 is equivalent to, for all
is equivalent to, for all 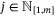 ,
,
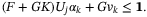 (18)
(18)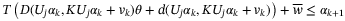
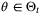 ,
, 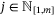 and
and 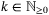 . This is equivalent (see e.g. Reference 22, Proposition 3.31) to the requirement that there exist matrices
. This is equivalent (see e.g. Reference 22, Proposition 3.31) to the requirement that there exist matrices 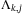 satisfying, for each prediction time step
satisfying, for each prediction time step 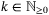 and each vertex
and each vertex  , the conditions
, the conditions
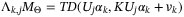 (19a)
(19a)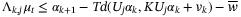 (19b)
(19b)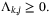 (19c)
(19c)3.3 Objective function
 (21)
(21)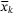 and
and 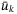 are elements of predicted state and control sequences generated by a nominal parameter vector
are elements of predicted state and control sequences generated by a nominal parameter vector 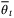 :
:
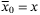 (22a)
(22a)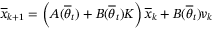 (22b)
(22b)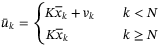 (22c)
(22c)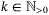 and where v = {v0, … , vN − 1}. Define
and where v = {v0, … , vN − 1}. Define 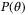 as the solution of the Lyapunov matrix equation
as the solution of the Lyapunov matrix equation
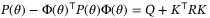 (23)
(23)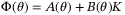 . Note that
. Note that 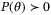 is well-defined for all
is well-defined for all 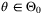 due to Assumption 4. Then (21) is equivalent to
due to Assumption 4. Then (21) is equivalent to
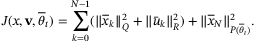 (24)
(24)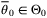 , which could be estimated using physical modeling or offline system identification, alternatively
, which could be estimated using physical modeling or offline system identification, alternatively 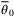 could be defined as the Chebyshev center of
could be defined as the Chebyshev center of 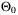 . For t > 0, we assume that
. For t > 0, we assume that 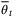 is updated by projecting
is updated by projecting 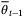 onto the parameter set estimate
onto the parameter set estimate 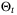 , that is
, that is
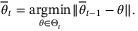 (25)
(25)
3.4 Augmented objective function and persistent excitation
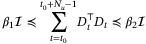 (26)
(26)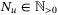 , some
, some 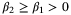 , and all times t0.4 Although the upper bound in (26) implies convex constraints on xt and ut, the lower bound is nonconvex. The bounds on convergence of the parameter set
, and all times t0.4 Although the upper bound in (26) implies convex constraints on xt and ut, the lower bound is nonconvex. The bounds on convergence of the parameter set 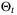 derived in Section 5 suggest faster convergence as
derived in Section 5 suggest faster convergence as 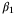 in the PE condition (26) increases.
in the PE condition (26) increases.Previously proposed MPC strategies that incorporate PE constraints consider the PE condition to be defined on an interval such as {t − Nu + 1, … , t}, where t is current time, which means that the PE constraint depends on only the first element of the predicted control sequence. Marafioti et al23 simplify the PE condition by expressing it as a nonconvex quadratic inequality in ut. Likewise, Lorenzen et al10 show that the PE condition is equivalent to a nonconvex constraint on the current control input. Lu and Cannon15 linearize the PE condition about a reference trajectory and thus obtain a sufficient condition for persistent excitation.
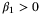 ,
,
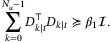 (27)
(27)The inclusion of predicted future states and control inputs in this PE condition allows for greater flexibility in meeting the constraint. To avoid nonconvex constraints, we derive a convex relaxation that provides a sufficient condition for (27).
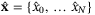 and
and 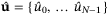 , approximating the optimal predicted state and control sequences, are available. To derive sufficient conditions for (27), we consider the difference between the reference and optimized sequences, denoted
, approximating the optimal predicted state and control sequences, are available. To derive sufficient conditions for (27), we consider the difference between the reference and optimized sequences, denoted 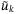 and
and 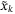 (ie,
(ie,  and
and 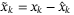 ). Since the prediction tube implies
). Since the prediction tube implies 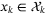 , we therefore have
, we therefore have 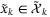 where
where 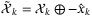 . Denote the vertices of
. Denote the vertices of 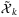 as
as 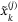 and for
and for 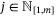 , we have
, we have
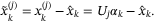
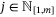 ,
,
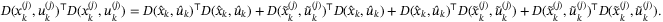
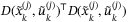 is a positive semidefinite matrix, and by omitting this term we obtain sufficient conditions for (27) as a set of LMIs in
is a positive semidefinite matrix, and by omitting this term we obtain sufficient conditions for (27) as a set of LMIs in 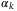 and vk. The following convex conditions are thus sufficient to ensure (27) whenever
and vk. The following convex conditions are thus sufficient to ensure (27) whenever 
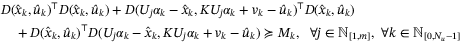 (28a)
(28a)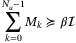 (28b)
(28b)where 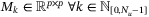 are intermediate variables.
are intermediate variables.
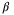 value for the PE constraint in the implementation. A larger value of
value for the PE constraint in the implementation. A larger value of 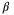 is generally desirable, but a large
is generally desirable, but a large 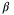 might make the optimization problem with the PE condition infeasible. In this article, we incentivize a large value of
might make the optimization problem with the PE condition infeasible. In this article, we incentivize a large value of 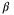 by modifying the MPC objective function as follows
by modifying the MPC objective function as follows
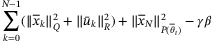 (29)
(29) is a weight that controls the relative priority given to satisfaction of the PE condition (27) and tracking performance. This modification does not affect the feasibility of the optimization.
is a weight that controls the relative priority given to satisfaction of the PE condition (27) and tracking performance. This modification does not affect the feasibility of the optimization.Although incorporating a condition such as (27) or the convex relaxation (28) and (29) into a MPC strategy does not ensure that the closed-loop system satisfies a corresponding PE condition, its effect on the convergence rate of the estimated parameter set is significant, as shown in the numerical example in Section 6. In addition, 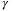 is a meaningful and straightforward coefficient to tune, and the PE constraint can be easily switched off by setting
is a meaningful and straightforward coefficient to tune, and the PE constraint can be easily switched off by setting  .
.
3.5 Proposed algorithm
- 1. Obtain the current state xt and set x = xt.
- 2. Update
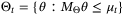 using (11) and the nominal parameter vector
using (11) and the nominal parameter vector 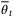 using (25), and solve (23) for
using (25), and solve (23) for 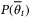 .
. - 3.
At t = 0 compute the initial reference state and control sequences
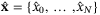 and
and  , for example, by solving the nominal problem described in Remark 4.
, for example, by solving the nominal problem described in Remark 4.At t > 0 compute the reference state and control sequences
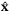 and
and 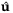 , using the solution
, using the solution 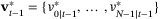 at t − 1, and
at t − 1, and
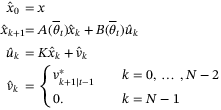 (30)
(30) - 4. Compute
 ,
, 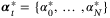 ,
, 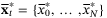 ,
, 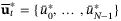 ,
, 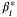 ,
, 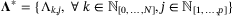 the solution of the semidefinite program (SDP):
the solution of the semidefinite program (SDP):
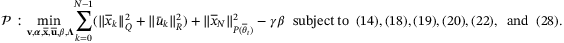
- 5. Implement the current control input
 .
.
Remark 2.In offline step 1, T can be chosen so that the polytope 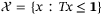 in Assumption 4 approximates a robust control invariant set of the form
in Assumption 4 approximates a robust control invariant set of the form 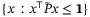 , where
, where 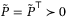 satisfies
satisfies 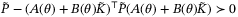 for some
for some 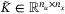 . Using the vertex representation of
. Using the vertex representation of 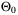 , the matrix
, the matrix 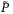 can be computed by solving a SDP (see e.g. Reference 24, Chapter 5). This approach allows the number of rows in T to be specified by the designer. However, T can alternatively be chosen so that
can be computed by solving a SDP (see e.g. Reference 24, Chapter 5). This approach allows the number of rows in T to be specified by the designer. However, T can alternatively be chosen so that 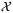 approximates the minimal robust positive invariant (RPI) set or the maximal RPI set for the system (1) and (2) under a specified stabilizing feedback law.22
approximates the minimal robust positive invariant (RPI) set or the maximal RPI set for the system (1) and (2) under a specified stabilizing feedback law.22
Remark 3.In offline step 3, the computation of 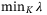 subject to (6) for given T can be performed by solving a LP using the vertex representation of
subject to (6) for given T can be performed by solving a LP using the vertex representation of 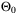 [ 22, chap. 7]. The objective of minimizing
[ 22, chap. 7]. The objective of minimizing 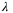 is chosen to make the constraints of problem
is chosen to make the constraints of problem 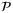 easier to satisfy. In particular, choosing K so that
easier to satisfy. In particular, choosing K so that 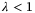 in (6) ensures that
in (6) ensures that 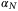 exists satisfying the terminal constraints (20b-d).
exists satisfying the terminal constraints (20b-d).
Remark 4.At t = 0, the reference sequences 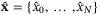 and
and  may be computed by solving
may be computed by solving
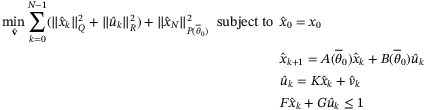 (31)
(31)
Remark 5.The online computation of the proposed algorithm may be reduced by updating 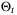 only once every Nu > 1 time steps. For example, in Step 2, set
only once every Nu > 1 time steps. For example, in Step 2, set 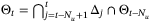 for t ∈ {Nu,2Nu, …} and
for t ∈ {Nu,2Nu, …} and 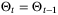 at all times t ∉ {Nu,2Nu, …}.
at all times t ∉ {Nu,2Nu, …}.
In Section 4, we use the property that 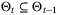 to show that the solution,
to show that the solution, 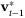 , of
, of 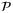 at time t − 1 forms part of a feasible solution of
at time t − 1 forms part of a feasible solution of 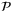 at time t. As a result, the reference sequences
at time t. As a result, the reference sequences 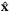 ,
, 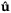 in Step 3 are feasible for problem
in Step 3 are feasible for problem 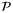 at all times t > 0.
at all times t > 0.
4 RECURSIVE FEASIBILITY AND STABILITY
4.1 Recursive feasibility
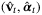 be defined in terms of the optimal solution
be defined in terms of the optimal solution 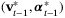 of
of  at time t − 1 by
at time t − 1 by
Proposition 1. (Recursive Feasibility)The online MPC optimization 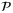 is feasible at all times
is feasible at all times 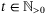 if
if 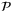 is feasible at t = 0 and
is feasible at t = 0 and 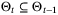 for all time t.
for all time t.
Proof.If 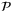 is feasible at t − 1, then at time t,
is feasible at t − 1, then at time t, 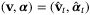 is: feasible for (14) because
is: feasible for (14) because 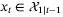 ; feasible for (18) and (19) for
; feasible for (18) and (19) for 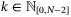 because
because  is feasible for (18) and (19) for
is feasible for (18) and (19) for 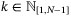 and
and 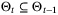 ; and feasible for (18) and (19) for k = N − 1 and feasible for (20) because
; and feasible for (18) and (19) for k = N − 1 and feasible for (20) because 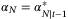 is feasible for (20) and
is feasible for (20) and 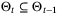 . Finally, we note that (22) is necessarily feasible and (28) necessarily holds for some scalar
. Finally, we note that (22) is necessarily feasible and (28) necessarily holds for some scalar 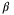 if
if 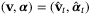 .
.
4.2 Input-to-state stability
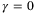 in problem
in problem 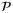 . Therefore, the objective of
. Therefore, the objective of 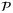 is
is 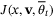 where J is the nominal cost (24). As a result of parameter adaption, the change of
where J is the nominal cost (24). As a result of parameter adaption, the change of 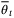 online might increase the cost, but this is absorbed in the ISS terms. To simplify notation we define a stage cost L(x,v) and terminal cost
online might increase the cost, but this is absorbed in the ISS terms. To simplify notation we define a stage cost L(x,v) and terminal cost  as
as 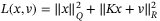 and
and 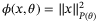 so that (24) is equivalent to
so that (24) is equivalent to
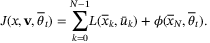
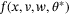 as
as
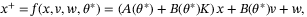
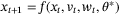 .
.
Lemma 2. (ISS-Lyapunov function [25])The system
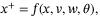 (32)
(32)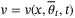 is ISS with region of attraction
is ISS with region of attraction 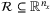 if the following conditions are satisfied.
if the following conditions are satisfied.(i). 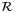 contains the origin in its interior, is compact, and is a robust positively invariant set for (32), that is,
contains the origin in its interior, is compact, and is a robust positively invariant set for (32), that is, 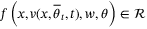 for all
for all 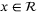 ,
, 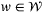 ,
, 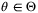 , and
, and 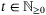 .
.
(ii). There exist 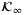 - functions
- functions 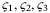 ,
, 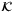 -functions
-functions 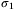 ,
, 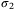 and a function
and a function 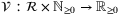 such that for all
such that for all 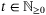 ,
, 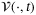 is continuous, and for all
is continuous, and for all 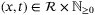 ,
,
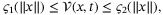 (33)
(33)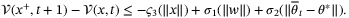 (34)
(34)In the following, we define 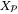 as the set of states x such that problem
as the set of states x such that problem 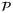 is feasible and assume that
is feasible and assume that 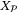 is nonempty. In addition, for a given state x, nominal parameter vector
is nonempty. In addition, for a given state x, nominal parameter vector 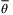 , and parameter set
, and parameter set 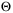 , we denote
, we denote 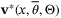 as the optimal solution of problem
as the optimal solution of problem 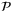 , and let
, and let 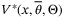 be the corresponding optimal value of the cost in (24), so that
be the corresponding optimal value of the cost in (24), so that 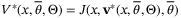 .
.
Theorem 1.Assume that 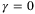 and the nominal parameter vector
and the nominal parameter vector 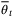 is not updated, that is,
is not updated, that is, 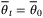 for all
for all 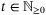 . Then for all initial conditions
. Then for all initial conditions 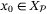 , the system (1) with control law
, the system (1) with control law 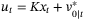 , where
, where 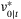 is the first element of
is the first element of 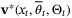 , robustly satisfies the constraint (2) and is ISS with region of attraction
, robustly satisfies the constraint (2) and is ISS with region of attraction 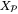 .
.
Proof.We first show that condition (i) of Lemma 2 is satisfied with 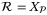 . If
. If 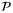 is feasible at t = 0, then (20) implies that
is feasible at t = 0, then (20) implies that 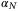 exists such that
exists such that 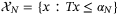 satisfies
satisfies
 (35)
(35)Therefore 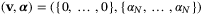 is feasible for
is feasible for 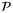 for all
for all 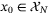 , and hence
, and hence 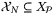 . In addition, the robust invariance of
. In addition, the robust invariance of 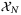 implied by (35) ensures that
implied by (35) ensures that 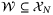 , and since
, and since 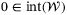 due to Assumption 1,
due to Assumption 1, 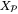 must contain the origin in its interior. Furthermore, Proposition 1 shows that if
must contain the origin in its interior. Furthermore, Proposition 1 shows that if  is initially feasible, then it is feasible for all t ≥ 0, so that
is initially feasible, then it is feasible for all t ≥ 0, so that 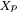 is positively invariant for (32). Finally,
is positively invariant for (32). Finally, 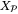 is necessarily compact by Assumption 3, and it follows that condition (i) of Lemma 2 is satisfied if
is necessarily compact by Assumption 3, and it follows that condition (i) of Lemma 2 is satisfied if 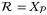 .
.
We next consider the bounds (33) in condition (ii) of Lemma 2. For a given state x, nominal parameter vector 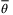 and parameter set
and parameter set  , problem
, problem 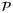 with
with 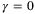 and Q, R ≻ 0 is a convex quadratic program. Therefore,
and Q, R ≻ 0 is a convex quadratic program. Therefore, 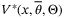 is a continuous positive definite, piecewise quadratic function of x26 for each
is a continuous positive definite, piecewise quadratic function of x26 for each 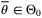 and
and 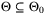 . Furthermore,
. Furthermore,  is compact due to Assumption 2 and it follows that there exist
is compact due to Assumption 2 and it follows that there exist 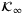 -functions
-functions 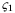 ,
, 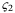 such that (33) holds with
such that (33) holds with
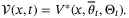
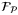 denote the set
denote the set 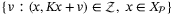 . Then, given the linear dependence of the system (1), the model parameterization (4), and the predicted control law (5) on the state x, disturbance w, and parameter vector
. Then, given the linear dependence of the system (1), the model parameterization (4), and the predicted control law (5) on the state x, disturbance w, and parameter vector 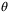 , and since
, and since 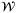 ,
, 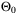 ,
, 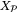 , and
, and 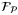 are compact sets by Assumptions 1,2, and 3, there exist
are compact sets by Assumptions 1,2, and 3, there exist 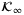 functions
functions 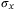 ,
, 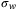 ,
, 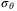 ,
, 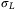 ,
, 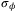 such that,
such that, 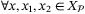 ,
, 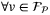 ,
, 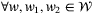 ,
, 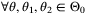 ,
,
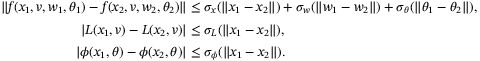
Following the proof of Theorem 5 in Limon et al25 and using the weak triangle inequality for 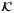 -functions,27 we obtain
-functions,27 we obtain
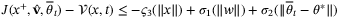
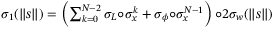 and
and 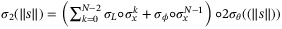 , and both
, and both 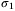 and
and  are
are 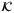 -functions. Since
-functions. Since 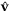 is a feasible but suboptimal solution of
is a feasible but suboptimal solution of 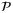 at x+, and since
at x+, and since 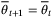 by assumption, the optimal cost function satisfies
by assumption, the optimal cost function satisfies 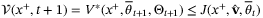 and hence
and hence
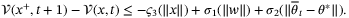
Corollary 1.Assume that  and the nominal parameter vector
and the nominal parameter vector 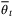 is updated at each time
is updated at each time 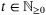 using (25). Then for all initial conditions
using (25). Then for all initial conditions 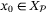 , the system (1) with control law
, the system (1) with control law 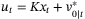 , where
, where 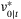 is the first element of
is the first element of  , robustly satisfies the constraint (2) and is ISS with region of attraction
, robustly satisfies the constraint (2) and is ISS with region of attraction 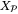 .
.
Proof.It can be shown that condition (i) of Lemma 2 and the bounds (33) in condition (ii) of Lemma 2 are satisfied with 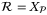 and
and 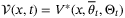 for some
for some  -functions
-functions  ,
,  using the same argument as the proof of Theorem 1. To show that (34) is also satisfied and hence complete the proof we use an argument similar to the proof of Theorem 1. In particular, as before we define
using the same argument as the proof of Theorem 1. To show that (34) is also satisfied and hence complete the proof we use an argument similar to the proof of Theorem 1. In particular, as before we define  using the optimal solution of
using the optimal solution of 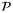 ,
, 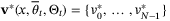 , and
, and

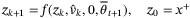
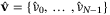 has
has 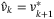 for
for 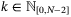 and
and 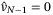 . Then
. Then 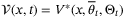 implies
implies
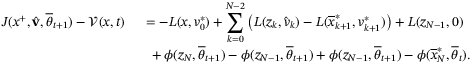 (36)
(36)The update law (25) ensures that 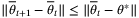 since
since 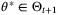 . Hence, for all
. Hence, for all 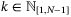 , we have
, we have
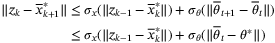
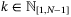 ,
,
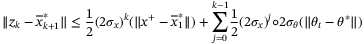
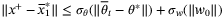 . In addition we have, for all
. In addition we have, for all 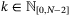

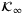 function
function 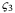 such that
such that 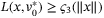 , while (23) implies
, while (23) implies
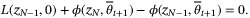
 and the solution
and the solution 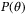 is unique for all
is unique for all 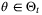 (see, eg, Reference 28) since
(see, eg, Reference 28) since 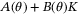 is by assumption stable. Therefore, by the implicit function theorem,
is by assumption stable. Therefore, by the implicit function theorem, 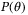 is Lipschitz continuous and
is Lipschitz continuous and 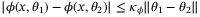 for all
for all 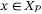 ,
, 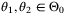 , for some
, for some 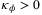 . Hence
. Hence
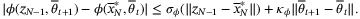
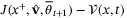 in (36), we obtain
in (36), we obtain
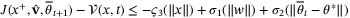
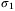 ,
, 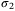 are
are  -functions. But by optimality we have
-functions. But by optimality we have 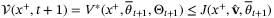 . Therefore (34) holds and hence all of the conditions of Lemma 2 are satisfied.
. Therefore (34) holds and hence all of the conditions of Lemma 2 are satisfied.
Remark 6.The ISS property implies that there exists a 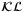 -function
-function 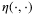 and
and 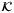 -functions
-functions 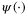 and
and 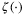 such that for all feasible initial conditions
such that for all feasible initial conditions 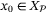 , the closed-loop system trajectories satisfy, for all
, the closed-loop system trajectories satisfy, for all 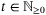 ,
,
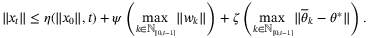
5 CONVERGENCE OF THE ESTIMATED PARAMETER SET
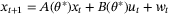 can be rewritten as
can be rewritten as
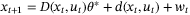 (37)
(37)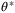 , and additive disturbance
, and additive disturbance 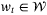 .
.Bai et al18 show that, for such a system, the diameter of the parameter set constructed using a set-membership identification method converges to zero with probability 1 if the uncertainty bound 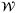 is tight and the regressor Dt is PE. We extend this result and prove convergence of the estimated parameter set in more general cases. Specifically, in this article we avoid the problem of computational intractability arising from a minimum volume update law of the form
is tight and the regressor Dt is PE. We extend this result and prove convergence of the estimated parameter set in more general cases. Specifically, in this article we avoid the problem of computational intractability arising from a minimum volume update law of the form 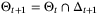 . Instead, we derive stochastic convergence results for parameter sets with fixed complexity and update laws of the form
. Instead, we derive stochastic convergence results for parameter sets with fixed complexity and update laws of the form 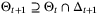 .
.
In this section, we first discuss relevant results for an update law that gives a minimal parameter set estimate for a given sequence of states (but whose representation has potentially unbounded complexity), before considering convergence of the fixed-complexity parameter set update law of Section 3.1. We then compute bounds on the parameter set diameter if the bounding set for the additive disturbances is overestimated. Finally, we demonstrate that similar results can be achieved when errors are present in the observed state, as would be encountered, for example, if the system state were estimated from noisy measurements. In each case we relate the PE condition to the rate of parameter set convergence. We also prove that the parameter set converges to a point (or minimal uncertainty set) with probability one.
In common with Bai et al,18, 29 we do not assume a specific distribution for the disturbance input. However, the set 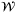 bounding the model disturbance is assumed to be tight in the sense that there is nonzero probability of a realization wt lying arbitrarily close to any given point on the boundary,
bounding the model disturbance is assumed to be tight in the sense that there is nonzero probability of a realization wt lying arbitrarily close to any given point on the boundary, 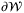 , of
, of 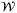 .
.
Assumption 5. (Tight disturbance bounds)For all  and any
and any 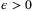 the disturbance sequence {w0,w1, …} satisfies
the disturbance sequence {w0,w1, …} satisfies 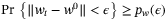 , for all
, for all 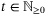 , where
, where 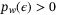 whenever
whenever 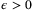 .
.
Assumption 6. (Persistent Excitation)There exist positive scalars 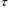 ,
, 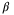 and an integer Nu ≥ ⌈p/nx⌉ such that, for each
and an integer Nu ≥ ⌈p/nx⌉ such that, for each 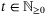 we have
we have 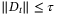 and
and

We further assume throughout this section that the rows of  are normalized so that
are normalized so that 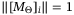 for all i.
for all i.
5.1 Minimal parameter set
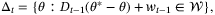 (38)
(38)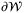 , then the normal cone
, then the normal cone  to
to 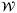 at w0 is defined
at w0 is defined
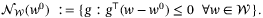 (39)
(39)
Proposition 2.For all 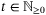 , all
, all 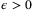 , and for any
, and for any 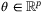 such that
such that 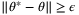 , under Assumptions 1, 5, and 6 we have
, under Assumptions 1, 5, and 6 we have
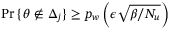
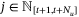 .
.
Proof.Assumption 1 implies that there exists  so that
so that 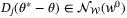 for any given
for any given 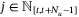 and
and 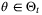 Therefore, if
Therefore, if 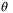 satisfies
satisfies 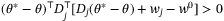 , then the definition (39) of
, then the definition (39) of 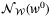 implies
implies 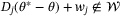 , and hence
, and hence 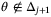 from (38). But
from (38). But
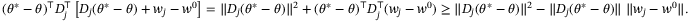
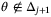 whenever
whenever 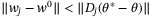 . Furthermore, for all
. Furthermore, for all 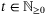 Assumption 6 implies
Assumption 6 implies
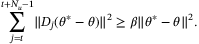
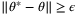 , then there must exist some
, then there must exist some 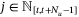 such that
such that
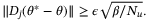
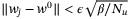 , then it follows that
, then it follows that 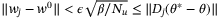 and thus
and thus 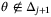 . Assumption 5 implies the probability of this event is at least
. Assumption 5 implies the probability of this event is at least 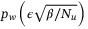 .
.
Proof.For the nontrivial case of t ≥ Nu we have 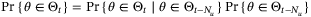 since
since 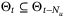 . Also
. Also 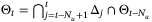 and Proposition 2
implies
and Proposition 2
implies 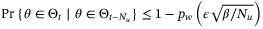 if
if 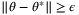 . Therefore,
. Therefore,

Proof.For any 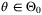 and
and 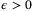 such that
such that 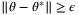 , Theorem 2 implies that
, Theorem 2 implies that 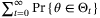 is necessarily finite, and since
is necessarily finite, and since 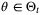 requires that
requires that 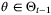 , the Borel-Cantelli lemma therefore implies that
, the Borel-Cantelli lemma therefore implies that 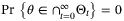 . It follows that
. It follows that 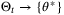 as t → ∞ with probability 1 since
as t → ∞ with probability 1 since 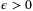 is arbitrary.
is arbitrary.
5.2 Fixed complexity parameter set
In order to reduce computational load and ensure numerical tractability, we assume that the parameter set 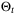 is defined by a fixed complexity polytope, as in (10) and (11). This section shows that, although a degree of conservativeness is introduced by fixing the complexity of
is defined by a fixed complexity polytope, as in (10) and (11). This section shows that, although a degree of conservativeness is introduced by fixing the complexity of 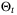 , asymptotic convergence of this set to the true parameter vector
, asymptotic convergence of this set to the true parameter vector 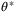 still holds with probability 1.
still holds with probability 1.
Theorem 3.If 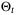 is updated according to (10), (11) and Remark 5, and Assumptions 1, 5, and 6 hold, then for all
is updated according to (10), (11) and Remark 5, and Assumptions 1, 5, and 6 hold, then for all 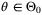 such that
such that 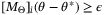 for some
for some 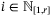 , we have, for all
, we have, for all 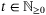 and any
and any 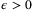 ,
,

Proof.For the nontrivial case of t ≥ Nu we have 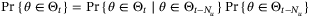 since
since 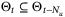 by Lemma 1. Consider therefore the probability that any given
by Lemma 1. Consider therefore the probability that any given 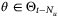 satisfying
satisfying 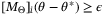 lies in
lies in 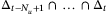 . Define vectors gj for
. Define vectors gj for  by
by
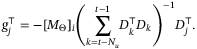 (40)
(40)Assumption 1 implies that, for any given 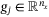 , there exists a
, there exists a 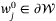 such that
such that 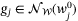 . Accordingly, choose
. Accordingly, choose 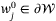 so that gj in (40) satisfies
so that gj in (40) satisfies 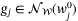 for each
for each 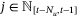 . Then
. Then
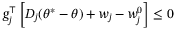 (41)
(41)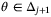 due to (38) and (39). But (40) and Assumption 6 imply
due to (38) and (39). But (40) and Assumption 6 imply

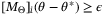 by assumption, and it follows from (41) that
by assumption, and it follows from (41) that 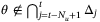 if
if 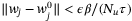 for all
for all 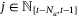 . From Assumption 5 and the independence of the sequence {w0,w1, …} we therefore conclude that
. From Assumption 5 and the independence of the sequence {w0,w1, …} we therefore conclude that
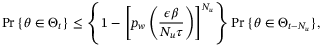
Corollary 3.Under Assumptions 1, 5, and 6, the fixed complexity parameter set estimate 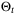 converges to
converges to 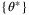 with probability 1.
with probability 1.
5.3 Inexact disturbance bounds
We next consider the case in which the set 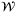 bounding wt in Assumption 1 does not satisfy Assumption 5. Instead, we assume that a compact set
bounding wt in Assumption 1 does not satisfy Assumption 5. Instead, we assume that a compact set 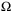 providing a tight bound on wt exists but is either unknown or nonpolytopic or nonconvex. We define the unit ball
providing a tight bound on wt exists but is either unknown or nonpolytopic or nonconvex. We define the unit ball 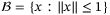 and use a scalar
and use a scalar 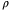 to characterize the accuracy to which
to characterize the accuracy to which 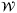 approximates
approximates 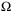 .
.
Assumption 7. (Inexact disturbance bounds)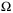 is a compact set such that
is a compact set such that 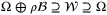 for some
for some  , and, for all
, and, for all 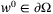 and
and 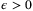 , the disturbance sequence {w0,w1, …} satisfies, for all
, the disturbance sequence {w0,w1, …} satisfies, for all 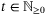 ,
, 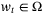 and
and 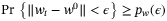 , where
, where 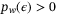 whenever
whenever 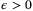 .
.
Remark 8.Assumption 7 implies that 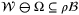 . As a result, every point in
. As a result, every point in 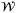 can be a distance no greater than
can be a distance no greater than 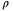 from a point in
from a point in 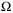 , that is
, that is  .
.
Theorem 5.Let Assumptions 1, 6, and 7 hold and let 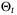 be the fixed complexity parameter set defined by (10), (11) with Remark 5. Then, for all
be the fixed complexity parameter set defined by (10), (11) with Remark 5. Then, for all 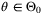 such that
such that 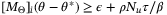 for some
for some 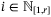 and any
and any 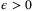 , we have, for all
, we have, for all 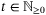 ,
,
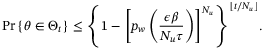
Proof.A bound on the probability that 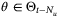 satisfying
satisfying 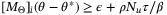 lies in
lies in  can be found using the same argument as the proof of Theorem 3. Thus, choose
can be found using the same argument as the proof of Theorem 3. Thus, choose 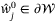 ,
, 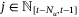 so that
so that 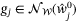 , where
, where
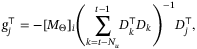
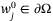 so that
so that 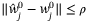 for each
for each 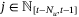 . Then, from
. Then, from 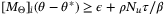 and Assumptions 6 and 7 we have
and Assumptions 6 and 7 we have
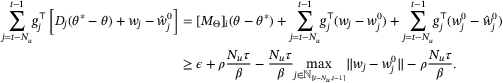
Therefore, if 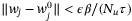 for all
for all 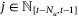 , then
, then 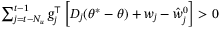 which implies
which implies 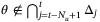 . From Assumption 7 and the independence of the sequence {w0,w1, …} we therefore conclude that
. From Assumption 7 and the independence of the sequence {w0,w1, …} we therefore conclude that
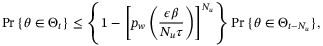
5.4 System with measurement noise
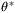 and measurement noise st:
and measurement noise st:
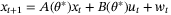 (42a)
(42a)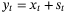 (42b)
(42b)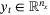 is a measurement (or state estimate) and the noise sequence {s0,s1, …} has independent elements satisfying
is a measurement (or state estimate) and the noise sequence {s0,s1, …} has independent elements satisfying 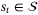 for all
for all 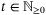 .
.
Assumption 8. (Measurement noise bounds)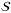 is a compact convex polytope with vertex representation
is a compact convex polytope with vertex representation 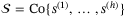 .
.
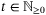 using the available measurements yt, yt − 1, the known control input ut − 1, and sets
using the available measurements yt, yt − 1, the known control input ut − 1, and sets 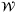 and
and 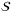 bounding the disturbance and the measurement noise. To be consistent with (42),
bounding the disturbance and the measurement noise. To be consistent with (42), 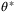 must clearly lie in the set
must clearly lie in the set 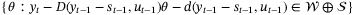 , and the smallest unfalsified parameter set based on this information is given by
, and the smallest unfalsified parameter set based on this information is given by
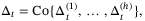 (43a)
(43a)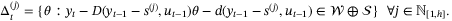 (43b)
(43b)Thus, Assumption 8 implies that the unfalsified set 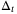 is a convex polytope and the parameter set
is a convex polytope and the parameter set 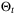 can be estimated using, for example, the update law (10), (11) if
can be estimated using, for example, the update law (10), (11) if 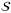 is known.
is known.
Assumption 9. (Tight measurement noise and disturbance bounds)For all  ,
, 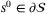 , and
, and 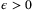 we have
we have
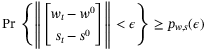
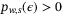 whenever
whenever 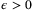 .
.
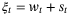 , then Assumption 9 implies
, then Assumption 9 implies
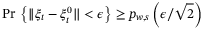
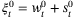 with
with 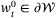 and
and 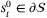 . This implies the following straightforward extensions of Theorems 2 and 3 and Corollaries 2
and 3.
. This implies the following straightforward extensions of Theorems 2 and 3 and Corollaries 2
and 3.
Corollary 6.Let Assumptions 1, 6, 8, and 9 hold and 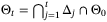 , with
, with 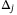 given by (43). Then for all
given by (43). Then for all 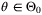 such that
such that 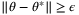 , for all
, for all  and all
and all 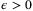 , we have
, we have
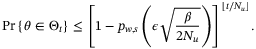
Corollary 7.Let Assumptions 1, 6, 8, and 9 hold and let 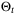 be the fixed complexity parameter set defined by (10), (11) with Remark 5 and (43). Then for all
be the fixed complexity parameter set defined by (10), (11) with Remark 5 and (43). Then for all 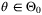 such that
such that  for some
for some 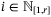 and any
and any 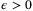 , we have, for all
, we have, for all 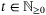 ,
,
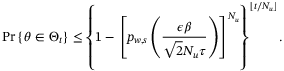
Corollary 8.Under Assumptions 1, 6, 8, 9 the parameter set 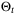 defined in Corollary 6 or 7 converges to
defined in Corollary 6 or 7 converges to 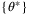 with probability 1.
with probability 1.
Remark 9.If measurement noise is present, modifications to the proposed algorithm in Section 3.5 are needed. If no additional output constraints are present, then, given the noisy measurement yt, the constraint (14) should be replaced by
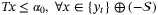
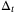 is in this case given by (43).
is in this case given by (43).
6 NUMERICAL EXAMPLES
This section presents simulations to illustrate the operation of the proposed adaptive robust MPC scheme. The section consists of two parts. The first part investigates the effect of additional weight 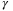 in optimization problem
in optimization problem 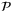 by using the example of a second-order system from Reference 30. The second part demonstrates the relationship between the speed of parameter convergence and minimal eigenvalue
by using the example of a second-order system from Reference 30. The second part demonstrates the relationship between the speed of parameter convergence and minimal eigenvalue 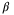 from the PE condition.
from the PE condition.
6.1 Objective function with weighted PE condition
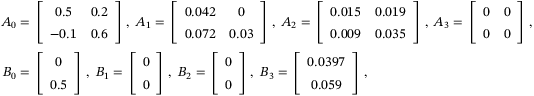
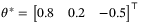 . The initial parameter set estimate is
. The initial parameter set estimate is 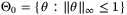 , and for all t ≥ 0,
, and for all t ≥ 0, 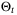 is a hyperrectangle, with
is a hyperrectangle, with 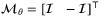 . The elements of the disturbance sequence {w0,w1, …} are independent and identically (uniformly) distributed on
. The elements of the disturbance sequence {w0,w1, …} are independent and identically (uniformly) distributed on 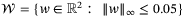 . The state and input constraints are [xt]2 ≥ −0.3 and ut ≤ 1. The MPC prediction horizon and PE window length are set to be N = 10 and Nu = 2, respectively. The matrix T is chosen according to Remark 2 and has 9 rows.
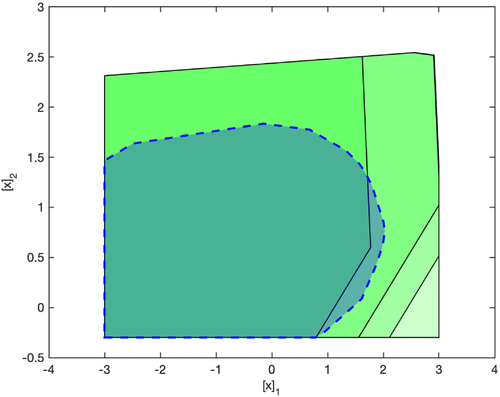
. The state and input constraints are [xt]2 ≥ −0.3 and ut ≤ 1. The MPC prediction horizon and PE window length are set to be N = 10 and Nu = 2, respectively. The matrix T is chosen according to Remark 2 and has 9 rows.All simulations were performed in Matlab on a 3.4 GHz Intel Core i7 processor, and the online MPC optimization 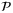 was solved using Mosek.31 For purposes of comparison, the same parameter set update law and nominal parameter update law were used in all cases. Robust satisfaction of input and state constraints and recursive feasibility were observed in all simulations, in agreement with Proposition 1. To illustrate satisfaction of the state constraint [x]2 ≥ −0.3, Figure 1 shows the cross-sections of the robust state tube predicted at t = 0, with initial condition x0 = (3,6), together with the closed-loop state trajectories for 10 different initial conditions.
was solved using Mosek.31 For purposes of comparison, the same parameter set update law and nominal parameter update law were used in all cases. Robust satisfaction of input and state constraints and recursive feasibility were observed in all simulations, in agreement with Proposition 1. To illustrate satisfaction of the state constraint [x]2 ≥ −0.3, Figure 1 shows the cross-sections of the robust state tube predicted at t = 0, with initial condition x0 = (3,6), together with the closed-loop state trajectories for 10 different initial conditions.
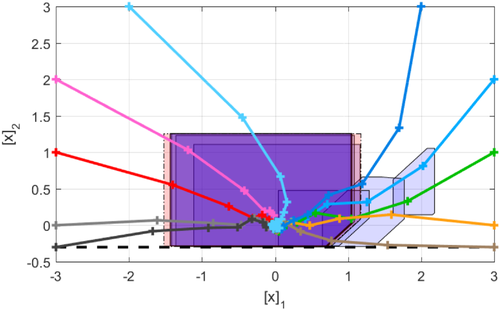
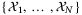 at t = 0 for initial condition x0 = (3,2), with
at t = 0 for initial condition x0 = (3,2), with 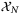 shown in red and enclosed by dashed line
shown in red and enclosed by dashed lineTable 1 compares the computational time and parameter sizes of the proposed algorithm and existing algorithms when the same initial conditions and disturbance sequences {w0,w1, … } are used. Algorithm (A) refers to the robust adaptive MPC in Section 3.4 of Lorenzen et al.10 Algorithm (B) is a modification of algorithm (A) that incorporates the PE constraint 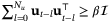 , which is implemented as described in Lu and Cannon15 with a fixed
, which is implemented as described in Lu and Cannon15 with a fixed 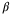 value:
value: 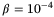 . Algorithms (C) and (D) are the algorithm proposed in Section 3.5, with and without the PE condition, respectively.
. Algorithms (C) and (D) are the algorithm proposed in Section 3.5, with and without the PE condition, respectively.
| (A) | (B) | (C) | (D) | |
|---|---|---|---|---|
| Algorithm | Homothetic tube (no PE)10a | Homothetic tube with PE10 | Proposed algorithm (no PE)a | Proposed Algorithm with PE (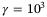 ) ) |
| Yalmip time (s) | 0.1825 | 0.7407 | 0.2053 | 0.2608 |
| Solver time (s) | 0.1354 | 0.2065 | 0.1016 | 0.0766 |
| Computational time (s) (Yalmip + solver time) | 0.3179 | 0.9472 | 0.3069 | 0.3374 |
 set size (%) set size (%) |
18.26 | 18.51 | 18.26 | 16.56 |
- aFor algorithms without PE constraint, a QP solver, Gurobi,32 is used instead of Mosek.
- Abbreviations: MPC, model predictive control; PE, persistently exciting.
Consider first algorithms (A) and (C) in Table 1. Although (C) uses a more flexible tube representation, there is negligible difference in overall computational time relative to (A). This is due to the use of a more efficient method of enforcing constraints on predicted tubes in (A) than (C), which introduces additional optimization variables to enforce these constraints. The more flexible tube representation employed in (C) provides a larger terminal set, as shown in Figure 2. Moreover, the formulation of (C) incorporates information on  in the constraints, and as a result, the terminal set increases in size over time as the parameter set
in the constraints, and as a result, the terminal set increases in size over time as the parameter set  shrinks. On the other hand, the homothetic tube MPC employed in (A) employs a terminal set that is computed offline and is not updated online.
shrinks. On the other hand, the homothetic tube MPC employed in (A) employs a terminal set that is computed offline and is not updated online.
Comparing algorithms (B) and (D) in Table 1, it can be seen that implementing the PE condition using an augmented cost function and linearized constraint (as in (D)) results in lower computation and faster parameter convergence than using a PE constraint with a fixed value of 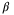 (as in (B)). Tuning the value of
(as in (B)). Tuning the value of 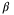 in algorithm (B) is challenging, since a value that is too small results in slow convergence whereas choosing
in algorithm (B) is challenging, since a value that is too small results in slow convergence whereas choosing 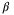 too large frequently causes the PE constraint to be infeasible. Moreover, whenever the PE constraint is infeasible in algorithm (B), the MPC optimization is solved a second time without the PE constraint, thus increasing computation.
too large frequently causes the PE constraint to be infeasible. Moreover, whenever the PE constraint is infeasible in algorithm (B), the MPC optimization is solved a second time without the PE constraint, thus increasing computation.
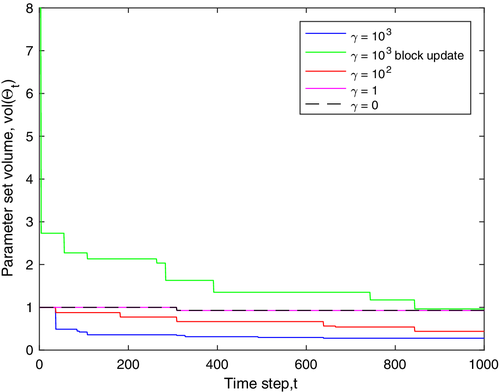
Figure 3 shows the effect of the weighting coefficient 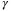 in the objective function (29) on the parameter set
in the objective function (29) on the parameter set 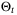 when the same initial conditions (x0 = [3, 4]⊤,
when the same initial conditions (x0 = [3, 4]⊤, 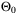 ,
, 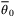 ) and disturbance sequences {w0,w1, …} are used. Larger values of
) and disturbance sequences {w0,w1, …} are used. Larger values of 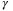 place greater weighting on
place greater weighting on 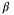 in the MPC cost (29), and thus on satisfaction of the PE condition (27). Therefore, increasing
in the MPC cost (29), and thus on satisfaction of the PE condition (27). Therefore, increasing 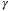 results in a faster convergence rate in the parameter set volume. When the same weighting coefficient
results in a faster convergence rate in the parameter set volume. When the same weighting coefficient 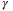 is used, performing the parameter set update periodically (as discussed in Remark 5) slows down the convergence rate of the parameter set, as shown by the green line. For this simulation, the parameter set update (online step 2 in Section 3.5) takes only 2% of the total computational time.
is used, performing the parameter set update periodically (as discussed in Remark 5) slows down the convergence rate of the parameter set, as shown by the green line. For this simulation, the parameter set update (online step 2 in Section 3.5) takes only 2% of the total computational time.
The relationship between weighting coefficient  and volume of parameter set
and volume of parameter set 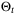 is shown in Figure 4. For values of
is shown in Figure 4. For values of 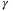 between 10−3 and 103, closed-loop simulations were performed with the same initial conditions, disturbance sequences, and initial nominal model and parameter set. The parameter set volume after 20 time-steps is shown. Figure 4 also shows that increasing
between 10−3 and 103, closed-loop simulations were performed with the same initial conditions, disturbance sequences, and initial nominal model and parameter set. The parameter set volume after 20 time-steps is shown. Figure 4 also shows that increasing 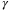 results in a faster parameter set convergence rate, in agreement with Figure 3.
results in a faster parameter set convergence rate, in agreement with Figure 3.

For the same set of simulations, Figure 5 shows the optimal value of 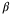 in (28) and (27) against
in (28) and (27) against 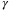 . From (29), it is expected that a larger
. From (29), it is expected that a larger 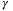 value will increase the influence of the term
value will increase the influence of the term 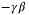 , thus pushing
, thus pushing 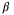 to be more positive. The left-hand figure shows the value of
to be more positive. The left-hand figure shows the value of  in the convexified constraint (28). As expected, the increase in
in the convexified constraint (28). As expected, the increase in 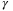 leads to a smooth increase in
leads to a smooth increase in 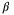 initially, but after a certain point, any further increase in the weighting factor
initially, but after a certain point, any further increase in the weighting factor 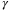 does not affect the calculated
does not affect the calculated 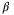 value. The right-hand figure shows the value of
value. The right-hand figure shows the value of 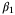 in the PE condition (27). The difference between
in the PE condition (27). The difference between 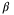 and
and 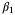 illustrates the conservativeness of the convexification proposed in Section 3.4. Note that this can be reduced by repeating steps (3) and (4) in the online part of the proposed algorithm, thus iteratively recomputing the reference sequences
illustrates the conservativeness of the convexification proposed in Section 3.4. Note that this can be reduced by repeating steps (3) and (4) in the online part of the proposed algorithm, thus iteratively recomputing the reference sequences 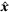 ,
, 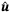 and reducing the conservativeness of linearization to any desired level. It is interesting to note that, although the optimal value of
and reducing the conservativeness of linearization to any desired level. It is interesting to note that, although the optimal value of 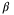 in (28) levels off at
in (28) levels off at 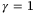 , the value of
, the value of 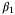 in the PE condition (27) increases monotonically between
in the PE condition (27) increases monotonically between 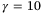 and
and 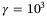 . The smaller
. The smaller 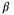 values observed with (27) also explain the lower rates of parameter convergence for small values of
values observed with (27) also explain the lower rates of parameter convergence for small values of 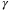 in Figure 4. In practice, it can be used as a guideline for the tuning of
in Figure 4. In practice, it can be used as a guideline for the tuning of 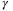 .
.
Table 2 illustrates the convergence of the estimated parameter set over a large number of time steps for the initial condition x0 = [2, 3]⊤ and a randomly generated disturbance sequence {w0,w1, … }. Here, 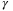 was chosen as 103 to speed up the convergence process. In agreement with Theorem 3,
was chosen as 103 to speed up the convergence process. In agreement with Theorem 3,  has shrunk to a small region around the true parameter value at t = 5000.
has shrunk to a small region around the true parameter value at t = 5000.
| Time step (t) | 0 | 1 | 5 | 50 | 100 | 500 | 1000 | 5000 |
|---|---|---|---|---|---|---|---|---|
 set size (%) set size (%) |
100 | 30.21 | 18.50 | 14.46 | 12.75 | 11.11 | 1.51 | 0.25 |
6.2 Relationship between PE coefficient and convergence rate
 ,
, 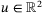 ,
, 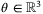 and
and
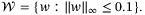
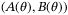 satisfy (4) with randomly generated Ai, Bi,
satisfy (4) with randomly generated Ai, Bi, 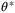 parameters and initial parameter set
parameters and initial parameter set 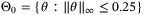 . In each case the estimated parameter sets
. In each case the estimated parameter sets 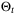 have fixed complexity, with face normals aligned with the coordinate axes in parameter space. A linear feedback law is applied, ut = Kxt, where K is a stabilizing gain. We use these systems to investigate the relationship between the coefficient
have fixed complexity, with face normals aligned with the coordinate axes in parameter space. A linear feedback law is applied, ut = Kxt, where K is a stabilizing gain. We use these systems to investigate the relationship between the coefficient 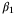 in the PE condition (27) and rate of convergence of the estimated parameter set.
in the PE condition (27) and rate of convergence of the estimated parameter set.Taking the window length in (27) to be Nu = 10, closed-loop trajectories were computed for 10 time steps and the parameter set 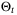 was updated according to (11). Simulations were performed for 500 different initial conditions, and the average value of
was updated according to (11). Simulations were performed for 500 different initial conditions, and the average value of 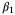 was computed for each initial condition using 100 random disturbance sequences {w0,w1, …}. Figure 6 illustrates the relationship between the average size of the identified parameter set
was computed for each initial condition using 100 random disturbance sequences {w0,w1, …}. Figure 6 illustrates the relationship between the average size of the identified parameter set 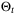 and the average value of
and the average value of 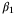 in the PE condition (27). Clearly, increasing
in the PE condition (27). Clearly, increasing 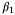 results in a smaller parameter set on average, and hence a faster rate of convergence of
results in a smaller parameter set on average, and hence a faster rate of convergence of 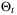 , which is consistent with the analysis of Section 5.2. The inner and outer radii shown in the figure on the left are the radii of the smallest and largest spheres, respectively, that contain and are contained within the parameter set estimate after 10 time steps. A similar trend can also be seen between the average volume of the parameter set
, which is consistent with the analysis of Section 5.2. The inner and outer radii shown in the figure on the left are the radii of the smallest and largest spheres, respectively, that contain and are contained within the parameter set estimate after 10 time steps. A similar trend can also be seen between the average volume of the parameter set 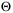 and the ensemble average value of
and the ensemble average value of 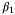 .
.
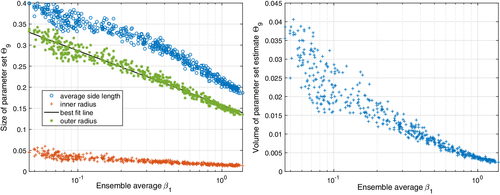
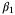 in the PE condition (27) with Nu = 10. The parameter set size and
in the PE condition (27) with Nu = 10. The parameter set size and 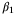 were computed for 500 different initial conditions. Left: mean side length and inner and outer radii of
were computed for 500 different initial conditions. Left: mean side length and inner and outer radii of 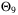 . Right: volume of
. Right: volume of 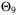
7 CONCLUSIONS
In this article, we propose an adaptive robust MPC algorithm that combines robust tube MPC and set membership identification. The MPC formulation employs a nominal performance index and guarantees robust constraint satisfaction, recursive feasibility and ISS. A convexified persistent excitation condition is included in the MPC objective via a weighting coefficient, and the relationship between this weight and the convergence rate of the estimated parameter set is investigated. For computational tractability, a fixed complexity polytope is used to approximate the estimated parameter set. The article proves that the parameter set will converge to the vector of system parameters with probability 1 despite this approximation. Conditions for convergence of the estimated parameter set are derived for the case of inexact disturbance bounds and noisy measurements. Future work will consider systems with stochastic model parameters and probabilistic constraints. Quantitative relationships between the convergence rate of the estimated parameter set and conditions for PE will be investigated further and methods of enforcing PE of the closed-loop system will be considered.



 and
and 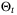 is defined by (
is defined by (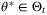 and
and 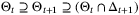 for all
for all 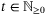 .
.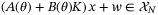 and (F + GK)x ≤ 1 for all
and (F + GK)x ≤ 1 for all 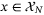 ,
, 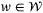 , and
, and 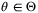 . Then (
. Then ( and
and 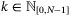 , and there exist matrices
, and there exist matrices 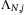 satisfying the conditions, for all
satisfying the conditions, for all 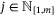
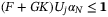
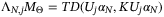
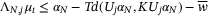
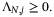
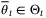 . However, subject to this constraint, alternative update laws for
. However, subject to this constraint, alternative update laws for 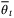 are possible; for example, a least mean squares estimate projected onto
are possible; for example, a least mean squares estimate projected onto 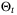 .
.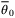 .
.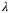 satisfying (
satisfying (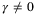 . However, if
. However, if 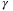 is replaced by a time-varying weight
is replaced by a time-varying weight 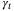 in the objective of problem
in the objective of problem 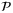 , then ISS can be guaranteed by setting
, then ISS can be guaranteed by setting 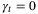 for all t ≥ t0, for some finite horizon t0.
for all t ≥ t0, for some finite horizon t0. and Assumptions
and Assumptions  such that
such that 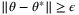 , for all
, for all 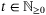 and any
and any 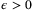 , we have
, we have
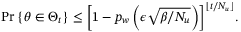
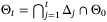 converges to
converges to 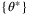 with probability 1.
with probability 1.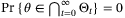 if
if  for some
for some 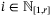 and
and 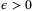 . Since
. Since 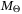 is assumed to be chosen so that
is assumed to be chosen so that 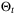 is compact for all
is compact for all 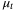 such that
such that 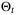 is nonempty, it follows that
is nonempty, it follows that 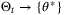 as t → ∞ with probability 1.
as t → ∞ with probability 1.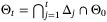 and Assumptions
and Assumptions 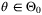 such that
such that  , for all
, for all 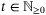 and any
and any 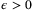 , we have
, we have
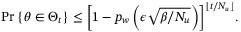
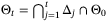 converges to
converges to 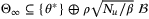 with probability 1.
with probability 1.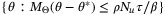 .
.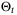 over time for a range of weights
over time for a range of weights 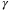 in the MPC objective function (
in the MPC objective function (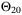 against weighting
against weighting  in the MPC objective function (
in the MPC objective function (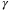 in the MPC objective function (
in the MPC objective function (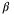 in the constraint (28). Right: computed value of the PE coefficient
in the constraint (28). Right: computed value of the PE coefficient 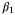 in (
in (