RESEARCH ARTICLE
H∞ model predictive control for constrained discrete-time piecewise affine systems
Peyman Sindareh Esfahani,
Jeffery Kurt Pieper,
Corresponding Author
Peyman Sindareh Esfahani
Department of Mechanical and Manufacturing Engineering, Schulich School of Engineering, University of Calgary, Calgary, AB, Canada
Correspondence
Peyman Sindareh Esfahani, Department of Mechanical and Manufacturing Engineering, Schulich School of Engineering, University of Calgary, Calgary, AB T2N 1N4, Canada.
Email: [email protected]
Search for more papers by this authorJeffery Kurt Pieper
Department of Mechanical and Manufacturing Engineering, Schulich School of Engineering, University of Calgary, Calgary, AB, Canada
Search for more papers by this authorPeyman Sindareh Esfahani,
Jeffery Kurt Pieper,
Corresponding Author
Peyman Sindareh Esfahani
Department of Mechanical and Manufacturing Engineering, Schulich School of Engineering, University of Calgary, Calgary, AB, Canada
Correspondence
Peyman Sindareh Esfahani, Department of Mechanical and Manufacturing Engineering, Schulich School of Engineering, University of Calgary, Calgary, AB T2N 1N4, Canada.
Email: [email protected]
Search for more papers by this authorJeffery Kurt Pieper
Department of Mechanical and Manufacturing Engineering, Schulich School of Engineering, University of Calgary, Calgary, AB, Canada
Search for more papers by this authorSummary
This paper investigates
stability analysis for piecewise affine (PWA) systems and specifically contributes a new
robust model predictive control strategy for PWA systems in the presence of constraints on the states and inputs and with l2 or norm-bounded disturbances. The proposed controller is based on piecewise quadratic Lyapunov functions. The problem of minimization of the cost function for model predictive control design is changed to minimization of the worst case of the cost function. Then, this objective is reduced to minimization of a supremum of the cost function subject to a terminal inequality by considering the induced l2-norm. Finally, the predictive controller design problem is turned into a linear matrix inequality feasibility exercise with constraints on the input signal and state variables. It is shown that the closed-loop system is asymptotically stable with guaranteed robust
performance. The validity of the proposed method is verified through 3 well-known examples of PWA systems. Simulation results are provided to show good convergence properties along with capability of the proposed controller to reject disturbances.
REFERENCES
- 1Cervantes I, Femat R, Leyva-Ramos J. Study of a class of hybrid-time systems. Chaos Solitons Fractals. 2007; 32(3): 1081-1095.
- 2Campos-Cantón E, Barajas-Ramirez JG, Solis-Perales G, Femat R. Multiscroll attractors by switching systems. Chaos Interdiscip J Nonlinear Sci. 2010; 20(1): 1-6.
10.1063/1.3314278 Google Scholar
- 3Bemporad A, Morari M. Control of systems integrating logic, dynamics, and constraints. Automatica. 1999; 35(3): 407-427.
- 4Bemporad A. Efficient conversion of mixed logical dynamical systems into an equivalent piecewise affine form. IEEE Trans Autom Control. 2004; 49(5): 832-838.
- 5Liberzon D. Switching in Systems and Control. Systems & Control: Foundations & Applications. Boston: Birkhauser; 2003.
10.1007/978-1-4612-0017-8 Google Scholar
- 6Skafidas E, Evans RJ, Savkin AV, Petersen IR. Stability results for switched controller systems. Automatica. 1999; 35(4): 553-564.
- 7Ferrari-Trecate G, Cuzzola FA, Mignone D, Morari M. Analysis of discrete-time piecewise affine and hybrid systems. Automatica. 2002; 38(12): 2139-2146.
- 8Lazar M, Heemels WP, Weiland S, Bemporad A. Stabilizing model predictive control of hybrid systems. IEEE Trans Autom Control. 2006; 51(11): 1813-1818.
- 9Lazar M, Heemels WP. Predictive control of hybrid systems: input-to-state stability results for sub-optimal solutions. Automatica. 2009; 45(1): 180-185.
- 10Johansson M. Piecewise linear control systems [PhD Thesis]. Sweden: Department of Automatic Control, Lund Institute of Technology; 1999.
- 11Imura JI, van der Schaft A. Characterization of well-posedness of piecewise-linear systems. IEEE Trans Autom Control. 2000; 45(9): 1600-1619.
- 12Bemporad A, Ferrari-Trecate G, Morari M. Observability and controllability of piecewise affine and hybrid systems. IEEE Trans Autom Control. 2000; 45(10): 1864-1876.
- 13Johansson M, Rantzer A. Computation of piecewise quadratic Lyapunov functions for hybrid systems. IEEE Trans Autom Control. 1998; 43(4): 555-559.
- 14Rantzer A, Johansson M. Piecewise linear quadratic optimal control. IEEE Trans Autom Control. 2000; 45(4): 629-637.
- 15Feng G. Controller design and analysis of uncertain piecewise-linear systems. IEEE Trans Circuits Syst I Fundam Theory Appl. 2002; 49(2): 224-232.
10.1109/81.983869 Google Scholar
- 16Zhu Y, Li DQ, Feng G. H∞ controller synthesis of uncertain piecewise continuous-time linear systems. IEE Proc-Control Theory Appl. 2005; 152(5): 513-519.
- 17Zhang J, Tang W. Output feedback optimal guaranteed cost control of uncertain piecewise linear systems. Int J Robust Nonlinear Control. 2009; 19(5): 569-590.
- 18Zhang J, Tang W. Output feedback H∞ control for uncertain piecewise linear systems. J Dyn Control Syst. 2008; 14(1): 121-144.
- 19Johansson M. Piecewise Linear Control Systems. New York: Springer; 2003.
10.1007/3-540-36801-9 Google Scholar
- 20Rodrigues L, Hassibi A, How JP. Output feedback controller synthesis for piecewise-affine systems with multiple equilibria. Paper presented at: Proceedings of the American Control Conference, Vol. 3; IEEE; 2000; Hyatt Regency Hotel Chicago, Illinois United States.
- 21Hassibi A, Boyd S. Quadratic stabilization and control of piecewise-linear systems. Paper presented at: Proceedings of the American Control Conference, Vol. 6; IEEE; June 21, 1998; Philadelphia, Pennsylvania USA.
- 22Pettersson S, Lennartson B. Hybrid system stability and robustness verification using linear matrix inequalities. Int J Control. 2002; 75(16-17): 1335-1355.
- 23Lin H, Antsaklis PJ. Switching stabilizability for continuous-time uncertain switched linear systems. IEEE Trans Autom Control. 2007; 52(4): 633-646.
- 24Feng G. Stability analysis of piecewise discrete-time linear systems. IEEE Trans Autom Control. 2002; 47(7): 1108-1112.
- 25Mirzazad-Barijough S, Lee JW. Robust stability and performance analysis of discrete-time piecewise affine systems with disturbances. Paper presented at: IEEE 51st IEEE Conference on Decision and Control (CDC), IEEE; December 10, 2012; Grand Wailea, Maui, Hawaii.
- 26Mirzazad-Barijough S, Lee JW. Stability and transient performance of discrete-time piecewise affine systems. IEEE Trans Autom Control. 2012; 57(4): 936-949.
- 27Gao Y, Liu Z, Chen H. Robust H∞ control for constrained discrete-time piecewise affine systems with time-varying parametric uncertainties. IET Control Theory Appl. 2009; 3(8): 1132-1144.
- 28Qiu J, Zhang T, Feng G, Liu H. Piecewise affine model-based H∞ static output feedback control of constrained non-linear processes. IET Control Theory Appl. 2010; 4(11): 2315-2330.
- 29Chen Y, Zhou Q, Fei S. Robust stabilization and l 2-gain control of uncertain discrete-time constrained piecewise-affine systems. Nonlinear Dyn. 2014; 75(1-2): 127-140.
- 30Qiu J, Feng G, Gao H. Approaches to robust
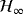static output feedback control of discrete-time piecewise-affine systems with norm-bounded uncertainties. Int J Robust Nonlinear Control. 2011; 21(7): 790-814.
- 31Sindareh-Esfahani P, Tabatabaei SS, Pieper JK. Model predictive control of a heat recovery steam generator during cold start-up operation using piecewise linear models. Appl Therm Eng. 2017; 119: 516-529.
- 32Sindareh-Esfahani P, Habibi-Siyahposh E, Saffar-Avval M, Ghaffari A, Bakhtiari-Nejad F. Cold start-up condition model for heat recovery steam generators. Appl Therm Eng. 2014; 65(1): 502-512.
- 33Ghaffari A, Bahmaie B, Nazari M. A mixed radiotherapy and chemotherapy model for treatment of cancer with metastasis. Math Methods Appl Sci. 2016; 39(15): 4603-4617.
- 34Sindareh-Esfahani P, Ghaffari A, Ahmadi P. Thermodynamic modeling based optimization for thermal systems in heat recovery steam generator during cold start-up operation. Appl Therm Eng. 2014; 69(1): 286-296.
- 35Kothare MV, Balakrishnan V, Morari M. Robust constrained model predictive control using linear matrix inequalities. Automatica. 1996; 32(10): 1361-1379.
- 36Mayne DQ, Raković SV, Findeisen R, Allgöwer F. Robust output feedback model predictive control of constrained linear systems. Automatica. 2006; 42(7): 1217-1222.
- 37Song Y, Wang Z, Ding D, Wei G. Robust model predictive control under redundant channel transmission with applications in networked DC motor systems. Int J Robust Nonlinear Control. 2016; 26(18): 3937-3957.
- 38Shi T, Wu ZG, Su H. Improved dynamic output feedback RMPC for linear uncertain systems with input constraints. Int J Robust Nonlinear Control. 2015; 26(12): 2729-2742.
- 39Sindareh-Esfahani P, Pieper JK. Online robust model predictive control for linear fractional transformation systems using linear matrix inequalities. Int J Mech Aerosp Ind Mechatronic Manuf Eng. 2017; 11(5): 1025-1031.
- 40Chen H, Scherer CW. An LMI based model predictive control scheme with guaranteed/spl Hscr//sub/spl infin//performance and its application to active suspension. Paper presented at: Proceedings of the 2004 American Control Conference,Vol. 2; IEEE; June 30, 2004; Boston Sheraton Hotel Boston, Massachusetts, United States.
- 41Benallouch M, Schutz G, Fiorelli D, Boutayeb M. H∞ model predictive control for discrete-time switched linear systems with application to drinking water supply network. J Process Control. 2014; 24(6): 924-938.
- 42Yang W, Gao J, Feng G, Zhang T. An optimal approach to output-feedback robust model predictive control of LPV systems with disturbances. Int J Robust Nonlinear Control. 2016; 26(15): 3253-3273.
- 43Khani F, Haeri M. Robust model predictive control of nonlinear processes represented by Wiener or Hammerstein models. Chem Eng Sci. 2015; 129: 223-231.
- 44Ghaffari V, Naghavi SV, Safavi AA. Robust model predictive control of a class of uncertain nonlinear systems with application to typical CSTR problems. J Process Control. 2013; 23(4): 493-499.
- 45Razi M, Haeri M. Design of an RMPC with a time-varying terminal constraint set for tracking problem. Int J Robust Nonlinear Control. 2016; 26(12): 2623-2642.
- 46Zou Y, Li S. Robust model predictive control for piecewise affine systems. Circuits, Systems. Signal Process. 2007; 26(3): 393-406.
- 47Thomas J. Robust predictive control for constrained uncertain piecewise linear systems using linear matrix inequalities. IFAC Proc Vol. 2014; 47(1): 165-170.
10.3182/20140313-3-IN-3024.00149 Google Scholar
- 48Zou Y, Li S. Robust constrained model predictive control of piecewise linear systems with bounded additive disturbances. Paper presented at: Proceedings of the 48th IEEE Conference on Decision and Control, 2009 held jointly with the 2009 28th Chinese Control Conference. CDC/CCC 2009, IEEE; December 15, 2009; Pudong Shangri-La, Shanghai International Converntion Center Shanghai, China.
- 49Orukpe PE, Jaimoukha IM, El-Zobaidi HM. Model predictive control based on mixed H2/H∞ control approach. Paper presented at: Proceedings of the 2007 American Control Conference; 2007; New York City, USA.
- 50Lee SM, Park JH. Robust H∞ model predictive control for uncertain systems using relaxation matrices. Int J Control. 2008; 81(4): 641-650.
- 51de Oliveira MC, Bernussou J, Geromel JC. A new discrete-time robust stability condition. Syst Control Lett. 1999; 37(4): 261-265.
- 52Cuzzola FA, Geromel JC, Morari M. An improved approach for constrained robust model predictive control. Automatica. 2002; 38(7): 1183-1189.
- 53Ojaghi P, Bigdeli N, Rahmani M. An LMI approach to robust model predictive control of nonlinear systems with state-dependent uncertainties. J Process Control. 2016; 47: 1-10.
- 54Boyd SP, El Ghaoui L, Feron E, Balakrishnan V. Linear Matrix Inequalities in System and Control Theory. Philadelphia: Society for Industrial and Applied Mathematics; 1994.
10.1137/1.9781611970777 Google Scholar
- 55Gao Y, Liu Z, Chen H. Robust observer-based control for uncertain discrete-time piecewise affine systems. J Control Theory Appl. 2012; 10(2): 236-243.
10.1007/s11768-012-9145-7 Google Scholar
- 56Feng G, Zhang T. Output tracking of discrete-time piecewise linear systems via error feedback. Paper presented at: 6th World Congress on Intelligent Control and Automation, IEEE; 2006; Dalian Univ. of Technology Dalian, China.
- 57Henson MA, Seborg DE. Nonlinear Process Control. Upper Saddle River, New Jersey: Prentice Hall PTR; 1997.
- 58Rodrigues L, Boyd S. Piecewise-affine state feedback for piecewise-affine slab systems using convex optimization. Syst Control Lett. 2005; 54(9): 835-853.
