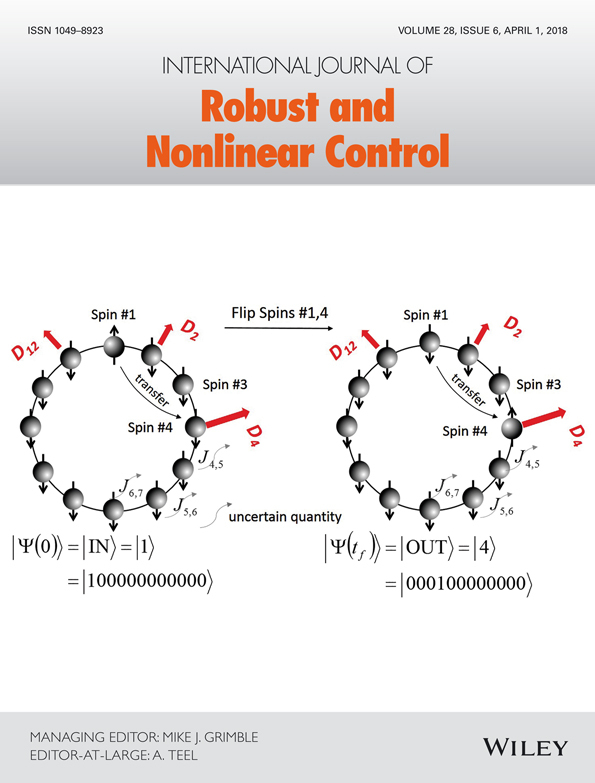
Finite-time stabilization of stochastic low-order nonlinear systems with FT-SISS inverse dynamics
Meng-Meng Jiang
Institute of Automation, Qufu Normal University, Qufu, China
Search for more papers by this authorCorresponding Author
Xue-Jun Xie
Institute of Automation, Qufu Normal University, Qufu, China
Correspondence
Xue-Jun Xie, Institute of Automation, Qufu Normal University, Qufu 273165, China.
Email: [email protected]
Search for more papers by this authorMeng-Meng Jiang
Institute of Automation, Qufu Normal University, Qufu, China
Search for more papers by this authorCorresponding Author
Xue-Jun Xie
Institute of Automation, Qufu Normal University, Qufu, China
Correspondence
Xue-Jun Xie, Institute of Automation, Qufu Normal University, Qufu 273165, China.
Email: [email protected]
Search for more papers by this authorSummary
This paper studies finite-time stabilization problem for stochastic low-order nonlinear systems with stochastic inverse dynamics. By characterizing unmeasured stochastic inverse dynamics with finite-time stochastic input-to-state stability, combining the Lyapunov function and adding a power integrator technique, and using the stochastic finite-time stability theory, a state feedback controller is designed to guarantee global finite-time stability in probability of stochastic low-order nonlinear systems with finite-time stochastic input-to-state stability inverse dynamics.
REFERENCES
- 1Yin JL, Khoo SY, Man ZH, Yu XH. Finite-time stability and instability of stochastic nonlinear systems. Automatica. 2011; 47(12): 2671-2677.
- 2Khoo SY, Yin JL, Man ZH, Yu XH. Finite-time stabilization of stochastic nonlinear systems in strict-feedback form. Automatica. 2013; 49(5): 1403-1410.
- 3Yin JL, Khoo SY. Continuous finite-time state feedback stabilizers for some nonlinear stochastic systems. Int J Robust Nonlinear Control. 2015; 25(11): 1581-1600.
- 4Gao FZ, Yuan FS. Finite-time stabilization of stochastic nonholonomic systems and its application to mobile robot. Abstr Appl Anal. 2012; Article ID 361269.
10.1155/2012/361269 Google Scholar
- 5Hou MZ, Deng ZQ, Duan GR. Finite-time
 filtering for nonlinear stochastic systems. Int J Syst Sci. 2016; 47(12): 2945-2953.
filtering for nonlinear stochastic systems. Int J Syst Sci. 2016; 47(12): 2945-2953.
- 6Luan X, Liu F, Shi P. Finite-time filtering for nonlinear stochastic systems with partially known transition jump rates. IET Control Theory Appl. 2010; 4(5): 735-745.
- 7Wang H, Zhu QX. Finite-time stabilization of high-order stochastic nonlinear systems in strict-feedback form. Automatica. 2015; 54(4): 284-291.
- 8Lan QX, Li SH, Khoo SY, Shi P. Finite-time stabilization for a class of stochastic nonlinear systems by output feedback. Int J Control. 2015; 88(3): 494-506.
- 9Zhao Y, Zhao P. Global finite-time stabilization by state-feedback for a class of stochastic nonlinear systems. J Syst Sci Math Sci. 2014; 34(12): 1604-1612.
- 10Huang SP, Xiang ZR. Finite-time stabilization of a class of switched stochastic nonlinear systems under arbitrary switching. Int J Robust Nonlinear Control. 2016; 26(10): 2136-2152.
- 11Tsinias J. Stochastic ISS and applications to global feedback stabilization. Int J Control. 1998; 71(5): 907-930.
- 12Tang C, Basar T. Stochastic stability of singularly perturbed nonlinear systems. Paper presented at: Proceedings of the 40th IEEE Conference Design Control; 2001; Orlando, FL.
- 13Liu SJ, Zhang JF, Jiang ZP. Decentralized adaptive output-feedback stabilization for large-scale stochastic nonlinear systems. Automatica. 2007; 43(2): 238-251.
- 14Liu SJ, Zhang JF, Jiang ZP. A notion of stochastic input-to-state stability and its application to stability of cascaded stochastic nonlinear systems. Acta Math Appl Sinica. 2008; 24(1): 141-156.
- 15Liu L, Xie XJ. State-feedback stabilization for stochastic high-order nonlinear systems with SISS inverse dynamics. Asian J Control. 2012; 14(1): 207-216.
- 16Liu L, Yin S, Gao HJ, Alsaadi F, Hayat T. Adaptive partial-state feedback control for stochastic high-order nonlinear systems with stochastic input-to-state stable inverse dynamics. Automatica. 2015; 51(1): 285-291.
- 17Zhao P, Feng W, Zhao Y, Kang Y. Finite-time stochastic input-to-state stability of switched stochastic nonlinear systems. Appl Math Comput. 2015; 268(10): 1038-1054.
- 18Qian CJ, Lin W. A continuous feedback approach to global strong stabilization of nonlinear systems. IEEE Trans Autom Control. 2001; 46(7): 1061-1079.
- 19Lin W, Qian CJ. Adaptive control of nonlinearly parameterized systems: the smooth feedback case. IEEE Trans Autom Control. 2002; 47(8): 1249-1266.
- 20Lei H, Lin W. Reduced-order observer, homogeneous domination and nonsmooth output feedback stabilization of high-order stochastic nonlinear systems with stochastic inverse dynamics. Paper presented at: 7th World Congress on Intelligent Control and Automation; 2008; Chongqing, China.
- 21Zhang XH, Zhang KM, Xie XJ. Finite-time stabilization of stochastic high-order nonlinear systems. Asian J Control. 2016; 18(6): 2244-2255.
- 22Yu X, Xie XJ. Output feedback regulation of stochastic nonlinear systems with stochastic iISS inverse dynamics. IEEE Trans Autom Control. 2010; 55(2): 304-320.
- 23Yu X, Xie XJ, Duan N. Small-gain control method for stochastic nonlinear systems with stochastic iISS inverse dynamics. Automatica. 2010; 46(11): 1790-1798.
- 24Duan N, Xie XJ, Yu X. State feedback stabilization of stochastic nonlinear systems with SiISS inverse dynamics. Int J Robust Nonlinear Control. 2011; 21(16): 1903-1919.
- 25Xie XJ, Duan N, Yu X. State-feedback control of high-order stochastic nonlinear systems with SiISS inverse dynamics. IEEE Trans Autom Control. 2011; 56(8): 1921-1926.
- 26Ito H, Nishimura Y. Stability of stochastic nonlinear systems in cascade with not necessarily unbound decay rates. Automatica. 2015; 62(1): 51-64.
- 27Ito H, Nishimura Y. An iISS framework for stochastic robustness of interconnected nonlinear systems. IEEE Trans Autom Control. 2016; 61(6): 1508-1523.