Recurrence relations for the evaluation of electron repulsion integrals over spherical Gaussian functions

Recurrence relations are derived for the evaluation of two-electron repulsion integrals (ERIs) over Hermite and spherical Gaussian functions. Through such relations, a generic ERI or ERI derivative may be reduced to “basic” integrals, i.e., true and auxiliary integrals involving only zero angular momentum functions. Extensive use is made of differential operators, in particular, of the spherical tensor gradient 𝒴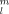(∇). Spherical Gaussians, being nonseparable in the x, y, and z coordinates, were not included in previous formulations. The advantages of using spherical Gaussians instead of Cartesian or Hermite Gaussians are briefly discussed. © 1993 John Wiley & Sons, Inc.