Atomic integrals containing r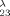 r
r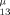 r
r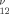 with λ, μ, ν ≥ −2
with λ, μ, ν ≥ −2
A. Lüuchow
Institut für Physikalische Chemie und Elektrochemie, Heinrich-Heine-Universität Düsseldorf, D-4000 Düsseldorf 1, Germany
Search for more papers by this authorH. Kleindienst
Institut für Physikalische Chemie und Elektrochemie, Heinrich-Heine-Universität Düsseldorf, D-4000 Düsseldorf 1, Germany
Search for more papers by this authorA. Lüuchow
Institut für Physikalische Chemie und Elektrochemie, Heinrich-Heine-Universität Düsseldorf, D-4000 Düsseldorf 1, Germany
Search for more papers by this authorH. Kleindienst
Institut für Physikalische Chemie und Elektrochemie, Heinrich-Heine-Universität Düsseldorf, D-4000 Düsseldorf 1, Germany
Search for more papers by this authorAbstract
In this paper, the efficient evaluation of the atomic integrals I =∫r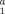 r
r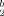 r
r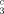 r
r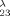 r
r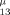 r
r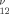 e−αr1−βr2−γr3dτ with one or two factors r
e−αr1−βr2−γr3dτ with one or two factors r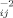 is described. These integrals are necessary for a lower-bound calculation for Li-like systems using the method of variance minimization or Temple's formula. © 1993 John Wiley & Sons, Inc.
is described. These integrals are necessary for a lower-bound calculation for Li-like systems using the method of variance minimization or Temple's formula. © 1993 John Wiley & Sons, Inc.
Bibliography
- 1 A. Lüchow and H. Kleindienst, Int. J. Quantum Chem. 41, 719 (1992).
- 2 H. Kleindienst and W. Altmann, Int. J. Quantum Chem. 10, 873 (1976).
- 3 H. Kleindienst and W. Müller, Theor. Chim. Acta 56, 183 (1980).
- 4
H. Kleindienst and
R. Emrich,
Numerical Treatment of Eigenvalue Problems,
Vol. 5
p. 131,
in J. Albrecht et al., Eds.,
Int. Series of Num. Math.,
Vol. 96
(Birkhäuser Verlag, Basel,
1991).
10.1007/978-3-0348-6332-2_10 Google Scholar
- 5 A. Weinstein and W. Stenger, Methods of Intermediate Problems for Eigenvalues (Academic Press, New York, 1972), p. 103.
- 6 A. A. Frost, Theor. Chim. Acta 1, 36 (1962).
- 7 S. Larsson, Phys. Rev. 169, 49 (1968).
- 8 F. W. King and M. P. Bergsbaken, J. Chem. Phys. 93, 2570 (1990).
- 9 D. K. McKenzie and G. W. F. Drake, Phys. Rev. A 44, R6973 (1991).
- 10 H. Kleindienst and A. Lüchow, Int. J. Quantum Chem. 45, 87 (1993).
- 11 J. F. Perkins, J. Chem. Phys. 48, 1985 (1968).
- 12 A. Lüchow, Diploma Thesis, Eq. (3.108), Düsseldorf (1990).
- 13 F. W. King, Phys. Rev. 44, 7108 (1991).
- 14 R. A. Sack, J. Math. Phys. 5, 245, Eq. (19) (1964).
- 15 E. O. Steinborn and E. Filter, Theor. Chim. Acta 38, 261 (1975).
- 16 G. Pauli and H. Kleindienst, Theor. Chim. Acta (Berl.) 64, 481 (1984).
- 17 H. James and A. Coolidge, Phys. Rev. 49, 694 (1936).
- 18 D. Levin, Int. J. Comput. Math. B3, 371 (1973).
- 19 I. S. Gradshteyn and I. M. Ryzhik, Table of Integrals, Series and Products (Academic Press, New York, 1980).
- 20
W. Gröbner and
N. Hofreiter,
Integraltafel
(Springer-Verlag, Vienna,
1966),
Vol. II.
10.1007/978-3-7091-3341-5 Google Scholar
- 21
P. Wynn,
Proc. Camb. Philos. Soc.
52, 663
(1956).
10.1017/S030500410003173X Google Scholar
- 22
P. Wynn,
Math. Tables Aids Comput.
10, 91
(1956).
10.2307/2002183 Google Scholar
- 23 C. Brezinski, C.R. Acad. Sci. Paris Ser. A 273, 727 (1971).
- 24 D. A. Smith and W. F. Ford, SIAM J. Numer. Anal. 16, 223 (1979).
- 25
E. J. Weniger,
Comput. Phys. Rep.
10, 189
(1989).
10.1016/0167-7977(89)90011-7 Google Scholar
- 26 E. J. Weniger, Comput. Phys. Commun. 64, 19 (1991).
- 27 C. Brezinski and M. Redivo Zaglia, Extrapolation Methods: Theory and Practice (North-Holland, Amsterdam, 1991).
- 28 Y. Öhrn and J. Nordling, J. Chem. Phys. 39, 1864 (1963).
- 29 R. Bhattacharya, D. Roy, and S. Bhowmick, Comput. Phys. Commun. 55, 297 (1989).
- 30 K. Knopp, Infinite Sequences and Series (Dover, New York, 1956).
- 31 C. de Boor, Mathematical Software, J. R. Rice, Ed. (Academic Press, New York, 1971).
- 32 M. Abramowitz and I. A. Stegun, Handbook of Mathematical Functions, (Dover Publications, New York, 1972), Eqs. (6.5.2), (6.3.2), and (6.3.4).
- 33 E. R. Hansen, A Table of Series and Products (Prentice-Hall, Englewood Cliffs, NJ, 1975), p. 115, Eq. 6.1.193.
- 34
K. Knopp,
Theorie und Anwendung der unendlichen Reihen
(Springer-Verlag, Berlin,
1964).
10.1007/978-3-642-49655-4 Google Scholar




