1 INTRODUCTION

Many researchers have investigated using the paramagnetic relaxivity effect of oxygen on longitudinal relaxation rate R1 (1/T1) as a means of inferring oxygenation levels. For example, measurements of R1 have been used to infer oxygen levels in vitreous fluid as a noninvasive alternative to the highly invasive oxygen electrodes used to measure retinal hypoxia,^1-3 bladder urine,⁴ and urine in the renal pelvis to create a non-invasive detection of renal dysfunction,⁵ and cerebrospinal fluid.^{4, 6} Additionally, measuring changes in R1 following the inspiration of increased fractions of oxygen is the basis for oxygen-enhanced MRI techniques,^7-9 which are used to study a range of conditions from tumor hypoxia^{8, 10, 11} to lung disease.^{12, 13}

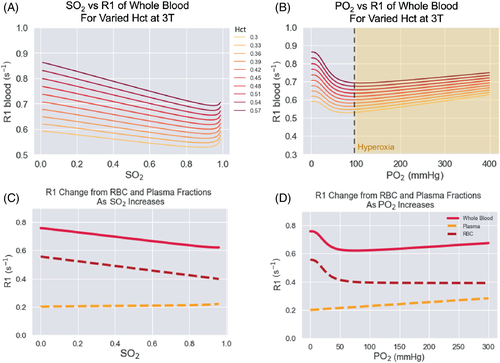
The linear relationship between the partial pressure of oxygen (PO₂) in a material and the resulting longitudinal relaxation rate (R1) has been measured in phantoms^{2-4, 6, 14} and bodily fluids such as vitreous fluid.² The relationship between R1 and PO₂ has been modeled as for a paramagnetic contrast agent, R1_Ox = R1₀ + r1_Ox*C, where R1_Ox is the relaxation rate in the solution with oxygen added, R1₀ is the relaxation rate in the solution without oxygen, C is the concentration of oxygen added, and r1_Ox is the relaxivity of oxygen in that solution, which is dependent on the magnetic field and temperature.¹⁵ Although this linear relationship has been demonstrated in phantoms and bodily fluids, studies on blood and tissues have sometimes reported so-called ”contradictory” R1 changes, where either no change or a negative change in R1 is observed.^{16, 17} It has been hypothesized that the source of this contradictory R1 change is paramagnetic deoxyhemoglobin since there is a positive linear relationship between R1 and deoxyhemoglobin concentration, i.e., an inverse correlation with blood oxygen saturation.¹⁸ The blood oxygen saturation, denoted by ‘SO₂’, is a measure of how much hemoglobin is currently bound to oxygen compared to how much hemoglobin remains unbound. In contrast, the partial pressure of oxygen (PO₂) in blood is a measure of the dissolved oxygen in the plasma.

To estimate changes in blood R1 following hyperoxia, Bluemke et al.¹⁹ created a general model to estimate the R1 of blood, accounting for hematocrit, oxygen saturation (SO₂), the partial pressure of oxygen (PO₂), and magnetic field strength under both normal physiological and hyperoxic conditions. That model showed that there are two competing effects on blood R1 that arise from increasing oxygen levels (paramagnetic oxygen and paramagnetic deoxyhemoglobin) and that the effect on R1 due to deoxyhemoglobin dominates at SO₂ levels below 99%, thus inducing a negative ΔR1 in venous blood after breathing 100% oxygen. While this model does explain the negative ΔR1 measured by Vatnehol et al. in venous blood during oxygen delivery experiment,¹⁶ it is not directly applicable to applications such as placental and tumor OE-MRI research where image voxels contain non-vascular tissue. In a tissue voxel, changing deoxyhemoglobin levels will only affect the portion of the voxel that is occupied by blood, and the R1 change of the tissue will dominate the remaining voxel volume. Therefore, in order to estimate the expected change in R1 of a tissue voxel, the blood model¹⁹ must be extended to contain a tissue compartment.

In this paper, we present a three-compartment model for estimating the changes in R1 that could be expected in healthy, hypoxic, and necrotic tissues depending on field strength, blood oxygen saturation, blood volume, hematocrit, oxygen extraction fraction, and change in partial pressure of oxygen. Since modeling tissue oxygen diffusion and consumption is a broad, active research area with many different approaches, this model has been designed to make it possible for a researcher to easily substitute their preferred model for tissue oxygen diffusion and consumption and tailor this model to their tissue of interest. For this paper, the model incorporates the classic Krogh tissue cylinder model for oxygen diffusion and the commonly used Michaelis–Menten equation for oxygen consumption. Last, we demonstrate the use of this model for estimating the expected R1 changes in tissues from breathing increased levels of oxygen and compare the R1 estimations with literature empirical measurements from oxygen-enhanced MRI research.^{8, 10, 11, 20, 21}

2 THEORY

2.1 Model background and overview

There have been two previous attempts at modeling the changes in tissue R1 following increased oxygen: both arise from the research field of OE-MRI.^{22, 23} In 2013, Holliday²² used a two-compartment model of blood to estimate ΔR1 in a capillary given a change in capillary PO₂ (Equation 1) and used a Krogh tissue cylinder model to estimate the corresponding tissue ΔPO₂ (ΔPO_2T), allowing the ΔR1 in tissue to be calculated by Equation (2).

$$$$ \Delta R{1}_{capillary}=\Delta P{O}_2\ast r{1}_{Ox}+\Delta \left(1-S{O}_2\right)\ast r{1}_{dHb} $$$$ (1)

$$$$ \Delta R{1}_{t\mathrm{i}s}=\Delta P{O}_{2\ tis}\ast r{1}_{Ox}. $$$$ (2)

Holliday used the r1_dHb at 1.5T reported by Blockley et al. (0.11 s⁻¹).¹⁸ The main limitation of Holliday's approach is that the resulting model contains many independently adjustable variables, such as the blood flow velocity, oxygen consumption rate, vessel geometry, and length of the capillary. In practice, these variables are often impossible to measure in tissues.

In 2018, Kindvall²³ proposed a much simpler equation to estimate the expected R1 change in pulmonary OE-MRI, in which the total ΔR1 is separated into the expected ΔR1 of the arterial blood (ΔR1_B,A), venous blood (ΔR1_B,V), and tissue ΔR1_T, and divided by 3 to yield an average ΔR1:

$$$$ \Delta R{1}_{tis}=\frac{\Delta R{1}_{B,A}+\Delta R{1}_{B,V}+\Delta R{1}_T}{3\ }. $$$$ (3)

Kindvall then used empirical measurements from previous experiments to estimate ΔR1 at a set magnetic field strength (4.7T): the ΔR1_B,A and ΔR1_T were set to be the same values (0.2 s⁻¹), and ΔR1_B,V was estimated to be −0.05 s⁻¹ based on the relaxivity of deoxyhemoglobin (r1_dHb) reported by Silvennoinen et al. (0.35 s⁻¹) and a rough estimate of the expected change in venous deoxyhemoglobin levels.²⁴ The main insight provided by Kindvall's approach was the benefit of separating the R1 changes in arterial blood and venous blood to observe the negative ΔR1 induced in deoxygenated blood, as opposed to Holliday's approach of estimating the ΔR1 of the capillary blood. However, the division by 3 assumes a 66% blood volume fraction in the voxel, which is too high for most tissue voxels.

Last, some substantial limitations to both of these approaches are: (A) the equations used to calculate the blood ΔR1 were of unknown accuracy and were not compared with literature values, (B) they did not take into account the blood hematocrit levels, and (C) the equations were not adjustable for magnetic field strength, which has a considerable effect on the relaxivity of oxygen.¹⁵

Therefore, we propose a new three-compartment model that calculates the expected ΔR1 of the arterial blood (ΔR1_B,A), venous blood (ΔR1_B,V), and tissue ΔR1_T as separate compartments, and, following Holliday, uses a Krogh tissue cylinder model to estimate the corresponding tissue ΔPO₂ (ΔPO_2T). The model takes into account the magnetic field strength (B0), blood SO₂, blood volume fraction (BV), hematocrit (Hct), oxygen extraction fraction of the tissue (OEF), and changes in PO₂ in both the blood and tissue. Last, the model uses the blood volume fraction to calculate the resulting ΔR1 of the voxel (ΔR1_voxel).

An overview of the model is illustrated in Figure 1. The model can be conceptually separated into four steps:

• Step 1. Calculate PO₂ along the capillary. The ΔR1_B,V and ΔR1_T and ΔR1_B,A are all related by a calculation of the SO₂ or PO₂ along the capillary length, which is determined by the arterial PO₂ (PaO₂) and the OEF of the tissue.
• Step 2. Calculate ΔPO₂ of each compartment. Knowing the PO₂ along the capillary allows the ΔPO₂ from oxygen administration to be calculated in the blood and tissue compartments, using the Krogh tissue cylinder to model the oxygen diffusion into the tissue, and the set OEF is related to the tissue oxygen consumption rate. The Krogh tissue cylinder radius is calculated from the set blood volume.
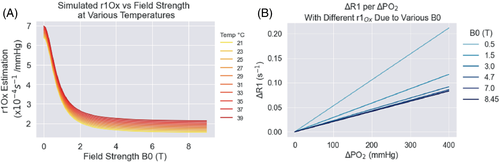
• Step 3. Calculate ΔR1 of each compartment. Knowing the ΔPO₂ in each compartment allows: (A) the ΔR1_T to be calculated using the relaxivity of oxygen (r1_Ox) as a function of the magnetic field, using the equation for r1_Ox by Bluemke et al.¹⁵; and (B) the ΔR1 of each blood compartment to be calculated using the Blood R1 model published by Bluemke et al.¹⁹
• Step 4. Calculate ΔR1 of the voxel. Once the ΔR1 in each compartment is calculated, the set blood volume fraction (BV) is used to calculate the resulting ΔR1 of the voxel (ΔR1_voxel).

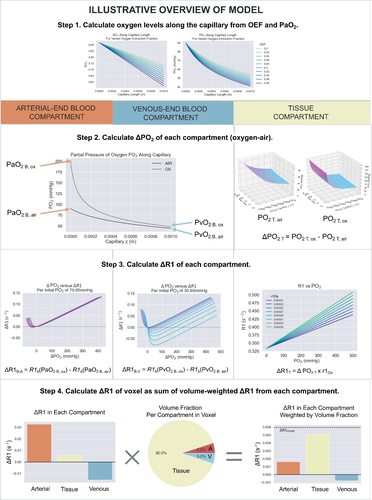
The theory and reasoning behind each part of this model are provided in the following sections. The model has been provided as a public code repository, and a graphical overview of the inputs and outputs of each function created to implement this model is provided in Figure 1. This model was created as a set of Python functions, the overview of which is provided in Figure 2.

2.4 Step 3. Calculating ΔR1 in the three compartments

2.4.1 Blood compartments

The ΔR1 induced from supplemental oxygen in the arterial (ΔR1_B,A) and venous (ΔR1_B,V) blood compartments can both be calculated from the following equation

$$$$ \Delta R{1}_B=R{1}_b\left(P{O}_{2, ox}\right)-R{1}_b\left(P{O}_{2, air}\right) $$$$ (17)

where R1_b(PO₂) is the general equation for calculating the R1 of blood by Bluemke et al.¹⁹ (shown in Figure 3):

$$$$ {\displaystyle \begin{array}{cc}R{1}_b\left(P{O}_2\right)& ={f}_e\left(R{1}_{eox}+r{1}_{dHb}\left[ Hb\right]\left(1-\frac{P{O_2}^n}{P{O_2}^n+P{50}^n}\right)\right)\\ {}& \kern1em +\left(1-{f}_e\right)\left(R{1}_p+r{1}_{pOx}P{O}_2\right)\end{array}} $$$$ (18)

where R1_b is the relaxation rate of whole blood, R1_eox is the relaxation rate of erythrocytes when SO₂ = 100%, [Hb] is the mean corpuscular hemoglobin concentration (5.15 mmol Hb tetramer/L plasma), r1_dHb is the molar relaxivity of deoxyhemoglobin (in s⁻¹ L plasma in erythrocyte/mmol Hb tetramer), n is the Hill exponent for hemoglobin (typically 2.7),³⁰ R1_p is the longitudinal relaxation rate of plasma (s⁻¹), and r1_pOx is the relaxivity of dissolved oxygen in the plasma in s⁻¹ mmHg⁻¹ oxygen. The variable f_e is the fraction of water in whole blood that resides in erythrocytes (0–1), which is described by the equation:

$$$$ {f}_e(Hct)=\frac{W_{RBC} Hct}{W_{RBC} Hct+{W}_{plasma}\left(1- Hct\right)} $$$$ (19)

where Hct is the hematocrit (0–1), W_RBC is the volume fraction of water within the erythrocyte (typically valued at 0.70 due to hemoglobin occupying approximately 30% of the erythrocyte volume), and W_plasma is the volume fraction of water within the plasma (typically valued at 0.95, where the other 5% volume is occupied by plasma proteins such as albumin).³² In addition, Bluemke et al.¹⁹ modeled R1_eox, R1_p, r1_dHb, and r1_pOx to have a linear dependence on B0 (where β₀ and β₁ are the y-intercept and slope for the linear fit):

$$$$ R{1}_{eox}(B0)={\beta}_{0,R{1}_{eox}}+{\beta}_{1,R{1}_{eox}}B0 $$$$ (20)

$$$$ R{1}_p(B0)={\beta}_{0,R{1}_p}+{\beta}_{1,R{1}_p}B0 $$$$ (21)

$$$$ r{1}_{dHb}(B0)={\beta}_{0,r{1}_{dHb}}+{\beta}_{1,r{1}_{dHb}}B0 $$$$ (22)

$$$$ r{1}_{pOx}(B0)={\beta}_{0,r{1}_{pOx}}+{\beta}_{1,r{1}_{pOx B0}}\ B0. $$$$ (23)

The values used for all empirically derived parameters and constants in the blood model are listed in the original publication.¹⁹ The behavior of this model is shown in Figure 3.

2.4.2 Tissue compartment

Between the air and oxygen states, the only paramagnetic factor changing in the tissue compartment is the concentration of oxygen dissolved either intracellularly or interstitially. Therefore, the ΔPO_2T calculated in Step 2 can be used to calculate the ΔR1_T using the following equation

$$$$ \Delta R{1}_T=r{1}_{Ox}\ast \Delta P{O}_{2\ T} $$$$ (24)

where the relaxivity of oxygen, r1_Ox, is dependent on field strength and calculated using the empirical model for r1_Ox published by Bluemke et al.¹⁵ (shown in Figure 4):

$$$$ r{1}_{Ox}=\frac{C_1}{1+{C}_2B{0}^2} + {C}_3+{C}_{Temp}\ast T $$$$ (25)

where the empirically derived constants are set to the parameters reported by Bluemke et al.,¹⁵ and in the context of this tissue model, temperature is assumed to be 37°C.

3 METHODS

4 RESULTS

To visualize the relationship between the independent variables, dependent variables, and ΔR1, the following plots were produced. The effect of all combinations of blood volume and OEF on the baseline tissue PO₂ (mean and minimum) and maximum oxygen consumption rate is shown in Supporting Information Figure S6. The effect of OEF on the ΔR1 of the venous, arterial, and tissue compartments individually, for varied PaO₂ changes induced from oxygen, is shown in Figure 5A–C, and the resulting ΔR1 for the voxel is shown in Figure 5D,E (all simulated at 1.5T). In this model, there is an inverse mathematical relationship between blood volume and the Krogh Radius R_t (shown in Supporting Information Figure S3), and therefore blood volume has an effect on the M₀ (see Supporting Information Figure S6C), where M₀ increases with blood volume fraction. In our model, blood volume is considered to be the independent variable while M₀ is dependent, however in biological reality, this is a highly intertwined feedback relationship where tissues with high metabolism recruit more blood vessels.⁴⁰ Blood volume also has an effect on the final ΔR1_voxel (see Figure 5D,E), which is due to the increased contributions from the arterial and venous components in Step 4 of the model. Interestingly, when there has been a smaller change in PaO₂ (i.e., less oxygen administered), the increase in the blood volume fraction allows the negative ΔR1 from the venous component to decrease the ΔR1 of the voxel, whereas this becomes dominated by the high increase in ΔR1 from the arterial component as more oxygen is administered.

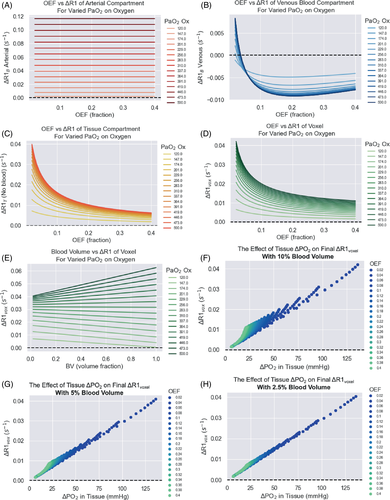
In this model, the OEF chosen has a large effect on ΔR1_voxel, which can be seen clearly in Figure 5D,E. Figure 5A,E shows that as OEF increases – in other words, as a higher fraction of oxygen is extracted from the tissue between the arterial and venous ends – there will be a lower change in PO₂ in the tissue (and hence smaller ΔR1_T), which is the largest contributor to the overall ΔR1 of the voxel. Last, the relationship between ΔPO₂ in the tissue compartment and ΔR1_voxel is shown in Figure 5F-H.

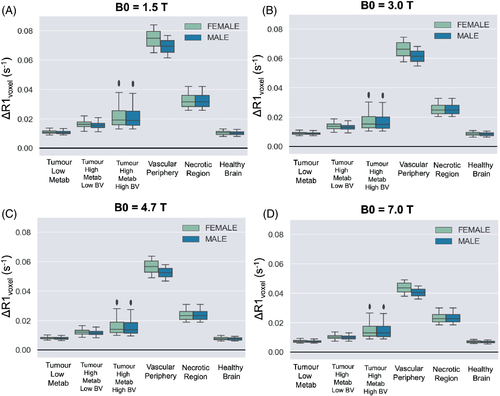
The resulting ΔR1 calculated from this model is plotted in Figure 6, calculated using different field strengths, and using all combinations of the chosen range of Hct, OEF, BV, P_crit listed in Table 1 for each respective tumor tissue type. Since hematocrit levels can vary between sexes, the results from using the female and male ranges for hematocrit have been shown separately to examine the expected difference in ΔR1. In this simulation, the largest difference in ΔR1 between the sexes was 0.0045 s⁻¹, which occurred in the vascular periphery due to containing the highest percentage of blood component and therefore most affected by differences in hematocrit. The difference in ΔR1 between the sexes was negligible in the other simulated tissue types.

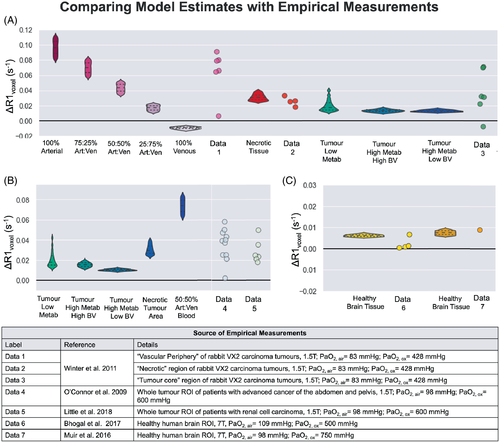
For a rough quantitative comparison, empirical _ΔR1 measurements from six tissue types, alongside the respective simulated ΔR1 according to the B0, PaO₂ and tissue type, are shown in Figure 7. It is not possible to know the composition of the whole tumors ROIs reported by O'Connor et al.¹¹ and Little et al.,⁸ or the “tumor core” reported by Winter et al.,¹⁰ however, each data point for empirical tumor ΔR1 falls within the range of ΔR1 simulated for each possible tumor tissue type; therefore, these whole tumor ROIs could reasonably be the sum of a composition of these different tumor tissue types. One notable exception to this is one “tumor core” data point reported by Winter et al.,¹⁰ which reaches a negative ΔR1 close to that of pure venous blood.

5 DISCUSSION

In this paper, we propose a three-compartment model for estimating the changes in R1 that could be expected in tumor tissues depending on field strength, blood SO₂, blood volume, hematocrit, oxygen extraction fraction, and changes in PO₂ in both the blood and tissue. This model has been developed with the aim of estimating the expected ΔR1 induced by the oxygen delivery in a voxel containing tumor tissue, however, it is generally applicable to OE-MRI research as well and has been designed to make it possible for a researcher to easily substitute their preferred model for tissue oxygen diffusion and consumption and make this model tailored to their tissue of interest, for example, placenta or liver.

Interestingly, the relationship between ΔPO₂ in the tissue compartment and ΔR1_voxel (Figure 5F-H) shows that the linear relationship between ΔPO₂ and ΔR1_voxel seen in phantoms almost holds true in tissue voxels containing lower blood volume; however, in voxels containing higher blood volume, the ΔR1 contribution from the blood compartment interrupts the linear relationship. This suggests that despite the influence of deoxyhemoglobin changes, measuring ΔR1 does provide an indication of the final change in PO₂ in the tissue. In practice, the efficiency of the oxygen delivery to the tissue via inhalation of increased oxygen fraction can be affected by by many factors, and therefore for convenience, Figure 5D simulated a large range of PaO₂ changes (120-500 mmHg) where the resulting change in the R1 (at 1.5T) of the voxel can be seen for each respective PaO₂. In addition, Figures 5F-H display the estimated corresponding ΔR1 for a large range of levels of changes in tissue PO₂ at 1.5T, allowing for a convenient estimate of the corresponding ΔR1 by quickly viewing the data points in Figure 5F-H.

It is known that the values estimated by the r1_Ox model and R1 Blood models by Bluemke et al.^{15, 19} both agree well with empirical measurements (R² = 0.93 and 0.93); however, since the tissue compartment of this model contains variables that were not measured at the time of OE-MRI data collection (i.e., hematocrit, changes in arterial PO₂, tumor blood volume), it is not possible to quantitatively compare the model ΔR1 predictions to the measured ΔR1 with metrics such as R² and MSE. Instead, we used a variety of reported ΔR1 from OE-MRI literature to gain a rough estimation of the accuracy of this model: qualitative ΔR1 responses, categorized by different tumor tissue types by the authors of the OE-MRI literature, are listed in Supporting Information Table S1. Overall, the simulated ΔR1 for each tissue type shown in Figure 6 does correspond with observations from OE-MRI literature: as seen in experiments by Winter et al.,¹⁰ the “vascular periphery” shows greater +ΔR1 than the “tumor core” and “necrotic” regions, and the “necrotic” regions show a greater +ΔR1 than the “tumor core” but less than “vascular periphery.” This is consistent with the distinctions between these three regions defined by Winter et al. — (1) necrotic region is avascular and filled with fluid, (2) the central tumor is cell-dense and has much lower vascularity than vascular periphery. As observed in experiments by Burrell et al.,⁴¹ the “less hypoxic” tumor type shows greater +ΔR1 than the “more hypoxic” tumor type. Last, in these simulations, the healthy brain tissue is predicted to show a very small ΔR1 that might end up ‘not detectable’, as observed by Bhogal et al.²⁰

For a select few OE-MRI studies that did report either measured or estimated PaO₂ changes, the simulated ΔR1 from the model did result in ΔR1 values that were in good agreement with the empirical data (Figure 7). The values for brain tissue and necrotic tissue were particularly accurate, and although it Is not possible to know the composition of the whole tumors ROIs, “vascular periphery,” or “tumor core,” each data point for empirical tumor ΔR1 fell within the range of ΔR1 simulated for each possible tumor tissue type. Therefore, the empirical ΔR1 could reasonably be the sum of a composition of these different tumor tissue types.

This model may be useful for OE-MRI researchers looking to predict the effect of certain factors, such as hematocrit. It is interesting that hematocrit differences in the male and female populations did have a slight effect on ΔR1 when the voxel contained larger blood volumes. In fact, this predicted difference has been empirically observed in lung tissue — where blood volume is approximately 33%–36%⁴² — Kindvall et al.¹² reported that age and sex were all predictors of ΔR1 in lung tissue, likely due to the hematocrit differences.

6 CONCLUSIONS

In conclusion, we have proposed a three-compartment model for estimating the changes in R1 that could be expected in various tissues depending on field strength B0, SO₂, BV, hematocrit, oxygen extraction fraction (OEF), and changes in blood and tissue PO₂. In a demonstration of the model, the resulting ΔR1 are consistent with reported literature OE-MRI results in a variety of tissues. This model has been designed to be easy for researchers to tailor to their tissue of interest by substituting their preferred model for tissue oxygen diffusion and consumption.