On Thermodynamics and Kinetics of Interface-Induced Crystallization in Polymers

1 Introduction

Crystallization of liquids is typically initiated at interfaces to foreign solid surfaces, such as substrates, the walls of containers, or small particles like impurities or nucleating agents. This process is especially relevant for polymers, as they are usually processed in a molten state and their crystalline state strongly depends on the crystallization conditions. A rationally selected solid surface can lead to enhanced crystallization kinetics and oriented overgrowth of the material, thus, enabling control of many physical properties of the material, for example, optical properties, charge transport, mechanical strength, selection of polymorph, etc.^{[1, 2]} Therefore, a detailed understanding of interface-induced crystallization in polymers is of great importance for fundamental and applied research in various disciplines of polymer science.

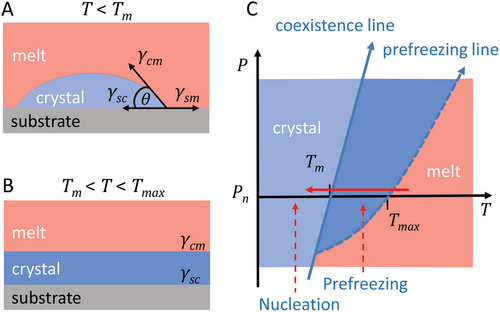
In general, a solid substrate can induce crystallization of liquids either by heterogeneous nucleation or by the less studied process of prefreezing.^[3-6] These two phenomena are very different from a thermodynamic perspective as described in Figure 1. Heterogeneous nucleation – the formation of crystal nuclei on foreign solid surfaces – is an activated process and occurs at a finite supercooling below the melting temperature T_m of the bulk crystal (Figure 1A).^[3] According to classical nucleation theory (CNT),^[3] a crystal nucleus must have at least the critical size to overcome the energy barrier and become stable. The formation of a crystal nucleus having supercritical size is the first step in crystallization via nucleation, which is followed by the growth of crystals from the already formed nuclei. In the case of heterogeneous nucleation on a flat substrate (Figure 1A), under CNT,^[3] the nucleus is assumed to have a shape of a spherical cap with a certain non-zero contact angle θ with the substrate.^[7] Compared to homogeneous nucleation – the formation of crystal nuclei in the bulk liquid material, a solid substrate can decrease the energy barrier for heterogeneous nucleation by a factor f(θ), which depends only on the contact angle θ. The value of θ of the crystal nuclei is determined by the interfacial free energies at the interface substrate-melt (γ_sm), substrate-crystal (γ_sc), and crystal-melt (γ_cm) according to Young's equation γ_sm = γ_sc + γ_cm × cos(θ).^[8] The reduced energy barrier for heterogeneous nucleation leads to an enhanced nucleation kinetics, which results in an increased crystallization temperature. Note that the assumptions made in CNT, primarily the so-called capillarity approximation of the sharp interface,^{[4, 9, 10]} limit its applicability and for complex systems result in a failure of exact quantitative predictions for the nucleation kinetics of homogeneous nucleation.^[9] However, the temperature or the pressure dependence of the nucleation rate was shown to be in a good qualitative agreement with the experimental and simulation data,^{[10, 11]} although the absolute value of the nucleation rate is often inaccurate. Moreover, approaches alternative to CNT mainly consider the non-ideal rough interface of the formed nuclei, while the predicted influence of the interfacial energies in the case of heterogeneous crystal nucleation remains the same as in CNT.^{[4, 9]} Thus, the contact angle θ of the crystal nuclei governed by the balance of the interfacial energies under Young's equation seems to be the main parameter affecting the nucleation kinetics. If, however, γ_sm > γ_sc + γ_cm, the contact angle θ becomes zero, implying that the energy barrier for nucleation vanishes. Under this condition, crystallization takes place above T_m via prefreezing,^[12] which in contrast to heterogeneous nucleation is an equilibrium phenomenon (Figure 1B). Here, instead of the spherical cap-shaped crystal nucleus, a thermodynamically stable crystalline layer forms under equilibrium conditions above T_m and coexists with the residual melt at a constant temperature (Figure 1B). Prefreezing is analogous and closely related to the well-known phenomenon of the vapor-liquid phase transition called prewetting – the formation of a stable liquid layer above vapor-liquid coexistence at the solid interface.^{[13, 14]} Similarly, the formation of a stable phase off-coexistence, either at the solid interface or at an interface to air, is also known in various other interfacial phase transitions, for example, surface freezing,^[15-23] surface melting,^[24-27] and premelting.^[28-31] The knowledge about prewetting can be generalized to a large extent to prefreezing with some differences, as discussed by Archer and Malijevský.^[32] The resulting phase diagram describing the process of prefreezing is shown in Figure 1C. Usually, the crystallization of a liquid occurs during cooling at ambient pressure. Depending on the balance between the interfacial energies, one of the two mentioned processes underlies interface-induced crystallization. If the difference of interfacial energies Δγ = γ_sm − (γ_sc + γ_cm) > 0, the prefrozen layer forms at T_max and grows further with decreasing temperature until, theoretically, the whole material crystallizes via prefreezing upon reaching T_m. Note that the requirement Δγ > 0 serves as a necessary condition for prefreezing. Without prefreezing, that is, at Δγ < 0, crystallization is initiated by nucleation at some finite supercooling. The growth of crystals from the formed nuclei proceeds with time and does not require temperature variation. Until recently, prefreezing was mainly investigated in simulations,^{[5, 12, 32-34]} and experimental observation has only been published for a colloidal system.^[35] Thus, this phenomenon of interface-induced crystallization has been poorly studied, especially in polymers.

The current perspective presents an overview of recent advances in both theoretical description and experimental observation of prefreezing in polymers, including direct observation of prefreezing and the influence of interfacial interactions on such thermodynamic properties of the prefrozen crystal as the transition temperature and the thickness of the prefrozen layer.^[36-40] The experimental investigation of prefreezing was realized for thin films of model polymers polyethylene (PE) and polycaprolactone (PCL) on different substrates by in situ atomic force microscopy (AFM).Another emphasis of this perspective is placed on the influence of interfacial interactions on the kinetics of heterogeneous nucleation and the resultant semicrystalline morphology studied in an ensemble of polyethylene oxide (PEO) droplets on selected substrates by microscopic techniques.^[41] Furthermore, we discuss the importance of interfacial interactions for crystallization of thin films of functional semiconducting polymers that has recently been discovered by the authors.^{[42, 43]}

2 Theoretical Framework of Interface-Induced Crystallization

2.1 Phenomenological Theory of Prefreezing

The phenomenological theory of prefreezing has been recently developed by the authors and provides a framework for the analysis of the equilibrium properties of the prefrozen crystal.^[38] The theory considers the difference of the grand canonical free energy per unit area of two states of the system – with and without a prefrozen layer on a solid substrate above T_m, as shown in Figure 2A,B. The corresponding free energy difference reads as:

$$$$\begin{eqnarray} \Delta {{\Sigma}}\left( {l,T} \right) &=& {{{\Sigma}}_2} - {{{\Sigma}}_1} = {\gamma _{{\rm{sc}}}} + {\gamma _{{\rm{cm}}}} - {\gamma _{{\rm{sm}}}} + {{\Delta}}S \times l \times \left( {T - {T_{\rm{m}}}} \right) \times \frac{T}{{{T_{\rm{m}}}}}\nonumber\\ &&+\ {\gamma _{{\rm{sm}}}} \times {e^{ - \frac{l}{{{l_0}}}}}\end{eqnarray}$$$$()

where ΔS is the entropy change per unit volume during crystallization, l is the thickness of the prefrozen layer, T is absolute temperature, T_m is the bulk melting temperature, and l₀ is the correlation length of the effective interaction between a substrate and a melt through a prefrozen layer. As discussed in the Introduction, Δγ = γ_sm − (γ_sc + γ_cm) > 0 is a necessary condition for prefreezing. Thus, the first three terms in Equation (1), which can be combined into − Δγ represent the only energy gain due to the formation of the prefrozen layer. The fourth term in Equation (1) describes the energy cost for crystallization above T_m. The last term is the repulsive potential approximating an effective interfacial interaction between substrate and melt separated by the crystalline layer of thickness l. The schematic plot of ΔΣ(l, T) is shown in Figure 1C and evidences a single minimum of the free energy difference at each temperature that corresponds to the equilibrium state of the system. The equilibrium thickness of the prefrozen layer as a function of temperature is thus obtained by minimizing ΔΣ(l, T) with respect to l:

$$$$\begin{eqnarray}{l_{{\rm{eq}}}}\left( T \right) = {l_0} \times ln\left( {\frac{{{\gamma _{{\rm{sm}}}} \times {T_{\rm{m}}}}}{{{{\Delta}}S \times {l_0} \times \left( {T - {T_{\rm{m}}}} \right) \cdot T}}} \right)\end{eqnarray}$$$$()

From the basic thermodynamic principles, it follows that the prefrozen crystalline layer forms when the equilibrium free energy change of the system ΔΣ_eq(T) (blue line in the free energy profile in Figure 1C) becomes zero that allows deriving the corresponding transition temperature T_max as follows:^[38-40]

$$$$\begin{eqnarray}{T_{{\rm{max}}}} = \frac{{{T_{\rm{m}}}}}{2}\left( {1 + \sqrt {1 + \frac{{4 \times \Delta {\gamma _{{\rm{eff}}}}}}{{{{\Delta}}S \times {l_0} \times {T_{\rm{m}}}}}} } \right)\end{eqnarray}$$$$()

where $$\Delta {\gamma _{{\rm{eff}}}} = \frac{{\Delta \gamma }}{{1 + {{{\Gamma}}^{ - 1}}( {2,\;\frac{{\Delta \gamma }}{{{\gamma _{{\rm{sm}}}}}}} )}}$$ is the effective interfacial free energy difference, which combines all interfacial interactions between melt, crystal, and the substrate. The function $${{{\Gamma}}^{ - 1}}( {2,\frac{{\Delta \gamma }}{{{\gamma _{{\rm{sm}}}}}}} )$$ is the inverse of the upper incomplete Gamma function that varies from infinity to zero when the ratio $$\frac{{\Delta \gamma }}{{{\gamma _{{\rm{sm}}}}}}$$ varies in the acceptable range of values from 0 to 1. Thereby, an increase in Δγ causes an increase in Δγ_eff, which in turn gives rise to T_max. The latter allows concluding that Δγ or, more precisely, Δγ_eff is the driving force for prefreezing. As such, Δγ_eff becomes the only parameter for T_max, which summarizes the influence of interfacial interactions on the transition temperature of prefreezing. Furthermore, if the energy cost for crystallization ΔS × l₀ × T_m is also considered, the transition temperature T_max is then determined by the interplay between the energy gain Δγ_eff and the energy cost ΔS × l₀ × T_m for prefreezing.

By substituting Equation (3) into Equation (2), the change of crystal thickness at T_max or the minimum order parameter l_min can be calculated in the following form:^[40]

$$$$\begin{eqnarray} {{ \def\eqcellsep{&}\begin{array}{l} {l_{{\rm{min}}}} = {l_{{\rm{eq}}}}\left( {{T_{{\rm{max}}}}} \right) = {l_0} \times {{{\Gamma}}^{ - 1}}\left( {2,\;\displaystyle\frac{{\Delta \gamma }}{{{\gamma _{{\rm{sm}}}}}}} \right) = {l_0} \times {{{\Gamma}}^{ - 1}}\left( {2,1 - \displaystyle\frac{{{\gamma _{{\rm{sc}}}} + {\gamma _{{\rm{cm}}}}}}{{{\gamma _{{\rm{sm}}}}}}} \right) \end{array} }}\nonumber\hspace*{-10pt}\\ \end{eqnarray}$$$$()

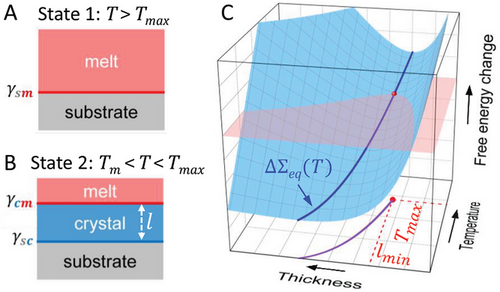
Equation (4) evidences that the normalized minimum order parameter $$\frac{{{l_{{\rm{min}}}}}}{{{l_0}}}$$ depends solely on the ratio of the interfacial energies $$\frac{{{\gamma _{{\rm{sc}}}} + {\gamma _{{\rm{cm}}}}}}{{{\gamma _{{\rm{sm}}}}}}$$. Recalling that for prefreezing Δγ > 0, the ratio $$\frac{{{\gamma _{{\rm{sc}}}} + {\gamma _{{\rm{cm}}}}}}{{{\gamma _{{\rm{sm}}}}}}$$ has the acceptable range of values from 0 to 1, as 1 or higher values violate the condition Δγ > 0, while 0 is physically unrealistic. For the indicated range of $$\frac{{{\gamma _{{\rm{sc}}}} + {\gamma _{{\rm{cm}}}}}}{{{\gamma _{{\rm{sm}}}}}}$$, l_min is always larger than 0. This important result implies that prefreezing is a first-order phase transition, since the formation of the prefrozen layer is abrupt and discontinuous. Moreover, from the comparison of Equations (3) and (4) it follows that T_max and l_min depend differently on the interfacial energies. Thus, the developed phenomenological theory predicts that the values of T_max and l_min can vary independently when the interfacial interactions, expressed in the interfacial energies, change.

2.2 Heterogeneous Nucleation in CNT

As discussed in the Introduction, nucleation is an activated process, since a crystal nucleus has to overcome an energy barrier ΔG* to become stable (Figure 3A). CNT is a well-known model used to describe the nucleation process. CNT yields the relationship between the energy barrier and the temperature-dependent nucleation rate as follows:^[3]

$$$$\begin{eqnarray}J = {J_0} \times exp\left( { - \frac{{\Delta {G^*}}}{{{k_{\rm{B}}}T}}} \right)\end{eqnarray}$$$$()

where k_B is the Boltzmann constant. The exponential factor in Equation (5) depends much stronger on temperature than the prefactor J₀, which is thus often considered constant. Consequently, the nucleation rate depends mainly on ΔG*. According to CNT, the energy barrier for homogeneous nucleation is derived as:

$$$$\begin{eqnarray}\Delta G_{hom}^* = \frac{{16\pi }}{3}\frac{{\gamma _{{\rm{cm}}}^3T_{\rm{m}}^2}}{{\Delta H_{\rm{m}}^2}}{\left( {\frac{1}{{{T_{\rm{m}}} - T}}} \right)^2}\end{eqnarray}$$$$()

where γ_cm is the interfacial energy at the crystal-melt interface and ΔH_m is the melting enthalpy. For the case of heterogeneous nucleation, it is assumed that the spherical cap-shaped crystal nucleus forms on a flat substrate with a contact angle θ (Figure 1A) that results in a reduction of the corresponding energy barrier $$\Delta G_{{\rm{het}}}^*$$ by a factor f(θ):

$$$$\begin{eqnarray} \Delta G_{{\rm{het}}}^* = \Delta G_{{\rm{hom}}}^* \times f\left( \theta \right) = \Delta G_{{\rm{hom}}}^* \times \frac{1}{4}\left( {2 + cos\left( \theta \right)} \right){\left( {1 - cos\left( \theta \right)} \right)^2}\nonumber\\ \end{eqnarray}$$$$()

where the contact angle θ is governed by the interplay of the interfacial energies according to Young's equation γ_sm = γ_sc + γ_cm × cos(θ).^[8] From Equation (7), it is straightforward to see that for the values of 0 < θ < π, the factor 0 < f(θ) < 1 and $$0 &lt; \Delta G_{{\rm{het}}}^* &lt; \Delta G_{{\rm{hom}}}^*$$. In other words, the energy barrier for heterogeneous nucleation is always smaller than that of homogeneous nucleation at a given temperature. The latter has a direct implication for the nucleation rate, which increases with the decreased $$\Delta G_{{\rm{het}}}^*$$ (Equation (5)). Figure 3B demonstrates that a lowered energy barrier for heterogeneous nucleation leads to a decrease in supercooling needed to initiate the nucleation event. As schematically shown in Figure 3B, the same value of logarithm of normalized nucleation rate ln(J/J₀) is realized by different amounts of supercooling (T_m − T). According to Equation (5), the latter condition can be expressed as:

$$$$\begin{eqnarray}\frac{{\Delta G_{{\rm{het}}}^*}}{{{k_{\rm{B}}}{T_{{\rm{het}}}}}} = \frac{{\Delta G_{{\rm{hom}}}^*}}{{{k_{\rm{B}}}{T_{{\rm{hom}}}}}}\end{eqnarray}$$$$()

where T_het and T_hom are the temperatures, at which the same nucleation rate is realized for heterogeneous and homogeneous nucleation, respectively. Substituting Equation (6) taken at T = T_hom, and Equation (7) taken at T = T_het into Equation (8) allows obtaining the factor f(θ) as follows:

$$$$\begin{eqnarray}f\left( \theta \right) = \frac{{{T_{{\rm{het}}}} \times {{\left( {{T_{\rm{m}}} - {T_{{\rm{het}}}}} \right)}^2}}}{{{T_{{\rm{hom}}}} \times {{\left( {{T_{\rm{m}}} - {T_{{\rm{hom}}}}} \right)}^2}}}\end{eqnarray}$$$$()

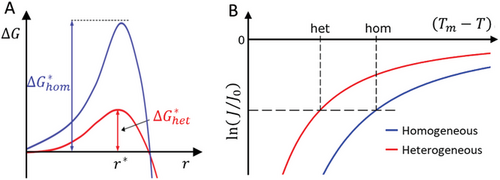
From Equation (9) it follows that information about the factor f(θ) can be obtained from the amounts of supercooling needed to initiate homogeneous and heterogeneous nucleation in a fixed sample volume during the cooling experiments with a constant rate. Furthermore, this information can be used to estimate the contact angle θ, a parameter that summarizes the influence of interfacial interactions on nucleation kinetics and is hardly accessible in experiments otherwise.

3 Experimental Investigation of Prefreezing in Polymers

3.1 Microscopic Observation and the Range of Existence

The experimental investigation of prefreezing in polymers was realized for thin polymer films deposited on a solid substrate.^{[36, 37, 39, 40]} Such a strategy enables accessing a detailed microscopic picture of crystallization in a well-defined system, as the substrate-material interactions are kept constant along the entire macroscopic-large film surface. This approach differs from conventional methods of dispersing nucleating agents in polymeric matrices, where the exact size, shape, and volume fraction of the nucleating agents are not always accurately known, and microscopic observation of crystallization in such systems is significantly difficult. As well-known, PE crystallizes epitaxially on graphite,^[44] which provides a strong indication for interface-induced crystallization in this system. In this regard, we investigated the crystallization of PE with well-defined molecular weight (M_n = 33 kDa, M_w/M_n = 1.04) on highly ordered pyrolytic graphite (HOPG).^[36] PE used in this work was produced by hydrogenation of 1,4,-polybutadiene and contains a small fraction of ethyl branches to avoid thickening of the lamellar crystals. Figure 4 shows AFM images of thin PE films on HOPG and a silicon wafer used for comparison. Both samples were measured at room temperature after slow cooling from the molten state. While the large-scale morphology of PE on silicon (Figure 4A) is represented by spherulites with clearly identifiable nucleation events in the centers of spherulites, the morphology of PE on HOPG (Figure 4B) is remarkably uniform and homogeneous. A closer inspection reveals a terraced structure of laterally growing lamellae on silicon (Figure 4C), whereas the epitaxial, presumably vertically grown, well-ordered PE lamellar crystals are visible on HOPG (Figure 4D). Furthermore, the X-ray scattering data measured for PE on HOPG (Figure 4D, inset) evidence a strong out-of-plane crystal orientation of PE with (110) crystal planes parallel to HOPG. These observations suggest that HOPG induces crystallization in PE by a different phenomenon than the nucleation observed on silicon. To disclose the crystallization mechanism underlying the morphology of PE on HOPG, ultrathin PE films were investigated at elevated temperatures by in situ AFM performed in the net attractive regime. Figure 5A–C shows AFM amplitude images recorded during melting (Figure 5A,B) and subsequent crystallization (Figure 5B,C) of ultrathin PE films on HOPG. As seen in Figure 5A, measured at 120 °C, which is well above the bulk melting temperature of PE T_m = 108 °C, several domains of crystalline lamellae epitaxially aligned with the underlying HOPG are partially covered by and coexist with the molten PE droplets. Complete melting of PE on HOPG occurs at T_max = 124 °C, so only liquid PE is visible at 125 °C (Figure 5B). Evidently, it is the interaction between the PE chains and the HOPG surface that stabilizes an ordered surface layer up to T_max. On cooling, the ordered PE structure reappears in the same temperature range above T_m (Figure 5C), confirming that the process is reversible. These experimental observations unequivocally prove that PE crystallizes on HOPG via prefreezing.

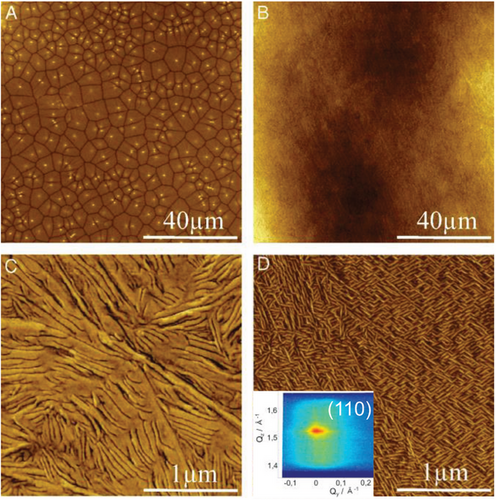
To demonstrate the influence of the substrate-material interactions on prefreezing, we directly compared the prefreezing of PE on HOPG to that on a molybdenum disulfide MoS₂ substrate.^[39] The results of an analogous in situ AFM investigation of ultrathin PE film on MoS₂ are displayed in Figure 5D,E. While the PE crystalline layer has a similar epitaxial relation with MoS₂, the temperature range of the existence of PE crystals is significantly extended compared to that on HOPG. A uniform lamellar crystalline layer of PE can be well identified around the featureless molten droplets in the AFM amplitude image at 140 °C (Figure 5D) and disappears at a temperature of at least 155 °C (Figure 5E). The schematic illustration in Figure 5F summarizes the observed melting of PE on the two used substrates. In addition, note that the crystalline PE layer adopts the same out-of-plane crystal orientation on MoS2 as on HOPG with (110) crystal planes parallel to the substrate surface.^[39] Thus, our results explicitly show that the prefrozen PE layer is stabilized over a larger temperature range on MoS₂ with T_max = 155 °C than on HOPG with T_max = 124 °C. The value of the transition temperature T_max of PE on MoS₂ even exceeds the equilibrium melting temperature of PE crystals, which provides convincing evidence of the key role of the substrate-material interactions for prefreezing.

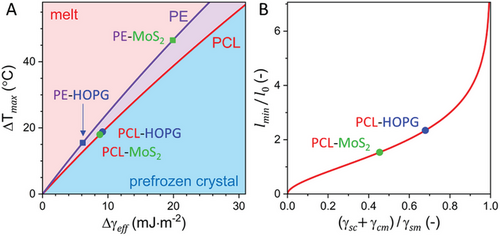
Furthermore, for a quantitative analysis of the substrate effect on prefreezing, we performed a detailed analysis of the series of AFM height images at elevated temperatures by determining the volume of molten PE droplets on HOPG and MoS₂ (Figure 5G,H). The experimental data were analyzed with the phenomenological theory of prefreezing presented in the theory section. The temperature dependence of the equilibrium melt volume can be derived from Equation (2) under the assumption of negligible volume difference between melt and crystal.^{[36, 39]} The corresponding fit curves in Figure 5G,H show well agreement between the theory and experimental data. Note that only a limited temperature range was used to fit the data for PE on MoS₂ (Figure 5H) because of the suppression of the autophobic dewetting of molten PE with decreasing crystalline layer thickness (molten PE dewets from the prefrozen layer but wets the MoS₂ substrate). The subsequent analysis of fitting parameters by the phenomenological theory of prefreezing allowed estimating the effective interfacial free energy difference Δγ_eff. Thereby, the values of Δγ_eff increase from 6.1 mJ m⁻² for PE on HOPG to 19.9 mJ m⁻² for PE on MoS₂.^{[39, 40]} So, as predicted by the phenomenological theory of prefreezing, the increase of T_max is attributed to the increase of the substrate-material interactions summarized in the values of Δγ_eff.

3.2 Order Parameter and Its Temperature Dependence

The experimental observation of prefreezing in PE, presented in Section 3.1., left open the question of the order of this interface-induced liquid-crystal phase transition. Indeed, as molten PE wets both HOPG and MoS₂ substrates, direct measurement of the prefrozen layer thickness or, in other words, the order parameter was not possible. We, thus, tackled this important question by studying the melting of thin films of a more polar polymer PCL (M_n = 23 kDa, M_w/M_n = 1.8) on the same two substrates – HOPG and MoS₂.^{[37, 40]} Figure 6A,B shows AFM amplitude images of PCL films on HOPG (Figure 6A) and MoS₂ (Figure 6B) measured at temperatures above the bulk melting point of PCL T_m = 57 °C, determined by differential scanning calorimetry (DSC).^[37] This observation confirms that PCL crystallizes on the two substrates via prefreezing, analogously to PE. The PCL film morphology is again similar to that observed in PE (Figure 5) and consists of a crystalline epitaxially aligned layer covered by molten PCL droplets. However, molten PCL wets HOPG and MoS₂ only partially,^{[37, 40]} as evidenced, for example, by small holes in the left upper and lower corners in Figure 6A. Such dewetted morphology of thin PCL film on HOPG and MoS₂ has advantages because it provides simultaneous access to the bare substrate surfaces and the stable prefrozen layer and, thus, allows measuring the thickness of the prefrozen layer as a function of temperature by extracting height profiles from the corresponding AFM height images. Thereby, the measured crystalline layer thickness as a function of superheating (T−T_m,fit) is displayed in Figure 6C, where T_m,fit is the bulk melting temperature obtained by fitting the experimental data with Equation (2). The value of T_m,fit = 62–63 °C is in close agreement with its experimental estimate from DSC and coincides with the offset of melting in DSC. The results in Figure 6C allow several important conclusions to be drawn. Prefreezing is a first-order phase transition, since the formation or melting of the prefrozen crystalline layer at T_max is abrupt and discontinuous. This experimental outcome fully meets the theoretical prediction discussed in Section 2.1. Moreover, while the minimum thickness or order parameter l_min is noticeably different for PCL on HOPG and MoS₂, the transition temperature T_max for these two systems is nearly the same (Figure 6C). Therefore, these results clearly demonstrate that l_min and T_max are independent properties of the prefrozen phase and, consequently, are varied separately. Indeed, as predicted by the phenomenological theory, T_max depends on Δγ_eff, whereas l_min is a function of $$\frac{{{\gamma _{{\rm{sc}}}} + {\gamma _{{\rm{cm}}}}}}{{{\gamma _{{\rm{sm}}}}}}$$.

To further illustrate the consistency between the experimental and theoretical results, the equilibrium superheating ΔT_max = T_max − T_m,fit and the normalized minimum order parameter $$\frac{{{l_{{\rm{min}}}}}}{{{l_0}}}$$ were calculated by Equations (3) and (4) as functions of their respective variables Δγ_eff and $$\frac{{{\gamma _{{\rm{sc}}}} + {\gamma _{{\rm{cm}}}}}}{{{\gamma _{{\rm{sm}}}}}}$$ for widely varied interfacial energies and using the results of fitting shown in Figure 5G,H and 6C. The experimental estimates of ΔT_max and $$\frac{{{l_{{\rm{min}}}}}}{{{l_0}}}$$, along with the respective values of Δγ_eff and $$\frac{{{\gamma _{{\rm{sc}}}} + {\gamma _{{\rm{cm}}}}}}{{{\gamma _{{\rm{sm}}}}}}$$, obtained from fitting for the four studied systems of PE and PCL on HOPG and MoS₂, are mapped together in Figure 7.^[40] As such, Figure 7 summarizes the influence of interfacial interactions on thermodynamics of prefreezing and show how versatile this influence can be. Namely, while changing the substrate from HOPG to MoS₂ entails a significant increase in ΔT_max for PE by about 30 °C, the value of ΔT_maxfor PCL on the two substrates remains nearly unchanged. On the other hand, the normalized minimum order parameter $$\frac{{{l_{min}}}}{{{l_0}}}$$ for PCL changes significantly when the substrate is changed from HOPG to MoS₂. These seemingly unexpected observations can be readily explained within the framework of the phenomenological theory of prefreezing. Indeed, the theory predicts a different dependence of ΔT_max and $$\frac{{{l_{min}}}}{{{l_0}}}$$ on the interfacial energies and identifies the corresponding decisive variables. Thus, the developed theoretical formalism provides a consistent explanation for the observed behavior of thermodynamic properties of prefreezing and demonstrates great predictive power.

4 Influence of Interfacial Interactions on Kinetics of Heterogeneous Crystal Nucleation and Microscopic Structure

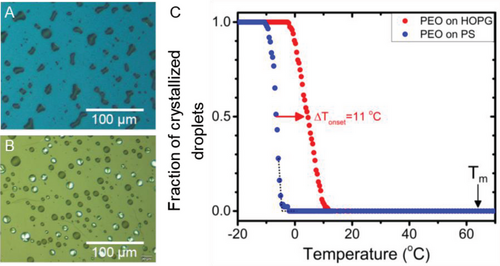
Сonfining material into small compartments or droplets supported on a substrate has previously been shown to be an elegant method for the experimental study of crystal nucleation.^[45] This approach was utilized by Dalnoki-Veress and co-workers to investigate crystal nucleation in PEO droplets on amorphous and semicrystalline polystyrene (PS).^[46-48] By analyzing the dependence of nucleation kinetics on the droplet size during isothermal crystallization experiments, it was concluded that PEO droplets crystallize via homogeneous nucleation on amorphous polystyrene (PS), while the nucleation of PEO changes to heterogeneous on semicrystalline PS.^[48] However, the energetics of heterogeneous nucleation and the influence of substrate-material interactions on the microscopic structure has remained unexplored. We addressed these fundamental questions of heterogeneous nucleation by analyzing crystallization in a model system – an ensemble of PEO droplets dewetted from the melt on HOPG and additionally on the amorphous PS substrate used as a reference system with homogenous nucleation.^[41] The crystallization in droplets was monitored using polarized light optical microscopy, where polarizers were nearly crossed. With this mutual arrangement of polarizers, amorphous droplets appear dark, whereas crystalline droplets appear bright due to birefringence. Figure 8A,B displays the selected optical microscopy images of PEO droplets crystallized on amorphous PS (Figure 8A) and HOPG (Figure 8B) during slow cooling from the melt at a rate of 0.4 °C min⁻¹. The recorded images demonstrate that PEO droplets start crystallizing at a higher temperature than those on PS, which results from different substrate-material interactions, although droplets on both substrates have similar length scales. To obtain more detailed information about the detected effects, the fraction of crystallized droplets in the frame of view was calculated as a function of temperature and is presented in Figure 8C. The results unambiguously confirm the enhanced crystallization of PEO on HOPG, whereby we conclude that it is due to heterogeneous nucleation. Furthermore, as discussed in Section 2.2., the temperature shift of the curves in Figure 8C can be used to access the factor f(θ). Hence, the temperatures at which the fraction of crystallized droplets reached 0.5 were taken as the corresponding crystallization temperatures and amounted T_het = 4.6 °C for PEO on HOPG and T_hom = −6.4 °C on PS. By applying Equation (9) and the bulk melting temperature of PEO used (M_n = 31.25 kDa, M_w/M_n = 1.04) T_m = 64 °C, the factor was estimated f(θ) = 0.741. Accordingly, the contact angle of crystal nuclei of PEO on HOPG was calculated from Equation (7): θ = 109.5°. The obtained value of contact angle θ, according to Young's equation, implies γ_sm < γ_cm and, thus, indicates that HOPG has a less energetic preference to be wetted by crystalline than by molten PEO. This interesting outcome should not be confusing, as even for γ_sm < γ_cm the energy barrier for heterogeneous nucleation is reduced simply because of the smaller total surface of spherical cap-shaped crystal nuclei, according to CNT.

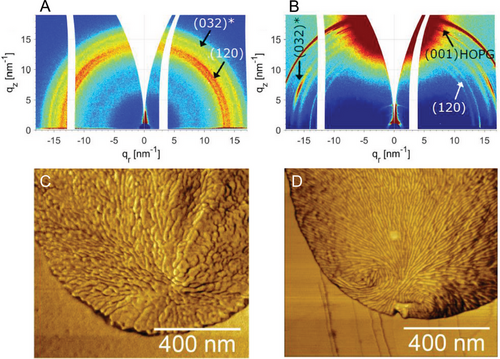
The effect of HOPG on the crystal orientation and semicrystalline morphology of PEO was studied by wide-angle X-ray scattering (WAXS) and AFM. The scattering patterns of PEO droplets on PS and HOPG are shown in Figure 9A,B, respectively. While isotropic WAXS pattern of PEO on PS is indicative of random crystal orientation, the narrowly distributed (032)^* crystal reflection of PEO on HOPG points to a preferred crystal orientation. Note that the (032)^* reflection of PEO indicated in Figure 9A is a superimposed signal of many different reflections of monoclinic crystal lattice of PEO.^[49] Because of the very intense (001) reflection of HOPG (Figure 9B), which obstructs the observation of the scattering signal from PEO, a more detailed analysis of PEO crystal orientation was not possible. Nevertheless, the results in Figure 9B demonstrate that the substrate-induced nucleation entails a preferred orientation of PEO crystals. Moreover, the semicrystalline morphology of PEO droplets inspected by AFM (Figure 9C,D) reveals that the PEO lamellae are oriented on HOPG, in contrast to the unoriented PEO lamellae on PS. As such, the AFM results support the conclusion about the crystal orientation drawn from WAXS. Importantly, no signs of epitaxy between PEO and HOPG are visible in Figure 9D. Thus, our results indicate that a solid substrate can enhance the crystal nucleation rate and induce a preferred crystal orientation without epitaxy, which is often seen as an important parameter for heterogeneous nucleation.^[50-52]

As discussed above, heterogeneous nucleation leads to a preferred out-of-plane crystal orientation, which can be preserved during the subsequent growth of the crystal phase, quite similar to that observed for prefreezing. This experimental outcome is of particular importance for thin film applications of semicrystalline polymers. Indeed, as recently shown in our works for model semiconducting polymer poly(3-hexylthiohene) (P3HT) on graphene,^[43] the interfaces to the substrate and vacuum induce different crystal orientations and thus play a decisive role in the overall crystal orientation of thin films of P3HT.^[42] As the upper interface to vacuum cannot be directly influenced by the substrate, we employed a different strategy and chemically modified the end groups of the P3HT side chains. Thereby, by introducing more polar end groups in poly[3-(6-bromohexyl)]thiophene (P3BrHT) but keeping the crystal structure similar,^[53] the influence of the interface to vacuum was reduced, which resulted in full face-on orientation in thin P3BrHT films on graphene. This example clearly shows that crystallization initiated at interfaces plays a significant role in the nanostructuring of functional semicrystalline polymers and, therefore, can be used advantageously for targeted control of their properties.

5 Conclusion and Outlook

The importance of a deep and detailed understanding of interface-induced crystallization in polymers is beyond any doubt, as any crystallizing polymer sample is at least confined to its shape and more practically – to containers, pores, nanodomains, etc. Moreover, numerous endeavors to find the “right” nucleating agent to control polymer crystallization are still abundant in both industry and academia, hence, indicating a need for profound comprehension of interface-induced crystallization. In this perspective, we present our recent progress in understanding the influence of substrate-material interactions on crystallization mechanism, thermodynamic properties, and morphology of interface-induced crystallization in polymers.

The equilibrium phenomenon of prefreezing is the first focus here. We show that the recently developed phenomenological theory of prefreezing evidences that it is a first-order phase transition and provides a physically reasonable connection between the transition temperature T_max and the minimum order parameter l_min of prefreezing and the respective interfacial energies. The latter theoretical outcome allowed unifying prefreezing with the well-established phenomenon of heterogeneous nucleation, where the interfacial energies are the main parameters. Moreover, the theory identifies the key variables for T_max and l_min and predicts that these two equilibrium properties of the prefrozen phase are, in fact, independent from each other and can be varied separately as the interfacial energies change. The independence of T_max and l_min was barely addressed not only for prefreezing, but also for other similar interfacial phase transitions, like surface freezing, liquid-crystalline phase transitions, etc. In this regard, our results contribute to the general fundamental understanding of interface-induced crystallization, and are not limited to polymer crystallization. A series of experimental studies of prefreezing in model polymers on different substrates by in situ AFM provided access to the microscopic picture of this crystallization phenomenon. Moreover, the experimental outcomes were quantitatively analyzed with the theory that confirmed the validity of the theoretical approach and allowed the creation of a comprehensive picture of substrate-material interactions for prefreezing. Besides, we could clearly show that prefreezing entails the out-of-plane oriented growth of polymer crystals.

The second accent of this work is on studying the energetics of heterogeneous nucleation and its impact on the formed microscopic structure. Although heterogeneous nucleation is a well-known phenomenon of interface-induced crystallization, the mentioned aspects has not been tackled before. By analyzing the enhancement of the crystal nucleation kinetics and by applying classical nucleation theory, we were able to estimate the contact angle of crystal nuclei on a solid surface – the quantity, which summarizes the influence of substrate-material interactions on heterogeneous nucleation. Furthermore, we showed that heterogeneous nucleation entails a preferential out-of-plane crystal orientation, an effect similar to that induced by prefreezing, which is especially relevant for modern thin film applications, for example, organic electronics.

Evidently, there is still a lot to be understood about interface-induced crystallization. The spectrum of open questions is quite broad and, in the following, we point to some of the most relevant. For all the examples of prefreezing studied, the epitaxial growth of polymer lamellae was clearly observed as a result of the substrate influence. The analogous to prefreezing phenomenon of surface freezing at the upper interface to vacuum obviously excludes any epitaxy. However, whether there is an analogy between these two phenomena concerning epitaxy remains open. Besides, the dependence of the equilibrium properties of prefreezing on the interfacial energies derived in our theory should hold its validity for surface freezing. An independent test of these predictions for the case of surface freezing would be very advantageous for a deeper understanding of these interfacial equilibrium phase transitions. Furthermore, it would also be important to study the discussed cases of prefreezing in simulations and calculate the theoretical values of the interfacial free energies, which are hardly accessible in experiments directly. The simulation results could be then compared with our findings. Another important aspect is the kinetics of prefreezing, which has not been tackled so far. Knowing the kinetics of prefreezing will help clarify whether prefreezing or heterogeneous nucleation is practically more suitable for efficient nucleation. Besides, the effects of both prefreezing and heterogeneous nucleation on crystal orientation discussed above pose a question whether these effects have limited correlation length and what the role of chain length and flexibility is here. Thus, we want to encourage the community to intensify both experimental and theoretical research on interface-induced crystallization.

Conflict of Interest

The authors declare no conflict of interest.