Sampling reference data is crucial in machine learning potential (MLP) construction. Inadequate coverage of local configurations in reference data may lead to unphysical behaviors in MLP-based molecular dynamics (MLP-MD) simulations. To address this problem, this study proposes a new on-the-fly reference data sampling method called radial distribution function (RDF)-based data sampling for MLP construction. This method detects and extracts anomalous structures from the trajectories of MLP-MD simulations by focusing on the shapes of RDFs. The detected structures are added to the reference data to improve the accuracy of the MLP. This method allows us to realize a reasonable MLP construction for liquid water with minimal additional data. We prepare data from an H₂O molecular cluster system and verify whether the constructed MLPs are practical for bulk water systems. MLP-MD simulations without RDF-based data sampling show unphysical behaviors, such as atomic collisions. In contrast, after applying this method, we obtain MLP-MD trajectories with features, such as RDF shapes and angle distributions, that are comparable to those of ab initio MD simulations. Our simulation results demonstrate that the RDF-based data sampling approach is useful for constructing MLPs that are robust to extrapolations from molecular cluster systems to bulk systems without any specialized know-how.

1 INTRODUCTION

Molecular dynamics (MD) simulation is a computational method for investigating the dynamic behaviors and interactions of atoms or molecules. It is applied in various fields, including life, material, astrochemical, and geological sciences.^1-7 In classical MD (CMD) simulations, energies and forces are obtained from an empirical force field. Various force fields have been developed^8-14 and applied in MD simulations. However, nearly all empirical force fields have been constructed by optimizing many parameters to reproduce the experimental results. Therefore, in conditions far from the environments that the empirical force fields can describe, CMD simulations often fail to reproduce the correct physical and chemical properties.^{15, 16} In addition, because the empirical force fields cannot incorporate quantum mechanical effects, CMD simulations cannot describe chemical reactions involving bond formation or breaking.¹⁷

Ab initio MD (AIMD) simulations contain few empirical parameters and provide more realistic atomic descriptions than CMD simulations. The systems evolve in time by obtaining energies and forces by performing on-the-fly single-point ab initio calculations based on the quantum mechanical equation. Therefore, AIMD has been performed to reveal the microscale properties of a wide variety of materials, including water, silicate and lithium-ion batteries.^18-20 However, because the computational cost is high due to solving the quantum mechanical equations, AIMD simulations are complex to perform over large space and time scales.

Machine learning potential (MLP) has recently been developed for large space- and time-scale AIMD simulations.^{21, 22} MLP is a machine-learning model that trains a potential energy surface (PES) in a system from reference data that contains information on atomic coordinates, energies, and forces, in which the local atomic environments of reference structures are converted to descriptors as inputs for neural networks. Neural network models for MLPs, such as the Behler–Parrinello high dimensional neural network²³ and deep potentials,²⁴ have realized invariance for the translation, rotation, and permutation of atoms, as well as the size scalability of MLPs.^{21, 22, 25-27} The accuracy of the energy and force values predicted by an adequately constructed MLP is equivalent to the ab initio computational level of the reference data. Furthermore, once the MLPs are constructed, the energies can be obtained by simply substituting the coordinates as in classical force fields. Therefore, MD simulations can be performed for large-scale systems at the ab initio computational level using MLPs.

In MLP construction, reference data is usually prepared from first-principles or quantum chemical (QC) calculations in periodic boundary and isolated cluster models. The calculations in the periodic boundary models are typically used for bulk systems, such as liquids, crystals, and amorphous materials,^{25, 28-31} whereas the calculations in the isolated cluster models are used for smaller systems, such as small molecular clusters or chemical reactions.^32-35 Recently, attempts to calculate large systems using MLPs constructed from QC calculations in the isolated cluster models have become increasingly popular. Two primary approaches have been developed. One approach involves reducing the computational cost of QC calculations for the calculation of the entire system. Liu et al. developed an electrostatically embedded generalized molecular fractionation method, which is fragment-based QC calculations, for large–size ion–water systems.^{36, 37} Other fragment-based or divide-and-conquer methods for QC calculations are also useful for preparing extensive system data while keeping the computational cost low.³⁸ Another approach is constructing MLPs with small molecular cluster data and applying them to large systems. The only successful extrapolation of water clusters to bulk water was performed by Zaverkin et al. using their original Gaussian moment neural network model.^39-41 Therefore, optimal MLP construction methods for large systems based on QC calculations are still in the exploratory phase.

The sampling of reference data is an essential issue in MLP construction. Reference data is usually sampled using MD or Monte Carlo simulations.^{42, 43} Enhanced-sampling methods are also utilized to sample rare events.^44-47 However, there are some cases where the reference data does not adequately cover the entire space of the local configurations, which could lead to unphysical behaviors in MLP-based MD (MLP-MD) simulations. Several data sampling methods have been proposed to improve the original dataset. For example, Nagai et al. proposed a self-learning hybrid Monte Carlo approach, which is a type of hybrid Monte Carlo simulation for materials science, combined with an MLP.⁴⁸ Zhang et al. proposed a procedure for MLP construction through exploration, labeling, and training.^{49, 50} Thus, efficient data sampling methods are required to compensate for the lack of reference data and improve the quality and accuracy of MLPs.

In this study, we propose an on-the-fly reference data sampling method using a radial distribution function (RDF) called RDF-based data sampling. We focused on the RDF shape obtained by MLP-MD simulations and demonstrated that it is possible to modify the anomalous RDF with a few additional data points. In RDF-based data sampling, the RDF of the MLP-MD trajectory was compared with a reference RDF to verify whether it was an anomalous structure. The detected anomalous structures were then added to the reference data as a kind of counterexample to facilitate the MLPs in generating an accurate PES. In addition, we applied this sampling method to a liquid–water system.

Here, we constructed MLPs using the reference data of H₂O molecular clusters obtained by QC calculations. Then, we verified whether the MLPs could extrapolate bulk water systems across the size-scale gap between the isolated and periodic boundary systems. The MLPs constructed without our method exhibited unphysical behaviors in MLP-MD simulations, such as atomic collisions. In contrast, our method provided a significant improvement in MLP accuracy. We also confirmed that MLP is robust to scaling up size.

2 METHODOLOGY

2.1 Radial distribution function-based data sampling

Radial distribution function-based data sampling was performed to detect and extract anomalous structures from MLP-MD trajectories. Then, we retrained the reference data using additional anomalous structures to improve the MLP accuracy. Figure 1 shows the simple computational flow of RDF-based data sampling. In this section, we briefly describe this approach. The detailed computational flow is provided in Supplementary Material.

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

A brief computational flow of the radial distribution function (RDF)-based data sampling for machine learning potential (MLP).

First, we prepared an initial reference dataset consisting of a set of coordinates and corresponding energies and forces. An MLP was constructed by training a neural network model with reference data. Then, the MLP was used to perform short MLP-MD simulations, and the RDFs for each trajectory were computed. Note that this RDF is the distribution of the density of a particle–particle distance in a system at a given time, which does not include the time average. In this study, we calculated the RDFs of oxygen–oxygen (OO), oxygen–hydrogen (OH), and hydrogen–hydrogen (HH) atoms in water.

Next, we detected anomalous structures using RDFs. We focused on two regions (A and B) in the RDFs (Figure 2). Region A corresponds to interatomic distances up to the front of the first peak position in the correct RDF. Therefore, the RDF values in region A must be zero because the structures have interatomic distances that are too short to be observed in the proper structures. If we detect anomalous structures with non-zero RDF values in region A of the MLP-MD simulations, we can assume that the MLP has not correctly learned these structures. Then, anomalous structures were added to the reference dataset as new data. The lower limit of region A was set to approximately the diatomic intramolecular distance. Interatomic distances shorter than those in region A were too short for convergence in the QC calculations. In addition, because structures with anomalies in this region have high energies, sampling those structures is not expected to improve MLP accuracy. Thus, we excluded this region from the detection of anomalous structures. The exact criteria are provided in Supplementary Material.

We compared the calculated RDF and reference RDF (ref-RDF) in region B. The ref-RDF can be derived from experimental results or CMD simulations. The difference between the calculated RDF (

g_{XY} (r)

) and ref-RDFs (

g_{XY}^{ref} (r)

) between atoms X and Y were estimated by the root mean square error (RMSE)

Δ g_{XY}

. We divided region B of the interval

[a, b]

into

N

equal parts and let

r_{0}, r_{1}, \dots, r_{i}, \dots, r_{N}

be each equinox. Here,

r_{0}

and

r_{N}

are the left (a) and right (b) ends, respectively. Then, the RMSE

Δ g_{XY}

is defined by

Δ g_{XY} = \sqrt{\frac{\sum_{i = 0}^{N} {(g_{XY} (r_{i}) - g_{XY}^{ref} (r_{i}))}^{2}}{N + 1}}

When

Δ g_{XY}

is higher than the threshold value, the original molecular cluster is added to the reference dataset. This verification process was conducted for regions A and B in that order.

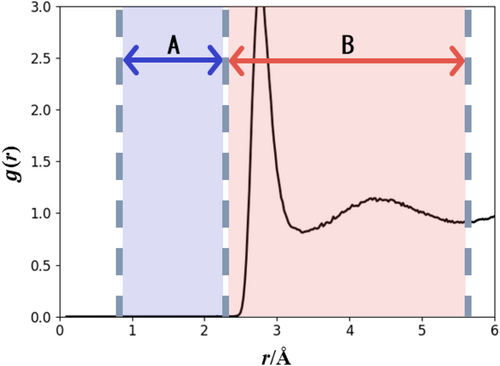
Any RDFs can function as ref-RDFs whenever the RDFs have features of the target system. In this study, we chose the TIP4P force field for the ref-RDFs generation, which is different force field used to generate training data structures. Ref-RDFs were prepared from CMD simulations with the Nose–Hoover thermostat^{51, 52} for temperature control in the NVT ensemble using the LAMMPS software.⁵³ Note that one can use other ref-RDF, such as those obtained from experiments, other computational methods, and so on. Because the TIP4P model⁵⁴ is a rigid-body model, the intramolecular distances of OH and HH are constant, and therefore, sharp peaks of the RDFs appear. These peaks are presumed to cause the large $Δ g_{OH}$ and $Δ g_{HH}$ values in region B owing to their large RDF values. To address this issue, we excluded these regions from the comparison. The series of processes from the MLP construction to anomalous structure sampling were repeated three times to improve the MLP. More detailed information on the boundary for regions A and B and the sampling thresholds for $Δ g_{XY}$ are shown in Supplementary Material.

2.2 Reference dataset

We prepared an initial reference dataset that included the geometries, energies, and forces of water cluster systems with 1, 10, 27, 64, and 100 H₂O molecules. A set of structures in the monomeric H₂O molecular system was constructed with two hydrogen atoms and one oxygen atom in a random arrangement. The structures of the other cluster systems were extracted from CMD simulations. The simulation cells had the same number of H₂O molecules as molecular clusters. After CMD simulations, we extracted the water cluster structures in the unit cell of each trajectory. Then, we calculated the energies and forces of the cluster structures using QC calculations and added them to the reference dataset. This two-step dataset construction strategy was proposed as an efficient method for initial data sampling.⁴² The CMD simulations were performed using the TIP3P force field under the NVT ensemble. The densities of water were 0.94, 1.00, and 1.13 g/cm³ at temperatures of 300 and 600 K, resulting in a total of six combinations of density and temperature conditions. The number of reference structures obtained is listed in Table 1; they were separated into training and validation data.

TABLE 1. The numbers of initial reference data for MLP construction for each H₂O cluster.

#H₂O	1	10	27	64	100
Total reference data	99	1200	3600	12,000	23,100
Training data^a	66	960	2880	10,200	18,600
Validation data^b	33	240	720	1800	4500

^a 60%–85% of total data.
^b Remainder of total data.

We construct the initial MLPs using the initial reference datasets. Subsequently, we updated only 100 H₂O molecular cluster data, while RDF-based data sampling cycles described in Section 2.1 and the other cluster size dataset remained unchanged.

2.3 Machine learning potential construction

This study used Deep Potential – Smooth Edition (DeepPot-SE)²⁴ of the DeepMD-kit package⁵⁵ as a neural network model to construct MLPs. In previous studies, DeepPot-SE was used for MLP construction in bulk water.^{30, 37, 42, 56} The sizes of the embedding and fitting networks of DeepPot-SE were set to (25, 50, 100) and (320, 160, 32, 16), respectively, and the learning steps were set to 1 × 10⁶ epoch per learning. In addition, five MLPs were created in parallel during one cycle to achieve a greater efficiency. Detailed training conditions are provided in Supplementary Material.

2.4 Machine learning potential-based molecular dynamics simulation

We performed MLP-MD simulations using the LAMMPS software⁵³ with the DeepMD plugin.⁵⁵ Short MLP-MD simulations in RDF-based data sampling cycles were performed over a period of 2 ps, extracting trajectory snapshots every 0.2 ps under the NVT ensemble using the Nose–Hoover thermostat with three densities (0.94, 1.00, and 1.13 g/cm³) at 300 K.

2.5 Quantum chemical calculation

Quantum chemical calculations were performed to prepare reference data using Gaussian 16 software.⁵⁷ To efficiently prepare the reference dataset, we employed the PM6 semi-empirical molecular orbital method⁵⁸ to calculate the energies and forces of the water molecular clusters.

3 RESULTS AND DISCUSSION

3.1 Conventional construction of machine learning potential

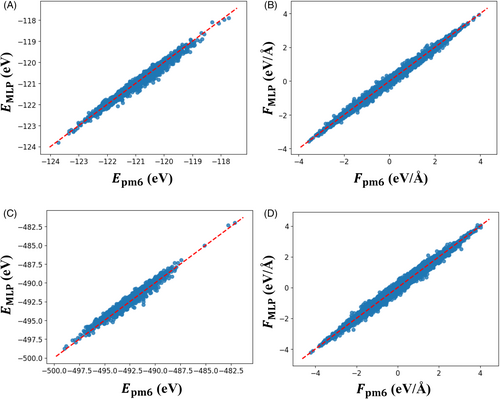
First, we construct an MLP without using the RDF-based data sampling method. Figure 3 shows parity plots of the energies and forces of the PM6 and MLP for reference data of 100 H₂O clusters. The energy and force data distributions are spread over a range of −253 to −237 eV and −4 to 4 eV/Å, respectively. The energy plots in Figure 3A are distributed with a slight downward bulge, and the obtained MLP tends to underestimate the energy. The RMSEs of the energies and forces for the validation data were 0.927 meV/atom and 38.4 meV/Å, respectively, which were smaller than the values of 1 meV/atom and 50 meV/Å that were recommended by Wen et al.⁵⁹

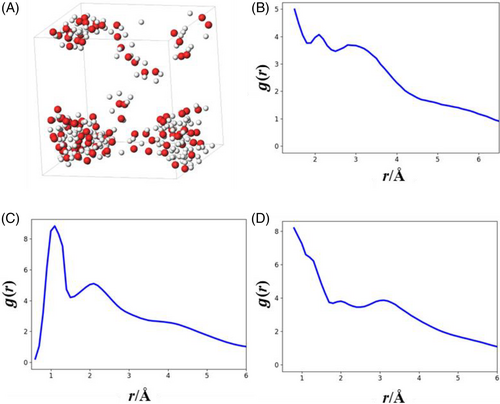
We performed an MLP-MD simulation for 50 ps in a unit cell containing 100 H₂O. A snapshot of the simulation (Figure 4A) shows the aggregation of oxygen and hydrogen atoms and unnatural chain structures. Figure 4B–D show the RDFs of OO, OH, and HH, respectively. These RDFs differ significantly from the RDFs of bulk water. These results suggest a case in which MLP-MD simulations show unphysical behaviors, even if the prediction accuracy of the MLPs seems satisfactory. This study prepared reference data by combining CMD simulations under different conditions with QC calculations. Nonetheless, the reference data does not cover a sufficient structural space. Therefore, appropriate reference data construction is necessary to perform MLP-MD simulations comparable to AIMD simulations.

3.2 Machine learning potential with radial distribution function-based data sampling

We applied our RDF-based data sampling method to improve the accuracy of MLP and MLP-MD simulations. After three sampling cycles, 231 additional structures were obtained. This number is sufficiently small compared to the original 100 H₂O cluster structures (23,100). In addition, the number of detected anomalous structures for each cycle was 149, 51, and 31, which is more than half of which were sampled in the first cycle. In the second and third cycles, anomalies were detected only in region B of the RDF, suggesting that the detected anomalous structures did not include those with extremely short interatomic distances. Even the detected anomalous structures slightly exceeded the thresholds of $Δ g_{XY}$ . These threshold exceedances are likely caused by the inconsistent RDFs of PM6 and TIP4P. As a result, we obtained at least the minimum structures required to improve the MLP accuracy.

Figure 5 shows the parity plots for the energies and forces of PM6 and improved MLP in the system with 100 H₂O clusters. The top end of the energy plots expanded from −240 (Figure 3A) to −180 eV (Figure 5A) through sampling. The force range also expanded from an initial range of −4 to 4 eV/Å (Figure 3B) to a final range of −30 to 30 eV/Å (Figure 5B). Additional structures caused these distribution spreads. In particular, the energy distribution indicated that structures could be obtained during the early stages of structural collapse. Strong repulsive interaction data was added to the reference data. The strong repulsion did not seem to have been estimated accurately by the MLP before applying this sampling method (Figure 4). Some water cluster structures added to the reference data are shown in Figure S3 (Supplementary Material). The RMSEs of the energy and force were 1.01 meV/atom and 43.9 meV/Å, respectively. The additional data caused this slight increase in the RMSEs.

We performed an MLP-MD simulation of the bulk water system to verify the appearance of any unphysical behaviors. The MLP-MD simulation was performed for 50 ps in the unit cell with 100 H₂O at a density of 1.00 g/cm³ and 300 K. For comparison, we also conducted a semi-empirical MD simulation at the PM6 level using the CP2K software.⁶⁰ Detailed information on the semi-empirical MD simulation is described in Supplementary Material.

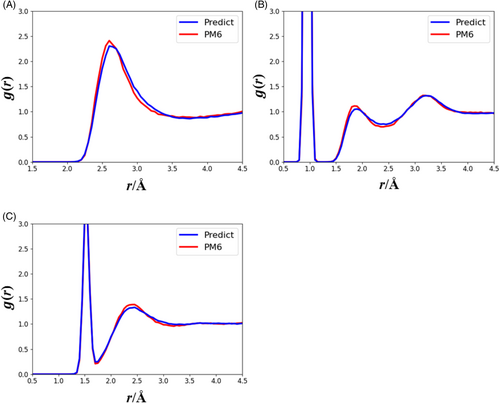
Compared with the RDFs computed by the MLP trained without RDF-based data sampling (Figure 4), we determined that the MLP improved by applying RDF-based data sampling and showed stable behaviors that reflected the characteristics of water. Figure 6 shows the RDFs of OO, OH, and HH derived from the MLP-MD and semi-empirical MD simulations. The RDF behaviors, such as the standing positions and heights of the peaks and valleys in the three RDFs, are consistent with the results of the MLP-MD (blue lines) and semi-empirical MD simulations (red lines). The shapes of the obtained RDFs are also consistent with those of previous PM6 studies.^{61, 62}

Furthermore, we computed the normalized frequency of the triplet OOO angles that consist of an oxygen atom and two of the four nearest-neighbor oxygen atoms (Figure 7A). The experimental results show that the triplet OOO angles are widely distributed at approximately 100°.^{63, 64} The results of the MLP-MD and semi-empirical MD simulations shown in Figure 7B show the same features, such as two peaks at approximately 60° and 100° and a decay of the distribution tail.

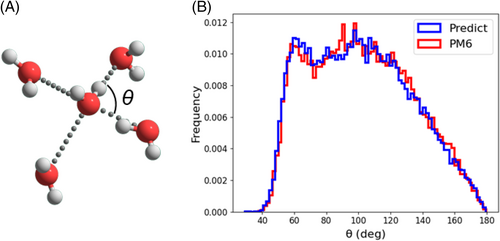
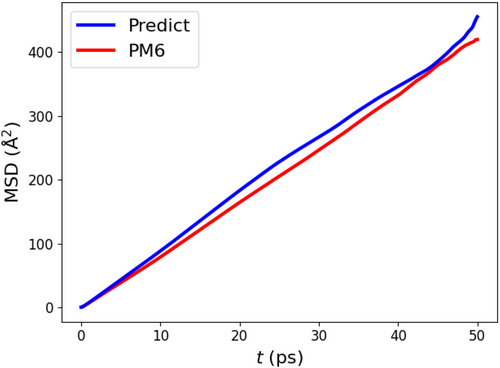
We also computed mean square displacement (MSD) and self-diffusion coefficient to verify the dynamical reproductivity. We performed 50 ps MLP-MD and semi-empirical MD simulations at 300 K. The MSD and the estimated self-diffusion coefficient were computed using MD Analysis library.^{65, 66} Figure 8 shows the calculated MSDs as a function of time. The self-diffusion coefficients for MLP-MD and semi-empirical MD simulations were 1.43 and 1.41 Å²/ps, respectively. These results show that the MLP-MD simulations are good reproductivity of the structural and dynamical characteristics.

To verify the amount of data required to construct an appropriate MLP, we also constructed an MLP trained with half the amount of the original reference data. We computed the RMSEs of the energy and force of validation data and the RDFs. The results are shown in Supplementary Material. Although the accuracy and reproducibility of the RDFs were slightly lower than those of the original MLP, they were still sufficiently practical, suggesting that our method is effective even when the amount of data is reduced. The tuning of hyperparameters, such as the number of neurons and epoch number, will help further improve the MLP accuracy.

We conclude that the quality of MLPs cannot be accurately measured only by energy and force predictions in some cases, and attention should be paid to the structures that appear in the MLP-MD simulations. Our method overcomes this problem by focusing on anomalous RDF shapes. Although the initial reference data did not cover sufficient structural space, the MLPs improved to the point where they could reproduce semi-empirical MD simulations.

3.3 Verification of cluster size extrapolation

In Sections 3.1 and 3.2, we showed that even when the prediction accuracy of the reference data is sufficient, MLP-MD causes unphysical behaviors owing to the incomplete dataset, and these phenomena are solved by RDF-based data sampling. In this section, we investigate the cluster size scalability of the MLP. Here, we tested whether the MLP could predict the energies and forces of molecular clusters with sizes not included in the reference dataset. We prepared the test data for 50 and 200 H₂O clusters as cases with clusters smaller and larger than 100 H₂O clusters, respectively. A total of 1500 test data points for both 50 and 200 H₂O clusters were newly prepared using CMD simulations to generate cluster structures and QC calculations at the PM6 level to obtain the energies and forces. Figure 9 shows the parity plots of the energies and forces of PM6 and MLP in systems with 50 and 200 H₂O clusters. The RMSEs of the energy and force of the 50 H₂O clusters were 0.872 meV/atom and 36.5 meV/Å, respectively, and those of the 200 H₂O clusters were 0.733 meV/atom and 44.0 meV/Å. All these values were lower than the recommended thresholds, ensuring cluster size scalability for our MLP. These results also indicated that as the cluster size increased, the RMSE of the energy per atom decreased. Therefore, we confirmed that our MLP exhibits size scalability for both bulk and cluster systems. In this work we applied our method only for pure water. When adding more other molecules in aqueous solution or changing the computational method of the training data, MLPs can be easily reconstructed by using transfer learning⁶⁷ or delta learning methods.⁶⁸

4 CONCLUSION

The preparation of sufficient reference data is essential for generating MLPs. Insufficient data causes unphysical behavior in MLP-MD simulations. In this study, we proposed a simple on-the-fly data sampling method, namely RDF-based data sampling, to improve the accuracy of the MLP. This method was applied to liquid–water systems. RDF-based data sampling detected anomalous structures made from MLP-MD simulations, focusing on the anomalous shapes of RDFs, and added those structures to the reference dataset. The MLP-MD simulation without RDF-based data sampling showed unphysical behaviors, such as aggregation of atoms or an unnatural chain structure, despite the good RMSE values of the predictions for the validation data. However, by applying RDF-based data sampling, the prediction accuracy of the MLP improved significantly with few additional data. Our final MLP-MD simulations produced appropriate RDFs, triplet OOO angle distributions, MSD, and self-diffusion coefficient, which were comparable with the results of semi-empirical MD simulations. These results indicate that RDF-based data sampling helps construct an MLP that is robust to extrapolation from molecular clusters to bulk systems. This simple sampling method can be applied to molecular aggregation systems other than water by appropriately changing specific parameters. Further improvements in MLP accuracy are expected when RDF-based data sampling is combined with different sampling methods or machine learning algorithms.

ACKNOWLEDGMENTS

This study was supported by Japan Society for the Promotion of Science Grants-in-Aid for Scientific Research [Grant Number JP24K17108, JP24KJ0486]; a Grant-in-Aid for Transformative Research Areas “Materials Science of Meso-Hierarchy” [Grant Number JP23H04879]; the Japan Science and Technology Agency, which is the establishment of university fellowships for the creation of science technology innovation [Grant Number JPMJFS2106]; Institute for Quantum Chemical Exploration, 2024 Research Grants-in-Aid; and the Multidisciplinary Cooperative Research Program at the Center for Computational Sciences, University of Tsukuba. Some of the computations were performed using computer facilities at the Research Institute for Information Technology, Kyushu University, for General Projects on the supercomputer “Flow” at the Information Technology Center, and Nagoya University.

CONFLICT OF INTEREST STATEMENT

The authors declare no competing financial interests.

Open Research

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are openly available in MLP-for-Water at https://github.com/Natsuww/MLP-for-Water.

Supporting Information

REFERENCES

1M. Karplus, G. Petsko, Nature 1990, 347, 631.
10.1038/347631a0
CAS PubMed Web of Science® Google Scholar
2T. Hama, N. Watanabe, Chem. Rev. 2013, 113, 8783.
10.1021/cr4000978
CAS PubMed Web of Science® Google Scholar
3G. C. Sosso, J. Chen, S. J. Cox, M. Fitzner, P. Pedevilla, A. Zen, A. Michaelides, Chem. Rev. 2016, 116, 7078.
10.1021/acs.chemrev.5b00744
CAS PubMed Web of Science® Google Scholar
4G. Kupgan, L. J. Abbott, K. E. Hart, C. M. Colina, Chem. Rev. 2018, 118, 5488.
10.1021/acs.chemrev.7b00691
CAS PubMed Web of Science® Google Scholar
5G. Enkavi, M. Javanainen, W. Kulig, T. Róg, I. Vattulainen, Chem. Rev. 2019, 119, 5607.
10.1021/acs.chemrev.8b00538
CAS PubMed Web of Science® Google Scholar
6T. R. Underwood, I. C. Bourg, J. Phys. Chem. C 2020, 124, 3702.
10.1021/acs.jpcc.9b11197
CAS Web of Science® Google Scholar
7D. Guo, L. H. Zhang, X. G. Li, X. Yang, Y. L. Zhao, X. Chen, Langmuir 2024, 40, 818.
10.1021/acs.langmuir.3c03011
CAS PubMed Google Scholar
8W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey, M. L. Klein, J. Chem. Phys. 1983, 79, 926.
10.1063/1.445869
CAS Web of Science® Google Scholar
9H. J. C. Berendsen, J. R. Grigera, T. P. Straatsma, J. Phys. Chem. 1987, 91, 6269.
10.1021/j100308a038
CAS Web of Science® Google Scholar
10J. Tersoff, Phys. Rev. B Condens. Matter 1988, 37, 6991.
10.1103/PhysRevB.37.6991
CAS PubMed Web of Science® Google Scholar
11J. Tersoff, Phys. Rev. Lett. 1988, 61, 2879.
10.1103/PhysRevLett.61.2879
CAS PubMed Web of Science® Google Scholar
12D. W. Brenner, Phys. Rev. B Condens. Matter 1990, 42, 9458.
10.1103/PhysRevB.42.9458
CAS PubMed Web of Science® Google Scholar
13A. D. J. MacKerell, D. Bashford, M. Bellott, R. L. J. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiórkiewicz-Kuczera, D. Yin, M. J. Karplus, Phys. Chem. B 1998, 102, 3586.
10.1021/jp973084f
CAS PubMed Web of Science® Google Scholar
14D. W. Brenner, O. A. Shenderova, J. A. Harrison, S. J. Stuart, B. Ni, S. B. Sinnott, J. Phys. B Condens. Matter 2002, 14, 783.
10.1088/0953-8984/14/4/312
CAS Web of Science® Google Scholar
15J. Sarnthein, A. Pasquarello, R. Car, Phys. Rev. B Condens. Matter 1995, 52, 12690.
10.1103/PhysRevB.52.12690
CAS PubMed Web of Science® Google Scholar
16C. Mischler, W. Kob, K. Binder, Comput. Phys. Commun. 2002, 147, 222.
10.1016/S0010-4655(02)00250-3
Web of Science® Google Scholar
17L. Koči, R. Ahuja, A. B. Belonoshko, J. Phys. Conf. Ser. 2008, 121, 012005.
10.1088/1742-6596/121/1/012005
Google Scholar
18K. Leung, J. L. Budzien, Phys. Chem. Chem. Phys. 2010, 12, 6583.
10.1039/b925853a
CAS PubMed Web of Science® Google Scholar
19Á. Cimas, F. Tielens, M. Sulpizi, M. P. Gaigeot, D. Costa, J. Phys. B Condens. Matter 2014, 26, 244106.
10.1088/0953-8984/26/24/244106
CAS PubMed Web of Science® Google Scholar
20M. Chen, H. Y. Ko, R. C. Remsing, M. F. Calegari Andrade, B. Santra, Z. Sun, A. Selloni, R. Car, M. L. Klein, J. P. Perdew, X. Wu, Proc. Natl. Acad. Sci. U. S. A. 2017, 114, 10846.
10.1073/pnas.1712499114
CAS PubMed Web of Science® Google Scholar
21J. Behler, Chem. Rev. 2021, 121, 10037.
10.1021/acs.chemrev.0c00868
CAS PubMed Web of Science® Google Scholar
22N. Yao, X. Chen, Z. H. Fu, Q. Zhang, Chem. Rev. 2022, 122, 10970.
10.1021/acs.chemrev.1c00904
CAS PubMed Web of Science® Google Scholar
23J. Behler, M. Parrinello, Phys. Rev. Lett. 2007, 98, 146401.
10.1103/PhysRevLett.98.146401
CAS PubMed Web of Science® Google Scholar
24L. Zhang, J. Han, H. Wang, W. A. Saidi, R. Car, E. Weinan, Adv. Neural Inf. Process. Syst. 2018, 31, 4436.
Google Scholar
25W. Li, Y. Ando, E. Minamitani, S. Watanabe, J. Chem. Phys. 2017, 147, 214106.
10.1063/1.4997242
PubMed Web of Science® Google Scholar
26A. M. Tokita, J. Behler, J. Chem. Phys. 2023, 159, 121501.
10.1063/5.0160326
CAS PubMed Web of Science® Google Scholar
27T. W. Ko, J. A. Finkler, S. Goedecker, J. Behler, Nat. Commun. 2021, 12, 398.
10.1038/s41467-020-20427-2
CAS PubMed Web of Science® Google Scholar
28L. Zhang, H. Wang, R. Car, E. Weinan, Phys. Rev. Lett. 2021, 126, 236001.
10.1103/PhysRevLett.126.236001
CAS PubMed Web of Science® Google Scholar
29R. Mathur, M. C. Muniz, S. Yue, R. Car, A. Z. J. Panagiotopoulos, Phys. Chem. B 2023, 127, 4562.
10.1021/acs.jpcb.3c00610
CAS PubMed Google Scholar
30I. Sanchez-Burgos, M. C. Muniz, J. R. Espinosa, A. Z. Panagiotopoulos, J. Chem. Phys. 2023, 158, 184504.
10.1063/5.0144500
CAS PubMed Google Scholar
31K. Wan, J. He, X. Shi, Adv. Mater. 2024, 36, 2305758. https://doi.org/10.1002/adma.202305758
10.1002/adma.202305758
CAS Google Scholar
32S. Jiang, Y. R. Liu, T. Huang, Y. J. Feng, C. Y. Wang, Z. Q. Wang, B. J. Ge, Q. S. Liu, W. R. Guang, W. Huang, Nat. Commun. 2022, 13, 6067.
10.1038/s41467-022-33783-y
CAS PubMed Web of Science® Google Scholar
33I.-B. Magdău, D. J. Arismendi-Arrieta, H. E. Smith, C. P. Grey, K. Hermansson, G. Csányi, Npj Comput. Mater. 2023, 9, 146.
10.1038/s41524-023-01100-w
CAS Google Scholar
34H. D. Wang, Y. L. Fu, B. Fu, W. Fang, D. H. Zhang, Phys. Chem. Chem. Phys. 2023, 25, 8117.
10.1039/D3CP00312D
CAS PubMed Web of Science® Google Scholar
35J. Zhang, H. Zhang, Z. Qin, Y. Kang, X. Hong, T. Hou, J. Chem. Inf. Model. 2023, 63, 1133.
10.1021/acs.jcim.2c01497
CAS PubMed Google Scholar
36J. Liu, L. W. Qi, J. Z. H. Zhang, X. He, J. Chem. Theory Comput. 2017, 13, 2021.
10.1021/acs.jctc.7b00149
CAS PubMed Web of Science® Google Scholar
37J. Liu, J. Lan, X. He, J. Phys. Chem. A 2022, 126, 3926.
10.1021/acs.jpca.2c00601
CAS PubMed Web of Science® Google Scholar
38K. Kato, T. Masuda, C. Watanabe, N. Miyagawa, H. Mizouchi, S. Nagase, K. Kamisaka, K. Oshima, S. Ono, H. Ueda, A. Tokuhisa, R. Kanada, M. Ohta, M. Ikeguchi, Y. Okuno, K. Fukuzawa, T. Honma, J. Chem. Inf. Model. 2020, 60, 3361.
10.1021/acs.jcim.0c00273
CAS PubMed Web of Science® Google Scholar
39G. Molpeceres, V. Zaverkin, J. Kästner, Mon. Not. R. Astron. Soc. 2020, 499, 1373.
10.1093/mnras/staa2891
CAS Web of Science® Google Scholar
40V. Zaverkin, D. Holzmüller, R. Schuldt, J. Kästner, J. Chem. Phys. 2022, 156, 114103.
10.1063/5.0078983
CAS PubMed Web of Science® Google Scholar
41S. Käser, L. I. Vazquez-Salazar, M. Meuwly, K. Töpfer, Digit. Discov. 2023, 2, 28.
10.1039/D2DD00102K
CAS PubMed Web of Science® Google Scholar
42M. S. Gomes-Filho, A. Torres, A. Reily Rocha, L. S. Pedroza, J. Phys. Chem. B 2023, 127, 1422.
10.1021/acs.jpcb.2c09059
CAS PubMed Google Scholar
43S. Liu, R. Dupuis, D. Fan, S. Benzaria, M. Bonneau, P. Bhatt, M. Eddaoudi, G. Maurin, Chem. Sci. 2024, 15, 5294.
10.1039/D3SC05612K
CAS PubMed Web of Science® Google Scholar
44D. Yoo, J. Jung, W. Jeong, S. Han, Npj Comput. Mater. 2021, 7, 131.
10.1038/s41524-021-00595-5
CAS Web of Science® Google Scholar
45M. Yang, L. Bonati, D. Polino, M. Parrinello, Cat. Today 2022, 387, 143.
10.1016/j.cattod.2021.03.018
CAS Google Scholar
46G. S. Jung, J. Y. Choi, S. M. Lee, Digit. Discov. 2024, 3, 514.
10.1039/D3DD00216K
Google Scholar
47T. Kobayashi, T. Ikeda, A. Nakayama, Chem. Sci. 2024, 15, 6816.
10.1039/D4SC01422G
CAS PubMed Google Scholar
48Y. Nagai, M. Okumura, K. Kobayashi, M. Shiga, Phys. Rev. B 2020, 102, 041124.
10.1103/PhysRevB.102.041124
CAS Web of Science® Google Scholar
49L. Zhang, D.-Y. Lin, H. Wang, R. Car, E. Weinan, Phys. Rev. Mater. 2019, 3, 023804.
10.1103/PhysRevMaterials.3.023804
CAS Web of Science® Google Scholar
50P. Zhang, N. Zhang, C. Gao, L. Zhang, Y. Gao, Y. Deng, D. Bluestein, Comput. Phys. Commun. 2016, 204, 132.
10.1016/j.cpc.2016.03.019
CAS PubMed Google Scholar
51S. Nosé, J. Chem. Phys. 1984, 81, 511.
10.1063/1.447334
CAS Web of Science® Google Scholar
52W. G. Hoover, Phys. Rev. A 1985, 31, 1695.
10.1103/PhysRevA.31.1695
CAS PubMed Web of Science® Google Scholar
53S. Plimpton, J. Comput. Phys. 1995, 117, 1.
10.1006/jcph.1995.1039
CAS Web of Science® Google Scholar
54J. L. Abascal, C. Vega, J. Chem. Phys. 2005, 123, 234505.
10.1063/1.2121687
CAS PubMed Web of Science® Google Scholar
55H. Wang, L. Zhang, J. Han, E. Weinan, Comput. Phys. Commun. 2018, 228, 178.
10.1016/j.cpc.2018.03.016
CAS Web of Science® Google Scholar
56M. C. Muniz, R. Car, A. Z. Panagiotopoulos, J. Phys. Chem. B 2023, 127, 9165.
10.1021/acs.jpcb.3c04629
CAS PubMed Google Scholar
57M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, H. Fox, Gaussian 16, revision B.01, Gaussian Inc, Wallingford, CT 2016.
Google Scholar
58J. J. Stewart, J. Mol. Model. 2007, 13, 1173.
10.1007/s00894-007-0233-4
CAS PubMed Web of Science® Google Scholar
59T. Wen, L. Zhang, H. Wang, D. J. Srolovitz, E. Weinan, Mater. Fut. 2022, 1, 022601.
10.1088/2752-5724/ac681d
CAS Google Scholar
60T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöß, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack, J. Hutter, J. Chem. Phys. 2020, 152, 194103.
10.1063/5.0007045
CAS PubMed Web of Science® Google Scholar
61G. Murdachaew, C. J. Mundy, G. K. Schenter, T. Laino, J. Hutter, J. Phys. Chem. A 2011, 115, 6046.
10.1021/jp110481m
CAS PubMed Web of Science® Google Scholar
62M. Welborn, J. Chen, L. P. Wang, T. Van Voorhis, J. Comput. Chem. 2015, 36, 934.
10.1002/jcc.23887
CAS PubMed Web of Science® Google Scholar
63A. K. Soper, C. J. Benmore, Phys. Rev. Lett. 2008, 101, 065502.
10.1103/PhysRevLett.101.065502
CAS PubMed Web of Science® Google Scholar
64R. A. DiStasio Jr., B. Santra, Z. Li, X. Wu, R. Car, J. Chem. Phys. 2014, 141, 084502.
10.1063/1.4893377
CAS PubMed Web of Science® Google Scholar
65R. J. Gowers, M. Linke, J. Barnoud, T. J. E. Reddy, M. N. Melo, S. L. Seyler, J. Domański, D. L. Dotson, S. Buchoux, I. M. Kenney, O. Beckstein, presented at Proc. 15th Python in Science Conference, Austin, TX, 2016, p. 98.
Google Scholar
66N. Michaud-Agrawal, E. J. Denning, T. B. Woolf, O. Beckstein, J. Comput. Chem. 2011, 32, 2319.
10.1002/jcc.21787
CAS PubMed Web of Science® Google Scholar
67V. Zaverkin, D. Holzmüller, L. Bonfirraro, J. Kästner, Phys. Chem. Chem. Phys. 2023, 25, 5383.
10.1039/D2CP05793J
CAS PubMed Web of Science® Google Scholar
68L. D. Jacobson, J. M. Stevenson, F. Ramezanghorbani, D. Ghoreishi, K. Leswing, E. D. Harder, R. Abel, J. Chem. Theory Comput. 2022, 18, 2354.
10.1021/acs.jctc.1c00821
CAS PubMed Web of Science® Google Scholar

Citing Literature

Volume45, Issue32

December 15, 2024

Pages 2949-2958

A machine learning potential construction based on radial distribution function sampling

Abstract

1 INTRODUCTION

2 METHODOLOGY

2.1 Radial distribution function-based data sampling

2.2 Reference dataset

2.3 Machine learning potential construction

2.4 Machine learning potential-based molecular dynamics simulation

2.5 Quantum chemical calculation

3 RESULTS AND DISCUSSION

3.1 Conventional construction of machine learning potential

3.2 Machine learning potential with radial distribution function-based data sampling

3.3 Verification of cluster size extrapolation

4 CONCLUSION

ACKNOWLEDGMENTS

CONFLICT OF INTEREST STATEMENT

Open Research

DATA AVAILABILITY STATEMENT

Supporting Information

REFERENCES

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A machine learning potential construction based on radial distribution function sampling

Abstract

1 INTRODUCTION

2 METHODOLOGY

2.1 Radial distribution function-based data sampling

2.2 Reference dataset

2.3 Machine learning potential construction

2.4 Machine learning potential-based molecular dynamics simulation

2.5 Quantum chemical calculation

3 RESULTS AND DISCUSSION

3.1 Conventional construction of machine learning potential

3.2 Machine learning potential with radial distribution function-based data sampling

3.3 Verification of cluster size extrapolation

4 CONCLUSION

ACKNOWLEDGMENTS

CONFLICT OF INTEREST STATEMENT

Open Research

DATA AVAILABILITY STATEMENT

Supporting Information

REFERENCES

Citing Literature

Figures

References

Related

Information