Delocalization-ratio analysis of 3-center bonding in position-space for closo-boranes and related systems: Approaching the styx picture and beyond
Abstract
Closo-boron hydrides BnHn2− (n = 5–12) are a conceptually well understood class of compounds. For these and a few related prototype compounds, both the local and the global picture of 3-center bonding are extracted from position-space quantities based on the electron density and the pair density. For this purpose, three-center delocalization indices between quantum theory of atoms in molecules (QTAIM) atoms in position space are used to develop a consistent set of local bond and triangle, and global cluster delocalization ratios (DRs), which are quantitatively compared with conceptual Γ values derived from the styx code for each cluster. Combination of the cluster DRs with associated effective numbers of skeletal electron sharing (SES) for selected cluster surface edges, triangles, or the whole cluster yields effective styx type values describing the trend and even the size of the conceptual styx codes for closo-boranes BnHn2− and related systems with increasing cluster size n reasonably well. For nonuniform cluster topologies, the different vertex degrees are shown to cause systematic 3-center wise bond delocalization effects for the associated edges and triangles of different average vertex degrees. Extension of DR analysis beyond the styx type triangular cluster-surface bonding corresponds to a triangulation of multicentric bonding. The cluster-wise results keep indicating consistency with the mixed 2- and 3-center bonding approach. The successfully established chemical meaning of the local edge, triangle, and global cluster DRs and their associated SES values constitutes the basis for systematic investigations of mixed 2- and 3-center bonding scenarios in particular in intermetallic and related (endohedral) cluster compounds in the future.
1 INTRODUCTION
Until today, there is still a lack of general valence theory of intermetallic compounds capable of conceptually explaining their diverse structures and chemical properties. The concepts and methods developed until now have apparently not been general enough to build up such a conceptual framework. In many intermetallic compounds, the number of covalently bonded neighbors around atomic species exceeds the number of electrons available for 2-center 2-electron bonding models. Moreover, the spatial arrangements of those neighbors may be not explainable within this type of models. In these respects, the molecular boron hydride clusters and related compounds display quite similar features. The introduction of the 3-center 2-electron bond formalism1, 2 has been the decisive feature to maintain the Lewis octet rule even for bonding scenarios, where the number of electrons is too short to form 2-center 2-electron bonds with all covalently bonded neighbors.
The styx conceptual framework of bonding in the boron hydride clusters consists of a sum of four different 2- and 3-center 2-electron skeletal bond types whose individual amounts denoted “s”, “t,” “y,” and “x” (forming the styx code of the cluster) are obtained from specific orbital, charge and hydrogen balance equations.3 This approach was shown to be a useful bonding model for systematization of structures and compositions of known and novel boron hydride compounds.4 With the Wade's observation,5 that already the reduced information contained in the number of skeletal electron pairs SEP = s + t + y + x6 is sufficient to set up a correlation with the novel structural topology systematics of the various cluster types,7 the styx approach became more and more superseded by the Wade's rules.
The Wade's rules are the result of the electron count for skeletal bond saturation,5, 8 which can be obtained from population analysis of canonical MO wavefunctions. The type of compounds successfully analyzed with the Wade-Mingos concept has been quickly extended from the borane, carborane, and carbocation compounds to metallaboranes and organometallic compounds, where the transition metal species are expected to follow the 18-electron rule and the isolobal concept.9
For a complete conceptual understanding of boranes and related compounds, both, the Wade and Mingos10 rules, and the Lipscomb's styx concept may be considered as necessary and important, each at its own level of understanding. While the Wade's rules relate the SEP number to the overall skeletal shapes of the clusters, the styx concept describes the underlying skeletal electronic structure in a conceptual way based on local 2- and 3-center 2-electron bond distributions capable of fulfilling the octet rule. In this sense, the way the bonds are formed, that is, the bonding architecture, creates the skeletal bond saturation at the respective electron count for the Wade's SEP rules. An important point not yet mentioned concerns the possible locally fractional-bond character of the octet-rule fulfilling bond distributions given by styx values. Especially in closo-boron hydrides, this is always the case. It is the result of the necessary resonance averaging of symmetry equivalent 2-electron bond allocations already at a conceptual level.3, 11
The knowledge obtained in many studies of this type can be considered to represent a robust basis for calibration of three- and multi-center bond treatments with new technologies.
Recently, the AdNDP (adaptive natural density partitioning) method,12 developed for the purpose of analyzing multicenter bonding scenarios, has been applied to closo-boron hydride molecules BnHn2− (n = 5–12).13 The resulting bonding picture for this prototype class of compounds reveals no relation to the Lipscomb's topological bonding scheme. The AdNDP localized orbital sets obtained with increasing cluster size n were shown to display a nonsystematic occurrence of 3-, 4-, 8-, and n-center 2-electron orbitals, and with skeletal 2-center 2-electron bonding orbitals completely missing. This scenario, classified as “flexible multicenter bonding” by the authors, represents a challenge for the conceptual understanding of the bonding architectures of closo-boranes and related compounds.
In the framework of position-space approaches to chemical bonding all difficulties of localized orbital representations with fractional bonding situations are avoided. The quantum theory of atoms in molecules (QTAIM) definition of an atom,14 electron localizability indicators in position space (ELF,15 and ELI-D16), and the delocalization indices (DIs, see below) between QTAIM atoms are derived from physical position-space quantities, the electron density and pair density.
Analysis of the ELF and ELI-D distributions in position space for selected closo boron hydrides and hexaborides revealed three different possible topologies, namely local maxima at (i) the deltahedral faces; (ii) the edges, or (iii) both, the faces and the edges.17, 18 While the detailed reasons for the different topologies remained unclear, it has been argued, that indications for skeletal edge and face bonding are related to the simultaneous presence of 2- and 3-center bonds in closo-boranes.18
In the framework of 3-center bond indices (BI, conceptually related to DIs) chemical bonding has been studied in certain nido- and arachno-boranes19 and also X2B3H3 (X = BH−, …) closo-borane homologues.20 The arguments for the presence of 3-center bonding have been based on the size of the corresponding 3c-BI being larger than a reasonably chosen boundary value of 0.1, and the occurrence of fractional 2-center effective bond orders with values significantly below 1.0 along the corresponding triangle edges. It has been found, that in the nido- or arachno-boranes investigated the type of 3-center bonds favored by Lipscomb and encoded into styx numbers do indeed have a significant contribution to the total electron count of the corresponding molecule. Moreover, domain averaged Fermi holes (DAFH) analysis has been applied to nido- and arachno-boranes.21 No further quantum chemical position-space studies have been reported to find quantitative connections to the styx code.
The goal of the present study is to set up a quantitative tool to detect and quantify 3-center bonding wherever it may occur, for example, in crystalline intermetallic compounds and in molecular multi-shell endohedral clusters as well. For calibration, the candidate tool (DRs) has to detect and quantify 3-center bonding in some prototype cases where we think to understand the 3-center bonding architectures already very well, that is, in closo-boranes and related systems. In a subsequent step, DR analysis is tested beyond the styx and the Wade's conceptual boundaries, namely beyond the deltahedral type of 3-center bond delocalization. As a result, a detailed view on the bonding architecture behind the overall Wade count of skeletal bonding MOs and styx values is obtained.
2 COMPUTATIONAL DETAILS
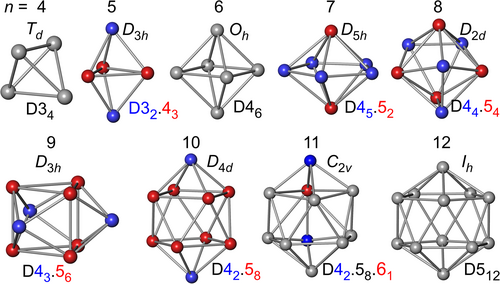
In order to assess the chemical meaning of DRs and their associated skeletal electron-sharing (SES) values, calibration studies on molecular systems B4H4, B4Cl4, BnHn2− (n = 5–12) and related molecules have been carried out on the basis of DFT-B3LYP22 calculations on optimized geometries. To exemplarily estimate the dependence of the results on the B3LYP functional used, for some compounds bonding analysis has been additionally carried out on DFT-PBE22 wavefunctions using the B3LYP optimized geometries for better comparison. The optimized structures of the molecules and their final wavefunctions were obtained from the Gaussian program.23 The skeletal structures, point group symmetries, and skeletal vertex compositions (see section 3.4) are given in Figure 1. For cubic CaB6 (Pm-3m, optimized a = 413.8 pm, xB = 0.2024) the solid state DFT (PBE) wavefunction obtained in Reference 18 using the ELK program system24 has been employed. The DFT (PBE) wavefunction for rhombohedral α-boron was computed with experimental structure parameters25 using the ELK program24 as well.
Partitioning of position space in terms of atomic regions was accomplished from their definition in position space using the QTAIM method.14 Calculation of the electron density, its subsequent topological analysis, and the calculation of the atomic overlap matrices was done with the DGrid program systems for molecular wavefunctions,26 and for solid-state wavefunctions.26 Calculation of 2- and 3-center delocalization indices from atomic overlap matrices, and of the various types of DR and SES values was done with program DISij.27
Calculation and analysis of tetrahedral B4H4 and C4H4 (Td) was performed for conceptual reasons, the Td structures correspond only to a vibrationally stable local minimum.28 For example, B4H4 is known to prefer a planar structure (Cs).
3 THEORY, CONCEPTS, AND COMPUTATION
Bond DRs G(A,B) (see below) have been initially defined in a bonding analysis study on solid state MB618 and subsequently employed for MB2 intermetallic compounds.29 The initial bond DRs can be used to consistently define triangle and full cluster DRs. These computational approaches are complementary to the conceptual ones of Wade and Lipscomb by including all types of real electronic structure features, for example, realistic charge distributions, bond-polarity effects, and electron sharing beyond nearest neighbors.
3.1 Delocalization ratios
The QTAIM definition of an atom A in a chemical system comprises the 3D spatial region belonging to the electron density basin Ω(A) and containing the nucleus of atom A. Electron sharing between these QTAIM atomic regions is described by delocalization indices.30, 31
Note, that the specific sequence of atoms in the 2- and 3-center DIs δ(A,B,C) is irrelevant. For example, all six site permutations (if A ≠ B ≠ C), and all three site permutations (A = B ≠ C) are included in the values of δ(A,B,C), and δ(A,A,C), respectively.
The last equality ensures the computability of G(A,B) from local quantities, which is important for crystalline systems, where the sum over 3-center DIs δ(A,B,X) (second equality) extends over an infinite number of terms.
This can be seen from the last equality, where the G3 value is given as a weighted sum of the G2 values of the edges.
This way, the total triangular DR G(A,B,C) of an atomic triangle (A,B,C) can be considered as the sum of a conceptually important part GkX;lY;mZ(A,B,C) and a conceptually neglected remainder. In the context of the present study, the deltahedral type of 3-center wise delocalization is the relevant part related to the styx concept. It employs only the skeletal edges and surface triangles of each n-vertex cluster deltahedron. In this case, each edge bond δ(A,B), δ(B,C), and δ(C,A) of the triangle (A,B,C) is restricted to delocalize to two atoms C and C′, A and A', and B and B′, respectively, because each deltahedral edge is connected to two deltahedral triangles. Lifting this restriction, one can also select more triangles, for example, by connecting each vertex to all other polyhedral atoms, which is investigated in section 4.2.
G(cluster) yields the same value as the individual G2 and G3 values, if all the edges or triangles included, respectively, are symmetrically identical.
While in Equation (14), there is no restriction on the edges A–B and triangles A–B–C chosen, that is, each combination of cluster atoms is included, it is conceptually decisive to be able to additionally analyze only the most important delocalization channels of each important edge, in a similar way as done in Equation (12). In the present context, we are especially interested in the bonding using the geometrically defined (important) edges and triangular faces of the deltahedral clusters. This restriction on edges and faces included is indicated by the superscript “Δ” (note, different writing of fluctuation variable Δ) in the following.
The calculation of the other two edge-employment frequencies n(B, C), and n(C, A) is done similarly. In the deltahedral cluster DRs GΔ(Bn), the edge-employment frequencies are always equal to 2, while for the ratios G(Bn) containing additional three-center wise delocalization channels they are always larger than 2 for all deltahedra besides the tetrahedron.
The partial DR of a triangle (A,B,C) with respect to the cluster value of the same set of {selected triangles} is calculated differently from the related value (Equation 12), because of the additional inclusion of the edge-employment frequencies required for the additivity property of partial DRs. This difference does not occur for partial DRs G2,part being identical to local G2 values. The deeper reason behind is that edges are clearly separated from each other, while the deltahedral triangles overlap at common edges.
As can be seen in Equations (18), 20, the G3,part values contain all selected cluster-wise delocalization channels of each edge. Restricting {sel. triangles} (Equation 18) to the deltahedral triangles yields the deltahedral partial G3 values denoted summing up to GΔ(cluster).
The local ses3,part values represent the bond-wise occupation of the corresponding triangle being associated with its G3,part value. Together, they yield the two pieces of information necessary to characterize and interpret 3-center bonding similar (but not identical) to the usual way, namely about its effective centricity (G value) and bond fraction (SES value).
3.2 Analytical DR, SESeff, and SEPeff values for model scenarios of n-center 2-electron bonding (n = 3–6)
With the general G-value scheme (Equations 5-21) at hand it is pertinent to investigate within a simple model, which values can be expected for different multicentric chemical bonding scenarios.
With this knowledge, all DIs and DRs can be analytically calculated (Table 1).
| System | δ(A,B) λ(A) | δ(A,B,C) δ(A,A,B) δ(A,A,A) | G(A,B) = G(A,B,C) = G(cluster) | SES2 = SES3 |
|---|---|---|---|---|
| Expressions | 4n−2 2n−2 |
12n−3 6n−3 2n−3 |
(n − 2) | 2(n − 1)n−1 |
n = 2 Linear |
1.0 0.5 |
0.0 0.75 0.25 |
0 | 1.0 |
n = 3 Ring |
|
|
1 | |
n = 4 Ring, tetrahedron |
0.25 0.125 |
0.1875 0.09375 0.03125 |
2 | 1.50 |
n = 5 Ring |
0.16 0.08 |
0.096 0.048 0.016 |
3 | 1.60 |
n = 6 Ring, octahedron |
|
|
4 |
For molecule H2 (n = 2), the 2-center DIs δ(H,H′) = 1, and δ(H,H,H′) = 6/8 is obtained. Since 3-center DI δ(H,H′,H″) does not exist here, there is no 3-center bond, which trivially confirms pure 2-center 2-electron bonding for this molecule. The same result is obtained, if a value of δ(H,H′,H″) = 0 had been given in the bond DR Equation (8) to yield G(H,H′) = 0.
For model-like H31+, we can imagine an equilateral triangle of H atoms, which has the right symmetry to justify S11σ(H) = 1/3. Note, that real H31+ has a non-nuclear electron-density maximum called NNM at the triangle center.33 In an explicit computation this would yield a total number of 4 QTAIM basins and a value of 1/3–x in the atomic overlap matrix of each H atom. In our model treatment, we consider the NNM basin and its occupation as infinitely small x ➔ 0, thus keeping with S11σ(H) = 1/3. This yields δ(H,H′,H″) = 0.44 and δ(H,H′,H″) = 0.22, from which G(H,H′) = 1 is obtained (Equation 8).18 From Equation (11), it is clear, that G(H,H′,H″) = G(H,H′) = 1, because of the identical weighting factor of 1/3 for each edge contribution. These are the G2 and G3 values expected for a system with ideal 3-center 2-electron type of bonding (Table 1).
The H42+ system is chosen as the largest model cluster Hn(n–2)+ explicitly discussed here, because it shows some peculiarities in common with the larger clusters n = 5, 6 which are worth noting. First, there are two geometric forms possible, the square and the tetrahedron, and with S11σ(H) = ¼ both yield exactly the same DI values δ(H,H′), δ(H,H′,H″), and δ(H,H,H′) (Table 1). These values do not even depend on the interatomic distance, which can be seen for the square with two HH distances available, namely the edge length d and the diagonal distance 21/2 d. For both of them the same value δ(H,H′) = 0.25 is obtained. Second, calculating G(H,H′) the fluctuation term Δfluc(H,H′) = δ(H,H′,H″) + δ(H,H′,H″’) has two contributions of equal size instead of only one as was the case for H31+ model. With δ(H,H,H′) = 6/64 and δ(H,H′,H″) = 12/64, the inclusion of only one contribution δ(H,H′,H″) into GH″(H,H′) = [12/64]/[12/64] yields a DR value of G1H(H,H′) = 1. With the additional inclusion of δ(H,H′,H″’), the final DR value G2H(H,H′) = 2 is obtained. It is the general result also obtained for 5- and 6-center 2-electron bonding models that in all these cases the step-wise inclusion of each of the n − 2 neighbors' 3-center DI into the G2 and G3 values increases it by an increment of 1. The incremental increase of 1 for the G value is considered the largest possible with the framework of DR analysis. Up to now, scenarios with significantly larger increments have not been found.
Summarizing, the values of the DRs G2, G3, and G(cluster) computed from 3-center delocalization indices give an indication, whether the actual bonding scenario within the selected unit is consistent with a mixed 2- and 3-center bonding situation or eventually even with higher-center bonding. Settling the latter case completely would clearly need further investigations and support from complementary methods beyond those employed in this study.
With an upper bound of G = 1 for perfect 3-center 2-electron bonding, and a lower bound of G = 0 (Equations 8, 11, 14, with Δfluc(A,B) = 0) for perfect 2-center 2-electron bonding, the question arises about the chemical meaning of intermediate values. The styx code for the closo-borane type of systems studied in the following suggests they are prototype examples for mixed 2- and 3-center 2-electron skeletal bonding, and this might be detected in the DR analysis shown in the following.
As a note for completeness, G can even adopt negative values, for example, for 3-center 4-electron bonding34 (e.g., linear H31−) the 3-center DI δ(H,H′,H″) < 0, and G(H,H′,H") = −0.11. All systems discussed in the present study, do not display significantly negative 3-center DIs.
Electron counting is an important technique in chemical bonding models, and the SES values represent bond counts in a sense different from what chemists are accustomed to, namely in the DI framework. From Table 1, it can be seen that in the various cases of n-center 2-electron bonding, the SES2 and SES3 values (SES2 = SES3 is valid only in this simple case) increase in a regular way from 1, the normally assumed value in case of 2-center 2-electron bonding, to 1.67 in case of 6-center 2-electron bonding.
These expressions are strictly valid for the n-center 2-electron type cases (SEC3 = 2) shown.
3.3 Connection with the styx concept: From SES and DR to SEP and styx
3.3.1 Computational skeletal electron sharing SES and conceptual SEP values
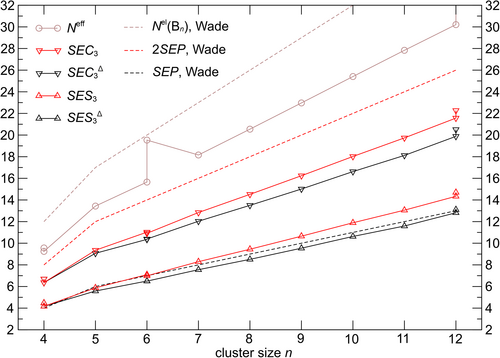
The decisive observation from a conceptual point of view is that the values of deltahedral electron sharing SES3Δ(Bn) are very close to the conceptual SEP values (Figure 2), while the best approximation to the 2SEP skeletal electrons counts SEC3Δ(Bn) is still missing an amount of electrons currently considered too high for detailed conceptual considerations. Thus, SES3Δ(Bn) is the quantum chemically computed quantity, that will be preferentially used to relate G3Δ(cluster) values to the Lipscomb picture. Noteworthy, this is not electron counting like the Wade's 2SEP is, but bond counting in the framework of delocalization indices.
3.3.2 Approaching closo styx values from skeletal SES and DR values
For boron hydrides and related systems, the chemical bonding scenario has been characterized as a mixture of 2-center and 3-center bonding as encoded in the styx code.3 In this code, parameter s denotes the number of skeletal 3-center 2-electron BHB bonds, t the number of skeletal 3-center 2-electron B–BB bonds, y the number of skeletal 2-center 2-electron BB bonds, and x the number of extra (besides the one always present exohedral bond per skeletal atom) 2-center 2-electron BH bonds.
A general description of the styx relations of 2- and 3-center bonding with increasing deltahedral cluster size n, is given in Supporting Information.
In order to establish a connection to the cluster G values above, a conceptual quantity has to be defined that has the same kind of principle behavior, namely boundary values 0 and 1 for pure 2- and 3-center bonding, respectively. For this purpose, two rather different conceptual frameworks have been connected. The styx values correspond to a conceptual framework completely different from the one of the G values, that is, t and y are not even conceptually similar to Δfluc and Δself, respectively. For example, while pure 3-center bonding without 2-center bonding, that is, y = 0 and t = n, is clearly conceivable, the situation Δself = 0, and Δfluc >0 is not possible. Thus, a one-to-one correspondence cannot even be expected to be found.
The key idea to circumvent this problem is to define from the initial two quantities of each framework, y and t, versus Δself and Δfluc, two derived quantities within each framework, Γ (concept) and SEP (concept) versus G and SES (and SEC), which can be used for pairwise comparison, Γ versus G, and SEP versus SES (and SEC), between the two frameworks. This will be shown in the following.
Another important difference between the styx picture and the present computational one employing quantities based on delocalization indices is the inclusion of an atomic definition, which leads to incorporation of bond-polarity effects not present in the conceptual styx picture. Effective atomic charges obtained from the actual DI calculations within the QTAIM framework has an effect on the cluster electron count and the cluster effective SES numbers. In order to relate conceptual quantities Γ and SEP to computational ones, this leads also to the additional requirement, that computational SES values are consistent with the corresponding G(cluster) values, that is, the same 2- and 3-center contributions have to be included. This way, to each DR G obtained for a certain 2-, 3-, or multiatomic unit (edge, triangle, cluster) there is also an exactly corresponding “bond count” SES, the former being the ratio, and the latter the sum of Δself and Δfluc. This is considered as the strength of the DR approach. Moreover, it is possible to relax this complete consistency between G values and associated SES values, by scaling the skeletal electron sharing values to yield skeletal electron counts SEC (Equation 27), which is an approximate procedure. The advantage gained is that SEC does represent an electron count like 2SEP and comparison between them is on the same footing, though the SEC values, while having the correct trend with cluster size, are significantly smaller (Figure 2) than the conceptual ones.
Summarizing, instead of chemically interpreting the initially obtained computational quantities Δself and Δfluc of the DI calculation, the two derived quantities G and SES will be shown to have a chemical meaning useful to discuss mixed 2- and 3-center bonding scenarios. They can be compared to conceptual Γ and SEPs, thus avoiding comparison of t, y with Δself and Δfluc.
In detail, the bond contributions used in the specific kind of G value for the borane cluster must be related to the Wade's number of skeletal electron pairs SEP implemented in the styx code, since SEP = t + y for closo-boranes. This has been achieved on the computational side by choosing the deltahedral variants GΔ(Bn) and the corresponding SES3Δ with the same 2- and 3-center DIs included.
Equations (37-40) have a conceptual meaning only if 0 ≤ GΔ(Bn) ≤ 1, such that values of , and , are positive.
3.4 Topological features of the closo-clusters' skeletal structures
The degree of a polyhedral vertex enumerates its number of connections (edges touching at that vertex).36 The vertex degrees of the n = 4, 6, 12 type of closo- deltahedra are uniform, that is, they are identical within each deltahedron, and display vertex degrees of 3, 4, and 5, respectively. This way, the n = 4, 6, 12 closo-deltahedra can be characterized by their vertex compositions D34, D46, and D512,11 where the subscript enumerates the number of vertices of given degree (Figure 1).
The remaining closo-deltahedra n = 5, 7–11 display a mixture of different vertex degrees, which can be indicated by their vertex compositions D3q.4r.5s.6u (n = q + r + s + u). The observation, that existing homoatomic closo-borane clusters prefer vertex compositions as uniform as possible points to an energetic advantage of the associated bonding situation. Therefore, the vertex composition of a deltahedral cluster is an important topological information besides its symmetry.
Each deltahedral edge can be characterized by its vertex composition as well, for example, the vertex compositions of the two types of edges in the pentagonal bipyramid is D4.4 (abbreviated D42) and D4.5 (Figure 1). This leads to deltahedral triangles composed of vertices of different degrees, for example, the pentagonal bipyramid displays one type of triangle with vertex composition to be denoted D42.5 in the following.
From comparison with the average deltahedral value (Equation 41), a selected vertex, edge, triangle can be topologically classified as under-, over-, or equi-connected. This will be used in the further discussion.
4 APPLICATION AND DISCUSSION
Bond DRs computed for some exemplary molecular systems, which are considered to feature typical 2-center bonds are given in Supporting Information.
4.1 3-center bonding within the deltahedral surface: Approaching the styx conceptual framework
4.1.1 Cluster-wise bonding
The relevant numerical results are given in Table 2. Comparison of the systematic evolution of the deltahedral boron hydride cluster DRs GΔ(cluster) with conceptual Γ(n) values (Figure 3) reveals a clear correspondence. The computational curve is always found displaced to higher values with slight variations of the intercurve distances. The positive deviations of GΔ(cluster) may be related to the electronic underpopulation of the B atoms obtained in all these clusters (Table 2), which has been already mentioned upon comparison of the computational Neff(Bn) with conception Nel(Bn) values (Figure 2). Already B4H4 displays a significant underpopulation of about 0.6 ve, and for the charged species the additional 2-charge of the clusters is not completely transferred to B as well. It leads to an electronic underpopulation of about 0.6–0.7 ve, which is expected to cause an increased 3-center character of deltahedral cluster bonding. This is what is actually observed. The case of B4H4 is an important test case for the DR methodology, because it represents the upper boundary case of pure 3-center 2-electron bonding characterized by Γ(4) = 1. The value obtained GΔ(B4) = 1.01 demonstrates that the specific setup of the DR formula (Equation 8) conceptually related to the 2-electron system H31+ also works for the multi-electron case. The slight overshooting of the conceptual boundary value of 1 is considered as nonsignificant. With this boundary value being fixed, it is obvious that cluster DR values between 0 and 1 conform to mixed 2- and 3-center character of bonding in multi-atomic multi-electronic chemical systems. As the conceptual counterpart C4H4 is discussed in the DR framework in Supporting Information.
| System, symm., vdfrq | SEP (styx) | Δ | ||||
|---|---|---|---|---|---|---|
| sum of edges; faces | s t y x | Γ(styx) | Δ | GΔ(Bn) | SES3Δ(Bn); SEC3Δ(Bn) | ; a |
| Nel(B) | G(Bn) | SES3(Bn); SEC3(Bn) | ; b | |||
B4H4, Td, D34 6 edges; 4 faces |
4 0 4 0 0 3.0 |
1.000 | 0.783 0.376 2.390 |
1.013 1.013 |
4.476; 6.700 4.476; 6.700 |
(4.53, −0.06); (3.39, −0.04) (4.53, −0.06); (3.39, −0.04) |
B4Cl4, Td, D34 6e; 4f |
4 0 4 0 0 3.0 |
1.000 | 0.725 0.322 2.310 |
0.895 0.895 |
4.165; 6.364 4.165; 6.364 |
(3.73, 0.44); (2.85, 0.33) (3.73, 0.44); (2.85, 0.33) |
B5H52−, D3h, D3243 9e; 6f |
6 0 3 3 0 3.40 |
0.500 | 0.682 0.218 2.685 |
0.614 0.692 |
5.582; 9.041 5.879; 9.353 |
(3.43, 2.15); (2.88, 1.64) (4.07, 1.81); (2.03, 0.90) |
B6H62−, Oh, D46 12e; 8f |
7 0 4 3 0 3.33 |
0.571 | 0.603 0.208 2.608 |
0.689 0.809 |
6.506; 10.358 7.101; 11.026 |
(4.48, 2.02); (3.57, 1.61) (5.74, 1.36); (4.46, 1.05) |
CaB6, Oh, D46 12e; 8f |
7 0 4 3 0 3.33 |
0.571 | 0.600 0.203 3.256 |
0.668 0.776 |
6.497; 10.392 6.987; 10.921 |
(4.34, 2.16); (3.47, 1.72) (5.42, 1.57); (4.24, 1.22) |
B7H72−, D5h, D45.52 15e; 10f |
8 0 5 3 0 3.29 |
0.625 | 0.560 0.193 2.593 |
0.687 0.826 |
7.553; 12.031 8.296; 12.839 |
(5.19, 2.36); (4.13, 1.89) (6.85, 1.44); (5.30, 1.12) |
B8H82−, D2d, D44.54 18e; 12f |
9 0 6 3 0 3.25 |
0.667 | 0.528 0.185 2.567 |
0.705 0.862 |
8.512; 13.504 9.446; 14.520 |
(6.00, 2.51); (4.76, 1.99) (8.14, 1.30); (6.26, 1.00) |
B9H92−, D3h, D43.56 21e; 14f |
10 0 7 3 0 3.22 |
0.700 | 0.507 0.185 2.551 |
0.744 0.907 |
9.542; 15.012 10.655; 16.241 |
(7.10, 2.44); (5.59, 1.92) (9.66, 0.99); (7.37, 0.75) |
B10H102−, D4d, D42.58 24e; 16f |
11 0 8 3 0 3.20 |
0.727 | 0.494 0.185 2.540 |
0.773 0.942 |
10.627; 16.622 11.893; 18.018 |
(8.22, 2.41); (6.42, 1.89) (11.20, 0.69); (8.48, 0.53) |
B11H112−, C2v, D425861 27e; 18f |
12 0 9 3 0 3.18 |
0.750 | 0.480 0.180 2.529 |
0.776 0.954 |
11.590; 18.117 13.057; 19.738 |
(8.99, 2.60); (7.03, 2.03) (12.46, 0.60); (9.42, 0.45) |
B12H122−, Ih, D512 30e; 20f |
13 0 10 3 0 3.17 |
0.769 | 0.475 0.185 2.516 |
0.815 0.982 |
12.817; 19.881 14.337; 21.570 |
(10.44, 2.37); (8.10, 1.84) (14.08, 0.26); (10.59, 0.19) |
α-B, D3d, D512 30e; 20f |
13 0 10 3 0 3.0 |
0.769 | 0.483 0.182 3.000 |
0.769 0.942 |
13.102; 20.511 22.272 |
(10.08, 3.03); (7.88, 2.37) (13.85, 0.85); (10.48, 0.65) |
- a Model GΔ(Bn),SES3Δ(Bn) and SEC3Δ(Bn), respectively.
- b Model G(Bn),SES3(Bn) and SEC3(Bn), respectively.

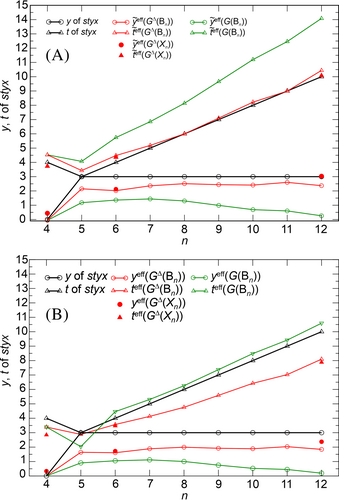
The 2- and 3-center bond orders , respectively, summing up to SES3Δ(Bn) are obtained from (Equations 37 and 38). The consistent usage of the same quantities Δself(Bn) and Δfluc(Bn) for GΔ(Bn) and SES3Δ(Bn) values leads to the characteristic trend of values, which agrees fairly well with conceptual t(n), y(n) of the styx code (Figure 4A). The tendency of the GΔ(Bn) values to increased 3-center character is visible in the separate and curves, where is slightly too high, and too low compared to styx values. Furthermore, the quantities denoted and (Figure 4B) correspond to electron pair counts (Equations 39 and 40) and have the same meaning as the Lipscomb styx values. They show the correct trend with increasing cluster size, but at too small values for both quantities. This is caused by the electronic underpopulation on the boron atoms compared to the Wade's 2SEP counts (Figure 2), which is directly passed also to SEC3Δ(Bn). In the remaining part of the contribution, the focus will be on the DRs and associated SES values, because they are directly related without a further approximation.
4.1.2 Local edge and triangle bonding
For the deltahedral boron hydride clusters n = 4, 6 12 with shapes of platonic solids all skeletal edges and faces are identical. In this case, the cluster-wise DR is identical to the local ones, that is, GΔ(Bn) = = .
The remaining clusters feature skeletal species (vertices) with different number of skeletal connections (vertex degrees), which yields topologically different edges and faces characterized by different average vertex degrees. Within the framework of octet-rule fulfillment in the delocalized TORI (topological octet-rule implementation) framework,11 it is found that locally averaged realizations of the styx code in the skeletal framework are dependent on local topological features as encoded in the average vertex degrees of each deltahedral edge and face. As a consequence, the skeletal edges and faces with higher average vertex degrees are expected to display the higher proportion of 3-center bonding contributions, that is, and values, respectively, than those with lower ones.
The results of this analysis are depicted in Figure 5.
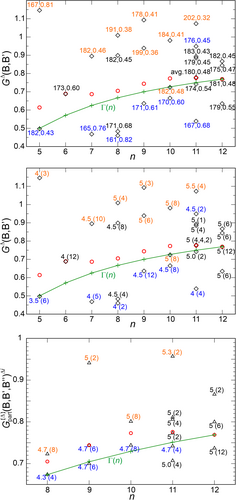
Among the remaining clusters, the cases n = 5, 7 are different from the other ones, because their symmetries allow for only one type of triangle. The presence of two topologically different types of vertices (atomic species), the apical (ap) and the equatorial (eq) ones, leads to two topologically different types of skeletal edges, namely Beq–Beq edges between vertices of like vertex degree and those between Bap–Beq vertices of different vertex degrees. The other clusters n = 8–11 generally display different types of edges and faces with different edge and vertex compositions.
In the triangular bipyramidal structure of B5H52− (D3h) with vertex composition D32.43 (Figure 1) and , the two apical and three equatorial atoms display skeletal vertex degrees of 3 and 4, respectively. The additional inclusion of the exo-ligand yields a classical 4-coordination of the former, and a 5-coordination of the latter species. This topological situation yields two types of skeletal connections (edges), the six shorter Bap–Beq edges of vertex composition D3.4 (topologically under-connected with respect to ), and the three longer Beq–Beq edges of composition D42 (over-connected). In contrast, in B7H72− (D3h) with composition D52.45 (Figure 1) and , the Bap–Beq edges (D4.5) are now overconnected, and Bap–Beq (D42) edges are under-connected.
Within the framework of octet-rule fulfillment, allowed local realizations of the styx code in the skeletal framework are obtained.11, 35 As a consequence, it is expected, that the longer over-connected edges display a higher proportion of 3-center bonding contributions (and smaller 2-center DIs) than the shorter under-connected ones.
Specifically, the under-connected edges Bap–Beq in B5H52− ( = 3.5), and Beq–Beq in B7H72− ( = 4.0), are expected to display lower (higher) G2 (2c-DI) values, than the over-connected edges Beq–Beq in B5H52− ( = 4), and Bap–Beq in B7H72− ( = 4.5).
The DR results are completely consistent with these expectations (Figure 5, top, middle). All deltahedral surface triangles Δ = (Bap,Beq,Beq’) are topologically and symmetrically equivalent, which leads to GΔ(Bn) = .
Compared to the n = 5, 7 clusters, the clusters n = 8–11 with their vertex compositions D4r.5s.6u (Figure 1) additionally display topologically different triangles characterized by different vertex compositions and average vertex degrees (Equation 43). Triangles with lower, higher or approximately equal average vertex degree than the cluster one , can be topologically classified as over-, under-, or equi-connected, respectively.
As discussed in detail for the n = 5, 7 clusters, these topological details of the polyhedral skeleton types are found to lead to local metric effects also in cluster structures n = 8–11 like edge-length variations, and concomitantly varying degrees of edge- and also triangle-wise electron delocalization, which can be monitored by delocalization indices and DRs. For deltahedral closo-boranes BnHn2− with n = 5, 7, 8, 9, 10 it is observed, that edges with lower average vertex degree display smaller edge lengths, higher δ(B,B′) values (Figure 5, top), lower values (Figure 5, middle), and lower values (Figure 5, bottom). In other words, edges and faces composed of atomic species on topologically under-connected sites display a lesser degree of three-center-wise delocalization than those composed of topologically overconnected sites, as generally expected. For clusters with n = 5, 7, 8, 9, 10 this relation is strictly valid. However, the occurrence of one clear exception from this correlation for n = 11 (Figure 5, top, middle bottom) shows, that there are in general additional effects at work that originate not only from average edge or triangle topology.
These types of effects are also responsible for the variations of the G2Δ values in crystalline α-Boron (Figure 5, middle), where all edges displaying the same vertex composition D52 are topologically similar. The α-Boron crystal structure displays distorted icosahedral B12 clusters with two chemically different B atoms and four chemically different skeletal connections. Nevertheless, they still feature the same D512 vertex composition as the undistorted B12H122− cluster; the observable variations of the G2Δ values (Figure 5, top) are not caused by topological features of the deltahedron.
For the closo-clusters with only one type of deltahedral triangle (n = 4–7), the local triangle DR value is already given by the global value GΔ(Bn). This is no longer the case for BnHn2− clusters for n = 8–11. It is interesting to analyze the spread of partial DRs for each type of triangle Δi in the less symmetrical clusters n = 8 to 11 and for the n = 12 distorted icosahedron in crystalline α-Boron. In analogy to the behavior found for the edges (Figure 5, top, middle), within each cluster also comparably large differences of local values can occur (Figure 5, bottom). With the exception of the n = 11 cluster, the sequence of increasing partial values again follows the sequence of average vertex composition for each triangle type Δi. The exceptional triangle with the lowest value (Figure 5, bottom) has an exceptional vertex composition of D4.5.6, which is indicated by the average vertex degree , while all other triangles with the same have composition D53 (indicated by ).
Especially large values are found in B9H92− and B11H112−, where they occur for the triangles with rather long edges of 199–199–199 pm (the only D53 type triangles in B9H92−) and 187–202–202 pm (the only D52.6 type triangles in B11H112−). These deltahedral triangles are characterized by small 3c-DIs (≈0.11) and small 2-center DIs (≈0.33) along the edges (Figure 5, top), which is quite different from the situation in B4H4 with similarly high values, but with large deltahedral 3c-DIs (0.38) and 2c-DIs (0.78) observed. These large triangles appear with only a rather small frequency of 2, and their contribution to the GΔ(cluster) values amounts to less than 10%. They seem to occur as a compromise for the sake of the overall cluster shape and stability.
Altogether, the local partial DR variations are well balanced, such that the GΔ(cluster) values resemble fairly well the conceptual Γ(Bn) (Figures 3 and 5) ones, and yield in combination with SES3Δ values computational () values (Equations 37 and 38) in fair agreement with the conceptual (t, y) ones (Figure 4).
4.2 Triangulation of the full-cluster multicentric bond delocalization
The scenario of complete inclusion of all types of endohedral three-atomic bonding by involvement of all possible intrapolyhedral triangles in addition to the geometrical deltahedral ones was skipped in the calibration part of the present study to investigate the relation to the styx picture of ligated closo-clusters. These additional triangles are denoted as “inner triangles” of the polyhedron. As an example, the deltahedral and the different types of inner triangles of an octahedron and icosahedron are depicted in Figure 6. The evaluation of the full-cluster 3-dimensional delocalization via DR values based on 3-center-DIs can be considered as a triangulation of the full-cluster multicentric bond delocalization. It is important to investigate the full-cluster 3-center bonding to see, whether in this more general topological framework the Lipscomb's mixed 2- and 3-center bonding picture remains, or whether strong signatures of higher bonding centricity destroy this classical picture already for the closo-boranes.

The idea of a triangulation of the full-cluster multicentric bond delocalization also has some interesting topological aspects. While the deltahedral DRs of the clusters with their edges and triangles corresponding in a 1:1 fashion to the geometrical structure and the common Euler characteristic of 2, this is no longer the case for the triangulated full-cluster delocalization models employed here. For the deltahedral models, the corresponding deltahedral graphs Dn37 incorporating all the deltahedral edges are planar ones that display no edge intersections in their Schlegel diagrams. This is no longer the case for the complete graphs Kn for n >4 describing the full-cluster bond delocalization. Already for n = 5 (trigonal bipyramid) the corresponding graph K5 mathematically represents the sufficient condition to prove its non-planarity (Kuratowski's theorem). As already noted by Mingos and Johnston,38 the representation of a cluster by its complete graph Kn is equivalent to considering it as hyperspherical in n − 1 dimensions. As a result, while all deltahedral cluster skeletons display the same Euler characteristic of 2, revealing a balanced increase of edges and face with cluster size (number of vertices) n, each hyperspherical cluster in n − 1 dimensions reveals a different balance of edges and faces and has its own Euler characteristic. A more detailed discussion based on simplicial 2-complexes39 is given in Supporting Information.
The different balance of edges and faces may be the deeper reason, why the absolute deviations of the SES3(Bn) values from the deltahedral ones SES3Δ(Bn) (and the conceptual SEP values as well) is monotonically increasing with cluster size (Figure 2). However, the relative increase of the SES3(Bn) values beyond the corresponding SES3Δ(Bn) ones is rather small, for example, comparing B6H62− and B12H122−, the relative increase amounts to 9% and 12%, respectively (Table 2). The overshooting of SES3(cluster) values with respect to Lipscomb-Wade SEP counts (Figure 2) is not an artifact of the DR approach. It is considered as a consequence of an extension beyond the styx approach. This relative increase may be considered as sufficiently small to be neglected within a conceptual framework for some but not for all cases and purposes.
The concomitant increase of related G3(Bn) compared to G3Δ(Bn) values (Figure 3, Table 2) is caused by additional 3-center DIs involving all possible triatomic skeletal atom combinations not contained in the deltahedral set. The number of such triangles is increasing stronger than the number of edges (see Supporting Information).
The computed (Equations 17-22) partial DRs G3,part, their weights, and associated partial ses3,part values of deltahedral and inner triangles related to the cluster G(Bn) and SES3(Bn) values (Table 2) are given in Table 3. For reconstruction of the G3(B6) value, the value for each individual triangle i is multiplied by the overall weight given in Table 3, which already includes the number of triangles of this type in the cluster. For the B6 skeleton, the 12 inner triangles' (it1) summed contributions even display a slightly higher overall weight (52% vs. 48%) than their deltahedral counterparts because of the 12/8 higher frequency of occurrence in the cluster. The same comparably low overall weight is obtained also for deltahedral partial contributions in the B12 skeleton case (Table 3).
| Triangle type | Edge lengths (pm) | Freq. | Weight (G3,part) (%) | ||
|---|---|---|---|---|---|
| B6H62− | |||||
| Δ | 173-173-173 | 8 | 0.79 | 47.9 | 0.423 |
| it1 | 173-173-245 | 12 | 0.82 | 52.1 | 0.310 |
| B12H122− | |||||
| Δ | 178-178-178 | 20 | 0.94 | 19.0 | 0.134 |
| it1 | 178-178-288 | 60 | 0.96 | 38.9 | 0.092 |
| it2 | 178-288-288 | 60 | 1.02 | 20.9 | 0.051 |
| it3 | 178-288-339 | 60 | 0.98 | 20.3 | 0.049 |
| it4 | 288-288-288 | 20 | 1.76 | 1.0 | 0.009 |
This indicates that the topological effect on the G3,part values of increasing number of triangles per edge compared to the deltahedral model overall dominates over the quantum chemical effect of 3-center wise bond delocalization. Thus, the decision of inclusion of certain polyhedral edges into the bonding model must be done before setting up and analyzing an all-inclusive DR model for the cluster. It might be decided from the fraction with respect to total cluster electron sharing being large enough, for example, covering about 90% with deltahedral bonding in the B6H62− case. Ultimately, it can be decided based on separate quantities that are related to covalent bond energies, that is, the IQA (interacting quantum atoms) type exchange-correlation bond energies (Exc(A,B)),40 if they are available. As an approximate alternative to Exc(A,B), the ratio δ(A,B) divided by the distance d(A,B) can be employed, which is approximately related to Exc(A,B) via the scaled point-charge approximation in the IQA methodological framework.40
An important result related to the idea of triangulation of multicentric intracluster bonding is the observation that the full cluster DR values G(Bn) for n = 5–12 values approach but do not exceed the value of 1. This is a clear indication, that the mixed 2- and 3-center bonding model is the pertinent framework. It appears to be as simple as is possible, but not too simple to discuss chemical bonding for this type of clusters even when the full 3D bond delocalization beyond the deltahedral model is analyzed. The methodological variability to select bonding contacts for investigations beyond current models' limitations could be especially important for better understanding of “disobedient skeletons”41 like oblatocloso-clusters42 and relations among Wade-Mingos, jellium-model, and other multi-shell clusters in future studies.
5 SUMMARY AND CONCLUSION
In general, the fairly close correspondence between GΔ(cluster) values and the styx derived Γ values suggests an interpretation of the DRs as effective mixing coefficients of 2-center and 3-center electron sharing, provided the DR values are between 0 and 1. In cases, where more than nearest neighbors with significantly different delocalization increments are included in the DR sum, they still keep the meaning as a measure of three-center wise bond delocalization. The associated SES3(cluster) values represent the corresponding effective bond sum of the cluster. Although SES3Δ (cluster) values are similar in size to the Wade's SEP values, they are different quantities, because they correspond to electron sharing (bond) counts, and not to electron (pair) counts.
The interpretation of the cluster DR GΔ(cluster) and SES3Δ(cluster) values, is passed on to their local G2Δ, G3Δ, and G3,part{Δ} variants and their associated sesΔ numbers. This opens the possibility for the bond and triangle decompositions of the cluster DRs to be used themselves for characterization of local bonding situations within clusters or in extended frameworks. The possibility to proceed beyond the initial styx restrictions of nearest neighbor surface bonding includes investigation of endohedral clusters with multiple atomic shells.
The reproduction of the conceptual t(n), y(n) trend with increasing cluster size n shows, that an imprint of the styx localized bond picture, despite finally becoming highly delocalized already by linear combinations of many resonance structures, can be identified and extracted in an orbital-independent way using DRs from 3-center DIs between QTAIM atoms.
The relation of GΔ(cluster) and associated SES3Δ(cluster) values to the corresponding conceptual Γ and SEP values may be increasingly difficult to interpret the larger markedly different effective atomic charges compared to the conceptual ones are found. These situations are often caused by high formal atomic or cluster charges, and counteracting effects included in the quantum chemical results are neglected in virtually all traditional concepts. For an understanding of the influence of these effects, setting up a scheme for model DI calculations would be useful in the future, that is, something like the Extended Hückel method is for conceptual MO theory.
The DIs represent electron sharing indices, and the energetic picture was excluded in this study. But on the same footing as the DI calculations an energy partitioning of the quantum chemically computed total energy into monoatomic and diatomic coulomb and exchange interactions is possible within the IQA (interacting quantum atoms) framework.40 This may finally guide the argument, whether or not a fractional 3-center bond is important enough to justify inclusion into a conceptual bonding model. As a rough guide, with only DIs at hand, the scaled point-charge approximation (sPCA)40 with constant scaling factor may be used for this purpose.
Definitively, the DRs G, like the DIs themselves, are dependent on the method of space partitioning chosen. The QTAIM method has been used for the present investigations because of the theoretical soundness of the whole QTAIM concept. However, the approach presented is not restricted to the QTAIM concept, it can be similarly applied using fuzzy atoms in position space, like, for example Hirshfeld partitioning,43 or some Hilbert space partitioning. In principle, the whole approach starts from atomic overlap matrices SijA computed with some atomic definition.
There is a certain dependence of the DIs and G values on the functional chosen, but at least for those cases in this study where this was checked, no significantly different results from B3LYP and PBE wavefunctions were found. Further studies of this issue also on other types of compounds (e.g., with transition metals) may be necessary to obtain a full picture.
Distinct conceptual bonding knowledge ends with the 3-center 2-electron bond. Of course, calculation on n-center delocalization indices would give small but non-zero values for all compounds investigated in this study, but this is not the conceptually important point made here. With the study of the G values for 2-electron N-center systems HN(n−2)+ an estimation of the validity of the 3-center 2-electron bonding model based on the G ratios was presented. This has to be further verified, for example, by analysis of electron population distribution functions,44 in future studies. At the presented conceptual chemical bonding level for the closo-borane type of compounds, there is no need to go beyond 3-center bonding as indicated by the total G values not significantly larger than 1. The DR approach presented appears to be as simple as is possible, but not too simple to discuss chemical bonding for this type of clusters even when the full 3D bond delocalization beyond the deltahedral model is analyzed. Of course, this does not contradict usage of n-center delocalization indices for studies of aromaticity45 in n-membered rings even with G(ring) ≤ 1.
Previous calculation of G2 values for intermetallic compounds of the CaB618 and AlB2 type (including transition metals) of structures,29 in FeGa3,46 in half-Heusler compounds,47 in NiB and SnNi21B20,48 ternary borides of the U3Si2 type of structure,49 and others50 seem to preliminarily indicate, that in polar intermetallics even containing transition metals the mixed 2- and 3-center bonding scenario is quite common. This has to be investigated in further systematic studies, for example, on compounds with more or less obvious rhomboid ring fragments,51 and extended for lower valence-electron concentrations. Recently, another type of electron-deficiency mechanism impeding 2-electron bonding has been vividly discussed for the NaBH3− molecule,52 which shows the ongoing interest in such kind of bonding scenarios.
ACKNOWLEDGMENTS
The author thanks Yuri Grin for discussions and critical reading of the manuscript. Open Access funding enabled and organized by Projekt DEAL.
Open Research
DATA AVAILABILITY STATEMENT
The data that support the findings of this study are available from the corresponding author upon reasonable request.




