In protein-ligand docking, the score assigned to a protein-ligand complex is approximate. Especially, the internal energy of the ligand is difficult to compute precisely using a molecular mechanics based force-field, introducing significant noise in the rank-ordering of ligands. We propose an open-source protocol (https://github.com/UnixJunkie/MMO), using two quantum mechanics (QM) single point energy calculations, plus a Monte Carlo (Monte Carlo) based ligand minimization procedure in-between, to estimate ligand strain after docking. The MC simulation uses the ANI-2x (QM approximating) force field and is performed in the dihedral space. On some protein targets, using strain filtering after docking allows to significantly improve hit rates. We performed a structure-based virtual screening campaign on nine protein targets from the Laboratoire d'Innovation Thérapeutique—PubChem assays dataset using Cambridge crystallographic data centre genetic optimization for ligand docking. Then, docked ligands were submitted to the strain estimation protocol and the impact on hit rate was analyzed. As for docking, the method does not always work. However, if sufficient active and inactive molecules are known for a given protein target, its efficiency can be evaluated.

1 INTRODUCTION

Several researchers have warned about the difficulty of precisely calculating the internal energy of a ligand using Molecular Mechanics (MM) based methods.^1-3 This fact has important implications for protein-ligand docking scores.

Tirado-Rives and Jorgensen formally investigated the fact that when a ligand binds to a protein, it is typically not in the same lowest-energy conformation as the unbound ligand.¹ The authors name “conformer focusing” the loss of conformational freedom in the ligand upon binding to a protein. The authors explain that misestimation or neglect of this free-energy change alone is sufficient to prevent proper rank-ordering of chemically diverse ligands in a protein-ligand docking screen: docking scores are noisy. With force-fields at the time (2006), the authors optimistically estimated that the error in calculating the free-energy change due to conformer focusing might be between five to 10 kcal/mol.

In the same vein, Winkler³ noticed that “The inability to properly account for entropy in the binding interactions is one of the contributors to the relatively poor performance of scoring methods even when the docking force fields can generate good poses.” So, while it is known that docking can predict the binding-mode of a known ligand (the “docking power”,^{4, 5} as assessed by redocking experiments), Winkler acknowledges that the virtual screening (VS) power^{4, 5} is lacking.

Peach and colleagues² did a literature review and gathered that estimates of ligand strain energy in protein crystal structures vary wildly (between zero to 25 kcal/mol). Brueckner et al.⁶ proposed a formula to compute an upper bound of ligand strain upon binding, solely based on the ligand's number of heavy atoms (HA): $S_{ub} = 0.3 (HA - 10)$ .

To those remarks about the inaccuracy of computing a ligand's conformer internal energy and so the significant noise in protein-ligand docking scores, we must add that to the best of our knowledge all flexible-ligand rigid-protein docking software only perform a heuristic search in a high dimensional space. For example, for a ligand with seven rotatable bonds, there are 13 degrees of freedom (three rotational plus three translational plus the seven ligand internal degrees of freedom). So, while a heuristic search can find a good solution in a timely manner, it does not guarantee it has found the global minimum. And, this global minimum might be several kcal/mol away from the found solution. In our opinion, this is another significant source of noise in protein-ligand docking scores.

Recently, researchers have tried to exploit ligand strain after docking.⁷ Rather than trying to “fix” docking scores, the authors propose to use a qualitative approach flagging docked ligands as “strained” or “non-strained.” One way they propose to do this is to compute the total ligand strain (measured in an unspecified “Torsion Energy Unit” [TEU]). Their approach uses an adapted version of the knowledge-based torsion library from Guba and colleagues.⁸ It is very fast, taking on average 0.04 s for one ligand conformer on their test computer. With their approach, if the total strain of a compound is ≤7.0 TEU, the conformer is classified as unstrained. Conversely, with a total strain $> 7.0$ TEU the conformer is deemed strained. In their benchmark on 40 database of useful decoys enhanced (DUD-E)⁹ targets and using DOCK3.7,¹⁰ the authors notice that with a total strain threshold of 7.0 TEU, 30 targets see an increase in $δ LogAUC$ ⁷ (a measure of early enrichment in VS). Encouraged by those results and recent developments in neural network potentials (NNP),^11-14 we decided to investigate if a quantitative approach to estimate ligand strain after docking was feasible and study its effect on post processing docking results from a commercial software (Cambridge crystallographic data centre [CCDC] genetic optimization for ligand docking [GOLD]) on the stringent Laboratoire d'Innovation Thérapeutique—PubChem assays (LIT-PCBA)¹⁵ dataset.

2 METHODS

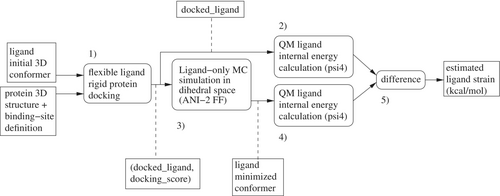
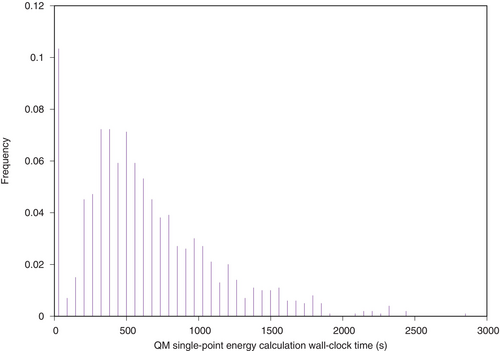
The standard definition of ligand strain is the difference in internal energy between the lowest energy conformer of a ligand in vacuum and its docked conformer on a protein.¹⁶ Unfortunately, we cannot guarantee that we are able to compute the lowest energy conformer of a ligand (a global minimum). Instead, we have opted to run a Monte Carlo (MC) simulation in the dihedral space starting from the docked ligand conformer. Bond lengths and bond angles are considered rigid. Only single bonds out of rings and not connecting a terminal atom (a heavy atom with degree one on the molecular graph) are considered rotatable during this simulation. The idea is that if there is a local energy minimum near the docked conformer, an MC simulation should be able to reach it. After looking into a few books,^17-19 we implemented Algorithm 1 in order to perform minimization of the docked ligand conformer in vacuum, with a force field (ANI-2x^11-14) described as reaching quantum mechanics (QM) accuracy. Our implementation uses the ANI-2x¹¹ model provided by the torchani²⁰ Python package. On our test computer, ANI-2x allows the ligand internal energy to be calculated about 100 times per second for a typical drug-like molecule. Experiments were run using MC simulations of $10 \times 10^{3}$ steps. ANI-2x enables running MC simulations at QM-accuracy, which would be computationally intractable using a standard QM method (cf. Figure 2). Using psi4, the average run-time of a single point ligand internal energy calculation is 633 s when using a single core of our computing node (the minimum run-time is 1 s, median 536 s and maximum $\sim 48$ min!). It would have been possible to run MC simulations using a MM force field, but such force fields are known to be of poor accuracy^1-3 when describing a ligand's internal energy. At each MC step, one of the rotatable bonds is selected uniformly at random. The angular value of the corresponding dihedral angle is tweaked by adding a uniform random quantity $δr \in [- dr, dr]$ , where $dr$ is the currently allowed maximal rotation increment for this bond ( $dr = 5^{°}$ at start). Every 100 MC steps, the selected bond is instead tried to be set to a new value in $[- π, π]$ . Acceptance or rejection of the last move (and hence of a new ligand conformer) is subject to the standard Metropolis criterion. If $n$ is the number of rotatable bonds of a ligand, every $100 n$ steps, each rotatable bond maximum rotation increment allowed ( $dr$ ) is updated using a hysteresis scheme taking into account the move acceptance ratio for this bond and the target acceptance ratio (Algorithm 1). In essence, the more likely moves are accepted for this bond, the more this bond will be allowed to rotate. For bonds which are more constrained, the opposite is true. These schemes are intended to make the conformational space exploration more efficient.¹⁷

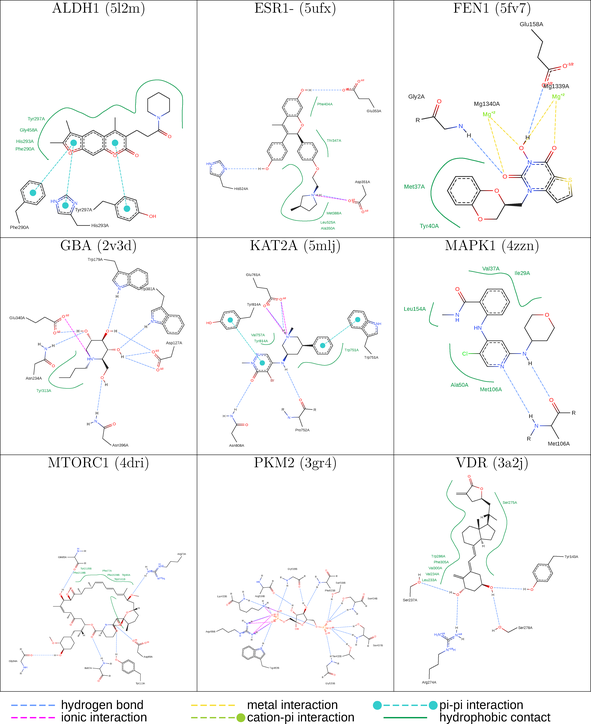
QM single point energy calculations (Figure 1) were performed using psi4²¹ driven by Mayachemtools;²² using the Becke, 3-parameter, Lee-Yang-Parr (B3LYP) method and the 6-31G** basis set (6-31+G** for sulfur containing compounds) (Tables 1, 2).

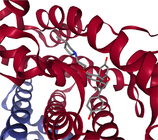
Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

Overview of the protocol to estimate ligand strain after docking: (1) Flexible-ligand rigid-protein docking. (2) QM calculation of the docked ligand's internal energy ( $E_{dock}$ ). (3) MC minimization of the docked ligand conformer in the dihedral space using the ANI-2x (QM approximating) NNP. (4) QM calculation of the minimized ligand's internal energy ( $E_{\min}$ ). (5) Calculation of the strain ( $E_{strain} = E_{dock} - E_{\min}$ ). MC, Monte Carlo; NNP, neural network potential; QM, quantum mechanics.

TABLE 1. The nine ligand-binding sites that were used for docking.

ALDH1 (5l2m)	ESR1-(5ufx)	FEN1 (5fv7)

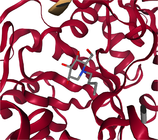
GBA (2v3d)	KAT2A (5mlj)	MAPK1 (4zzn)

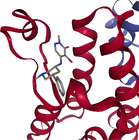
MTORC1 (4dri)	PKM2 (3gr4)	VDR (3a2j)

Note: The protein target name is on top of each binding-site with the corresponding protein data bank (PDB) id between parenthesis. Figures made at www.rcsb.org using NGL²³ viewer.

TABLE 2. Possible protein-ligand interactions identified in crystal structures by PoseEdit²⁴ (https://proteins.plus); legend at the bottom of the figure.

ALGORITHM 1. LIGAND-ONLY (VACUUM) MONTE CARLO SIMULATION IN THE DIHEDRAL SPACE. THE FORCE FIELD IS ANI-2X. COMMENTS ARE PREFIXED WITH //

function $ligand_only_MC (rng, steps, t, l)$

param $rng$ // properly initialized random number generator

param $steps$ // number of MC steps to perform

param $t$ // simulation temperature in Kelvin (for Metropolis criterion)

param $l$ // ligand with previously identified rotatable bonds

output $(l_{best}, E_{best})$ // minimized ligand conformer and its energy

// initial maximum rotation allowed per rotatable bond is ±5°

$set_default_rbonds_dr (l, \frac{5 π}{180})$

$a \leftarrow 0.5$ // target acceptance ratio

$low \leftarrow a - 0.05$ // hysteresis low bound

$high \leftarrow a + 0.05$ // hysteresis high bound

$num_rbonds \leftarrow ∣ get_rbonds (l) ∣$

$block \leftarrow 100 \times num_rbonds$

$E_{prev} \leftarrow + \infty$

$E_{best} \leftarrow + \infty$

$l_{prev} \leftarrow l$

$l_{best} \leftarrow l$

for $frame$ in $1 . . steps$ do

$l \leftarrow tweak_rbond (rng, l)$ // a single rotatable bond is affected

$E_{curr} \leftarrow ene_intra (l)$ // the force field is ANI-2x

if $E_{curr} \leq E_{prev} \lor metropolis_criterion (rng, t, E_{prev}, E_{curr})$ then

$E_{prev} \leftarrow E_{curr}$

$l_{prev} \leftarrow l$

end if

// record lowest energy conformer

if $E_{curr} < E_{best}$ then

$E_{best} \leftarrow E_{curr}$

$l_{best} \leftarrow l$

end if

if $frame \mod block = 0$ then

// update maximum rotation allowed per rotatable bond

$update_rbonds_dr (low, high, l)$

end if

end for

return $(l_{best}, E_{best})$

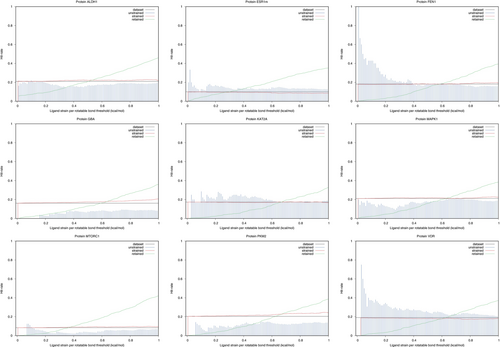
In order to compare diverse molecules, the calculated strain is divided by the number of rotatable bonds in a molecule; giving an average dihedral strain. To compute hit rates among strained or unstrained molecules, docked ligands were first sorted by increasing strain (Figures 6 and 7).

3 DATASET

3.1 A subset of the LIT-PCBA dataset

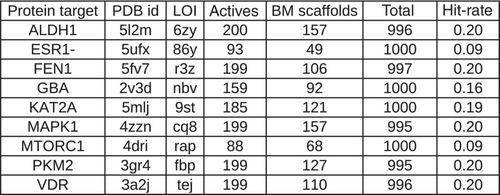
Structure-based virtual screening (SBVS) experiments were conducted on nine protein targets from the LIT-PCBA dataset¹⁵ (Figures 1-3). LIT-PCBA was designed to benchmark ligand and SBVS methods. It was carefully curated from 149 PubChem²⁶ assays. It contains 7844 confirmed actives and 407381 inactive molecules. In LIT-PCBA, for a given protein target a true positive is a molecule passing all LIT-PCBA filters¹⁵ for “true active” (only C, H, N, O, P, S and halogens allowed, dose-response curve with Hill slope $0.5 < h < 2.0$ , molecule not a known PubChem aggregator or luciferase inhibitor or autofluorescent). A true negative is a molecule which is not detected as a hit in the corresponding PubChem assay, but still has to pass all LIT-PCBA filters (organic compound, adequate property ranges, etc.); cf. the LIT-PCBA article¹⁵ for details. LIT-PCBA is a tough but realistic dataset for VS experiments. Our nine targets were selected based on the existence of at least 100 known active molecules, so that hit rates are calculated using a significant number. Then, inactive molecules were randomly selected to achieve a total of about 1000 molecules per protein, to keep the computational cost reasonable. Numbers vary slightly (Figure 3) because some molecules fail the ligand preparation protocol or QM calculation with psi4²¹ or scoring with ANI-2x.¹¹ One protein structure protein data bank (PDB) was selected for each protein (Figure 3), mostly based on the high resolution of the crystallographic data (LIT-PCBA proposes several PDB entries for each protein target).

3.2 Protein preparation and docking

Each protein was prepared using the Hermes graphical interface from CCDC GOLD. Starting from PDB files downloaded from rcsb.org (5l2m, 5ufx, 5fv7, 2v3d, 5mlj, 4zzn, 4dri, 3gr4 and 3a2j), hydrogen atoms were added, all water molecules and the cognate ligand were removed, then the protein was saved in MOL2 format. The cognate ligand's geometric center in combination with a radius of 10 Å were used as the binding-site definition (GOLD's defaults). All other parameters were left to their default values. Only the highest scoring pose per ligand was considered for further analysis (default ChemPLP scoring function).

3.3 Ligands preparation prior to docking

Starting from the SMILES provided by LIT-PCBA: OpenEye tautomers²⁷ was used to generate one reasonable tautomer at pH 7.4 for each ligand. Then, OpenEye OMEGA^{28, 29} was used to generate one low energy conformer per protonated ligand. Finally, OpenEye molcharge³⁰ was used to assign partial charges to each conformer using merck molecular force field 94.³¹

4 RESULTS

Experiments were run on computers running Linux CentOS-7.9; equipped with 2.6 GHz Intel Xeon CPUs (56 threads per node) and 256 GB of RAM.

4.1 Flexible-ligand/rigid-protein docking VS performance

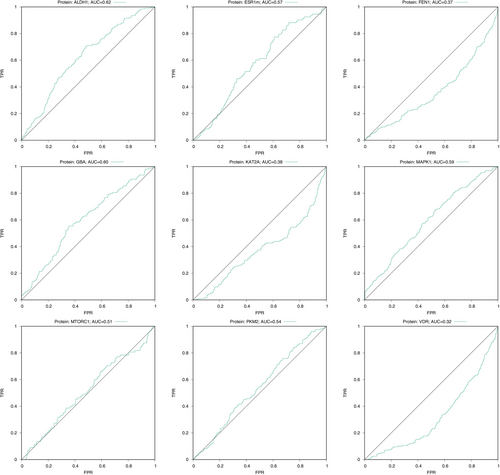
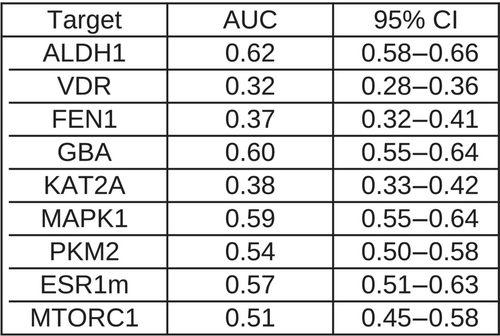
In Figure 4, Receiver operating characteristic (ROC) area under the curve (AUC) curves corresponding to the VS performance of CCDC GOLD are shown. If one considers the virtual screen to have acceptable performance only if the two following conditions are met: (1) the AUC's 95% confidence interval^{32, 33} is higher than 0.5 (Figure 5) and (2) the early enrichment is better than random (i.e., the left part of the ROC curve, between 0% false positive rate [FPR] and 5%, 10% or 20% FPR, is higher than the diagonal line), then only three targets are amenable to a docking screen: ALDH1 (AUC = 0.63), GBA (AUC = 0.6) and MAPK1 (AUC = 0.59). On ESR1m, the ROC AUC is borderline (AUC = 0.57), but the early enrichment is random or slightly worse. On three proteins (FEN1, KAT2A and VDR), with respective AUC values (0.37, 0.38 and 0.32), the VS performance is significantly worse than random. On the remaining two protein targets MTORC1 and PKM2, the AUC values (0.51 and 0.54 respectively) are dangerously close to 0.5, indicating random VS performance. While such results might be surprising, they are in line with our own past experience³⁴ when trying to dock the full LIT-PCBA dataset (only five out of 15 protein targets had an acceptable enrichment factor at 1% and only six had an AUC ≥ 0.6). Some other facts about protein-ligand docking are worrisome: in a recent study on the PDBScan22³⁵ dataset, Flachsenberg and colleagues³⁵ found that only $\sim 30 %$ of ligands were positioned at most 2 Å away from the crystal ligand in a large, fully automated redocking study. In terms of Enrichment Factor at 1% (EF_1%), the LIT-PCBA authors used Surflex-Dock and observed an average ${EF}_{1 %} \geq 2.0$ on only six out of 21 protein targets.

4.2 Effect of ligand strain filtering on hit rates

In Figure 6, the impact of strain filtering on hit rates is shown. On two protein targets (FEN1 and VDR), the method could be used to improve hit rates among selected molecules regardless of docking scores. For FEN1, the background hit rate is about 20%. Using a strain threshold of maximum 0.15 kcal/mol (average ligand strain per rotatable bond) the hit rate can be improved to 30%. Using a strain threshold of maximum 0.1 kcal/mol, the hit rate can be doubled. On the VDR protein, a threshold of 0.2 kcal/mol allows to improve the background hit rate from 20% to 30%. Deciding on a threshold to double the hit rate on this protein does not seem advisable: the range is too narrow and the filter would reject too many molecules. One has to keep in mind that the smaller the strain threshold, the more docked molecules are going to be rejected by the filter. In Figure 6, the green curve indicates the fraction of the docked molecules which pass the filter. For the two proteins where the method looks useful (FEN1 and VDR), a 0.2 kcal/mol strain threshold would keep about 5% of the docked molecules. We do not see a usable strain threshold for the seven other protein targets (ALDH1, ESR1m, GBA, KAT2A, MAPK1, MTORC1, PKM2). Especially, for five proteins (ALDH1, GBA, MAPK1, MTORC1 and PKM2), there is not any advisable strain filtering threshold. Strain filtering would be detrimental to the hit rate among docked molecules for those proteins.

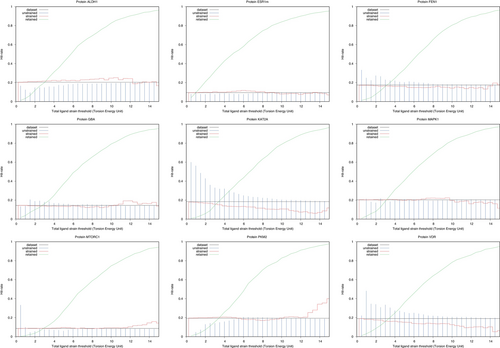
4.3 Effect of total ligand strain filtering on hit rates

To check our results, we also analyzed our dataset using the method of Gu and colleagues.⁷ ¹ When considering total ligand strain, our method has a positive but small Spearman $ρ$ correlation with the University of California, San Francisco (UCSF) method⁷ ( $0.4 \leq ρ \leq 0.5$ depending on the protein target). Looking at Figure 7, the method looks advisable on one protein target (KAT2A), and to some extent to two others (FEN1 and VDR). On KAT2A, a total ligand strain threshold of four TEU allows to bump the hit rate from about 20% to 30%. Such a threshold would keep about 25% of the docked molecules. A strain filter of two TEU allows to double the hit rate. On FEN1, a total ligand strain threshold of two to three TEU allows to bump the hit rate slightly, from 20% to about 25% to 30%. On VDR, a similar strain filter of two to three TEU bumps the hit rate from 20% to 30%. On the six other protein targets (ALDH1, ESR1m, GBA, MAPK1, MTORC1 and PKM2), we do not see an advisable total strain filtering threshold. Finally, the two different approaches agree on two protein targets (FEN1 and VDR) where strain filtering might be useful.

5 DISCUSSION

5.1 Advantages

While we would have loved to see the method work on a majority of protein targets, this is not the case but the same can be told for docking. Docking's VS performance is acceptable on ALDH1, GBA and MAPK1 while strain filtering works on FEN1 and VDR. Strain filtering can be used regardless of the performance of docking in terms of VS power. That is, docking can be trusted to optimize non-bonded protein ligand interactions (optimizing a ligand's conformer into the binding site), then strain filtering used to select molecules instead of relying on docking scores.

5.2 Drawbacks

The method does not seem applicable in general and needs to be benchmarked on a given protein target of interest. The proposed protocol (Figure 1) is not fail-safe: in about 4% of the 7895 ligands analyzed after docking, the MC simulation failed to minimize the docked conformer. That is, the calculated strain was negative. Of course, such points were excluded from the hit rate calculations and figures. We attribute this to some local disagreement between the ANI-2x NNP and an actual QM calculation. We also wonder about the transferability of the analysis. Probably, results for one protein structure should not be used to infer anything about other structures. Also, results obtained using one docking software and docking parameters are probably not advisable for another docking software or set of docking parameters. For example, Gu and colleagues, using DOCK3.7¹⁰ on DUD-E⁹ recommend a seven TEU total strain filtering threshold. In our benchmark and using CCDC-GOLD, it seems that the optimal total strain filtering threshold lies between two to four TEU (if and when the method is advisable).

The filter is very selective (cf. the retained curves in Figure 6). With a too low strain filtering threshold, no molecule will pass the filter.

While our protocol is computationally tractable for a thousand molecules and one protein target using at least one massively multi-core computer, it does take a few hours to run all the QM single-point energy calculations (cf. the outliers in Figure 2).

Following a suggestion from an anonymous reviewer, we did rerun all calculations with geometry optimization at the QM level (bond lengths and bond angles only; rotatable bonds were fixed) for the docked ligands prior to running the rest of the pipeline. Indeed, this could make the estimated strain values less noisy. However, this resulted in an explosion of the required computing power (we estimate, by a factor of at least $20 \times$ ). Also, only about 10% of the molecules for each protein target survived such treatment without any error. cf. Figure S1 for results. Using this more accurate protocol, three protein targets seem amenable to strain filtering: ALDH1, ESR1- and VDR. Interestingly, in all those three cases, a threshold filtering range of maximum 0.2 kcal/mol per rotatable bond seems adequate. Also, we note that VDR is the only protein target that seems amenable to strain filtering whatever protocol we were using. We do note that the crystallographic ligand in this protein is completely buried inside a protein cavity and almost completely desolvated (PDB: 3A2J, ligand of interest identifier: TEJ), unlike all other protein-ligand complexes that were studied.

We leave to courageous researchers investigating if taking into account solvation³⁶ during the QM single-point energy calculation might make such strain filtering protocol more generally applicable.

6 CONCLUSION

In this study, we have performed a SBVS campaign (protein-ligand docking) on nine protein targets of the LIT-PCBA dataset using CCDC GOLD. An open-source protocol taking advantage of the ANI-2x NNP was developed then used to estimate ligand strain after docking. The effect of strain filtering on hit rate was analyzed. The protocol was also checked against a torsion library⁸ based method.⁷

Because of the computational cost of the method and the low number of protein targets where it does benefit, we recommend potential users to first consider simpler and faster methods like pharmacophore filtering,³⁷ Protein-Ligand Interaction Fingerprints^{38, 39} or maybe some rescoring function.⁴⁰

ACKNOWLEDGMENTS

This work was supported by AMED grant JP20NK0101111. KT acknowledges an academic license from OpenEye for tautomers, OMEGA and molcharge.

CONFLICT OF INTEREST STATEMENT

The authors declare no conflict of interest.

Endnote

¹ A script can be downloaded after user registration at tldr.docking.org.

Open Research

DATA AVAILABILITY STATEMENT

Our source code is released as open-source under the BSD license at https://github.com/UnixJunkie/MMO (accessed March 19, 2024). The dataset used in this study can be downloaded from https://zenodo.org/records/10846630 (accessed March 21, 2024).

Supporting Information

REFERENCES

1J. Tirado-Rives, W. L. Jorgensen, J. Med. Chem. 2006, 49, 5880.
10.1021/jm060763i
CAS PubMed Web of Science® Google Scholar
2M. L. Peach, R. E. Cachau, M. C. Nicklaus, J. Mol. Recognit. 2017, 30, e2618.
10.1002/jmr.2618
CAS Web of Science® Google Scholar
3D. A. Winkler, J. Chem. Inf. Model. 2020, 60, 4421.
10.1021/acs.jcim.0c01146
CAS PubMed Web of Science® Google Scholar
4M. Su, Q. Yang, Y. Du, G. Feng, Z. Liu, Y. Li, R. Wang, J. Chem. Inf. Model. 2019, 59, 895.
10.1021/acs.jcim.8b00545
CAS PubMed Web of Science® Google Scholar
5J. Gabel, J. Desaphy, D. Rognan, J. Chem. Inf. Model. 2014, 54, 2807.
10.1021/ci500406k
CAS PubMed Web of Science® Google Scholar
6A. C. Brueckner, Q. Deng, A. E. Cleves, C. A. Lesburg, J. C. Alvarez, M. Y. Reibarkh, E. C. Sherer, A. N. Jain, J. Med. Chem. 2021, 64, 3282.
10.1021/acs.jmedchem.0c02159
CAS PubMed Web of Science® Google Scholar
7S. Gu, M. S. Smith, Y. Yang, J. J. Irwin, B. K. Shoichet, J. Chem. Inf. Model. 2021, 61, 4331.
10.1021/acs.jcim.1c00368
CAS PubMed Web of Science® Google Scholar
8W. Guba, A. Meyder, M. Rarey, J. Hert, J. Chem. Inf. Model. 2016, 56, 1.
10.1021/acs.jcim.5b00522
CAS PubMed Web of Science® Google Scholar
9M. M. Mysinger, M. Carchia, J. J. Irwin, B. K. Shoichet, J. Med. Chem. 2012, 55, 6582.
10.1021/jm300687e
CAS PubMed Web of Science® Google Scholar
10R. G. Coleman, M. Carchia, T. Sterling, J. J. Irwin, B. K. Shoichet, PLoS One 2013, 8, 1.
10.1371/annotation/b9b4a26a-4eb1-482f-b99d-e248f8ca31fa
Web of Science® Google Scholar
11C. Devereux, J. S. Smith, K. K. Huddleston, K. Barros, R. Zubatyuk, O. Isayev, A. E. Roitberg, J. Chem. Theory Comput. 2020, 16, 4192.
10.1021/acs.jctc.0c00121
CAS PubMed Web of Science® Google Scholar
12J. S. Smith, O. Isayev, A. E. Roitberg, Chem. Sci. 2017, 8, 3192.
10.1039/C6SC05720A
CAS PubMed Web of Science® Google Scholar
13Z. Liu, T. Zubatiuk, A. Roitberg, O. Isayev, J. Chem. Inf. Model. 2022, 62, 5373.
10.1021/acs.jcim.2c00817
CAS PubMed Web of Science® Google Scholar
14D. Anstine, R. Zubatyuk, O. Isayev, AIMNet2: A Neural Network Potential to Meet your Neutral, Charged, Organic, and Elemental-Organic Needs. 2023.
Google Scholar
15V.-K. Tran-Nguyen, C. Jacquemard, D. Rognan, J. Chem. Inf. Model. 2020, 60, 4263.
10.1021/acs.jcim.0c00155
CAS PubMed Web of Science® Google Scholar
16B. K. Rai, V. Sresht, Q. Yang, R. Unwalla, M. Tu, A. M. Mathiowetz, G. A. Bakken, J. Chem. Inf. Model. 2019, 59, 4195.
10.1021/acs.jcim.9b00373
CAS PubMed Web of Science® Google Scholar
17M. J. Field, A Practical Introduction to the Simulation of Molecular Systems, Cambridge University Press, Cambridge 1999.
Google Scholar
18M. P. Allen, D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, Oxford 2017.
10.1093/oso/9780198803195.001.0001
Google Scholar
19A. R. Leach, Molecular Modelling: Principles and Applications, Pearson Education, London 2001.
Web of Science® Google Scholar
20X. Gao, F. Ramezanghorbani, O. Isayev, J. S. Smith, A. E. Roitberg, J. Chem. Inf. Model. 2020, 60, 3408.
10.1021/acs.jcim.0c00451
CAS PubMed Web of Science® Google Scholar
21D. G. A. Smith, L. A. Burns, A. C. Simmonett, R. M. Parrish, M. C. Schieber, R. Galvelis, P. Kraus, H. Kruse, R. Di Remigio, A. Alenaizan, A. M. James, S. Lehtola, J. P. Misiewicz, M. Scheurer, R. A. Shaw, J. B. Schriber, Y. Xie, Z. L. Glick, D. A. Sirianni, J. S. O'Brien, J. M. Waldrop, A. Kumar, E. G. Hohenstein, B. P. Pritchard, B. R. Brooks, I. Schaefer, F. Henry, A. Y. Sokolov, K. Patkowski, I. DePrince, A. Eugene, U. Bozkaya, R. A. King, F. A. Evangelista, J. M. Turney, T. D. Crawford, C. D. Sherrill, J. Chem. Phys. 2020, 152, 184108.
10.1063/5.0006002
CAS PubMed Web of Science® Google Scholar
22M. Sud, J. Chem. Inf. Model. 2016, 56, 2292.
10.1021/acs.jcim.6b00505
CAS PubMed Web of Science® Google Scholar
23A. S. Rose, A. R. Bradley, Y. Valasatava, J. M. Duarte, A. Prlic, P. W. Rose, Bioinformatics 2018, 34, 3755.
10.1093/bioinformatics/bty419
CAS PubMed Web of Science® Google Scholar
24K. Diedrich, B. Krause, O. Berg, M. Rarey, J. Comput. Aided Mol. Des. 2023, 37, 491.
10.1007/s10822-023-00522-4
CAS PubMed Web of Science® Google Scholar
25G. W. Bemis, M. A. Murcko, J. Med. Chem. 1996, 39, 2887.
10.1021/jm9602928
CAS PubMed Web of Science® Google Scholar
26S. Kim, P. A. Thiessen, E. E. Bolton, J. Chen, G. Fu, A. Gindulyte, L. Han, J. He, S. He, B. A. Shoemaker, J. Wang, B. Yu, J. Zhang, S. H. Bryant, Nucleic Acids Res. 2016, 44, D1202.
10.1093/nar/gkv951
CAS PubMed Web of Science® Google Scholar
27 Software, O. S, QUACPAC 2.1.3.0: tautomers. http://www.eyesopen.com. Accessed June 02, 2024
Google Scholar
28 Software, O. S, OMEGA 4.1.2.0. http://www.eyesopen.com. Accessed June 02, 2024
Google Scholar
29P. C. D. Hawkins, A. G. Skillman, G. L. Warren, B. A. Ellingson, M. T. Stahl, J. Chem. Inf. Model. 2010, 50, 572.
10.1021/ci100031x
CAS PubMed Web of Science® Google Scholar
30 Software, O. S, QUACPAC 2.1.3.0: molcharge. http://www.eyesopen.com. Accessed June 02, 2024
Google Scholar
31T. A. Halgren, J. Comput. Chem. 1996, 17, 490.
10.1002/(SICI)1096-987X(199604)17:5/6<490::AID-JCC1>3.0.CO;2-P
CAS Web of Science® Google Scholar
32E. R. DeLong, D. M. DeLong, D. L. Clarke-Pearson, Biometrics 1988, 44, 837.
10.2307/2531595
CAS PubMed Web of Science® Google Scholar
33X. Robin, N. Turck, A. Hainard, N. Tiberti, F. Lisacek, J.-C. Sanchez, M. Müller, BMC Bioinf. 2011, 12, 77.
10.1186/1471-2105-12-77
PubMed Web of Science® Google Scholar
34F. Berenger, A. Kumar, K. Y. J. Zhang, Y. Yamanishi, J. Chem. Inf. Model. 2021, 61, 2341.
10.1021/acs.jcim.0c01452
CAS PubMed Web of Science® Google Scholar
35F. Flachsenberg, C. Ehrt, T. Gutermuth, M. Rarey, J. Chem. Inf. Model. 2024, 64, 219.
10.1021/acs.jcim.3c01573
CAS PubMed Web of Science® Google Scholar
36J. Tomasi, B. Mennucci, R. Cammi, Chem. Rev. 2005, 105, 2999.
10.1021/cr9904009
CAS PubMed Web of Science® Google Scholar
37X. Qing, X. Yin Lee, J. De Raeymaeker, J. Tame, K. Zhang, M. De Maeyer, A. Voet, J. Recept. Ligand Channel Res. 2014, 7, 81.
CAS Google Scholar
38G. Marcou, D. Rognan, J. Chem. Inf. Model. 2007, 47, 195.
10.1021/ci600342e
CAS PubMed Web of Science® Google Scholar
39J. Desaphy, E. Raimbaud, P. Ducrot, D. Rognan, J. Chem. Inf. Model. 2013, 53, 623.
10.1021/ci300566n
CAS PubMed Web of Science® Google Scholar
40V.-K. Tran-Nguyen, S. Simeon, M. Junaid, P. J. Ballester, Curr. Res. Struct. Biol. 2022, 4, 206.
10.1016/j.crstbi.2022.06.002
CAS PubMed Web of Science® Google Scholar

Citing Literature

Volume46, Issue1

January 5, 2025

e27478

An ANI-2 enabled open-source protocol to estimate ligand strain after docking

Abstract

1 INTRODUCTION

2 METHODS

ALGORITHM 1. LIGAND-ONLY (VACUUM) MONTE CARLO SIMULATION IN THE DIHEDRAL SPACE. THE FORCE FIELD IS ANI-2X. COMMENTS ARE PREFIXED WITH //