We describe a method to run simulations of ground or excited state dynamics under extremely high pressures. The method is based on the introduction of a fictitious ideal gas that exerts the required pressure on a molecular sample and is therefore called XP-GAS (eXtreme Pressure by Gas Atoms in a Sphere). The algorithm is most suitable for approximately spherical clusters of molecules described by quantum chemistry methods, Molecular Mechanics or mixed QM/MM approaches. We compare the results obtained by the algorithm here presented and by the XP-PCM approach, based on a continuum description of the environment. As a test case, we study the conformational dynamics of 1,3-butadiene either as an isolated molecule (“naked” butadiene) or embedded in a cluster of argon atoms, under pressures up to 15 GPa. Overall, our results show that the XP-GAS QM/MM simulation method is in good agreement with the XP-PCM QM/Continuum model (Cammi model) in describing the effect of the pressure on static properties as the equilibrium geometry of butadiene in the ground state. Furthermore, the comparison of XP-GAS simulations with naked butadiene and butadiene in argon shows the importance, for XP-GAS and related methods, of a realistic representation of the medium in modelling pressure effects.

1 INTRODUCTION

Molecular properties and chemical reactions under extremely high pressures (XP, i.e., several GPa) generated by diamond or tungsten carbide anvils are currently studied, mainly by spectroscopic methods.^1-6 It has been shown that photoinduced processes can also be affected, even at lower pressures ( $< 1$ GPa).^{7, 8} Theoretical studies have shed light on the peculiar features of XP chemistry.^{6, 9-21} The extension of the Polarizable Continuum Model²² put forward by one of us^11-13 accounts for the structural, electronic and energetic changes induced by high pressures on molecular systems, both at stable geometries and at transition states. The XP-PCM method (eXtreme Pressure Polarizable Continuum Model) has been therefore applied to study XP effects on thermal reaction kinetics and equilibria.^{12, 15, 16} Excited state energetics are also accessible, so data relevant to understanding the photochemistry can be provided by XP-PCM.¹⁴ However, the field of excited state molecular dynamics simulations in the extreme high pressure regime is, to the best of our knowledge, still completely unexplored.

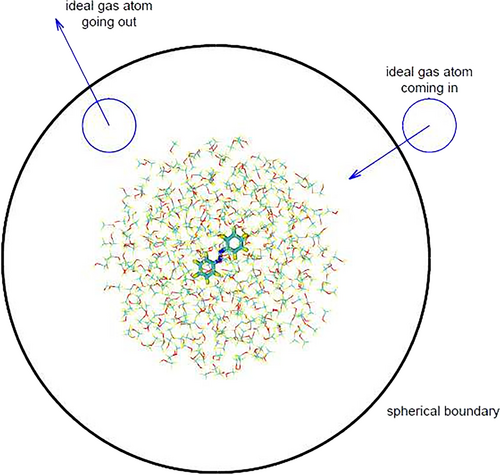
Our aim in this paper is to develop a basic ingredient to perform such type of studies, namely a suitable barostat for extreme high pressures that should be added in the simplest way to the algorithms describing molecular dynamics by semiclassical methods, such as surface hopping.^23-25 In this context, the environment is often represented as a finite cluster, an approximation compatible with many short time processes (in the range of tens of picoseconds or less) occurring in photochemistry and photophysics. The QM/MM approach is normally adopted, whereby the chromophore(s) and the reaction center are described by quantum chemistry methods and the environment by Molecular Mechanics.^26-28 Molecular Dynamics simulations have been run under high pressure conditions with periodic boundary conditions (PBC).^{9, 19-21, 29} However, performing QM/MM excited state dynamics with PBC requires ad hoc approximations and extensive modifications of the software.^30-35 This is why we prefer the cluster models, whereby the pressure can be imposed by an external computational device, without changing the algorithms describing the dynamics of the physical system. For approximately spherical systems (for instance, liquid droplets) one can use spherical boundary conditions,³⁰ but to apply an isotropic pressure to a sample of different shape, one needs some sort of model fluid. Fictitious atomic liquids with model interatomic potentials were first proposed.^36-39 Next, Grünwald and Dellago^40-42 introduced an even simpler medium, namely an ideal gas bath, made of particles that interact only with the atoms of the sample. Their approach was later modified by Plotnikov and Martínez.⁴³ In both variants of the method, the trajectories of the gas particles are only computed within a bounding box of variable shape, not much larger than the physical sample. For the sake of efficiency, the bounding box has the minimal volume compatible with its planar walls and the radius of interaction between the gas particles and the real atoms. Here we present a new version of Grünwald and Dellago's method, where the main innovation is the use of a spherical box, more suitable for clusters of solvent molecules or other (possibly isotropic) media surrounding a reaction center. However, as already noted, the applicability of the method is quite general as to the shape of the sample and its modelization (QM, MM or QM/MM). The new barostat will be called XP-GAS (eXtreme Pressure by Gas Atoms in a Sphere).

We describe the XP-GAS method in Sections 2 and 3. The XP-PCM method is briefly recalled in Section 4. We compare the results obtained with XP-GAS and XP-PCM as applied to the conformational dynamics of butadiene in Section 5. The XP-GAS simulation is based on a QM/MM description of butadiene in a cluster of Ar atoms, with the molecule treated at QM level by a semiempirical method.²⁵

2 THE XP-GAS METHOD

The whole system taking part in the dynamics is made of two subsystems. One is the molecular sample under study (hereafter, the “sample”), which is realistically described by quantum chemistry methods (QM), or Molecular Mechanics (MM), or a combination of both (QM/MM). The other subsystem is the fictitious ideal gas (hereafter, the “gas”) which exerts on the sample the desired pressure, as uniform as possible, due to the repulsive interactions between the gas and sample atoms (see Figure 1). Following Grünwald and Dellago,⁴⁰ to model such interactions we employed the potential (same for all kinds of sample atoms):

u (r) = \{\begin{array}{l} ϵ {(\frac{σ_{g}}{r})}^{12} - 2^{- 12} ϵ & for r < 2 σ_{g} \\ 0 & for r \geq 2 σ_{g} \end{array}

(1)

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

A cluster of molecules (the sample) contained in the spherical surface through which the ideal gas atoms enter and leave the system.

Here we arbitrarily fix $ϵ = 1$ kJ/mol, while $σ_{g}$ is a user defined parameter. The cutoff radius $r_{c} = 2 σ_{g}$ determines the interaction zone between the sample and a gas atom. Computational efficiency suggests to choose small values of $σ_{g}$ and $r_{c}$ , in order to reduce the number of interactions to be computed. Moreover, as we shall see, decreasing $r_{c}$ also decreases the number of gas atoms to be considered. On the other hand, if $σ_{g}$ is too small the gas atoms can easily penetrate the sample instead of applying a pressure on it. Reasonable values of $σ_{g}$ are of the order of few Å.

Given a temperature $T$ , which is the same for the sample and the gas, at equilibrium, the pressure $P$ can be controlled by adjusting the number density $ρ_{g}$ of the gas particles, since they do not interact among themselves: $P = k_{B} T ρ_{g}$ . Note that $ρ_{g}$ is the density in the region where the gas atoms do not interact with the sample: where such interactions are not negligible, the density is altered in a non trivial way. The ideal gas properties are therefore exploited by considering a sphere $S$ that contains the whole system. The surface of the sphere $S$ is external to the region where the gas atoms interact with the sample. By going through the surface of $S$ the gas atoms enter or leave the system. The inward flux is regulated according to the ideal gas laws.

We choose to put the center $C$ of the sphere $S$ in the center of mass of the sample. If $r_{\max}$ is the distance of the farthest atom of the sample from $C$ , the radius $R$ of the sphere must be at least $r_{\max} + r_{c}$ , so that the gas atoms entering the sphere are initially in the region of no interaction with the sample. To be on the safe side, we set $R = r_{\max} + 1.1 \cdot r_{c}$ . The volume contained inside the sphere $S$ , where we must calculate the trajectories of the gas atoms, quite clearly increases with $r_{c}$ , and the same is true for the number $N$ of the gas atoms themselves.

The basic strategy is to simulate the input of gas atoms in the system through the surface of the sphere

S

, and to integrate the trajectories of those atoms until they exit the sphere. The numerical integration is done with the same algorithm (Beeman's^{25, 44}) and the same time step

Δ t

used for the sample. In the following the expression “at time step

i

” will mean at time

i Δ t

, while “during the time step” will mean in the interval

[i Δ t, (i + 1) Δ t]

. During each time step, a variable number

N_{i n}

of gas atoms enter the system. We assume that all the gas atoms with negative radial component of the velocity

v_{r}

, found at the beginning of the time step in the spherical shell limited by the radii

R

and

R + | v_{r} | Δ t

, will enter the sphere

S

during the time step. This is actually an approximation, because atoms with a large tangential velocity may escape sideways without hitting the sphere: however, this is a rare event if

Δ t

is small. The volume of the spherical shell is

V = \frac{4}{3} π {(R + | v_{r} | Δ t)}^{3} - \frac{4}{3} π R^{3} ≃ 4 π R^{2} | v_{r} | Δ t

(2)

This is again a good approximation with small

Δ t

. Then, the average number of atoms entering the system with a radial velocity between

v_{r}

and

v_{r} + d v_{r}

\begin{align} d ⟨N_{i n}⟩ & = ρ_{g} V p (v_{r}) d v_{r} ≃ \\ ≃ P R^{2} Δ t {(8 π m_{g})}^{1 / 2} {(k_{B} T)}^{- 3 / 2} \exp (- \frac{m_{g} v_{r}^{2}}{2 k_{B} T}) | v_{r} | d v_{r} \end{align}

(3)

where

p (v)

is the normalized distribution of any single velocity component

v

in the ideal gas:

p (v) = {(\frac{m_{g}}{2 π k_{B} T})}^{1 / 2} \exp (- \frac{m_{g} v^{2}}{2 k_{B} T})

(4)

Here

m_{g}

is the mass of a gas atom. By integrating expression (3) we get the average number of gas atoms going in during a time step:

⟨N_{i n}⟩ ≃ P R^{2} Δ t {(\frac{8 π}{m_{g} k_{B} T})}^{1 / 2}

(5)

The mass $m_{g}$ is an arbitrary parameter. With a larger number of incoming gas atoms we can obtain a more uniform pressure, so it is convenient to choose $m_{g}$ as small as possible. However, the smaller $m_{g}$ , the higher will be the atom velocities, which can deteriorate the integration accuracy and require to reduce the time step $Δ t$ . As a compromise, we choose $m_{g} = 1$ a.m.u. = $1.66054 \cdot 1 0^{- 27}$ kg, close to the mass of the hydrogen atom, that is, the smallest mass normally present in the sample. With a pressure $P = 1$ GPa, $T = 300$ K, a reasonably large sphere ( $R = 30$ Å) and $Δ t = 0.1$ fs as normally used in nonadiabatic dynamics, we get 1.7 incoming gas atoms per time step, in the average.

Since the average

⟨N_{i n}⟩

is not an integer, at each time step the integer number of incoming atoms

N_{i n}

is determined by a random choice that guarantees the correct average. Given the largest integer

I \leq ⟨N_{i n}⟩

and a random number

r \in [0, 1]

, we set

N_{i n} = I

⟨N_{i n}⟩ - I < r

and

N_{i n} = I + 1

otherwise. Note that the correct distribution of integers is not limited to

I

and

I + 1

: it obeys the Poisson law

p (N_{i n}) = \frac{{⟨N_{i n}⟩}^{N_{i n}}}{N_{i n}!} e^{- ⟨N_{i n}⟩}

(6)

However, using the Poisson formula is computationally more expensive and we have left this alternative as a user option. Of course, for each time step the Poisson distribution is much broader than the choice between two integers implies, but the combination of many binary choices along a simulation partially reduces this discrepancy. Moreover, our aim is not to generate a fictitious ideal gas with the correct statistical properties (including fluctuations), but rather to apply a steady, uniform and isotropic pressure on the sample. A comparison of the two options is presented in Section S1.1.

3 ALGORITHM

In this section we shall see all the operations that must be performed to progress from time $t_{i} = i \cdot Δ t$ to time $t_{i + 1} = (i + 1) \cdot Δ t$ . We shall attach to all dynamical quantities a subscript indicating the time step: for instance, $R_{i}$ and $C_{i}$ will be the sphere parameters, $r_{i}$ , $v_{i}$ and $a_{i}$ the vectors of the gas atom positions, velocities and accelerations. Since gas atoms enter and exit the system during every time step, we must update the list of gas atoms and their total number, $N_{i}$ . The Beeman trajectory integrator,^{25, 44} applied to the sample atoms as well, yields the position and velocity vectors $r_{i + 1}$ , $v_{i + 1}$ and requires the knowledge of $r_{i}$ , $v_{i}$ , $a_{i - 1}$ and $a_{i}$ . The accelerations, including also $a_{i + 1}$ , are computed once the corresponding position vector is known, as $a_{j} = - {(\nabla_{r} U)}_{r_{j}} / m_{g}$ , where $U$ is the potential energy function that also depends on the positions of the sample atoms.

The center of mass of the sample, and with it the center of the sphere $C_{i}$ , does move, if nothing else because of the random force exerted by the gas. Moreover, the radius of the sphere $R_{i}$ can also change in time, therefore the spheres at time steps $i$ and $i + 1$ do not coincide. Part of the volume of the latter, the sphere $S_{i + 1}$ , may be external to the former, the sphere $S_{i}$ . Then, it must be populated with gas atoms, choosing their positions and velocities randomly, according to the ideal gas laws seen above. Viceversa, part of the volume of $S_{i}$ may not belong to $S_{i + 1}$ , which means the gas atoms contained in it must be removed from the list.

At time

t_{0} = 0

the positions, velocities and accelerations of the sample atoms are known. The accelerations at time

- Δ t

, required by the Beeman integrator, are set equal to those at

t = 0

. No gas atoms are present (

N_{0} = 0

). At each step

i

we perform the following operations to go to the next step,

i + 1

Compute the number of gas atoms $N_{i n}$ that will enter the sphere $S_{i}$ , as seen at the end of the previous section.
Assign to each of the “new” gas atoms a random entry position on the surface of the sphere $S_{i}$ . We use a system of polar coordinates centered in $C_{i}$ : $θ$ , $ϕ$ and $r = R_{i}$ . We assign $θ \in [0, π]$ with the probability proportional to $s i n (θ)$ using von Neumann's rejection technique, and $ϕ \in [0, 2 π]$ with no probability bias.
Assign to each of the “new” gas atoms the radial and the tangential components of the velocity. The negative radial component is randomly sampled from the distribution $| v_{r} | e^{- v_{r}^{2} / 2 σ^{2}}$ , where $σ = \sqrt{k_{B} T / m_{g}}$ . This distribution derives from Equation (3) by dividing both members by $d v_{r}$ and ignoring all factors not dependent on $v_{r}$ . The other two components are instead sampled from the distribution (4).
Assign to each of the “new” gas atoms its position at the beginning of the time step. We make use of its entry position $r_{s p h}$ on the spherical surface, with polar coordinates $θ, ϕ, R_{i}$ assigned at point 2, and of its velocity $v$ assigned at point 3. Its initial position is set as $r_{i n i} = r_{s p h} - v Δ t^{'}$ , with $Δ t^{'}$ randomly chosen in the range $[0, Δ t]$ . This means the gas atom is found at time $i Δ t$ in a randomly chosen point of its linear trajectory, such that during the next time step $Δ t$ it will enter the sphere $S$ .
Compute the “external” pressure $P_{ext}$ that would be exerted, during the time step $i$ , if the ingoing gas atoms would bounce back. $P_{ext}$ is proportional to the sum of the modules of the radial velocities of the ingoing atoms:
$P_{e x t} = \frac{m_{g}}{2 π R_{i}^{2} Δ t} \sum_{α = 1}^{N_{i n, i}} | v_{α, r, i} |$ (7)
where, as before, the index $i$ denotes the time step and the index $α$ is introduced to label the gas atoms (it is omitted for simplicity when describing operations that concern one atom at a time).
Propagate to time $(i + 1) Δ t$ the positions of all the particles of the system with Beeman's formula. Since we need the accelerations at step $i - 1$ , we set to zero those of the newly generated gas atoms, that do not interact with the sample yet.
Compute the accelerations at time $(i + 1) Δ t$ with the new positions and propagate the velocities to time $(i + 1) Δ t$ .
Remove the gas atoms that, because of their own motion, have left the sphere $S$ . At the same time, compute the “internal” pressure $P_{i n t}$ that would be exerted, during the time step, if the outgoing gas atoms would bounce back:
$P_{i n t} = \frac{m_{g}}{2 π R_{i}^{2} Δ t} \sum_{α = 1}^{N_{o u t, i}} | v_{α, r, i} |$ (8)

where $N_{o u t, i}$ is the number of outgoing atoms during step $i$ . See Section S1.2 for the determination of the radial velocities.
Compute the temperature $T_{i + 1}$ of the gas particles in the sphere $S_{i}$ : $T_{i + 1} = \frac{2 E_{k i n}}{3 k_{B} N^{'}}$ , where $E_{k i n}$ is the total kinetic energy computed with the velocities $v_{i + 1}$ and $N^{'}$ is the number of gas atoms at this stage (further changes will occur at points 11 and 12 to complete the transition from $N_{i}$ to $N_{i + 1}$ ). Note that, in the long run, the gas inside the sphere will have the same temperature $T$ which is imposed to the ingoing gas atoms, and will also act as a thermostat on the sample. However, the gas thermostatic action on a large sample (thousands of atoms or more) would be quite slow. In the simulations discussed in Section 5 we applied a more efficient thermostat⁴⁵ directly to the sample atoms.
Update the center of the sphere and its radius according to their definitions given in the previous section, from $C_{i}, R_{i}$ to $C_{i + 1}, R_{i + 1}$ .
Remove from the list the gas atoms contained in the sphere $S_{i}$ but not in the sphere $S_{i + 1}$ . See Section S1.3 for details.
Add new gas atoms in the region of sphere $S_{i + 1}$ not belonging to $S_{i}$ . See again Section S1.3 for details. The number of gas atoms is now $N_{i + 1}$ .

The barostat here described is implemented in a version of the semiempirical MOPAC program⁴⁶ called MOPAC-PI,⁴⁷ modified and developed by the Pisa research group on excited state dynamics. MOPAC-PI has been coupled with the TINKER software⁴⁸ to perform QM/MM calculations. The MOPAC-PI package is currently used to run simulations of nonadiabatic dynamics by the surface hopping method, either for isolated molecules^{49, 50} or for more complex systems.^{26-28, 51}

4 XP-PCM METHOD

We compared the results of simulations conducted with the method described in Sections 2 and 3 with those of XP-PCM,^{11, 12} using its latest version.¹³ XP-PCM is an extension of the PCM (Polarizable Continuum Model²²), whereby the molecular “target”, described quantum-mechanically, interacts electrostatically with the polarizable continuum medium (the “solvent”) in which it is embedded. The potential energy surface (PES) of the system is then modified and takes the status of a free energy, because the solvent is represented by its equilibrium average properties. The molecular target is contained in a cavity made of interlocking spheres centered on the nuclei of the constituent atoms. Another contribution to the total free energy is the cavitation energy, that is, the work done to separate the solvent molecules when the cavity is created to accommodate the target: such energy term becomes very important at high pressures.

Within XP-PCM, the effect of the external pressure on a molecular target is introduced by a repulsive potential that represents Pauli's repulsion and limits the volume accessible to the electrons of the target. The repulsive potential vanishes inside the cavity, while outside it takes the constant value $𝒵$ , proportional to the electron density of the solvent. The latter is equal to the number density of the solvent molecules times the number of their valence electrons. The radii of the interlocking spheres are those of Bondi (see Table 1), scaled by a factor $f$ which depends on pressure and is normally $f (0) = 1.2$ at $P = 0$ . The volume $V$ of the cavity then also changes with pressure, and the factor $f$ is adjusted to satisfy the thermodynamic relationship $P = - {(d G / d V)}_{T}$ . The repulsion $𝒵$ contains a factor that depends on the pressure through the cavity volume: $𝒵 (P) = 𝒵 (0) {[V (0) / V (P)]}^{1 + η / 3}$ , where $η$ is a user supplied semiempirical parameter. The repulsive potential, as well as the electrostatic interactions, is added to the electronic hamiltonian. This way, the electronic wavefunctions and properties of the target, along with the PESs, are modified by the applied pressure.

TABLE 1. OPLS-AA parameters^{48, 53}

ϵ

(kcal/mol) and

σ

(Å) used in the simulations and Bondi's van der Waals radii⁵⁴ (Å), scaled by the factor 1.2, as used in the calculation of the sample volumes.

Atom	OPLS-AA		Bondi's
	$ϵ$	$σ$	radii
C	0.0760	3.550	2.040
H	0.0300	2.420	1.440
Ar	0.2339	3.401	1.880

In the present application, energies and optimized geometries were computed with the DFT method, using the B3LYP hybrid functional and Dunning's cc-pVDZ basis set. Liquid argon was used as a compressing external medium (dielectric constant $ϵ_{r} = 1.43$ , density 1.3954 g/cm $^{3}$ ). The value of the Pauli repulsion parameter was $η = 3$ . The scaling factor $f$ ranged from 1.2 to 0.9. The geometry optimizations were performed using the Z-Matrix internal coordinates with the constraints of $C_{2}$ symmetry. For compressed butadiene, three kinds of calculations were performed: potential energy curves as functions of the dihedral angle $τ_{CCCC}$ , with the geometries obtained in vacuo ( $P = 0$ ); geometry optimizations at selected values of $τ_{CCCC}$ , for the bond lengths only, with bond angles and dihedrals fixed at their $P = 0$ values to speed up convergence; the same with the CCC bond angles also optimized. All the XP-PCM calculations were performed using a locally modified version of the Gaussian 16 suite of programs.⁵²

5 SIMULATIONS OF THE CONFORMATIONAL DYNAMICS OF BUTADIENE

Although the main purpose of the development of XP-GAS is the simulation of photochemistry at extreme pressures, we can as well simulate ground state dynamics. The latter is inherently simpler and lends itself to comparison with the XP-PCM method. Therefore, as a first test, we choose to simulate the effect of pressure on the equilibrium geometries and the conformational dynamics of 1,3-butadiene. No high pressure experiments concerning 1,3-butadiene were previously performed, to the best of our knowledge, with the exception of a study of the phase diagram of solid butadiene.⁵⁵ The purpose of the simulations here presented is not to assess the accuracy of our predictions versus experimental results. In fact, the overall accuracy depends more on the quality of the ground state PES of butadiene than on the details of the barostat. Our aim is rather to provide an example of the working of XP-GAS and of the kind of information one can extract from the high pressure simulations. Moreover, we run distinct simulations with a “naked” butadiene molecule and with the same molecule surrounded by a cluster of Ar atoms, in order to test the importance of a realistic description of the medium.

5.1 Reparameterization of the semiempirical hamiltonian

Since we compute the wavefunction and PES of butadiene by a semiempirical method, we found necessary to modify its parameters for better accuracy. In particular, we are interested in the energy relationships between the stationary points found along the torsional coordinate for the central C-C bond (

τ_{CCCC}

dihedral): the

s

t r a n s

and

g a u c h e

minima, the barrier between them, and the

s

c i s

maximum which is the transition state (TS) between the two

g a u c h e

enantiomeric conformers. In the following, we shall adopt the following shorthands to design these structures:

TBD for $s$ - $t r a n s$ -butadiene;
GBD for $g a u c h e$ -butadiene;
CBD for $s$ - $c i s$ -butadiene;
TS $_{t g}$ for the transition state between TBD and GBD.

A very accurate study of such stationary points was performed by Feller and Craig.⁵⁶ They made use of the coupled clusters theory at the CCSD(T) level, with the cc-pVQZ basis set, plus further corrections. Their results are in excellent agreement with Raman spectroscopy data by Engeln et al.⁵⁷ We then took these computational and experimental results as reference for the reparameterization of the semiempirical hamiltonian.

We performed geometry optimizations of the four critical points TBD, GBD, CBD and TS $_{t g}$ . Table 2 shows that the semiempirical methods implemented in MOPAC^{46, 47} (MNDO, AM1, PM3, PM5) with their standard parameters fail to predict the correct energy differences between the target critical points. Overall the potential energy curve as a function of the torsion angle $τ_{CCCC}$ is too flat in comparison with the computational⁵⁶ and experimental⁵⁷ references. A plausible explanation could be the well known weakness of dispersion and repulsion potentials of PM3 and related semiempirical hamiltonians.⁵⁸ Therefore, we added Lennard-Jones potentials between all pairs of C and H atoms, using the parameters and rules of OPLS-AA^{48, 53} (see Table 1). This modification results in a modest improvement, as shown in Table 2. The low values of the TS $_{t g}$ energy obtained with all the tested semiempirical methods suggest that the conjugation effect is underestimated.

TABLE 2. Relative energies (

E

in eV) with respect to TBD and dihedral angles

τ_{CCCC}

(degrees) obtained with different methods.

Method	$τ_{CCCC}$	$E$	$E$	$τ_{CCCC}$	$E$
	GBD		CBD	TS $_{t g}$
ab initio^a	35.5	0.131	0.151	101.7	0.278
B3LYP^b	29.9	0.159	0.168	100.0	0.328
Raman^c	42.5	0.123	0.173	103.4	0.257
MNDO	36.0	0.013	0.020	92.6	0.020
AM1	14.3	0.033	0.034	91.1	0.085
PM3	26.7	0.031	0.031	92.1	0.065
PM5	35.4	0.005	0.016	97.6	0.037
MNDO+LJ	55.8	0.011	0.025	89.7	0.013
AM1+LJ	35.4	0.050	0.055	89.0	0.075
PM3+LJ	35.6	0.046	0.058	88.3	0.055
PM5+LJ	47.0	0.014	0.037	95.6	0.028
R-AM1+LJ	33.9	0.133	0.169	101.6	0.250

Note: For TBD, $τ_{CCCC} = 18 0^{\circ}$ and for CBD, $τ_{CCCC}$ =0. Four semiempirical hamiltonians were tested, with or without the addition of Lennard-Jones potentials as indicated by the +LJ label (see text). The last line refers to the reparameterized AM1 hamiltonian with the addition of Lennard-Jones terms.
^a Feller and Craig.⁵⁶
^b This work, B3LYP with the cc-pVDZ basis set.
^c Engeln et al.⁵⁷

We then proceeded to reparameterize the semiempirical hamiltonian. The procedure⁵⁹ consists in defining a set of relevant target values (energy differences, equilibrium coordinates, vibrational frequencies) that are known with sufficient accuracy, and to train the semiempirical method to reproduce them as best as possible. The target data were: the energies of the CBD, GBD and TS $_{t g}$ critical points with respect to TBD; the C-C bond lengths and C-C-C bond angles of the four critical points; the $τ_{CCCC}$ and $τ_{HCCC}$ dihedral angles of the GBD and TS $_{t g}$ structures (the $τ_{HCCC}$ dihedral refers to the terminal H atom which is close to be eclipsed); and, the four lowest vibrational frequencies⁶⁰ of TBD. All data, with the exception of the experimental vibrational frequencies, were taken from Feller and Craig.⁵⁶ Twelve parameters were optimized, that is, all those involved in the determination of the semiempirical wavefunctions and pertaining to the C atoms. The parameters of the core-core potentials and all those of the H atoms were left unchanged. Details of the procedure and of its outcome are given in Section S2. The best results were obtained by starting from the AM1 parameters with the addition of Lennard-Jones potentials. The last line of Table 2, labelled R-AM1+LJ (reparameterized AM1 + Lennard-Jones), summarizes such results. We see that the $τ_{CCCC}$ dihedrals we obtained are very close to the target ones.⁵⁶ Also the energy differences are well reproduced: actually, the two energy data that show relatively large discrepancies with respect to the targets (CBD and TS $_{t g}$ ) are closer to the experimental estimates.⁵⁷

5.2 XP-GAS simulations

We ran two sets of simulations: in the first set the sample was just one molecule of butadiene (“naked” butadiene), while in the second the butadiene molecule was surrounded by a large cluster of argon atoms (butadiene in Ar). In both cases the simulations lasted 20 ps and two initial conformations were tried, TBD and GBD. Pressures up to 15 GPa were applied, including $P = 0$ , that is, the free sample in vacuo. The radius of the gas atoms was set to $σ_{g} = 6$ Å. In all simulations the temperature was $T = 300$ K. We applied the Langevin thermostat⁴⁵ to the sample atoms.

Butadiene was represented by the R-AM1+LJ semiempirical method. The pair interactions Ar-Ar, Ar-C and Ar-H were computed by the OPLS-AA force-field, which in this case reduces to Lennard-Jones potentials (see Table 1 for the parameters). The Ar cluster was approximately spherical, with radius of about 20 Å, and contained initially 1048 atoms, spaced by 3.76 Å (twice the van der Waals radius). Some atoms in the center were removed to host the butadiene molecule, so the cluster surrounding TBD reduced to 1036 Ar atoms, and the one with GBD, to 1039. All simulations, with the exception of those with $P = 0$ , were preceded by an equilibration run of at least 6 ps, whereby the sample atoms did not move, in order to save computing time. During the equilibration we monitored the internal pressure $P_{i n t}$ , which was initially zero. We stopped the equilibration at the time $t$ , when the time average of $P_{i n t}$ over the interval $[t / 2, t]$ was found to differ from the desired value $P$ by less than $1 %$ .

One of the relevant properties of the sample is its volume, which was evaluated by considering all atoms as spheres with fixed radii. We used the van der Waals radii as compiled by Bondi,⁵⁴ scaled by a factor 1.2, that is, the same radii taken as reference in XP-PCM (see Table 1). The atom spheres in a molecule do overlap, and computing the volume of such a solid is a non-trivial problem. We used the algorithm developed by Buša et al.⁶¹ and their freely available software ARVO.

As we see in Figure 2, the volume of the sample TBD in Ar decreases during the first 1–2 ps under the effect of pressures

\geq 1

GPa, and then remains stable. Quite clearly, within 2 ps the compression propagates from the surface of the cluster towards the center, and the Ar atoms get closely packed while the average distance between neighbors decreases. After 2 ps, monitoring the volume offers no evidence of further structural changes. With

P = 0

, on the contrary, the volume keeps slowly increasing, because Ar atoms “evaporate” from the cluster and the whole structure expands. The limiting volume, that is reached when all the spheres of the Ar atoms do not overlap any more, is about 50000 Å

^{3}

. The time averaged volumes

⟨V_{S}⟩

in the interval

[2, 20]

ps are plotted in the right panel of Figure 2 as a function of pressure, and can be conveniently fitted by the function

{⟨V_{S}⟩}_{P} = V_{\infty} + \frac{V_{0} - V_{\infty}}{1 + A P}

(9)

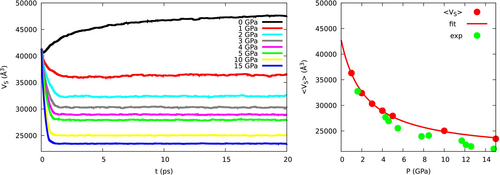
Here $A = 0.42$ GPa $^{- 1}$ is a compressibility parameter, $V_{0} = 42.8 \cdot 1 0^{3}$ Å $^{3}$ is the extrapolation of the volume at vanishing pressure (the $⟨V_{S}⟩$ value at $P = 0$ was not included in the fitting), while $V_{\infty} = 20.6 \cdot 1 0^{3}$ Å $^{3}$ is the asymptotic value that would be reached at large pressures of the order of 100 GPa. Almost identical results are obtained with GBD instead of TBD, since the contribution of butadiene to the $V_{S}$ volume is small, and the difference between the two conformers, as we shall see, is less than 0.3 Å $^{3}$ . These data compare well with the experimental ones, obtained by static measurements,⁶² but the difference tends to increase at the highest pressures, because the OPLS potential is slightly too repulsive at short Ar-Ar distances (see Patkowski et al.⁶³ for a very accurate potential).

5.3 Conformational dynamics

As a preliminary consideration, it is worth to compare the volumes of the four optimized conformations for the isolated molecule: we list them in Table 3, along with the C-C bond distances, the $θ_{C_{1} C_{2} C_{3}}$ and $θ_{C_{2} C_{3} C_{4}}$ bond angles and the $τ_{CCCC}$ dihedral. According to the R-AM1+LJ semiempirical geometry optimizations, the two stable conformers show the largest volume difference: $Δ V_{G - T} = V_{G B D} - V_{TBD} = - 0.257$ Å $^{3}$ . At the B3LYP geometries the volume changes follow a similar pattern, but the $Δ V_{G - T}$ difference is smaller ( $- 0.123$ Å $^{3}$ ) and the volume of CBD is smaller than that of GBD. In both cases, GBD and CBD are stabilized with respect to TBD at high pressures because of their smaller volumes. The GBD $-$ TBD free energy difference is also decreased by the entropic contribution $- R T l n (2)$ , due to the existence of two GBD enantiomers: at $T = 300$ K, this amounts to $- 0.018$ eV.

TABLE 3. Internal coordinates (distances in Å, angles in degrees) and volumes (Å

^{3}

) of four different conformations of butadiene.

	R-AM1+LJ				B3LYP/cc-pVDZ
	TBD	GBD	CBD	TS $_{t g}$	TBD	GBD	CBD	TS $_{t g}$
$R_{C_{1} C_{2}}$	1.374	1.373	1.371	1.370	1.343	1.341	1.342	1.337
$R_{C_{2} C_{3}}$	1.468	1.470	1.468	1.476	1.459	1.471	1.473	1.488
$θ_{C_{1} C_{2} C_{3}}$	117.7	121.1	124.4	119.5	124.3	125.9	127.3	124.8
$τ_{CCCC}$	180.0	33.9	0.0	101.6	180.0	30.6	0.0	99.0
Volume	98.120	97.863	97.895	98.261	99.283	99.160	99.050	99.553

Note: For all geometries, $R_{C_{3} C_{4}} = R_{C_{1} C_{2}}$ and $θ_{C_{2} C_{3} C_{4}} = θ_{C_{1} C_{2} C_{3}}$ . The volumes are computed by the ARVO method,⁶¹ whereby the atoms are overlapping spheres with the radii listed in Table 1. The molecular geometries were optimized by our R-AM1+LJ semiempirical method, or by DFT/B3LYP/cc-pVDZ as in the XP-PCM calculations.

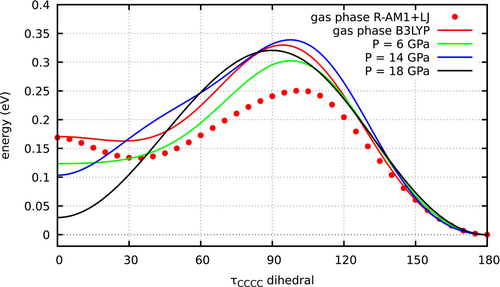
The molecular volumes do change when applying large pressures, mainly due to deformations of the molecular geometry but also to the confinement of the electronic cloud. The XP-PCM method takes into account both effects. In Figure 3 we show the potential energy curves of butadiene in gas phase, as a function of the torsion angle $τ_{CCCC}$ , obtained by optimizing all the other internal coordinates at B3LYP/cc-pVDZ and R-AM1+LJ levels. Three more curves represent the free energies obtained at $P = 6$ , 14 and 18 GPa by the XP-PCM method (remember that by XP-PCM the PESs acquire the status of free energies–see Section 4–yet can be directly compared with ordinary PES computed for the isolated molecule). Taking as starting point the geometries obtained in vacuo, the bond lengths were reoptimized, keeping the bond angles and the dihedrals fixed. The further optimization of the C-C-C bond angles did not result in noticeable changes in the geometries and free energies (see Table S4). The effect of pressure is to stabilize CBD with respect to TBD: at 18 GPa, the free energies of the two conformers only differ by about 0.03 eV. This effect is mainly due to bond shortening, rather than to the confinement of the electronic cloud. In fact, the free energy curves computed by XP-PCM with the in vacuo geometries show a much smaller dependence on pressure (see Figure S4 and Table S4).

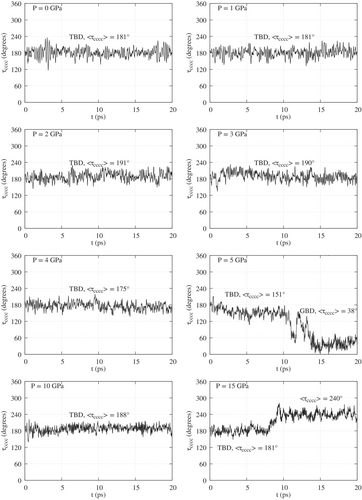
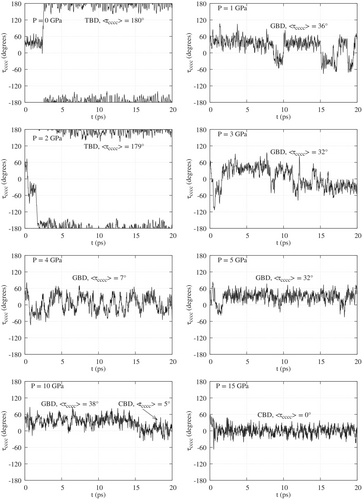
The conformations of butadiene are mainly characterized by the torsion angle $τ_{CCCC}$ . The values of $τ_{CCCC}$ as a function of time are shown in Figures 4 and 5, respectively for simulations starting with TBD and GBD in Ar, at different pressures. Figures S6 and S7 display the same data for a “naked” butadiene molecule. To facilitate the reading of the figures, the symbols TBD, GBD or CBD and the corresponding average values of $τ_{CCCC}$ mark the time intervals where one finds (meta)stable conformations, as detailed in Tables S5–S8. We see that TBD is favored at low pressures and GBD at high pressures, as expected from their relative volumes. GBD can switch frequently between its enantiomers or, at 10 or 15 GPa in argon, stabilize in the intermediate CBD conformation. The TBD $⇄$ GBD interconversion is instead much slower, due to the higher barrier, and occurs once or not at all in the simulations of standard duration (20 ps). In order to observe a statistically significant number of conformational transitions, we ran two much longer simulations (200 ps) for butadiene in argon, starting from either TBD or GBD geometries (Figure S5). We chose the pressure of 5 GPa, whereby we had observed a TBD $\to$ GBD transition during the first 20 ps. In the simulation starting from TBD we observed eight TBD $\to$ GBD and seven GBD $\to$ TBD transitions in 200 ps. On the contrary, the initial GBD conformer did not convert to TBD during the whole simulation (Figure S5). This result shows the important effect of the cage of Ar atoms at high pressures: when the cage is modelled on the flat TBD geometry, 5 GPa is about the pressure that makes the two conformers equally probable. On the contrary, the cage shaped around GBD makes the conversion to TBD much less likely.

Of course, the cage itself can rearrange in response to conformational changes of the hosted molecule, but apparently this event occurs in a still longer time scale at such extreme pressures. The dynamics of fast photoprocesses may also require the disruption of the high pressure cage. However, to really affect the photodynamics, the cage change must occur in a short time, namely before the quenching of excitation and the loss of vibrational energy to the environment have dissipated the energy excess acquired by photon absorption. So, slow cage rearrangements are likely irrelevant to our main goal, that is, to run high pressure simulations of photodynamics.

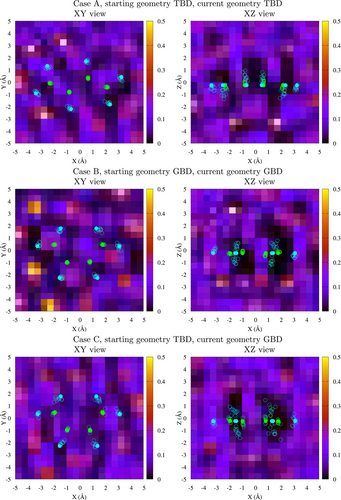
Figure 6 shows three different density maps of Ar atoms at 5 GPa: around TBD in the simulation starting at the TBD geometry (case A); around GBD in the simulation starting at the GBD geometry (case B) and around GBD obtained starting at the TBD geometry (case C). The B and C maps show marked differences: namely, the positions of the Ar atoms in case C are much less defined than in case B, meaning the butadiene molecule is more mobile with respect to the Ar cage. The maps were obtained as projections on two different planes of the densities computed for a cubic box of 10 Å side (see Section S6 for details). The average number of Ar atoms contained in the $1 0^{3}$ Å $^{3}$ box is 35.95 for TBD (case A), 36.07 for the “native” GBD (case B) and 36.41 for GBD derived from TBD (case C). Since the volume occupied by an argon atom at this pressure can be estimated between 25 and 27 Å $^{3}$ , the excluded volume difference $Δ V_{t - g}$ between the TBD and GBD at 5 GPa is about 3 and 12 Å $^{3}$ for cases B and C, respectively. These differences are much larger than those computed for the isolated molecule (see Table 3), showing that GBD is more compressible than TBD.

In conclusion, the two methods, XP-GAS/R-AM1+LJ and XP-PCM/B3LYP/cc-pVDZ show overall the same trends as to the effect of pressure on the conformational equilibrium between TBD and GBD/CBD. However, at the R-AM1+LJ semiempirical level the conformational equilibrium of butadiene is more sensitive to pressure than at XP-PCM/B3LYP/cc-pVDZ level. In fact, in the latter case we have seen that pressures of the order of 20 GPa are needed to make CBD and TBD about equally stable. Sources of this difference can be that the geometry optimizations performed at XP-PCM level did not consider all the internal coordinates, and possibly an overestimated compressibility of GBD and CBD with respect to TBD, at R-AM1+LJ level. Another minor difference is that both GBD and CBD can be found as relatively stable structures in the XP-GAS simulations, while XP-PCM does not predict a GBD minimum at any of the three pressures investigated. This is in part due to the fact that, even in vacuo, the GBD minimum is much shallower by B3LYP/cc-pVDZ than by R-AM1+LJ.

5.4 Effect of pressure on molecular geometries

As already noted, the compressibility of a single butadiene molecule is mainly due to changes in its internal coordinates. The averages and standard deviations of the latter are listed in Tables S5 and S6 for the simulations of butadiene in argon, and in Tables S7 and S8 for the naked butadiene. The averages were computed for well defined conformations, that is, along time ranges in which the $τ_{CCCC}$ dihedral oscillates around some fixed value. When appropriate, such time ranges are labelled TBD, GBD or CBD in Figures 4, 5, S6 and S7. The $τ_{CCCC}$ averages for the TBD structure were computed with reference to the $[0, 36 0^{\circ}]$ interval, while for GBD and CBD the interval was $[- 18 0^{\circ}, 18 0^{\circ}]$ (see notes in Tables S6, S7 and S8 for further details). With few exceptions described below, the average structures are symmetric, that is, $R_{C_{1} C_{2}} ≃ R_{C_{3} C_{4}}$ and $θ_{C_{1} C_{2} C_{3}} ≃ θ_{C_{2} C_{3} C_{4}}$ . For pressures up to 4 GPa the average $⟨τ_{CCCC}⟩$ of TBD does not deviate by more than 11° from the equilibrium value of 180°. In this range of pressures, the largest deviations from planarity are found for butadiene in Ar, at 2 and 3 GPa (Table S5). At 5 GPa we find $⟨τ_{CCCC}⟩ = 15 1^{\circ}$ , and Figure 6(case A, XZ view) clearly shows that the distorsion is due to the shape of the Ar atoms cage. An even larger distortion ( $⟨τ_{CCCC}⟩ = 24 0^{\circ}$ ) is found at 15 GPa, along with a slightly asymmetric structure ( $⟨θ_{C_{1} C_{2} C_{3}}⟩ \neq ⟨θ_{C_{2} C_{3} C_{4}}⟩$ ). GBD in most cases, especially at relatively low pressures, has $⟨τ_{CCCC}⟩$ between $2 7^{\circ}$ and $3 8^{\circ}$ (equilibrium value, $33 . 9^{\circ}$ ). At higher pressures (10 or 15 GPa) we observe three different behaviours: in Ar, starting from the GBD geometry, the symmetric CBD conformation prevails, with low $⟨τ_{CCCC}⟩$ values (see Table S6); the naked butadiene, initially TBD, assumes an asymmetric geometry with $⟨τ_{CCCC}⟩ = 7 1^{\circ}$ or, almost equivalently, 292° (Table S7); and again the naked butadiene, initially GBD, becomes strongly asymmetric and almost flat, with $⟨τ_{CCCC}⟩ ≃ \pm 1 6^{\circ}$ (Table S8).

The dependence of the internal coordinates on pressure is shown in Figure 7, where we plot the time averages listed in Tables S5, S6, S7 and S8. Since most of the structures are symmetric, we plot the averages $⟨R_{C_{1} C_{2}} + R_{C_{3} C_{4}}⟩ / 2$ and $⟨θ_{C_{1} C_{2} C_{3}} + θ_{C_{2} C_{3} C_{4}}⟩ / 2$ instead of the single distances and angles. Under the label TBD, we plot data belonging to conformations with $⟨τ_{CCCC}⟩ \in [15 0^{\circ}, 21 0^{\circ}]$ . The label GBD collects conformations with $⟨τ_{CCCC}⟩ \in [- 4 0^{\circ}, 4 0^{\circ}]$ , so including also geometries close to CBD. In few cases we have two values for the same conformer, pressure and environment (with or without Ar), because that conformer was obtained starting from the TBD and from the GBD geometries: in such cases, the averaged coordinates derived from the two simulations are quite close to each other. The XP-PCM results for TBD are also represented in Figure 7 and are in good agreement with the XP-GAS simulations of TBD in argon. TBD, among other molecules, was recently taken as a test case for the eXtended Hydro-static Compression Force Field (X-HCFF) model.¹⁸ X-HCFF is based on a relatively simple mechanochemical approach, whereby the pressure is converted into forces acting on the atoms of the sample. The bond lengths obtained by X-HCFF were also in good agreement with the present calculations.

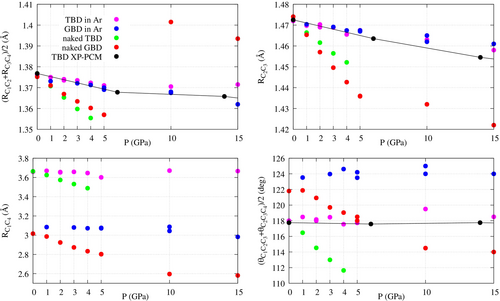
In Figure 7 we see that the C=C and C-C bond lengths decrease regularly with pressure up to 5 GPa. The dependence on pressure is much more marked for naked butadiene than in argon. At higher pressures the presence of more distorted and asymmetric geometries as discussed above makes the progression less regular. The CCC bond angles also decrease with pressure for naked butadiene, producing more compact geometries. On the contrary, for the angles of butadiene in Ar one cannot identify a decreasing trend. By inspecting the density maps of Figure 6, we see that the closest Ar atoms are placed above and below the (approximate) molecular plane and avoid being on top of the C atoms. Given their positions, the Ar atoms, pressed towards the butadiene molecule, can force a bond angle to increase or decrease, mainly depending on whether they are internal or external to the angle in the XY view. The $C_{1} - C_{4}$ distance, which can be taken as a proxy of the overall length of the molecule, depends mainly on the bond angles rather than on the bond lengths: in fact, it can change much more than the latter and it follows the same trends as the former. Of course, it is also affected by the $τ_{CCCC}$ dihedral, as shown by the large difference in $R_{C_{1} C_{4}}$ between TBD and GBD.

Overall, the plots of Figure 7 show striking differences between butadiene in Ar and naked butadiene. The latter behaves in a more straightforward way, reducing bond lengths and bond angles so as to decrease the molecular volume. The cage of Ar atoms very effectively reduces the pressure action, in part because of the Ar-Ar repulsive forces that hinder the shrinking of the cage itself. Moreover, depending on their position, some Ar atoms pushing against the molecule tend to open the C-C-C bond angles instead of closing them. These considerations show the importance of introducing a realistic description of the medium in modelling pressure effects by XP-GAS and similar methods.^40-43

6 CONCLUSIONS

We present the XP-GAS barostat for extremely high pressures, well suited to run simulations of molecules in different environments, described at MM, QM or QM/MM levels. The XP-GAS approach consists in embedding the molecular sample in a fictitious ideal gas as in previous proposals,^40-43 so producing the wanted uniform and constant pressure with good approximation. The major new feature of XP-GAS is the shape of the boundary containing the ideal gas, which is spherical, to guarantee isotropy. The barostat is implemented in the Pisa version of the semiempirical MOPAC package, called MOPAC-PI,⁴⁷ currently used to run simulations with nonadiabatic trajectories.^{25-28, 49-51}

While the main purpose of the XP-GAS barostat is to investigate the dynamics of photoprocesses at extreme pressures, in this work we tested it by simulating the conformational behaviour of 1,3-butadiene. Two kinds of simulations were run, where the sample subject to extreme pressures was, respectively, a single molecule of “naked” butadiene and the same embedded in a cluster of Ar atoms, as common in nano-anvil experiments. The transitions between the $s$ - $t r a n s$ , $s$ - $c i s$ and $g a u c h e$ conformations, as well as the geometry changes induced by pressure, show important differences when comparing naked butadiene with butadiene in argon. We found a good agreement between the time-averaged bond lengths and bond angles computed by XP-GAS simulations of butadiene in argon, and the geometries optimized by the XP-PCM method, put forward by one of us.^11-13 Overall, these results show that the XP-GAS QM/MM simulation method is in good agreement with the XP-PCM QM/Continuum model (Cammi model) in describing the effect of the pressure on static properties as the equilibrium geometry of butadiene in the ground state. Furthermore, the comparison of XP-GAS simulations with naked butadiene and butadiene in argon shows the importance, for XP-GAS and related methods,^40-43 of a realistic representation of the medium in modelling pressure effects.

ACKNOWLEDGMENTS

We are grateful to Dr. Lorenzo Cupellini for valuable suggestions. This work was supported by grants of the University of Pisa. GG acknowledges funding from CN1, "HPC, Big Data, Quantum Computing", Spoke 6, Multiscale Modeling and Engineering Applications. Open access publishing facilitated by Universita degli Studi di Pisa, as part of the Wiley - CRUI-CARE agreement.

Open Research

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available within the article and its supplementary material. These data were derived from the following resources available in the public domain: MOPAC-PI package, https://gitlab.com/granucci/mopacpi.

Supporting Information

REFERENCES

1V. Schettino, R. Bini, Chem. Soc. Rev. 2007, 36, 869.
10.1039/b515964b
CAS PubMed Web of Science® Google Scholar
2X.-D. Wen, L. Hand, V. Labet, T. Yang, R. Hoffmann, N. W. Ashcroft, A. R. Oganov, A. O. Lyakhov, Proc. Nat. Acad. Sci. 2011, 108, 6833.
10.1073/pnas.1103145108
CAS Web of Science® Google Scholar
3T. Scheler, M. Marqués, Z. Konôpková, C. L. Guillaume, R. T. Howie, E. Gregoryanz, Phys. Rev. Lett. 2013, 111, 215503.
10.1103/PhysRevLett.111.215503
PubMed Web of Science® Google Scholar
4H.-K. Mao, B. Chen, J. Chen, K. Li, J.-F. Lin, W. Yang, H. Zheng, Matter Rad. Extr. 2016, 1, 59.
10.1016/j.mre.2016.01.005
Web of Science® Google Scholar
5J. Sun, X. Dong, Y. Wang, K. Li, H. Zheng, L. Wang, G. D. Cody, C. A. Tulk, J. J. Molaison, X. Lin, Y. Meng, C. Jin, H. K. Mao, Angew. Chem., Int. Ed. 2017, 56, 6553.
10.1002/anie.201702685
CAS PubMed Web of Science® Google Scholar
6B. Chen, R. Hoffmann, N. W. Ashcroft, J. V. Badding, E. Xu, V. Crespi, J. Am. Chem. Soc. 2015, 137, 14373.
10.1021/jacs.5b09053
CAS PubMed Web of Science® Google Scholar
7T. A. Singleton, K. S. Ramsay, M. M. Barsan, I. S. Butler, C. J. Barrett, J. Phys. Chem. B 2012, 116, 9860.
10.1021/jp3060872
CAS PubMed Web of Science® Google Scholar
8T. Kinoshita, S. Nakamura, M. Harada, T. Hasobe, G. Fukuhara, Chem. Sci. 2023, 14, 3293.
10.1039/D3SC00312D
CAS PubMed Google Scholar
9M. Mugnai, G. Cardini, V. Schettino, Phys. Rev. B 2004, 70, 020101.
10.1103/PhysRevB.70.020101
Web of Science® Google Scholar
10Z. Cui, Y. Sun, J. Qu, J. Comput. Theor. Nanosci. 2008, 5, 1646.
10.1166/jctn.2008.842
CAS Google Scholar
11R. Cammi, C. Cappelli, B. Mennucci, J. Tomasi, J. Chem. Phys. 2012, 137, 154112.
10.1063/1.4757285
CAS PubMed Web of Science® Google Scholar
12R. Cammi, J. Comput. Chem. 2015, 36, 2246.
10.1002/jcc.24206
CAS PubMed Web of Science® Google Scholar
13R. Cammi, B. Chen, J. Chem. Phys. 2022, 157, 114101.
10.1063/5.0104269
CAS PubMed Web of Science® Google Scholar
14R. Fukuda, T. Yang, R. Cammi, J. Chem. Theory Comput. 2015, 11, 2063.
10.1021/ct5011517
CAS PubMed Web of Science® Google Scholar
15T. Yang, R. Fukuda, R. Cammi, M. Ehara, J. Phys. Chem. A 2017, 121, 4363.
10.1021/acs.jpca.7b02805
CAS PubMed Web of Science® Google Scholar
16B. Chen, R. Hoffmann, R. Cammi, Angew. Chem., Int. Ed. 2017, 56, 11126.
10.1002/anie.201705427
CAS PubMed Web of Science® Google Scholar
17M. Rahm, R. Cammi, N. W. Ashcroft, R. Hoffmann, J. Am. Chem. Soc. 2019, 141, 10253.
10.1021/jacs.9b02634
CAS PubMed Web of Science® Google Scholar
18T. Stauch, J. Chem. Phys. 2020, 153, 134503.
10.1063/5.0024671
CAS PubMed Web of Science® Google Scholar
19T. Pongratz, P. Kibies, L. Eberlein, N. Tielker, C. Hölzl, S. Imoto, M. B. Erlach, S. Kurrmann, P. H. Schummel, M. Hofmann, O. Reiser, R. Winter, W. Kremer, H. R. Kalbitzer, D. Marx, D. Horinek, S. M. Kast, Biophys. Chem. 2020, 257, 106258.
10.1016/j.bpc.2019.106258
CAS PubMed Web of Science® Google Scholar
20S. Imoto, D. Marx, Phys. Rev. Lett. 2020, 125, 086001.
10.1103/PhysRevLett.125.086001
CAS PubMed Web of Science® Google Scholar
21C. Förster, H. Osthues, D. Schwab, N. L. Doltsinis, K. Heinze, ChemPhysChem 2023, 24, e202300165.
10.1002/cphc.202300165
CAS PubMed Web of Science® Google Scholar
22J. Tomasi, B. Mennucci, R. Cammi, Chem. Rev. 2005, 105, 2999.
10.1021/cr9904009
CAS PubMed Web of Science® Google Scholar
23A. V. Akimov, Foundamentals of Trajectory Based Methods for Nonadiabatic Dynamics, in Comprehensive Computational Chemistry, Vol. 4 (Eds: M. Yáñez, R. J. Boyd), Elsevier, Amsterdam 2023, p. 235.
Google Scholar
24M. Persico, G. Granucci, D. Accomasso, The Quantum Decoherence Problem in Nonadiabatic Trajectory Methods In Comprehensive Computational Chemistry, Vol. 4 (Eds: M. Yáñez, R. J. Boyd), Elsevier, Amsterdam 2023, p. 273.
Google Scholar
25G. Granucci, M. Persico, A. Toniolo, J. Chem. Phys. 2001, 114, 10608.
10.1063/1.1376633
CAS Web of Science® Google Scholar
26P. Mondal, G. Granucci, D. Rastädter, M. Persico, I. Burghardt, Chem. Sci. 2018, 9, 4671.
10.1039/C8SC00072G
CAS PubMed Web of Science® Google Scholar
27J. Fregoni, G. Granucci, M. Persico, S. Corni, Chem 2020, 6, 250.
10.1016/j.chempr.2019.11.001
CAS Web of Science® Google Scholar
28S. Osella, G. Granucci, M. Persico, S. Knippenberg, J. Mat. Chem. B 2023, 11, 2518.
10.1039/D2TB02767D
CAS PubMed Google Scholar
29S. M. J. Rogge, L. Vanduyfhuys, A. Ghysels, M. Waroquier, T. Verstraelen, G. Maurin, V. Van Speybroeck, J. Chem. Theory Comput. 2015, 11, 5583.
10.1021/acs.jctc.5b00748
CAS PubMed Web of Science® Google Scholar
30T. Vasilevskaya, W. Thiel, J. Chem. Theory Comput. 2016, 12, 3561.
10.1021/acs.jctc.6b00269
CAS PubMed Web of Science® Google Scholar
31H. Nishizawa, H. Okumura, J. Comput. Chem. 2016, 37, 2701.
10.1002/jcc.24497
CAS PubMed Web of Science® Google Scholar
32Y. Kawashima, K. Ishimura, M. Shiga, J. Chem. Phys. 2019, 150, 124103.
10.1063/1.5048451
CAS PubMed Web of Science® Google Scholar
33M. Bondanza, M. Nottoli, L. Cupellini, F. Lipparini, B. Mennucci, Phys. Chem. Chem. Phys. 2020, 22, 14433.
10.1039/D0CP02119A
CAS PubMed Web of Science® Google Scholar
34S. Bonfrate, N. Ferré, M. Huix-Rotllant, J. Chem. Phys. 2023, 158, 021101.
10.1063/5.0133646
CAS PubMed Google Scholar
35S. Bonfrate, N. Ferré, M. Huix-Rotllant, J. Chem. theory Comput. 2024, 20, 4338. https://doi.org/10.26434/chemrxiv-2024-5tzsf
10.1021/acs.jctc.4c00201
PubMed Google Scholar
36S. Kodiyalam, R. K. Kalia, H. Kikuchi, A. Nakano, F. Shimojo, P. Vashishta, Phys. Rev. Lett. 2001, 86, 55.
10.1103/PhysRevLett.86.55
CAS PubMed Google Scholar
37S. Kodiyalam, R. K. Kalia, A. Nakano, P. Vashishta, Phys. Rev. Lett. 2004, 93, 203401.
10.1103/PhysRevLett.93.203401
CAS PubMed Web of Science® Google Scholar
38R. Martoňák, L. Colombo, C. Molteni, M. Parrinello, J. Chem. Phys. 2002, 117, 11329.
10.1063/1.1523894
CAS Google Scholar
39B. J. Morgan, P. A. Madden, Nano Lett. 2004, 4, 1581.
10.1021/nl049403d
CAS Web of Science® Google Scholar
40M. Grünwald, C. Dellago, Mol. Phys. 2006, 104, 3709.
10.1080/00268970600968052
CAS Google Scholar
41M. Grünwald, E. Rabani, C. Dellago, Phys. Rev. Lett. 2006, 96, 255701.
10.1103/PhysRevLett.96.255701
CAS PubMed Web of Science® Google Scholar
42M. Grünwald, C. Dellago, P. Geissler, J. Chem. Phys. 2007, 127, 154718.
10.1063/1.2790431
CAS PubMed Web of Science® Google Scholar
43N. Plotnikov, T. Martínez, J. Phys. Chem. C 2016, 120, 17898.
10.1021/acs.jpcc.6b04924
CAS Web of Science® Google Scholar
44D. Beeman, J. Comp. Phys. 1976, 20, 130.
10.1016/0021-9991(76)90059-0
Web of Science® Google Scholar
45W. F. van Gunsteren, H. J. C. Berendsen, Mol. Phys. 1982, 45, 637.
10.1080/00268978200100491
Web of Science® Google Scholar
46J. J. P. Stewart, Mopac, Fujitsu Limited, Tokyo, Japan 2002.
Google Scholar
47G. Granucci, M. Persico, D. Accomasso, E. Sangiogo Gil, S. Corni, J. Fregoni, T. Laino, M. Tesi, A. Toniolo, MOPAC-PI package. https://gitlab.com/granucci/mopacpi
Google Scholar
48J. A. Rackers, Z. Wang, C. Lu, M. L. Laury, L. Lagardère, M. J. Schniders, J.-P. Piquemal, P. Ren, J. W. Ponder, J. Chem. Theory Comput. 2018, 14, 5273.
10.1021/acs.jctc.8b00529
CAS PubMed Web of Science® Google Scholar
49D. Accomasso, M. Persico, G. Granucci, J. Mat. Chem. A 2021, 9, 21897.
10.1039/D1TA04766C
CAS Google Scholar
50C. Pieroni, F. Becuzzi, L. Creatini, G. Granucci, M. Persico, J. Chem. Theory Comput. 2023, 19, 2430.
10.1021/acs.jctc.3c00024
CAS PubMed Web of Science® Google Scholar
51E. Sangiogo Gil, M. Persico, G. Granucci, J. Chem. Phys. 2022, 157, 161101.
10.1063/5.0122109
CAS PubMed Web of Science® Google Scholar
52M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc, Wallingford, CT 2016.
Google Scholar
53W. L. Jorgensen, D. S. Maxwell, J. Tirado-Rives, J. Am. Chem. Soc. 1996, 118, 11225.
10.1021/ja9621760
CAS Web of Science® Google Scholar
54S. Batsanov, Inorg. Mat. 2001, 37, 871.
10.1023/A:1011625728803
CAS Web of Science® Google Scholar
55M. Citroni, M. Ceppatelli, R. Bini, V. Schettino, Chem. Phys. Lett. 2003, 367, 186.
10.1016/S0009-2614(02)01693-7
CAS Web of Science® Google Scholar
56D. Feller, N. C. Craig, J. Phys. Chem. A 2009, 113, 1601.
10.1021/jp8095709
CAS PubMed Web of Science® Google Scholar
57R. Engeln, D. Consalvo, J. Reuss, Chem. Phys. 1992, 160, 427.
10.1016/0301-0104(92)80010-S
CAS Web of Science® Google Scholar
58A. S. Christensen, T. Kubař, Q. Cui, M. Elstner, Chem. Rev. 2016, 116, 5301.
10.1021/acs.chemrev.5b00584
CAS PubMed Web of Science® Google Scholar
59T. Cusati, G. Granucci, E. Martínez-Núñez, F. Martini, M. Persico, S. Vázquez, J. Phys. Chem. A 2012, 116, 98.
10.1021/jp208574q
CAS PubMed Web of Science® Google Scholar
60Y. N. Panchenko, J. V. Auwera, Y. Moussaoui, G. R. De Maré, Struct. Chem. 2003, 14, 337.
10.1023/A:1024445810013
CAS Google Scholar
61J. Buša, J. Džurina, E. Hayryan, S. Hayryan, C. Hu, J. Plavka, I. Pokorný, J. Skřivánek, M. Wu, Comp. Phys. Commun. 2005, 165, 59.
10.1016/j.cpc.2004.08.002
CAS Web of Science® Google Scholar
62M. Ross, H. K. Mao, P. M. Bell, J. A. Xu, J. Chem. Phys. 1986, 85, 1028.
10.1063/1.451346
CAS Web of Science® Google Scholar
63K. Patkowski, G. Murdachaew, C.-M. Fou, K. Szalewicz, Mol. Phys. 2005, 103, 2031.
10.1080/00268970500130241
CAS Web of Science® Google Scholar

Volume45, Issue32

December 15, 2024

Pages 2848-2861

This article also appears in:

Special Issue to Celebrate Professor Hans Lischka's 80th Birthday

An algorithm for very high pressure molecular dynamics simulations

Abstract

1 INTRODUCTION

2 THE XP-GAS METHOD

3 ALGORITHM

4 XP-PCM METHOD

5 SIMULATIONS OF THE CONFORMATIONAL DYNAMICS OF BUTADIENE

5.1 Reparameterization of the semiempirical hamiltonian

5.2 XP-GAS simulations

5.3 Conformational dynamics

5.4 Effect of pressure on molecular geometries

6 CONCLUSIONS

ACKNOWLEDGMENTS

Open Research

DATA AVAILABILITY STATEMENT

Supporting Information

REFERENCES

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

An algorithm for very high pressure molecular dynamics simulations

Abstract

1 INTRODUCTION

2 THE XP-GAS METHOD

3 ALGORITHM

4 XP-PCM METHOD

5 SIMULATIONS OF THE CONFORMATIONAL DYNAMICS OF BUTADIENE

5.1 Reparameterization of the semiempirical hamiltonian

5.2 XP-GAS simulations

5.3 Conformational dynamics

5.4 Effect of pressure on molecular geometries

6 CONCLUSIONS

ACKNOWLEDGMENTS

Open Research

DATA AVAILABILITY STATEMENT

Supporting Information

REFERENCES

Figures

References

Related

Information