1 INTRODUCTION

Alzheimer's disease (AD) is an irreversible neurological condition that impairs patients' memory, cognition, and behavior [1]. The complexity of analyzing AD biomarkers and the variability of measures obtained from different imaging modalities challenges the effective early identification and treatment of AD [2]. Given the lack of significant advancements in developing modalities to treat AD, previous research has looked at providing feasible and affordable options to offer AD patients the care and treatment they need. For instance, the studies reported in Gavidia-Bovadilla and colleagues [3-5] aim at helping AD patients in their day-to-day activities and offer some forms of neural training.

However, detecting how AD is gradually progressing in a patient is crucial to implement early intervention plans [6]. Traditional time series-based methods and machine learning (ML) algorithms have been widely employed in the literature to categorize and predict AD severity, such as the works described in Gavidia-Bovadilla and colleagues [3, 4, 7-11]. Despite these encouraging developments, several complex modeling issues remain unexplored [12]. Most of the literature has focused on modeling the course of diseases rather than predicting their progression. This entails estimating the state of disease progression at known times based on the data available or in the event of limited observations, concentrating primarily on identifying the stages of its progression.

Various ML approaches have been used in the literature to find biomarkers for AD progression and optimize detection performance. A widely used approach to address image classification problems is the support vector machine (SVM). SVM was used in several studies to predict AD progression, such as in Zhang and colleagues [13-18]. In Zhang et al. [13], a multitask learning approach combined with SVM was employed to detect AD progression with 73.9% accuracy and 68.6% sensitivity. The study reported in Cheng et al. [14] achieved an accuracy of 79.4% and a sensitivity of 84.5%.

A linear discriminant analysis based on the cortex thickness data was utilized, which showed 63% sensitivity and 76% specificity [19]—the results for AD progression detection improved by integrating multimodality data and removing redundant AD-related biomarkers from modalities. Using a combination of cerebral spinal fluid, magnetic resonance imaging (MRI), and cognitive performance biomarkers, 68.5% accuracy, 53.4% sensitivity, and 77% specificity were noted in the studies reported in Ewers et al. [20] and Kim et al. [21]. These studies also used deep convolutional autoencoders to examine the data analysis process of AD progression using MRI data. While previous studies have investigated modeling AD, the AD progression issues using recurrent models remain unexplored. Given that AD is a progressive and irreversible disease, it is challenging to detect its progression over time using only the cognitive features of a patient. However, the timely structural changes from cognitive normal (CN) to mild cognitive impairment (MCI) and from MCI to AD can help trace the features affecting the progression of the disease [22].

To this end, as far as our knowledge is concerned, a single study has worked on the detection of patients with a progressive nature [23], which has utilized a univariate recurrent neural network (RNN). In contrast, our study proposes a multivariate long short-term memory (M-LSTM) for the detection of AD subjects with a progressive nature. The study has focused on two types of experiments. The first experiment involves patients who are in a state of progressive disease. Detection is then carried out by confirming their progressive and nonprogressive states. In the second experiment, the study involved only patients whose disease status was updated with time. It then observes the spread of the disease over some time. The performance of the proposed M-LSTM model is evaluated using The AD Prediction of Longitudinal Evolution (TADPOLE) challenge [24]. The results show that the proposed model outperformed the competing models (BiPro and AdaBoost) regarding detection.

The remainder of this paper is structured as follows. Section 2, 2 briefly describes the related studies on predictive modeling. Section 3, 3 presents the details of the proposed methodology. Sections 4, 4 and 5 report the experiments that compare the proposed model's performance with other published approaches. Lastly, Section 6 presents the conclusions of this study.

2 BACKGROUND

RNNs have been widely used in the literature to identify patterns in time series data [25]. Recent studies have shown the success of RNNs in disease detection and prediction. Examples include using gated recurrent units (GRUs) as a diagnostic tool [26]. Moreover, GRU was also used to predict the medication needed for patients' subsequent visits in the early onset of cardiac failure [27]. LSTM models are also used to predict multiple conditions' onset [28]. In addition, LSTM is used for the diagnostic classification of patients in the pediatric intensive care unit (PICU) [29]. The relevant studies have applied different RNN models for medical detection by using longitudinal data on a patient over time.

Research into the detection of AD progression can be classified into three subareas: AD progression categorization [30], AD progression modeling [31, 32], and AD progression estimation [33]. In the categorization framework, studies strive to determine the patient's status regarding non-conversion or conversion over time. Those with progressive MCI are distinguished from patients with stable MCI by learning deep nonlinear representations of the neuroimaging data as the output of a convolutional neural network [34]. In terms of the modeling, a study used a many-to-one extended RNN architecture to facilitate the temporal shift to mimic AD progression in patients on successive visits [35]. The method covered a variety of visit periods of AD subjects. In addition, the Bayesian progression score model is suggested to predict the biomarker trends from normal to MCI and AD [31]. In the context of estimation, a study presented a multisource multitask learner to estimate cognitive scores, such as mini-mental state examination (MMSE) and AD assessment scale-cognitive subscale [2]. These scores may be used to measure the degree and progression of cognitive impairment caused by AD. With the help of recurrent components, valid observations, and static relations considered, the temporal relation for imputation for AD [36].

Contrary to a standard bidirectional RNN, the timing of the inputs to the salient layers is reversed in a forward-and-backward direction. These imputed values were dynamically updated during training until they were optimal (dynamic relation). The study used an RNN for missing value imputation in time series data and then fed the imputed values to an LSTM cell to forecast both the diagnosis of AD and MRI biomarkers [37]. The model inspects the temporal and multivariate relations of measurements (dynamic relations) for missing value imputation (and is called LSTM-I in our comparisons below). Another study proposed a minimal RNN called MinRNN to predict patients' clinical diagnoses, cognition, and ventricular volume [38]. Their model has fewer parameters than other RNN models, such as the LSTM, and therefore is less prone to overfitting [38]. A study modified the LSTM cell by using a progressive module to compute the progression score of each biomarker between the given time point and the baseline through a negative exponential function [39].

3 METHODS

This study examined the detection of AD progression using AdaBoost, an ensemble ML model, and M-LSTM, a deep recurrent network. Two experiments are performed on the TADPOLE challenge data set [24] cohort from the Alzheimer's Disease Neuroimaging Initiative (ADNI) database, which contains ADNI-1, ADNI-2, and ADNI-GO. The first experiment involved patients with AD progression and detected their progressive or nonprogressive states with the help of AdaBoost. In the second experiment, the study considered only the patients whose disease status was updated with time and observed the disease's progression over time. The data set is prepared and preprocessed, followed by progressive nature detection using M-LSTM. Finally, the performance of the proposed methodology is evaluated on the data set, and the results are compared with the state-of-the-art literature.

3.3 Methodology for Experiment 2

In Experiment 2, this study included all the cognitive and neuroimaging features in a time-series pattern to study patients' AD progression. There were subjects in the data set that had single or double visits. Therefore, subjects with more than 3 years of consecutive visits were considered, while the remaining patients were removed. Given that every ML or DL model requires a fixed input length, the total number of visits of all the selected patients was equalized using

$$$V=\sum _{(i=1)}^{n}{W}_{i}({\mathrm{label}}_{i\mu }+\text{labe}{{\rm{l}}}_{i\sigma }),$$$()

where

$$${W}_{i}=\frac{{\mathrm{label}}_{i}}{\mathrm{Total}},$$$

label_i is the current label, and $$V\,\epsilon \,\mathrm{Whole}\mathrm{numbers}$$ since the number of visits should belong to the set of whole numbers. Patients with more than $$V$$ visits are dropped from the processing data. Those patients whose number of visits was less than $$V$$ are equalized with the help of the simple moving average (SMA) defined as follows:

$$$\begin{array}{ccc}{\mathrm{SMA}}_{k,\mathrm{next}} & = & \frac{1}{k}\sum _{i=n-k+2}^{n+1}{p}_{i,}\\ {\mathrm{SMA}}_{k{,}\mathrm{next}} & = & \frac{1}{k}({p}_{n-k+2}+{p}_{n-k+3}+{p}_{n-k+4}+\ldots +{p}_{n}\\ && +{p}_{n+1}+{p}_{n-k+1}-{p}_{n-k+1}),\\ {\mathrm{SMA}}_{k,\mathrm{next}} & = & \frac{1}{k}({p}_{n-k+1}+{p}_{n-k+2}+\ldots +{p}_{n})\\ && -\frac{{p}_{n-k+1}}{k}+\frac{{p}_{n+1}}{k},\\ {\mathrm{SMA}}_{k,\mathrm{next}} & = & {\mathrm{SMA}}_{k,\mathrm{current}}+\frac{1}{k}({p}_{n+1}-{p}_{n-k+1}).\end{array}$$$()

According to Equation (6), the moving average filter can be formulated quickly on real-time data using a circular or first in, first out (FIFO) buffer with three arithmetic operations. First, the sampling window is equal to the size of the data set at the first filling of the FIFO or circular buffer. Thus k = n, and the average calculation is done as a cumulative moving average. An M-LSTM is trained on the cleaned data set after data preprocessing. The LSTM structure is provided in the following section.

3.3.1 M-LSTM

The M-LSTM is a well-known DNN model. The fundamental architecture of the M-LSTM, an RNN [27], is shown in Figure 1. A single time-series data set can be classified, and sorted, and detection can be made using the M-LSTM. The ability of M-LSTM to estimate time-series data has also been explored and utilized previously, such as in Schafer and Graham [25]. The output value was first calculated in the M-LSTM structure to calculate the predictive time-series data. Then the input value from the current time was used as input to the forget gate. The processing results from the forget gate were then calculated using

$$${f}_{t}=\sigma ({W}_{{\rm{f}}}\otimes [{h}_{t-1},{x}_{t}]+{b}_{{\rm{f}}}),$$$()

where $${W}_{{\rm{f}}}$$ represents the weights of the forget gate, $${b}_{{\rm{f}}}$$ shows the bias value applied to the forget gate, $${x}_{t}$$ is the input value for the current time, and $${h}_{t-1}$$ shows the previous processing time output value. The $${f}_{t}$$ follows the range (0, 1). Additionally, the output value and state of the candidate cell at the input gate are determined after computation. Both the input value extracted from the most recent time and the output value taken from the last time are fed to the input gate, refer to

$$${\widetilde{C}}_{t}=\tanh ({W}_{{\rm{C}}}\otimes [{h}_{t-1},{x}_{t}]+{b}_{{\rm{C}}}),$$$()

where $${W}_{{\rm{C}}}$$ is the weight of the gate input candidate, and $${b}_{{\rm{C}}}$$ is the bias value of the gate input candidate. The next stage in the M-LSTM model is the process of adjusting the cell values or the model parameters shown as

$$${C}_{t}={f}_{t}\otimes {C}_{t-1}+{i}_{t}\otimes {\widetilde{C}}_{t},$$$()

where $${C}_{t}$$ follows the range (0, 1). At processing time $$t$$, the output value $${h}_{t-1}$$ and the input value $${x}_{t}$$ become the input for the output gate, and the output from the gate output is calculated using

$$${O}_{t}=\sigma ({W}_{{\rm{o}}}\otimes [{h}_{t-1},{x}_{t}]+{b}_{{\rm{o}}}),$$$()

where $${O}_{t}$$ follows the range (0, 1), $${W}_{{\rm{o}}}$$ is the weight of the gate output, and $${b}_{{\rm{o}}}$$ is the bias value of the gate output. Finally, the final output value of the M-LSTM is generated by the output gate and is the result of the calculation using

$$${h}_{t}={O}_{t}\otimes \tanh ({C}_{t}),$$$()

$$\tanh $$ is a hyperbolic tangent function is an activation function that can be tailored to the needs and characteristics of the problem to be resolved. M-LSTM has been used in this work as it can process recorded data in a specific time sequence. Additionally, M-LSTM has been commonly used in the literature for analyzing and modeling time-series data [26, 27].

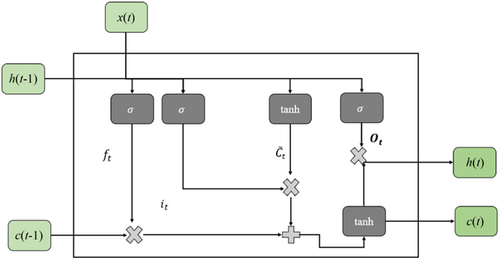
3.3.2 Data processing for Experiment 2

Experiment 2 studies the patients who have visited the consultants for over 3 years. The total number of these patients is 1030, who have made 10545 visits to the specialists. On average, each of the 476 patients with a progressive nature has made 10.56 visits to the consultants. The number of patients with a nonprogressive nature was 554, who consulted 5519 times, averaging 9.96 visits per patient. The numbers of patients with more than 3 years of visits are given in Table 3. After applying the SMA, the total number of visits increased from 10,545 to 14,420. The data preprocessing follows the settings described in Experiment 1.

Table 3. Statistics for Experiment 2.

Processing	Type (nature)	Patient	Visits	Average	Standard deviation
Before data preparation	Total	1030	10,545	10.23	3.67
	Progressive	476	5026	10.56	3.98
	Nonprogressive	554	5519	9.96	3.36
After data preparation	Total	1030	14,420	10.23	3.67
	Progressive	476	6664	14	–
	Nonprogressive	554	7756	14	–

• Note: Represents not taking standard deviation.

The data set is preprocessed for Experiment 2 with filtration, missing data handling, and normalization like the processes conducted in Experiment 1. Then, the data set was fed to the M-LSTM model using the process detailed in Section 3.3.1. Finally, the M-LSTM model is trained as a classification problem on the preprocessed data set. The model architecture used in this study is given in Table 4.

Table 4. M-LSTM model architecture.

Layer type	Output shape	Parameters
M-LSTM	(None, 256)	278,528
Fully connected	(None, 128)	32,896
Dropout	(None, 128)	0
Fully connected	(None, 2)	258
Total parameters: 311,682
Trainable parameters: 311,682
Nontrainable parameters: 0

• Abbreviation: M-LSTM, multivariate long short-term memory.

4 RESULTS

4.1 Experiment 1

After five-cross validation, the AdaBoost model reported an average accuracy, precision, recall, and F1 score of 77.52%, 75.21%, 81.48%, and 78.22%, respectively. After tuning the model's parameters, the accuracy improved to ∼80%. Previously, the best accuracy to classify AD as progressive or nonprogressive was 58.47% [23]. The achieved accuracy with AdaBoost with effective preprocessing has improved by 21.34% compared to the literature, reaching 80%. Figure 2 demonstrates the model's performance in Experiment 1 regarding accuracy, precision, recall, and F1 score. AdaBoost models have performed well and better after fine-tuning.

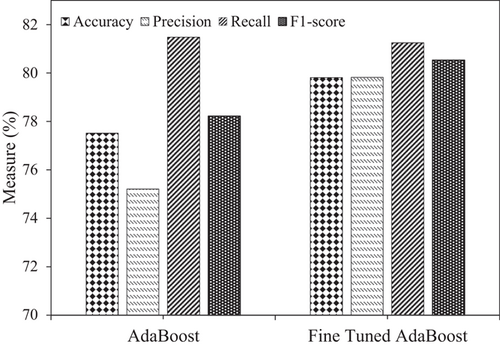
To demonstrate the effectiveness of the proposed model with the baseline work presented in Ho et al. [23], Table 5 provides the accuracy, precision, and recall of both models for AD progression and nonprogression classification, respectively. There is a significant increase in the observed accuracy with AdaBoost. The accuracy and precision of 58.47% and 59.25%, respectively, are increased with the BiPro [23] to 77.52% and 75.21% with AdaBoost. A significant increase in accuracy of 21.34% and precision of 20.57% is achieved with our proposed methodology. The confusion matrix for AD progression and nonprogression is illustrated in Figure 3.

Table 5. Performance analysis with baseline [23].

Model	Accuracy (%)	Precision (%)	Recall (%)
BiPro [23]	58.47	59.25	57.78
AdaBoost	77.52	75.21	81.48
Fine Tuned AdaBoost	79.81	79.82	81.25

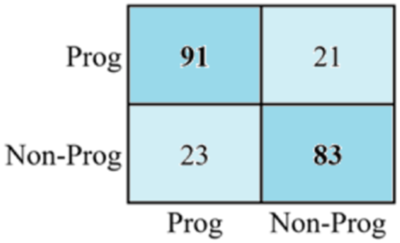
The first-row cell in the first column represents true positives. It indicates that 91 positive instances have been classified correctly. Similarly, the first-row cell in the second column indicates a false positive, meaning 21 negative values were confused with positive labels. The value of the second-row cell in the first column represents a false negative, meaning that 23 of the positive labels were identified as negative. Finally, the values of the second-row cell of the second column show true positives, which means that 83 of the positive samples were correctly classified.

4.2 Experiment 2

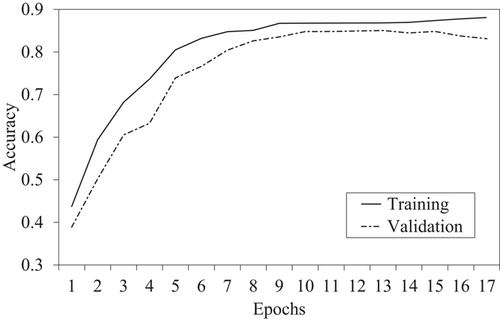
The M-LSTM model for detecting AD progression state is trained and tested on the data set with a split ratio of 80:20, that is, 80% data for training and 20% for testing. Initially, the model achieved an accuracy of ∼80%. However, after fine-tuning the parameters and hyperparameters of the M-LSTM model, the model accuracy increased to ∼82%. The training and validation accuracy of the proposed model is plotted in Figure 4.

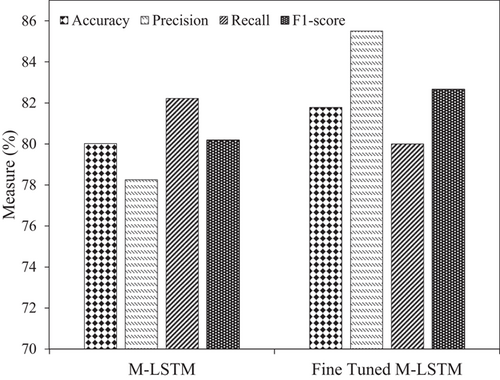
The M-LSTM model in this study reported an average accuracy, precision, recall, and F1 score of 80.02%, 78.25%, 82.21%, and 80.18%, respectively. After tuning the model's parameters, the accuracy improved to ∼82%. Previously in Experiment 1, the best accuracy to classify the AD as progressive or nonprogressive was 79.81% with AdaBoost and 58.47% with BiPro [23]. However, the achieved accuracy with M-LSTM and excellent preprocessing was improved to ∼82%. M-LSTM improved accuracy by 23.53% over BiPro and 2.18% with AdaBoost, respectively. In addition, the precision and recall with M-LSTM increased from 78.25% and 82.21% with AdaBoost to 85.5% and 82.66%, respectively. Figure 5 shows the performance of the M-LSTM model for AD progression in Experiment 2 using accuracy, precision, recall, and F1 score, respectively.

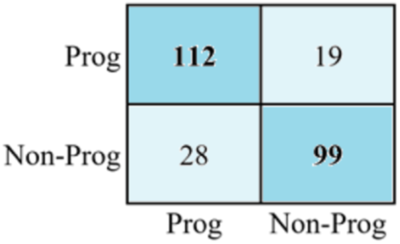
The confusion matrix for AD progression and nonprogression is illustrated in Figure 6. According to the matrix computed, 112 of the positive values were classified correctly. Similarly, the value of the first-row cell and the second column indicates a false positive which means that 19 negative values are confused with positive labels. Likewise, the number of false negatives is 28, meaning the positive labels are identified as negative. Finally, a total of 99 positive samples are correctly classified.

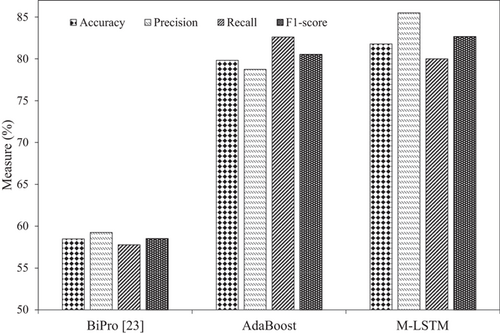
To demonstrate the effectiveness of the M-LSTM model over AdaBoost, Table 6 summarizes the accuracy, precision, recall, and F1 score. Better AD progression detection is achieved with M-LSTM compared to AdaBoost with efficient data engineering. Figure 7 demonstrates the achieved performance with both experiments and the baseline to predict AD progression. There is a 2.18% accuracy improvement with M-LSTM, the best classification accuracy for AD progression. The precision and F1 scores of 78.25% and 80.53% with the AdaBoost classifier have increased to 85.5% and 82.66%, achieving 7.25% and 2.13% gains, respectively.

Table 6. Performance analysis with AdaBoost.

Model	Experiment	Accuracy	Precision	Recall	F1 score (%)
M-LSTM	2	81.78	85.50	80.00	82.66
AdaBoost	1	79.81	79.82	81.25	80.53

• Abbreviation: M-LSTM, multivariate long short-term memory.

5 DISCUSSION

This study aimed to develop and evaluate two different models, that is, AdaBoost and M-LSTM, for classifying the nature of AD subjects as progressive or nonprogressive. In this study, we conducted two experiments to evaluate the performance of the selected models to classify patients with AD progression. The results of both experiments demonstrate significant improvements in accuracy, precision, recall, and F1 score compared to previous literature and baseline models.

In Experiment 1, the AdaBoost model achieved an average accuracy of 77.52%, precision of 75.21%, recall of 81.48%, and F1 score of 78.22% after five cross-validations. After fine-tuning the model's parameters, the accuracy improved to approximately 80%. This improvement is substantial compared to the best accuracy reported in the literature, which was 58.47% [23]. The achieved accuracy with AdaBoost, coupled with effective preprocessing, represents a remarkable 21.34% improvement over the previous best result, reaching 80%. The performance of the AdaBoost model is further visualized in Figure 2, illustrating its accuracy, precision, recall, and F1 score.

In Experiment 2, the M-LSTM model was trained and tested on the data set. The initial average performance measures achieved by the M-LSTM model were accuracy of 80.02%, precision of 78.25%, recall of 82.21%, and F1 score of 80.18%. After parameter tuning, the accuracy further improved to approximately 82%. Compared to Experiment 1, where the best accuracy was achieved with AdaBoost (79.81%) and the baseline BiPro model (58.47%) [23], the M-LSTM model demonstrated superior performance with an accuracy of approximately 82%. This improvement in accuracy corresponds to a 23.53% gain over the BiPro model and a 2.18% gain over the AdaBoost model. Additionally, the precision and recall of the M-LSTM model increased from 78.25% and 82.21% with AdaBoost to 85.5% and 82.66%, respectively. The performance of the M-LSTM model for AD progression is visualized in Figure 5, showcasing accuracy, precision, recall, and F1 score.

Our findings indicate that the M-LSTM model outperforms AdaBoost in detecting AD progression. The superiority can be attributed to the M-LSTM's ability to effectively process time series data, capturing temporal dependencies crucial in understanding disease progression dynamics. Unlike AdaBoost, which may struggle with the sequential nature of cognitive and neuroimaging indicators, M-LSTM's memory gates enable a more nuanced analysis. The broader implications of these findings in clinical settings are significant. Improved accuracy in classifying AD progression, as demonstrated by M-LSTM, holds promise for enhancing early diagnosis and treatment planning. The ability to capture temporal nuances in patient data opens avenues for more personalized and timely interventions, ultimately improving patient outcomes.

Overall, the results obtained from both experiments highlight the effectiveness of the proposed models, AdaBoost and M-LSTM, in accurately classifying AD progression. The improvements achieved in accuracy, precision, recall, and F1 score compared to the literature and baseline models demonstrate the potential of these models for clinical applications. These findings have important implications for the early diagnosis and treatment of AD, as accurate classification of disease progression can aid in implementing appropriate interventions.

6 CONCLUSIONS

AD is an irreversible neurological condition that impairs memory, cognition, and behavior. Therefore, early detection is crucial to halt its progression. Timely identification of structural changes from CN to MCI and MCI to AD can aid in detecting progression factors to halt AD progression. Various ML and deep learning models are used for the detection process. This study performed two experiments, that is, one using an ensemble ML model, AdaBoost, and the other using the deep learning model, M-LSTM. First, an efficient preprocessing pipeline for the TADPOLE data set is introduced before digging into the detection part of the progression state. AdaBoost is applied to the prepared data set and results in the detection of subjects involved in AD progression. Different performance measures show better results than a recent state-of-the-art method, BiPro. Furthermore, the second experiment observed the disease's spreading over time using M-LSTM, detected the subject's progressive nature regarding AD, and outperformed the AdaBoost.

AdaBoost is an ensemble ML model that trains the classifier iteratively on the prepared samples, which results in better performance than other classical ML methods. Similarly, M-LSTM is a powerful DL model that uses memory gates to process time series data. However, training the M-LSTM for a classification problem is more challenging and time-consuming than training AdaBoost. But the results achieved on the prepared data set from M-LSTM are more convincing than AdaBoost and a recent literature method. This research has preprocessed an already existing data set, which is collected for stages detection rather than the detection of AD progressive nature. Furthermore, the preprocessing data pipeline used in this research can be further enhanced by applying custom preprocessing steps rather than standard steps.

Deep learning models are powerful but require excessive computational power and time to process time series data. Most of the datasets have limited information and are unlabeled. Preprocessing the data set and labeling could be useful to avoid the model's overfitting and underfitting problems because the more data available, the better the detection of the AD progression state will be.

AUTHOR CONTRIBUTIONS

Muhammad Irfan: Conceptualization; software, formal analysis; investigation; data curation; writing—original draft preparation; visualization. Muhammad Irfan and Seyed Shahrestani: Methodology. Muhammad Irfan, Seyed Shahrestani, and Mahmoud Elkhodr: Validation. Seyed Shahrestani and Mahmoud Elkhodr: Resources; project administration; supervision; writing—review and editing; funding acquisition.

CONFLICT OF INTEREST STATEMENT

The authors declare no conflict of interest.

ETHICS STATEMENT

This study exclusively utilized data from the Alzheimer's Disease Neuroimaging Initiative (ADNI) database. The ADNI was launched in 2003 as a public–private partnership, led by Principal Investigator Michael W. Weiner, MD. The primary goal of ADNI has been to test whether serial magnetic resonance imaging, positron emission tomography, other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment and early Alzheimer's disease. For the use of ADNI data, this study adhered to all guidelines and policies set forth by the ADNI and complied with the ethical standards of the relevant institutional and national research committees. Please refer to the acknowledgment statement provided by ADNI. This research involved the use of existing, publicly available data from the ADNI. The ADNI obtained informed consent from all participants involved in the original data collection.

INFORMED CONSENT

Not applicable to this study. This research involved the use of existing, publicly available data from the Alzheimer's Disease Neuroimaging Initiative (ADNI). The ADNI obtained informed consent from all participants involved in the original data collection.