The neural basis of metacognitive monitoring during arithmetic in the developing brain
Funding information: Fund for Scientific Research Flanders, Grant/Award Number: G.0638.17
Abstract
In contrast to a substantial body of research on the neural basis of cognitive performance in several academic domains, less is known about how the brain generates metacognitive (MC) awareness of such performance. The existing work on the neurobiological underpinnings of metacognition has almost exclusively been done in adults and has largely focused on lower level cognitive processing domains, such as perceptual decision-making. Extending this body of evidence, we investigated MC monitoring by asking children to solve arithmetic problems, an educationally relevant higher-order process, while providing concurrent MC reports during fMRI acquisition. Results are reported on 50 primary school children aged 9–10 years old. The current study is the first to demonstrate that brain activity during MC monitoring, relative to the control task, increased in the left inferior frontal gyrus in children. This brain activity further correlated with children's arithmetic development over a 3-year time period. These data are in line with the frequently suggested, yet never empirically tested, hypothesis that activity in the prefrontal cortex during arithmetic is related to the higher-order process of MC monitoring.
1 INTRODUCTION
Cognitive neuroscience has made considerable progress in understanding the neural basis of cognitive performance in several academic domains, such as arithmetic. Much less is known, however, about how the brain generates metacognitive (MC) awareness of task performance (Fleming & Dolan, 2012) during academic performance. Understanding the neural basis of metacognition is essential, as this higher-order process supports reflection upon and control of other cognitive processes, and occupies a central role in human cognition (Flavell, 1979). Metacognition is defined as “thinking about your thinking,” or more specifically, one's ability to monitor and regulate one's mental operations. Its age-related improvements are widely recognized to underlie cognitive development, such as age-related improvements in accuracy on a wide variety of tasks (e.g., Lyons & Ghetti, 2010), for example, arithmetic (Rinne & Mazzocco, 2014). In view of the extensive behavioral work on the importance of metacognition in academic performance (e.g., Roebers, Cimeli, Röthlisberger, & Neuenschwander, 2012; Schneider & Artelt, 2010; Schraw, Crippen, & Hartley, 2006), there is a need to further our understanding of MC processes in the context of academic skills at the level of the brain.
Metacognition is considered to be a higher brain function that strongly depends on the prefrontal cortex or PFC (see Pannu & Kaszniak, 2005; Shimamura, 2000, for reviews). In brain imaging research, metacognition is often more narrowly defined and operationalized as MC monitoring. MC monitoring is an important aspect of metacognition, and is defined as the subjective self-assessment of how well a cognitive task will be/is/has been performed (Nelson & Narens, 1990). It is usually measured with MC monitoring judgments of performance (e.g., judgments on the accuracy of one's response to a task). Adult studies on the neural correlates of MC monitoring judgments across different tasks have pointed to a consistent involvement of a frontoparietal network (e.g., Fleming & Dolan, 2014; see Vaccaro & Fleming, 2018, for a meta-analysis). There are, however, three critical limitations in the current literature on the neurobiological underpinnings of metacognition that motivated the current study. First, and to the best of our knowledge, the existing body of data is solely based on adult studies. Therefore, the results cannot be generalized to the neural basis of metacognition in children without thorough empirical investigation. Second, this adult work has almost exclusively been done in lower level cognitive processing domains, such as perceptual decision-making (Fleming & Dolan, 2014; Fleming, Huijgen, & Dolan, 2012; Shimamura, 2000; Vaccaro & Fleming, 2018). Yet, there is evidence to suggest that there is specificity, that is, regional specialization within the PFC, concerning the neural basis of metacognition with respect to MC processes in different tasks and domains. For example, Baird, Smallwood, Gorgolewski, and Margulies (2013) found distinct patterns of functional connectivity that correlated with individual differences in the perceptual domain versus memorial judgments, and McCurdy et al. (2013) found different structural patterns associated with metacognition in perceptual and memory tasks. Hitherto, it remains unknown what the neural correlates of metacognition on high-level cognitive processing, such as arithmetic, are. Thirdly, Vaccaro and Fleming (2018) indicated that some aspects of the neural basis of metacognition have been overlooked. Most research has focused on brain activity related to MC confidence judgments in task performance or related to the extent to which an MC monitoring judgment effectively tracks task performance (i.e., MC monitoring ability). Yet, the fundamental question of which brain regions are involved in engaging in an MC monitoring task regardless of participants' behavioral performance (in other words, the level of confidence that participants indicate, and/or their MC monitoring ability) has been neglected. Answering this question is crucial to understand the underlying neurocognitive architecture supporting MC abilities. This was precisely the aim of the current study. We therefore examined MC monitoring judgment-related activity in itself, namely activation that results from contrasts comparing the requirement of MC monitoring judgment against a control condition.
The current study tackles these important issues by investigating them for the first time in children. We investigated which brain region(s) are active when engaging in an MC monitoring task through the use of retrospective MC monitoring judgments in a higher-level cognitive process, namely arithmetic.
Investigating brain activity during MC monitoring of arithmetic also adds to the existing body of developmental brain imaging studies that have studied brain activity during arithmetic (Arsalidou, Pawliw-Levac, Sadeghi, & Pascual-Leone, 2018 for a meta-analysis; Peters & De Smedt, 2017 for a systematic review), as this might lead to a better understanding of the activity in prefrontal regions, which has been consistently observed during arithmetic. Indeed, it has been frequently suggested that this prefrontal activation during arithmetic reflects MC monitoring as well as working memory load or goal-directed problem solving (e.g., Ansari, Garcia, Lucas, Hamon, & Dhital, 2005; Arsalidou et al., 2018; Houdé, Rossi, Lubin, & Joliot, 2010; Kaufmann et al., 2006; Kaufmann, Wood, Rubinsten, & Henik, 2011; Kucian, von Aster, Loenneker, Dietrich, & Martin, 2008; Menon, 2015; Rivera, Reiss, Eckert, & Menon, 2005). However, this suggestion that the control networks that are active during arithmetic might point, at least partially, to the involvement of MC processes, has never been empirically tested.
This suggestion is not far-fetched, as behavioral work has revealed that MC monitoring is a unique predictor of individual differences in arithmetic in children (Bellon, Fias, & de Smedt, 2019; Rinne & Mazzocco, 2014). Interestingly, Ansari et al. (2011) showed in adults that medial and lateral regions of the PFC were correlated with the detection of arithmetic errors and deployment of control following an arithmetic error. These authors suggested that activation of these regions might suggest greater awareness of mistakes during calculation, pointing to the role of metacognition.
In sum, the current study empirically investigated which brain regions are involved in engaging in MC monitoring within a higher-order cognitive processing domain (i.e., arithmetic), and to do so in primary school children. Investigating this also sheds light on the frequently suggested, but never empirically tested hypothesis that MC monitoring processes, which were found to be an important predictor of arithmetic skills in behavioral research, could partially explain the increases in prefrontal activation that are often observed when doing arithmetic.
We examined these questions in primary school children aged 9–10, as they are in the midst of an important developmental period of both arithmetic (e.g., Vanbinst, Ceulemans, Ghesquière, & de Smedt, 2015) and metacognition (e.g., Schneider, 2010). Children participated in an fMRI experiment in which they were asked to solve arithmetic problems and to answer either MC questions (i.e., experimental condition) or to make a color judgment (i.e., control condition) while they were in the scanner. To further explore the association between brain activity during MC monitoring and children's arithmetic development, we specifically recruited children that took part in a larger longitudinal behavioral project in which developmental arithmetic data were collected. This allowed us to explore associations between children's brain activity during MC monitoring and their arithmetic development.
It is important to note that firm hypotheses on a specific location of brain activation when engaging in MC monitoring in arithmetic in children were not possible, as there is a lack of prior research in this specific area. Against the background of the results from the MC and arithmetic research fields described above, we hypothesized that increasing activation during MC monitoring in children would be located in the prefrontal cortex and that this would overlap with the prefrontal regions that have been found to increase in activity during arithmetic.
2 METHODS AND MATERIALS
2.1 Participants
Participants were 55 children (30 girls; 2 left-handed), aged 9–10 years old (Mage = 10 years 2 months, SD = 3 months, [9 years 7 months–10 years 7 months]). After correction for movement in the scanner (see below), the final sample consisted of 50 participants (27 girls; 2 left-handed), aged 9–10 years old (Mage = 10 years 2 months, SD = 3 months, [9 years 7 months–10 years 7 months]). All children were recruited from an ongoing 3-year-longitudinal study on the role of MC monitoring in arithmetic (Bellon et al., 2019). They were all typically developing children, who had no diagnosis of a developmental disorder, nor reported a history of psychiatric or neurological illness. They had normal or corrected-to-normal vision, and a dominantly middle- to high-socioeconomic background. For every participant, written informed parental consent was obtained. In return for participating, all children were given a financial compensation. The study was approved by the Medical Ethical Committee of KU Leuven (S59167).
2.2 Imaging task
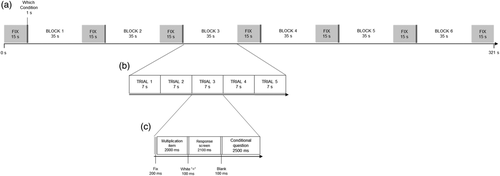
An arithmetic task was performed by the children in the scanner. This task was specifically designed to tap into both arithmetic and MC processes, using a specific protocol adapted from recent behavioral research (Bellon et al., 2019; Rinne & Mazzocco, 2014). Similar MC protocols have also been used in adult neuroimaging research (e.g., Chua, Schacter, & Sperling, 2009; Fleming et al., 2012; Hilgenstock, Weiss, & Witte, 2014). An overview of the arithmetic task, including its timing is illustrated in Figure 1. The task was presented across five functional runs in a block fMRI design. In each run, 30 multiplication items were presented in which children were asked to indicate which of the two presented solutions (i.e., one on either side of the screen) was correct. Two conditions were administered (i.e., experimental condition and control condition, see Figure 2) within each run. Each run was divided into six blocks: experimental (n = 3) and control (n = 3) blocks were alternated. A block comprised of a long fixation (15 s), an indication of which condition would follow (1,000 ms), five arithmetic trials of the same condition (35 s) and an end fixation (15 s); see Figure 3. Each arithmetic trial consisted of a short fixation (200 ms), a presentation of the multiplication item and a response screen (in total 4,300 ms), a short black screen (100 ms) and an additional question depending on the condition (2,500 ms). A multiplication item consisted of the presentation of the arithmetic problem (2,000 ms), the presentation of a white equality sign (100 ms), the presentation of a colored equality sign and two solutions to the arithmetic problem (i.e., one lure and one correct solution; 2,100 ms), and a black screen (100 ms). Children answered using buttons on a response box corresponding to the location of the response options on the screen. The duration of each run was approximately 5 min.

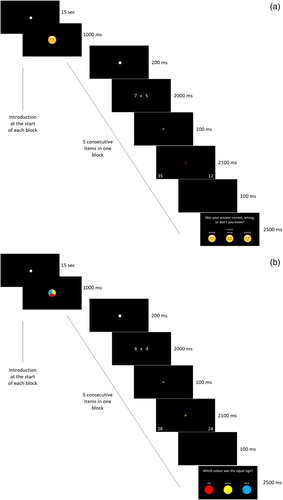
Each participant was presented with a set of 150 multiplication items. A list of the items is included in the Appendix S1, Supplementary Information and on the Open Science Framework page of this project (https://osf.io/7phm5/). Multiplication was chosen as arithmetic operation of interest to ensure considerable inter- and intra-individual variability in performance by using items of different difficulty levels, while still using a task with which children were very familiar, and which was as ecologically valid as possible. To maximize variability in both arithmetic performance and metacognition processes (experimental condition, see below) a wide range of multiplication items was included, ranging from easy items (n = 50; i.e., single-digit multiplications items with 0–1 and 2–9 as operands, and single times double digit items with 0–1 or 10–11 and 12–19 or 2–9, respectively, as operands) over standard multiplication tables (n = 50; i.e., single-digit multiplications with 2–9 as operands) to hard items (n = 50; i.e., single- times double-digit multiplications with 2–9 and 12–19 as operands). We did not include ties, standard single-digit items that were considered “too easy” (i.e., 2 × 3, 2 × 4, 3 × 4 and their commutative pairs), and hard items that were considered “too difficult” (i.e., operands 17–19 combined with operands 7–9). In each run, the same number of single-digit items as well as single-times double-digit items was presented. The number of times a specific operand was presented in one run was equally distributed across runs. Commutative pairs were never presented within the same run.
All multiplication items were presented horizontally, in white (Calibri, font size 80) on a black background and in Arabic digits. On presentation of the two solutions to the arithmetic problem, the children were asked to indicate where the correct solution was presented by pressing the leftmost or rightmost button on the response boxes for the left or right response alternatives, respectively. Lure solutions were one of five possible categories, namely the correct solution plus or minus the value of the largest operand, the correct solution plus or minus the value of the smallest operand or the solution to the corresponding addition. As a result, most of the proposed incorrect solutions were table related products. Lures from each category were evenly distributed over blocks and conditions. The position of the correct answer was balanced.
To truly isolate the act of engaging in MC processes, two conditions were created, namely an experimental condition in which an MC question was asked after the arithmetic item, and a control condition, in which every aspect of the arithmetic task was identical, and only for the nature of the question that was asked after the arithmetic item. In this control condition, a question on color was asked.
2.2.1 Experimental condition: MC question
In the MC condition, after each arithmetic item children were asked to report their judgment on the accuracy of their arithmetic answer, by indicating whether they thought their answer was “Correct,” “Incorrect” or whether they “Did not know.” We used emoticons in combination with the options to make the task more attractive and feasible for the children (see Figure 2, left panel). The participating children were very familiar with this task, as they already participated in an ongoing longitudinal study in which this protocol to assess MC monitoring was used (Bellon et al., 2019).
2.2.2 Control condition: Color question
In the control condition, after each arithmetic item, children were asked which of three colors the equality sign (presented simultaneously with the two solutions) had. Importantly, the equal sign was colored in both conditions, to make conditions as similar as possible. Only in the control condition, children were asked to report on the color (see Figure 2, right panel). This specific control condition was used, to engage similar memory processes as during the MC monitoring judgment (i.e., both involve thinking back), yet the content of the cognitive process was entirely different, as in the MC condition the children think back to their own performance, while in the color condition, they have to remember the color they saw.
Taken together, the two conditions were exactly the same in terms of timing, nature of the stimuli and arithmetic task. The only difference between them was that in the experimental condition they had to make a judgment on their own performance on the item, while in the control condition they had to make a judgment about color of the item.
In Figure 3, an overview of a block in both conditions is presented, in which detailed information of the course of an arithmetic item can be found.
Stimuli were presented using a script written in MATLAB (The MathWorks Inc., 2018), displayed using PsychToolbox 3 (Brainard, 1997), via a projector (NEC Display Solutions) onto a screen, which was made visible through a mirror attached to the head coil, located approximately 46 cm behind the participants' eyes.
2.2.3 Scanning parameters
Structural and functional images were collected via a 3.0T Philips Ingenia CX MRI Scanner with a SENSE 32-channel head coil, located at the Department of Radiology of the University Hospital in Leuven, Belgium. Soft padding was used to stabilize the children's heads in order to minimize head motion. For the fMRI data, slices were recorded in ascending order, using a EPI sequence (52 slices, 2.19 × 2.19 × 2.2 mm voxel size, 2.2 mm slice thickness, 0.3 mm interslice gap, TR = 3,000 ms, TE = 29.8 ms, 90° flip angle, 96 × 96 acquisition matrix) and covered the whole brain (field of view: 210 × 210 × 130 mm). Each run consisted of 107 measurements. Furthermore, a high-resolution T1-weighted anatomical image (MPRAGE sequence, 182 slices, resolution 0.98 × 0.98 × 1.2 mm3, TE = 4.6 ms, 256 × 256 acquisition matrix, 8° flip angle, 250 × 250 × 218 mm field of view) was acquired for each participant.
2.3 Behavioral task outside the scanner
Arithmetic fluency was assessed by the Tempo Test Arithmetic (TTA; de Vos, 1992); a standardized pen-and-paper test of arithmetical fluency which comprises five columns of arithmetic items (one column per operation and a mixed column), each increasing in difficulty. Participants got 1 min per column to provide as many correct answers as possible. The performance measure was the total number of correctly solved items within the given time (i.e., total score over the five columns).
Because all participants were enrolled in a longitudinal study (Bellon et al., 2019), performance on the TTA was not only available from the behavioral session that accompanied the MRI session, but also from when these participants were in second and third grade (i.e., 7–8 and 8–9 years old, respectively). These data were further included in the current study.
2.4 Procedure
Each child participated in two sessions. During the first session, children were extensively informed about the scanning procedure. They were familiarized with the MRI environment and procedures using a mock scanner in which every step of the MRI procedure was practiced while the noise of the scanner was simulated. They also completed an arithmetic fluency test (see below). Additionally, an extensive cognitive test battery was administered, as part of an ongoing longitudinal study in which these children participated, including executive functioning, numerical magnitude processing, reading ability, and mathematics anxiety. The data from this behavioral test battery were not considered for the current study. During the second session, brain imaging data were collected. Both functional data (during an arithmetic task) and structural data were acquired (for scanning parameters see below). The full MRI-protocol lasted approximately 50 min.
2.5 Data analysis
All preprocessing was conducted with the Statistical Parametric Mapping (SPM) software package for MATLAB (SPM12, Wellcome Department of Cognitive Neurology, London). Functional images were corrected for slice-timing differences and for head motion artifacts by realigning all images to the mean image, and were co-registered to the high-resolution anatomical image. Both functional and anatomical images were normalized to the standard Montreal Neurological 152-brain average template. As a final preprocessing step, functional images were spatially smoothed using a Gaussian kernel of 6 mm full-width at half-maximum.
To avoid a decrease in data quality due to movement during scanning, two motion criteria (see also (Peters, Bulthé, Daniels, op de Beeck, & de Smedt, 2018) were used to identify excessive movement during functional runs. First, all runs in which participants moved more than one voxel size (2.2 mm) in the x-, y-, or z-direction on two consecutive images, were discarded. Second, runs in which an Euclidean distance measure (i.e., an additive measure of the amount of motion in all directions from one time point to another), exceeded one voxel size, were also removed. Participants with less than three runs without excessive movement, were discarded in all analyses on both the imaging and behavioral data. This criterion led to the discarding of five participants, leading to a final sample of 50 children. Of these remaining participants, 7% of the runs were discarded from the analyses due to excessive motion.
After preprocessing, as a part of the first level analysis, the effect of the experimental condition per voxel was estimated by creating a general linear model per participant. Onset and duration of each block of each condition were modeled. These regressors were convolved with a canonical hemodynamic response function. The six motion realignment parameters for each subject were included as regressors of no interest in the general linear models, to further control for variation due to movement artifacts.
To measure the neural correlates of MC monitoring, a “metacognition contrast” was created in the first-level analysis by subtracting the average BOLD response of the control condition (i.e., color task) from the experimental condition (i.e., MC question), resulting in voxel-wise t-statistics maps for each participant.
Finally, a second-level group analysis was performed on the first level contrast images of the “metacognition contrast” using a one-sample t test to identify brain regions with higher activity during MC monitoring judgment than during the control condition. We studied activation at a whole brain level, threshold of p < .05 after family wise error (FWE) correction, to control for multiple comparisons. Anatomical labels of results were defined using the xjView toolbox for SPM (https://www.alivelearn.net/xjview).
To further understand the results of the MC contrast, functionally defined region(s) of interest (ROI) were generated from significantly activated cluster(s) in this contrast, using the MarsBaR toolbox for MATLAB (Brett, Anton, Valabregue, & Poline, 2002). From the ROI(s), we extracted the contrast estimates of the MC contrast, also using MarsBaR. High values indicated a large difference between the activation in the MC condition versus the control condition. These contrast estimates were then used for examining brain–behavior correlations.
As in the adult literature specific regions were found depending on the studied MC aspect (e.g., judgment-related activity, judgment level or MC monitoring ability; Vaccaro & Fleming, 2018), we first explored whether the activation found for engaging in MC thought (i.e., judgment-related activity) was correlated with these other MC aspects (i.e., absolute MC monitoring judgment and MC monitoring ability), which were inferred from the behavioral data of in-scanner performance. Pearson correlations were calculated between the contrast estimates of the MC contrast and the different MC aspects, that is, absolute MC monitoring judgment and MC monitoring ability. For the absolute MC monitoring judgment, a score of 3 was given if children indicated they were certain their arithmetic answer was correct, a score of 2 if they indicated they were unsure about their arithmetic answer, a score of 1 if they thought their arithmetic answer was incorrect. For MC monitoring ability, a score of 2 was obtained if their MC monitoring judgment corresponded to their actual performance (i.e., metacognitively judged as Correct and indeed correct academic answer; metacognitively judged as Incorrect and indeed incorrect academic answer), a score of 0 if their MC judgment did not correspond to their actual performance (i.e., metacognitively judged as Correct and in fact incorrect academic answer; metacognitively judged as Incorrect and in fact correct academic answer), and a score of 1 if children indicated they were Uncertain about the correctness of their academic answer.
Second, against the background of behavioral research in which MC monitoring was an important predictor of arithmetic performance, we further explored whether the activation found for engaging in MC thought was associated with children's arithmetic and its development. Therefore, we used developmental behavioral data from the longitudinal study in which these children were enrolled (Bellon et al., 2019). Specifically, children's score on the TTA was used as an indicator of their arithmetic fluency, which were collected at each time point (Grades 2, 3, and 4). From these data, a linear regression was calculated to predict their arithmetic fluency. For each individual we derived an intercept and slope, which reflected the starting level and the change over time, respectively. These behavioral measures were subsequently correlated with the extracted contrast estimates of the MC contrast.
3 RESULTS
3.1 In-scanner behavioral results
In-scanner behavioral results were only analyzed for runs that were included in the imaging analyses. Descriptive statistics of the in-scanner behavioral results are displayed in Table 1. Additional secondary analyses confirmed the validity of the in-scanner arithmetic task (see Appendix S1, Supplementary information).
| n | M | SD | Range | Theoretical maximum | |
|---|---|---|---|---|---|
| In-scanner arithmetic performance | |||||
| Arithmetic response rate a | 50 | 0.84 | 0.11 | [0.59–1.00] | 1.00 |
| Arithmetic correct responses b, c | 50 | 0.82 | 0.08 | [0.62–1.00] | 1.00 |
| In-scanner absolute metacognitive monitoring judgment | |||||
| Absolute accuracy judgment b, d | 50 | 2.62 | 0.17 | [2.08–2.94] | 3.00 |
| In-scanner metacognitive monitoring ability | |||||
| Monitoring ability b, e | 50 | 1.65 | 0.15 | [1.26–1.95] | 2.00 |
- a A score of 0 was given if participants failed to answer the arithmetic item within the time limit of 2,100 ms, and a score of 1 when they were able to answer within the time frame.
- b Only items on which participants were able to provide an arithmetic answer within the time frame were included in this measure.
- c A score of 0 was obtained if the arithmetic answer given was incorrect, a score of 1 if the arithmetic answer was correct.
- d A score of 3 was given if children indicated they were certain their arithmetic answer was correct, a score of 2 if they indicated they were unsure about their arithmetic answer, a score of 1 if they thought their arithmetic answer was incorrect.
- e A score of 2 was obtained if their metacognitive monitoring judgment corresponded to their actual performance (i.e., metacognitively judged as Correct and indeed correct academic answer; metacognitively judged as Incorrect and indeed incorrect academic answer), a score of 0 if their metacognitive judgment did not correspond to their actual performance (i.e., metacognitively judged as Correct and in fact incorrect academic answer; metacognitively judged as Incorrect and in fact correct academic answer), and a score of 1 if children indicated they Did not know about their academic answer.
- Abbreviation: MC, metacognitive.
To verify whether the two conditions of the arithmetic task in the scanner (i.e., MC condition and color [C] condition) differed in task difficulty level, we first compared (a) whether or not participants were able to provide an answer to the arithmetic item within the given time frame (i.e., 2,100 ms), independent of the accuracy of that answer (i.e., a score of 0 was given if participants failed to answer within the time limit; a score of 1 when they were able to answer within the time frame) and (b) the number of correct arithmetic responses that were given within the time limit (i.e., a score of 0 when participants chose the incorrect solution to the arithmetic item; a score of 1 when they chose the correct solution). Importantly, trials in which participants did not respond, or responded too late due to the time limit, were excluded from the correct responses scores. No differences between the conditions were found on either of the arithmetic performance measures (independent sample t-test arithmetic response rate: MMC = 0.85, SDMC = 0.10; MC = 0.83, SDC = 0.13; t(98) = 0.83, p = .41; independent sample t-test correct arithmetic responses: MMC = 0.81, SDMC = 0.09; MC = 0.83, SDC = 0.8; t(98) = −1, p = .32). Bayes factors for these analyses indicated evidence for the null hypothesis of no difference between the conditions (both BF10's < 0.33). This equivalence indicates there was no difference in degree of cognitive demand in the arithmetic task between the two conditions, and thus ensures that differences in brain activity between these conditions are not due to variation in arithmetic task performance.
Second, we compared performance measures on the MC and color question. It should be noted that we did not compare the two conditions on the number of correct responses that were given within the time limit, because in the MC condition, determining an accuracy measure was not possible as there is no correct or incorrect response. Namely, the MC question that was asked is a question on what the child thinks about the correctness of his/her answer. As such, accuracy in the experimental condition comes down to MC accuracy. In the color condition, on the other hand, there is indeed one correct response (i.e., the color of the equal sign). As a result, a comparison of “accuracy” between the two conditions to investigate task difficulty was not possible. The response rate of both conditions, on the other hand, can be compared to give an indication of potential differences in task difficulty. Using independent samples t test, we compared whether or not participants were able to provide an answer to the MC or color question within the given time frame (i.e., 2,500 ms), independent of the accuracy of that answer (i.e., a score of 0 was given if participants failed to answer within the time limit; a score of 1 when they were able to answer within the time frame). The results indicated that there was no difference in response rate (MMC = 0.94, SDMC = 0.06; MC = 0.94, SDC = 0.05; t(98) = −0.58, p = .57, BF10 = 0.25). The Bayes factor indicated evidence for the null hypothesis of no difference in response rate between the conditions, thus pointing to equivalence in task difficulty.
3.2 Imaging results
To isolate areas of functional significance during which participants metacognitively judged the accuracy of their arithmetic answer, we examined the difference in neural activation between the MC condition and the control (i.e., color) condition, that is, the metacognition contrast. An overview of the clusters that were more active during the metacognition than during the color condition can be found in Table 2. A visualization of this contrast is displayed in Figure 4. These differences were FWE corrected at p < .05. Our findings revealed that engaging in an MC task was associated with stronger activation in the left inferior frontal gyrus (IFG). There were no other clusters that showed increased activity during the metacognition as compared to the control condition. In secondary analyses (see Appendix S1, Supplementary information), we also used a less stringent control for multiple comparisons. Using a false discovery rate (FDR) correction at p < .05, we found largely similar results as those presented with the FWE correction.
| Peak coordinates | |||||
|---|---|---|---|---|---|
| Cluster | x | y | z | k | t |
| Metacognition > control condition | |||||
| Left IFG | −47 | 30 | −5 | 75 | 7.04 |
| −56 | 21 | 13 | 10 | 4.94 | |
- Abbreviations: IFG, inferior frontal gyrus; MC, metacognitive.

3.3 Brain–behavior correlations
The significant cluster found in the left IFG was used as ROI to further understand the results of the MC contrast. From this ROI, the contrast estimates of the MC contrast were extracted. These beta-values, which represent the activation difference between the MC and the control condition, were correlated with MC and arithmetic performance indices (see below).
3.3.1 Absolute MC monitoring judgment and MC monitoring ability
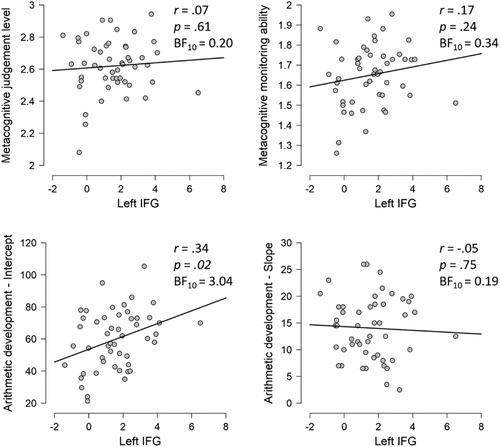
We explored whether the activation found for engaging in MC thought (i.e., activation in the left IFG) was also significantly correlated with other MC aspects (i.e., MC monitoring judgment level and MC monitoring ability; Figure 5). No significant correlations were found between brain activation for engaging in an MC monitoring task and MC monitoring judgment level or MC monitoring ability. Bayes factors pointed to evidence for the null hypotheses.
3.3.2 Arithmetic
The results of the TTA on three time points are displayed in Table 3. Significant age-related changes in TTA score were found, with performance in each time point significantly differing from the other time points (F(2,147) = 29.80, p < .001; post hoc tests using Bonferroni correction: all p's < .02). The intercept and slope of that change over time were calculated, indicating that on average children started with a performance of around 60 arithmetic items solved in 5 min, and each year, they were able to solve on average 14 items more.
| n | M | SD | Range | |
|---|---|---|---|---|
| TTA T1 (Grade 2) | 50 | 72.62 | 16.37 | [41–108] |
| TTA T2 (Grade 3) | 50 | 90.32 | 19.34 | [52–127] |
| TTA T3 (Grade 4) | 50 | 100.72 | 19.34 | [65–142] |
| Intercept | 50 | 59.79 | 18.31 | [21.33–105.33] |
| Slope | 50 | 14.05 | 5.83 | [2.5–26.0] |
- Abbreviation: TTA, Tempo Test Arithmetic.
We further explored whether the activation found for engaging in MC thought was associated with arithmetic development, as measured by intercept and slope of the regression line of TTA performance on three time points (Figure 5). A significant correlation was found between brain activation for engaging in an MC monitoring task and the intercept of arithmetic development. There was no significant correlation with slope in arithmetic development and Bayes factors pointed to evidence for the null hypothesis. Secondary, post hoc analyses (see Appendix S1, Supplementary information) further revealed that the significant association between activation in the left IFG in the MC contrast and the intercept of arithmetic development was not merely the result of a negative correlation with the control condition.
4 DISCUSSION
The current study tackled an important gap in the existing literature on how the brain generates MC awareness of task performance. While there is already some evidence on this ability in adults (Fleming & Dolan, 2012), there are no brain imaging data available on this issue in children. Moreover, research focused predominantly on lower level cognitive processing and has mostly neglected particular aspects of the neural basis of metacognition, namely, which brain regions are involved in engaging in an MC monitoring task.
Addressing these gaps in the literature, the current study was the first to explicitly investigate the brain activation underlying the engagement in MC monitoring in children, and during MC monitoring in an academic task. We observed increased activation in the left IFG relative to the control task. No other increases in brain activity during MC monitoring were observed. Brain–behavior correlations indicated that brain activity related to engaging in MC monitoring and behavioral arithmetic performance were associated. These data are in line with the suggestion that prefrontal activation in the arithmetic brain network may be, at least partially, related to metacognition.
A comparison of the existing literature, which is exclusively based on adults, and the current data in children, demonstrates both similarities and differences in the neural basis of engaging in MC monitoring. Our results are in line with Chua et al. (2009), who found greater activity in the left inferior frontal region (BA 47) in adults for retrospective MC monitoring compared to a prospective feeling-of-knowing. Our data are also in accordance with results in adults, which consistently show activation increases in prefrontal regions during MC monitoring. However, the exact location where this increased activation in the prefrontal cortex is found, differs depending on the very diverse study characteristics in the existing literature. These include operationalization of MC monitoring and the MC aspect under study (e.g., confidence versus MC monitoring ability), used contrasts (e.g., monitoring versus fixation or task performance), and the domain in which MC monitoring was studied (e.g., perceptual decision-making versus memory domain). For example, using low versus high confidence as MC measure compared to fixation Chua, Schacter, Rand-Giovannetti, and Sperling (2006) found activation differences in the PFC including anterior, dorsolateral, and posterior regions of the bilateral IFG. Yet, when comparing confidence rating and a recognition task instead of fixation, they found different activation patterns (e.g., right orbitofrontal regions). Yokoyama et al. (2010) found that, in adults who were good at predicting the correctness of their recognition memory performance (i.e., as measured by a significantly positive gamma), brain regions exhibiting higher activity during confidence rating compared to a perceptual task included bilateral superior frontal regions.
Using a similar design as in the current study, a small number of studies in adults have examined the brain activity of engaging in MC monitoring independent of participants actual behavioral task performance; that is, the brain activity regardless of which MC monitoring judgment (e.g., “I think I'm (in)correct”) is given and regardless of whether one's MC monitoring judgment is aligned with the actual task performance. Specifically, Fleming et al. (2012) found that, in adults, in a perceptual decision-making task, the right rostrolateral PFC showed greater activity during self-report compared to a matched control condition.
Because of this large variability in characteristics of the studies that investigated the neural basis of MC monitoring, it is desirable to follow a meta-analytic approach to obtain a reference to which the results of the current study can be compared. The activation likelihood estimation (ALE) composite meta-analysis of metacognition-related activity by Vaccaro and Fleming (2018) revealed a consistent involvement of a frontoparietal network, including a cluster in the left IFG (peak coordinate in MNI: −36 28 –6; volume in mm3 = 1,432; maximum ALE value = 0.0318). The current results in children are in line with this observation. Our results also align with their meta-analysis investigating retrospective MC monitoring judgments and revealing consistent activation in the left IFG (Vaccaro & Fleming, 2018). It is worth noting that both meta-analyses also revealed other significant clusters in MC monitoring in adults (e.g., bilateral parahippocampal), which were not found in the current study in children.
To more quantitatively compare MC monitoring related activation found in our study to those associated with monitoring in the broader, existing adult literature, we obtained the association test maps for the term “monitoring” and the term “judgment” from Neurosynth (www.neurosynth.org; Yarkoni, Poldrack, Nichols, van Essen, & Wager, 2011; accessed November 2019), a platform for automatically synthesizing the results of many different neuroimaging studies using text-mining and meta-analyses to generate mappings between neural and cognitive states. Data on the term “metacognition” were not available in Neurosynth. The meta-analytical map associated with the term “monitoring” describes the likelihood that a region will be activated if the study contains the term “monitoring” over and above other terms in the database including 1,335 terms, 507,891 activations reported in 14,371 studies. The automated meta-analysis of 465 studies containing “monitoring” revealed a map that contained a cluster in the left IFG (FDR criterion of .01), of which the peak value was −34 24 –4. This suggests some overlap between the current result (i.e., peak value −47 30 –5, k = 75, voxel size 2.2) and the Neurosynth data for “monitoring.” The automated meta-analysis of 290 studies containing “judgment” also revealed a map that contained a cluster in the left IFG, which included the peak value found in the current study. Taken together, the existing meta-analytic data are thus overlapping with our results on the neural basis of MC monitoring using retrospective MC monitoring judgments.
The current study adds to the existing literature, as we explicitly investigated the neural basis of MC monitoring in children of a narrow age range and in higher order cognitive processing. Research with such a specific focus is of utmost importance to functionally specify brain activation associated with MC processes. This furthers our understanding of the underlying neurocognitive architecture supporting MC abilities. Investigating the activation tracking the requirement for an MC monitoring judgment in particular, is an essential area of research, as a detailed meta-analysis of research in this area (Vaccaro & Fleming, 2018) demonstrated a lack of studies investigating this, even in the adult population. The current study addressed that lacuna.
Because we specifically isolated the brain regions involved in MC monitoring in arithmetic in children, the current study yields a unique opportunity to explore the overlap between MC monitoring processes and arithmetic in children. During arithmetic, children are known to activate various parietal and frontal areas (Peters & de Smedt, 2017), a network that also includes the left IFG. Kucian et al. (2008) and Kawashima et al. (2004) also found significant activation increases during exact calculation and multiplication, respectively, in the left IFG. The current results, identifying the left IFG as the neural basis for engaging in MC monitoring, are in line with the frequently suggested hypothesis (Ansari et al., 2005; Arsalidou et al., 2018; Houdé et al., 2010; Kaufmann et al., 2006; Kaufmann et al., 2011; Kucian et al., 2008; Menon, 2015; Rivera et al., 2005), that part of this prefrontal activation that is consistently found during arithmetic in children points to MC awareness.
The exploratory brain–behavior correlations further reveal an association between brain activity related to engaging in MC monitoring and arithmetic performance: Higher activation in the left IFG while engaging in MC monitoring on arithmetic performance, is associated with better arithmetic performance. This is aligns with Peters et al. (2018), who found higher activation during arithmetic in the left IFG for children with better arithmetic performance. Importantly, our data are not reflective of individual differences in error making or posterror responses, as such an association would reveal a negative correlation between arithmetic performance and left IFG activation, instead of the currently found positive association. Moreover, there was no difference in arithmetic accuracy between the MC and the control condition, making it unlikely that activation related to errors would be captured in the MC contrast estimates.
Future research should build on our results to deepen our understanding of how the brain generates MC awareness of task performance. Such studies should examine age-related changes in the neural basis of metacognition in higher-order processes, via comparing different age groups or by using longitudinal data. This is particularly relevant as MC monitoring gradually shifts from being a more domain-dependent ability to a more domain-general process (Geurten, Meulemans, & Lemaire, 2018). As such, an interesting avenue for future research is to study whether the current results are specific for arithmetic or whether the left IFG is generally involved in MC monitoring in other domains. Additional research is also needed to investigate whether brain activation differs between different MC monitoring judgments (e.g., “I think I'm correct” vs. “I think I'm incorrect”) and between correct versus incorrect arithmetic trials, a possibility that we could not examine given the design of the current study. By building on this first empirical study of the neural basis of MC monitoring in children in arithmetic, subsequent studies might further clarify the role of MC monitoring in arithmetic that was found in earlier behavioral research, at the level of the brain.
To conclude, this study is the first to reveal the neural basis of MC monitoring in children during an educationally relevant higher-order process in the left IFG. The current design yielded a unique opportunity to explore the overlap between the neural basis of MC monitoring and arithmetic performance in children, as it has been frequently suggested, but was never empirically tested, that prefrontal activation during arithmetic performance pointed to control mechanisms such as metacognition. Our results are in line with this suggestion.
ACKNOWLEDGMENTS
The authors would like to thank all participants, their parents, and the Department of Radiology of the University Hospital in Leuven for their support. The authors would also like to thank Dr Jessica Bulthé for her important contribution to the scripting of the fMRI experiment and the scripts for data-analysis in MATLAB and Dr Lien Peters for her helpful comments on our data-analysis.
CONFLICT OF INTEREST
The authors declare that they have no conflict of interest.
AUTHOR CONTRIBUTIONS
Elien Bellon, Wim Fias, and Bert De Smedt: Conceptually designed the study. Elien Bellon: Designed the experiments, collected the data, analyzed the results, and wrote a first draft of the article. Daniel Ansari, Wim Fias, and Bert De Smedt: Provided suggestions for analyses and provided critical comments, suggestions, and reviews of the article.
Open Research
DATA AVAILABILITY STATEMENT
The data underlying the results presented in the study will be made available from the Open Science Framework (https://osf.io/7phm5/) upon acceptance of the manuscript.




