Semi-empirically modelling barrier sediment transport in response to hydrodynamic forcing using UAV-derived topographical data (Holgate, New Jersey)
Abstract
We conducted monthly surveys, from October 2020 to May 2021, of coastal topography in Holgate, New Jersey. Using unmanned aerial vehicle (UAV)-photogrammetry and RTK-GNSS equipment, we generated digital elevations models and cross-section profiles, capturing spatiotemporal variability in volumetric change. We measured a total loss of 27 500 ± 10 500 m3 of subaerial sediment through the study. From October 2020 to February 2021, over 59 600 ± 10 500 m3 of sediment was eroded, followed by 32 100 ± 10 500 m3 of deposition from February to May 2021. We developed a semi-empirical model correlating the measured geomorphological change to wave energy and water-level variations. The calibrated model identified storm conditions that caused erosion and that waves from the south to southeast caused more erosion than those from the east to northeast. These results emphasise that alongshore transport represents a critical component of sediment transport dynamics relevant to beach erosion. Using the calibrated model, we quantified the impact of water-level variations and wave energy on net sediment transport for a stretch of barrier coastline. Specifically, a water-level increase of 0.14 m (equivalent to a 1σ variation) generated slightly less erosion (1.18 m3/m per 48 h) than the same variance-based increase in wave energy, which generates 1.44 m3/m of erosion per 48 h. These variables strongly covary. Alongshore transport modulates the relationship, increasing erosion 0.9 m3/m per 48 h with a 1σ shift in wave energy directed alongshore. Forcing from strong storms, hindcast from 8 years of data, can produce 15–20 m3/m of erosion per 48 h. This modelling approach represents a methodology to produce estimates of potential erosion under predicted storm conditions, which is inherently valuable to coastal management and resilience planning. Our study demonstrates cost-effective data collection and robust analytical methods that can be applied globally to benefit both the understanding of coastal geomorphology and local communities through data-driven natural resource management.
1 INTRODUCTION
Beaches are valuable natural resources that offer substantial environmental, commercial, recreational and cultural benefits to the 600 million people residing in coastal areas globally (Fitzgerald et al., 2008; Mcgranahan, Balk, & Anderson, 2007). As beaches erode, the natural resource they constitute is lost and it is, therefore, inherently valuable to develop metrics that describe and quantify how coastlines respond to the influence of coastal processes (Carapuço et al., 2016). To better understand the evolution of coastlines under different environmental conditions, there is a need for frequently collected and highly accurate topographical data to delineate geomorphological change that can be coupled with data representative of primary oceanographic forcing, such as waves and elevated water levels that facilitate erosion associated with storms (Dolan & Davis, 1992; Fenster & Dominguez, 2022; Splinter et al., 2014), and robust analytical methods to establish the correlations (e.g. Callaghan et al., 2008; Kriebel & Dean, 1993).
NOAA (National Oceanic and Atmospheric Administration) offers hourly wave height, wave direction and water-level measurements that, considered in conjunction, correlate with processes like wave runup and alongshore sediment transport flux. However, topographical data collected in the coastal environment is generally sparsely sampled and, as a result, it has been challenging to calibrate and improve models that relate hydrodynamic forcing to coastal morphodynamic response (Sherwood et al., 2022). Densely sampled topographical records that can be used to assess geomorphological response to discrete processes are rare and notably challenging to collect. It is especially difficult, technically and logistically, to capture the effects of individual storms over a representative area (Hoagland et al., 2023), although efforts are being made to coordinate the collection of data before and after major storms that impact coastal areas (Raubenheimer, 2020). Data collected over longer periods can be analysed to assess the broader cumulative effects of the observed processes and potentially isolate signals representative of discrete process characteristics and magnitudes. Unfortunately, there are also very few coastal topography records spanning decades (e.g. Turner et al., 2016), and those that exist are often sampled at intervals spanning kilometers or collected only a few times a year (e.g. along the northeastern US coastline; Farrell et al., 2008, Psuty et al., 2017). While airborne lidar (Bonisteel et al., 2009; Brock et al., 2002) can cover large expanses of coastline (Brock & Purkis, 2009), it is too expensive to collect data frequently enough for event-scale analysis (i.e. the overlap of the event/engineering scale of Castelle and Masselink, 2023 spanning days to years and tens of metres to kilometres). New emerging sources of data, like drone-based photogrammetry (e.g. Chen et al., 2018; Long et al., 2016; Ruessink et al., 2018), that can provide cost-effective high-resolution data have yet to prove transformative in terms of facilitating an improved understanding of the influence of coastal processes on coastal topography, and scarcity of data remains the greatest challenge to improvement of morphodynamic models (Sherwood et al., 2022). Moreover, despite advances in process-based modelling approaches (e.g. Larson, Wise, & Kraus, 2004; Lesser et al., 2004; Roelvink et al., 2009), predicting barrier system morphodynamics at the kilometre-scale over months to years is limited by the inherent compromise between detailed process-based dynamic modelling and manageable computational costs (Hoagland et al., 2023).
In this study, we employ a semi-empirical modelling approach (e.g. Rahmstorf, 2007) to evaluate the drivers of volumetric change along a stretch of barrier coastline over several months. Although the physics of sediment transport are not specifically accounted for in semi-empirical models, either dynamically or through parameterised equations (e.g. Kriebel & Dean, 1993, Bailard, 1981, Bailard & Inman, 1981), they represent an efficient tool to accurately reconstruct and predict coastal change over a variety of timescales (Castelle et al., 2014; Davidson & Turner, 2009; Ibaceta et al., 2022; Miller & Dean, 2004; Yates, Guza, & O'reilly, 2009). Moreover, statistically establishing theoretical relationships between coastal processes and geomorphological changes likely represents an increasingly powerful technique considering developments in the collection of high-resolution topographical data and high-performance computing resources.
Specifically, our study aims to address three primary objectives: (1) to determine whether a statistically parameterised set of functions can reconstruct unmanned aerial vehicle (UAV)-derived estimates of volumetric change occurring on a barrier coastline provided only measurements of wave height, wave direction and water level; (2) to calculate the sensitivity of the model output to parameterised model component functions that are likely correlated with specific modes of sediment transport along this stretch of coastline; and (3) to identify the wave- and water-level conditions that produce significant erosion and quantify how much erosion is predicted to be generated in storm conditions based on 8 years of past wave- and water-level data. Here, we assess that accurate high-resolution data collected at a monthly interval over kilometres of coastline can be used to calibrate a statistical model that can yield an accurate reconstruction of volumetric change of beaches and dunes using wave buoy and tide gauge data. Moreover, the modelling methods we apply offer detailed insights pertaining to how coastal processes affect kilometre-scale stretches of coastline over days to months.
2 LITERATURE REVIEW
2.1 Study site
Our study area is a 2-km stretch of coastline, Holgate (Long Beach Township), located on Long Beach Island, a 29-km long barrier island in southern New Jersey (Figure 1). The modern barrier systems in the mid-Atlantic Bight, including Long Beach Island, were generally formed during the end of the Holocene transgression (~2–5 ka). As global mean geocentric sea level (GMGSL) slowed to ~2 mm/yr by 5 ka (Lambeck et al., 2014; Miller et al., 2020) and to a near-zero rate of change from 4 ka to 1850 CE (Kemp et al., 2018; Walker et al., 2021), the rates of relative sea level (RSL) rise in New Jersey (1.5–2 mm/yr; Psuty, 1986, Engelhart & Horton, 2012, Horton et al., 2013, Walker et al., 2021) were low enough to facilitate the development and preservation of the modern barrier systems including Long Beach Island. The modern beaches of Long Beach Island are medium-grained (0.25 to 0.4 mm; Mcmaster, 1954) sand, and comprise the upper portion of ~10-m thick stratigraphic unit of beach and marine sand that is intermixed with shell fragments and pebbles/gravel (Uptegrove et al., 2012). The berm of the beach at Holgate is ~2–2.5 m in elevation through the study period, and the width of the beach ranges from ~30 to 40 m towards the southern end of the study area to ~70 m towards the northern boundary.
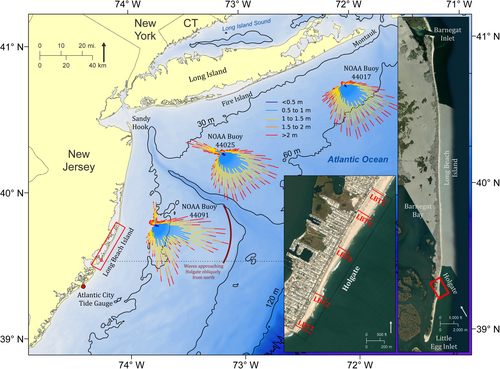
Over the past century, Long Beach Island has endured several major storms like the Ash Wednesday Storm (1962), a Nor'easter (1992) and Superstorm Sandy (2012), causing substantial damage to its coastal infrastructure. Smaller storms have also altered the topographical configuration of beach and dune sediments, impacting long-term geomorphological stability and resilience. Coastal engineering projects have been undertaken to protect the infrastructure and tourism industry. Since 1989, the NJ DEP, alongside the U.S. Army Corp of Engineers (USACE), has carried out offshore dredging and sand renourishment projects along the New Jersey coastline, exceeding $375 million and 49 million yards of sand (Farrell, 2009). In April 2018, 700 000 yd3 of dredged sediment was dumped on the beaches and dunes at Holgate (NJDEP [New Jersey Department of Environmental Protection] 2018). An artificial dune was constructed to an elevation greater than 6.5 m above the North American Vertical Datum of 1988 (NAVD88, vertical datum that reflects the geoid in the continental United States) along the length of the site after Superstorm Sandy, but a portion of it (central third of the site) has eroded and created a steep cliff in the backshore. This dune was planted with dune grass shortly after the construction, and sand fences, that are now mostly buried, were installed at the dune toe. A steel terminal groin has also been constructed at Holgate (completed in 2019), and beach scraping is commonly employed.
Waves typically approach from due east or southeast, with more of the larger storm-generated waves originating from due east (Figure 1). From 2014 to 2022, the mean of half-hourly significant wave height (SWH) measurements from NOAA Buoy 44091 is 1.26 m, and the tidal range is 1.23 m at the Atlantic City tide gauge (Figure 1). We note significant coastal erosion events occur locally when water levels exceed 2.15 m relative to mean lower low water (MLLW) with a SWH greater than 3.3 m measured at the wave buoy, conditions that facilitate run up to exceed the elevation of the berm surface and occur approximately 3–5 times per year. A hindcast study by the USACE (1999) suggests that the net longshore transport rate at Long Beach Island is approximately 75 000 to 150 000 m3 per year to the south, driven predominately by the prevailing wave direction relative to the shoreline orientation. Residual current flow on the shelf is to the south and southeast (Butman, Noble, & Folger, 1979; Uptegrove et al., 2012). Hapke et al. (2011) estimate that Long Beach Island loses ~1 m of shoreline position per year, and the Holgate section erodes at a rate of ~2–4 m per year (since 1880). Ashley, Susan and Christopher (1986) identified Barnegat Inlet (Figure 1) as a nodal point in the alongshore transport regime in New Jersey, primarily caused by the confluence of the change in the orientation of the shoreline at this location with the dissipation of the sheltering effect of Long Island, New York that limits the influence of northerly waves on longshore transport along the northern New Jersey Coast (USACE, 1999).
2.2 Sediment transport dynamics as a conceptual basis for the semi-empirical modelling approach
Constructing a semi-empirical model that accurately reflects the relationship among wave energy, water level and measured volumetric change requires consideration of the relevant, underlying coastal processes and the expected geomorphological response. This approach simplifies complex sediment transport processes that are simulated in hydrodynamic models at significant computational cost. The accuracy of a semi-empirical model is dependent on the ability of the model functions to emulate the effect of those complex physical processes, the uncertainty of parameterisation and the calibration dataset (D'anna et al., 2020; Kroon et al., 2020; Ruessink, 2005; Schmelz et al., 2024). Our semi-empirical model of volumetric change at Holgate mirrors others that relate shoreline position or beach profile change to underlying wave- or water-level data (e.g. Jaramillo et al., 2020; Miller & Dean, 2004), as it has a foundation in concepts that relate the geomorphological response of the beach to variation in wave energy and water levels.
This conceptual basis justifies the expectation that the model can closely emulate the measured volumetric changes of the beach through time provided wave energy and water-level data. Our model generates erosion or accumulation when these variables deviate from parameterised equilibrium levels. Empirical evidence shows nearshore sediments are transported landward by low-energy, fair-weather waves that contribute to the growth of the beach (Davidson-Arnott, Bauer, & Houser, 2019). This sediment, often sourced from nearshore bars deposited in the upper shoreface (outermost zone of active sediment exchange within the beach and nearshore system; Hamon-Kerivel et al., 2020, Hallermeier, 1980) during storms (Lee, Nicholls, & Birkemeier, 1998), is deposited at high elevations on the beach during rising tides. This transfer of material to higher elevations through swash-related processes during flood tidal stages can build the berm surface and increase subaerial volume, but deplete the lower sections of the beach profile (Duncan, 1964). During falling tides, the sediments deposited in the upper beach during the flood stage are abandoned, and lower portions of the beach profile are reworked. Additionally, slip-face or ridge-and-runnel type intertidal bars are observed at Holgate. They are likely to migrate shoreward during high tide because of shoaling wave asymmetry, and at low tide because of swash-related processes. However, they may be eroded because of bed return flow during flood or ebb stages (Masselink, Kroon, & Davidson-Arnott, 2006). These bars, often formed after storms, may meld to the beach face and add significant volumes of subaerial sediment during extended periods of fair-weather conditions.
Storm events, characterised by elevated water levels and strong waves, tend to erode beaches (Hopkins, Elgar, & Raubenheimer, 2018; Komar & Holman, 1986; Morton, 2002). These events increase the concentration of sediment just above the near-bed layer of the water column (10–20 cm), where currents flow seaward in the surf zone (Davidson-Arnott, Bauer, & Houser, 2019). Additionally, the increased velocity of undertow in storm conditions facilitates erosion and the transport of eroded sediments from the beach and intertidal/nearshore/foreshore bars (<100 m from shoreline) to those developed in deeper water (100–400 m from shoreline) during storms (Gallagher, Elgar, & Guza, 1998; Goff et al., 2015; Thornton, Humiston, & Birkemeier, 1996). Clusters of storms can quickly erode the dunes, beaches and nearshore/foreshore areas (Splinter et al., 2014; Vousdoukas, Almeida, & Ferreira, 2012), while also leading to rapid deposition of material in the upper shoreface (Lee, Nicholls, & Birkemeier, 1998). High winds and low atmospheric pressures associated with meteorological storms produce storm surges (Pugh, 1987), raising water levels and intensifying setup, swash, and run-up (Holman, 1986; Holman & Sallenger, 1985), conditions that cause beach erosion (Plant & Stockdon, 2012; Stockdon et al., 2007), particularly in the upper beach (Brenner et al., 2018). Severe events with higher water levels and stronger run-up may result to the erosion and overtopping of dunes, the deposition of washover in the backshore, and damage to developed properties (Ruggiero et al., 2001; Sallenger, 2000).
Coastal topography evolves within a constant state of disequilibrium adjusting towards an equilibrium state dictated by the wind, waves, tides, currents and antecedent topography, all of which inevitably change on a timescale of hours. To reflect this, some of our model functions have time-varying equilibrium values, trending towards the current state with residual memory of the past. This produces a mechanism that allows for, among other effects, accelerated beach recovery immediately following storms, a process that begins as the storm itself wanes in intensity (Roberts, Wang, & Puleo, 2013). Other model functions that represent more pervasive process–response relationships, like accretion of the beach prolonged periods of fair weather conditions (Thom & Hall, 1991), do not contain a time-varying equilibrium value.
Our model does not stipulate sediment mass balance, as beach recovery from storms may only result in the accumulation of a fraction of the beach volume lost (Anderson, Frazer, & Fletcher, 2010). Some eroded sediments may be permanently lost from the nearshore zone, transported offshore in strong storm-generated near-bed flows (Dyhr-Nielsen & Sørensen, 1970) that are directed offshore along the upper shoreface and inner shelf (Goff et al., 2015). Coastal set-up can generate bottom layer current velocities strong enough to transport, or even resuspend, sand across the entire shelf (Glenn et al., 2008), possibly moving sediment out of reach for nearshore transport that is typically directed onshore in fair weather near our site (Styles & Glenn, 2005). Sediment can also be lost from the dune/beach/nearshore system to washover deposits. Antecedent topography affects the amount of sediment lost to the backbarrier through overwash (Schmelz & Psuty, 2022), although the sediment ‘lost’ to washover deposits contributes to the landward movement of the barrier system as a whole (Lorenzo-Trueba & Ashton, 2014) and may be reincorporated into the nearshore sediment budget as a barrier system continues in a phase of transgression.
Alongshore currents generated by coastal setup also play a role in the transport of sediments alongshore, particularly during storm events (Swift et al., 1985) when alongshore sediment flux increases (Miller, 1999) by as much as 60 times (Kana & Ward, 1980). Factors like incoming wave power, incident wave angle, grain size and slope of the beach are determinants of transport flux (Komar & Inman, 1970). Spatial variation in any factor that contributes to alongshore sediment flux, especially those related to the characteristics of the beach itself or bathymetry offshore, can generate convergence or divergence of flux that relates to progradation or erosion of the beach (Rosati, 2005). Some semi-empirical models account for gradients in alongshore transport with an extra linear term (Splinter et al., 2017) or by explicitly modelling the alongshore gradients in flux (Roelvink et al., 2020; Vitousek et al., 2017). We estimate the fraction of wave energy directed alongshore as a function of incident wave angle and relate these data to accumulation or erosion of the site that is likely influenced by spatial variability in alongshore transport rate in variable conditions.
The model parameterisation also plays a role in linking the data, the physical processes represented by the model functions and the observations of change in the coastal topography. Therefore, model parameter error also contributes to misalignment of the model output and the actual topographical change. The dynamic nature of coastal evolution can result in non-stationary values of semi-empirical model parameters (Ibaceta et al., 2022), especially over longer time frames (years to decades). We assume temporally constant parameter values and apply a Bayesian approach that incorporates a Markov Chain Monte Carlo (MCMC) algorithm (Hastings, 1970; Metropolis et al., 1953) to sample posterior distributions of the parameter set and the model output to generate a robust statistical representation of the data, the model output and the model parameter uncertainties.
3 METHODOLOGY
Our semi-empirical modelling approach is based in a statistical transformation of wave energy, wave approach angle, and absolute water level to topographical change. We apply this statistical model to emulate the processes governing volumetric change along a 2-km stretch of barrier coastline at Holgate, NJ (Figure 1). Conceptually, the model should capture general sediment transport dynamics such as the landward transport of material by fair-weather waves, loss of material to the offshore during storms and redistribution of material alongshore in response to variable incident wave conditions.
We collected the topographical data used to calibrate the model over 8 months between October 2020 and May 2021. To generate digital elevation models (DEMs), we collected aerial imagery with a UAV (Figure 2a) and ground control points (GCPs) with RTK-GNSS equipment (Figure 2b). From these data, we generated highly accurate high-resolution DEMs that defined the topography of the beach and dunes at the times the data were collected. We calculated the volumetric changes from October 2020 to May 2021 using the UAV-derived DEMs.

We also obtained hourly water level (NOAA, 2021a) and half-hourly wave (NOAA, 2021b) data that overlapped the timing of the topographical data collection. We fit a semi-empirical model that related cumulative forcing represented by these data to the volumetric changes observed in the beaches and dunes along this stretch of coastline using the topographical data. The calibrated semi-empirical model was then provided with a synthetic dataset sampled from a correlated distribution of wave and tidal events to evaluate how certain events would likely affect the coastline. We applied a multiple regression analysis to the synthetic dataset and the model output values derived using it, which produced metrics of expected volumetric gain or loss per unit change in water level and wave energy.
3.1 Field surveys and generation of DEMs
Aerial imagery was collected monthly between October 2020 to May 2021 to generate DEMs that recorded the topography of the beach and dunes at Holgate. The imagery was collected with a DJI Mavic 2 Pro quadcopter (Figure 2) equipped with a Hasselblad L1D-20c camera and an internal GPS + GLONASS GNSS system. The preprogrammed flight path for each UAV survey was generated and optimised for photogrammetric data collection using Pix4D software. During the flight, the drone collected images at regular intervals, ensuring 70% overlap for adjacent photos from both the front and side. The images capture 20–30 ground control points that were readily identifiable on multiple orthophotos and measured with RTK-GNSS equipment to determine their precise position in three-dimensional space. The average pixel resolution for the images collected across all surveys is 1.48 cm (Table 1). The data collection was scheduled during early afternoons at low tide during a spring tide to minimise shadows and maximise exposure of the beach.
| Survey | Total images | GCPs | Image resolution (cm/pixel) | Tie points | RMSD rel. to GCPs (cm) | DEM resolution (cm/pixel) |
|---|---|---|---|---|---|---|
| 17 Oct 2020 | 1203 | 26 | 1.42 | 1 568 846 | 2.168 | 3.11 |
| 3 Nov 2020 | 1063 | 30 | 1.55 | 1 142 090 | 1.21 | 3.35 |
| 11 Dec 2020 | 578 | 30 | 1.5 | 717 818 | 3.31 | 1.64 |
| 27 Jan 2021 | 1234 | 32 | 1.44 | 2 011 080 | 5.06 | 3.14 |
| 17 Feb 2021 | 1135 | 26 | 1.41 | 1 706 616 | 4.92 | 3.11 |
| 27 Mar 2021 | 1140 | 28 | 1.49 | 1 974 976 | 3.05 | 3.25 |
| 26 Apr 2021 | 711 | 27 | 1.55 | 1 033 497 | 0.01 | 3.33 |
| 27 May 2021 | 1095 | 22 | 1.5 | 2 030 800 | 1.79 | 3.25 |
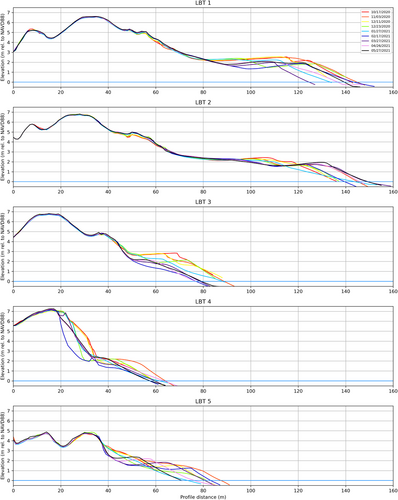
GCP data were collected during every survey with a low-cost, multi-frequency differential GNSS survey system that uses Arduino-based Ardusimple GNSS boards equipped with the U-blox ZED-F9P GNSS module. We constructed this survey system that consists of a RaspberryPi powered base station that broadcast data that enabled real-time kinematic (RTK) correction for the ‘rover’ data collection unit in the field. The base station antenna was set up over the same survey benchmark during each of the UAV surveys. This RTK survey system facilitates topographical data collection with an accuracy of 4-cm vertical root mean square error (RMSE; Schmelz et al., 2020). In addition to the GCPs, topographical data were collected using the RTK-GNSS equipment along five cross-shore profile lines (Figure 3; following methods in Psuty et al., 2012). These data were also used as independent control points (data independent from the creation of the DEM; ICPs) to evaluate DEM accuracy. Portions of the dune area surveyed along topographical profiles LBT1, LBT2 and LBT3 did not experience change in elevation across the surveys (Figure 3). Using data collected in these locations, we calculate a vertical precision of 2.72 cm RMSE (n = 612) for the RTK data, which is similar to the precision of data collected with Trimble and Leica equipment (2.61 cm RMSE; n = 71) over the same substrate (Schmelz & Psuty, 2019).
Agisoft Metashape Pro software and photogrammetric/structure from motion (SFM) methods were used to create a DEM of the study area from each set of images collected during each monthly survey. The DEMs we generated have a vertical RMSE of ranging from 10 to 19 cm that was calculated using the ICPs (Table 2). The average error for the ICPs across all surveys is −1 cm and normally distributed. The average error for individual surveys ranged from −16 to 7 cm. We use the standard deviation of the average error for the eight surveys, 7.0 cm, to represent a variance-based estimate of average error across a survey, which would affect calculated volume. We calculate the estimated variability of volumetric change attributable to survey error for each survey (~3.98 m3/m) and the error for calculation of volumetric change from the initial survey (~5.65 m3/m; Table 2). The error for the volumetric change estimates is used to calibrate the semi-empirical model. Several coastal monitoring studies have incorporated photogrammetry/SFM processes (e.g. Chen et al., 2018; Guillot & Pouget, 2015; Long et al., 2016; Moloney et al., 2018; Ruessink et al., 2018; Scarelli et al., 2017; Talavera et al., 2018) similar to those we apply here, and we follow the guidelines proposed by James et al. (2019). Gaps in data coverage were filled using a spatiotemporal Gaussian process regression model. More information about the processing of the UAV data can be found in the supporting information SOI 1 and SOI 2.
| Survey | ICPs (n) | Average error (m) | RMSE (m) | Area above NAVD88 (m2) | Volume above NAVD88 error (m3/m; 1σ) | Volume change error (m3/m; 1 σ) |
|---|---|---|---|---|---|---|
| 17 Oct 2020 | 105 | 0.07 | 0.14 | 105 439 | 4.01 | - |
| 3 Nov 2020 | 60 | −0.04 | 0.12 | 106 661 | 4.05 | 5.71 |
| 11 Dec 2020 | 109 | 0.01 | 0.13 | 105 169 | 4.00 | 5.67 |
| 27 Jan 2021 | 109 | −0.16 | 0.18 | 104 184 | 3.96 | 5.64 |
| 17 Feb 2021 | 102 | −0.03 | 0.14 | 105 005 | 3.99 | 5.66 |
| 27 Mar 2021 | 91 | 0.00 | 0.10 | 102 840 | 3.91 | 5.60 |
| 26 Apr 2021 | 96 | 0.01 | 0.15 | 103 367 | 3.93 | 5.62 |
| 27 May 2021 | 95 | 0.05 | 0.19 | 105 520 | 4.02 | 5.67 |
3.2 Modelling the effect of variations in oceanographic forcing on geomorphological change
3.2.1 Calculation of volumetric change through time
The UAV-derived DEMs are used to measure the changes in net sediment transport from October 2020 to May 2021, using the methods of Psuty, Schmelz, & Habeck (2018). We apply these methods to obtain total volumetric change for each survey, as well as change within 74, 25-m wide alongshore compartments to evaluate spatial variability within the study area. These volumetric changes (Figure 4) represent observations that the semi-empirical model is fit using.
3.2.2 Defining variations in water levels and their effect on net sediment transport
The NOAA Atlantic City tide gauge (Station No. 8534720; Figure 1), located 25 km south of Holgate, provides hourly water-level data between 1 October 2020 and 31 May 2021 (NOAA, 2021a). We generate two semi-empirical model components with the tide gauge data, (Equation S4) and (Equation S5), to relate absolute water-level variations, which are altered by storm events, to net sediment transport. The first metric, , is the integral of all water-level values above a threshold value, , from the time of the first survey, , and time . An increasing value in this metric is indicative of a period of time that has been relatively stormy.
3.2.3 Defining variations in wave energy and direction
NOAA Buoy Station 44091 (Figure 1) provides half-hourly measurements of SWH and mean wave direction (MWD) between 17 October 2020 and 31 May 2021. The MWD was converted to cartesian angles relative to the shoreline, which is oriented at an angle of 58° from east. MWD is thereby reassigned as the angle of approach where a value of 0° indicates a wave approaching perpendicularly. As a pre-processing step, wave measurements recorded as originating from onshore at the buoy location were removed from the dataset.
3.2.4 A parameterised semi-empirical model relating wave energy and water levels to geomorphological change
The model of is calibrated using volumetric change measured at Holgate, and the hourly water-level data, that is, , and wave data, that is, and , between 17 October 2020 and 1 June 2021. The model is fit to these values of volumetric change using a MCMC algorithm in a Bayesian statistical framework. This framework is constructed to (1) learn the parameter values that result in the best fit of to the measured volumetric change; (2) to learn the uncertainty of and its underlying components and ; and (3) to provide insight into how the beach might respond to specific wave- and water-level conditions. We sample the posterior distribution of the 10 model parameters using the MCMC algorithm, which establishes the sensitivity of the model output to the parameters. The posterior distribution of parameter values is provided in Table S3. Additional information can be found in SOI 3 of the supporting information.
The calibration dataset only contains eight measurements, so we use a leave-one-out cross-validation scheme (LOOCV) to evaluate the predictive power of the model. We calibrated the model 7 times, once for each datapoint except the initial survey. We compared the prediction made for each LOOCV model calibration to the observation left out of the volumetric change dataset (Figure 5e), which provided a framework to assess the accuracy of the model predictions in the time between the surveys.
| Parameter | Value | S.E. |
|---|---|---|
| 0.72 m3/m | 0.03 | |
| −8.65 m3/m m−1 | 0.22 | |
| −0.50 m3/m kJ−1 | 0.06 | |
| −0.38 m3/m kJ−1 | 0.07 | |
| 0.55 m3/m kJ−1 | 0.02 |
4 RESULTS
4.1 Measurement of geomorphological change
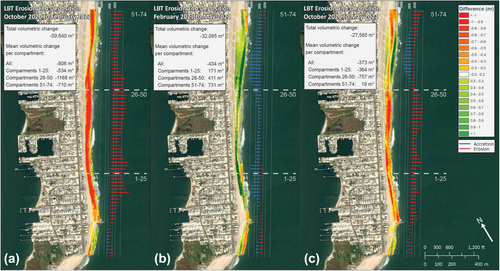
Both the cross-section profiles and the calculations of volumetric change show the beach and dunes at Holgate lost sediment to the nearshore/offshore from October 2020 to February 2021. The center third of the study area lost the most total volume during this time (Figure 4a), while the southern end of the center third of the study area was the only portion to lose a substantial volume of sediment from the dune (see LBT2 in Figure 3). The sediment loss was particularly evident after Nor'easter ‘Orlena’ occurred in early February 2021. The erosion of the dune within the center third of the study area (i.e. near LBT2; Figure 1) created large dune scarps/cliffs 4- to 5-m high in some locations. These cliffs were captured by the survey data (Figure 3) and images taken on-site. From October to February, Holgate lost 59 600 ± 10 500 m3 of sediment above NAVD88. This sediment loss equates to an average of ~30 ± 5.65 m3 of sediment per metre of shoreline alongshore (Figure 5d), or approximately 14 m of landward shoreline position change, on average, across the study area.
From February/March 2021 to the final survey at the end of May, the beach recovered 32 100 ± 10 500 m3 of the sediment lost over the winter (Figure 4b). The greatest recovery of the beach was observed in the northern third of the study area (compartments 51–74), where ~730 ± 140 m3 per 25 m compartment of volumetric change was measured. This amounts to a smaller amount more sediment (~460 m3) than this area lost over the winter. Some sediment recovery occurred where the dune and/or upper berm was eroded, such as in the southern to middle thirds of the study area. The dune was partially reconstructed in the location of LBT2 through beach scraping, which created an artificially sloping scarp that can be seen in the LBT2 cross-section profile collected in the February survey (Figure 3). Despite the combination of recovery and some anthropogenic intervention, the area never recovered its original elevation by May 2021, resulting in net erosion in the southern and middle thirds of the study area (Figures 3 and 4c). The sand used to reconstruct the dune in the vicinity of LBT2 was scraped from the beach.
From the initial survey in October 2020 to the final survey in May 2021, the beaches and dunes at Holgate lost approximately 27 500 ± 10 500 m3 of sediment (Figure 4c). There was little to no volumetric change in the northern third of the study area (compartments 51–74), 20 ± 140 m3 per 25-m compartment. The central (compartments 26–50) and southern (compartments 1–25) thirds of the study area lost ~760 ± 140 and ~370 ± 140 m3 per 25-m compartment (30 and 14 m3 per metre of shoreline), respectively. Per metre of shoreline alongshore, Holgate lost 15 ± 5.65 m3 of sediment over the 8-month study (Figure 5d).
4.2 Modelling the changes in geomorphology
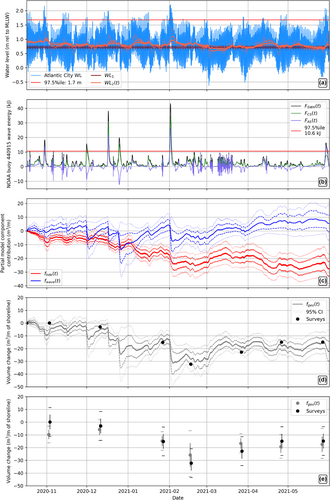
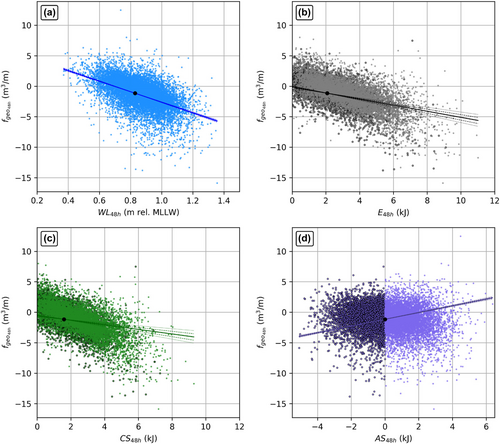
The calibrated statistical model, , relates wave and water-level data to net sediment transport at Holgate. The modelled output captures the volumetric loss within the study area through the winter and recovery of the beach in the spring (Figure 5d). A LOOCV analysis of the model shows it with a mean error (average of error for the ‘left out’ observations) of −0.93 m/m3. The model predicted the observed volumetric change data points with an RMSE of 5.8 m/m3 (n = 7), and the confidence intervals of the model output and the volumetric change observations overlap for each iteration of the cross-validation analysis (Figure 5e). Fewer data points to calibrate the model result in a less accurate prediction of net sediment transport (12.1 m/m3 RMSE, three calibration points; 9.1 m/m3 RMSE, five calibration points). To evaluate volumetric change likely to have been produced over short periods of time, we ran the semi-empirical model with 48-h samples of input data from Holgate between 2014 and 2022 (Figures 6 and 7). We fit a multiple regression model (Equation 7) to summarise the resulting dataset (r = 0.8).
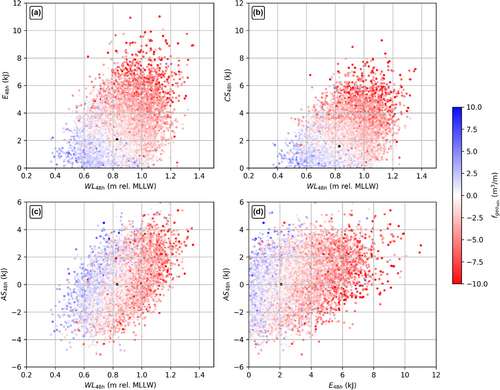
The two semi-empirical model subcomponents, and , (Figure 5c) quantify the instantaneous effect of wave energy and water-level conditions on coastal topography. The negative calibrated parameter values for , and (Equations 1 and 5; Table S2) indicate that higher water levels and larger significant wave heights resulted in more erosion (Figure 6a and b, respectively). Water levels and wave energy ( and , respectively) are also positively correlated (Figure 7). The direction of wave approach also contributes to the variation in net sediment transport at Holgate. The model accounts for the incident wave angle through , as and account for (Figure 5b). The value of is greater, for a given value of , when waves approach more perpendicularly to the shoreline. is also closely correlated with , and the negative covariance between and (Figure 6c) mirrors that of and (Figure 6b). Positive values in , indicating wave approach from the east to northeast, tend to help grow the beach, as evidenced by the positive model coefficient (Equation 5 and Table S2) and regression coefficient (Equation 7 and Table 3). Conversely, for every 1σ decrease (1.6 kJ) in 48-h mean AS(t), indicating a more southerly wave approach, the beach will tend to be 0.9 m3/m per 48 h more erosive (Figure 6d). For a given value of WL(t) or SWH(t), a more southerly approach of wave leads to a greater probability of erosion (Figure 7c and d).
The model also indicated that the beach is likely to have eroded during discretely identifiable storms (Figure 5c and d) independent of the UAV/RTK-GNSS measurements, including Nor'easter ‘Orlena’. Considering multivariate distributions of the water level and wave data from 2014 to 2022, the model predicts that over 15 m3/m of sediment can be eroded in large storms, which equates to ~6 m of shoreline position loss averaged across the study area. A 1σ variation in 48-h average water level is 0.14 m, which relates to erosion of 1.18 m3/m per 48 h in the semi-empirical model according to the multiple regression analysis (Figure 6). The 1σ variation in total wave energy averaged over 48 h is 1.7 kJ, which results in 0.85 m3/m of erosion over that time. A similar 1σ variation in the wave energy directed cross-shore results in 0.59 m3/m of erosion over 48 h. Combined, these regression model components representative of total wave energy generate 1.44 m3/m of erosion per 48 h.
5 DISCUSSION
This study represents a demonstration of semi-empirical modelling to reconstruct subaerial sediment transport along a stretch of coastline over time. This case study offers insights regarding the mechanisms of sediment transport at Holgate by establishing relationships between data that correlate with forcing produced by coastal processes and observations of volumetric change. The successful application of these methods serves to validate a computationally manageable approach, relative to process-based/morphodynamic modelling methods, to deriving detailed information about coastal dynamics, and also what is likely a valuable tool for predicting and managing future coastal changes. Here, we discuss the modelled reconstruction of volumetric change to the beach at Holgate, along with insights derived from the calibrated statistical model. We also speculate on potential implications for coastal management practices and identify the limitations of the study and methodology.
5.1 Reconstruction of coastal geomorphological change through semi-empirical modelling and insights from the calibrated model
The study demonstrated that volumetric change to beaches and dunes can be effectively reconstructed using semi-empirical modelling methods. The model, , captured the primary changes observed during the study period as demonstrated by the LOOCV analysis. Specifically, Holgate experienced ~30 ± 5.65 m3 of erosion of per metre of shoreline during the winter storms and a recovery of subaerial sediment in the spring, hindcast with an accuracy of ±5.8 m3 per metre of shoreline through the 8-month study period. Notably, the model output was able to generate the values of the rapid erosion caused by large storms and emulate recovery in intervening periods. The insights into mechanisms of sediment transport at Holgate that this application of semi-empirical methods offers demonstrates the utility of this framework to study the dynamics of coastal geomorphological change, albeit sacrificing detailed physics-based representations of the morphodynamics for computational feasibility.
Fundamentally, the model suggests that large waves that occur with elevated water levels associated with storm surges will be more erosive, which is largely congruent with basic coastal geomorphological theory. In isolation, elevated water level and high wave energy result in erosion in the model (Figure 6a and b), but these variables are also correlated. Water levels tend to amplify the effect of wave energy, leading to more erosion at a given wave energy when the corresponding water level is higher (Figure 7a). The model also suggests a slightly lesser sensitivity of the geomorphology to variations in water levels than wave height. A 1σ variation in 48-h average water level causes 1.18 m3/m of erosion, compared with 1.44 m3/m of erosion for an equivalent variation in wave energy.
The results also suggest that incident wave angle affects net sediment transport. Waves approaching from the east tend to promote the growth of the beach at Holgate, whereas waves approaching from the south to southeast are more likely to erode the beach (Figure 6d). Additionally, there is strong covariance between and (Figure 7c), indicating that higher water levels are associated with waves approaching from a more easterly direction. However, waves approaching from the south produce more erosion at a given water-level value (Figure 7c). Similarly, wave energy, and are positively correlated, as large waves are more likely to approach from the east. While larger waves are more likely to produce erosion, this relationship is modulated by the angle of approach, as waves approaching from a direction closer to south or southeast tend to generate more erosion for waves of a given SWH value (Figure 7d).
This relationship between and is likely caused by the terminal groin that has been constructed at the southern end of Holgate. This structure does not allow any sediment to bypass from south to north. As a result, when waves approach from the south to southeast, there is no updrift source of sediment to feed the beaches of Holgate. Conversely, waves approaching from the east to northeast are likely to direct alongshore transport to the south, and a fraction of that material is likely to be captured by the terminal groin.
The semi-empirical modelling framework offers the ability to quantify these relationships for a given stretch of coastline with relatively minimal computational expense over months to years, a prohibitively long duration for morphodynamic models. This context is significant considering sea level rise and climate change, as it is an expectation that beaches like Holgate will be exposed to a more frequent recurrence of erosive events. The quantitative inferences that can be derived from the calibrated semi-empirical model can offer a basis to predict how this might affect the future sediment budget.
5.2 Broader implications of the demonstration of this methodological approach
This case study at Holgate, NJ demonstrates semi-empirical methods that can be calibrated to evaluate volumetric sediment transport along any stretch of coastline globally over time periods ranging from months to years. Even the results from this short, 8-month study can offer residents and local decision-making authorities some insight into coastal vulnerability and resilience. Of particular value is the ability of the model to offer predictions for erosion based on specific storm conditions. Coupled with past data defining the range of possible conditions, probabilistic assessments of vulnerability represent a logical extension of the predictions our model can provide. This empirically derived understanding of how sediment is transported in response to storm events can potentially inform infrastructure and mitigation planning, such as the placement of coastal engineering structures, beach scraping and nourishment frequency. This study also highlights the potential for unintentional impacts of engineered intervention in the coastal system. Structures like the terminal groin at the south-end of our study area can make areas of the beach more susceptible to erosion under certain conditions. Although the net flow of sediment alongshore is from north to south, the results here suggest that there are times when flow is reversed and erosion is exacerbated at Holgate as a result.
With coastlines increasingly affected by rising sea levels and other effects of climate change, there is a greater need for accurate and frequently collected topographical data. Our use of the Arduino based GNSS boards and consumer-grade UAVs demonstrates that low-cost equipment can be used to collect accurate topographical data in the coastal environment. This technology may help facilitate more widespread collection of coastal monitoring data. More frequently collected data across a range of coastlines regionally and globally might represent a starting point towards defining specific responses to discrete combinations of quantifiable process variables, and the combination of oceanographic data and semi-empirical methods presented here provide analytical tools to do so.
5.3 Limitations of the study and suggestions for future work
The model effectively replicates the cumulative gains and losses of sediment captured by the monthly surveys. However, there are two significant limitations caused by the short data record from which the model was calibrated. First, short-term topographical gain and loss, including discrete impacts of storm events, are not well-constrained by the observations. The short-term volumetric loss is likely more realistically represented than the rate of recovery. More frequent measurements would help constrain the rate at which the study area recovers from storm-induced erosion, but a longer data record would also be helpful. Direct tests of storm events are planned as future work. Second, the established relationships cannot be reliably extrapolated to determine medium- to long-term effects without a longer record constraining the relevant trends. The short data record precludes evaluation of geomorphology over an annual cycle, which is significant on the US mid-Atlantic Coast considering that winters are typically more storm prone. A dataset spanning at least 2 years would significantly improve the model calibration, allowing for a more precise correlation of geomorphological changes with specific wave and water-level events over time.
Finally, the model we construct is entirely statistical in nature and would benefit from being informed by theoretical or energetics-based relationships (e.g. those defined in Komar & Inman, 1970, Bailard, 1981, Bailard & Inman, 1981). Additionally, this model would need to be calibrated locally for any beach that it is to be applied, and the predictive power of a locally calibrated model is dependent on the quality and length of the data record underlying it. Although we have accounted for the directional approach of the waves relative to the shoreline in this model, the model does not consider the refraction of the waves as they travel over the nearshore bathymetry between the wave buoy and the study site, which would affect the incident wave angle. Accounting for this effect may better tie the wave data and the model output considering the theoretical relationship between incident wave angle alongshore sediment transport, although the model as constructed does possess sufficient predictive power to derive meaningful information from it. We view exploring these limitations and details of the model construction as a direction for future work to build on our results.
6 CONCLUSIONS
From October 2020 to May 2021, we collected 8 monthly UAV and RTK-GNSS topographical surveys along a 2-km stretch of barrier coastline at Holgate, NJ. From these surveys, we generated DEMs and cross-section profiles that facilitated the volumetric measurement of coastal geomorphological change. The beach and dunes at Holgate lost 59 600 ± 10 500 m3 of sediment above NAVD88 during fall and winter storms, and recovered 32 100 ± 10 500 m3 during the spring. The total sediment loss of 27 500 ± 10 500 m3 during the entire study period equates to ~6.5 m of shoreline position retreat.
We constructed a parameterised semi-empirical model that related the observed volumetric changes to wave- and water-level conditions. The calibrated model not only captures the larger trends in volumetric change but also generates event-scale estimates of erosion, capturing the effect of major storms like Nor'easter ‘Orleana’ in February 2021. The model suggests that a powerful storm, defined using water levels and wave characteristics sampled from 8 years of wave- and water-level data, could cause more than 15 m3 of sediment loss per metre of shoreline over 48 h, or ~6.5 m of shoreline position retreat. The calibrated model also suggests that incident wave angle modulated the geomorphological outcomes. This is likely because of the terminal groin at the southern end of the study area that cuts off the alongshore transport of material into the site when waves approach from the south to southeast.
Overall, this study demonstrates the efficacy of utilising accurate, cost-efficient data collection methods, coupled with semi-empirical modelling methods, to monitor coastal erosion and a basis to predict conditions that produce it. Further, the methods we apply to derive an empirical correlation of coastal processes and net sediment transport along a barrier coastline also offer a framework to evaluate how sediment transport pathways may change as coastal processes change with climate.
ACKNOWLEDGEMENTS
We acknowledge the support and feedback received through the Coastal Climate Risk and Resilience (C2R2) graduate certificate programme. The programme awarded a certificate to Ashlyn Spector for her work that contributed to this research. The authors acknowledge the Office of Advanced Research Computing (OARC) at Rutgers University for providing access to high-performance computing resources. We also sincerely thank Kristen Joyse, J.N. Stanley, Christian Rowan and Melissa Boyd of Rutgers University for their help collecting the topographical data we have analysed herein.
Open Research
DATA AVAILABILITY STATEMENT
A database of all topographical data and Python scripts generated for the Gaussian process regression and the semi-empirical analysis applied in this paper have been made publicly available and are stored on Zenodo and GitHub, respectively (Schmelz et al., 2024; https://doi.org/10.5281/zenodo.14296621). The tide gauge (NOAA, 2021a) and wave buoy data (NOAA, 2021b) are publicly available from NOAA.




