Source Apportionment and Geostatistics: An Outstanding Combination for Describing Metals Distribution in Soil
Abstract
The purpose of this paper is to present the potential of the combination of source apportionment methods and geostatistics. We want to outline the possibilities of this combination for the investigation of soil pollution. Therefore, we focused on the identification of sources in the vicinity of an iron smelter and the different element distribution in this area. We determined the concentration of 15 elements in the aqua regia digestion of 60 soil samples in an area of 12 km2. In the current study, the application of two different source apportionment methods onto the data set and comparison of the results are presented. The focus was on absolute principal components score analysis with multiple linear regression and multivariate curve resolution with alternating least-squares. Four different sources in the region of interest could be detected. The source composition profiles and contribution profiles for both methods are alike. Furthermore, the distribution of the elements caused by each source with isoline plots could be visualized. The distribution is unique for each source and hence, element- and source-specific. Thus, the combination of the results of source apportionment methods with geostatistics is a powerful tool to evaluate and describe the content and distribution of metals in soil.
Abbreviations
-
- APCS-MLR
-
- absolute principal components scores analysis followed by multiple linear regression
-
- MCR-ALS
-
- multivariate curve resolution with alternating least-squares
-
- PMF
-
- positive matrix factorization
-
- RMSEP
-
- root mean squared error of prediction
1 Introduction
Source apportionment modeling methods are commonly used for examining environmental data. Typical examples are the absolute principal components scores analysis followed by multiple linear regression (APCS-MLR) 1, 2, multivariate curve resolution with alternating least-squares (MCR-ALS) 3, 4, and positive matrix factorization (PMF) 2, 3, 5. Here, the focus was on the former two because PMF considers also the standard deviation matrix in the computations 6, whereas the application of APCS-MLR and MCR-ALS considers the original data matrix. Therefore, the results can be compared directly. Whereas receptor modeling methods are well established in atmospheric deposition studies 1, 5, only few publications consider this technique in soil science 7, 8. Often, just the combination of geostatistics with classical methods of the multivariate data analysis is presented 9-11.
In this investigation, the focus was on the distribution of metals in soil in an area mainly influenced by iron production. The study area is located in Germany and in the 1990s, the production changed from pig iron to electric steel. Former studies dealt with the spatial distribution of elements in this region, but no source apportionment was applied 12, 13. The application of statistical methods allows an objective assessment of pollution sources and their distribution. As pointed out in a former paper, the combination of source apportionment models with geostatistics is possible 14. In the present study, the best technique was examined and the results of two different source apportionment methods and emphasized the strength of its combination with geostatistics were compared.
2 Materials and methods
2.1 Investigation area, soil sampling, preparation, and analysis
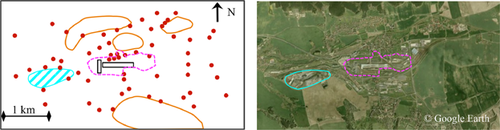
The investigation area Unterwellenborn is located in the Free State of Thuringia in the central part of Germany. The iron- and steelworks in Unterwellenborn, now belonging to the Stahlwerk Thüringen GmbH (SWT), have a long tradition. Since 1872 iron and steel were produced. In the 1990s, the production was changed from pig iron production in blast furnace to an electric steel manufacturing plant (www.stahlwerk-thueringen.de). In the vicinity of the Stahlwerk Thüringen 60 soil samples were collected in an area of about 12 km2 (see Fig. 1). The samples were taken on an irregular grid due to different anthropogenic interventions, for example, the newly built circuitous roads or residential areas. Buildings, streets, the railway, cultivated fields, industrial buildings, and even industrial monuments characterize this area. At each sampling point, five subsamples from the upper 0–20 cm layer under comparable conditions were taken, which were mixed to one composite soil sample. The soil samples were dried (105°C), homogenized, and passed through a 2-mm-sieve. Microwave digestion with aqua regia (21 mL 12 M HCl and 7 mL 15.8 M HNO3) was performed according to EN 13346:2000 15. The digestion was performed twice with 0.5 g soil for each sampling point. Each solution was filled up to 100 mL with diluted HNO3 (0.5 M) and the concentration of 15 elements was analyzed. The concentration of Cd, Co, Cr, Cu, Ni, Pb, and V was determined with the ICP-MS Elan 6000 (PerkinElmer) using multi-element standard and Rh as internal standard for the calibration 16. The As concentration was determined with the flow injection hydride generation AAS-5100 ZL (PerkinElmer) and the concentration of Ca, Fe, K, Mg, Mn, Na, and Zn with the flame-AAS-3110 (PerkinElmer). All elements were detected with concentrations above the detection limit, calculated according to the German DIN-standard 17 and the certified reference material IAEA/SOIL-7 18 was analyzed to verify the trueness (p = 95%) of the analytical method.
2.2 Basic principles of the applied chemometric methods
2.2.1 Data pre-treatment
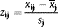 (1)
(1)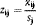 (2)
(2)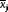 s the mean value of variable j, i is the index of the feature, and j is the index of the object.
s the mean value of variable j, i is the index of the feature, and j is the index of the object.2.2.2 Applied source apportionment methods
Source apportionment methods are well established in atmospheric deposition studies but rarely used in soil sciences. The purpose of these methods is to find (emission) sources, which influence the investigated area profoundly. Thereby, each source influences the behavior or distribution of only some of the examined elements or compounds. With the so-called source composition profiles we can present up to which amount the elements are characterized by each source. The other important result of source apportionment studies is the so-called source contribution profile. This presents the impact of the sources onto the different sampling points, respectively, investigation area.
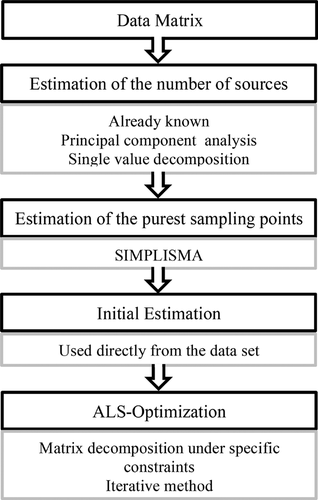
Performing a complete source apportionment survey of environmental data is a rather complicated task. Several steps must be carried out in order to achieve the composition and contribution profiles. Figures 2 and 3 present the flowcharts for the used methods APCS-MLR respectively MCR-ALS.
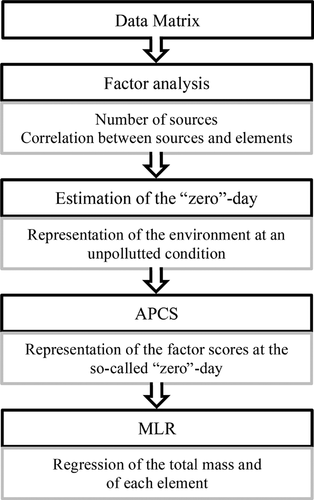
In order to find the hidden sources, a factor analysis must be performed to complete APCS-MLR. The factor analysis results in the number of sources and the correlation between the sources and elements. These results are used in the proceeding steps. In a perfect environmental condition no pollution would be occurring. This state presents the theoretical “zero”-day. It is also assumed, that sources only emit substances and, therefore, increase the pollution in the environment. With these considerations, the absolute principal component scores are calculated. In addition, the mass balance in order to accomplish APSC-MLR was needed. Then, a multiple linear regression between the APCS and the total mass was performed to obtain the source distribution profiles. Then, a multiple linear regression for each element was performed and the results were transformed into the source composition profiles.
Again, different steps must be done to accomplish MCR-ALS. First, the number of sources must be revealed. Common methods are principal component analysis or single value decomposition. If the number of sources is known, we have to select the proper sampling points. These have to represent each source specifically. These sampling points are used for the initial estimation and the alternating least squares algorithm is performed for the matrix decomposition. This results directly in the composition and distribution profiles.
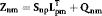 (3)
(3)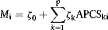 (4)
(4)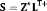 (5)
(5)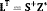 (6)
(6)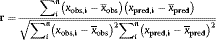 (7)
(7)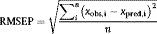 (8)
(8)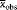 s the mean value of the observed variable, xpred,i is the predicted variable for object i, and
s the mean value of the observed variable, xpred,i is the predicted variable for object i, and 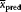 s the mean value of the predicted variable.
s the mean value of the predicted variable.2.2.3 Geostatistical methods
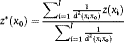 (9)
(9)2.3 Software
Excel 2010 (Microsoft) was used for general calculations of the data matrix, STATISTICA 6.1 (StatSoft) for factor analysis and multiple linear regression of the APCS-MLR-models, and MATLAB 7.9.0.529 (R2009b) (The MathWorks) for Windows 7 for the calculation of SIMPLISMA (spectral-mva-toolbox), and the MCR-ALS-model (MCR-ALS-toolbox). The toolboxes MCR-ALS and spectral-mva were downloaded from the following websites: www.mcrals.info and www.mathworks.com/matlabcentral/fileexchange/15391-multivariate-analysis-and-preprocessing-of-spectral-data. Surfer 9 (Golden Software) was used to calculate and illustrate the isoline plots.
3 Results and discussion
The main goal of this study is to present the advantages of the combination of different source apportionment methods with geostatistics. First, the results of the source apportioning with absolute principal components scores followed by multiple linear regression were compared with the results of multivariate curve resolution followed by alternating least-squares. Secondly, after choosing the better model for the combination with geostatistics, the distribution of the elements with isoline plots was illustrated.
3.1 Source apportionment methods
In environmental studies pollution, sources are often unknown and must be revealed by statistical tools. Factor analysis uncovers these sources and must be carried out to accomplish APCS-MLR 29. The principal components extraction method was used and the resulting factor loadings were rotated with Varimax rotation 19. Six factors were extracted with communalities >0.8 for each element. Two factors were described by a single element each and are, therefore, feature-own factors. These elements (K and Na) were removed for the succeeding source apportionment modeling analysis. Thus, the source apportionment studies were accomplished with 13 remaining elements (As, Ca, Cd, Co, Cr, Cu, Fe, Mn, Mg, Ni, V, Pb, and Zn). Now, the factor analysis results in three eigenvalues >1. Another possibility for the selection of relevant factors uses communalities. The communalities of factor 4 are >0.8 for all elements (see Table 1). Using communalities also suggests four factors instead of three.
| Factor 1 | Factor 2 | Factor 3 | Factor 4 | |
|---|---|---|---|---|
| As | 0.364 | 0.582 | 0.919 | 0.956 |
| Ca | 0.245 | 0.678 | 0.833 | 0.952 |
| Cd | 0.635 | 0.637 | 0.756 | 0.969 |
| Co | 0.361 | 0.467 | 0.971 | 0.975 |
| Cr | 0.722 | 0.903 | 0.920 | 0.958 |
| Cu | 0.699 | 0.731 | 0.947 | 0.947 |
| Fe | 0.772 | 0.889 | 0.891 | 0.904 |
| Mg | 0.040 | 0.748 | 0.814 | 0.940 |
| Mn | 0.802 | 0.837 | 0.866 | 0.917 |
| Ni | 0.662 | 0.736 | 0.771 | 0.814 |
| Pb | 0.443 | 0.707 | 0.830 | 0.901 |
| V | 0.725 | 0.902 | 0.907 | 0.952 |
| Zn | 0.646 | 0.646 | 0.770 | 0.978 |
The amount of the explained variance increased from 86% using three factors to 94% using four factors. With three factors, the variances of the heavy metals cadmium, nickel, and zinc are described insufficiently. Therefore, it is necessary to use four factors for the succeeding computation of the source apportionment studies.
The first important result of the source apportionment study is the percentage of explained variance for each source. The variance for both models differs due to the different requirements for the matrix decomposition. Table 2 summarizes the explained variance for both methods.
| APCS-MLR (%) | MCR-ALS (%) | |
|---|---|---|
| Source 1 | 36 | 45 |
| Source 2 | 17 | 23 |
| Source 3 | 22 | 25 |
| Source 4 | 19 | 33 |
| Complete model | 94 | 97 |
The requirements for the MCR-ALS-method do not include orthogonality, respectively, independence of the sources. Hence, the variances overlap. In this case, the variances overlap for almost 30%. Both models show resemblance: The explained variance for the complete model is very similar. The order of the sources is also alike. Only the results for source 4 (waste dump) differ: While the APCS-MLR-model explains 19% of the variance, the MCR-ALS-model explains 33%. The methods describe the impact of the waste dump onto the examined area differently.
To evaluate the quality of both models, the correlation coefficient and the relative prediction errors for both methods are given in Table 3.
| APCS-MLR-model | MCR-ALS-model | |||
|---|---|---|---|---|
| Correlation coefficient | Relative RMSEP in % | Correlation coefficient | Relative RMSEP in % | |
| Complete model | 0.990 | 11 | 0.962 | 22 |
| As | 0.974 | 17 | 0.968 | 20 |
| Ca | 0.979 | 33 | 0.960 | 34 |
| Cd | 0.979 | 18 | 0.984 | 16 |
| Co | 0.988 | 9 | 0.988 | 9 |
| Cr | 0.979 | 23 | 0.976 | 22 |
| Cu | 0.971 | 20 | 0.964 | 22 |
| Fe | 0.942 | 25 | 0.954 | 20 |
| Mg | 0.962 | 22 | 0.974 | 20 |
| Mn | 0.946 | 38 | 0.944 | 37 |
| Ni | 0.900 | 23 | 0.910 | 24 |
| Pb | 0.932 | 25 | 0.949 | 22 |
| V | 0.977 | 16 | 0.973 | 18 |
| Zn | 0.983 | 16 | 0.989 | 13 |
The quality parameters for both models are also very similar. Only for the complete model the results of MCR-ALS are slightly worse. The correlation coefficient is for all elements >0.9. The relative prediction error is below 25% for all elements except for calcium and manganese. These results are satisfactory for a real model. Therefore, both models are useful to describe the existing sources in the examined region.
After comparing the general results of both models, the sources need to be discussed in more detail. The summarized results for both models are listed in Table 4.
| Interpretation | APCS-MLR-Model | MCR-ALS-Model | |
|---|---|---|---|
| Source 1 | Iron Industry | Cd, Cr, Cu, Fe, Mn, Ni, V, Zn | Cr, Fe, Mn, Ni, V |
| Source 2 | Limestone | Ca, Mg, Pb | Ca, Mg, Pb |
| Source 3 | Red Mountain | As, Co, Cu | As, Co, Cu |
| Source 4 | Waste Dump | Cd, Pb, Zn | Cd, Pb, Zn |
| Unexplained | – | Cd, Ni | Ca, Cd, Cr, Fe, Mn, V, Zn |
The grouping of the elements is very reasonable for all sources and enables a rational interpretation. Source 1 includes typical elements for steel production. Therefore, source 1 was interpreted as iron industry emissions. In source 2 calcium and magnesium are grouped together. They indicate an interpretation of this source as limestone. In this region, limestone exists geologically and is quarried since 1963 (www.tagebau-kamsdorf.de). Source 3 includes arsenic, cobalt, and copper. These elements have also a geogenic origin and characterize the so-called Red Mountain 30. This mountain is rich of asbolane – a cobalt enriched ore. Source 4 includes cadmium, lead, and zinc. These elements are also related to the iron industry, but they are not emitted by it. It is likely, that these elements are still being deposited on the waste dump. There is one important difference between both methods. The number of elements, which are not described sufficiently by either one of the sources, varies considerably.
For a substantial interpretation, the source composition profiles need further discussion (Fig. 4). The source composition profiles allow a closer look on elements instead on sources. The loadings of the MCR-ALS-model had to be normalized to unity 31 for a better comparability of the two models. Additionally, the negative amounts of the composition profiles were set to zero, because sources can only emit elements and cannot force them to disappear.
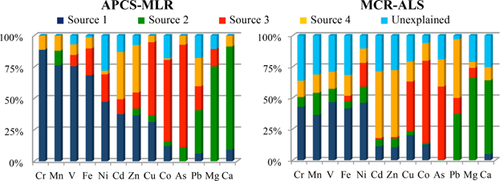
The source composition profiles differ remarkable, especially for sources 1 and 4. The most important difference is the high amount of unexplained variance for the MCR-ALS-model. Even though the loadings overlap due to the constraints in MCR-ALS, a lot of the variance is still unexplained. Another important difference is that the APCS-MLR-model assigns the elements more directly to one specific source instead of all existing ones. None of the elements is just characterized by one source. Usually three sources influence each element, sometimes even all four.
To complete the interpretation, the source contribution profiles for both models will be discussed (Figs. 5 and 6). The intensity of the source contribution profiles was normalized to compare the results of both models more easily.
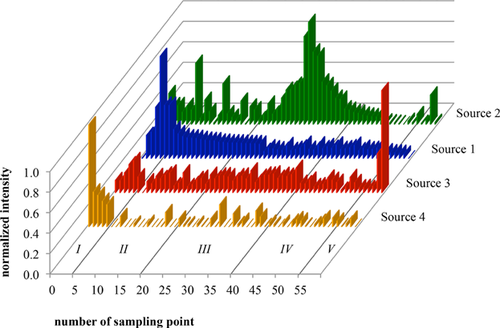
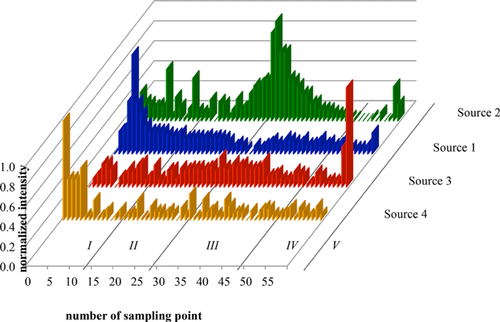
The source contribution profiles illustrated in Figs. 3 and 4 show a similar behavior for both methods. Source 1 influences mainly some sampling points (I + IV), source 2 a couple of sampling points (III), source 3 a few sampling points (V), and source 4 mainly one and partly up to five sampling points (I). These results also emphasize the interpretation of the sources. Source 2 is of geogenic origin, hence, a lot of sampling points are mainly influenced by this source. Source 4, however, is of anthropogenic origin and, therefore, characterizes only a few sampling points.
The results of both methods are similar. The main difference is the high amount of unexplained variance in the MCR-ALS-model. This can be seen as the weakness of this method. Even though the loadings overlap, a high amount (for some elements even up to 30%) of unexplained variance still exists. Furthermore, negative amounts for some elements for the source composition profiles appeared which would imply an element disappearance instead of emission. This is unrealistic for environmental studies. Elements are emitted from sources and do not vanish; especially in soil sciences because elements accumulate in soil.
3.2 Combination of geostatistics and source apportionment
It is possible to combine the results of the source contribution profiles with geostatistical methods. This can be done either for the results of MCR-ALS or APCS-MLR. Because the results of APCS-MLR are slightly better and can be used directly without further calculations, the distribution plots for this method are presented.
Therefore, the source-specific distribution of each element was interpolated. Altogether, 41 source-specific isoline plots out of 52 theoretical ones could be calculated. Because the sources do not influence all elements, there exist less isoline plots than theoretically could be expected. The source-specific element distribution plots illustrate very well the impact of each source onto the examined area. For example, in Fig. 7 the source-specific distribution of copper is illustrated.
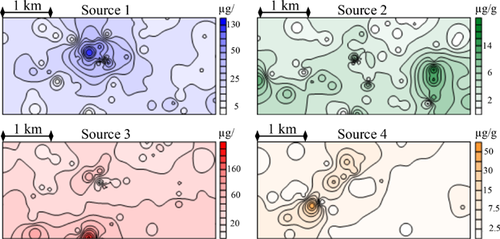
It is notable, that each source causes different hotspots. Source 1 has one big hotspot in the center of the area. Source 2 is responsible for hotspots in the eastern and western part of the region, source 3 in the southern part and the center and source 4 mainly in the southwestern part of the region. This implies that each source influences the region differently and the sources may influence the element distribution at more than one place.
The other source-specific element-distribution-plots are similar to the shown example in Fig. 5. This proves that the distribution caused by the sources is independent of the amount of emitted element. By considering not only the shape of each isoline plot but also the unit, a quantitative analysis is also possible. The impact of source 2 is about 18 μg/g at the hotspots and for source 3 up to 180 μg/g. This illustrates once more the results of the source apportionment. Source 3 characterizes the distribution of copper about 60% and source 2 only about 5%. In this case, the units of the source-specific isoline plots vary about one order of magnitude.
Another possibility to illustrate the source-specific distribution is to overlap them in one single plot. Figure 6 shows this overlapped source-specific distribution allowing a comprehensive interpretation.
The isoline plots illustrate the source-specific distribution very clearly (Fig. 8). Source 1 causes the main element distribution of chromium, iron, manganese, nickel, and vanadium. The hotspot of this source is located in the center of the region of interest. Samples in the immediate vicinity of the ironworks were taken, where the former iron industry smelter was located. Source 2 influences the distribution of calcium and magnesium. These elements have their highest contents where agricultural fields are located. They represent the limestone, which dominates this landscape. Source 3 characterizes the distribution of arsenic, cobalt, and copper. The highest content for these elements was found in the south of the examined area. At this point the so-called Red Mountain is located, where arsenic and copper enriched ore can be found 30. Source 4 describes mainly the distribution of cadmium, lead, and zinc. The highest content of these elements was found in the southwestern part of the examined area where the waste dump is situated. Furthermore, two smaller hotspots are near the source 1 hotspot. Without calculating the source-specific distribution, they would wrongly be linked to source 1 instead of source 3.
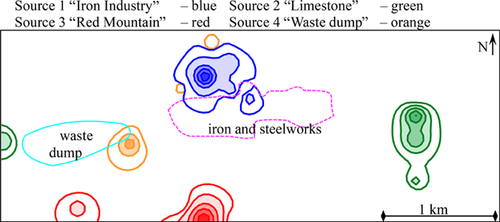
The visualization of the distribution of the elements confirms the results of the two source apportionment methods very well.
3.3 Advantages of the combination of receptor modeling methods with geostatistics
The combination of both methods can reveal hidden information. A clear distinction between different sources is possible. In addition, the elemental distributions caused by each source can be illustrated. Furthermore, the pattern of each source and the amount of emitted element could be visualized. The source description is quantitative and the impact of the source can be described very precisely. Therefore, the combination enables a reasonable interpretation of the data.
4 Concluding remarks
The two different source apportionment methods result in similar conclusions. This proves that source apportionment methods are applicable to the investigation of soil and not only to the investigation of the atmosphere, where these methods are well established. The same four sources, describing the distribution of the different elements, were identified with both methods, proving the trueness independently. The main difference between APCS-MLR and MCR-ALS is the amount of unexplained variance. The APCS-MLR model leaves less variance unexplained. The selection of the appropriate number of factors should be done using communalities instead of eigenvalues and Varimax rotation should be used afterwards.
By using only factors with an eigenvalue>1, a significant part of the variance can get lost. It also occurs, that after Varimax rotation one factor with a small eigenvalue explains more variance than other factors with original high eigenvalues.
The combination of the results of source apportionment with geostatistics allows a profound and reasonable interpretation of the element respective source distribution. The obtained isoline plots of the sources have a different pattern. Usually they have their hotspot at different locations. Displaying only one isoline plot for each source can be sufficient to describe the distribution of all elements. A prediction of the elemental behavior of all elements is possible, by combining the source-specific isoline plots with the source composition profiles.
These results show the powerful combination of receptor modeling methods and geostatistics for the description of the spatial pollution in soils. Both source apportionment methods lead to similar results and are suited for the investigation of contaminations in soils. The authors recommend this combination for a profound description of environmental studies in soil sciences.
The authors have declared no conflicts of interest.




