Chemie Ingenieur Technik
Volume 93, Issue 3 pp. 353-363
Gewusst wie!
Open Access

Tropfenbewegung und Stofftransport in technischen Flüssig/flüssig-Systemen. Teil 1: Einzeltropfensedimentation ohne Grenzflächeneffekte

Fluid Dynamics and Mass Transfer in Technical Grade Liquid-Liquid Systems. Part 1: Sedimentation of Single Droplets in Absence of Interfacial Effects

Joschka M. Schulz, 

Corresponding Author

Joschka M. Schulz

Technische Universität Berlin, Fachgebiet Verfahrenstechnik, Ackerstraße 76, 13355 Berlin, Deutschland

Correspondence: Joschka M. Schulz ([email protected]), Technische Universität Berlin, Fachgebiet Verfahrenstechnik, Ackerstraße 76, 13355 Berlin, Deutschland.Search for more papers by this author
Marc Petzold, 

Marc Petzold

Technische Universität Berlin, Fachgebiet Verfahrenstechnik, Ackerstraße 76, 13355 Berlin, Deutschland

Search for more papers by this author
Lutz Böhm, 

Lutz Böhm

Technische Universität Berlin, Fachgebiet Verfahrenstechnik, Ackerstraße 76, 13355 Berlin, Deutschland

Search for more papers by this author
Matthias Kraume, 

Matthias Kraume

Technische Universität Berlin, Fachgebiet Verfahrenstechnik, Ackerstraße 76, 13355 Berlin, Deutschland

Search for more papers by this author
First published: 03 February 2021
https://doi.org/10.1002/cite.202000246
Citations: 3

Abstract

de

Für die Dimensionierung von Flüssig/flüssig-Kontaktapparaten sind Fluiddynamik und Stofftransport in der Dispersion von entscheidender Bedeutung. Schwarm- und Grenzflächeneffekte führen zu komplexen Interaktionen und erschweren die Vorhersage von Betriebsparametern. Anhand von Einzeltropfenuntersuchungen kann eine grundlegende Vorhersage für fluiddynamisches Verhalten und Stofftransportleistung auf Basis einfacher Experimente und zahlreicher publizierter Korrelationen und Theorien getroffen werden. Dieser zweiteilige Beitrag befasst sich mit den Grundlagen von Fluiddynamik und Stofftransport von Einzeltropfen sowie der Auswirkung von Grenzflächeneffekten und für technische Systeme üblichen Verunreinigungen auf die Transportprozesse in dispersen Systemen.

Abstract

en

The design of a liquid-liquid contact apparatus necessitates the knowledge of fluid dynamics and mass transfer in the dispersion. Since swarm effects and interfacial phenomena induce complex interactions the prediction of process parameters is a challenging task. Single-drop investigations are suited to enable a sophisticated dimensioning based on few simple experiments in combination with published theories and correlations available from literature. This two-part article deals with the fundamentals of fluid dynamics and mass transfer of single droplets and evaluates occurrence and impact of interfacial effects as well as impurities typical for technical applications.

1 Einleitung

Fluiddynamik und Stofftransport beeinflussen wichtige Betriebsparameter in Kontaktapparaten, wie Holdup, Separationseffizienz oder Flutcharakteristik. Ihr Verständnis und ihre Vorhersage sind sowohl essenziell für die Dimensionierung neuer Apparate als auch als Hilfsmittel zur Evaluation und Optimierung bestehender Prozesse und können zu Troubleshooting-Zwecken herangezogen werden.

Nur in den seltensten Fällen finden sich in industriellen Prozessen reine Stoffsysteme. In technischen Flüssig/flüssig-Systemen sind oftmals lediglich die Hauptkomponenten bekannt, nicht aber sämtliche Begleitstoffe und/oder Verunreinigungen, die selbst in geringen Anteilen einen signifikanten Einfluss auf die Performance des Apparates ausüben können. 1, 2

Üblicherweise liegen grenzflächenaktive Spezies als Verunreinigungen vor, entstanden als Neben- bzw. Folgeprodukt, oder werden bewusst beispielsweise als Lösevermittler hinzugefügt. Da sie sowohl den Stofftransport als auch die Fluiddynamik stark beeinflussen, ist es erforderlich beeinflussende Stoffe zu identifizieren oder zumindest eine Abschätzung hinsichtlich des möglichen Einflusses vorzunehmen. Auf Basis theoretischer Betrachtungen und einfacher Schlüsselversuche, beispielhaft seien hier Einzeltropfenexperimente oder Absetzversuche mit und ohne gezielte Zugabe von Ionen genannt, kann eine Grundlage geschaffen werden, um zu bewerten, inwiefern und ab welchen Konzentrationen sich eine positive oder negative Beeinflussung der Transportprozesse bemerkbar macht. Die Entscheidung, ob eine etwaige Vorbehandlung für die Prozesseffizienz sinnvoll wäre oder sich die Stoffe bewusst zur Prozessintensivierung hinzufügen lassen, muss auf Basis der ganzheitlichen Betrachtung des Gesamtprozesses erfolgen.

In diesem zweiteiligen Artikel wird ein Überblick über die Effekte und den Einfluss verschiedener Stoffklassen gegeben, die als Verunreinigung oder Begleitkomponente auftreten bzw. dem Prozess bewusst hinzugefügt werden können. Die Unterteilung erfolgt dabei einerseits in Komponenten, bei denen die Adsorption an der Phasengrenzfläche maßgeblich ist, was insbesondere die Klasse der grenzflächenaktiven Substanzen betrifft, wie Tenside und Amphiphile, es werden aber ebenfalls partikuläre Systeme, insbesondere Nanopartikel, und das Auftreten von Ionen berücksichtigt. Andererseits werden die lokalen Grenzflächenspannungsunterschiede und die daraus resultierenden Grenzflächenphänomene betrachtet, die z. B. beim Stofftransport einer Übergangskomponente auftreten. Diese Einflussfaktoren und das durch ihre Anwesenheit in technischen Flüssig/flüssig-Systemen zu erwartende Transportverhalten wird im zweiten Teil dieser Reihe detailliert betrachtet. Weitere zur Prozessintensivierung einsetzbare Betriebsparameter, wie z. B. elektromagnetische Felder oder die Temperatur, werden u. a. in Saien und Jafari 3 bezüglich ihrer Gesamtperformance evaluiert.

Hervorzuheben ist allgemein, dass beim Auftreten von Grenzflächeneffekten eine komplexe Verknüpfung von Impuls- und Stofftransport auftritt 4, weshalb das Tropfenverhalten und auftretende Grenzflächenprozesse häufig die Ursache für praktische Probleme darstellen 5.

Bevor im zweiten Teil dieses Beitrags auf die einzelnen Effekte eingegangen wird, werden in dem hier vorliegenden ersten Teil zuerst die Grundlagen für die unbeeinflusste Phasengrenzfläche für die Grenzfälle der starren und fluiden Partikel dargestellt. Diese werden als Referenzwerte herangezogen und ermöglichen eine Abschätzung der zu erwartenden Sedimentationsgeschwindigkeiten und Stofftransportkoeffizienten auf Basis der physikalischen Stoffdaten und Tropfengrößen des betrachteten Stoffsystems.

In Abb. 1 werden die betrachteten Phänomene und Referenzfälle strukturiert dargestellt. Das Schema erläutert gleichzeitig die Gliederung beider Teile dieses Beitrags und stellt einen möglichen Entscheidungsbaum zur Bewertung der Transportprozesse in potenziell kontaminierten oder unter Einfluss von Grenzflächeneffekten stehenden Systemen dar.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Strukturierung von fluiddynamischen und Stofftransportphänomenen in Flüssig/flüssig-Systemen und deren Erläuterung in diesem zweiteiligen Beitrag.

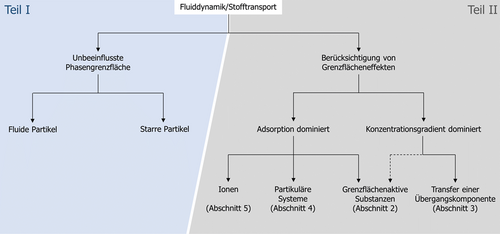
Dieser Artikel gibt Hinweise, wann solche Effekte potenziell auftreten, welche Auswirkungen sie ausüben, wie groß deren Einfluss sein kann und inwiefern Einzeltropfenexperimente darüber Aufschluss geben können, um eine aussagekräftige Abschätzung zu erhalten. Dabei wird eine kompakte Darstellungsweise angestrebt, für ausführliche Erläuterungen werden entsprechende Literaturstellen angegeben.

Durch die intensive Wechselwirkung zwischen Impuls- und Stofftransport ist mit dem Auftreten der o. g. Grenzflächenphänomene in der Regel ein charakteristisches Sedimentationsverhalten verbunden, das als sensitiver Indikator zur Vorhersage des Stofftransports dienen kann 1, 6. Der Artikel konzentriert sich auf Einzeltropfenexperimente, deren Einsatz als Schlüsselexperiment bspw. im Bereich der Flüssig/flüssig-Extraktion erfolgreich praktiziert wird. Die Betrachtung repräsentativer Tropfen erfolgt dabei zur Parametrisierung von Simulationen auf Basis von Kompartiment-Modellen oder Populationsbilanzen und wird ausführlich in Bart et al. 7 und Leleu und Pfennig 2 evaluiert. Aktuelle Anwendungen sind beispielsweise in Ayesterán et al. 8 oder Weber und Jupke 9 zu finden. Wie dort gezeigt wird, können Laborversuche an Einzeltropfen in Kombination mit weiteren standardisierten Experimenten, insbesondere zur Bestimmung des Koaleszenzverhaltens, erfolgreich eingesetzt werden, um Betriebsparameter wie die Trenneffizienz und die Flutcharakteristik von gerührten und gepulsten Trennkolonnen in der industriellen Anwendung zu beschreiben. Auch zur Wirtschaftlichkeitsbetrachtung können sie herangezogen werden, s. bspw. 10. Übersichten zu numerischen und experimentellen Einzeltropfenstudien geben ebenfalls Saien und Jafari 3 sowie Zhang et al. 11.

2 Modellierung von Einzeltropfen in Flüssig/flüssig-Systemen

Die Modellierung eines repräsentativen Tropfens, stellvertretend für die in Kontaktapparaten auftretenden Schwärme, erfolgt auf Basis von theoretischen, empirischen oder halb-empirischen Ansätzen. Diese ermöglichen für den Fall der ungestörten Phasengrenzfläche bereits rein auf Basis der physikalischen Größen oder mit minimalem experimentellem Aufwand eine Vorhersage der Bewegungsgeschwindigkeit und des Stofftransports. 2

Dabei werden die Grenzfälle der fluiden Partikel mit mobiler Phasengrenzfläche und der starren Partikel mit unbeweglicher Phasengrenzfläche als Referenzfälle herangezogen, wobei ersterer die größtmöglichen Bewegungsgeschwindigkeiten für ein gegebenes System beschreibt, während letzterer die langsamsten zu erwartenden Tropfen charakterisiert 1. Der nötige technische Aufwand, um reine oder zumindest “vernachlässigbar kontaminierte” Systeme experimentell zu erhalten (s. bspw. 12), zeigt, dass in technischen Anwendungen in der Regel keine fluiden Partikel mit ideal mobiler Phasengrenzfläche zu erwarten sind, sondern vielmehr Geschwindigkeiten zwischen der fluiden und der starren Partikel auftreten, wie in Abschn.  3.1.2 anhand von in der Literatur verfügbaren Messdaten illustriert wird. Interessant ist bei Betrachtung der beiden Grenzfälle außerdem deren Abweichung voneinander, die insbesondere vom Viskositätsverhältnis und dem Durchmesser abhängt 13 und in Abschn.  3.1.3 genauer betrachtet wird. Die Betrachtung fluider und starrer Partikeln ermöglicht zusätzlich eine Vorhersage der zu erwartenden Stofftransportgeschwindigkeit, so dass diese Grenzfälle auch bei Auftreten von Grenzflächeneffekten als Referenzfälle dienen.

3 Beschreibung reiner Systeme als Referenzfall ohne Grenzflächeneffekte

Im Folgenden werden die Berechnung und Voraussage der Zielgrößen

  • stationäre Sedimentationsgeschwindigkeit (Abschn.  3.1)

  • sowie Stoffübergangskoeffizient bzw. transienter Konzentrationsverlauf (Abschn.  3.2)

auf Basis physikalischer Größen vorgestellt. Dabei kann durch Berücksichtigung der Konzentrationsabhängigkeit der Stoffgrößen der Einfluss von Mischungsgrößen ebenfalls einbezogen werden.

3.1 Fluiddynamik

Zur Voraussage der Verweilzeit und des Holdups sowie des Stofftransportkoeffizienten wird die Sedimentationsgeschwindigkeit der Partikel benötigt. Die Kräftebilanz um ein Einzelpartikel unter Berücksichtigung der Trägheits-, Gravitations-, Auftriebs- sowie der Widerstandskraft ermöglicht die Berechnung der transienten Geschwindigkeit eines Einzelpartikels 14. Der instationäre Anteil ist in reinen Systemen mit einer Ausdehnung von wenigen Hundertstel- bis Zehntelsekunden in der Regel so gering, dass er an dieser Stelle vernachlässigt werden kann. Somit ergibt sich für die stationäre Sedimentationsgeschwindigkeit vp unter Vernachlässigung der Trägheitskraft die Bewegungsgleichung des Einzelpartikels 14:
urn:x-wiley:0009286X:media:cite202000246-math-0001()

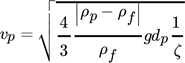mit der Dichte des Partikels ρp und des Fluids ρf, dem Partikeldurchmesser dp, der Erdbeschleunigung g sowie dem Widerstandsbeiwert ζ. Da der Widerstandsbeiwert eine Funktion der Reynoldszahl ist, wird Gl. 1 in der Regel numerisch gelöst. Für starre Partikel lässt sich bspw. durch Wahl der Korrelation nach Martin 15 ein expliziter Ausdruck herleiten 14. Des Weiteren existiert eine analytische Lösung für die schleichende Strömung mit Re ≪ 1 16, 17.

3.1.1 Berechnung der Sedimentationsgeschwindigkeit auf Basis gängiger Modelle

Zum iterativen Lösen von Gl. 1 werden Widerstandsgesetze verwendet, die den Widerstandsbeiwert ζ als Funktion der Reynoldszahl und für Fall der fluiden Partikel zusätzlich in Abhängigkeit des Viskositätsverhältnisses korrelieren 1. Der Widerstandsbeiwert spiegelt die an dem Partikel auftretenden Druck- und Reibungskräfte wider und berücksichtigt die Charakteristika der Phasengrenzfläche sowie eine etwaige Verformung des Partikels.

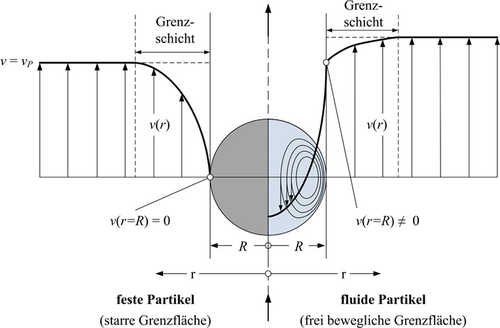
Abb. 2 zeigt das Strömungsfeld um ein Einzelpartikel für die Grenzfälle des starren und fluiden Partikels. Dabei wird das starre Partikel durch eine unbewegliche Phasengrenzfläche und folglich vernachlässigbare Bewegung im Inneren charakterisiert. Das Gegenstück stellt das fluide Partikel mit ideal beweglicher Phasengrenzfläche dar, bei dem die Schubspannung über die Phasengrenzfläche übertragen und somit eine innere Zirkulation induziert wird. Daraus resultiert die höhere Aufstiegsgeschwindigkeit fluider Partikel, wobei die Ausprägung dieser Diskrepanz insbesondere vom Viskositätsverhältnis abhängig ist, worauf in Abschn.  3.1.3 detaillierter eingegangen wird.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Geschwindigkeitsprofil bei Umströmung eines Einzelpartikels mit starrer und fluider Phasengrenzfläche (aus 1, leicht modifiziert).
Abb. 3 zeigt Ansätze zur Berechnung der stationären Bewegungsgeschwindigkeit von Einzelpartikeln. Dazu sind exemplarisch die Aufstiegsgeschwindigkeiten für verschiedene Tropfendurchmesser des Referenzsystems Toluol/Wasser 18 dargestellt, die auf Basis der in Tab. 1 angegebenen Stoffdaten berechnet wurden. Folgende Fälle und Widerstandsgesetze wurden hier verwendet:

  • sphärische, fluide Partikel nach Feng und Michaelides 13(—)

  • sphärische, starre Partikel nach Martin 15 (· · ·)

  • verformte, fluide Partikel nach Thorsen et al. 19 (– · –)

  • kontaminierte Systeme nach Grace et al. 20 (– – –).

Table 1. Stoffdaten bei 25 °C nach Misek et al. 18 sowie an die Messdaten von Wegener und Paschedag 21 angepasste Übergangsparameter für das Modell nach Henschke 29 für das Stoffsystem Toluol/Wasser.

 

Wasser

Toluol

Dichte ρ [kg m−3]

997,02

862,3

Viskosität η [mPas]

0,8903

0,552

dum [mm]

→ 0

α15 [–]

2,11

α16 [–]

4,17

Grenzflächenspannung γ [mN m−1]

36

  • a) Die Parameter wurden für die Annahme dum → 0 angepasst. Bei Anpassung des ganzen Parametersatzes ergibt sich: dum = 1,25 mm, α15 = 2,11, α16 = 4,18.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Vergleich gemessener und berechneter stationärer Sedimentationsgeschwindigkeiten in Abhängigkeit des Partikeldurchmessers für das Stoffsystem Toluol/Wasser, Stoffdaten gemäß Tab. 1, experimentelle Daten nach Wegener und Paschedag 21, 22, Unterteilung der fluiddynamischen Zustände nach Henschke 29 ( | ) in die Bereiche starre, bewegliche, oszillierende sowie deformierte Partikel mit steigendem Durchmesser.

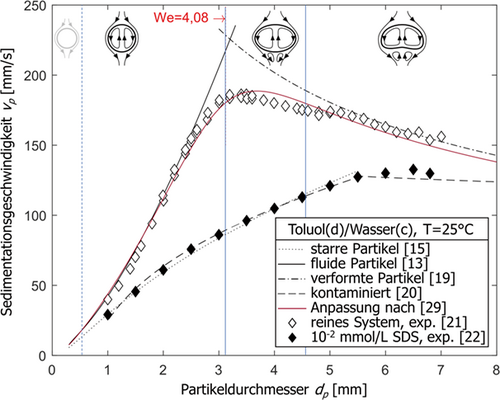
Die der Berechnung zugrunde liegenden Gleichungen können den jeweiligen Quellen entnommen werden. Eine Übersicht weiterer gängiger Widerstandsgesetze inklusive der dazugehörigen Gültigkeitsbereiche ist bei Wegener et al. 1 zu finden. Zum Vergleich sind die maximal erreichbaren Geschwindigkeiten im System Toluol/Wasser aus Wegener und Paschedag 21 (◊) sowie, exemplarisch für kontaminierte Systeme, die mittleren Aufstiegsgeschwindigkeiten in Anwesenheit von 10−2 mmol L−1 des ionischen Tensids SDS im selben Stoffsystem 22 (⧫) dargestellt. Es ist hervorzuheben, dass die dargestellte Tensidkonzentration lediglich circa einem Promill der kritischen Mizellbildungskonzentration (CMC) entspricht, die für SDS in Toluol bei 8,35 mmol L−1 23 liegt. Des Weiteren zeigt die Grenzflächenspannung einen nur geringen Abfall in der Größenordnung von 4 % 22. Dies zeigt, dass bereits kleine Mengen an grenzflächenaktiven Verunreinigungen das Verhalten eines Partikels mit unbeweglicher Phasengrenzfläche hervorrufen können; ein Fakt, der für grenzflächenaktive Substanzen gängig ist und im zweiten Teil dieses Beitrags, der den Einfluss von Grenzflächeneffekten behandelt, genauer betrachtet wird.

Zum Abschätzen des für die Verformung kritischen Durchmessers evaluieren Wegener et al. 1 verschiedene Korrelationen. Unter anderem kann die Weberzahl We = 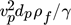urn:x-wiley:0009286X:media:cite202000246-math-0003, mit der Grenzflächenspannung zwischen den beiden Phasen γ, herangezogen werden, für die Winnikow und Chao 24 einen Wert von Wekrit = 4,08 vorschlagen (3,58 25, 4 26, 4,04 27)1, der ebenfalls in Abb. 3 eingezeichnet ist. Einen alternativen Ansatz zur Bestimmung der Partikelform stellt die grafische Darstellung der Reynolds- über der Eötvöszahl nach Grace et al. 20 dar 28.

Ein alternativer Ansatz zur Beschreibung der Sedimentationsgeschwindigkeit nach Henschke 29 ist ebenfalls in Abb. 3 dargestellt (rote Linie). Dort werden Übergangsparameter zum Wechsel zwischen den beschreibenden Gleichungen an Einzeltropfenexperimente angepasst. Dabei beschreibt dum den Tropfendurchmesser, bei dem der Übergang vom starren zum fluiden Partikel signifikant wird, α15 das Niveau der Geschwindigkeit oszillierender Tropfen und α16 den Übergang vom viskosen in den grenzflächenspannungsdominierten Bereich 29. Die an die Messdaten von Wegener und Paschedag 21 für das Referenzsystem Toluol/Wasser angepassten Parameter können Tab. 1 entnommen werden. Es zeigt sich eine gute Übereinstimmung zwischen den Verläufen. Mangels Messdaten für Partikel mit dp < 1 mm und aufgrund der hohen Reinheit bei den durchgeführten Versuchen, lässt sich der Übergang vom starren zum fluiden Partikel, und damit der Parameter dum, für kleine Partikeldurchmesser anhand der Messdaten nicht exakt bestimmen, sofern er aufgrund der Reinheit des Systems überhaupt auftreten würde. Durch Reduktion von dum kann die Modellierung der Aufstiegsgeschwindigkeiten kleiner Toluol-Tropfen durch die Annahme dum → 0 verbessert werden.

3.1.2 Vergleich mit experimentellen Daten

Zum Vergleich mit experimentellen Daten ist in Abb. 4a ein Paritätsplot nach Wegener et al. 1 dargestellt. Gezeigt werden 414 Datenpunkte für unkontaminierte, binäre Stoffsysteme diverser Autoren, wobei als organische Phase Toluol, Butylacetat, Butanol, Tetrachlormethan oder Methylenbromid eingesetzt wurden und Wasser jeweils die kontinuierliche Phase darstellte. Die Berechnung der zu erwartenden Sedimentationsgeschwindigkeiten erfolgt auf Basis der verfügbaren Stoffdaten, wozu lediglich die Dichten und Viskositäten beider Phasen sowie die Grenzflächenspannung vonnöten sind. Zum Vergleich ziehen Wegener et al. 1 verschiedene, in der Literatur verfügbare Ansätze heran: Für fluide, sphärische Partikel die Widerstandsgesetze nach Hamielec et al. 30, Feng und Michaelides 13 und Saboni und Alexandrova 31, für nicht-sphärische Partikel die Ansätze nach Thorsen et al. 19 und Harper 26 sowie für den gesamten Durchmesserbereich den grafischen Ansatz nach Grace et al. 20.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Paritätsplot zum Vergleich der theoretischen und experimentellen stationären Aufstiegsgeschwindigkeit für a) reine, binäre Systeme (Messdaten diverser Autoren und Berechnungsansätze 13, 19, 20, 26, 30, 31 nach Wegener et al. 1), b) technische Systeme mit Stofftransport (Messdaten diverser Autoren und Modellierungsansatz nach Weber et al. 32).

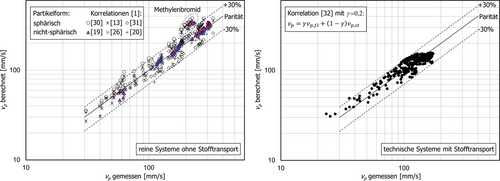
Nahezu alle Messpunkte in Abb. 4a zeigen eine geringere Abweichung als 30 %, die stärker abweichenden Daten für das Stoffsystem Methylenbromid/Wasser sind auf eine Bifurkation, das Auftreten zweier möglicher Geschwindigkeiten bei bestimmten Durchmesser- und Stoffdatenkombinationen, zurückzuführen. Für eine detaillierte Beschreibung der zugrunde liegenden Daten und Ergebnisse sei auf Wegener et al. 1 verwiesen, eine Betrachtung der Bifurkation im Stoffsystem Toluol/Wasser ist beispielsweise in Wegener und Paschedag 21 zu finden.

Abb. 4b nach Weber et al. 32 illustriert das Sedimentationsverhalten technischer Systeme. Die Autoren schlagen eine Modellierung der Sedimentationsgeschwindigkeit von Einzeltropfen basierend auf einer linearen Interpolation zwischen Korrelationen für fluide und starre Partikel vor, wobei der Gewichtungsfaktor γ an Einzeltropfenexperimente angepasst wird und für γ = 1 die Geschwindigkeit der fluiden Partikel bzw. für γ = 0 die der starren Partikel beschreibt. Auf Basis von 491 Messreihen verschiedener Autoren, in denen Stofftransport und etwaige, technisch übliche Verunreinigungen auftreten, bestimmen Weber et al. 32 einen Wert von γ = 0,2. Dieser Wert dient in Abb. 4b als Grundlage zum Vergleich der experimentellen Daten mit den für γ = 0,2 erhaltenen theoretischen Aufstiegsgeschwindigkeiten und illustriert eine starke Reduktion der Aufstiegsgeschwindigkeiten in technischen Systemen. Der zugrunde liegende Mechanismus, inwiefern Stofftransport und Verunreinigungen in technischen Systemen eine Reduktion der Aufstiegsgeschwindigkeit induzieren und welche Wechselwirkung mit dem Stofftransport besteht, steht im zweiten Teil dieses Beitrags im Fokus.

3.1.3 Einfluss des Viskositätsverhältnisses

Die Abweichung zwischen den Aufstiegsgeschwindigkeiten fluider und starrer Partikel zeigt insbesondere eine Sensitivität bezüglich des Viskositätsverhältnisses η* = ηd/ηc von disperser zu kontinuierlicher Phase. Abb. 5 illustriert auf Basis der beiden Referenzsysteme Toluol/Wasser (η* = 0,62) und 1-Octanol/Wasser (η* = 10,2) das Verhältnis dieser Geschwindigkeiten. Dazu wurden dieselben Gesetzmäßigkeiten wie in Abb. 3 zugrunde gelegt und die Geschwindigkeit der fluiden Partikel nach Feng und Michaelides 13 auf die der starren Partikel nach Martin 15 bezogen. Die Abhängigkeit des Übergangs zum oszillierenden Partikel von der Viskosität der dispersen Phase wird dabei vernachlässigt und sphärische Partikel in Analogie zu Abb. 3 näherungsweise bis zum Erreichen der kritischen Weberzahl von We = 4,08 (rote Linie) angenommen.

Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Einfluss des Viskositätsverhältnisses auf das Verhältnis der Bewegungsgeschwindigkeiten fluider 13 und starrer 15 sphärischer Partikel im Vergleich mit experimentellen Daten für die Stoffsysteme Toluol/Wasser 21 und 1-Octanol/Wasser.

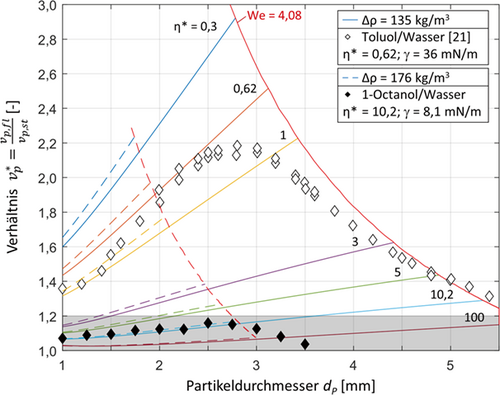
Durch Variation der Viskosität der dispersen Phase ηd wird das Viskositätsverhältnis verändert, wobei die durchgezogenen Linien mit den Stoffdaten aus Tab. 1 berechnet wurden und der Verlauf für η* = 0,62 dem oben gezeigten Referenzsystem Toluol/Wasser entspricht. Zum Vergleich sind die Messdaten nach Wegener und Paschedag 21 (◊) dargestellt.

Es zeigt sich ein ausgeprägter Unterschied der Sensitivität bzgl. des Viskositätsverhältnisses im Bereich von Verhältnissen kleiner 10, wobei mit steigendem Viskositätsverhältnis die Sensitivität stark abnimmt. Zusätzlich beträgt die Abweichung zwischen fluidem und starrem Partikel ab einem Viskositätsverhältnis von 10 lediglich für große Tropfen mehr als 20 % (grau hervorgehobener Bereich). Der Unterschied der Geschwindigkeit fluider und starrer Partikel wird demzufolge vernachlässigbar. Dieses Verhalten bestätigt sich anhand der für das Stoffsystem 1-Octanol/Wasser dargestellten Messdaten mit einem Viskositätsverhältnis von η* = 10,2 (⧫). Die gestrichelten Verläufe wurden zum Vergleich mit den Stoffdaten aus Paul et al. 6 berechnet.

Vom Dichteverhältnis ist der Widerstandsbeiwert hingegen nahezu unabhängig 13, 33, wodurch die Abschätzung bezüglich Dichteänderungen auf Basis von Gl. 1 erfolgen kann.

3.2 Stofftransport

Üblicherweise wird der Stofftransportwiderstand beim Stoffdurchgang von einer Phase I in eine zweite nicht-mischbare Phase II in drei Anteile unterteilt: den Transport vom Bulk der Phase I an die Phasengrenzfläche, der Transport durch die Phasengrenzfläche hindurch und den anschließenden Transport von der Phasengrenzfläche in den Bulk von Phase II. Dabei wird unter normalen Bedingungen davon ausgegangen, dass der durch die Phasengrenzfläche hervorgerufene Widerstand vernachlässigbar klein ist 34. Die relevanten Widerstände werden im Stoffdurchgangskoeffizienten kd zusammengefasst. 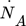Die Gleichung zur Berechnung des Stoffstroms urn:x-wiley:0009286X:media:cite202000246-math-0004 einer Komponente A mit Bezug auf die disperse Phase lautet
urn:x-wiley:0009286X:media:cite202000246-math-0005()

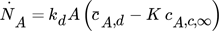wobei 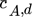urn:x-wiley:0009286X:media:cite202000246-math-0006 die mittlere Konzentration in der dispersen Phase, 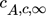urn:x-wiley:0009286X:media:cite202000246-math-0007 die mittlere Konzentration bzw. die Konzentration außerhalb der Konzentrationsgrenzschicht in der kontinuierlichen Phase und A die für den Transport zur Verfügung stehende Oberfläche repräsentieren.

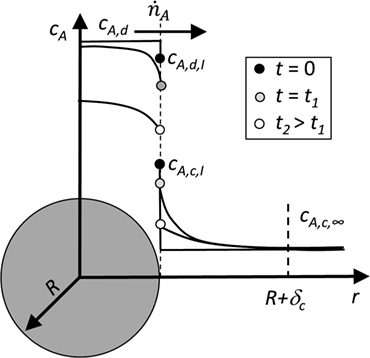
Zur Vorhersage der auftretenden Stofftransportkoeffizienten und des zeitlichen Verlaufs der Konzentrationen innerhalb beider Phasen sind die auftretenden Konzentrationsgradienten maßgeblich. Abb. 6 zeigt den transienten Verlauf des radialen Konzentrationsprofils in und um eine Einzelpartikel für den Fall, dass sowohl der innere als auch der äußere Transportwiderstand berücksichtigt werden müssen. Man spricht in diesem Fall von einem konjugierten Problem. Während bei einem Innenproblem der Widerstand in der dispersen Phase dominiert, ist bei einem Außenproblem der Widerstand in der kontinuierlichen Phase entscheidend. Wenn einer der beiden Widerstände vernachlässigbar ist, tritt in dieser Phase kein Konzentrationsgradient auf. Die Phasengrenzfläche wird vereinfachend mit vernachlässigbarer Ausdehnung angenommen und die angrenzenden Phasen stehen dort im thermodynamischen Gleichgewicht. Damit ist das Verhältnis der Konzentrationen in der dispersen und der kontinuierlichen Phase direkt an der Phasengrenzfläche (cA,d,I bzw. cA,c,I) durch den Verteilungskoeffizienten K festgelegt. Eine tiefergehende Betrachtung der Konzentrationsverläufe an und innerhalb der Phasengrenzfläche unter Anwendung der Dichtegradienten-Theorie ist beispielsweise in Danzer und Enders 35 zu finden. Aktuelle Untersuchungen berücksichtigen den berechneten Einfluss der Anreicherung einer Komponente in der Phasengrenzfläche auf den Stofftransport 36, 37.

Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
Transienter Verlauf des radialen Konzentrationsprofils beim Stofftransport am Einzeltropfen, Stofftransportrichtung d → c (aus Wegener et al. 1).

3.2.1 Berechnung des Stofftransports auf Basis gängiger Modelle

Zur Berechnung der Stofftransportkoeffizienten finden sich in der Literatur jeweils entkoppelt für das Außen- und das Innenproblem etablierte Korrelationen und Gesetzmäßigkeiten, wie sie bspw. in Clift et al. 28, Kumar und Hartland 38 und Wegener et al. 1 zusammengestellt sind. Abb. 7 zeigt die dimensionslose Darstellung des transienten Konzentrationsverlaufs bei der Einzeltropfensedimentation. 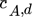Dabei wird die mittlere Konzentration im Tropfen urn:x-wiley:0009286X:media:cite202000246-math-0008 gemäß
urn:x-wiley:0009286X:media:cite202000246-math-0009()

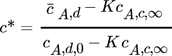derart dimensionslos dargestellt, dass die zur Kontaktzeit t noch vorhandene treibende Konzentrationsdifferenz in Relation zur maximal möglichen Differenz, gebildet mit der Anfangskonzentration cA,d,0 im Tropfen, gesetzt wird. Die Kontaktzeit t wird in Form der Fourierzahl wie folgt dimensionslos dargestellt: Fod = 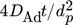urn:x-wiley:0009286X:media:cite202000246-math-0010.

Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
Zeitlicher Verlauf der Konzentration in dimensionsloser Darstellung für einen Tropfen mit 2 mm Durchmesser, Berechnung des Innenproblems (IP) bei unterschiedlichen Bedingungen sowie des Außenproblems (AP) für das Stoffsystem Toluol/Aceton/Wasser mit DAd = 2,78·10−9 m2s−1 und DAc = 1,15·10−9 m2s−1 nach 18.
Die Betrachtung erfolgt für sphärische Tropfen für das Innenproblem (IP) mit den Korrelationen für

  • die starre Partikel nach Newman 39 (–––) und Calderbank und Korchinski 40 mit R = 1 (blaue Linie),

  • die fluide Partikel nach Kronig und Brink 41 (– – –) und Calderbank und Korchinski 40 mit R = 2,25 (blau gestrichelt)

  • sowie die turbulente Vermischung nach Handlos und Baron 42 (– · –).

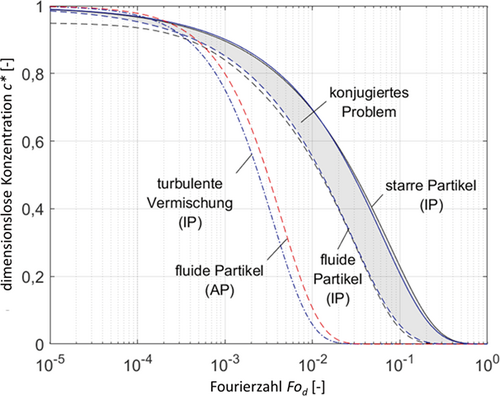
Für die Modellierung des Außenproblems (AP) wurde nach Wegener et al. 1 die Berechnung des Konzentrationsverlaufs nach Clift et al. 28 mit der Korrelation für den außenseitigen Stofftransport nach Lochiel und Calderbank 43 (rot gestrichelt) kombiniert. Da sowohl bei der Modellierung des Außenproblems als auch der turbulenten Vermischung die Sedimentationsgeschwindigkeit eine Rolle spielt, wurde erneut beispielhaft das EFCE-Referenzsystem Toluol/Wasser mit der Übergangskomponente Aceton zugrunde gelegt 18 (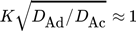urn:x-wiley:0009286X:media:cite202000246-math-0011) und die Aufstiegsgeschwindigkeit eines 2-mm-Tropfens mithilfe der o. g. Korrelation nach Feng und Michaelides 13 berechnet.

Neben der Modellierung auf Basis gängiger Korrelationen existieren analog zur Betrachtung der Fluiddynamik Stofftransportmodelle, die an experimentelle Daten angepasst werden können. Entsprechende Anpassungsparameter finden sich zum Beispiel im Modell nach Henschke und Pfennig 44 mit der Instabilitätskonstanten CIP sowie im Modell nach Calderbank und Korchinski 40 mit dem Verhältnis der effektiven Diffusivität R. Diese spielen insbesondere bei Auftreten von Grenzflächeneffekten eine Rolle und finden im zweiten Teil dieses Beitrags an den entsprechenden Stellen Anwendung. Zum Vergleich ist in Abb. 7 das Modell von Calderbank und Korchinski 40 dargestellt, bei dem durch geeignete Wahl der effektiven Diffusivität R auch das Verhalten des fluiden und des starren Partikels (R = 2,25 bzw. R= 1) abgebildet werden kann. Analog ließe sich das o. g. Modell nach Henschke und Pfennig 44 mit CIP ≈ 3,5 × 104 für das fluide und 2 × 106 ≤ CIP < ∞ für das starre Partikel verwenden.

Durch Anwendung der Additionsregel
urn:x-wiley:0009286X:media:cite202000246-math-0012()

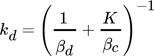die den Stoffdurchgangskoeffizienten kd aus den Stoffübergangskoeffizienten der dispersen und der kontinuierlichen Phase βd bzw. βc bestimmt, lässt sich durch Kombination des Außen- und Innenproblems der Stoffdurchgang für den Fall des konjugierten Problems berechnen. Die Ergebnisse für den zugehörigen zeitlichen Konzentrationsverlauf liegen zwischen der Lösung für die ideale fluide Partikel nach Calderbank und Korchinski 40 und der rein diffusiven Betrachtung nach Newman 39, s. grau hervorgehobener Bereich in Abb. 7.

In welchen Grenzen die für konjugierte Systeme gängige Additionsregel der Stofftransportwiderstände Gültigkeit besitzt und in welche Richtung Abweichungen auftreten, evaluieren u. a. Juncu 45 und Rachih et al. 33 numerisch. Eine Übersicht über numerische Betrachtungen und die zugrunde liegenden numerischen Ansätze zur Einzeltropensedimentation ist in Zhang et al. 11 zu finden. Es hat sich gezeigt, dass im Falle eines konjugierten Problems in der Regel eine aufwendigere numerische Evaluierung nötig ist 1 und die Additionsregel zur Berechnung des Stoffdurchgangskoeffizienten kd gemäß Gl. 4 nur eine unzureichende Genauigkeit besitzt 33, 45.

3.2.2 Abschätzung des dominierenden Transportwiderstandes

Zur Auswahl geeigneter Korrelationen erfolgt sinnvollerweise zuerst eine Abschätzung bezüglich der Lage des Stofftransportwiderstands. Dazu wird das Produkt aus dem Verteilungskoeffizienten K und der Wurzel aus dem Verhältnis der Diffusionskoeffizienten D* = DAD/DAc von disperser und kontinuierlicher Phase berechnet und folgende Unterteilung vorgenommen:

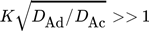  • urn:x-wiley:0009286X:media:cite202000246-math-0013: Hauptwiderstand in der kontinuierlichen Phase (Außenproblem)

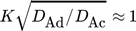  • urn:x-wiley:0009286X:media:cite202000246-math-0014: beide Widerstände relevant (konjugiertes Problem)

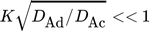  • urn:x-wiley:0009286X:media:cite202000246-math-0015: Hauptwiderstand in der dispersen Phase (Innenproblem).

Eine Abschätzung der Diffusionskoeffizienten kann beispielsweise durch Gruppenbeitragsmethoden erfolgen 46. Alternativ lässt sich das Verhältnis der Diffusionskoeffizienten unter Annahme identischer hydrodynamischer Radien mithilfe der Stokes-Einstein-Gleichung 47 auf das Verhältnis der Viskositäten zurückführen 1: D* ≈ 1/η*.

Eine abschätzende Bestimmung des vorliegenden Problems für sedimentierende Partikel in Abhängigkeit von der Peclétzahl Pe = vpdp/DAd ist z. B. auf Basis der in Abschn.  3.2.1 eingeführten Additionsregel für die Transportwiderstände (s. Gl. 4), in Anlehnung an Schulze 48 möglich. Durch Einsetzen der Sherwoodzahlen des konjugierten Problems Shk = kddp/DAd sowie der dispersen und der kontinuierlichen Phase (Shd = βddp/DAd bzw. Shc = βcdp/DAc) resultiert die dimensionslose Form von Gl. 4:
urn:x-wiley:0009286X:media:cite202000246-math-0016()
wobei der Term 1/Shd den dispersseitigen und KD*/Shc den Teilwiderstand in der kontinuierlichen Phase repräsentiert. Mit der Annahme, dass einer der Teilwiderstände als dominant erachtet werden kann, sofern dessen Anteil mindestens 90 % des Gesamtwiderstandes im konjugierten Fall ausmacht, folgt für das Vorliegen eines Innen- bzw. Außenproblems die Bedingung:
urn:x-wiley:0009286X:media:cite202000246-math-0017()

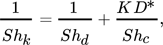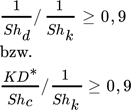Durch Einsetzen dieser Bedingung in Gl. 5 und Verwendung der in Abschn.  3.2.1 betrachteten Berechnungsansätze zur Bestimmung der Sherwoodzahlen für die disperse und die kontinuierliche Phase lassen sich in Abhängigkeit von der Peclétzahl und dem Verhältnis Shc/Shd Grenzen für das Vorliegen eines Innen- bzw. Außenproblems berechnen.

Ansätze wie dieser stellen eine einfache Möglichkeit dar, um die Lage des Hauptwiderstandes für ein gegebenes Stoffsystem auf Basis der Stoffdaten und der chemischen Zusammensetzung abzuschätzen. In Abb. 8 wird der resultierende Zusammenhang beispielhaft in Anlehnung an Schulze 48 für D* = η* = 1 grafisch illustriert. Dabei werden für den ruhenden Tropfen und folglich rein diffusiven Stofftransport der asymptotische Wert der analytischen Lösung nach Newman 39 Shd = 6,58 für das Innenproblem und die für den diffusiven Transport um ein sphärisches Partikel gültige Sherwoodzahl von Shc = 2 für das Außenproblem verwendet. Der von Plöcker und Schmidt-Traub 49 für ruhende Systeme vorgeschlagene Bereich von 0,03–30 für 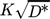urn:x-wiley:0009286X:media:cite202000246-math-0018 als Gültigkeitsbereich für das konjugierte Problem ist in Abb. 8 ebenfalls hervorgehoben.

Details are in the caption following the image
Figure 8
Open in figure viewerPowerPoint
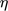Lage der Stofftransportwiderstände für D* = 1 und urn:x-wiley:0009286X:media:cite202000246-math-0019* = 1 in Anlehnung an Schulze 48.

Für sedimentierende Tropfen werden die Modelle von Kronig und Brink 41 und Lochiel und Calderbank 43 zur Berechnung der Sherwoodzahlen herangezogen. Es zeigt sich eine gute Übereinstimmung mit dem von Piarah 50 numerisch ermittelten Gültigkeitsbereich des konjugierten Problems von 0,1 bis 10 für Pe = 104 und Re = vpdp/νf = 100.

Der grau hervorgehobene Bereich zwischen den Grenzlinien für das Innen- und das Außenproblem stellt den Bereich des konjugierten Problems dar. Mit steigenden Peclétzahlen verschiebt sich der Bereich des konjugierten Problems hin zu größeren Verteilungskoeffizienten, wodurch bei gleichbleibendem Verteilungskoeffizienten eine Verschiebung in Richtung des Innenproblems erfolgt. Dies ist auf die Abnahme des Widerstandes in der kontinuierlichen Phase mit steigender Peclétzahl zurückzuführen. Bei Betrachtung einer festen Peclétzahl begünstigen höhere Verteilungskoeffizienten das Auftreten eines Außenproblems, was durch die abnehmende Konzentrationsdifferenz bzw. durch einen kleineren Konzentrationsgradienten in der kontinuierlichen Phase hervorgerufen wird.

4 Zusammenfassung und Ausblick

Die Wechselwirkung zwischen Impuls- und Stofftransport in Flüssig/flüssig-Apparaten zeigt eine starke Abhängigkeit vom Verhalten der Phasengrenzfläche. Im ersten Teil dieses Artikels werden einerseits Ansätze zur Modellierung von Flüssig/flüssig-Systemen auf Basis der vorhandenen Fachliteratur, die über das Lehrbuchwissen hinausgehen, vorgestellt und geeignete Literatur für eine Vertiefung der Sachverhalte angeben. Andererseits wird durch Kombination der verschiedenen Ansätze und den Vergleich mit experimentellen Ergebnissen ein tieferer Einblick und ein besseres Verständnis des Verhaltens von Flüssig/flüssig-Systemen ermöglicht. Dabei fokussiert sich die vorgestellte Übersicht vor allem auf Einzeltropfenexperimente, um ein besseres Verständnis der Transportvorgänge zu erreichen und die Kopplung mit Schwarmeffekten zu eliminieren.

Das hier dargestellte Verhalten dient im zweiten Teil des Beitrags als Referenz. Dort wird der Einfluss von technisch üblichen Verunreinigungen und des Stofftransports selbst auf die Transportprozesse in Flüssig/flüssig-Systemen detailliert betrachtet. Es zeigen sich unterschiedliche Tendenzen für die verschiedenen Stoffklassen, wobei die gängigen Beobachtungen mit Beispielen illustriert sowie anhand verschiedener Literaturquellen verglichen werden. Beim Einsatz der Fluiddynamik als sensitive Messmethode und als Indikator für das Auftreten von Grenzflächenphänomenen stellen die hier präsentierten Grundlagen geeignete Referenzfälle dar, um das Verhalten der Phasengrenzfläche besser zu verstehen.

Acknowledgements

Gefördert durch die Deutsche Forschungsgemeinschaft (DFG) – TRR 63 ”Integrierte chemische Prozesse in flüssigen Mehrphasensystemen” (Teilprojekt A10) – 56091768.

Abb. 2 und Abb. 6: Reprinted and translated, with permission from Elsevier, from M. Wegener, N. Paul, M. Kraume, Fluid dynamics and mass transfer at single droplets in liquid/liquid systems, Int. J. Heat Mass Transfer 2014, 71, 475–495.

Besonderer Dank gilt Benedikt Weber, Christian Meyer und Andreas Jupke für die Bereitstellung der Rohdaten aus 32 zur Erstellung der Abb. 4b sowie Mirco Wegener und Niklas Paul für die Vorarbeiten und Bereitstellung der Daten aus 1. Veröffentlichung ermöglicht und organisiert durch Projekt DEAL.

    Formelzeichen

  1. A [m2]

  2. Oberfläche

  3. C [–]

  4. Instabilitätskonstante des Modells nach Henschke und Pfennig 44

  5. c [mol m−3]

  6. Stoffmengenkonzentration

  7. c* [–]

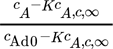
  8. dimensionloses Konzentrationsverhältnis, urn:x-wiley:0009286X:media:cite202000246-math-0020

  9. D [m2s−1]

  10. Diffusionskoeffizient

  11. D* [–]

  12. dimensionsloses Diffusionskoeffizientenverhältnis, DAD/DAc

  13. d [m]

  14. Durchmesser

  15. Fod [–]

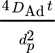
  16. Fourierzahl (dispersseitig), urn:x-wiley:0009286X:media:cite202000246-math-0021

  17. g [m s−2]

  18. Erdbeschleunigung

  19. K [–]

  20. Verteilungskoeffizient

  21. k [m s−1]

  22. Stoffdurchgangskoeffizient

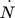  23. urn:x-wiley:0009286X:media:cite202000246-math-0022 [mol s−1]

  24. Stoffstrom

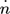  25. urn:x-wiley:0009286X:media:cite202000246-math-0023 [mol m−2s−1]

  26. spezifischer Stoffstrom

  27. Pe [–]

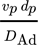
  28. Pecletzahl, urn:x-wiley:0009286X:media:cite202000246-math-0024

  29. R [m]

  30. Radius

  31. R [–]

  32. effektive Diffusivität

  33. r [m]

  34. radiale Koordinate

  35. Re [–]

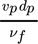
  36. Partikel-Reynoldszahl, urn:x-wiley:0009286X:media:cite202000246-math-0025

  37. Shc [–]

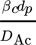
  38. Sherwoodzahl der kontinuierlichen Phase, urn:x-wiley:0009286X:media:cite202000246-math-0026

  39. Shd [–]

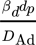
  40. Sherwoodzahl der dispersen Phase, urn:x-wiley:0009286X:media:cite202000246-math-0027

  41. Shk [–]

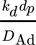
  42. Sherwoodzahl des konjugierten Problems, urn:x-wiley:0009286X:media:cite202000246-math-0028

  43. T [°C]

  44. Temperatur

  45. t [s]

  46. Zeit

  47. v [m s−1]

  48. Geschwindigkeit

  49. v* [–]

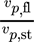
  50. dimensionsloses Geschwindigkeitsverhältnis, urn:x-wiley:0009286X:media:cite202000246-math-0029

  51. We [–]

  52. Weberzahl, urn:x-wiley:0009286X:media:cite202000246-math-0030

    53. Griechische Symbole

  53. α [–]

  54. Parameter des Modells nach Henschke 29

  55. β [m s−1]

  56. Stoffüberganskoeffizient

  57. γ [–]

  58. Gewichtungsfaktor des Modells nach Weber et al. 32

  59. γ [N m−1]

  60. Grenzflächenspannung

  61. δ [m]

  62. Grenzschichtdicke

  63. η [Pa s]

  64. dynamische Viskosität

  65. η* [–]

  66. dimensionsloses Viskositätsverhältnis, ηd/ηc

  67. ν [m2s−1]

  68. kinematische Viskosität

  69. ζ [–]

  70. Widerstandsbeiwert

  71. ρ [kg m−3]

  72. Dichte

    73. Indizes

  73. A

  74. Komponente A

  75. c

  76. kontinuierliche Phase

  77. d

  78. disperse Phase

  79. f

  80. Fluid

  81. fl

  82. fluid

  83. k

  84. konjugiert

  85. krit

  86. kritischer Wert

  87. p

  88. Partikel

  89. um

  90. Umschlag zwischen starrer und fluider Partikel

  91. st

  92. starr

  93. 0

  94. Anfangswert für t = 0

  95. 1

  96. Zeitpunkt

  97. 2

  98. Zeitpunkt

  99. 15

  100. Niveau der Geschwindigkeit oszillierender Partikel

  101. 16

  102. Übergang viskoser zu grenzflächendominierter Bereich

  103. I

  104. Interface/Wert an der Phasengrenzfläche

  105. ∞

  106. außerhalb der Grenzschicht/Bulk

    107. Abkürzungen

  107. AP

  108. Außenproblem

  109. IP

  110. Innenproblem

  111. SDS

  112. Natriumdodecylsulfat

    • 1) Feng und Michaelides 13 führen eine Übergangsfunktion zwischen zwei gängigen Widerstandsgesetzen für Blasen und starre Partikel ein, um den gesamten Bereich der Viskositätsverhältnisse von 0 < η* < ∞ abzudecken. Bei dem auf Moore 51 basierenden Gesetz für Blasen hat sich in 13 und folglich in diversen sich darauf beziehenden Publikationen ein Vorzeichenfehler eingeschlichen. 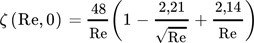Die korrekte Form des Widerstandsgesetzes für Blasen, das im Fall η* ≤ 2 Anwendung findet, lautet in Anlehnung an 51 und 28: urn:x-wiley:0009286X:media:cite202000246-math-0002.
    • 2) 40 führen basierend auf dem Modell nach Vermeulen 52 eine empirische Korrelation ein, bei der R das Verhältnis zwischen effektiver und molekularer Diffusion beschreibt. Eine gute Übereinstimmung mit den Modellen nach Newman 39 für den dispersseitigen Stofftransportwiderstand für starre Partikel und Kronig und Brink 41 für die fluide Partikel mit idealer innerer Zirkulation ergibt sich für R = 1 bzw. R = 2,25. Durch die innere Zirkulation ergibt sich folglich eine Intensivie„rung der molekularen Diffusion um den Faktor 2,25.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.