Chemie Ingenieur Technik
Volume 93, Issue 5 pp. 789-795
Communication
Open Access

Simulation of Fluid Flow During Direct Synthesis of H2O2 in a Microstructured Membrane Reactor

Laura L. Trinkies, 

Corresponding Author

Laura L. Trinkies

Karlsruhe Institute of Technology, Institute for Micro Process Engineering (IMVT), Hermann-von-Helmholtz-Platz, 76344 Eggenstein-Leopoldshafen, Germany

Correspondence: Laura L. Trinkies ([email protected]), Karlsruhe Institute of Technology, Institute for Micro Process Engineering (IMVT), Hermann-von-Helmholtz-Platz, 76344 Eggenstein-Leopoldshafen, Germany.Search for more papers by this author
Andrea Düll, 

Andrea Düll

Karlsruhe Institute of Technology, Institute for Micro Process Engineering (IMVT), Hermann-von-Helmholtz-Platz, 76344 Eggenstein-Leopoldshafen, Germany

Search for more papers by this author
Benedikt J. Deschner, 

Benedikt J. Deschner

Karlsruhe Institute of Technology, Institute for Micro Process Engineering (IMVT), Hermann-von-Helmholtz-Platz, 76344 Eggenstein-Leopoldshafen, Germany

Search for more papers by this author
Alexander Stroh, 

Alexander Stroh

Karlsruhe Institute of Technology, Institute of Fluid Mechanics (ISTM), Kaiserstraße 10, 76131 Karlsruhe, Germany

Search for more papers by this author
Manfred Kraut, 

Manfred Kraut

Karlsruhe Institute of Technology, Institute for Micro Process Engineering (IMVT), Hermann-von-Helmholtz-Platz, 76344 Eggenstein-Leopoldshafen, Germany

Search for more papers by this author
Roland Dittmeyer, 

Roland Dittmeyer

Karlsruhe Institute of Technology, Institute for Micro Process Engineering (IMVT), Hermann-von-Helmholtz-Platz, 76344 Eggenstein-Leopoldshafen, Germany

Karlsruhe Institute of Technology, Institute of Catalysis Research and Technology (IKFT), Hermann-von-Helmholtz-Platz 1, 76344 Eggenstein-Leopoldshafen, Germany

Search for more papers by this author
First published: 19 March 2021
https://doi.org/10.1002/cite.202000232
Citations: 5

Abstract

A microstructured membrane reactor has been developed to overcome the safety and productivity challenge of the direct synthesis of hydrogen peroxide. A single membrane is employed for separate, continuous dosage of the gaseous reactants hydrogen and oxygen to the solid catalyst present in the aqueous solvent. Using a custom OpenFOAM® model, the impact of catalyst-coated static mixers with different mixer geometries is studied. It is demonstrated that the custom fluid guiding elements outperform the investigated commercial static mixer under the flow conditions relevant to this application.

1 Introduction

Hydrogen peroxide (H2O2) is a promising “green” oxidant with application in paper, pulp and also wastewater treatment 1. The most common production route for H2O2 today uses the anthraquinone auto-oxidation process 2, responsible for more than 95 % of the total H2O2 production 3. With its high capital expenditures and required wastewater treatment 4, the process is currently only implemented at large scale, since it relies on the economy of scale to achieve viability 5. An alternative reaction route is the direct synthesis of H2O2 by selective conversion of H2 and O2 over a solid catalyst 6, 7. Different combinations of active material, support and reaction medium for the direct synthesis of H2O2 exist, with an extended overview given in 5. Nevertheless, all reaction systems studied for the direct synthesis route are facing the same safety concerns resulting from the direct contact of hydrogen and oxygen given the wide flammability range of the mixture 8, 9.

One of the approaches to cope with this issue are membrane reactors 9, 10. They prevent direct hydrogen/oxygen contact by dosing one or both reactants through a membrane into an organic or inorganic solvent, which contains the solid catalyst 6, 10-12. The major challenge in this kind of reactor is the development of a robust membrane 13. Another concept to tackle the safety concerns are microreactors. Their narrow channels hinder the propagation of an explosion and therefore massively increase the range of safe operation 14. The reactor concept presented in this paper combines both reactant separation with a membrane as well as microfluidic flow synergistically, targeting a new technology for on-site synthesis of ready-to-use hydrogen peroxide solutions 6, 15.

In order to decrease the diffusion length at any fluid velocity contrary to suspension flow catalysis 6, we investigated catalytically coated inserts in the flow channels. Specifically, we used the design of so-called fluid guiding elements (FGEs), recently developed in our institute 16. The impact of the inserts was investigated numerically in a CFD simulation using OpenFOAM® (OF) 17. Special attention is given to the impact of the residence time and channel insert geometry on the reaction.

2 Materials and Methods

2.1 Design of the Membrane Reactor

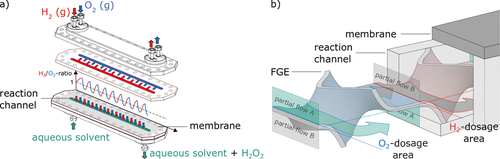
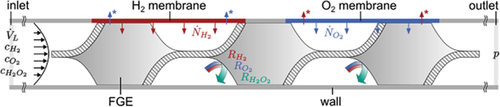
Fig. 1a illustrates the reactor concept, which was adapted from an earlier reaction module designed in our institute 6. The FGEs are produced using an additive manufacturing technology (laser-beam powder bed fusion, LB-PBF) which places some restrictions on the geometry, in particular avoiding overhangs 18. For this reason, the curvilinear liquid channel design introduced by Selinsek et al. 6 was altered to a straight geometry while the gaseous reactants hydrogen and oxygen were introduced in an alternating manner over the dosing membrane, as illustrated in Fig. 1b. The FGEs do not generate turbulence but aim for a laminar guiding of the fluid flow to keep the pressure drop low by smart division and recombination of the flow and generated partial flows, respectively 16. After partial flow A had contact with the mass transferring region for resaturation, the O2- or H2-dosage area in Fig. 1b, it is directly guided away from the place of exchange to the channel bottom to equilibrate. Then, the next equilibrated partial flow B is led to the region of transfer. The contact time of the fluid with the gas was kept short to keep the diffusion depth of the resaturating gas considerably small in order to guarantee a large concentration gradient and thereby enhance the mass transfer. The same principle has previously been described for heat transfer .

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Sketch of the microstructured membrane reactor for the direct synthesis of H2O2 with gas resaturation, adapted with permission from Ref. 15 (a) and detailed scheme of the arrangement of a FGE in a microchannel covered by a PDMS membrane, adapted with permission from Ref. 34 (b).

2.2 Material Properties

The transport and material properties are summarized in Tab. 1, with all properties corresponding to a temperature of 298 K (simulations were run at this temperature, and future experiments will be conducted at this temperature). The influence of the additives H2SO4 and NaBr on the fluid properties of the aqueous reaction medium were neglected. Similarly, due to the low solute concentrations expected, it was assumed that the dissolved species H2, O2 and H2O2 did not alter the fluid properties. Only binary diffusion of the individual solutes in the liquid reaction medium as described by the Fickian diffusion model was considered. The simple solution diffusion model, as described in 19, was used to model the mass transport through the dense polymer membrane.

Table 1. Transport and material properties at 298 K.

Property

H2

O2

H2O2

H2O

Reference

Di,H2O [m2s−1]

3.894 · 10−9

2.488 · 10−9

2.298 · 10−9

–

20

νH2O [m2s−1]

–

–

–

8.927 · 10−7

21

Hi [mol m−3Pa−1]

7.800 · 10−6

12.000 · 10−6

–

–

22

Ρi [mol m−2s−1Pa−1]

1.77 · 10−7

1.12 · 10−7

0

0

23
A 5-wt % Pd/TiO2 catalyst was chosen as model catalyst for this study applied as a coating onto the microstructured channel inserts. This palladium loading is among the highest reported for defined nanocatalysts 24 and was therefore selected for an enhanced but realistic reactor productivity. Since the kinetics are yet to be determined in a purely aqueous reaction medium containing 0.15 mol m−3 H2SO4 and 4 mol m−3 NaBr, the numerical simulation adapted the kinetic model from Voloshin et al. 25-28 for a system with close resemblance to the specific combination of catalyst and reaction medium present. The adapted kinetic rate expressions considered in the numerical simulation are presented in Eqs. 1 and 5 with the adapted constants given in Eqs. 2–4 and (6)–(8) 25-28.
urn:x-wiley:0009286X:media:cite202000232-math-0001()
with
urn:x-wiley:0009286X:media:cite202000232-math-0002()
urn:x-wiley:0009286X:media:cite202000232-math-0003()
urn:x-wiley:0009286X:media:cite202000232-math-0004()
urn:x-wiley:0009286X:media:cite202000232-math-0005()
with
urn:x-wiley:0009286X:media:cite202000232-math-0006()
urn:x-wiley:0009286X:media:cite202000232-math-0007()
urn:x-wiley:0009286X:media:cite202000232-math-0008()

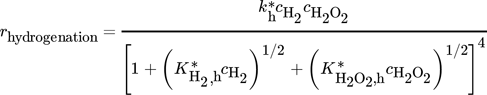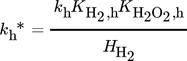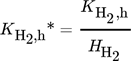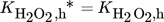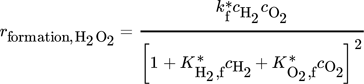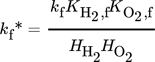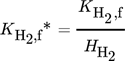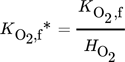Moreover, a layer thickness of 4 µm with a porosity ε of 0.4 and tortuosity τ of 6, reported for silica coatings employed in the direct synthesis was assumed for all simulated structures 29. Although Gemo et al. 30 provided the experimental proof of negligible internal mass transfer limitations within a comparable operation range for a spherical catalyst of 15 µm diameter, the impact of mass transfer limitations within the catalyst coating layer on the macroscopic reaction rates of the direct synthesis of H2O2 was considered by effectiveness factors. This allowed further studies of a wider catalyst layer range. The effectiveness factors were calculated using Matlab®. All kinetic parameters used are listed in Tab. 2 and 3.

Table 2. Kinetic constants of the proposed rate expressions: pre-exponential factors k0 and sorption equilibrium constants Ki at system temperature according to 25, 27; subscripts: h for the hydrogenation reaction path and f for the H2O2 formation reaction path.

Property

Value

k0,h [molH2O2kgcat−1s−1]

25.57 · 106

K0,H2,h [Pa−1]

3.36 · 10−10

K0,H2O2,h [m3mol−1]

2.95 · 10−4

k0,f [molH2O2kgcat−1s−1]

1.60 · 103

K0,H2,f [Pa−1]

2.76 · 10−4

K0,O2,f [Pa−1]

3.38 · 10−8

Table 3. Kinetic constants of the proposed rate expressions: activation energy Ea and reaction enthalpy ΔHi according to 25, 27; subscripts: h for the hydrogenation reaction path and f for the H2O2 formation reaction path.

Property

Value

Ea,h [kJ mol−1]

43.7

ΔHH2,h [kJ mol−1]

−23.1

ΔHH2O2,h [kJ mol−1]

−4.7

Ea,f [kJ mol−1]

22.3

ΔHH2,f [kJ mol−1]

10.1

ΔHH2O2,f [kJ mol−1]

−12.2

2.3 Numerical Model of the Reactor

OF provides a finite-volume-based framework for the creation of custom computational solvers for continuum mechanics problems 17. The CAD model of the FGEs generated in Autodesk® Inventor® was used via STL format import to create the numerical grid using OF meshing tools. The simulation domain consisted of a rectangular channel, which contained the microstructured FGE inserts. The channel used for the investigations had a width of 6 mm, a height of 1.97 mm and a length of 44.5 mm. Additional inlet and outlet zones of 11 mm length each were implemented in order to guarantee a fully developed flow. These zones equal the maximum expected hydrodynamic entrance length calculated analytically.

In the simulation, the flow regime present in the liquid channel was assumed to be laminar, due to the low liquid flow rates in the range of milliliters per minute as used in the concept presented in 6 and 15 as well as channel geometries in the millimeter range. The maximum expected Reynolds number Re calculated in a void rectangular channel with a width of 6 mm and a height of 1.97 mm for an estimated, elevated flow rate of 16 mL min−1 was 75, which confirmed the validity of this assumption. Moreover, the system was considered isothermal and the flow field incompressible due to the nature of the aqueous reaction medium under the conditions given.

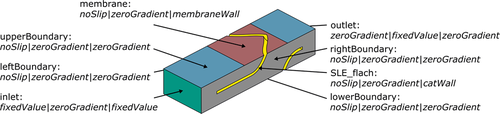
Three phases are present in the actual reactor, namely the gaseous H2 and O2 flowing through separate reactor channels, the solid membrane and the solid catalyst applied onto microstructured FGEs as well as the liquid reaction medium. To simplify the problem, a single-phase model was adopted for the simulation by merely considering the liquid phase with the dissolved reactants and the product. Thus, the membrane and the catalyst coating were defined as system boundaries. Moreover, it was assumed that the feeding gas phases remain constant in their composition, even in case of possible cross-contamination of the H2-gas channel with O2 by desaturating gas and vice versa. This is justified in case of the gas channels being flushed sufficiently and permanently with the corresponding pure gas. Fig. 2 shows a schematic representation of the simulated geometry. The implemented patches of the simulation and the applied boundary conditions can be taken from Fig. 3.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Schematic representation of the simulated geometry, showing the boundaries, fixed quantities and species flows across the system boundaries; transmembrane flows causing H2/O2 cross-contamination indicated with an asterisk (*).
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Boundary conditions applied to velocity (U) | pressure (p) | concentration (c) fields at the different patches.

OF's blockMesh utility was used for the background mesh, while snappyHexMesh was used to generate the computational grid so that the FGE features were captured correctly and high gradient regions were resolved particularly well. Mass diffusion processes impose much stricter constraints on mesh resolution than fluid dynamics 31. Thus, at least three cell layers were used within the concentration boundary layer to ensure the proper capture of concentration gradients and mass transport phenomena as recommended by Bothe and Reusken 31. Correspondingly, three additional grid layers were added within a distance of 0.03 mm, which is lower than the expected minimum concentration boundary layer thickness estimated from mass transfer correlations. To ensure sufficient grid refinement, different grid resolutions were investigated and their maximum residuals as well as the resulting maximum species imbalances were evaluated as control quantities. The acceptable residual for a stable result was set to 1 · 10−4 for the concentration. The errors obtained from mass and individual species balances applied to the overall system had to be below the threshold of 1 %. A grid of 7 million cells of an average size of 10−13 m−3 was finally used in the simulation.

To evaluate the velocity, the iterative solver smoothSolver with symmetric Gauss-Seidel smoother (symGaussSeidel) was used in OF to solve the conservation of mass equation (Eq. 9) for an incompressible fluid with the nabla operator ∇ (Eq. 10).
urn:x-wiley:0009286X:media:cite202000232-math-0009()
urn:x-wiley:0009286X:media:cite202000232-math-0010()
For the pressure, on the other hand, the iterative solver GAMG with Gauss-Seidel smoother (GaussSeidel) was employed to solve the momentum conservation equation (Eq. 11) under the assumption of incompressible flow, constant dynamic viscosity μ and absence of volume forces.
urn:x-wiley:0009286X:media:cite202000232-math-0011()
To solve the species conservation equation (Eq. 12) for the concentration, PBiCGStab with diagonal-based incomplete LU preconditioner (DILU) was used.
urn:x-wiley:0009286X:media:cite202000232-math-0012()
In order to include the description of the catalyst-coated FGEs, a Neumann boundary condition catWall derived from the OF class fixedGradientFvPatchFields was implemented. During the evaluation of the species conservation equation, the catWall boundary face concentrations were then determined from the corresponding values at the cell centroid and the previously calculated effective reaction rates as formulated in Eq. 13 and (14)
urn:x-wiley:0009286X:media:cite202000232-math-0013()
with
urn:x-wiley:0009286X:media:cite202000232-math-0014()
At every face belonging to a membraneWall patch, the boundary face value ci,bf was calculated from the cell value in dependence of the species's partial pressure in the gas phase pi,G, the membrane permeance Ρi, properties such as the Henry constant Hi and diffusion coefficient Di as well as the cell's face-to-center distance δbf-c according to Eq. 15.
urn:x-wiley:0009286X:media:cite202000232-math-0015()

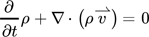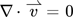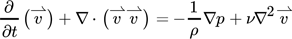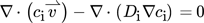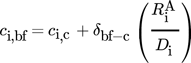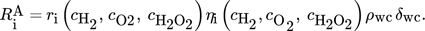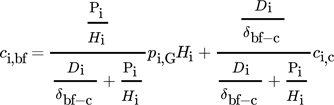The derived solver was verified by the comparison with the (semi-)analytical solutions of three different configurations of a simplified, cylindrical channel geometry evaluated using Matlab®.

2.4 Considered Case: Influence of the Geometry of the Microstructured Channel Insert on Reactor Performance

As the catalyst is applied as a coating onto the microstructured channel inserts, the inserted structure's geometry is expected to have a considerable influence on the reactor performance. This was investigated by carrying out CFD simulations with two different geometries of mixing inserts. A commercial static mixer (SMX®, from Sulzer AG, Winterthur, Switzerland) with a geometry adapted from 32 was compared with a customized FGE developed in our institute. While the inserts' overall widths, heights and lengths are identical, the surface area of SMX® available for the application of catalyst exceeds the FGE's surface area with an area ratio SSMX/SFGE of 2.27. Similarly, the volume reduction of the liquid flow channel due to the inserted structure was higher in case of the SMX® resulting from its slightly bigger volume. This leads to a volume ratio of the resulting liquid volumes of VL,SMX/VL,FGE = 0.94. The influence of the volumetric flow rate was evaluated by carrying out simulations with both geometries over range between 0.7 and 15.9 mL min−1. The system pressure and temperature were set to 2 bar and 298 K. In all simulations, a membrane arrangement of alternating H2 and O2 dosing zones of 2 mm length each and a distance of 1.27 mm in between was chosen.

3 Results and Discussion

A comparison of the pressure drop over the length of the liquid flow channel for the case of no insert, the SMX® insert and FGE insert is shown in Fig. 4. At low residence times (corresponding to higher flow velocities) the pressure drop for SMX® inserts is significantly higher than for FGE inserts. At higher residence times, the difference between the pressure drop for SMX® versus FGE is smaller. The calculated H2O2 outlet concentrations cH2O2,out achieved with the two different types of microstructured channel inserts are compared in Fig. 5a. Fig. 5b shows the comparison of the H2O2 outlet concentrations cH2O2,out per surface area of the respective insert Sinsert. As a reference, the corresponding values for a void channel without inserts but with catalyst coated lower and side walls are given additionally in all graphs.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
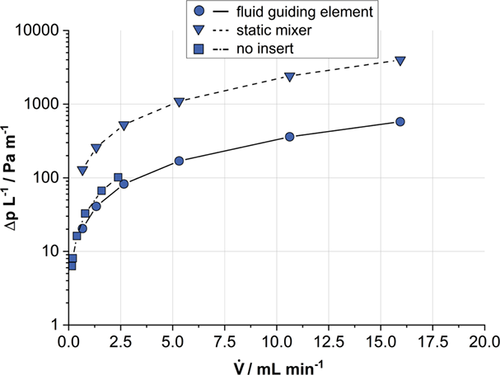
Pressure drop Δp over the length of the reactor as a function of the volumetric flow rate urn:x-wiley:0009286X:media:cite202000232-math-0016 with the 45 mm long SMX® and FGE serving as channel inserts at 2 bar and volume flows between 0.7 and 15.9 mL min−1.

At all investigated modified residence times (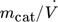urn:x-wiley:0009286X:media:cite202000232-math-0017), the performance of the reactor with SMX® inserts in terms of cH2O2,out appears to be superior to the one with FGE inserts (Fig. 5a). This is to be attributed to the SMX's higher surface area and the corresponding increased amount of catalyst present in the system, the H2O2 outlet concentration ratio cH2O2,SMX/cH2O2,FGE exceeds the surface area ratio SSMX/SFGE at all residence times. This may be explained by an enhancement of the SMX's mixing properties at increased liquid velocities in the laminar flow regime, which is consistent with findings of Rahmani et al. 33. On the other hand, the FGE is beneficial in terms of the overall pressure drop (Fig. 4) over the length of the liquid flow channel as the structure does not contain any abrupt changes in its geometry and thus imposes less resistance to the liquid flow 16. It can also be seen from Fig. 5b that the achieved H2O2 outlet concentration relative to the insert's surface area of the FGE (i.e., the productivity per catalyst mass) is even significantly higher than the one of the SMX® at all residence times. With H2O2 hydrogenation as consecutive reaction path in the reaction network, comparably low residence times (high tmod) proved to be beneficial 15, which is why it may be concluded that the implementation of catalyst-coated FGEs has a beneficial effect on the reaction system.

Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Average product outlet concentration cH2O2,out in dependence of the modified residence time tmod. 45 mm long SMX® and FGE serving as channel inserts at 2 bar and volume flows between 0.7 and 15.9 mL min−1 (a). Influence of the geometry of the microstructured channel insert's geometry on the achieved cH2O2,out relative to the insert's surface area Sinsert under the same flow conditions (b).

4 Conclusion

In the simulations presented, the influence of the microstructured insert's geometry on the reactor performance quantified by the H2O2-outlet concentration cH2O2,out was investigated at different volumetric flow rates by comparing a FGE insert with a standard SMX® at different flow rates. Higher product concentrations in general were found to be achieved with the latter. This is attributed to the static mixer's higher surface area and therefore high amount of catalyst present in the system. The use of FGEs, however, is beneficial in terms of pressure drop at lower residence times and higher productivity relative to a defined catalyst mass is achieved.

To conclude, the basis has been laid for the optimization of a microstructured membrane microreactor for the direct synthesis of H2O2 facilitated by spatially resolved CFD simulations. Further research will validate the implemented solver against experimental results, paving the way to a precise reaction control of this demanding multiphase reaction.

Acknowledgements

Financial support by the German Research Foundation (DFG) through the Research Unit 2383 ProMiSe under Grant No. DI 696/13-2 is gratefully acknowledged. The authors acknowledge support by the state of Baden-Württemberg through bwHPC. Open access funding enabled and organized by Projekt DEAL.

    Symbols used

  1. Di,H2O [m2s−1]

  2. Fickian diffusion coefficient of gas i in H2O

  3. c [mol m−3]

  4. molar concentration

  5. ci,bf [mol m−3]

  6. concentration of the gas i at the boundary face

  7. ci,inlet [mol m−3]

  8. concentration of the gas i at the inlet of the simulated field

  9. ci,sat [mol m−3]

  10. saturation concentration of the gas i, according to Henry's law

  11. Hi [mol m−3Pa−1]

  12. Henry constant of gas i

  13. ΔHi [J mol−1]

  14. reaction enthalpy

  15. K [Pa−1]

  16. sorption equilibrium constant

  17. k [–]

  18. kinetic rate constant

  19. k0 [–]

  20. pre-exponential factor (reaction rate)

  21. L [m]

  22. length

  23. mcat [g]

  24. catalyst mass

  25. pi [Pa]

  26. partial pressure of gas i

  27. Ri [–]

  28. rate of generation or destruction of species i due to chemical reactions

  29. r [mol s−1kg−1]

  30. reaction rate per catalyst mass

  31. T [K]

  32. temperature

  33. tmod [gcoats mL−1]

  34. modified residence time

  35. SSMX/FGE [m2]

  36. surface area of the inserts (SMX®/FGE)

  37. Sinsert [m2]

  38. surface area of the respective insert

  39. v [m s−1]

  40. velocity

  41. VL,SMX/FGE [m−3]

  42. volume in the liquid channel after implementing the insert (SMX®/FGE)

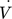  43. urn:x-wiley:0009286X:media:cite202000232-math-0018 [mL min−1]

  44. volumetric flow rate

    45. Greek letters

  45. δ [m]

  46. distance, thickness

  47. ε [–]

  48. porosity

  49. η [–]

  50. catalyst effectiveness factor

  51. μ [Pa s]

  52. dynamic viscosity

  53. νH2O [m2s−1]

  54. kinematic viscosity of H2O

  55. τ [–]

  56. tortuosity

  57. ρ [kg m−3]

  58. material density

  59. Ρi [mol m−2s−1Pa−1]

  60. membrane permeance of gas i

    61. Sub- and Superscripts

  61. A

  62. per unit area

  63. bf

  64. boundary face

  65. c

  66. center

  67. G

  68. gas

  69. H2

  70. hydrogen

  71. H2O2

  72. hydrogen peroxide

  73. L

  74. liquid

  75. O2

  76. oxygen

  77. wc

  78. wallcoat

  79. *

  80. adapted property

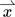
  81. urn:x-wiley:0009286X:media:cite202000232-math-0019

  82. vector quantity x

    83. Abbreviations

  83. FGE

  84. fluid guiding element

  85. PDMS

  86. polydimethylsiloxane

  87. PET

  88. polyethylene terephthalate

  89. PI

  90. polyimide

  91. OF

  92. OpenFoam®

      93. The full text of this article hosted at iucr.org is unavailable due to technical difficulties.