Trennfunktion für den stationären Siebprozess
Grade Efficiency Function for the Stationary Screening Process
Abstract
deEs wird eine neue Trennfunktion T(x, α′, β) für den stationären Siebprozesses vorgestellt. Sie ist eine Funktion der Partikelgröße x, der Trennschärfe α′ und der neue eingeführten Trenneffizienz β. Mit der neuen Trennfunktion kann der Siebklassierprozess sehr gut beschrieben werden, insb. im Fein- und Grobgutbereich ist eine sehr gute Übereinstimmung mit den Messwerten zu beobachten. Ein Vergleich der Trennfunktionen berechnet mit dem Trennschärfeparameter α′ und der Trenneffizienz β zu den Trennfunktionen, die nur mit α′ ermittelt wurden, zeigt, dass durch T(x, α′, β) eine wesentliche Verbesserung der Charakterisierung des stationären Siebklassierprozesses möglich ist. Das neue Modell der Trennfunktion T(x, α′, β) liefert eine wesentlich bessere Übereinstimmung mit den Messwerten als andere Modelle und ist somit zur Beschreibung einer Trennfunktion für den stationären Siebprozess sehr gut geeignet ist.
Abstract
enA new grade efficiency function T(x, α′, β) for the stationary screening process is presented. It is a function of particle size x, separation sharpness α′, and the newly introduced separation efficiency β. With this new grade efficiency, the screening classification process can be described exactly. Especially in the fine and coarse material range, a very good correlation with the measured values can be observed. A comparison of the grade efficiency function with separation sharpness α′, separation efficiency β and only with the measure for separation efficiency has shown that the new grade efficiency allows a significant improvement in the characterization of the stationary screen classification process. The new model of the grade efficiency function T(x, α′, β) shows a significant higher correlation with the measured values compared to other models, and is therefore very well suited to describe a grade efficiency for the stationary screening process.
1 Einleitung
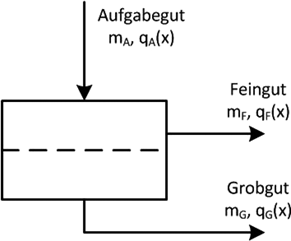
Die Siebtechnologie ist eine verfahrenstechnische Grundoperation, die in sehr vielen Prozessen angewandt wird. Je nach Zielsetzung unterscheidet man drei unterschiedliche Anwendungsfelder. Die Schutzsiebung ist ein Prozess zur Entfernung von Verunreinigungen, Fremdkörpern oder groben Fehlchargen aus dem Produkt. Bei diesem Siebprozess sind die Siebgutpartikel deutlich kleiner als die Maschenweite w > xmax. Die Entstaubungssiebung dient zur Trennung von vor allem zu feinen Partikeln in einem Produkt. Bei diesem Prozess muss die kleinste Produktpartikelgröße wesentlich größer als Maschenweite xmin > w sein. Im Rahmen dieser Arbeit wird vorwiegend der Siebklassierprozess betrachtet. Die Siebklassierung dient zur Separation von Produktströmen mit breiten Partikelgrößenverteilungen in zwei oder mehrere Größenklassen (Abb. 1). Kennzeichnend für diesen Prozess ist die gleiche Größenordnung der Partikelgröße x und der Maschenweite w der Siebe (x ∼ w). Bei diesem Prozess wird ein disperses Partikelkollektiv über eine bewegte Oberfläche transportiert und durch ein Sieb getrennt. Für diesen Trennvorgang müssen zwei Voraussetzungen erfüllt sein. Die Partikel müssen auf ihrem Weg über den Siebboden die Gelegenheit haben, sich über einer Sieböffnung anzuordnen und es muss eine hinreichend große Kraft vorhanden sein, die das Partikel durch die Sieböffnung befördert. Die Möglichkeit, dass sich die Partikel über einer Sieböffnung anordnen können, hängt u. a. entscheidend von der Schichtdicke des Siebgutes auf dem Sieb ab. Bei einer Dickschichtsiebung muss durch Auflockerung oder Umwälzung des Siebgutes die erforderliche Relativbewegung der Partikel gewährleistet werden. Bei einer Dünnschichtsiebung hingegen hängt die Kinetik des Siebvorgangs nur von den Bedingungen ab, die die Partikeln für das Passieren der Sieböffnungen vorfinden. Hier ist die Transportgeschwindigkeit, die Sieblänge und somit die Verweilzeit maßgeblich für den Trennerfolg verantwortlich. Während dieses Vorgangs erfolgt ein ständiger geometrischer Vergleich der Partikelgröße x des Aufgabegutes mit der Maschenweite w des Siebbodens. Bei einem erfolgreichen Transport der Partikel durch die Siebmasche erfolgt eine Trennung des Aufgabegutes in eine Fraktion Grobgut (g) und eine Feingutfraktion (f).
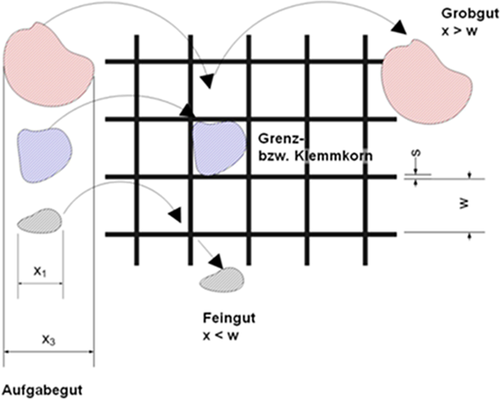
Ob und mit welcher Wahrscheinlichkeit ein Partikel eine Sieböffnung passiert, hängt insbesondere von dem Verhältnis der Partikelgröße zur Maschenweite (x/w), der Partikelform, der Maschenform, der Orientierung des Partikels zum Kontaktzeitpunkt und dem Auftreffwinkel gegenüber der Siebebene ab. Abb. 2 zeigt schematisch die Verhältnisse bei der Korrespondenz eines Partikels der Größe x mit der Siebmasche. Für den Sieberfolg ist das im Aufgabegut vorhandene Grenzkorn (x ∼ w) von besonderer Bedeutung.
Die Qualität eines Siebprozesses wird neben den Parametern des Aufgabegutes, wie die Partikelgrößenverteilung QA(x), Partikelform und -dichte sowie dem Wechselwirkungspotenzial des dispersen Systems, auch durch die Masse des Aufgabegutes, die Art der verwendeten Siebmaschine und die Ausführung der Siebe (z. B. die Maschenweite oder die offene Siebfläche) bestimmt. Der Erfolg einer Siebklassierung wird durch die Trennfunktion T(x) bzw. durch die Trennschärfe gekennzeichnet 1, 2.
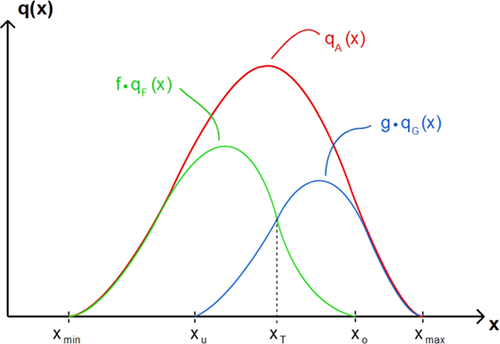
Mit einem Siebklassierprozess kann in der Regel keine ideale Klassierung realisiert werden. Ein gewisser Anteil der Partikel des Aufgabegutes mit x < w bleibt auf dem Sieb zurück und befindet sich somit im Grobgut und ein weiterer Anteil größerer Partikel kann z. B. durch Ausbildungsfehler der Sieböffnungen als Überkorn ins Feingut gelangen. Dieser Anteil an Partikeln wird als Fehlkorn (Fehlunterkorn oder Fehlüberkorn) bezeichnet (s. Abb. 3).
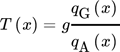 ()
()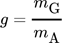 ()
()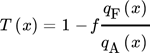 ()
()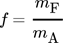 ()
()Die Trennfunktion T(x) liegt im Wertebereich 0 ≤ T(x) ≤ 1 und charakterisiert das Trennverhalten eines Klassierapparates.
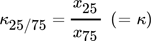 ()
()Zur Charakterisierung einer Trennung müssen im Vorfeld die Verteilungssummenfunktionen für das Aufgabegut Q3,A(x), das Grobgut Q3,G(x) oder das Feingut Q3,F(x) sowie die Massenströme ermittelt werden.
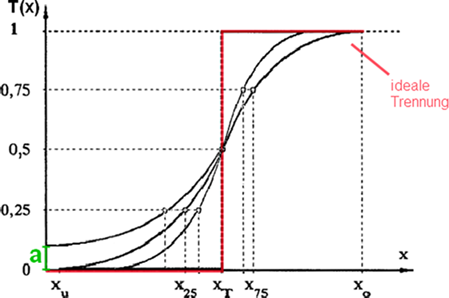
2 Trennfunktionen für den stationären Siebprozess
Zur Beurteilung von Siebklassierprozessen ist die Kenntnis der Trennfunktion T(x) des Prozesses ein sehr wichtiger Bestandteil 3, 4. Aus der Literatur sind einige wenige Modelle zur Beschreibung einer Trenncharakteristik bekannt. Beispielhaft seien hier folgende Trennfunktionen genannt.
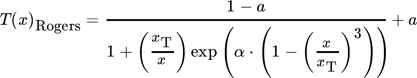 ()
()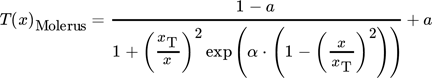 ()
() ()
()-
a: toter Fluss, Funktionswert für T(x = 0); es gilt: 0 ≤ a ≤ 1
-
α: Maß für die Trennschärfe; es gilt 0 < α < ∞
-
xT: Trenngrenze, Medianwert der Trennfunktion, bei a = 0
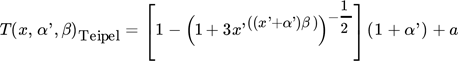 ()
()Hierin sind (wie oben beschrieben) a der tote Fluss und α′ ein Maß für die Trennschärfe (0 < α′ < ∞) sowie der neu eingeführte Parameter β, der ein Maß für die Trenneffizienz der Siebklassierung darstellt. Für β gilt: 0 < β < ∞.
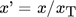 ()
()3 Material und Methode
Im Rahmen dieser Validierungsuntersuchungen der neuen Trennfunktion T(x,α′,β)Teipel wurden vier verschiedene Stoffsystem untersucht: Quarzpartikelfraktionen, zerkleinerter Kalkstein, Maisgrieß und Seramis Pflanzengranulat (s. Abb. 5).

Alle Partikelgrößenverteilungen der Aufgabegüter und der Fraktionen nach dem Siebklassierprozess wurden mittels Bildanalyse mit dem CamSizer der Firma Retsch gemessen. Abb. 6 zeigt die Partikelgrößenverteilungen der Aufgabegüter. Wie ersichtlich ist, wurden zwei Schüttgüter mit engerer Partikelgrößenverteilung und zwei Materialien mit sehr breiten Partikelgrößenverteilungen für die Untersuchungen ausgewählt.
Vor den Siebversuchen wurde die Grundgesamtheit mit einem Probeteiler entsprechend konditioniert. Die Siebversuche wurden jeweils mit einer entsprechenden Maschenweite mit zwei unterschiedlichen Amplituden (1 und 2,5 mm) auf einer Vibrationssiebmaschine der Firma Retsch bei drei Siebzeiten 1 min, 5 min und 10 min durchgeführt.
4 Ergebnisse
4.1 Die neue TrennfunktionT(x, α′, β)
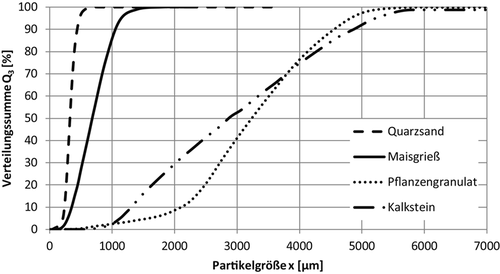
In Abb. 7 sind beispielhaft für das Material Quarz die Verteilungssummenfunktionen für das Aufgabegut, das Grob- und Feingut nach dem Siebprozess dargestellt.
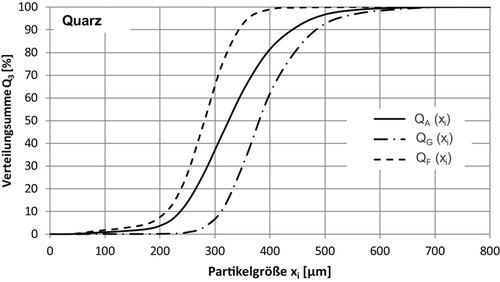
Abb. 8a–d zeigt die Messwerte der Siebversuche und die mit der neuen Funktionsgleichung (Gl. 9) berechneten Trennfunktionen T(x, α′, β). Die Berechnung der neuen Trennfunktion erfolgte auf Basis der jeweiligen Messwerte mit der Vorgabe, dass für den Funktionswert bei T(x = 0) der tote Fluss a = 0 gilt. Unter Berücksichtigung der Methode der kleinsten Fehlerquadrate werden die jeweiligen Trennfunktionen mit der Trennschärfe α′ und der neue eingeführte Trenneffizienz β berechnet. Zur Darstellung der Reproduzierbarkeit wurden jeweils 5 Messungen durchgeführt und berechnet. In Abb. 8a sind für das Stoffsystem Quarz die Ergebnisse der Versuche mit einer Amplitude von 1 mm und einer Siebzeit von 5 min dargestellt.
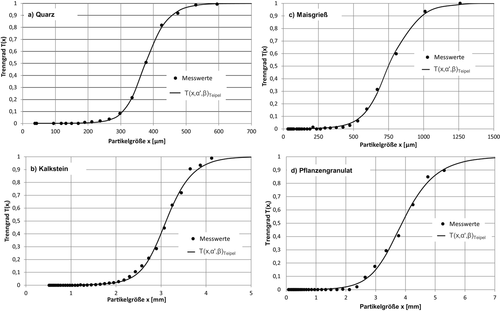
Wie Abb. 8a zeigt, ermöglicht die neue Funktion T(x, α′, β) (Gl. 9) eine exakte Berechnung der Trennfunktion dieses Siebklassierprozesses. Sowohl im Feingutbereich wie auch im Grobgutbereich lässt sich die Trennfunktion sehr genau ermitteln und basierend auf den Messdaten darstellen. Bei diesem Beispiel ergibt sich eine Fehlerquadratsumme von f 2 = 5,95 · 10−3. Die Trennschärfe berechnete sich in diesem Beispiel zu α′ = 0,1241 und die Trenneffizienz β zu β = 13,354. Die Trenngrenze xT ergibt sich in diesem Beispiel zu xT = 375,56 μm.
Die in Abb. 8b–d dargestellten Trennfunktionen T(x, α′, β) wurden ebenfalls alle mit einer Siebzeit von 5 min und bei einer Amplitude von 1 mm ermittelt. Auch Abb. 8b macht deutlich, dass die Trennfunktion T(x,α′,β) für den stationären Siebprozess den Prozess für dieses Partikelsystem sehr gut beschreiben kann. Die Fehlerquadratsummen lagen für alle Untersuchungen im Bereich 3 · 10−4 ≤ f 2 ≤ 7 · 10−2. Für das Beispiel der Kalksteinpartikel (Abb. 8b) ergab sich eine Trennschärfe von α = 0,0766, Trenneffizienz von β = 13,2934 und eine Trenngrenze xT = 3,113 mm. Dieses Ergebnis ist insbesondere von Bedeutung da sich zeigt, dass auch eine Siebklassierung von Stoffsystemen mit breiter Partikelgrößenverteilung des Aufgabegutes sehr gut mit der neuen Funktion beschrieben werden kann.
Für die Maisgrießproben (Abb. 8c) ergab sich eine Trennschärfe α′ = 0,27096, eine Trenneffizienz β = 8,29211 und eine Trenngrenze von xT = 0,7537 mm und für das Stoffsystem Pflanzengranulat (Abb. 8d) wurde eine Trennschärfe von α′ = 0,51974, eine Trenneffizienz von β = 6,1718 und eine Trenngrenze xT = 3,883 mm ermittelt.
Auch für diese Stoffsysteme, die sich durch unterschiedliche Partikelformen auszeichnen, in zwei verschieden Partikelgrößenbereichen liegen und eine deutlich unterschiedliche Dispersität aufweisen, können die Trennfunktionen T(x, α′, β) sehr gut dargestellt werden.
Zusammenfassend kann festgestellt werden, das der stationäre Siebprozess mit der neuen Trennfunktion T(x, α′, β) sehr gut beschrieben werden kann. Insbesondere im Feingutbereich ist eine sehr gute Übereinstimmung der berechneten Funktionen mit den Messwerten zu beobachten. Die gewählten Stoffsysteme weisen Partikelgrößen von unteren µm-Bereich bis in den Millimeterbereich und insbesondere engere und breite Größenverteilungen auf, was bedeutet, das die neue Trennfunktion unabhängig von dem Größenbereich der Partikelfraktionen und der Dispersität zur Beschreibung der Trenncharakteristik stationärer Siebprozesse eingesetzt werden kann.
4.2 Einfluss der Trenneffizienzβauf die Trennfunktion
Zur Ermittlung des Einflusses der Trenneffizienz β auf die Trennfunktion wurden basierend auf den Messwerten die Trennfunktionen T1(x, α′, β) gemäß Gl. 9 berechnet. Wie in Abschn. 4.1 wurde der tote Fluss a = 0 gesetzt. Für die Bestimmung der Funktion T2(x, α′) wurde ebenfalls die Berechnung der Trennfunktion nach Gl. 9 durchgeführt, aber der Wert für die Trenneffizienz β = 1 gesetzt. Abb. 9a zeigt das Ergebnis für das Partikelsystem Quarz. Die Siebzeit betrug hier ebenfalls t = 5 min und die Amplitude 1 mm.
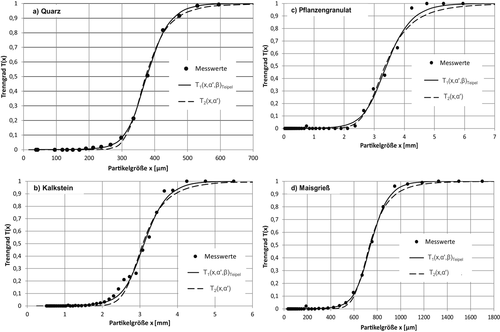
Es zeigt sich deutlich, dass sowohl im Feingutbereich zwischen xi1 ≈ 200 µm und xi2 ≈ 350 µm wie auch im Grobgutbereich zwischen xi3 ≈ 450 µm und xi4 ≈ 700 µm die Einführung der Trenneffizienz β einen wesentlichen Vorteil zur Beschreibung der Trennfunktion für den stationären Siebprozess bietet. Für dieses Beispiel ergibt sich nach der Trennfunktion T1(x, α′, β) eine Trennschärfe von α′1 = 0,1235 und eine Trenneffizienz von β1 = 13,3636. Bei der Funktion T2(x, α′) ergibt eine Trennschärfe von α′2 = 14,1615.
Für das Partikelsystem Kalkstein (Abb. 9b), das eine wesentlich größere Partikelgröße und eine breitere Partikelgrößenverteilung aufweist, ergibt sich eine nicht ganz so zufriedenstellende Beschreibung der Trennfunktion der Siebklassierung. Aber auch hier zeigt sich die deutlich verbesserte Beschreibung der Trennfunktion im Fein- und Grobgutbereich durch die neue Trennfunktion T1(x, α′, β). Die ermittelte Trennschärfe ergibt sich in diesem Beispiel zu α′1 = 0,0425 und die Trenneffizienz zu β1 = 13,3083. Bei der Funktion T2(x, α′) ergibt eine Trennschärfe von α′2 = 12,8771.
Für die beiden Systeme Pflanzengranulat und Maisgrieß (Abb. 9c und 9d) ergeben sich folgende Parameter: Für das Produkt Pflanzengranulat eine Trennschärfe von α′1 = 0,3348 und die Trenneffizienz von β1 = 8,4140. Bei der Funktion T2(x, α′) ergibt eine Trennschärfe von α′2 = 9,4618. Für die kleineren Maisgrießpartikel berechnet sich die Trennschärfe zu α′1 = 0,1554 und die Trenneffizienz zu β1 = 11,4851. Bei der Funktion T2(x, α′) ergibt eine Trennschärfe von α′2 = 11,7098.
In Abb. 9d ist zu beobachten, dass auch hier im Fein- und Grobgutbereich eine wesentlich bessere Charakterisierung des Siebklassierprozesses durch die neue Trennfunktion T(x, α′, β) möglich ist. Bei Verwendung der neuen Trennfunktion T(x, α′, β) ergeben sich für den Trennschärfeparameter α′ Werte im Bereich 0,04 ≤ α′1 ≤ 0.4 und Trenneffizienzparameter im Bereich 8 ≤ β ≤ 14. Hingegen ergaben sich Trennschärfeparameter bei Berechnung mit der Trennfunktion T2(x, α′) im Bereich von 8 ≤ α′2 ≤ 15. Durch die Einführung der Trenneffizienz β konnte eine deutliche Reduzierung der Summe der kleinsten Fehlerquadrate, teilweise um den Faktor 10, erreicht werden. Durch den Vergleich der Trennfunktionen bei Berücksichtigung des Parameters β und ohne die Trenneffizienz β konnte gezeigt werden, dass die neue Trennfunktion T(x, α′, β) eine wesentlich Verbesserung für die Charakterisierung des Siebklassierprozesses ermöglicht.
In Abb. 10 wurde am Beispiel der Messwerte des Stoffsystems Quarz bei konstantem Trennschärfeparameter α′ = 0,1241 der Einfluss des Trenneffizienzparameters β ermittelt. Die Trenneffizienz wurde in den Grenzen von 2 ≤ β ≤ 30 variiert.
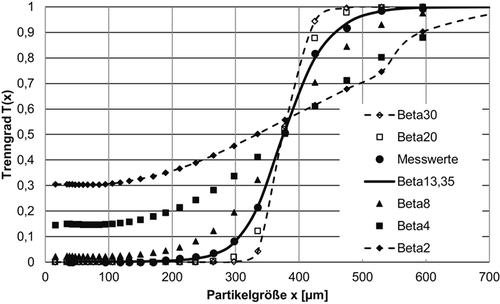
Es zeigt sich, dass bei kleinerem Trenneffizienzparameter β als der optimal berechnete Trenneffizienzparameter β ≤ 13,35 die Funktionen einen deutlich flacheren Verlauf aufweisen. Durch diese Funktionsverläufe würde ein toter Fluss simuliert. Die Funktionen mit einem Trenneffizienzparameter β ≥ 13,35 weisen einen steilen Funktionsverlauf mit schärferen Krümmungsradien als die wirkliche Trennfunktion auf.
4.3 Vergleich der Trennfunktionen
Die Trennfunktionen für den stationären Siebklassierprozess (s. Abschn. 2) sind bespielhaft für ein Stoffsystem in Abb. 11 dargestellt. Die Trennfunktionen wurden gemäß der verschiedenen Modelle nach Rogers (Gl. 6), Molerus (Gl. 7), Plitt (Gl. 8) und dem neu vorgestellten Modell T(x, α′, β) (Gl. 9) berechnet.
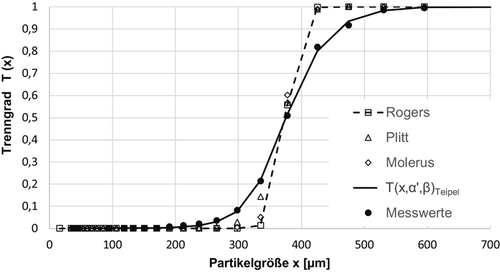
Für die Modelle von Rogers und Molerus ergeben sich sehr ähnliche Funktionsverläufe und für das Modell von Plitt wird ein geringfügig anderer Verlauf dargestellt. Alle diese Modelle zeigen keine Übereinstimmung mit den Messwerten. Im Feingut- und auch im Grobgutbereich konnten keine Übereinstimmungen mit den Messwerten festgestellt werden. Das neue hier vorgestellte Modell einer Trennfunktion für stationäre Siebklassierprozesse T(x,α′,β) zeigt eine deutlich bessere Übereinstimmung mit den experimentellen Daten und beschreibt somit die Trennfunktion eines Siebklassierprozess wesentlich genauer.
5 Zusammenfassung
Die Siebtechnologie ist eine verfahrenstechnische Grundoperation, die in sehr vielen industriellen Prozessen eingesetzt wird. Die Siebklassierung dient hierbei zur Separation von Produktströmen mit breiten Partikelgrößenverteilungen in zwei oder mehrere Größenklassen und zur Beurteilung dieser Siebklassierprozesse ist die Kenntnis einer Trennfunktion T(x) des Prozesses von großer Bedeutung. Im Rahmen der vorstellten Untersuchungen zur Validierung der neuen Trennfunktion T(x,α′,β) wurden die partikulären Stoffsysteme Quarz, Kalkstein, Maisgrieß und Pflanzengranulat untersucht. Es wurden zwei Partikelsysteme mit engerer und zwei Stoffsysteme mit breiter Partikelgrößenverteilung ausgewählt.
Die hier vorgestellte neue Trennfunktion T(x,α′,β) für den stationären Siebprozess ist eine Funktion der Partikelgröße x, der Trennschärfe α′ und der neu eingeführten Trenneffizienz β. Mit dieser neuen Trennfunktion kann der Siebklassierprozess für die untersuchten Stoffsysteme sehr gut beschrieben werden. Insbesondere im Fein- und Grobgutbereich ist eine sehr gute Übereinstimmung der berechneten Funktionen mit den Messwerten zu beobachten. Aufgrund der unterschiedlichen Dispersitäten der untersuchten Partikelfraktionen zeigt sich, dass die Ermittlung der Trennfunktion T(x,α′,β) unabhängig von der Größenverteilung des Systems ist.
Durch den Vergleich der Trennfunktionen unter Berücksichtigung des Trennschärfeparamters α′ und des Trenneffizienzparameters β (T(x,α′,β)) mit den Trennfunktionen ohne Berücksichtigung des Trenneffizienzparameters β (T(x,α′)) konnte gezeigt werden, dass durch die neue Trennfunktion eine wesentliche Verbesserung der Charakterisierung des stationären Siebklassierprozesses möglich ist. Im Vergleich mit den anderen in dieser Arbeit aufgeführten Modellen zeigte sich, dass die Modelle von Rogers und Molerus sehr ähnliche Funktionsverläufe ergaben und für das Modell von Plitt ein geringfügig anderer Verlauf dargestellt wird. Alle diese Modelle zeigen aber keine Übereinstimmung mit den Messwerten, insbesondere im Fein- und im Grobgutbereich. Das neue Modell der Trennfunktion T(x, α′, β) liefert eine wesentlich bessere Übereinstimmung mit den Messwerten und ist somit zur Beschreibung einer Trennfunktion für den stationären Siebprozess sehr gut geeignet.
Acknowledgements
Open Access Veröffentlichung ermöglicht und organisiert durch Projekt DEAL
Formelzeichen
-
- a [–]
-
toter Fluss: Funktionswert für T(x = 0)
-
- f [–]
-
Feingutmassenanteil
-
- g [–]
-
Grobgutmassenanteil
-
- mA [kg]
-
Masse Aufgabegut
-
- mF [kg]
-
Masse Feingut
-
- mG [kg]
-
Masse Grobgut
-
- QA [%]
-
Verteilungssummenfunktion Aufgabegut
-
- QF [%]
-
Verteilungssummenfunktion Feingut
-
- QG [%]
-
Verteilungssummenfunktion Grobgut
-
- qA [% µm−1]
-
Verteilungsdichtefunktion Aufgabegut
-
- qG [% µm−1]
-
Verteilungsdichtefunktion Grobgut
-
- qF [% µm−1]
-
Verteilungsdichtefunktion Feingut
-
- x [µm]
-
Partikelgröße
-
- xT [µm]
-
Trenngrenze
Griechische Symbole
-
- α [–]
-
Maß für die Trennschärfe
-
- α′ [–]
-
Maß für die Trennschärfe
-
- β&[–]
-
Maß für die Trenneffizienz




