Bentonite-PDMS composite foams for oil spill recovery: Sorption performance and kinetics
Funding information: Ministry of Education, Science and Technological Development, Republic of Serbia, Grant/Award Number: 451-03-68/2022-14/200124
Abstract
The aim of this article is the synthesis and characterization of bentonite-filled siloxane foams for oil spills recovery. Composite foams at varying filler content in the range 35–45 wt% were investigated. The sorption kinetics and capacity of composite foams in different oils (e.g., kerosene, virgin naphtha, pump oil) were assessed. As a reference, water absorption capacity was also evaluated. Among all, the composite foam filled with 40 wt% bentonite (B-40 batch) shows the lowest affinity with water and good absorption capacity with oils (mainly light oils) reaching an absorption capacity at saturation equal to 10.3 and 518.2 wt% in water and virgin naphtha, respectively. Furthermore, isothermal absorption curves were analyzed using three kinetic models: pseudo-first order, pseudo-second order, and Elovich models. The equilibrium isotherm fitting results were optimal using the pseudo-second order model, indicating that chemisorption phenomena play a key role in the speed of the absorption phase for these PDMS-based composite foams. Finally, a correlation was addressed between morphology, foam microstructure, absorption capacity, and kinetics.
1 INTRODUCTION
Oil spills represent a huge ecological problem. The sea-oil spills are generally much more harmful than land oil spills because oil can be spread on a huge surface by a thin oil slick. Possible tanker accidents, equipment failures on oil platforms, war, terrorist attacks, and illegal oil spills, during which large amounts of oil can spill into the oceans and rivers have various effects on an entire ecosystem. The biggest oil spill was in 1991, in Kuwait, involving the discharge of about 142 million liters of crude oil.1 As a result of this ecological catastrophe, a large number of plant and animal species have irretrievably disappeared. Another huge environmental disaster, which left a big mark, was the Exxon Valdez oil tanker accident in 1989. Despite the fact that Exxon alone spent more than two billion dollars to clean up the sea and coast from pollution, serious environmental issues were noticed. According to some experts, cleaning attempts were wrong, because used detergents and various chemicals additionally polluted the sea.
Due to their potential danger to the environment and human health, various remediation techniques have been developed to mitigate hazards to the environment. Mehmood et al.2 reported several methods for removing crude oil from water. These methods include physical removal of oil waste, using oil skimmer and containment booms, and biological methods, such as biodegradation and bioremediation of oil spills by microorganisms.
Other methods of remediation are detergent-like products, flocculation, coagulation, membrane filtration, and vacuuming.3-5 But the most promising method remains the use of absorbent materials.
Different sorbents are used in oil recovery and their development to enhance the oil-recovery capacity is currently a science trend. A wide range of materials, including natural, thermodegradable, synthetic, and hybrid, could be used.6 Due to the serious risk of oil pollution and growing concerns about the sustainability of absorbent materials, there are significant research interests in the development of economical, reusable and environmentally friendly absorbents derived from renewable resources.7
Foam-based materials are attractive, due to the possibility of squeezing oil out and reusing it, which reduces cleanup costs. The new generation of airogel materials or cellulose sponges, which succeed silica and synthetic polymer-based absorbents, combine the intriguing characteristics of airogel-type materials with further advantages of cellulose, abundantly present in nature, such as natural renewability, biodegradability, and easy surface modification.8-10 But, the pore structure of cellulose aerogels critically depends on the choice of drying processes. Usually, freeze and supercritical dryings are the most commonly used methods for the preparation of cellulose aerogels.11 Organo-clay were widely studied as a great alternative to oil spill natural remedies, as demonstrated by Carmody et al.12 The main factors affecting sorbents selection are oil viscosity, surface roughness, the critical surface tension of the sorbents, the thickness of a floating layer, oil retention, contact angle, temperature, sorbent buoyancy, and strength.13 In particular, the hydrophobicity of the absorbent material plays a fundamental role. This, in fact, contributes to the selectivity of oil recovery, increasing the efficiency of the recovery action. For this reason, bentonite, as well as other types of clays are considered possible absorbent materials.14 Furthermore, the study of their properties with also the investigation on the oil absorption kinetics provide important information on recovery times.15 Clay materials have been extensively studied as additives to polymers to obtain high-performance composite materials to be used in wastewater technologies for a sustainable environment. Recently, Senol et al. added kaolinite to polyacrylamide to obtain an optimal UO22+ ions absorbent.16 Simsek et al.17 investigated the use of vermiculite to obtain a functional polyacrylamide composite.
The present study aims to scrutinize the effect of the addition of bentonite, a low cost clay, in a siloxane-based foam, added to increase the oil/water selectivity for oil spill recovery application. In such a context, the sorption capacity of the composite foams in different oils (kerosene, naphtha, and pump oil) is evaluated. The experimental campaign was addressed to define a relationship among the composite materials' macroporous morphology, oil characteristics, and sorption capacities. Finally, a kinetic modeling approach is applied to quantitively compare the sorption rate and performances of the bentonite-siloxane foams at varying oil pollutant and filler content. Three kinetic mass transfer models (pseudo-first order, pseudo-second order, and Elovich model) are applied, to evaluate the tested materials' oil/water selective capacity. The related absorption mechanics, based on a careful comparison of the kinetic rate parameters, equilibrium capacity, and the correlation coefficients for each model were also considered.
2 EXPERIMENTAL PART
2.1 Materials and characterization methods
2.1.1 Filler material
As filler material, bentonite powder was used. The material (bentonite clay) was obtained from the company “Nemetali,” Vranjska Banja, South Serbia. Before further modification, bentonite was thermally treated at 120°C for 3 h.
The three samples of bentonite-filled siloxane foams were prepared, with bentonite shares of 35%, 40%, and 45%. The structure of the investigated filler was characterized by X-ray diffraction (XRD), using a D8 Advance Bruker diffractometer (Billerica, MA, USA), in the Bragg–Brentano theta-2theta configuration, Cu Kα, 40 V, 40 mA, 0.1°/s scan rate. Furthermore, the sample morphology was investigated using a scanning electron microscope (SEM, FEI Quanta 450, Thermo Fisher Scientific, Waltham, MA, USA), in Low Vacuum, at an acceleration voltage of 5 kV. The foam static water/oil contact angle was measured by means of an Attension Theta Tensiometer equipment (Biolin Scientific, Västra Frölunda, Sweden), according to the sessile drop technique. A distilled water/oil droplet (3 μl) was put on the sample surface at room temperature (25°C). A micro CCD camera equipped onsite recorded the images of the droplets to be further analyzed by suitable PC Attension software (OneAttension V. 2.3). Ten replicas of contact angle measurements for each liquid were performed.
2.1.2 Synthesis of the composite foams
The synthesis of composite foams was carried out according to the simple procedure proposed in.18, 19 All reagents were used as provided without any further purification. The silicone foam was manufactured using a direct dehydrogenative reaction as foaming reaction.20 At first, poly(dimethylsiloxane-co-methylhydrosiloxane), trimethylsilyl terminated, PMHS, M.W. 5500–6500 CAS: 68037-59-2 and silanol terminated polydimethylsiloxane, PDMS, M.W. 110,0000 CAS: 70131-67-8 compounds, both supplied by Gelest (Morrisville, USA) were mixed in ethanol solution under magnetic stirring (PDMS/PMHS weight ratio 2:1) for 60 s. Afterward, the bentonite was gradually added always under stirring, and continuously mixed until to obtain a homogenous slurry. In order to reduce the viscosity of the slurry, bidistilled water and ethanol were used.20, 21 Then, a catalyst, tin(II)2-ethylhexanoate(Sn(II)) (density: 1.251 g/ml, purity >92.5%) purchased from Sigma Aldrich (USA) was added still under stirring to activate the dehydrogenative reaction. Finally, it was poured into a cylindrical mold (diameter 2 cm) to define the sample shape during the foaming phase. According to Reference 22, the porous structure of the foam is due to a dehydrogenative reaction between the siloxane constituents (PDMS and PMHS) that leads to the formation of hydrogen gas that provokes the bubbling phenomenon. This reaction occurs already at room temperature. Soft curing at 70°C for 24 h in the air was performed to cure the siloxanes completely. The synthesis set-up of the clinoptilolite-silicone foam and details of the produced formulations are shown in Figure 1 and Table 1, respectively.

| B-0 | B-35 | B-40 | B-45 | ||
|---|---|---|---|---|---|
| PDMS | Siloxane | 41.7% | 31.2% | 30.8% | 28.8% |
| PMHS | Siloxane | 20.8% | 15.6% | 15.4% | 14.4% |
| Water | Solvent | 12.5% | 9.3% | 6.2% | 5.8% |
| Ethanol | Solvent | 14.6% | 10.9% | 9.2% | 8.6% |
| Sn(II) | Catalyst | 10.4% | 7.8% | 7.6% | 7.1% |
| Bentonite | Filler | 0.0% | 25.2% | 30.8% | 35.3% |
| Bentonite versus foam (wt%) | 0.0% | 35.0% | 40.0% | 45.0% | |
2.1.3 Sorption capacity tests
2.2 Sorption kinetics models
- pseudo-first order model
- pseudo-second order model
- Elovich model
For each sorption model, the correlation coefficient, R2 (R-squared), was calculated to better evaluate the correlation between experimental and fitting data.
2.2.1 Pseudo-first order kinetic model
2.2.2 Pseudo-second order kinetic model
In the t/qt versus time plot, the slope and intercept of the line can be used to determine the second-order rate constant, K2, and the sorption capacity at equilibrium, qe, respectively.
2.2.3 Elovich model
3 RESULTS AND DISCUSSION
3.1 Filler characterization
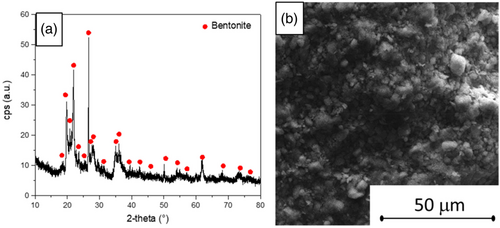
The structure of the investigated filler is homogeneous. As evidenced by XRD analysis (Figure 2a), no impurities are detected. SEM image (Figure 2b) shows a slight regular morphology of the filler characterized by particle size in the range of 1–5 μm.
3.2 Morphological evaluation
Figure 3 shows the SEM images of all the batches. The silicone foam (Figure 3a) exhibits by a macroporous structure with quite regular and homogenously distributed bubbles. The pores are interconnected due to bubble agglomeration or microchannels pores. The foam exhibits a quite isotropic morphology, with bubble size about 1.75 mm and a density of 970 kg/m3. The macroporous morphology of the foam is preserved after adding the bentonite filler. Although, some discrepancies, compared with the unfilled foam, can be identified.

The compactness of the composite foam (Figure 3b–d) increases by increasing the filler content. Therefore, a reduction in bubble size and distribution regularity can be observed, implying that the density of the foam is higher the larger the bentonite content.
This behavior can be related synergistically to both the higher viscosity of the synthesis composite slurry, due to the addition of the bentonite filler in the PDMS based mixture, and to a favored bubble nucleation mechanism activated by the bentonite filler in the slurry.19
In particular, the B-45 batch showed the smallest pore size and the highest density: 0.82 mm and 1659 kg/m3, respectively.
The foam density and porosity are affected by the chemical reactions that take place between the siloxane mixture constituents, PDMS and PHMS, and the hydroxyl-terminated surface groups of the bentonite clay that promote the chemo-physical bubbling.28 Furthermore, the bubble flow and coalescence are hindered in high viscosity solutions. Indeed a low viscosity siloxane-bentonite solution favors the bubbles agglomeration during the crosslinking foaming stage.29 Therefore, the coalescence is promoted for low viscosity slurry (e.g., B-35 foam) and large and circular-shaped bubbles are obtained. Instead, the bubble aggregation is hindered for high viscosity slurry (e.g., B-40 and B-45 foams) and foam porosity is heterogeneous and not regular in shape.30 As seen in Figure 3c,d, foam morphology is characterized by irregular-shaped bubbles. In particular, a bimodal bubble distribution, constituted by small and medium sized clusters, can be qualitatively identified.
The low flexibility of the material increases the structural heterogeneity of the composite foam due to the high bentonite content,31 thus evolving toward a stiff and brittle composite structure.32
3.3 Sorption performances
Figure 4 shows the sorption capacity, expressed as weight uptake, at increasing sorption time in water, pump oil, kerosene, and naphtha for all foams. All curves exhibit a monotonic trend with a progressive increase in uptake at increasing time, until the saturation is reached, where oil uptake stabilizes, and a plateau is reached. Evaluating the curve trend, three phases can be distinguished: (i) at low sorption times, the uptake increases rapidly, demonstrating a high sorption rate at this stage of the sorption process; (ii) at intermediate sorption times, the oil uptake evolves exhibiting a reduced slope in the uptake versus time curve; (iii) at high sorption times, an equilibrium sorbent-sorbate is achieved. At this stage, the sorption capacity is hampered, due to the limited free surfaces in the sorbent, suitable for a further entrapment of the sorbate.33

A high pollutant uptake is reached in low-density oils, such as kerosene and naphtha (Figure 4c,d, respectively). Indeed, all foams exhibit a weight increase at least 300%. Conversely, a low sorption capacity is observed in high-density liquids: water and pump oil (Figure 4a,b, respectively).
Further relevant considerations can be drawn by evaluating the sorption properties in the different oils of the composite foams compared with the unfilled one.
All composite foams exhibit a lower oil absorption capacity than B-0 foam. This effect is particularly relevant for naphtha oil, where a sorption capacity reduction of about 30% can be found at saturation for all composite foams. However, by analyzing the trend of the curves in this oil, it is possible to extrapolate some qualitative information on the sorption rate. Although it leads to a lower absorption capacity at saturation, the addition of the bentonite also induces an increase in the slope of the uptake versus the time curve. This implies that the initial absorption phase is kinetically faster and the saturation condition is reached for shorter immersion times.
In particular, in pump oil (characterized by a density of 858 kg/cm3 and a viscosity of 0.123 Pa*s) the unfilled silicone foam (B-0) reaches an equilibrium in sorption capacity at 121% after about 180 s sorption time (defined as saturation time, ts). The saturation time (ts) is significantly reduced for bentonite composite foams. Furthermore, this value decreases increasing the filler content, reaching a minimum for B-45 foam where ts of about 60–90 s can be observed. Analogous consideration can be argued in low density oils. For example, in naphtha oil (characterized by a density, ρ, equal to 630 kg/cm3 and a viscosity, μ, equal to 0.0012 Pa*s) the unfilled foam acquires a sorption at saturation after about 200 s with a maximum oil uptake of 768%. Instead, the composite foams absorb at saturation an amount of naphtha equal to 500% but in half the time (te is about 90 s).
Evaluating the water absorption trend (Figure 4a), fascinating valuable information, useful for oil spill remediation application can be drawn.
In the unfilled foam, the water absorption capacity is relatively low, despite its low viscosity. Besides, the saturation conditions are reached relatively long (about 360 s) compared with oils. This behavior can be attributed to the hydrophobic nature of the siloxane matrix, which slows down the absorption process and the maximum absorption equilibrium capacity. Although, capillarity phenomena can trigger mass transport phenomena toward the interconnected channels of the foam,34 favoring unwanted water absorption conditions at intermediate or long sorption time.
The choice of an active filler able to limit the diffusion mechanisms that stimulate water absorption is a necessary condition to guarantee the material's applicability for the recovery of the spilled oil. In this context, the option to add a clay filler aims to increase the surface hydrophobicity without compromising the hydrophilic nature of the material.
The results presented in Figure 4a clearly illustrate that the bentonite filler significantly collapses the water absorption capacity of the macroporous foam. The best results are obtained for the B-40 foam for which a water absorption capacity of 10.3% saturation is reached with a saturation time, te, of 120 s. This behavior could be attributed to a double action of enhancement of the water repellency and morphological modification of the foam porosity. As observed in literature, in fact, bentonite clay has a hydrophobic nature.35 It shows a hydrophobic interaction with the recovering oil, tending to absorb oil, and reject water.35
Moreover, the liquids diffusion in the interconnected macroporous structure evidences a resistance to deformation for microporous structures.36 For foam morphologies, characterized by small pore size, a higher force is required to absorb the oil into the open porosity of the foam. Consequently, the bentonite-PDMS foam morphology hinders the water absorption. But, considering the good affinity of the foam constituents with the oils37 the oil absorption capacity is slightly preserved.
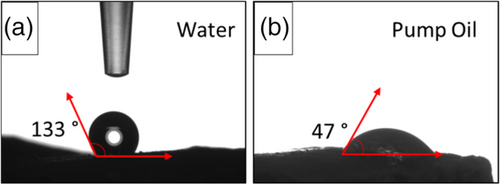
Table 2 summarizes the sorption capacity at equilibrium, Se, and the referred time at with it is reached (identified as time at equilibrium, te,) for all the investigated sorbate liquid at varying bentonite content in the absorbent foam. As previously discussed, the unfilled foam exhibits the highest sorption capacity at equilibrium in water (115.2% in 360 s) about 80%–90% higher than in composite foams. On the contrary, the bentonite-PDMS matrix hinders the surface affinity with polar liquids leading to B-40 foam's Se of 10.3% at 120 s, confirming at the same time a meager and fast sorption capacity at saturation. This confirms that the unfilled siloxane foam is characterized by a greater affinity to water, causing a conspicuous hydrophilic behavior of the foam surface. The bentonite addition could stabilize the surface polarity of the PDMS matrix, thus decreasing the polar surface energy with a beneficial effect in terms of water hydro-repellency of the foam.35 as confirmed by contact angle measurements reported in Figure 5. A relevant difference between contact angle in water and in pump oil can be identified, for B-40 foam. The contact angle in water is about 130° (Figure 5a), above the hydrophobicity threshold of 90°, in pump oil it decreases to 47° (Figure 5b), underlining the oleophilic behavior of the foam.
| Water | Pump oil | Kerosene | Naphtha | ||
|---|---|---|---|---|---|
| B-0 | Se (%) | 115.2 ± 17 | 121 ± 21 | 544 ± 51 | 768 ± 31 |
| te (s) | 360 | 180 | 300 | 200 | |
| B-35 | Se (%) | 14.3 ± 5 | 66 ± 6 | 328.3 ± 24 | 544.0 ± 32 |
| te (s) | 190 | 150 | 180 | 130 | |
| B-40 | Se (%) | 10.3 ± 3 | 73 ± 4 | 385.8 ± 13 | 518.2 ± 18 |
| te (s) | 120 | 90 | 90 | 100 | |
| B-45 | Se (%) | 19.6 ± 7 | 97 ± 19 | 385.4 ± 10 | 534.9 ± 23 |
| te (s) | 120 | 60 | 90 | 90 |
Indeed, evaluating the sorption capacity at equilibrium in oils of the composite foam, an apparent reduction of Se value can be identified. However, the mass flow diffusion of the pollutant in the macroporous structure of these foams is faster than the unfilled one. This aspect can be scrutinized evaluating the trend of te for unfilled and bentonite-filled foams. For high bentonite content (B-40 and B45 batches) the te values is about three time lower than the B-0 one. This suggests that although the absorption capacity is not very high, the addition of bentonite in the siloxane foam implies a significant improvement in the kinetics absorption mechanisms in oils, with substantial benefit on the performance in operation conditions during the recovery phases of the spilled oils.
The oil/water selectivity index, determined as ratio between the Se value in oil and water, reported in Figure 6, validates the previous considerations, allowing at the same time to indirectly quantify the effectiveness in separating oils from the water dispersing environment.
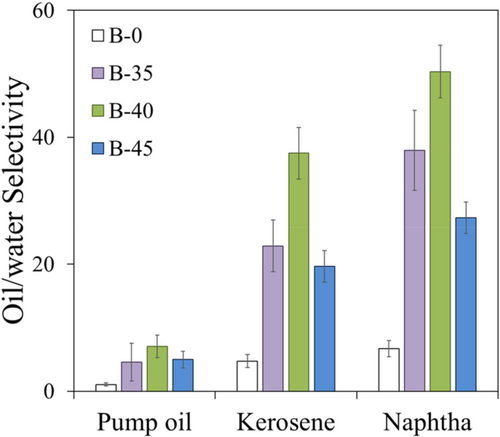
In the composite foams, B-45 batch shows the poorest selectivity to oil, preserving anyway a selectivity about five time higher than the B-0 one. A worsening of the selective efficacy is visible in heavy oils (pump oil) in which selectivity falls at about ~5.0–7.0, unlike lighter oils, such as virgin naphtha and kerosene, the reached values are ~25–35 and ~25–50, respectively.
Interesting considerations can be argued evaluating the selectivity performances of the composite foam with intermediate bentonite content (B-40 batch). Undeniably, in virgin naphtha and kerosene, while showing a lower absorption capacity than B-0 (518% vs 768% for B-45 and B-0, respectively, in naphtha), a faster absorption rate (te 100 vs 200 s for B-45 and B-0, respectively, in naphtha) and the highest oil/water selectivity (Figure 6) are evidenced. This behavior is also found for the recent composite foams obtained by the addition of clinoptilolite filler, but in the latter case, the absorbent capacity in virgin naphtha is evidently lower (518.2% and 362.9%, for B-40 and 40% filled clinoptilolite foam, respectively).38
The very low water absorption of the B-40 foam allows to obtain highest selectivity indices in all oils.
It shows the best selectivity in light oils, virgin naphtha, and kerosene oils, where oil/water sorption capacity ratios are above 50 and 37, respectively. The selectivity index is low in pump oil, but it remains the highest compared with the other foams (7.1 for B-40 and 4.6 and 5.0 for B-35 and B-45, respectively).
Considering the high flexibility and compressibility of the siloxane based composite foams, the squeezing was performed by simply manual compression for three times in an adsorbent paper.
This parameter, as defined, can be used to evaluate the reusability of the foam at the end of an oil absorption cycle. The higher the SC values, the more oil is manually removed. Consequently, the oils absorbed in the foam can be extracted from the foam by simple compression and collected in specific containers to collect it, optimizing their disposal. The adsorbent foam can thus be reused for multiple absorption cycles with obvious advantages in terms of management costs of the spilled oils recovery phase.
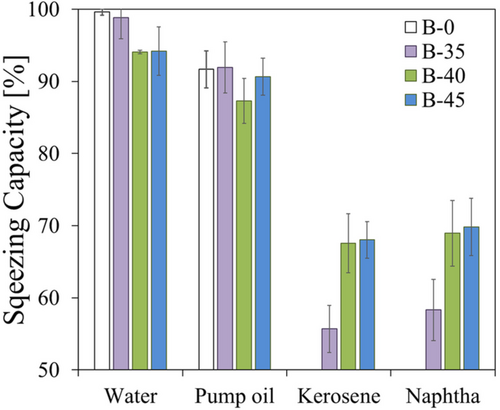
Figure 7 shows the SC evolution at varying oils for all investigated foams. All foams always showed an SC index above 50% regardless of the used oil. These results confirm that the foam has a good compressibility and deformability to allow the recovery of the absorbed material, and allow its potential reuse for different absorption cycles. The optimal SC values were found in water and pump oil, for which an absorbed recovery index is generally higher than 90%. The values of light oils (kerosene and naphtha) vary between 55% and 70%, depending on the foam batch. In particular, the foams with a high bentonite content (B-40 and B-45 batches) exhibited very high squeezing efficiency in these oils. This result, coupled with the good water/oil selectivity of B-40 (Figure 6), identifies this batch as the potentially most promising one for its use for oil spill recovery application.
3.4 Kinetic modeling and sorption mechanism
The kinetics of the absorption capacity of the different foams at varying oils has been assessed to better interpret the multiple mechanisms that govern the absorption phenomenon and its uptake evolution. The absorption phenomena are correlated to the surface interaction between the absorbed oil and the active sites of the absorbent. Depending on the triggered interaction, physical (physio-absorption), chemical (chemo-absorption) or a combination of these mechanisms will be activated and support the mass transport of the sorbate in the adsorbent. Especially, three different kinetic models were compared with evaluate the acquired experimental absorption data: pseudo-first order (Lagergren model), pseudo-second order, and EM.39 The kinetic parameters of each model, as well as their correlation coefficients (R2), are compared in Tables 3–6 for all batches.
| Pseudo-first order | Pseudo-second order | Elovich | ||||
|---|---|---|---|---|---|---|
| Water | qe | 107.54 | qe | 120.20 | Omega | 2.85E-02 |
| K1 | 6.08E-03 | K2 | 8.59E-05 | alpha | 1.87 | |
| h0,1 | 0.65 | h0,2 | 1.24 | Re | 0.35 | |
| R2 | 0.98 | R2 | 0.99 | R2 | 0.98 | |
| Pump oil | qe | 59.71 | qe | 119.94 | Omega | 5.61E-02 |
| K1 | 7.85E-03 | K2 | 5.34E-04 | alpha | 43.12 | |
| h0,1 | 0.47 | h0,2 | 7.68 | Re | 0.16 | |
| R2 | 0.83 | R2 | 1.00 | R2 | 0.95 | |
| Kerosene | qe | 409.84 | qe | 549.91 | Omega | 8.86E-03 |
| K1 | 9.70E-03 | K2 | 7.82E-05 | alpha | 38.52 | |
| h0,1 | 3.97 | h0,2 | 23.66 | Re | 0.21 | |
| R2 | 0.97 | R2 | 1.00 | R2 | 0.98 | |
| Virgin Naphtha | qe | 574.48 | qe | 776.98 | Omega | 5.22E-03 |
| K1 | 1.04E-02 | K2 | 5.23E-05 | alpha | 33.34 | |
| h0,1 | 5.96 | h0,2 | 31.57 | Re | 0.26 | |
| R2 | 0.94 | R2 | 1.00 | R2 | 0.92 | |
| Pseudo-first order | Pseudo-second order | Elovich | ||||
|---|---|---|---|---|---|---|
| Water | qe | 40.00 | qe | 19.14 | Omega | 2.28E-01 |
| K1 | 2.16E-02 | K2 | 4.91E-04 | alpha | 0.37 | |
| h0,1 | 0.86 | h0,2 | 0.18 | Re | 0.31 | |
| R2 | 0.82 | R2 | 0.95 | R2 | 0.97 | |
| Pump oil | qe | 48.32 | qe | 67.30 | Omega | 2.50E-01 |
| K1 | 2.24E-02 | K2 | 1.93E-03 | alpha | 3394.09 | |
| h0,1 | 1.08 | h0,2 | 8.75 | Re | 0.06 | |
| R2 | 0.94 | R2 | 1.00 | R2 | 0.98 | |
| Kerosene | qe | 188.63 | qe | 352.23 | Omega | 1.72E-02 |
| K1 | 1.36E-02 | K2 | 1.19E-04 | alpha | 61.49 | |
| h0,1 | 2.57 | h0,2 | 14.74 | Re | 0.18 | |
| R2 | 0.91 | R2 | 1.00 | R2 | 0.85 | |
| Virgin Naphtha | qe | 506.52 | qe | 577.81 | Omega | 1.31E-02 |
| K1 | 2.07E-02 | K2 | 9.01E-05 | alpha | 352.97 | |
| h0,1 | 10.50 | h0,2 | 30.07 | Re | 0.14 | |
| R2 | 0.98 | R2 | 1.00 | R2 | 0.94 | |
| Pseudo-first order | Pseudo-second order | Elovich | ||||
|---|---|---|---|---|---|---|
| Water | qe | 10.47 | qe | 11.31 | Omega | 4.70E-01 |
| K1 | 1.81E-02 | K2 | 2.59E-03 | alpha | 0.94 | |
| h0,1 | 0.19 | h0,2 | 0.33 | Re | 0.21 | |
| R2 | 0.85 | R2 | 0.99 | R2 | 0.89 | |
| Pump oil | qe | 55.02 | qe | 74.37 | Omega | 1.66E-01 |
| K1 | 2.41E-02 | K2 | 1.70E-03 | alpha | 4457.27 | |
| h0,1 | 1.33 | h0,2 | 9.42 | Re | 0.08 | |
| R2 | 0.97 | R2 | 1.00 | R2 | 0.87 | |
| Kerosene | qe | 318.02 | qe | 402.23 | Omega | 2.11E-02 |
| K1 | 2.29E-02 | K2 | 1.91E-04 | alpha | 670.47 | |
| h0,1 | 7.30 | h0,2 | 30.92 | Re | 0.12 | |
| R2 | 0.90 | R2 | 1.00 | R2 | 0.85 | |
| Virgin Naphtha | qe | 295.12 | qe | 530.73 | Omega | 2.07E-02 |
| K1 | 2.48E-02 | K2 | 2.83E-04 | alpha | 10525.75 | |
| h0,1 | 7.33 | h0,2 | 79.61 | Re | 0.09 | |
| R2 | 0.96 | R2 | 1.00 | R2 | 0.78 | |
| Pseudo-first order | Pseudo-second order | Elovich | ||||
|---|---|---|---|---|---|---|
| Water | qe | 24.10 | qe | 22.01 | Omega | 2.22E-01 |
| K1 | 2.31E-02 | K2 | 1.25E-03 | alpha | 1.43 | |
| h0,1 | 0.56 | h0,2 | 0.61 | Re | 0.23 | |
| R2 | 0.97 | R2 | 0.99 | R2 | 0.91 | |
| Pump oil | qe | 76.00 | qe | 100.75 | Omega | 9.87E-02 |
| K1 | 2.47E-02 | K2 | 9.91E-04 | alpha | 659.53 | |
| h0,1 | 1.88 | h0,2 | 10.06 | Re | 0.10 | |
| R2 | 0.99 | R2 | 1.00 | R2 | 0.83 | |
| Kerosene | qe | 123.25 | qe | 392.99 | Omega | 2.86E-02 |
| K1 | 1.05E-02 | K2 | 2.38E-04 | alpha | 941.45 | |
| h0,1 | 1.29 | h0,2 | 36.72 | Re | 0.09 | |
| R2 | 0.73 | R2 | 1.00 | R2 | 0.80 | |
| Virgin Naphtha | qe | 211.13 | qe | 548.72 | Omega | 2.07E-02 |
| K1 | 2.56E-02 | K2 | 2.73E-04 | alpha | 1546.83 | |
| h0,1 | 5.41 | h0,2 | 82.13 | Re | 0.09 | |
| R2 | 0.93 | R2 | 1.00 | R2 | 0.77 | |
Preliminarily, by analyzing the values of the correlation coefficient R2, among all the studied models, it is possible to observe a better applicability of the second-order kinetic model (R2 ≈ 1) to describe the kinetic and uptake rate in oils of all the composite foams.
Moreover, the qe value determined by PSOM is the closest to the experimental one, confirming the good ability to predict the absorption capacities at equilibrium of the different batches in all oils.
As reference, Figure 8 shows the experimental data and fitting results referred to pseudo-second order kinetics in water (Figure 8a), pump oil (Figure 8b), kerosene (Figure 8c), and naphtha (Figure 8d) for the B-35 foam.
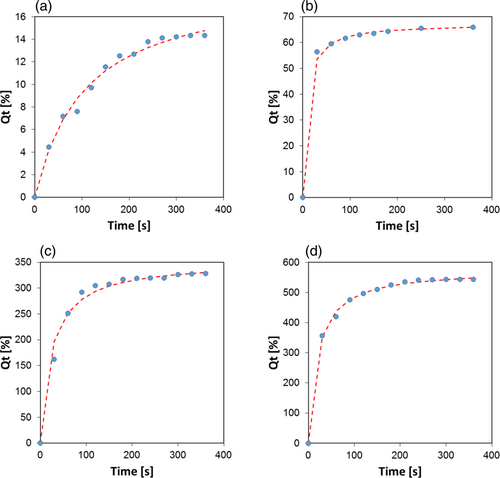
The good fitting of the experimental data with the PSOM suggests that the absorption phenomenon in bentonite-based composite foams could be related to a chemisorption mechanism. In this case, the absorbent–adsorbate surface interaction is based on an intermolecular interaction with a strength similar to chemical bonds.
Instead, PFOM and EM models exhibited a lower predictive capacity, albeit with an acceptable correlation coefficient (R2 > 0.75), especially for composite foams with significant filler content.
Based on the results summarized in Tables 3–6, the fitting accuracy of the investigated kinetic models can be classified as in the following: pseudo-second order > pseudo-first kinetic model > Elovich.
These results emphasized that the chemisorption phenomenon is the driving factor controlling the oil absorption rate,40, 41 addressing that the occupation capacity of suitable binding sites is squared proportional to the amount of still active sites (not yet occupied) on the surface of the absorbent foam.33 However, an additional factor that synergistically influences the absorption capacity and the mass transport phenomena inside the absorbent is represented by the porosity and bubble diameter of the foam. The interconnection of the open/closed bubble in the PDMS based foam plays a relevant role in the sorption capacity of spilled oils.42 Besides, macro-porous light-weight foams exhibits faster sorption performances in oil than microporous heavy-weight foams.43 Consequently, the morphology of the foam can influence the absorption capacity and related SC in water and oils. Surely, B-40, characterized by an intermediate pore size (0.98 mm) and a density of 1582 kg/m3, exhibited an effective absorption capacity at saturation in oils (for B-40 foam, 73%, 386%, and 518% in pump oil, kerosene, and virgin naphtha, respectively). Accordingly, thanks to a well-interconnected macro-cellular structure, the foam exhibited furthermore a suitable SC both in heavy and light oils. An increase in particle size favors mass diffusion phenomena, mainly for high viscosity liquids.43
At the same time, the phenomena of diffusion by capillarity to the absorbent are more limited. A large pore size provokes an unwanted oil release during the oil spill removal due to a low retention force of the oil in the foam.44 This implies that there is an optimal size of the bubbles, a compromise between capillarity and mass transport phenomena, which facilitate the absorption of the absorbed products inside the porous matrix.
Based on the absorption evolution and referred kinetic models of the composite foams in the oils, different competing absorption stages can be identified45, 46: (i) external mass transfer (transport from the bulk solution to the sorbent surface); (ii) film diffusion; (iii) intraparticle pore diffusion; (iv) chemical surface interaction at the active sites. Based on the intrinsic porous microstructure of the foam, the mass transfer of the oil into foam pores is stimulated by the presence of preferential pathways along the interconnected porous channels of the foam itself. Therefore, the external mass transfer and film diffusion mechanism are significantly fast. Meanwhile, the intraparticle diffusion and the chemical surface interaction can be identified as the limiting factor of the absorption process.
The diffusion phenomenon in the composite foam begins with the oil flowing from the bulk toward the active surface of the absorbent. The oil impregnates this latter following the combined action of capillarity and concentration gradient effect of the contaminant in the liquid bulk which synergistically favor the mass diffusion of the oil inside the foam porosity.14
At this stage, secondary phenomena can be activated to increase the absorption capacity further. Peculiarly, a chemical phenomenon, in the active sites on the foam surface, takes place due to physical (molecular van der Waals forces) and/or chemical (electron transfer between absorbent and absorbed) interactions of the pollutant molecules with the substrate.33 Therefore, although the process is conveyed by the combination of physical and chemical phenomena, the good fitting of the transient absorption capacity by the PSOM suggests that chemisorption mechanism plays a predominant role in the absorption of the contaminating oils in the bentonite-silicone composite foams. Subsequently, the absorption rate decreases cause of the progressive decrease of free active sites on the porous foam surface.47 During this stage, the oil uptake slightly increases due to a limited diffusion of the pollutant toward not embedded foam pores.48
The oil absorption is also influenced by the micro- and macro-structure of the foam, making the design of an optimal foaming ratio is an essential condition for its effective use for oil spill recovery.42
In this concern, the bentonite acts both on the morphology of the foam and on the surface interaction with oil and water. In fact, the filled composite foam showed a markedly hydrophobic and oleophilic behavior, thus revealing a clear oil/water selectivity.18
These preliminary results showed these macroporous composite materials as potentially suitable reusable absorbent systems for the oil spill recovery. Furthermore, a correlation was identified between morphology, foam microstructure, absorption capacity, and kinetics. In this sense, a future increase in knowledge on the structure–property relationship of the PDMS-bentonite composite foams could be helpful to better tailor the product performances for its future application in oil recovery systems.
4 CONCLUSIONS
Since oil spills represent a major environmental issue, suitable techniques for oil removal from water should be used. One of the techniques that could be used is crude oil sorption on sorbents that fulfill specific criteria. Synthesized and characterized bentonite-filled siloxane foams were applied for oil spills recovery experiments. Composite foams with a range of filler content of 35, 40, and 45 wt% were evaluated. Sorption kinetics and capacity of composite foams with various filler range in different oils (e.g., kerosene, virgin naphtha, pump oil) was assessed and compared with water absorption capacity. The composite foam filled with 40 wt% bentonite (B-40 batch) showed the lowest affinity with water and good absorption capacity with oils reaching an absorption capacity at saturation equal to 10.3% and 518.2% in water and virgin naphtha, respectively. Unfilled siloxane foam showed a greater affinity for water because of its more extensive hydrophilic behavior. After bentonite addition surface polarity of the PDMS matrix was stabilized by decreasing the polar surface energy with a beneficial effect for water hydro-repellency of the foam. The very low water absorption of the B-40 foam allows obtaining the highest selectivity indices in all investigated oils. SC experiments confirmed the reusability of B-40 for multiple absorption cycles. The simple synthesis process, the low cost of reagents, the highly performing behavior and the reusability of bentonite foam, in particular B-40, make this composite material promising for oil spill applications. Future studies will focus on the bentonite treatments in order to increase the sorption capacity of this kind of composites in heavy oils, such as pump oil.
AUTHOR CONTRIBUTIONS
Elpida Piperopoulos: Conceptualization (equal); data curation (equal); formal analysis (equal); investigation (equal); methodology (equal); validation (equal); writing – original draft (equal). Luigi Calabrese: Conceptualization (equal); data curation (equal); formal analysis (equal); investigation (equal); methodology (equal); validation (equal); writing – original draft (equal). Vesna Stankov Jovanovic: Data curation (supporting); investigation (supporting); validation (supporting); writing – original draft (equal). Jelena Nikolic: Investigation (supporting); validation (supporting); writing – original draft (supporting). Slobodan Ciric: Investigation (supporting); validation (supporting); writing – original draft (supporting). Candida Milone: Writing – original draft (equal); writing – review and editing (equal). Edoardo Proverbio: Supervision (lead); writing – review and editing (equal).
ACKNOWLEDGMENT
The authors thank to the Ministry of Education, Science and Technological Development, Republic of Serbia (Contract No: 451-03-68/2022-14/200124). Open Access Funding provided by Universita degli Studi di Messina within the CRUI-CARE Agreement.
CONFLICT OF INTEREST
The authors declare that they have no competing interests.
Open Research
DATA AVAILABILITY STATEMENT
All data generated or analyzed during this study are included in this published article.




