Are Redox-Active Centers Bridged by Saturated Flexible Linkers Systematically Electrochemically Independent?
Abstract
The extent to which electrophores covalently bridged by a saturated linker are electrochemically independent was investigated considering the charge/spin duality of the electron and functionality of the electrophore as a spin carrier upon reduction. By combining computational modeling with electrochemical experiments, we investigated the mechanism by which tethered electrophores react together within 4,4′-oligo[n]methylene-bipyridinium assemblies (with n=2 to 5). We show that native dicationic electrophores (redox state Z=+2) are folded prior to electron injection into the system, allowing the emergence of supra-molecular orbitals (supra-MOs) likely to support the process of the reductive σ bond formation giving cyclomers. Indeed, for Z=+2, London Dispersion (LD) forces contribute to flatten the potential energy surface such that all-trans and folded conformers are approximately isoenergetic. Then, upon one-electron injection, for radical cations (Z=+1), LD forces significantly stabilize the folded conformers, except for the ethylene derivative deprived of supra-MOs. For radical cations equipped with supra-MOs, the unpaired electron is delocalized over both heterocycles through space. Cyclomer completion (Z=0) upon the second electron transfer occurs according to the inversion of redox potentials. This mechanism explains why intramolecular reactivity is favored and why pyridinium electrophores are not independent.
Introduction
It is generally accepted that for two identical electrophores tethered by saturated linkers, and in contrast to what happens in the case of unsaturated linkers,1 potential inversion cannot occur. Indeed, as the length of the spacers increases, both the Coulombic repulsion energy rapidly falls below the estimated error and the electrophoric components become electronically independent. Thus, the standard potential separation ▵E0 eventually becomes practically equal to the statistical limit (RT/F)ln4, i.e. 35.6 mV at 25 °C.2-6 Such molecules with multiple electronically-independent redox centers exhibit current-potential responses of the same shape as that obtained for a molecule containing only a single center.5, 7
Let′s consider the case study of two identical electrophoric components carrying cationic charges, namely N-methylpyridiniums, which are connected by saturated and flexible oligomethylene linkers. Here we show that these electrophores are not necessarily independent in terms of their electronic/redox properties even though they are apparently reduced at the same potential. In fact, we give here a contradictory example in questioning the manner in which electron “spin-spin interaction” (SSI) actually takes place in the process of reductive formation of cyclomers8 derived from 4,4′-oligomethylene-bipyridinium species. These 4,4′-bridged compounds are referred to as γ-bridged species (Figure 1).9-13 For N,N′-bridged isomers (Figure 1), the reader is referred to references.8, 14-18 Electrochemistry allows to prove the inversion of standard potentials within these saturated assemblies. Beyond reactivity (e.g. the propensity to σ bond formation) of single-electron reduced electrophoric species (i.e., pyridinyl19 radicals), it is worth also considering the through space orbital interactions.20, 21
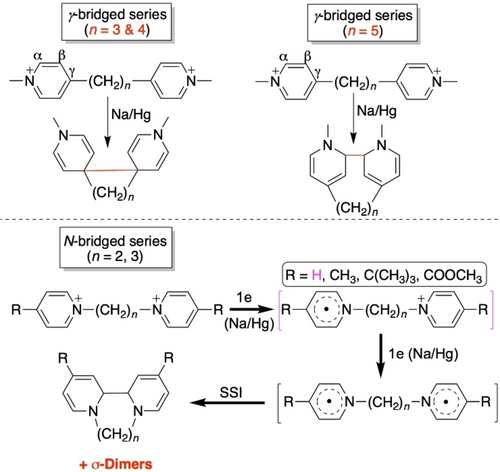
In fact, N-methylpyridiniums as redox-active building blocks of multicomponent systems can interact (intramolecularly) in different ways, either through bonds, through space, or both. The structure-electrochemistry relationships are highly dependent on the connection schemes of the pyridiniums. Essentially three electrochemical paradigms can be identified among assemblies composed of two redox-active components (Figure 2). They include pyridiniums (1) connected tail-to-tail via their C(γ), such as methylviologen (MV2+; Weitz paradigm), (2) connected head-to-tail, such as “expanded bipyridiniums” (EBP2+), and (3) held approximately cofacially and connected via their C(γ) by a (semi-)rigid redox-innocent spacer (“structronic” paradigm). These three connection patterns result in three different electrochemical behaviors, which are the following:
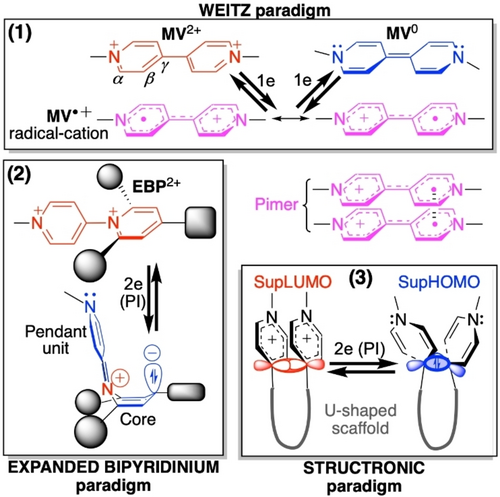
Three electrochemical paradigms. PI denotes potential inversion and EBP2+ refers to expanded bipyridinium native dication. For SupLUMO and SupHOMO terminology, see text.
-
Weitz type electrochemical paradigm is characterized by a two-step reversible redox system22 yielding a rather stable radical cation upon one-electron reduction.23 In concentrated solutions or in diluted solutions within purposely pre-organized covalent assemblies24 (and in the solid state), this radical cation in turn shows a propensity to form dimers in the form of closed-shell stacks whose cohesion is colloquially recognized to be maintained by intermolecular π–π interactions (“pimers” in Figure 2). In fact, it has recently been found that existing covalent π (and σ) contributions are by far small compared to the huge -attractive- London Dispersion (LD) forces25 of highly polarizable π orbitals (namely π singly occupied molecular orbitals, π-SOMOs), which allow circumventing the coulombic repulsion of cations.26
-
“Expanded Bipyridinium” paradigm27 is characterized by a reversible single-step two-electron reduction yielding a distorted, neutral (zwitterionic) and EPR silent (closed shell) species.28 Actually, the radical cation is a transient reaction intermediate that cannot be isolated because an inversion of the standard reduction potentials (hereafter referred to as “potential inversion”, PI) takes place, meaning that the second monoelectronic reduction is energetically less demanding than the first one because of a correlated redox-triggered intramolecular structural reorganization.2, 29 SSI is thus averaged over the entire system.
-
Structronic paradigm allows a two-electron reduction that proceeds with PI, resulting in the formation of a covalent σ bond stable at room temperature,30, 31 thereby providing a means to store two electrons in an elongated carbon-carbon bond as a reservoir.20, 30, 31 The key requirement for achieving this paradigm is the existence of a Lowest Unoccupied Supra-Molecular Orbital (hereafter referred to as SupLUMO; Figure 2) that propagates through the space between the electrophoric subunits and strides over the bond network of the U-shaped scaffold. This SupLUMO is built from a σ-type overlap of the 2pz atomic orbitals (AOs) of the proximal Cγ of vicinal pyridiniums (with the distance between Cγ atoms smaller than or equal to 3.40 Å, the van der Waals contact). SSI is limited here to spin pairing within the SupLUMO to yield the corresponding SupHOMO (Figure 2), i.e., the elongated CC σ bond. The U-shaped scaffold that more or less strictly pre-organizes the spatial arrangement of redox centers is usually a rigid (e.g., 1,8-naphthyl)30 or semi-rigid (e.g., biphenyl)31 linker.
In the present study, the situation is reversed: U-shaped folding of superelectrophores30, 31 is anticipated to result from LD-driven interactions between oligomethylene-linked pyridinium termini (short n-alkane molecules with H-terminals normally adopt a linear all-trans conformation).
With these three electrochemical paradigms in mind, we can approach the reductive formation of cyclomers using SSI as a yardstick. The question to be answered is whether molecular folding leading to σ bond formation occurs (1) at the early stage of electrophoric units in their native cationic state (N-methylpyridinium groups), or (2) at the later stage of their one-electron reduced form, i.e. N-methylpyridinyl radicals, as postulated in previous work9-13 (Figure 3; see also section S2 in the SI). In the former case, supramolecular MOs (supra-MOs) such as SupLUMO (and SupSOMO) may emerge, which are likely to annihilate the independence of the redox centers despite the saturated nature of the oligomethylene linkers. The existence of supra-MOs is traced back by demonstrating single-step two-electron reductions with PI.
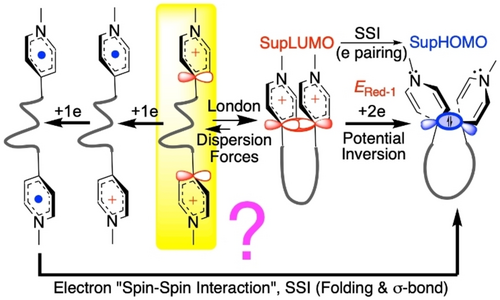
Two possible pathways for cyclomer formation. Right: Implementation of the working principle of the Structronic paradigm with a flexible linker, the London Dispersion forces promoting the folding, that is, pre-organization of electrophoric components. Left: Independent monoelectronic reductions prior to folding for σ bond formation (“intramolecular dimerization”) according to previous work.
Thus, the main question addressed in the present work is mechanistic in nature. By combining molecular electrochemistry with computational chemistry at the density functional theory (DFT) level, we show here that statement (1) accurately accounts for both our experimental results (electrochemistry) and those previously reported in the literature (Figure 1, top), provided that key ingredients are added, namely, the often-underestimated LD forces and supra-MOs.
Results and Discussion
The characterization of -predominant- (see Figure 4) cyclomers derived from the chemical reduction with Na/Hg amalgam of 4,4′-oligomethylenebipyridinium superelectrophores was performed and the identity of the compounds was unambiguously established (see Figure 1, top).9-13 For reasons of consistency and to avoid subtle effects coming from the surrounding medium, we performed our electrochemical and theoretical studies in the same solvent as in previous works, namely acetonitrile. Indeed, preliminary calculations show that there is a pronounced environmental effect when changing the solvent (e.g. from acetonitrile to dichloromethane), which affects both the relative stability of the conformers and the electrochemical behavior, i.e. the standard reduction potential (see section S3.6 in the SI). This is essentially due to different dielectric constants (charge screening) and Gutman donor numbers (solvation).
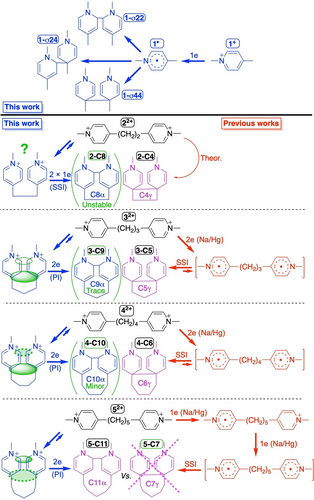
Top: reductive σ-dimerization of the reference N-methyl-4-picolinium cation 1+ (this work). Bottom: reduction schemes for dicationic assemblies 22+ to 52+, left side in blue: this work (electrochemistry); right side in red: previous work (reduction with Na/Hg).9-13 Purple color: issued from both previous work and this work. In red square brackets: postulated but not detected (EPR, UV/Vis.-NIR). PI stands for potential inversion. Green solid (or dashed) ellipsoids: SupLUMO through-space contribution (see text).
For the necessity of our electrochemical studies, all five molecules (1 to 5; Figure 4) were resynthesized as hexafluorophosphate (PF6−) salts. The complete characterization of molecules 1 to 5 and the single-crystal X-ray diffraction of 2 to 4 are provided in Sections S5 and S6 of the SI.
Computational Strategy. Impact of London Dispersion Forces
For a given charge state Z=+2 (native), Z=+1 (one-electron reduced) or Z=0 (two-electron reduced), the stabilization energy (▵Estab, kcal/mol) of folded (U-shaped) conformers with respect to their corresponding all-trans (extended) conformers is calculated as ▵Estab=(Efolded−Eall-trans). The energy of each conformer is computed using the large def2-TZVPP basis set32 together with the PBE0 global hybrid density functional33 after structure optimization at the same level of theory. The D3(BJ) empirical dispersion correction,34 later called D3, is added to the DFT computation to properly account for the effects of weak—medium range—forces such as LD, which decreases as a function of 1/dLD6 (where dLD is the distance between interacting molecular moieties).
Table 1 summarizes ▵Estab values calculated without (PBE0) and with the empirical D3 corrections (PBE0-D3), for the superelectrophores distinguished both by their oligomethylene linker and by the connectivity (α-α/γ-γ) of their corresponding cyclomers (from C4γ to C11α; Figure 4). The more negative ▵Estab value is, the more stable is the folded conformation. The stabilization of the folded native structure (Z=+2) is systematically increased by about 1 to 5 kcal/mol (depending on the linker) by the addition of the dispersion correction. From a structural point of view, this energy stabilization is reflected in a tighter stacking of the pyridinium rings in the transition from PBE0 to PBE0-D3. The same behavior is observed for one- and two-electron reduced species (Z=+1 and 0), respectively. For Z=+2, folding is referred to as a “promoted pre-organization”. It follows that the dispersion forces play a determining role regardless of Z, making folded and extended conformers nearly isoenergetic (within 1 kcal/mol) for dicationic native species. Notably, folding is unnatural for short n-alkanes, which tend to adopt the all-trans conformation,35-37 hence the role of pyridinium termini as LD-responsive components.
|
▵Estab (PBE0) |
▵Estab (PBE0-D3) |
d(C−C)[a]/Å |
||||||
|---|---|---|---|---|---|---|---|---|---|
Z |
+2 |
+1 |
0 |
+2 |
+1 |
0 |
+2 |
+1 |
0 |
2: n-Ethylene (C4γ) |
+0.81 |
+1.48 |
−11.83 |
−0.38 |
+0.23 |
−19.15 |
3.040 |
3.091 |
1.629 |
2: n-Ethylene (C8α) |
+0.81 |
+2.60 |
+3.63 |
−0.38 |
+0.23 |
−2.72 |
5.466 |
4.368 |
1.679 |
3: n-Propylene (C5γ) |
+1.76 |
+0.35 |
−16.78 |
+0.32 |
−4.57 |
−21.45 |
3.709 |
2.764 |
1.595 |
3: n-Propylene (C9α) |
+1.76 |
−3.34 |
+3.74 |
+0.32 |
−8.79 |
−3.81 |
6.835 |
3.468 |
1.658 |
4: n-Butylene (C6γ) |
+5.94 |
−1.67 |
−20.31 |
+0.91 |
−8.39 |
−26.49 |
3.227 |
2.844 |
1.598 |
4: n-Butylene (C10α) |
+5.94 |
−1.67 |
−7.01 |
+0.91 |
−7.79 |
−14.35 |
4.054 |
3.246 |
1.621 |
5: n-Pentylene (C7γ) |
+2.76 |
+0.68 |
+14.41 |
−0.76 |
−6.17 |
+5.33 |
4.458 |
3.855 |
3.580 |
5: n-Pentylene (C11α) |
+2.76 |
+0.68 |
−7.20 |
−0.76 |
−6.17 |
−15.89 |
3.788 |
3.176 |
1.628 |
- Boldface: discrepant values (see text).[a] d(Cγ−Cγ) or d(Cα−Cα) computed at PBE0-D3 level. See also Figure S1 in the SI.
As LD is shown to be a relevant attractive force for the series of superelectrophores, it is worth considering hereafter the correspondingly computed data (PBE0-D3) that include it.
The second interesting general observation is that the stabilization of the folded structure increases with the reduction state, i.e. from Z=+2 to Z=+1 to Z=0, regardless of whether LD is considered. Exceptions to this trend (bold in Table 1) will be explained below. This tendency thus indicates the existence of a stabilizing interaction unrelated to SSI when considering the intermediate ranking of ▵Estab(Z=+1) involving a single electron. We ascribe this role to the intervention of a supramolecular orbital (supra-MO) and, more specifically, the semi-occupied supra-MO, i.e. SupSOMO of the radical cation (see Figure 5).
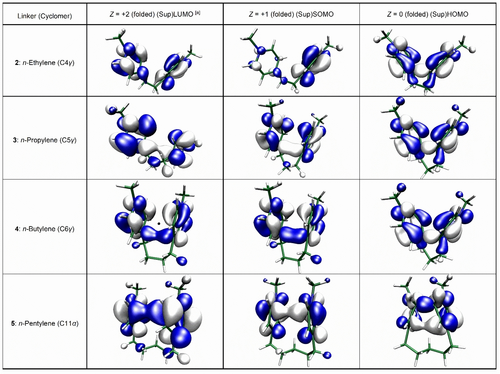
MOs (2) and supra-MOs (3–5) computed from PBE0-D3-optimized folded (U-shaped) prevalent conformers according to Table 1. Isocontour value is set at 0.04 a.u.[a] Isocontour values of SupLUMO of C5γ and C11α are respectively set at 0.02 a.u. and 0.025 a.u. for clarity.
Supramolecular Orbitals
The first question to be answered is whether a negative value for ▵Estab(Z=+2), implying that a folded (cisoid) conformer is more stable than its extended (transoid) counterpart, indicates the existence of a SupLUMO. We show that in the case of the ethylene linker, ▵Estab(Z=+2) is negative (−0.38 kcal/mol), while supra-MOs do not exist for symmetry reasons (see Figure 5). On the contrary, for derivatives of propylene and butylene having ▵Estab(Z=+2)>0 as well as for pentylene with ▵Estab(Z=+2)<0, SupLUMOs are effectively computed, as shown in Figure 5.
Mechanisms of Cyclomerization
Returning to the case study of the ethylene linker (molecule 2), computations show that the cyclobutane derivative (C4γ; Figure 4) is indeed more stable than the extended parent diradical by 19 kcal/mol (Table 1), despite a significantly elongated σ bond (d(Cγ−Cγ)=1.629 Å). Regarding the higher-membered cyclomer with a σ bond at α sites, namely C8α, the compound is computed to be barely stable (if formed) with an ultralong C(α)−C(α) bond of 1.679 Å.38 From the deprivation of supra-MOs, it follows that the formation of C4γ is expected, but following a cyclization mechanism reminiscent of that of the bimolecular σ dimerization, with σ bond formation occurring intramolecularly8 as a result of SSI (see also Figure S2 in the SI). Moreover, as far as the folded radical cation is concerned, inspection of Figures 5 and 6 reveals that the SOMO and spin density are localized on one of the two electrophoric subunits, instead of being delocalized over both heterocyclic spin carriers, as is the case for the other prevalent species that are conversely equipped with supra-MOs. This localization is likely to promote reactivity such as (bimolecular) σ dimerization. The above mechanism based on the SSI, referred to as EC2 mechanism in electrochemistry,39, 40 also implies that we are basically dealing with one-electron processes.
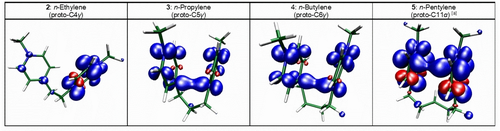
Spin density computed from PBE0-D3-optimized folded (U-shaped, Z=+1) prevalent conformers. Isocontour value is set to 0.004 a.u. (blue: increase, red: depletion).[a] Isocontour value is set to 0.002 a.u. for better visualization of C(α)−C(α) site.
A single one-electron process is involved in the formation of the σ dimer, or two one-electron processes are involved in the formation of the cyclomers C4γ and C8α.
On the other hand, for those superelectrophores with a SupLUMO, a one-step two-electron process of reductive σ bond formation is postulated, as is typical for the Structronic paradigm (Figures 2, 3 and 4).20 This potential inversion (PI) makes the radical cation elusive, which explains why no EPR signal could be detected from it, as noted in the literature.10-12 It is at the SupSOMO stage that U-shaped (cisoid) conformers are significantly stabilized as reflected by the considerable variation of both ▵Estab(Z=+1) and distances between C atoms about to be involved in σ bond formation, which approach the critical distance 3.40 Å of van der Waals contact (Table 1). Although the folded radical cations (Z=+1, SupSOMO) and the corresponding folded dicationic conformers (Z=+2, SupLUMO) have geometries that are close to each other except for the distances between the proximal carbon atoms, it is from the radical cation that the ▵Estab(Z) values begin to diverge, again highlighting the key role of SupSOMO in determining the formation of the γ-based or α-based cyclomers. The main structural relaxation, i.e. the driving force for PI, is the tetrahedralization (hybridization change from sp2 to sp3) of two C atoms directly involved in σ bond formation, which occurs upon the second electron transfer. Thus, the increase in energy stabilization ▵Estab(Z) in the transition from radical cation to two-electron reduced cyclomer (Z=0, SupHOMO) is of greater magnitude than that obtained in the first one-electron reduction, except for the lower-membered cyclomer C7γ from the pentylene derivative, which is predicted to simply not exist (▵Estab(Z=0)=+5.33 kcal/mol and d(Cγ−Cγ)=3.580 Å). Again, this result is consistent with the experimental work on cyclomer formation from 4,4′-pentylene bipyridinium reduced with Na/Hg (Figure 4).13
Regarding the reduction processes, they are governed first by the (Sup)LUMO of different proto-cyclomers and then by the (Sup)SOMO for the second one-electron reduction. Thus, their energies are computed, together with those of the (Sup)HOMOs, as a function of the limiting conformations, namely the fully extended (i.e. all-trans) or the pre-organized for cyclomer formation, i.e. folded (Figure 7 and Table S1 in the SI).
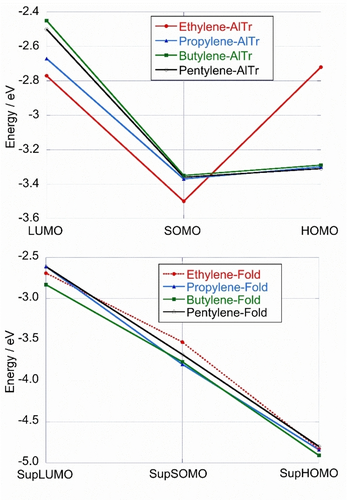
Energies (eV) of the (Sup)LUMO, (Sup)SOMO and (Sup)HOMO as a function of conformation: all-trans (AlTr) (top) and folded (Fold) (bottom) computed at the PBE0-D3 level. For SupSOMO and SupHOMO, the dominant species were considered. Dotted line actually corresponds to MOs of 2 (see text).
First of all, it should be recalled that extended all-trans conformers are described by regular MOs, whereas the reactivity of folded (pre-organized) conformers is governed by supra-MOs, with the exception of the ethylene derivative (deprived of supra-MOs). Looking at Figure 7, it appears that the energy of the (supra-)MOs depends on the conformation of the electrophores.
For all-trans conformations, an energy decrease of about 0.75 eV (from about −2.6 eV to −3.35 eV) is first observed in going from LUMOs to SOMOs, before a plateau is reached in the transition to HOMOs. The only discrepant behavior is related to the ethylene linker, which shows a decrease in energy when going from LUMO (−2.77 eV) to SOMO (−3.50 eV), followed by a marked destabilization of the HOMO (−2.72 eV). In other words, the diradical of the ethylene derivative (whether singlet or triplet, see Table S1 in the SI) is unstable.
On the contrary, for folded conformers, the energy decreases steadily by 2.1 eV from (Sup)LUMOs (ca. −2.70 eV) to (Sup)HOMOs (ca. −4.80 eV) via (Sup)SOMOs (ca. −3.75 eV). Notably, SupSOMOs are on average 0.25 eV more stable than SOMOs. The ethylene-linked electrophore (red trace in Figure 7) is also distinguishable, but this time only moderately.
Taken together, we observe that the folding pathway of conformers is energetically favored over that of extended diradical species, regardless of the spin multiplicity of the latter (see Table S1 in the SI). This is also true for the ethylene derivative deprived of supra-MOs. These results indicate that the process of prior folding is critical in the formation of cyclomers. Radical cations are shown to play a key role by taking over LD forces. This scenario is not in line with the mechanism proposed so far in the literature, which assumes the formation of diradical species prior to the folding process.9-13
Electrochemical Correlations
As a final step of our computational analysis, the standard potentials for the first (E10) and second (E20) one-electron reduction are calculated on the basis of our mechanistic model of cyclomer formation (Table 2; see also Section S1.3 and Table S2 in the SI). Indeed, these results can be confronted with experimental results based on cyclic voltammetry in order to assess the relevance of the description of the cyclomerization process based on the pre-organization of superelectrophores and supra-MOs.
Z=+2/Z=+1 |
E10/V |
Z=+1/Z=0 |
E20/V |
|---|---|---|---|
22+/2⋅+ (AlTr) |
−1.75 |
2⋅+/2⋅⋅ (AlTr) |
−2.77 [−2.14] |
22+/2⋅+ (Fold) |
−1.83 |
2⋅+/2-C4 (2⋅+/2-C8) |
−2.06 (−2.86) |
32+/3⋅+ (AlTr) |
−1.90 |
3⋅+/3⋅⋅ (AlTr) |
−2.12 [−2.10] |
32+/3⋅+ (Fold) |
−1.73 |
3⋅+/3-C5 (3⋅+/3-C9) |
−1.51 (−2.56) |
42+/4⋅+ (AlTr) |
−1.99 |
4⋅+/4⋅⋅ (AlTr) |
−2.08 [−2.05] |
42+/4⋅+ (Fold) |
−1.63 |
4⋅+/4-C6 (4⋅+/4-C10) |
−1.46 (−2.03) |
52+/5⋅+ (AlTr) |
−1.97 |
5⋅+/5⋅⋅ (AlTr) |
−2.10 [−2.07] |
52+/5⋅+ (Fold) |
−1.84 |
(5⋅+/5-C7) 5⋅+/5-C11 |
(−2.66) −1.87 |
- [a] Compound labeling is shown in Figure 4. For Z=0, diradicals of the all-trans (AlTr) conformation are computed as singlets or [triplets]. For folded species (Fold), redox couples in parentheses have small contributions (if any). Underlined values should be compared with experimental values (see Electrochemistry section).
Except for the peculiar case of 2, folded conformers are systematically easier to reduce than the corresponding all-trans conformers.
Let′s first consider the all-trans conformers that end up as diradical species after two-electron reduction. Again, the ethylene derivative (2) shows a discrepant behavior with a potential gap (▵E0=E10−E20) of about +1 V, indicating that the second reduction is much more demanding than for other derivatives (▵E0 ranges from +0.09 V to +0.22 V; average +0.147 V), while the E10 values of 3 to 5 are all close to the average value of −1.95 V. This observation suggests that in the case of 2, two one-electron reductions are not independent, indicating communication of redox centers via the alkane chain. Incidentally, STM-break junction experiments performed on the transoid dipyridyl-ethane analog allowed the measurement of a conductance value.41 In this sense, it is also worth noting that, with the exception of 2, calculated E20 values assuming triplet states for diradical superelectrophores are quasi-degenerate with those assuming singlet states (Table 2), consistent with the absence of through-bond mediated magnetic coupling between pyridinyl termini as radical carriers. In contrast to the ethylene linker, the other all-trans linkers behave as true “insulators”.
For the folded conformers that give rise to cyclomers according to our mechanistic model, E10 and E20 potentials are inverted (▵E0<0 V) giving ▵E0(3)=−0.22 V and ▵E0(4)=−0.17 V or coalescent giving ▵E0(5)=+0.03 V. This is in contrast to the cisoid ethylene derivative for which ▵E0(2)=+0.23 V. PI and, to a lesser extent, potential coalescence are diagnostic features for the presence of supra-MOs, which are electrochemically translated as single-step two-electron transfer processes.30, 31 PI also explains why the radical cation is elusive, as observed experimentally (no EPR signal detected during the reduction process).10-12 Regarding 2, it is expected that the two-electron reduction will proceed stepwise with two peaks close to each other.
Electrochemistry
The main characterization of the four superelectrophores (2 to 5) together with the reference N-methyl-4-picolinium hexafluoro-phosphate (1) is achieved by performing their cyclic voltammetry under different conditions (mainly concentration C and scan rate v). Typical cyclic voltammograms (CVs) recorded under the same conditions are shown in Figure 8.
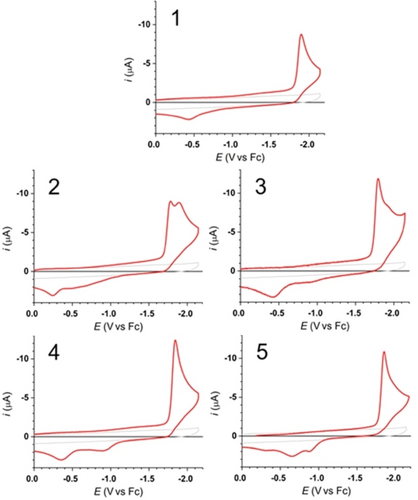
Cyclic voltammograms (CVs) in the absence (grey curves) and presence (red curves) of 10−3 M solution of 1 to 5 solutions in 0.1 M of TBAPF6 and acetonitrile recorded at scan rate of 10 V s−1.
The first observation is that all compounds exhibit a single irreversible reduction peak (Epc(1)~−1.90 V; Epc(3)~−1.80 V; Epc(4)~−1.84 V and Epc(5)~−1.86 V), as expected, with the exception of 2, with ethylene linker, which exhibits two closely spaced cathodic peaks at Epc1(2)~−1.78 V and Epc2(2)~−1.89 V.
Exhaustive electrolysis (coulometry) of two representative molecules 2 and 4 at −2.1 V allows to verify that both reduction processes involve two electrons per electrophoric assembly confirming transfer of two electrons for 2 to 5.
Let′s first consider the special case of 2. The experimental results are as follows. First, the variation of the first cathodic peak potential Epc1(2) as a function of the logarithm of the scan rate (see Figure S3 in the SI) shows that Epc1 shifts cathodically by 19.5±0.6 mV per decade, which is consistent with a variation of 19.7 mV/n per decade, where n is the number of electrons equal to 1 under the EC2 mechanistic scheme assumption corresponding to the intermolecular dimerization process.40 Secondly, Epc1 shifts by 18.8±1.2 mV per decade to positive potentials with increasing concentration of 2 (Figure 9), to be compared with the theoretical value of 19.7 mV per decade under the EC2 assumption.40 For example, in the case of dimerization of reference molecule 1, Epc shifts by 21.6±1.3 mV per decade to positive potentials with increasing concentration. Finally, Figure 8 shows that the heights of the peak currents for Epc(1) and Epc1(2) are virtually identical, indicating that a single electron is involved. Taken together, these results point to the same fate for the first one-electron transfer, i.e., intermolecular (bimolecular) σ dimerization. This is consistent with the computations, since the spin density mapping of 2 (Z=+1) shows that the first electron is localized on one of the two pyridiniums (see Figure 6), yielding a reactive pyridinyl radical (but see caveat in section S4.2 of the SI). Regarding the fate of the second one-electron process leading to the diradical species: the latter is computed to be much more stable in its folded conformation than in its all-trans conformation (Figure 7 and Table S1 in the SI). Under this assumption of a dominant folding for 2, the two separate and closely spaced standard potentials computed for two one-electron reduction processes (Table 2) agree well with the experiment (Figure 8). According to Table 1, the more stable cyclomer of the two possibilities is by far the γ-linked one (2-C4 in Figure 4).
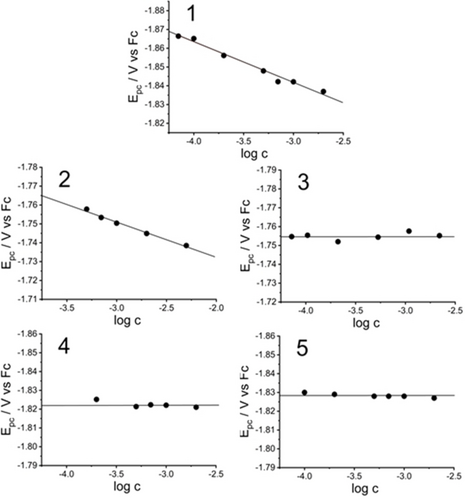
Plot of the first reduction potential Epc versus the logarithm of the concentration for molecules 1 to 5. Cyclic voltammograms were obtained in 0.1 M TBAPF6 in acetonitrile using a Pt working electrode at a scan rate of 0.025 V s−1 (molecule 1) and 0.5 V s−1 (molecules 2 to 5). The potential is referred to the Fc+/Fc couple.
Concerning the superelectrophore 4, as a representative of the redox-active assemblies 3 to 5, it should be noted that the height of its peak current ipc(4) for Epc(4) is ~12 μA, i.e. higher than for Epc(1) and Epc1(2), as is expected for a two-electron process. Importantly, and in contrast to molecules 1 and 2, the peak potential Epc(4) of the chemically irreversible reduction does not shift with increasing concentration, as shown in Figure 9. This finding suggests that we are dealing with an intramolecular process. Considering the electrochemical irreversibility, we deduce that the reduction mechanism consists of two one-electron transfer steps followed by a chemical step, i.e. an EEC process of intramolecular σ bond formation. The question now is whether the electron transfers are independent, as postulated by the SSI assumption (previous work), or not as suggested by the present theoretical study, which evidenced supra-MOs within folded superelectrophores (Figure 5) and which calculated the potential inversion for 3 and 4 (see Table 2). First reduction process in Figure 8 for all molecules 1 to 5 was submitted to semi-integration analysis to provide the semi-integrated current versus potential curves known as neopolarograms, see Figures S4 to S6 of the SI. The log-plot analysis of thus computed neopolarograms for molecules 1 and 2 give a straight line (Figures S4 and S5 in the SI) providing a variation of 56 mV per decade for 1 and 51 mV per decade for 2, which is close to the expected value of 59 mV per decade for one-electron transfer process.
Figure 10 shows the log-plot analysis of neopolarograms for 3 to 5 confirming the potential inversion for these molecules. The neopolarogram of 4 (Figure S6) has a simple shape, indicating that the first and second electrons are strongly correlated, as expected for electrons in the same orbital (supra-MOs). For both molecules 3 and 5, the neopolarograms show a post-reduction adsorption wave, which is clearly visible as bumps in the corresponding CVs (Figure 8). The effects of this adsorption, which have been properly accounted for (see section S4 in the SI), do not change the fact that the two monoelectronic transfers are also strongly correlated. The log-plot analysis in Figure 10 does not yield a straight line with a variation of about 30 mV per decade, which would be consistent with potential inversion of a large magnitude,4, 42, 43 as predicted by calculations (about 200 mV; see Table 2). Instead, as in the case of 5 (for which potential coalescence was predicted computationally), traces of a barely discernible S-shape (diagnostic feature for moderate potential inversion) are obtained, delimited by two asymptotes with the same slope approaching 59 mV per decade. This is an experimental finding that not only indicates that two one-electron transfers are fast, but also allows the determination of their formal reduction potentials E10 and E20. It turns out that these potentials are indeed experimentally inverted, but only moderately, with values of ▵E0=E10−E20 of −16 mV for 3, −28 mV for 4, and −26 mV for 5. Further discussion related to the EEC mechanism is provided in the section S4.3 of the SI. In short, the electron transfer steps are electrochemically-reversible with the rate-limiting step being the diffusion of molecules to the electrode. The fact that the process appears irreversible (no counter-wave) is due to chemical irreversibility: the reduced species are converted to the product(s) very quickly, which is consistent with our proposal. In summary, potential inversion has been experimentally confirmed for molecules 3 to 5, but due to the apparent weakness of the phenomena,44 the potential difference is only within the range −10 mV to −30 mV.
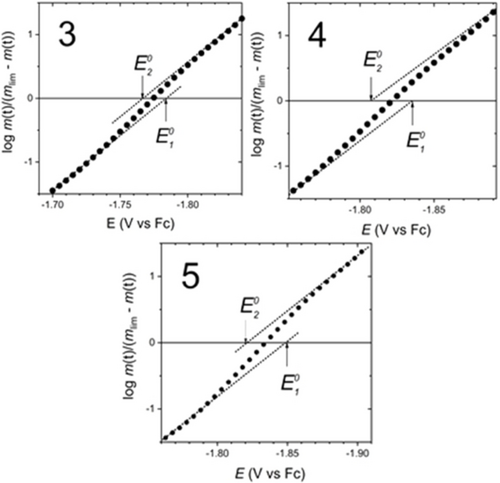
Log-plot analysis for superelectrophores 3 to 5 calculated for reduction of 1 mM solutions in 0.1 M TBAPF6 in acetonitrile, Pt electrode, scan rate 10 V s−1.
Conclusion
Contrary to currently accepted paradigms we showed that two pyridinium units separated by a saturated alkane chain fold as a consequence of the contribution of LD forces acting within the spin carriers both in the early stage of their diamagnetic native state (dicationic species) and in the subsequent stage of their one-electron reduced state (radical cation species). Folding, referred to as the pre-organization process, is thus induced in the native superelectrophore by the interaction of two pyridinium moieties. Folded assemblies, which resemble encounter pairs of electrophoric units, allow the onset of supra-MOs, with the exception of the ethylene derivative (2). If the SupLUMO by itself has no energetic impact on the stability of the folded -native- assemblies for 3 to 5, it plays a determining role in terms of the electrochemical mechanism. The LD forces-assisted formation of supra-MOs within 3 to 5 explains why virtually no σ-dimer is formed (bimolecular processes), but only intramolecularly σ-bonded cyclomeric assemblies are observed in (almost) quantitative yields (Figures 1 and 4); it also provides a rationale for the elusive character of radical cations (potential inversion).
Existence of the SupLUMO within molecules 3 to 5 explains why the two monoelectronic reductions are not independent but correlated, even though they take place at apparently the same potential to yield a two-electron wave. The radical cation in its folded conformation (SupSOMO), despite its elusive existence, explains the distribution pattern of γ–γ and α–α isomers of cyclomers as a function of linker length.
On the other hand, the redox-active assembly 2 is worth considering as a bis-electrophore properly described with regular MOs localized on pyridinium terminals with a residual electronic communication mediated through the ethylene bonds.
Overall, we show that electrophoric moieties that can legitimately be considered electrochemically independent due to the saturated nature of their linker are in fact strongly coupled (supra-MOs-driven σ bond formation) when folded and upon reduction. Although this coupling remains dependent on an equilibrium between all-trans and folded native conformers, it is easily shifted toward folding as the critical formation of the radical cation proceeds. The mechanism is upstream-driven by weak van der Waals forces, namely LD forces.
Supporting Information
The authors have cited additional references within the Supporting Information.45-55
Acknowledgments
Financial support by the Grant Agency of the Czech Republic (21-13458S), and the Academy of Sciences of the Czech Republic (RVO: 61388955), the Ministry of Education of the Czech Republic (Barrande Project 8J21FR016), the French Ministries of Europe and Foreign Affairs (MAE) and of Advanced Education, Research and Innovation (MESRI) (PHC Barrande, Project No. 46775VG), and the French National Research Agency, ANR (ANR-20-CE05-0041 and ANR-21-CE29-0003), is gratefully acknowledged. M.H., R.S. and E.V. acknowledge the assistance provided by the Advanced Multiscale Materials for Key Enabling Technologies project, supported by the Ministry of Education, Youth, and Sports of the Czech Republic. Project No. CZ.02.01.01/00/22_008/0004558, Co-funded by the European Union. EB also acknowledges the TGCC center for HPC resources (Project AD010810359R1).
Conflict of interests
The authors declare no conflict of interest.
Open Research
Data Availability Statement
The data that support the findings of this study are available in the Supporting Information.




