Agribusiness
Volume 39, Issue 3 pp. 691-702
RESEARCH ARTICLE
Open Access

Beef and pork processing plant labor costs

Christopher N. Boyer, 

Corresponding Author

Christopher N. Boyer

Department of Agricultural and Resource Economics, University of Tennessee, Knoxville, Tennessee, USA

Correspondence Christopher N. Boyer, Department of Agricultural and Resource Economics at University of Tennessee, Knoxville, TN, USA.

Email: [email protected]

Search for more papers by this author
Dayton M. Lambert, 

Dayton M. Lambert

Department of Agricultural Economics, Oklahoma State University, Stillwater, Oklahoma, USA

Search for more papers by this author
Charles C. Martinez, 

Charles C. Martinez

Department of Agricultural and Resource Economics, University of Tennessee, Knoxville, Tennessee, USA

Search for more papers by this author
Joshua G. Maples, 

Joshua G. Maples

Department of Agricultural Economics, Mississippi State University, Mississippi, Mississippi, USA

Search for more papers by this author
First published: 08 March 2023
https://doi.org/10.1002/agr.21804

Abstract

Federal and state legislators recently enacted policies to fund new and renovated small and local meat processors expansion with the aim of increasing the meat-processing sector's resiliency. Wages must be competitive to attract employees for these new and renovated plants to be competitive. No previous studies have examined what has happened to employee labor costs at United States (US) meat-processing plants since the early 2000s. This study estimates how meat-processing firm size affects employee wages in the US. We use average employee wages for beef and pork processing plants from 2007 to 2019. We find larger plants pay higher wages than smaller ones, which is likely attributable to lower fixed costs resulting from economies of scale. Findings suggest that facilities with more than 500+ employees will most likely offer wage that are high enough to recruit workers in for this industry. Small plants will need to increase real wages that are higher than historical averages. Thus, if smaller facilities increase the sector's resiliency, then it will likely come at a cost in terms of higher wage bills. [EconLit Citations: Q12, Q18].

Abbreviations

  • FI
  • Federal Inspected
  • HMC-NUTS
  • Hamiltonian Monte Carlo and No U-turn Sampler
  • MAR
  • Missing at Random
  • MCAR
  • Missing Completely at Random
  • NAICS
  • North American Industry Classification System
  • NMAR
  • Not Missing at Random
  • US
  • United States
  • USDA
  • United States Department of Agriculture

    • 1 INTRODUCTION

    Examining the resiliency and flexibility of the United States (US) meat processing supply chain emerged as an important research topic in the initial wake of COVID-19 (Bina et al., 2022; Ma & Lusk, 2021; Ijaz et al., 2021; Wahdat & Lusk, 2023). Across the US, meat-processing plants experienced numerous COVID-19 outbreaks, resulting in temporary shutdowns and a reduction in output. These events led to serious disruptions along protein supply chains (Krumel & Goodrich, 2022; Taylor et al., 2020) and rapid declines in animal prices combined with higher meat prices (Martinez et al., 2021). Policy makers focused efforts on to expand industry capacity (United States [US] Department of Agriculture [USDA], 2021b). Along with these investments, additional funding targeted meat processing workforce development and supported the development of lending programs to finance the capital needed to build these plants (USDA, 2021a).

    State and federal initiatives share the same goal of providing more opportunities for meat processing at smaller plants that cater to local demand for their services. A rationale of policies to expand smaller and more localized meat processing plants is to increase supply chain resiliency and flexibility or the time it takes for a firm to return to performance levels after experiencing a shock. Bina et al. (2022) found that such policies may generate unintended outcomes, given that labor is a key constraint for US meat processors (Bina et al., 2022; Hobbs, 2021; Ma & Lusk, 2021; Wahdat & Lusk, 2023). Meat processing industry employment has decreased over the last decade (Luckstead et al., 2022). More recently, the risk of COVID-19 spreading among meat processing employees and the shutdown of production lines due to a reduction in workers were the primary drivers of these disruptions (Luckstead et al., 2021, 2022; Ramsey et al., 2021). The pandemic exposed how vulnerable the animal slaughtering and the processing industry are to labor shocks in terms of gross output (Wahdat & Lusk, 2023).

    These proposed policy goals also reverse a general trend in the meat-processing sector over the past half-century of consolidation toward fewer large processing plants. Crom (1988) reported the number of US livestock physical slaughter plants declined by 46% from 1967 to 1986. Crom (1988) noted that a few large plants were built and operated more intensively using double shifts and 6-day work weeks. This trend continued through the 1990s (Hornung, 2004; Ward & Hornung, 2005). Hornung (2004) concluded that, by 1980, there were 520 beef federally inspected (FI) slaughtering plants that harvested 24.5 million head of steers and heifers annually. By 2000, total FI steer and heifer slaughter increased to 29.39 million head per year from fewer larger plants. After 2000, the US FI cattle slaughter industry saw a permanent decline in physical capacity following the closure of several plants, for example, Conagra in 2001, Tyson in 2008, and Cargill in 2013. A similar trend of fewer, but larger processing plants developed for the pork industry as well (MacDonald & Ollinger, 2000; MacDonald et al., 2000). The primary drivers of this structural change in the US meatpacking industry were economies of scale and size. Aggregate industry average total costs decreased as slaughter facility output increased (Koontz & Lawrence, 2010; MacDonald & Ollinger, 2000; Ward, 1990, 1993).

    Previous research suggests that these new and renovated small and local meat processors will need to offer sufficiently higher wages to attract workers in their effort to reduce the threat of labor vulnerabilities and increase the resiliency of the meat-processing supply chain. Wages must also be economically sustainable for the processing plant to remain profitable. MacDonald and Ollinger (2000) showed that labor costs at pork processing plants increased as the volume of processing increased from the 1970s to 1992, with larger plants paying employees more than smaller processors due to economies of scale. However, MacDonald and Ollinger (2005) found hourly wages were lower for large beef and hog processors than small plants in 1997 and 2002. A recent study by Luckstead et al. (2022) found that the current average wage for a meat-processing employee was lower than employee willingness to accept these jobs. They concluded that the average willingness to accept a wage offer at a meat processing facility was $22.77 per hour, which is higher than the national average of $15 per hour. Since the early 2000s, no previous studies have examined what happened to employee labor costs at US meat-processing plants across firm sizes.

    The objective of this study is to determine how several factors, including the size of meat processing facilities, affect employee wages in the US. We use average employee wages for beef and pork processing plants from the Statistics of US Business data tables, 2007 to 2019. The results provide insight into meat-processing wages across different plant sizes and locations. These findings could inform policy maker and agency decisions regarding the distribution of program funds to support wages in effort to stabilize the meat-processing labor force. Results also provide insight into the value of detailed labor data that could address important questions pertaining to the resiliency of the US meat processing supply chain.

    2 DATA

    Data are from the US Census Bureau for animal slaughtering plants (excluding poultry) (US North American Industry Classification System [NAICS] code 311611) from 2007 to 2019 (US Census Bureau, 2022). The data include establishments that slaughter hogs and cattle across the US. The data also include the number of processing establishments (equivalently, firms), total annual payroll, the number of employees by state, year, and facility processing size. The data are classified into firm size categories with ranges of less than 4 employees, 5–9 employees, 10–19 employees, 20–99 employees, 100–499 employees, and 500 or more employees. We calculate the average annual salary per employee at slaughtering plants by state, year, and size by dividing the total annual payroll by the number of employees. All payroll dollars were adjusted to 2019 dollars using the Employee Cost Index (US Federal Reserve Bank of St. Louis, 2022). We dropped plants located in Alaska, Nevada, New Hampshire, Delaware, Rhode Island, Connecticut, Massachusetts, and Vermont because these states did not report data for all these years. This left us with 2514 observations.

    Table 1 reports the summary statistics for annual employee salaries and the number of processing establishments according to size, which is based on the employment categories. Like MacDonald and Ollinger's (2000) findings for pork processors, we find larger processors pay higher salaries. Assuming a 50-week year and a 40-h work week, the average hourly wage was around $12 per hour for plants with less than 20 employees, around $15 per hour for plants with 20–99 employees, and around $18 per hour for plants with more than 100 employees. These statistics are similar to Luckstead et al.'s (2022) industry average estimates but are below the employee willingness to work in a processing facility. Table 1 also shows there are more processing plants with less than four employees than any other size category. The number of firms declines as size increases, which aligns with the industry concentration reported in previous studies.

    Table 1. Summary statistics of annual employee salary and number of firms for cattle and hog processing plants from 2007 to 2019.
    Size Variable Observations Mean SD Minimum Maximum
    Less than 4 employees Annual Employee Salary 346 25,810 13,679 9455 162,750
    Number of Firms 536 14 8 1 43
    5 to 9 employees Annual Employee Salary 382 21,830 7310 8532 95,611
    Number of Firms 517 9 6 1 28
    10 to 19 employees Annual Employee Salary 317 24,987 8750 5939 89,337
    Number of Firms 457 6 3 1 21
    20 to 99 employees Annual Employee Salary 209 32,582 8502 14,615 70,178
    Number of Firms 401 5 3 1 15
    100 to 499 employees Annual Employee Salary 84 38,440 7932 18,803 56,468
    Number of Firms 269 3 2 1 9
    500 plus employees Annual Employee Salary 151 39,179 5606 30,393 53,500
    Number of Firms 334 3 2 1 10

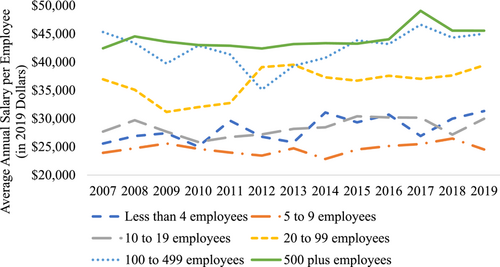
    Firm size and salary have changed over time. Figure 1 shows the percentage change in the number of beef and hog processing firms by size from 2007 to 2019. Plants with less than four employees have seen a 37% decline in establishments, starting from 691 firms in 2007 to 436 firms in 2019. Plants with more than 500 employees are essentially unchanged, from 84 in 2007 to 83 firms in 2019. Overall, the number of hog and cattle processing plants has declined by 25% from 2007 to 2019 (1565–1178 establishments, respectively) with most of the decline due to smaller processing plants. This trend has been documented since the late 1960s (Crom, 1988; Hornung, 2004; MacDonald & Ollinger, 2000; MacDonald et al., 2000).

    Details are in the caption following the image
    Figure 1
    Open in figure viewerPowerPoint
    Percentage change in the number of beef and hog processing establishments and annual employee salary by size from 2007 to 2019.

    Figure 1 also reports the percentage change on average adjusted salary per employee per year by firm size from 2007 to 2019. In 2019 dollars, average annual salary paid to workers increased by 7%, from $33,652 in 2007 to $35,972 in 2019. The largest percentage change occurred for firms with less than four employees. These wages increased from $25,579 (in 2007) to $31,335 (in 2019), but the increase was below the industry average (Figure 2). This could indicate that, while the plants with less than four employees increased wages, the increase was well below the industry average. However, higher wage costs might be associated with the decline in small establishments. This is a researchable question but outside the scope of the current study. Figure 2 reports the average adjusted salary from 2007 to 2019. The figure shows that larger firms are able pay higher wages compared to firms with a smaller payroll.

    Details are in the caption following the image
    Figure 2
    Open in figure viewerPowerPoint
    Average annual salary per employee (in 2019 dollars) of beef and hog processing firms by size from 2007 to 2019.

    3 METHODS AND PROCEDURE

    We estimate a log-linear regression of adjusted salary per employee per year by firm size on observed covariates using a Bayesian procedure introduced by Geweke (1993). Geweke's procedure models the distribution of heteroskedastic disturbances as a mixture of normal models, which, under certain regularity conditions, is equivalent to a Student- t $t$ distribution for the error terms. Koop et al. (2007), Starz (2015), and Gelman et al. (2013) provide additional details on Bayesian estimation of the Student- t $t$ linear model. The procedure used here to estimate the linear model with Student- t $t$ errors is based on the approach outlined by the Stan Development team (Stan Development Team, 2022).

    The response model with Student- t $t$ errors is:
    y itj ~ Normal ( μ itj , σ ∙ ω itj − 1 ) , ${y}_{{itj}}\unicode{x0007E}\text{Normal}({\mu }_{{itj}},\sigma \bullet {\omega }_{{itj}}^{-1}),$ ()
    where y itj ${y}_{{itj}}$ is the natural logarithm of average annual salary per employee in 2019 dollars for i $i$  = 1, …,   n $n$ states; t $t$ indexes years; j $j$ indexes establishment size according to employees; μ itj ${\mu }_{{itj}}$ is a mean function for the log of salary; σ $\sigma $ is the standard deviation for the model errors; and ω itj ${\omega }_{{itj}}$ is heteroskedastic term that varies across observations. Note that this parameterization is agnostic concerning any formalized heteroskedastic function.
    The mean response is parametrized as:
    μ itj = β 0 + β 1 ∙ estab itj + s j + c n + τ t , ${\mu }_{{itj}}={\beta }_{0}+{\beta }_{1}\bullet {{estab}}_{{itj}}+{s}_{j}+{c}_{n}+{\tau }_{t},$ ()
    with s j ${s}_{j}$ fixed effects for facility size class j $j$  = establishment with less than 4 employees, 5–9 employees, 10–19 employees, 20–99 employees, and 100–499 employees (500 plus employees are the reference group); c n ${c}_{n}$ are fixed effects for state n $n$ = 1, …, 42 (Wyoming is the reference state); and τ t ${\tau }_{t}$ are yearly fixed effects for t $t$  = 2007…2018 (2019 is the reference year). The variable estab ${estab}$ is the number of animal processing establishments.
    Priors for the population effects are normal, weakly informative, and centered on zero with a standard deviation of 100:
    β 0 , β 1 , s j , c n , τ t ~ Normal ( 0 , 100 ) . ${\beta }_{0},{\beta }_{1},{s}_{j},{c}_{n},{\tau }_{t}\unicode{x0007E}\text{Normal}(0,100).$ ()
    The normal distribution is used as the prior for the model parameters because (1) the probability the parameter lies below or above zero is the same, and (2) it is centered on zero, which corresponds with our null hypotheses, β = 0 $\beta =0$ (McElreath, 2020). The prior for the model's error standard deviation is Half-Cauchy with a lower bound of zero and a relatively diffuse prior on the scalar term's variance:
    σ ~ Half Cauchy ( 0,100 ) . $\sigma \unicode{x0007E}\text{Half Cauchy}(\mathrm{0,100}).$ ()

    The Cauchy distribution has wide, flat tails and is amenable to modeling potential residual outliers.

    The prior for the heteroskedastic terms, ω $\omega $ , is:
    ω i 2 ~ Gamma ν 2 , ν 2 , ${\omega }_{i}^{2}\unicode{x0007E}\text{Gamma}\left(\frac{\nu }{2},\frac{\nu }{2}\right),$ ()
    which is a function of a degrees-of-freedom parameter, ν $\nu $ . The model's degrees of freedom are estimated jointly with the other model parameters. Joint estimation of the degrees of freedom parameter with the other model parameters allows the data to determine the width of the Student- t $t$ tails for the error terms. Chung et al. (2013) recommended the following prior for the degrees-of-freedom term:
    ν ~ Gamma ( 2 , 0.1 ) , $\nu \unicode{x0007E}\text{Gamma}(2,0.1),$ ()
    with a lower bound of two. This parametrization ensures that the likelihood estimate is roughly one standard deviation from zero when the estimate of ν $\nu $ is approximately zero.

    3.1 Modeling missingness

    The US Census Bureau's data does not disclose wages and salaries paid to employees when the number of firms in a reporting district is small enough to identify employers. For this analysis, the number of records was 2514 observations, of which 41% (1025) observations for the dependent variable, salary, were suppressed due to administrative protocol. Isserman and Westervelt (2006) found that suppression is particularly common for establishments located in rural communities since one or several firms may employ a significant share of the community's population.

    The effect of missingness on inference depends on the mechanism causing missing values. If records with missing data are dropped, one implicitly assumes that the missing values are missing completely at random (MCAR) (Rubin, 1976). The MCAR assumption maintains that missing patterns are independent of other missing values and of other observed covariates. In this case, dropping records with missing values could reduce the power of tests but otherwise inference proceeds as usual.

    The other case, which is relevant here, assumes that suppressed salary records are missing at random (MAR). Unlike MCAR, MAR assumes that the likelihood of suppression is unrelated to other missing values for salary but its missingness is related to other observed data (Rubin, 1976). US Census suppresses employment and salary when an establishment, or several establishments, are identifiable in a surveyed region. Naturally, the pattern of missingness is a function of the number of firms because this is a leading criterion for suppression. Other factors, such as the categorical number of employees, annual-, and state-level effects could ostensibly codetermine suppression along with establishment count. The missing firm information is not “not missing at random” (NMAR) because the missing data mechanism is uncorrelated with missing values for salary and for the reason why the number of firms is candidate predictor of missingness.

    Several methods are available for contending with suppressed data issues. The first includes two imputation methods. The first imputation method, proposed by Isserman and Westervelt (2006), uses a hierarchical mathematical programming procedure to impute missing employment and salary information. Lower levels of missingness are filled in using matrix-balancing algorithms such as RAS (Schneider & Zenios, 1990). For example, state level totals are downscaled to county levels, conditioned on variation in employment across industry sectors and states as targets. Use of Isserman and Westervelt's procedure in this study would entail a two-step estimation procedure of the statistical model, with imputation of missing salaries in the first stage, and estimation of the statistical model in the second stage. The second imputation approach uses statistical procedures to generate pseudo-datasets with missing values replaced with predicted values estimated with complete cases. Examples of this procedure include “hot deck” imputation (Lohr, 2010) or the use of multiple imputation by chained equations (“mice”) (Zhang, 2016). These procedures also entail a two-step estimation procedure, with imputation in the first stage and estimating the statistical model with the imputed data sets in the second stage.

    We use a model-based approach to estimate simultaneously the statistical model and to impute MAR values for the dependent variable; salary. The model-based approach taken here considers missing records as unknown but estimable parameters that share a joint distribution with the population effects and other model components. The advantage of the model-based approach over the previously mentioned imputation procedures is that it specifies a joint density function of the missingness mechanism and the statistical model. The likelihood function of the joint distribution is maximized to estimate both MAR values for salary along with population effects and other model components. In theory, specification of a joint distribution function for MAR outcomes and the statistical model used here should increase the efficiency of parameter estimates. Future studies could compare the relative efficiencies of competing procedures using Monte Carlo experiments.

    In this analysis, the likelihood that salary is missing depends on the number of firms in a reporting district and other observable characteristics, but not on the other missing values of salary. Gelman et al. (2013) label similar cases as MAR with an ignorable missing mechanism and proposed a latent variable approach to condition observed and missing values on model covariates. Latent outcomes are:
    y itjk * = y itjk obs , if salary is observed, y itjk mis , otherwise. ${y}_{{itjk}}^{* }=\left\{\begin{array}{c}{y}_{{itjk}}^{{obs}},\,\text{if salary is observed,}\\ {y}_{{itjk}}^{{mis}},\,\,\text{otherwise.}\end{array}\right.$ ()
    Let w $w$ index all observations and W $W$ the total number of observations. The variable y w * ${y}_{w}^{* }$ is observed and equal to y w ${y}_{w}$ for w $w$  = 1, 2, …,  m $m$ , m $m$  <  W $W$ . The dependent variable is missing for all other w $w$  =  m $m$  + 1, m $m$  + 2, …,  W $W$ observations. In this case, the joint distribution for the observed and missing values for salary is:
    y obs y mis ~ Normal ( μ , σ ∙ Ω − 1 ) , $\left[\begin{array}{c}{{\bf{y}}}^{{obs}}\\ {{\bf{y}}}^{{mis}}\end{array}\right]\unicode{x0007E}\text{Normal}({\boldsymbol{\mu }},\sigma \bullet {{\boldsymbol{\Omega }}}^{-1}),$ ()
    with Ω = diag ( ω 1 , ω 2 , … , ω W ) ${\boldsymbol{\Omega }}{\boldsymbol{=}}\text{diag}{\boldsymbol{(}}{\omega }_{1}{\boldsymbol{,}}{\omega }_{2}{\boldsymbol{,}}\text{\unicode{x02026}}{\boldsymbol{,}}{\omega }_{W}{\boldsymbol{)}}$ and bold font indicating vectors and matrices. The prior distribution for y mis ${{\bf{y}}}^{{mis}}$ is truncated-normal with a lower bound of zero and a standard deviation of 100.

    3.2 Estimation procedures

    The complete cases ( n $n$  = 1025) and missing at random models ( n $n$  = 2514) are estimated with R-Stan's Hamiltonian Monte Carlo and No U-turn Sampler (HMC-NUTS) (Stan Development Team, 2022). The performance of the HMC-NUTS algorithm is superior to Gibbs or standard Metropolis-Hastings algorithms in terms of the number of iterations typically required to achieve convergence and the relative speed the algorithm affords compared to other samplers (Hoffman & Gelman, 2014).

    We ran the HMC-NUTS sampler on four parallel chains with 5000 iterations per chain and a warm-up (“burn in”) period of 5000 iterations. Every fifth sample was saved following the warm-up period, resulting in 4000 posterior samples for each model parameter. Gelman and Rubin's (1992) R ˆ $\hat{R}$ -statistic is used to confirm chain convergence. A R ˆ $\hat{R}$ diagnostic approaching one indicates convergence.

    4 RESULTS

    We organize the results by first discussing significant independent variables included in both models, followed by discussion of estimated salaries for workers at different sized facilities. Finally, we connect these findings back to the literature to build on the discussion of labor costs for hog and beef processing facilities. Table 2 reports the model statistics and estimated parameters. All R ˆ $\hat{R}$ -statistics are less than 1.01, indicating that both models converged. The posterior log likelihood value was larger for the model using the completed cases than when modeling with missingness; however, there is little difference in the estimated parameters and their significance.

    Table 2. Estimated parameters for US hog and cattle processing plant employee salary
    Complete cases Modeling missingness
    Variable Estimate Z-score Estimate Z-score
    Establishments (count) 0.0013 0.87 0.0022 1.47
    less than 4 employees −0.4414 −14.42 −0.4899 −16.55
    5–9 employees −0.5465 −21.18 −0.5844 −22.83
    10–19 employees −0.4389 −17.99 −0.4652 −19.63
    20–99 employees −0.1874 −7.47 −0.2031 −8.22
    100–499 employees −0.0459 −1.44 −0.0316 −1.04
    Year fixed effects Yes Yes
    State fixed effects Yes Yes
    Sample size 1025 2514
    Posterior log likelihood −830 −4770

    Annual salary varied across time and state, but the year and state fixed effects are not reported or discussed here. The year fixed effects are included to capture variation in beef and pork demand changes, wage inflation, and employment. State fixed effects are difficult to interpret because employment laws vary across states, but these variables serve as a proxy for this unobserved heterogeneity. Predicted values of salaries by state are reported in an appendix figure.

    For both models, the sign and significance of the estimated parameters were similar. These data are MAR, but there does not seem to be any inferential differences in salary for hog and beef processing facilities with or without the missing salary data. This finding is important, considering 41% of the salary data were missing.

    The number of firms in a state and by size was not significant in either model. However, the estimated parameters for beef and hog processing facilities with less than 4 employees, 5–9 employees, 10–19 employees, and 20–99 employees were significant and negative. Thus, the labor costs at smaller-sized processing facilities were lower than the labor cost at facilities with 100–499 employees and 500+ employees. There was no difference in annual labor costs for at facilities with 100–499 employees and 500+ employees.

    Figure 3 summarizes the estimated predicted annual cost per employee by enterprise size with the completed cases and modeling the missing data. We find the average annual labor cost for employees at US beef and hog meat processing facilities increased as volume increased. This finding corresponds with MacDonald and Ollinger (2000)'s findings for pork processors. The average annual salary was between $25,000 and $30,000 for facilities with less than 20 employees. Facilities with 20–99 employees paid an average annual salary of $37,858, while the facilities with 100–499 employees paid an average annual salary of $44,900 and 500+ employees paid an average annual salary of $46,400. The estimated predicted annual salary per employee was similar for both models.

    Details are in the caption following the image
    Figure 3
    Open in figure viewerPowerPoint
    Predicted average annual salary per employee (in 2019 dollars) of beef and hog processing firms by size.

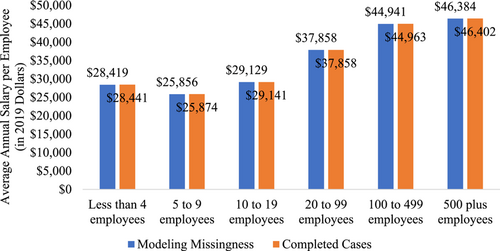
    Luckstead et al. (2022) estimated the average willingness to accept employment at a meat processing facility was $22.77 per hour. Assuming a 50-week year and a 40-h work week, they estimated an average annual salary of $45,540. This is higher than what we predict for plants with less than 500 employees. However, the estimated predicted annual salary for plants with more than 500 employees was above this willingness to accept level. Data used in this analysis was in 2019 dollars, while Luckstead et al.'s (2022) estimate in nominal wage for 2020. Regardless, facilities with more than 500 employees are the size that will most likely achieve wage levels needed to recruit workers in for this industry.

    Smaller plants, which are the target of proposed and active policies, have been historically unable to compete with larger facilities in terms of wages. However, this might be the salary level at which a smaller facility is profitable. Economies of scale and size were the drivers of the shift to fewer, larger meat processing plants (Koontz & Lawrence, 2010; MacDonald & Ollinger, 2000; Ward 1990, 1993). Scale economies are also likely the reason that larger plants can pay higher wages because they have lower per animal fixed costs than smaller plants. Smaller, local meat processing plants that offer higher wages in effort to attract employees increase variable costs, which are subsequently passed upstream to producers or downstream to customers. This finding supports Krumel (2017)'s forecast of how changes in the labor force for meatpacking impact consumers. Krumel's paper focused on anti-immigration reform policies on meatpacking costs. Krumel argued that policies that increased labor costs or cause labor shortages reduce overall economic welfare. Overall, the findings are consistent with Bina et al. (2022)'s study. Bina et al. concluded that policies supporting the expansion of processing capacity might produce unintended outcomes because labor would remain a constraint. Luckstead et al. (2022) surveyed results and found that other benefits, like a signing bonus, could be another way to attract meat-processing workers. Smaller plants currently promoted through newly implemented polices might consider how to utilize other types of employee benefits.

    5 CONCLUSIONS

    Recently, federal and state policies have been enacted to fund the expansion of small and local meat processors. For these policies to increase the meat-processing sector's resiliency, new and renovated plants will need to offer competitive wages to attract employees. However, to our knowledge, no previous study has examined what happened to employee labor costs at US meat-processing plants across various sizes since the early 2000s. This study determined how the size of meat processing facilities affects employee wages in the US. We used average employee wages for beef and pork processing plants from the Statistics of US Business data tables, 2007–2019.

    These findings could help policy makers and agency funders make decisions regarding the distribution of funding to the meat-processing sector that would support wages to stabilize the meat-processing labor force. Results could also provide insight into the value of detailed labor data that could address important questions pertaining to the resiliency of the US meat processing supply chain.

    We find annual employee wages vary across meat processing plant size. Larger plants can pay a higher wage than the smaller plants, which is likely due to lower fixed costs attributable to economies of scale. The paper finds that small plants, which are the target of these proposed and active policies, have historically been unable to pay employees the wages needed to retain workers. The results suggest that policies that add physical processing capacity to improve resiliency may generate unintended outcomes, given labor constraints.

    A shortcoming of this study is that employee wages at a plant were modeled as an average of all employees. We know that not all jobs within a meat processing facility are created equally, and thus wages will vary by job title within a plant. Some jobs will, which require more skill in processing, likely get paid a higher wage than other positions (i.e., the person splitting the carcass vs. the person that collects trimmings). High skill jobs are the ones that will have the biggest implications on meat processing resiliency. These are the employees that are harder to train, retain, and replace. This study is unable to estimate wages by job across plant size. That said, the results provide insight into the challenges smaller new or renovated plants will face with labor costs.

    ACKNOWLEDGMENTS

    This research was partially funded by United States Department of Agriculture Office of the Chief Economist grant number 58-0111-21-019.

      CONFLICT OF INTEREST STATEMENT

      The authors declare no conflict of interest.

      ETHIC STATEMENT

      Not applicable.

      Biographies

      • Christopher N. Boyer is a professor in the Department of Agricultural and Resource Economics at University of Tennessee. His research is focused on farm management and risk management. He received is PhD from Oklahoma State University.

      • Dayton M. Lambert is a professor and Willard Sparks Chair in the Department of Agricultural Economics at Oklahoma State University. His research area is econometrics, rural economics, and production economics. He received his PhD from Purdue University.

      • Charles C. Martinez is an assistant professor in the Department of Agricultural and Resource Economics at University of Tennessee. Dr. Martinez is an Extension Specialist in farm and financial management. He received his PhD from Texas A&M.

      • Joshua G. Maples is an associate professor in the Department of Agricultural Economics at Mississippi State University. Dr. Maples is an Extension livestock specialist and his research interest is in agricultural markets. He received is PhD from Oklahoma State University.

      DATA AVAILABILITY STATEMENT

      These data are publicly available and location cited in the manuscript.

        The full text of this article hosted at iucr.org is unavailable due to technical difficulties.