From Hyperinsulinemia to Cancer Progression: How Diminishing Glucose Storage Capacity Fuels Insulin Resistance
ABSTRACT
Background
Type 2 diabetes (T2D) is a complex metabolic disorder characterized by insulin resistance, hyperglycemia, and hyperinsulinemia. A significant portion of individuals with T2D are unaware of their condition until it has reached advanced stages. T2D is also associated with an increased risk and worse prognosis of cardiovascular disease, cognitive decline, and cancer. Understanding the mechanisms underlying the emergence of insulin resistance is critical for improving early detection and therapeutic interventions.
Methods
An updated framework is proposed to describe the emergence of insulin resistance that precedes the development of T2D. The model focuses on the impact of diminishing capacity to store excess glucose, which can occur due to a multitude of factors, including age-related muscle loss. The model is used to simulate responses to oral glucose tolerance tests (OGTTs) to capture the transition from a normal to a diabetic phenotype, as defined by the Kraft criteria. Additionally, the model is used to explore how the metabolic environment influences tumor progression, drawing on experimental data regarding the impact of transient diabetic phenotypes and hyperinsulinemia on cancer therapy efficacy.
Results
The model successfully demonstrates that reduced glucose storage capacity can qualitatively reproduce the progression from normal to diabetic phenotypes observed in OGTT responses. Furthermore, it shows that tumor progression or regression is highly dependent on the host's metabolic environment, particularly hyperinsulinemia. This aligns with experimental results that connect drug-induced hyperinsulinemia to a loss of therapeutic efficacy against tumors, whereas the reversal of the diabetic phenotype could restore drug sensitivity and treatment response.
Conclusions
This study highlights the critical role of hyperinsulinemia, even in normoglycemic individuals, in both the progression of T2D and the modulation of cancer therapy outcomes. Addressing hyperinsulinemia emerges as a promising strategy to enhance cancer treatment efficacy and improve overall health outcomes in patients with or at risk for T2D.
1 Introduction
Type 2 diabetes (T2D) is a complex metabolic disorder that is characterized by insulin resistance (IR) and hyperinsulinemia, followed by progressive decline in the capacity of pancreatic beta cells to produce insulin [1]. According to Ogurtsova et al. [2], in 2021 almost a quarter of adults in North America were unaware of having T2D, whereas in West Africa, Western Pacific, and Southeast Asia, this number can be more than 50%. The incidence of pre-diabetes is estimated to be even higher [3], with nearly 70% of individuals with pre-diabetes expected to progress to overt diabetes within their lifetime [4, 5].
This observation is particularly troubling because hyperinsulinemia can occur in individuals with normal blood glucose and is frequently undetected. In a classic study, Kraft et al. [6] analyzed the response of 3650 patients to an oral glucose tolerance test (OGTT), where a bolus of 100 g of glucose was administered to each person, and their blood glucose and insulin levels were assessed at baseline, 30, 60, 120, and 180 min [6]; the analysis was subsequently redone on a larger patient dataset by Crofts et al. [7] to address technical limitations of the original work. Five different patterns of glucose–insulin dynamics were identified. Pattern I described the norm, with fasting insulin levels maintained below 30 µIU/L, with a peak occurring at 30–60 min, followed by return to baseline by 180 min; the pattern of postprandial (after the meal) glucose increase and return to baseline is normal. Pattern II described individuals with still normal glucose dynamics but delayed return to baseline of insulin levels, suggesting that more insulin was becoming needed to stabilize glucose levels. Pattern III showed delayed insulin peak and higher postprandial glucose levels, as well as a longer return to baseline. Finally, Kraft IV pattern revealed both higher postprandial levels of glucose, longer time to return to baseline and higher baseline levels of both insulin (over 50 µIU/L) and glucose, consistent with patterns observed in people with T2D; for these individuals, insulin production from the pancreas was not sufficient to lower blood glucose levels to normal levels. (Notably, Pattern V was also identified, where insulin levels never rose above 30 µIU/L, whereas blood glucose levels were very high; this pattern is more reminiscent of type 1 diabetes [T1D] and is omitted in the subsequent analysis presented in this work, which is aimed at simulating the emergence of IR, leading specifically to T2D.) Critically, Crofts et al. [7] identified that over half of participants showed hyperinsulinemia despite normal glucose clearance [7], indicating that metabolic dysregulation begins significantly prior to it being detectable on blood glucose tests.
In addition to being associated with a higher incidence of complications, including chronic kidney disease and retinopathy, T2D is also associated with a higher incidence and worse prognosis of many other conditions, including cardiovascular disease, cognitive decline, and cancer [8-11]. Intriguingly, it was recently demonstrated in animal models that a diabetic phenotype can cause resistance to certain types of cancer therapy. Specifically, in Hopkins et al. [12], the authors showed that administration of PI3K inhibitors to mice with implanted tumors caused an emergence of both hyperglycemia and most importantly hyperinsulinemia, which in turn caused the development of resistance to therapy. However, sensitivity to therapy was restored in all 12 tested tumor models when the authors corrected the diabetic phenotype through either administration of metformin, which reduces liver gluconeogenesis [13], through administration of sodium glucose cotransporter protein-2 (SGLT2) inhibitors, which increase glucose excretion in the urine, or via carbohydrate-restricted ketogenic diet. The authors confirmed that although elevated glucose may have contributed to an emergence of resistance through providing cancer cells with extra substrate, it was the correction of specifically hyperinsulinemia that caused the restoration of sensitivity to therapy. In fact, it is well established that insulin can act as a powerful growth factor for cancer cells [14-17] and that individuals with elevated insulin-like growth factors (IGF) have an elevated a risk of developing multiple types of cancer, ranging from breast cancer to hematological malignancies to glioblastoma [18-21]. Normalizing baseline insulin levels can diminish a proliferative signal, thereby allowing for the cytotoxic effects of the drug to outweigh the insulin-augmented growth of the tumor.
The classical paradigm for understanding the emergence of IR is through loss of sensitivity to signaling between the hormone insulin and its receptor. A classical metaphor used to describe this interaction is “lock and key,” where insulin (the “key”) binds to a lock (“insulin receptor”), causing the translocation of an insulin-dependent glucose transporter, such as GLUT4, allowing glucose to enter the cell. If such an interaction is faulty (the metaphor of a “jammed lock,” in which the key cannot turn), then glucose cannot enter the cells and remains in the blood [22]. An alternative mechanism to understand the emergence of IR is that of a full train car: if the number of passengers in the train car is low, it is easy to let new passengers in. However, if the train car is full, opening more doors or keeping them open longer will not permit more passengers to enter until some have exited. Therefore, within this framework, the cause of elevated blood glucose is not the inability of insulin–receptor interaction to “open the door,” but the lack of capacity of a cell to store additional glucose.
There exist numerous mathematical models of varying complexity to describe glucose–insulin dynamics [23], with the unifying goal of most models to capture the emergence of IR as a function of different internal and external factors. The three best known detailed models of glucose–insulin dynamics are the Hovorka model, the Sorensen model, and the UVAPadova model, the latter being accepted by the Food and Drug Administration (FDA),[24]. These models have very high dimensionality and aim at capturing the many details of glucose–insulin interactions throughout the different tissue compartments in the body in as complete a detail as possible. An excellent summary of the key similarities and differences between these models is given in [25]. A smaller but still very detailed physiologically-based glucose–insulin model was developed by Alvehag and Martin [26], where the authors describe the feedback control of glucose regulation, keeping track of glucose and the three hormones insulin, glucagon, and incretins, and their distributions through multiple compartments in the body, including brain, liver, heart, lung, pancreas, and kidneys. There also have been developed several minimal models of glucose–insulin interactions aimed at answering more focused questions. For example, a recent minimal model with a delay by Murillo et al. [27] is used to analyze the impact of plasma free fatty acids on the emergence of IR. One of the keystone minimal models, however, was developed by Bergman et al. [28]. In this work, the authors were able to quantify the relationships between blood glucose and insulin based on experimental data available at the time; a fascinating account of the development and history of this model can be found in [29]. A qualitative update to the model has been developed by Topp et al. [30], where the authors included emerging understanding of the impact of high blood glucose on insulin-producing beta cells, which allowed capturing a wider range of physiologically plausible behaviors compared to the original Bergman model; an excellent account of both mathematical and physiological considerations underlying this modification can also be found in [31].
In what follows, we further update the minimal insulin–glucose model to include the limit on the body's ability to store excess glucose as a key factor that can affect the emergence of IR. Although glucose is primarily stored in the liver, adipose tissue, and skeletal muscle, we focus particularly on the latter as the largest modifiable storage depot. We show that variation in just one parameter can qualitatively reproduce the Kraft patterns of postprandial glucose–insulin dynamics, capturing the transition between normal glucose–insulin dynamics (Kraft I) to hyperinsulinemia and hyperglycemia, characteristic of Kraft IV (diabetes). We further analyze the relative impact of other factors on change in fasting insulin and glucose levels and show that metabolic environment may determine whether a microscopic tumor might regress or progress. We conclude with a discussion of the emerging evidence that medications developed for managing diabetes could become exciting combination partners to cancer therapy.
2 Model Description
The proposed model is a modification of the classical models by Bergman et al. [28] and Topp et al. [30], describing the change over time of blood glucose , insulin and beta cells , with the addition of an equation for intracellular glucose . The equation for food is added to simulate the effects of an ingested meal on blood glucose and insulin, as one would measure in a standard OGTT, to illustrate the ability of the model to qualitatively capture the key patterns of the four Kraft criteria.
It is assumed that a bolus of glucose is absorbed at a rate m, increasing the blood glucose level. Blood glucose can also increase as a result of gluconeogenesis [32], where the liver produces and releases glucose during fasting periods. The presence of insulin can additionally inhibit gluconeogenesis [33] as a mechanism of tight regulation of homeostatic blood glucose concentrations; these processes are described by the term .
We then assume that glucose can be cleared in an insulin-dependent and insulin-independent manner. Insulin-independent glucose clearance could involve rapid glucose absorption to meet immediate metabolic needs, or it could occur through insulin-independent transporters, such as GLUT1 [34]. Insulin-dependent glucose clearance involves binding between the insulin molecule and its receptor, which causes the translocation of the GLUT4 transporter on the surface of the cell, allowing the glucose to enter [35, 36]. Here, we describe this process similarly to Bergman et al. [28] and Topp et al. [30] as , where is the rate of insulin-mediated glucose clearance, also often defined as parameter of insulin sensitivity. The ranges for parameter were chosen on the basis of results reported in Figures 1 and 2 of Kahn et al. [37], where the authors report on the inverse relationships between insulin sensitivity parameters and fasting insulin concentrations.
We then modify this functional form by assuming that extracellular glucose is transported into an intracellular glucose storage compartment , which has a total carrying capacity . Excess glucose is assumed to be primarily stored in adipose tissue and skeletal muscle. As a result, the term for insulin-dependent glucose clearance becomes .
The equation for intracellular glucose then has an insulin-dependent inflow term described above and insulin-restricted clearance, an assumption that comes from the observations made by Jensen et al. [38]. In their study, the authors evaluated the relationship between insulin concentration and lipolysis (fat breakdown). They found that lipolysis was very sensitive to insulin, with higher insulin concentrations resulting in significantly lower lipolysis, whereas lower concentrations of insulin corresponded to greater fat breakdown. This inverse relationship between lipolysis and insulin is captured by the term , such that larger values of insulin reduce the rate of clearance of intracellular glucose. Parameters and were chosen to qualitatively capture the relationships between lipolysis and insulin in Figure 4 of Jensen et al. [38] for nondiabetic subjects.
The dynamics of blood insulin and beta cells are captured similarly to the classic model by Topp et al. [30]. It is assumed that insulin is produced by beta cells in the pancreas. Insulin secretion by is well-described by , a classical Hill function [39, 40], which reaches its half-maximal value when glucose concentration is , and where the steepness of the Hill function is determined by parameter n. In Alcazar and Buchwald [41], the authors measured the concentration–response relationship of insulin secretion in both human and murine islets, reporting the slope of the Hill function to be 3.4 for murine and 3.2 for human islets, with half-maximal concentration of glucose being approximately 14 mM for mice versus 8 mM for human cells. As such, parameters and in were chosen to be 3.2 and 8, respectively. It is also assumed that insulin is cleared at a normal rate .
The equation for the dynamics of beta cells comes from [30], where the authors capture the inverse quadratic relationship between glucose concentration and beta cell expansion and reduction, a phenomenon known as glucotoxicity. It was quantified experimentally by Efanova et al. [42], where rodent beta cell islets were co-incubated with different concentrations of glucose. The authors showed that beta cell viability increased, up to a point, proportionally to increase in glucose concentrations, presumably to match the necessary insulin production to maintain glucose homeostasis; however, high concentrations of glucose were toxic [42]. It has been proposed by Karin and Alon [43] that such a mechanism exists as a protection against the emergence of mutant cells that may perceive low glucose concentrations as higher than they are and compensate by excessive insulin production, thereby causing potentially fatal hypoglycemia. The simple quadratic equation proposed by Topp et al. [30] captures this relationship; parameters a, β, and c in Table 1 were taken from Topp et al. [30] and converted to corresponding units. Parameter p, describing the beta-cell-dependent insulin secretion rate, was also adapted from Topp et al. [30] and converted to corresponding units.
| Parameter | Description | Value | Units | Refs |
|---|---|---|---|---|
| m | Glucose absorption rate | 0.1 | 1/min | Estimated |
| Gin | Glucose production from the liver (gluconeogenesis) | 0.2 | mM/min | Estimated |
| Insulin-dependent reduction of gluconeogenesis | 0.008 | 1/min | Estimated | |
| kg | Insulin-independent glucose clearance | 0.017 | 1/min | Estimated |
| Rate of insulin-dependent glucose absorption into cells | 0.001 | 1/µIU/L | [37] | |
| K | Carrying capacity for storing excess glucose | 50 | mM | n/a |
| Rate of beta-cell-dependent insulin production | 0.03 | 1/min | [30] | |
| n | Parameter of steepness of the Hill function describing glucose-dependent insulin secretion by beta cells | 3.2 | n/a | [41] |
| Glucose concentration for half-maximal insulin production by beta cells | 8 | mM | [41] | |
| dI | Normal insulin clearance | 0.04 | 1/min | Estimated |
| b | Rate constant for beta-cell glucotoxicity | 5.833e − 7 | 1/mM^2/min | [30, 42] |
| a | Rate constant for glucose-mediated beta cell expansion | 0.27e − 4 | 1/mM/min | [30, 42] |
| c | Beta cell death rate | 1.667e − 9 | 1/min | [30, 42] |
| dgc | Rate of insulin-restricted lipolysis | 0.03 | µIU/L/min | Estimated from [38] |
| λ | Phenomenological parameter for capturing observed rate of insulin-restricted lipolysis | 0.4 | Unitless | Estimated from [38] |
| r | Rate of insulin-mediated tumor proliferation | 0.002 | 1/µIU/L/min | Estimated |
| aT | Rate of glucose consumption by the tumor | 0.003 | 1/mM | Estimated |
| hT | Handling/processing time for one unit of glucose | 0.1 | 1/min | Estimated |
| dT | Normal tumor death rate | 0.001 | 1/min | Estimated |
The summary of the key mechanisms described by the proposed model and their connection to the Kraft criteria described in Section 1 is given in Figure 1. Parameter values used in subsequent simulations are summarized in Table 1.
It should be noted that glucose concentrations are typically reported in the literature either in the units of mmol/L or in the units of mg/dL, with 1 mg/dL of glucose = 18.018 mM. Normal fasting glucose concentrations are typically around 5.5 mM, with normal fasting glucose concentrations of around 100 mg/dL. Insulin data are typically reported either in conventional insulin concentration units (pmol/L) or international units (IU/mL) , where 1 µIU/mL = 6.0 pmol/L [44]. The data reviewed and digitized for this work used both sets of units. Henceforth for consistency, we use mM for glucose and µIU/L for insulin; literature data, when needed, were converted to these units using aforementioned conversion factors.
3 Results
The first step of the subsequent analysis is to evaluate whether the model described in System (1) can reproduce the experimentally observed patterns of transition from normal glucose–insulin dynamics (Kraft pattern I) to diabetic (Kraft pattern IV). All subsequent analysis was done in Matlab v2020a using an ode23s numerical solver. Parameter values are taken from Table 1 unless indicated otherwise in the figure captions.
3.1 Capturing Emergence of IR Through Diminishing Capacity to Store Glucose
The classical understanding of the emergence of IR and subsequent transition to T2D suggests that the key parameter underlying this process is parameter of insulin sensitivity s [37]; lower insulin sensitivity results in lower value of the term , thereby leaving more glucose in the blood. We propose that even for fixed s, it is possible to qualitatively replicate the four main Kraft patterns solely through a variation of the parameter of carrying capacity in the updated term .
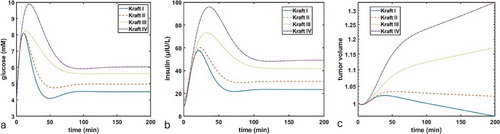
In Figure 2, we simulated the administration of a single bolus of glucose using equation F(t). We varied the value of parameter from (Figure 2a) to (Figure 2b) to (Figure 2c) to (Figure 2d). The values of parameter were chosen arbitrarily due to lack of data that would enable its more precise estimate; nevertheless, even with an arbitrarily selected value of one can see that diminishing capacity to take up excess glucose from the blood results in transitions from normal insulin–glucose dynamics to both higher baseline levels and longer time needed to return to baseline levels. Furthermore, as one can see particularly in transition from Kraft II (Figure 2b) to Kraft III (Figure 2c), the shape of both curves changes, with a more delayed insulin peak (blue curve) and a less rapid decline of glucose (red curve). These results demonstrate that it is possible to capture the features of the Kraft criteria and emergence of IR solely through a progressive decrease of the body's ability to store excess glucose.
Next, we wanted to evaluate the change in equilibrium fasting levels of both glucose and insulin as a function of decreasing carrying capacity . To generate these results, we ran simulations until time t = 2000 (time point chosen arbitrarily to allow the system to fully equilibriate) for different values of , ranging from 100 to 0.1, and collected the corresponding equilibrium values of glucose and insulin. The results are shown in Figure 3. Notably, we highlighted the typical cutoffs for diagnosing pre-diabetes and diabetes for glucose, where normal blood glucose is considered to be <5.5 mM; 5.6–6.9 mM is considered to be the pre-diabetes range; over 7.0 mM fasting glucose indicates diabetes [45]. For insulin, there do not exist such clear cut-off values, with typical values expected to be under 25 µIU/L [46, 47], although Kraft I criteria suggest normal fasting insulin levels to be <30 µIU/L, with patients meeting Kraft III criteria having fasting insulin up to 50 µIU/L, and Kraft IV criteria patients having fasting insulin >50 µIU/L [7].
As can be seen in Figure 3, assuming a maximum value of K = 100, decreasing its value starts to impact baseline fasting levels of glucose and insulin only around when only 15%–20% of capacity to store excess glucose remains, which indicates that there exists a large buffer allowing the body to maintain normal levels of glucose and insulin even as decreases.
Next, we wanted to evaluate the impact of variation of both parameter and the parameter of insulin sensitivity s on the average fasting values of both insulin and blood glucose. Parameter was varied from 0.01 to 40, as analysis reported in Figure 3 revealed that larger values of are not expected to affect glucose and insulin fasting levels; parameter s was varied from 0.0001 to 0.002 to fall within the range of values for insulin sensitivity reported in Kahn et al. [37]. Similar to the previous set of simulations, we varied parameters s and K and reported the corresponding fasting levels of glucose and insulin. As one can see in Figure 4, at very low values of s (extremely low insulin sensitivity), even high capacity to store excess glucose does not protect from elevated fasting glucose and insulin. However, for larger values of s (normal insulin sensitivity), parameter K plays a key role. Together, these results add another dimension to understanding the impact of insulin sensitivity on fasting glucose and insulin levels: even when one's insulin sensitivity is high, it is still possible to develop IR, hyperglycemia, and hyperinsulinemia through diminishing ability to store excess glucose.
3.2 Impact of Hyperinsulinemia on Cancer Cell Proliferation
In Hopkins et al. [12], the authors demonstrated that hyperinsulinemia was the driver of emergence of resistance to PI3K inhibitors in mouse cancer models regardless of etiology; furthermore, they showed that reversing hyperinsulinemia was sufficient to restore sensitivity to the drug for all 12 tested cancer cell lines. They proposed that the underlying mechanism for their observations was not elevated glucose acting as additional fuel but instead elevated insulin acting as an accelerant of tumor growth.
As one can see in Figure 5, the same tumor can grow or regress depending on the metabolic state of its host. In this set of simulations, the tumor will regress for an individual with Kraft I or II metabolic profile as the death term > . However, for Kraft III and IV, due to higher levels of insulin and glucose, cumulative growth term , resulting in net tumor growth.
Next, we simulated the impact of parameters s and K on whether a microscopic tumor might progress or regress. For this, we once again varied parameter K from 0.01 to 40 and parameter s from 0.0001 to 0.002. We ran the simulation till t = 2000 and calculated whether the difference between the initial tumor size and its size at t = 2000 was positive (tumor progression) or negative (tumor regression). As one can see in Figure 6, there exists a region of low insulin sensitivity (which, as was seen in Figure 4, corresponds to regions of higher fasting glucose and insulin levels), where, should a tumor appear, it is expected to progress. However, for individuals with higher insulin sensitivity, larger capacity to store excess glucose and therefore lower fasting glucose and insulin levels can prevent an emerging tumor from progressing.
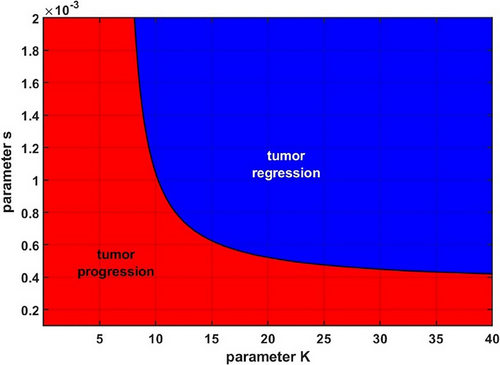
Although the parameters for tumor proliferation and death rates in this model were chosen arbitrarily, the simulations nevertheless serve to illustrate how hidden hyperinsulinemia can act to promote the overall growth of a microscopic tumor that would not thrive in a more metabolically healthy environment.
4 Discussion
Emergence of IR and subsequent hyperinsulinemia frequently occur in individuals with normal fasting glucose [6, 7]. Chronic hyperinsulinemia that precedes hyperglycemia, characteristic of T2D, can contribute to the elevated risk of cardiovascular disease, dementia, and cancer [9, 10, 49, 50]. Classical understanding of the emergence of IR assumes loss of functional signaling between insulin and its receptor and thus a lower sensitivity to insulin signaling [37]. Here, we describe an updated framework of describing glucose–insulin dynamics, where the emergence of IR that precedes hyperglycemia characteristic of T2D is a result not necessarily of loss of sensitivity to insulin but of diminishing capacity to store excess glucose (Figure 1).
The implications of this framework are studied using a modification introduced into the well-established minimal models of glucose–insulin dynamics, developed by Bergman et al. [28] and Topp et al. [30]. We demonstrate that the reduction of the carrying capacity parameter K is sufficient to qualitatively describe both the key features of the four key patterns [6, 7] of glucose–insulin dynamics during a standard OGTT (Figure 2), and the incremental increases in fasting levels of both glucose and insulin, capturing the transition from norm to pre-diabetes to T2D with a single parameter (Figure 3). We demonstrate that even for individuals with high insulin sensitivity, it is still possible to develop IR, hyperglycemia, and hyperinsulinemia through diminishing ability to store excess glucose.
Finally, we build upon the observations of Hopkins et al. [12], where the authors showed that development of diabetic phenotype in mouse cancer models resulted in an emergence of reversible therapeutic resistance to PI3K inhibitors due to growth signals from elevated insulin overwhelming the cytotoxic effects of the drug. Using the proposed model, we demonstrate that change in metabolic environment and increased fasting glucose and insulin can enable the microscopic tumor to transition from regression to progression (Figure 5). This prediction is consistent with observations that preexisting T2D is associated with worse prognosis for many cancer types [11, 51, 52]. Furthermore, our results suggest that hidden hyperinsulinemia, which can occur independently of T2D and in individuals with normal glucose tolerance, which was the case in over half (n = 4185) of participants in the analysis done by Crofts et al. [7], can prime the environment for tumor progression, should a cancer arise. Finally, we demonstrated that change in one's ability to store excess glucose can be an important modifiable factor in promoting cancer regression versus progression (Figure 6).
Excess glucose can be stored in three main compartments: adipose tissue, liver, and skeletal muscle. The capacity for how much excess glucose can be stored in the adipose tissue is likely in part genetic, with some individuals having larger carrying capacity, allowing them to accumulate fat tissue without acquiring a diabetic phenotype, whereas others may have a smaller carrying capacity and thus begin to exhibit elevated glucose and insulin levels even in the absence of high body fat [53, 54]. Interestingly, in an elegant experiment, Gavrilova et al. [55] showed that surgical transplantation of wild-type adipose tissue into severely diabetic lipoatrophic mice reversed the diabetic phenotype by effectively increasing the adipose carrying capacity and creating a compartment into which excess glucose could be stored.
Storing too much excess glucose as fat in the liver can lead to the development of nonalcoholic fatty liver disease (NAFLD), which currently has a global prevalence of approximately 25% [56]. In the early stages, NAFLD is fully reversible [57, 58]. However, if it is left unchecked, it can lead to nonalcoholic steatohepatitis (NASH), which in turn can lead to cirrhosis; at the current rate, cirrhosis with NASH is poised to become the leading indication for liver transplantation in the next decade [59, 60].
Finally, the largest storage depot for excess glucose is skeletal muscle, which is also the most modifiable factor for varying carrying capacity K. It can be increased through exercise, or lost through sedentary lifestyle [61, 62], as a result of the normal aging process [63], or even as a result of bed rest, particularly for older adults [64]. In fact, according to the catabolic crisis model, loss of muscle mass as a result of time necessary for recovery from injuries, which occur at a higher rate and take longer to recover from in an aging population, is hypothesized to significantly accelerate age-related muscle loss [65]. Interestingly, exercise additionally enables the activation of insulin-independent glucose clearance mechanisms, a strategy that has been used by T1D patients to reduce the need for exogenous insulin [66, 67].
Advances in glucose monitoring technology have enabled understanding of the dynamics of glucose not only during an OGTT but throughout the day, which has been an extremely important tool for blood sugar management for both T1D and T2D patients. Continuous glucose monitors are small devices with a thin membrane-coated wire that inserts into subcutaneous tissue. After coming in contact with interstitial fluid, they generate electrochemical signals, which are received by a transmitter on top of the sensor, where an algorithm converts the electrochemical signal to a glucose value [68]. Notably, the ability to measure glucose in the interstitial space using an enzymatic method, which does not require multiple washes, is what allows for the continuous measurement of glucose in these devices. Unfortunately, measuring insulin requires using either ELISA or radioimmune assays [69], thereby currently making immediate readings impossible. Nevertheless, even in the absence of continuous insulin monitors, it may be possible to monitor postprandial glucose levels within the frameworks of Kraft patterns.
Pharmacologically, metformin is still typically recommended as first-line therapy for management of pre-diabetes and T2D. It has also been studied extensively as a combination agent with cancer treatment, with mixed results. Many report positive impact of combination with metformin [70, 71], whereas some studies report no improvement [72, 73]. Importantly, the patients in these analyses were not stratified based on the drug's impacts on their underlying hyperinsulinemia. Furthermore, the ability of metformin to control specifically hyperinsulinemia appears to be mixed as well, with several teams reporting positive effect of metformin on lowering fasting insulin [74, 75], several groups reporting no effect [76, 77]; one team even reported increase in insulin levels in Hispanic women with polycystic ovary syndrome [78]. Therefore, alternative medications that are superior with respect to improving both hyperglycemia and hyperinsulinemia might be better combination partners. It should also be noted that in Hopkins et al. [12], metformin had the least impact on normalizing hyperglycemia and therefore hyperinsulinemia. Ketogenic diet, which was significantly more efficacious in this set of experiments, has also been shown to have different effects depending on the type of cancer. For example, Arfelli et al. [79] showed that ketone bodies might support expansion of leukemia cells. This suggests that the ketogenic diet, which increases ketone bodies, could actuall promote acute myeloid leukemia by providing an energy source for leukemia cells. It remains to be investigated if this effect may be relevant in other cancer types, where the additional fuel provided by ketone bodies may outweigh the benefits of normalizing fasting glucose and insulin levels through this type of intervention. Therefore, alternative glucose and insulin management approaches may be more efficacious.
Until recently, after metformin, typical treatments for T2D involved medications aimed at increasing insulin production from pancreas, such as sulfonylureas [24], as well as administration of exogenous insulin when the capacity of the pancreas to produce insulin is pharmacologically maximized. In the last two decades, a new class of drugs for normalizing blood glucose has emerged. Of particular note are SGLT2 inhibitors, which block the activity of cotransporter protein responsible for up to 90% of glucose reabsorption in kidneys. As a result, blockade of SGLT2 increases the renal excretion of glucose without additional insulin, thereby systematically lowering the amount of excess glucose in the blood without the need to store it in the body [80, 81]. Furthermore, SGLT2 is expressed in certain types of cancer [82, 83], making it a potential target for cancer therapy as well. Indeed, in an observational study that included nearly 25,000 patients diagnosed with non-small cell lung cancer (NSCLC) between 2014 and 2017 who had a preexisting diagnosis of T2D, Luo et al. [84] assessed whether taking SGLT2 affects NSCLC prognosis and survival. Among patients who had used an SGLT2 inhibitor for over 12 months, the authors showed a 46% relative reduction in all-cause mortality compared to non-users. Whether the benefit came solely from blocking the mechanism of action of SGLT2, affecting cancer cell metabolism, or from the systemic lowering of glucose and insulin, remains to be evaluated, as does the impact and the combination potential with other emerging classes of medications, including GLP-1 agonists, such as semaglutides. If so, then some of the drugs that act to normalize both blood glucose and insulin might be exciting future combination partners for cancer therapy.
Conflicts of Interest
The author declares the following conflicts of interest: I.K. is an employee of EMD Serono, the US business of Merck KGaA. The author declares no non-financial conflicts of interest. The views expressed in this manuscript are the author's own views and do not necessarily represent the views of EMD Serono.
Open Research
Data Availability Statement
The author has nothing to report.




