Abstract and Applied Analysis
Volume 2014, Issue 1 953151
Research Article
Open Access

Revisiting Blasius Flow by Fixed Point Method

Ding Xu, 

Ding Xu

State Key Laboratory for Strength and Vibration of Mechanical Structures, School of Aerospace, Xi′an Jiaotong University, No. 28, Xianning West Road, Xi′an 710049, China xjtu.edu.cn

Search for more papers by this author
Jinglei Xu, 

Corresponding Author

Jinglei Xu

School of Jet Propulsion, Beijing University of Aeronautics and Astronautics, Xueyuan Road, No. 37, Beijing 100191, China

Search for more papers by this author
Gongnan Xie, 

Gongnan Xie

School of Mechanical Engineering, Northwestern Polytechnical University, Xi′an, Shaanxi 710072, China npu.edu

Search for more papers by this author
First published: 12 January 2014
https://doi.org/10.1155/2014/953151
Academic Editor: Mohamed Fathy El-Amin

Abstract

The well-known Blasius flow is governed by a third-order nonlinear ordinary differential equation with two-point boundary value. Specially, one of the boundary conditions is asymptotically assigned on the first derivative at infinity, which is the main challenge on handling this problem. Through introducing two transformations not only for independent variable bur also for function, the difficulty originated from the semi-infinite interval and asymptotic boundary condition is overcome. The deduced nonlinear differential equation is subsequently investigated with the fixed point method, so the original complex nonlinear equation is replaced by a series of integrable linear equations. Meanwhile, in order to improve the convergence and stability of iteration procedure, a sequence of relaxation factors is introduced in the framework of fixed point method and determined by the steepest descent seeking algorithm in a convenient manner.

1. Introduction

The Navier-Stokes equations are the fundamental governing equations of fluid flow. Usually, this set of nonlinear partial differential equations has no general solution, and analytical solutions are very rare only for some simple fluid flows. However, in some certain flows, the Navier-Stokes equations may be reduced to a set of nonlinear ordinary differential equations under a similarity transform [1, 2]. These similarity solutions could not only provide some physical significance to the complex Navier-Stokes equations but also act as a benchmarking for numerical method. The well-known Blasius flow [3–5] is possibly the simplest example among these similarity solutions. It describes the idealized incompressible laminar flow past an semi-infinite flat plate at high Reynolds numbers, which is mathematically a third-order nonlinear two-point boundary value problem:
(1)
subject to the boundary conditions:
(2)
where the prime denotes differentiation to the variable η and f(η) is the nondimensional stream function related to the stream function ψ(x, y) as follows:
(3)
is the similarity variable, where U∞ is the free stream velocity, ν is the kinematic viscosity coefficient, and x and y are the two independent coordinates. The two velocity components are then determined:
(4)
According to (1) and (2) the solution is defined on a semi-infinite interval η ≥ 0, and one of the boundary conditions is asymptotically assigned on the first derivative of function at infinity, which are the main challenges on solving the Blasius flow. The solution to this problem has the following asymptotic property [6, 7]:
(5)
where B is a constant and the benchmarking value provided by Boyd [6, 7] is B = −1.720787657520503.

As known, no simple closed-form solution to the Blasius problem is available, despite the simple form and such a long history of it since 1908 [3]. Much attention has been paid to this problem. Blasius [3] himself firstly investigated this problem by the perturbation method and obtained an approximate solution by matching a power series solution for small η to an asymptotic expansion for large η. However, this procedure may be improper because of somewhat restricted radius of convergence in the first power series [8]. Later, this problem was handled by Bender et al. [9] with δ-expansion in a smart manner. The approximate solutions were obtained by He [10], Liao [11, 12], and Turkyilmazoglu [13–16] with the variational iteration method, homotopy analysis method, and homotopy perturbation method, respectively. Wang [17] also investigated this problem by the Adomian decomposition method. Meantime, there are a lot of numerical methods emerging to handle the Blasius problem including, but not limited to, shooting method, finite differences method, and spectral method [18–31]. A vast bibliography of numerical methods has developed for this problem, so a full account of them is out of the scope of this paper, and readers are suggested to refer to the review articles [6, 7]. It is noted that the existing numerical methods usually integrate this problem over a finite interval η ∈ [0, η∞], although the Blasius problem is originally defined on the semi-infinite interval η ∈ [0, +∞). Thus the value of η∞ should be chosen sufficiently large to assure the accuracy of the asymptotical boundary condition at infinity. However, the appropriate value η∞ could not be determined beforehand, so usually the trial-and-error approach is involved, and some different values should be tried to find the appropriate η∞ to satisfy the demanded accuracy.

In order to exactly assure the boundary conditions (2) and obtain a uniformly valid solution on the semi-infinite interval η ∈ [0, +∞), two transformations not only for the independent variable η but also for function f(η) are introduced in this paper. The transformed nonlinear differential equation is subsequently investigated with the fixed point method (FPM) [33], which transforms the nonlinear differential equation into a series of integrable linear differential equations. Hence, an approximate semianalytical solution to the Blasius problem is finally obtained, which is valid on the whole domain and can satisfy the asymptotic property automatically. Meantime, in order to improve the convergence and stability of iteration procedure, a sequence of relaxation factors is introduced in the framework of FPM, which are determined by the steepest descent seeking algorithm. Thus, the accuracy of this approximate solution could be improved step by step in a convenient manner.

2. Revisiting the Blasius Equation by Fixed Point Method

2.1. Transformations

As mentioned in Section 1, the main challenge on handling the Blasius problem originates from the semi-infinite interval η ∈ [0, +∞) and the asymptotic boundary condition lim η→∞f′(η) = 1. In order to overcome these difficulties, two transformations are introduced for independent variable η and function f(η), respectively,
(6)
where λ (>0) is a free parameter. 1/λ stands for the length dimension and its physical meaning is related to the scale of boundary layer thickness. The influence of λ on the solution will be discussed in detail in Section 3.2.
Hence, the original Blasius equation becomes
(7)
with the following boundary conditions:
(8)
where the prime denotes differentiation to the new variable z. It is clear that the semi-infinite interval η ∈ [0, +∞) is mapped to the bounded interval −1 ≤ z ≤ 1, and the original asymptotic boundary condition lim η→∞f′(η) = 1 becomes
(9)
which is beneficial to the acquirement of the valid solution in the whole domain.

2.2. The Idea of Fixed Point Method (FPM)

The fixed point, a fundamental concept in functional analysis [34], has been widely adopted in studying the existence and uniqueness of solutions by pure mathematicians. Recently, the fixed point concept has been used to handle nonlinear differential equations, and the fixed point method (FPM) has been proposed to obtain the explicit approximate analytical solution to the nonlinear differential equation [33].

To outline the idea of FPM, let us consider the following nonlinear differential equation:
(10)
where 𝒜[·] is a nonlinear operator and u is an unknown function. Here, ℬ+[u] = 0 is the boundary condition and/or initial condition for u.
𝒯[·] is a contractive map:
(11)
where ℒC[·] is a linear continuous bijective operator, named as the linear characteristic operator of the nonlinear operator 𝒜[·] and is the inverse operator of ℒC[·]. ϖ is a real nonzero free parameter, named as the relaxation factor, which could improve the convergence and stability of iteration procedure. The optimal value ϖ is usually dependent on the problem to be solved [33]. Then, a solution sequence {un|n = 0,1, 2,3, …} can be obtained from the following iteration procedure:
(12)
(13)
If the convergence of the solution sequence {un|n = 0,1, 2,3, …} is ensured, it is clear that the limit value u* is exactly the zero point of the original nonlinear operator 𝒜[·]:
(14)
and u* is also named as a fixed point of the contractive map 𝒯[u].

In [33], only one relaxation factor ϖ is introduced and determined by the so-called ϖ-curves in a heuristic manner. Here, a sequence of relaxation factors {ϖn | n = 1,2, 3, …} is introduced in (12), which will be decided according to the steepest descent seeking algorithm in the following Section 2.3.

2.3. The Steepest Descent Seeking Algorithm (SDS)

As mentioned in Section 2.2, the relaxation factor {ϖn|n = 1,2, 3, …} could improve the convergence and stability of iteration procedure, and usually the optimal value of relaxation factor is dependent on the problem to be solved. Here, an algorithm, named as the steepest descent seeking algorithm (SDS), is adopted to determine the optimal value of the relaxation factor.

Let Resn denote the square residual error of the aforementioned iteration procedure in (13):
(15)
where Ω is the definition domain of the variable and Resn is a kind of global residual error and can evaluate the accuracy of the approximation un. Then it is suggested that the optimal value of relaxation factor ϖn,opt corresponds to the value ϖn such that Resn obtains the minimum value min (Resn). For example, when n = 1, the square residual error Res1(ϖ1) is a function of ϖ1 only and thus the optimal value ϖ1,opt can be obtained by solving the nonlinear algebraic equation:
(16)
When n = 2, the square residual error Res2(ϖ1, ϖ2) is dependent on ϖ1 and ϖ2. Because the optimal value ϖ1,opt is known from the previous step, the optimal value ϖ2,opt is governed by the following nonlinear algebraic equation:
(17)
Similarly, for the nth-higher order, the square residual error Resn actually contains an unknown relaxation factor ϖn only, so the optimal value ϖn,opt is determined by the following nonlinear algebraic equation:
(18)

The name of the steepest descent seeking algorithm just comes from the aforementioned approach; that is, every optimal value ϖn,opt is sought to minimize the corresponding square residual error Resn. According to this approach, only one nonlinear algebraic equation should be solved in every iteration step, and the elements of the sequence {ϖn|n = 1,2, 3, …} are obtained sequentially and separately.

2.4. Iteration Procedure

Now, for (7), let us choose the linear characteristic operator:
(19)
and construct an iteration procedure as follows:
(20)
(21)
The initial guess g0 is conveniently chosen as
(22)
which satisfies the following equation:
(23)

3. Result and Discussion

3.1. Results as λ = 1/5

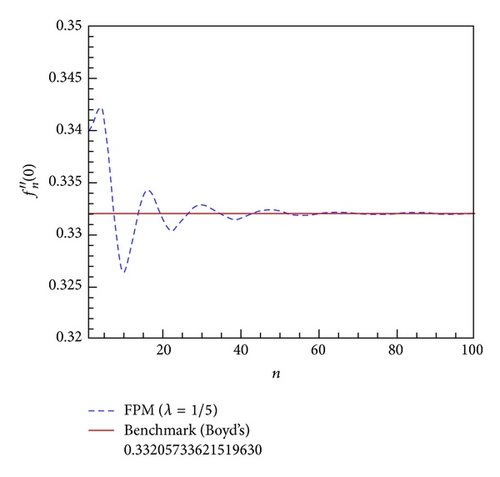
Before the acquirement of approximate solution according to the iteration procedure (21), the free parameter λ should be determined. It is found that the iteration procedure converges rapidly when the value of 1/λ takes the scale of boundary layer thickness. Here, the value of λ is firstly set to λ = 1/5 and the influence of λ value on the solution will be studied in Section 3.2.

In order to demonstrate FPM, the procedure to obtain the first-order approximation g1(z) is given here in detail. Firstly, the governing equation for g1(z) is deduced according to (21):
(24)
Then the first order approximation g1(z) takes the following form:
(25)
It is clear that the first-order approximation g1(z) in (25) is dependent on the relaxation factor ϖ1, whose optimal value could be determined by the steepest descent seeking algorithm (SDS) as mentioned in Section 2.3. Here, the square residual error Resn of the original equation (1) is introduced:
(26)
Then, the square residual error of f1(η) is as follows:
(27)
and the optimal value ϖ1,opt and the minimum of Res1 are
(28)
Hence, the first-order approximation g1(z) is finally determined:
(29)

For the higher-order approximation gn(z), the procedure is similar, and an explicit semianalytical solution could be deduced by the symbolic computation software, such as MAXIMA, MAPLE and MATHEMATICA.

In consideration of the transformation (6), the corresponding approximate solution fn(η) to the original Blasius equations (1) and (2) is
(30)

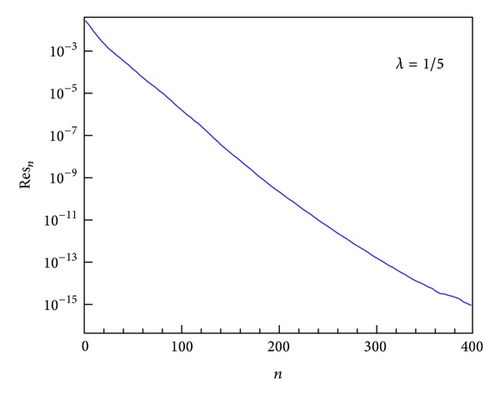
The convergence history of the square residual error Resn is illustrated in Figure 1, which clearly shows that Resn is gradually reduced during the iteration procedure, so the accuracy of the approximate solution could be improved step by step to any possibility.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
The convergence history of Resn (λ = 1/5).
The second derivative f′′(0) is a measure of the shear stress on the plate and plays a critical role in the Blasius problem [4, 5]. The relationship between and can be deduced as follows:
(31)
The convergence history of is displayed in Figure 2, which shows that the difference between the approximation and Boyd’s [6, 7] benchmarking result f′′(0) = 0.33205733621519630 decreases during the iteration procedure. Meanwhile, the comparison between the present result and others given in [6, 7, 31, 32] is tabulated in Table 1, which shows that is the same as Boyd’s benchmarking result within 7 significant digits when n ≥ 300 and within 12 significant digits when n ≥ 800.
Table 1. Comparison of f′′(0) between FPM (λ = 1/5) and others.
Present (FPM)

Fazio

[31]

 Zhang and Chen [32] Boyd [6, 7] (Benchmark)
n
1 0.3399132521631 0.3320575595 0.33205733621 0.33205733621519630
25 0.3314634706964
50 0.3322299008614
100 0.3320852976636
150 0.3320560696476
200 0.3320572413724
250 0.3320573781489
300 0.3320573415043
400 0.3320573362780
600 0.3320573362198
800 0.3320573362153
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
The convergence history of (λ = 1/5).

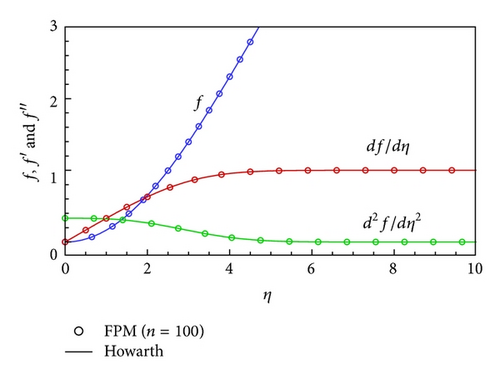
The approximate semianalytical solutions and the well-known Howarth’s [32] accurate numerical result of f(η), f′(η), and f′′(η) are compared in Figure 3 and simultaneously tabulated in Tables 2–4, which shows that the present result obtained by FPM is of high accuracy.

Table 2. Comparison of f between FPM (λ = 1/5) and Howarth.
η f
FPM

Howarth

[21]
n = 50 n = 200 n = 800
0 0. 0. 0. 0
0.2 0.006644529362447 0.006640995986591 0.006640999714597 0.00664
0.4 0.02657431250127 0.02655986911996 0.02655988401799 0.02656
0.6 0.05976777037563 0.05973460409079 0.05973463749804 0.05974
0.8 0.1061682229933 0.1061081617252 0.1061082208390 0.10611
1.0 0.1656669946990 0.1655716339700 0.1655717257893 0.16557
1.2 0.2380877115384 0.2379485860317 0.2379487172889 0.23795
1.4 0.3231726092163 0.3229813967422 0.3229815738295 0.32298
1.6 0.4205717973682 0.4203205366053 0.4203207655016 0.42032
1.8 0.5298364510983 0.5295177515398 0.5295180377438 0.52952
2 0.6504167979655 0.6500240214585 0.6500243699353 0.65003
3 1.397637112752 1.396807516637 1.396808230870 1.39682
4 2.307039632340 2.305745294404 2.305746418462 2.30576
5 3.284986166454 3.283272129531 3.283273665156 3.28329
6 4.281691879364 4.279618989982 4.279620922514 4.27964
7 5.281627551984 5.279236492841 5.279238811029 5.27926
8 6.281851614090 6.279210729689 6.279213431346 6.27923
10 8.282182252512 8.279208870686 8.279212342934 /
15 13.284515240195 13.27920694573 13.279212342479 /
20 18.283646215099 18.27920502276 18.279212342479 /
Table 3. Comparison of f′ between FPM (λ = 1/5) and Howarth.
η f′
FPM

Howarth

[21]
n = 50 n = 200 n = 800
0 0. 0. 0. 0
0.2 0.06644347995228 0.06640775477474 0.06640779209625 0.06641
0.4 0.1328378289536 0.1327640864649 0.1327641607610 0.13277
0.6 0.1990509318305 0.1989371417431 0.1989372524222 0.19894
0.8 0.2648643497350 0.2647089925007 0.2647091387231 0.26471
1.0 0.3299775414929 0.3297798506391 0.3297800312497 0.32979
1.2 0.3940157297864 0.3937758909492 0.3937761044339 0.39378
1.4 0.4565422496657 0.4562615202332 0.4562617647051 0.45627
1.6 0.5170757864638 0.5167565112060 0.5167567844226 0.51676
1.8 0.5751123265865 0.5747578444754 0.5747581438894 0.57477
2 0.6301509546266 0.6297654136655 0.6297657365024 0.62977
3 0.8465117311855 0.8460440464746 0.8460444436580 0.84605
4 0.9559675373580 0.9555178143322 0.9555182298107 0.95552
5 0.9919283302451 0.9915414951870 0.9915419001644 0.99155
6 0.9993091537696 0.9989724827440 0.9989728724358 0.99898
7 1.000215077512 0.9999212208137 0.9999216041479 0.99992
8 1.000195058002 0.9999958903313 0.9999962745353 1.00000
10 1.000231913519 0.9999996129000 0.9999999980154 /
15 1.000224523350 0.9999996133026 1.000000000000 /
20 0.9997789079310 0.9999996166005 1.000000000000 /
Table 4. Comparison of f′′ between FPM (λ = 1/5) and Howarth.
η f′′
FPM Howarth [21]
n = 50 n = 200 n = 800
0 0.3322299008614 0.3320572413724 0.33205733621526 0.33206
0.2 0.3321681255428 0.3319836510534 0.33198383711462 0.33199
0.4 0.3316651431123 0.3314696606323 0.33146984420144 0.33147
0.6 0.3302835149673 0.3300789475208 0.33007912757428 0.33008
0.8 0.3275995678839 0.3273890950354 0.32738927014924 0.32739
1.0 0.3232190113859 0.3230069482211 0.32300711668693 0.32301
1.2 0.3167975457228 0.3165890310990 0.31658919106110 0.31659
1.4 0.3080647180157 0.3078652421801 0.30786539179016 0.30787
1.6 0.2968484699253 0.2966633238744 0.29666346145571 0.29667
1.8 0.2830971363448 0.2829308930580 0.28293101725975 0.28293
2 0.2668953087923 0.2667514357803 0.26675154569727 0.26675
3 0.1613836232798 0.1613602778747 0.16136031954088 0.16136
4 0.06418469140538 0.06423412147661 0.064234121091696 0.06424
5 0.01584093436570 0.01590681516643 0.015906798685320 0.01591
6 2.367987742194e − 3 2.402051505611e − 3 2.4020398437568e − 3 0.00240
7 1.526040209602e − 4 2.201705391867e − 4 2.201689552708e − 4 0.00022
8 −9.161215077567e − 4 1.223887615942e − 5 1.224092624324e − 5 0.00001
10 1.667970449293e − 4 9.650715210973e − 9 8.442915877193e − 9 /
15 2.499528919705e − 4 −1.207941083287e − 10 1.426848065722e − 17 /
20 1.244076430614e − 4 1.815564827202e − 9 4.736242910970e − 18 /
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Comparison of FPM result (λ = 1/5, n = 100) with Howarth’s numerical result.

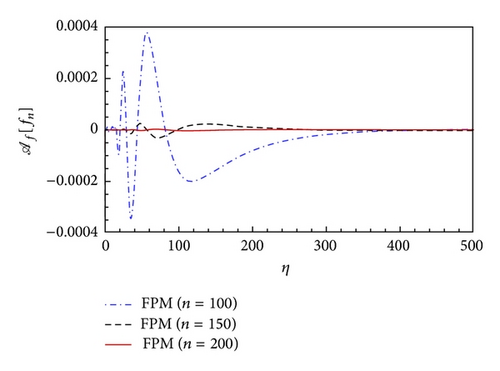
The residual error function is plotted in Figure 4, which also reveals that the error of approximate solutions gradually decreases during the iteration procedure. Moreover, the present approximate solutions are uniformly valid in the whole region.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
The residual error function (λ = 1/5).
Based on the asymptotic property of f(η) given in (5), we obtain
(32)
The approximate value of B could be obtained as follows:
(33)
The comparison between the approximate value of B obtained by FPM (n = 800, λ = 1/5) and the benchmarking result B = −1.720787657520503 provided by Boyd [6, 7] is given in Table 5, which shows that the present result is the same as Boyd’s benchmarking result within 7 significant digits when η ≥ 9 and within 13 significant digits when η ≥ 13.
Table 5. The asymptotic property of f for large positive η (λ = 1/5, n = 800).
η f − η   (Benchmark) [6, 7]
5 −1.716726334844 −1.720787657520503
6 −1.720379077486
7 −1.720761188971
8 −1.720786568654
9 −1.720787629355
10 −1.720787657066
11 −1.720787657516
12 −1.720787657520
13 −1.720787657521
14 −1.720787657521
15 −1.720787657521
20 −1.720787657521
25 −1.720787657521
30 −1.720787657521

3.2. The Influence of λ Value on the Solution

It is clear that 1/λ takes the length dimension in consideration of transformation (6). In order to investigate the influence of λ value on the solution, some different λ values are considered in the following calculations, and the comparison of Resn at different λ values is displayed in Figures 5(a) and 5(b). It is found that all Resn corresponding to different λ values are gradually reduced during the iteration procedure, and Resn based on λ = 1/5 converges more rapidly than others. What is the physical meaning of λ? Let us try to find the answer from the Prandtl’s boundary layer theory [5].

Details are in the caption following the image
Figure 5 (a) Comparison among λ = 0.4, λ = 1/3, λ = 1/4, and λ = 1/5
Open in figure viewerPowerPoint
The influence of λ value on the square residual error Resn.
Details are in the caption following the image
Figure 5 (b) Comparison among λ = 1/5, λ = 1/6, λ = 1/7, λ = 1/8, λ = 1/9, and λ = 1/10
Open in figure viewerPowerPoint
The influence of λ value on the square residual error Resn.

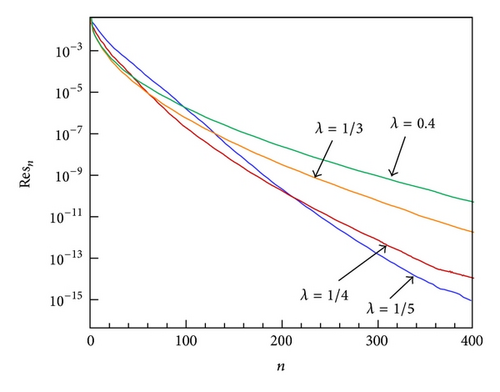
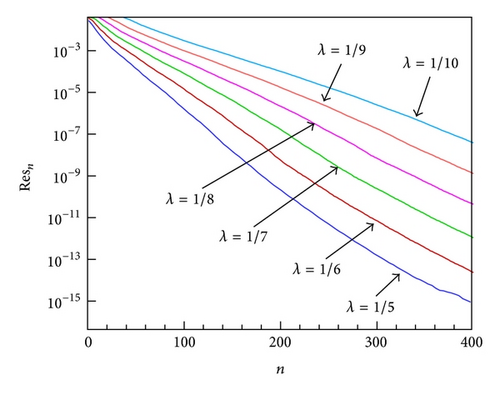
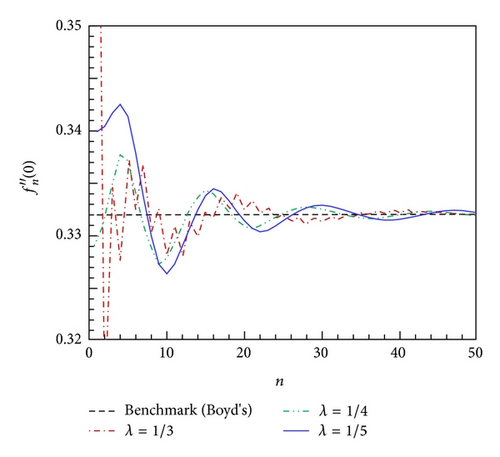
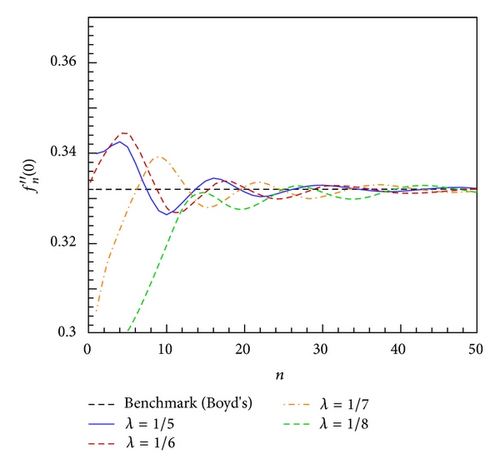
According to Prandtl’s boundary layer theory, the effect of viscosity is mainly confined to the boundary layer such that η < δ, and the outer flow (η > δ) could be considered as inviscid flow. From Table 3, the thickness of the boundary layer is just about δ ≈ 5, where u/U∞ = f′ ≈ 0.99. Now, the physical meaning of λ becomes clear. 1/λ has the same scale of boundary layer thickness δ. In consideration of transformation (6), the region −1 ≤ z ≤ 1 is divided into two equal parts, and the viscous flow (η < δ ≈ 5) and inviscid flow (η > δ ≈ 5) correspond to −1 ≤ z < 0 and 0 < z < 1, respectively. Although this determination of λ is in a heuristic manner, it is fortunate that the solution is quite insensitive to λ so long as 1/λ is of the same order-of-magnitude as δ ≈ 5. The influence of λ on the convergence of is given in Figures 6(a) and 6(b), which also reveals that the limit values of with different λ values agree well with each other. Hence, the selection of λ is nonessential to the final solution.

Details are in the caption following the image
Figure 6 (a) Comparison among λ = 1/3,  λ = 1/4, and λ = 1/5
Open in figure viewerPowerPoint
The influence of λ value on the convergence of .
Details are in the caption following the image
Figure 6 (b) Comparison among λ = 1/5,  λ = 1/6,  λ = 1/7, and λ = 1/8
Open in figure viewerPowerPoint
The influence of λ value on the convergence of .

4. Conclusion

In this paper, the well-known Blasius flow is revisited by the fixed point method (FPM). In order to overcome the difficulties originated from the semi-infinite interval and asymptotic boundary condition, two transformations are introduced for not only the independent variable but also the dependent variable. Under these transformations, all the boundary conditions are exactly assured for every order approximate solution. In the meanwhile, a free scale parameter λ is introduced in the transformation, and its physical meaning is related to the thickness of the boundary layer. Moreover, a sequence of relaxation factors {ϖn | n = 1,2, 3, …} is introduced to improve the convergence and stability during iteration procedure, and its elements are obtained in a convenient manner by the steepest descent seeking algorithm. Finally, the comparison of the present results with other scholars’ numerical results, especially with the benchmarking results provided by Boyd, shows that FPM is an effective and accurate approach to obtain the semianalytical solution to nonlinear problems.

Nomenclature

  • U∞:
  • Free stream velocity, m/s
  • u:
  • x-components of the velocity, m/s
  • v:
  • y-components of the velocity, m/s
  • ψ(x, y):
  • Stream function, m2/s
  • f(η):
  • Nondimensional stream function
  • ν:
  • Kinematic viscosity coefficient, m2/s.

    • Conflict of Interests

    The authors declare that there is no conflict of interests regarding the publication of this paper.

    Acknowledgments

    The work is supported by the National Natural Science Foundation of China (Approval no. 11102150) and the Fundamental Research Funds for the Central Universities.

        The full text of this article hosted at iucr.org is unavailable due to technical difficulties.