ORIGINAL ARTICLE

Open Access

Modelling the impact of antimicrobial use and external introductions on commensal E. coli colistin resistance in small-scale chicken farms of the Mekong delta of Vietnam

Corresponding Author

Jonathan Bastard

[email protected]

orcid.org/0000-0001-8531-1614

Université Paris-Saclay, UVSQ, Univ. Paris-Sud, Inserm, CESP, Anti-Infective Evasion and Pharmacoepidemiology Team, Montigny-le-Bretonneux, France

Institut Pasteur, Epidemiology and Modelling of Antibiotic Evasion Unit, Paris, France

MESuRS laboratory, Conservatoire national des arts et métiers, Paris, France

PACRI unit, Institut Pasteur, Conservatoire national des arts et métiers, Paris, France

Correspondence

Jonathan Bastard, Université Paris-Saclay, UVSQ, Univ. Paris-Sud, Inserm, CESP, Anti-infective evasion and pharmacoepidemiology team, F-78180, Montigny-le-Bretonneux, France.

Email: [email protected]

Search for more papers by this author

Nguyen Thi Nhung,

Nguyen Thi Nhung

Oxford University Clinical Research Unit, Ho Chi Minh, Vietnam

Search for more papers by this author

Vo Be Hien,

Vo Be Hien

Sub-Department of Animal Health and Production, Dong Thap, Vietnam

Search for more papers by this author

Bach Tuan Kiet,

Bach Tuan Kiet

Sub-Department of Animal Health and Production, Dong Thap, Vietnam

Search for more papers by this author

Laura Temime,

Laura Temime

MESuRS laboratory, Conservatoire national des arts et métiers, Paris, France

PACRI unit, Institut Pasteur, Conservatoire national des arts et métiers, Paris, France

Search for more papers by this author

Lulla Opatowski,

Lulla Opatowski

Université Paris-Saclay, UVSQ, Univ. Paris-Sud, Inserm, CESP, Anti-Infective Evasion and Pharmacoepidemiology Team, Montigny-le-Bretonneux, France

Institut Pasteur, Epidemiology and Modelling of Antibiotic Evasion Unit, Paris, France

Search for more papers by this author

Juan Carrique-Mas,

Juan Carrique-Mas

Oxford University Clinical Research Unit, Ho Chi Minh, Vietnam

Centre for Tropical Medicine and Global Health, Oxford University, Oxford, UK

Search for more papers by this author

Marc Choisy,

Marc Choisy

Oxford University Clinical Research Unit, Ho Chi Minh, Vietnam

Centre for Tropical Medicine and Global Health, Oxford University, Oxford, UK

Search for more papers by this author

Jonathan Bastard,

Corresponding Author

Jonathan Bastard

[email protected]

orcid.org/0000-0001-8531-1614

Université Paris-Saclay, UVSQ, Univ. Paris-Sud, Inserm, CESP, Anti-Infective Evasion and Pharmacoepidemiology Team, Montigny-le-Bretonneux, France

Institut Pasteur, Epidemiology and Modelling of Antibiotic Evasion Unit, Paris, France

MESuRS laboratory, Conservatoire national des arts et métiers, Paris, France

PACRI unit, Institut Pasteur, Conservatoire national des arts et métiers, Paris, France

Correspondence

Jonathan Bastard, Université Paris-Saclay, UVSQ, Univ. Paris-Sud, Inserm, CESP, Anti-infective evasion and pharmacoepidemiology team, F-78180, Montigny-le-Bretonneux, France.

Email: [email protected]

Search for more papers by this author

Nguyen Thi Nhung,

Nguyen Thi Nhung

Oxford University Clinical Research Unit, Ho Chi Minh, Vietnam

Search for more papers by this author

Vo Be Hien,

Vo Be Hien

Sub-Department of Animal Health and Production, Dong Thap, Vietnam

Search for more papers by this author

Bach Tuan Kiet,

Bach Tuan Kiet

Sub-Department of Animal Health and Production, Dong Thap, Vietnam

Search for more papers by this author

Laura Temime,

Laura Temime

MESuRS laboratory, Conservatoire national des arts et métiers, Paris, France

PACRI unit, Institut Pasteur, Conservatoire national des arts et métiers, Paris, France

Search for more papers by this author

Lulla Opatowski,

Lulla Opatowski

Université Paris-Saclay, UVSQ, Univ. Paris-Sud, Inserm, CESP, Anti-Infective Evasion and Pharmacoepidemiology Team, Montigny-le-Bretonneux, France

Institut Pasteur, Epidemiology and Modelling of Antibiotic Evasion Unit, Paris, France

Search for more papers by this author

Juan Carrique-Mas,

Juan Carrique-Mas

Oxford University Clinical Research Unit, Ho Chi Minh, Vietnam

Centre for Tropical Medicine and Global Health, Oxford University, Oxford, UK

Search for more papers by this author

Marc Choisy,

Marc Choisy

Oxford University Clinical Research Unit, Ho Chi Minh, Vietnam

Centre for Tropical Medicine and Global Health, Oxford University, Oxford, UK

Search for more papers by this author

First published: 13 April 2022

https://doi.org/10.1111/tbed.14558

Citations: 5

[Correction added on 15 June 2022, after first online publication: The copyright line was changed.]

Share a link

Email
Wechat
Bluesky

Abstract

Colistin is a critically important antimicrobial for human medicine, and colistin-resistant Escherichia coli are commonly found in poultry and poultry products in Southeast Asia. Here, we aim at disentangling the within-farm and outside-farm drivers of colistin resistance in small-scale chicken farms of the Mekong delta of Vietnam. Nineteen Vietnamese chicken farms were followed up along a whole production cycle, during which weekly antimicrobial use data were recorded. At the beginning, middle and end of each production cycle, commensal E. coli samples from birds were collected, pooled and tested for colistin resistance. Twelve models were fitted to the data using an expectation–maximization algorithm and compared. We further tested the spatial clustering of the occurrence of resistance importations from external sources using the local Moran's I statistic. In the best model, colistin resistance in E. coli from chickens was found to be mostly affected by importations of resistance, and, to a lesser extent, by the use of antimicrobials in the last 1.73 weeks [0.00; 2.90], but not by the use of antimicrobials in day-olds, nor their colistin resistance carriage from hatchery. The occurrence of external source importations proved to be sometimes spatially clustered, suggesting a role of local environmental sources of colistin resistance.

1 INTRODUCTION

Antimicrobial resistance (AMR) is a major threat worldwide and it is hastened by excessive antimicrobial use (AMU) (Ferri et al., 2017). Antimicrobials intended for veterinary use amount to a substantial fraction of total AMU (Carrique-Mas et al., 2020; ECDC et al., 2017), and AMU and AMR in food-producing animals are thought to contribute to the burden of resistance in human populations (Puyvelde et al., 2017), especially in low- and middle-income countries (Nadimpalli et al., 2018).

Polymyxins, a class of antibiotics that includes colistin (polymyxin E), are last resort antimicrobials for multidrug-resistant Gram-negative bacterial infections, and are thus classified as critically important antimicrobials for human medicine by the World Health Organization (WHO, 2019). The fact that resistance of Enterobacterales to colistin is reported in livestock worldwide, specifically in Asia, is a serious public health concern (Apostolakos & Piccirillo, 2018; Boeckel et al., 2019; Kempf et al., 2016).

In particular, high levels of colistin resistance have been reported in Escherichia coli collected from chicken products (Yamaguchi et al., 2018) and chicken flocks (Kawahara et al., 2019; Nguyen et al., 2016) in Southeast Asia. Chicken is the most consumed meat in this region and is the livestock production sector that grows the fastest (OECD & FAO, 2020). Moreover, the zoonotic potential of colistin-resistant bacteria carried by poultry has been shown in chicken farms in Vietnam (Trung et al., 2017).

Previous studies have investigated the factors that drive AMR in food-producing animals and, among them, some have specifically focused on colistin resistance in chicken farms. Hypothesized factors include AMU (Majewski et al., 2020; Nguyen et al., 2016), carry-over from a previous flock raised in the same building (Mo et al., 2019) or colistin resistance in day-old chicks on arrival at the farm (Baron et al., 2014). A major limit of these studies is that they rarely consider external sources of contamination that may impact levels of resistance measured on farms, for example, transmission from the surrounding environment such as water sources, or from humans to the flock (Lee et al., 2020). Indeed, such accidental resistance importations from outside the farm are difficult to detect directly (as compared with measuring AMU for instance), requiring the use of specific methods to account for these unobserved data. The multiplicity of potential resistance selection and transmission mechanisms renders the identification of an association between use and resistance difficult to unravel at the scale of a farm, and spatial (in addition to temporal) analyses become necessary (Rosenkrantz et al., 2019; Singer et al., 2006).

In this study, we analyze longitudinal AMU and colistin resistance data collected from small-scale commercial chicken farms of the Mekong delta in Vietnam, a region that accounts for ∼13% of Vietnam total chicken production (Truong et al., 2021). We apply an expectation–maximization algorithm to (i) assess the contributions of within-flock factors (such as AMU) on colistin resistance in chickens during production and (ii) estimate for each farm the probability of importation of resistance from external sources. We finally assess the spatial distribution of this probability, to investigate the presence of local hotspots of introduction of colistin resistant bacteria into chicken flocks.

2 MATERIALS AND METHODS

2.1 Study farms and data collection

The study took place in 19 farms raising chickens for meat located in the districts of Thap Muoi and Cao Lanh, Dong Thap province (Mekong Delta region of Vietnam), as part of the baseline phase of the ViParc research project described in Carrique-Mas and Rushton (2017) and Phu et al. (2021). Briefly, all farmers registered in the two districts and raising more than 100 meat chickens as single age (i.e. 200–300 farm owners in each district) were invited to participate to the project. 102 farms were included in the ViParc project (Phu et al., 2021), among which 19 were randomly selected for this study. These 19 farms correspond to small-scale commercial productions, with flock size between 100 and 2000 chickens of the same age (all-in/all-out system), raised over production cycles of 4–5 months in a dedicated area of the farm, and fed and watered manually. The use of antimicrobials in the flocks was recorded on a weekly basis by the farmers (Figure 1). All commercial containers were kept to ensure the generation of reliable AMU data (Cuong et al., 2019).

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

Description of the data collection. Rows correspond to the 19 chicken production cycles. The colour of the square indicates the weekly use of antimicrobials. Black crosses indicate weeks of pooled faecal sample collection, which happened on three occasions for each cycle: on restocking, in the middle and at the end of the production cycle. For each pooled sample, growth curves of *E. coli* were determined by optical density, in presence of different colistin concentrations. The metric of colistin resistance in our study is the area between the growth curve under 1 mg/L of colistin and the growth curve under 0 mg/L of colistin (see Section 2.2)

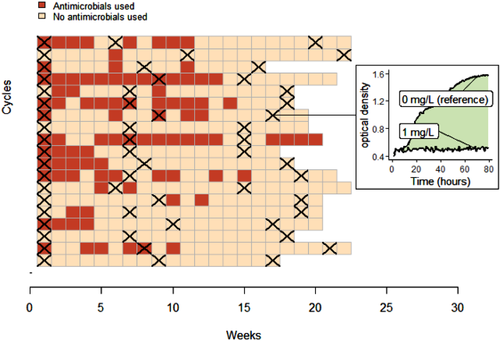
In each flock, three rounds of faeces sampling were performed: on arrival of day-old chicks (restocking), in the middle and at the end of the production cycle (Figure 1). The day before each sampling visit, farmers were asked to place a tarp on the pen's floor, in order to collect commensal E. coli from chickens’ gut flora. Indeed, E. coli is a classical indicator of AMR in commensal gut bacteria in human and animal populations (EFSA & ECDC, 2021; Tadesse et al., 2012). The faeces samples collected from the whole flock on the tarp were pooled for each sampling round of each flock, resulting in 19 × 3 samples.

2.2 Estimation of colistin resistance in samples

From each pooled sample of faeces, 30–50 colonies of E. coli were selected and pooled to have a resulting sample representative of the population of commensal E. coli in the collected faeces on each farm at each time point. Growth curves of E. coli were determined by growing a standardized suspension and measuring its OD_600nm (optical density), in presence of different colistin concentrations: 0, 0.5, 1, 2, 4, 8, 12 and 16 mg/L (Supplementary Material SM1). For each sample, this measure was repeated twice and averaged. The method, validated by Nhung et al. (2021), aims to obtain an aggregated estimate of colistin resistance among a representative sample of the whole E. coli population circulating in the guts of all the chickens of the flock of each farm and at each time point.

The chosen metric of colistin resistance is the area between the growth curve of E. coli in presence of colistin and the reference growth curve in absence of colistin (Figure 1 and SM1). If, for a given non-null colistin concentration, the growth curve is lower than the reference, the bacteria are considered susceptible to this concentration of colistin.

Because the objective is to explain the variance in the colistin resistance measured in samples, we first pre-select concentrations showing both low-growth (susceptible bacteria) and high-growth curves (resistant bacteria) (SM1). In order to increase the power of our analysis, we then select the colistin concentration c that provides the maximal standard deviation of our resistance metric. A robustness analysis on the value of c is also performed (see Section 2.7).

Because the distribution of the metric is bimodal (see SM1), we use a Gaussian Mixture Model with two components to determine the probability for each sample to belong to the ‘resistant’ or ‘susceptible’ categories. The value of probability 0.5 is the threshold for considering a sample either as ‘resistant’ or ‘susceptible’ (SM1).

Note that the classification we make between susceptible and resistant strains is based on a statistical rationale only (based on the bimodality of the resistance metric) and not on a clinical breakpoint. Indeed, the objectives of this study are to assess the factors increasing or decreasing the level of colistin resistance, independently of the threshold conventionally used to characterize colistin resistant versus susceptible bacteria.

2.3 Models

For each sample (i,j) collected in the flock i at the jth sampling round of the production cycle (j∈{2;3}), that is, 2 × 19 = 38 samples, we aim at explaining the observed resistance status R_ij, 0 for ‘susceptible’ and 1 for ‘resistant’.

The resistance status is assumed to follow the Bernoulli trial:

\begin{equation*}{R_{{\rm{ij}}}}\sim B\left( {{p_{{\rm{ij}}}}} \right)\end{equation*}

where p_ij, the probability for bacteria in sample (i,j) to be resistant, is defined as:

\begin{equation*}{\rm{\;}}{p_{ij}} = \frac{1}{{1 + {e^{ - [\mu + \alpha .{L_{ij}} + \varphi .{S_i} + \mathop \sum \nolimits_{k \in \left\{ {1;\;j - 1} \right\}} \left( {{\lambda _k}.{R_{ik}}} \right)]}}}}\;\;{\rm{if}}\;\;{Z_{ij}} = 0\end{equation*}

\begin{equation*}\;{p_{ij}} = \eta \;{\rm{if}}\;\;{Z_{ij}} = 1\end{equation*}

where (Table 1):

α is the effect of using antimicrobials before the sampling week. L_ij is the number of weeks of AMU during the β weeks preceding the jth sampling round in flock i (see SM2 for illustration), where β is estimated (Table 1). L_ij is defined as:
$\begin{equation*}{\rm{\;}}{L_{ij}} = \mathop \int \limits_{{t_{ij}} - 1 - \beta }^{{t_{ij}} - 1} {U_i}\left( t \right){\rm{d}}t\;\end{equation*}$

where t_ij is the week of sampling round j in flock i. U_i(t) = 1 if antimicrobials were used in the flock i during week t, and U_i(t) = 0 otherwise (SM2).

φ is the effect of using antimicrobials at the beginning of the production cycle. S_i is a measure of the AMU occurring during the first δ weeks of the production cycle of flock i (SM2), where δ is estimated (Table 1). S_i is similarly defined as:
$\begin{equation*}{\rm{\;}}{S_i} = \mathop \int \limits_0^\delta {U_i}\left( t \right){\rm{d}}t\;\end{equation*}$
λ₁ and λ₂ represent the effect of the resistance in the previous samples of the same flock (assuming potential autocorrelation), R_i₁ and R_i₂ (Table 1).
μ is the baseline within-flock acquisition of colistin resistance, without AMU nor previous resistance measured (Table 1).
Z is a latent (unobserved) binary variable, such that Z_ij= 1 (j∈{2;3}) if an unobserved event of importation from external sources increased the load of colistin resistance in the flock i between the sampling rounds j − 1 and j, and Z_ij= 0 otherwise. Therefore, if Z_ij= 1, the probability of the sample to be resistant is η, a fixed parameter with a value close to 1 (but cannot be equal to 1 to allow model fitting) (Table 1). On the contrary, if no importation event occurred (Z_ij= 0), the probability of resistance p_ij follows a logistic function accounting for AMU and the resistance in the previous samples of the same flock.

TABLE 1. Parameters used in the analysis

Parameter	Description	Value	Unit	Domain of definition
c	Colistin concentration chosen for the colistin resistance metric in samples	1 (See Section 2.2 and SM1)	mg/L	–
α	Effect of AMU shortly before sampling (recent AMU) on colistin resistance	Estimated	–	]−∞; +∞[
β	Number of weeks considered for the effect of recent AMU (see SM2)	Estimated	Weeks	]0; 5[
φ	Effect of AMU during the first few weeks of the production cycle (initial AMU) on colistin resistance	Estimated	–	]−∞; +∞[
δ	Number of initial weeks in the production cycle considered for the effect of initial AMU (see SM2)	Estimated	Weeks	]0; 5[
η	Probability of colistin resistance of the sample after an importation of resistance from external sources	0.999 (assumption)	–	–
λ_k	Effect of the colistin resistance previously measured in the kth round of sampling (autocorrelation)	Estimated	–	]−∞; +∞[
μ	Baseline within-flock acquisition of colistin resistance, without AMU nor previous resistance measured	Estimated	–	]−∞; +∞[
D	Distance used to compute the local' Moran I statistic (see Section 2.6)	Tuned	km	[0.1; 24]

We consider 12 versions of the model, described in Table 2, that are particular cases of the full model detailed above. We note θ the set of model parameters.

TABLE 2. Variants of the model

Model	Previous resistance		Antimicrobial use
Model	R_i₁	R_i₂	Initial	Recent
1
2	X
3	X	X
4			X
5	X		X
6	X	X	X
7				X
8	X			X
9	X	X		X
10			X	X
11	X		X	X
12	X	X	X	X

All models are particular cases of the full model (model 12) described in Section 2. Crosses indicate, for each model in rows, the inclusion in the model of the variables in columns. The different models are all possible combinations of the variables, excepted those based on R_i₂ without R_i₁. Indeed, those would represent a situation where the autocorrelation of E. coli resistance in chickens would affect sampling round 3 but not sampling round 2.

2.4 Estimation using the expectation–maximization algorithm

For a given model, let Y_m be the vector of values of the observed variables for sample m = (i,j), including R_m and the explanatory variables. Because our model includes both observed Y and unobserved data Z, we use an expectation–maximization algorithm (Dempster et al., 1977) to (i) estimate the parameters of the model, noted θ, and (ii) determine for each sample m the probability to have Z_m= 1, that is, the probability that an external source importation of resistance occurred. This algorithm comprises two steps detailed in SM3. In the expectation step, we determine for each observation the probability that an external source importation occurred given a set θ⁽^s⁾ of parameters for the model, that is, P(Z_m= 1|Y_m, θ⁽^s⁾). In the maximization step, we estimate θ⁽^s⁺¹⁾ by maximizing the complete-data LogLikelihood (also called Q function, see SM3), based on the value of P(Z_m= 1|Y_m, θ⁽^s⁾) computed in the previous expectation step. The algorithm is terminated once the complete-data likelihood of the model has converged.

2.5 Model selection

Classic criteria for models’ comparison and selection, such as the Akaike information criterion (AIC), most often depend on the likelihood based on the observed data, and are not directly suited for incomplete data problems like ours. Therefore, we use the IC_H,Q criterion, defined in Ibrahim et al. (2008), that is similar to the AIC if we set the penalty term to two times the effective number of parameters (see SM4 for details). The model presenting the lowest value of IC_H,Q is selected as the best model.

To validate the method, we simulate mock resistance data according to four scenarios, and apply the E–M algorithm and model selection process to each of these scenarios. The method is validated if, for each scenario, the best model retrieves the simulated relationships between explanatory variables and the outcome (see details in SM5).

2.6 Investigation of local spatial clusters of the occurrence of external source importations of resistance

As a result of the E–M algorithm, for each observation (sample) m = (i,j), we obtain an estimate of P^inf_m = P(Z_m= 1|Y_m, θ*), the probability of occurrence of an external source importation at convergence of the E–M algorithm, in the best model. Here, we test if the values of P^inf from each location are spatially clustered. We compute the local Moran's I statistic (Anselin, 1995; Zhu et al., 2019), defined for any observation m as:

\begin{equation*}{\rm{\;}}{I_m} = \frac{{\left( {P_m^{{\rm{inf}}} - \overline {{P^{{\rm{inf}}}}} } \right)}}{{{S^2}}}\;\;\mathop \sum \limits_n {W_{mn}}\left( {P_n^{{\rm{inf}}} - \overline {{P^{{\rm{inf}}}}} } \right)\end{equation*}

where S² is the variance of P^inf, and W_mn = 1 (resp. = 0) if the distance between samples m and n is ≤D (resp. > D). D is a tuning parameter that is searched exhaustively (Table 1).

The more positive (resp. negative) I_m is, the more P^inf_m is similar (resp. dissimilar) to neighbouring values of P^inf. This allows to classify observations as high–high, low–low, high–low, low–high or not significant. A high–high (resp. low–low) point has a high (resp. low) value of P^inf surrounded by other high (resp. low) values of P^inf, which corresponds to a significant spatial cluster of high (resp. low) probability of external source importation. A high–low (resp. low–high) point has a high (resp. low) value of P^inf surrounded by low (resp. high) values of P^inf, forming an outlier. To compute this statistic, we use the R package spdep version 1.1-3 (Bivand & Wong, 2018).

2.7 Robustness of the results

We test the robustness of our results with regard to the assumed value of two parameters: the colistin concentration used to measure colistin resistance, c (among the pre-selected values, see Section 2.2), and the assumed probability of colistin resistance of the sample after an external source importation, η. We run the analysis five additional independent times using respectively (c; η) = (2; 0.999), (4; 0.999), (1; 0.99), (2; 0.99) and (4; 0.99), on top of the baseline analysis using (c; η) = (1; 0.999) (see Table 1). All analyses are performed using R version 3.6.1 (R Core Team, 2019).

3 RESULTS

3.1 Measure of colistin resistance

Among the seven non-null colistin concentrations used to determine E. coli growth curves from the pooled sampled, we pre-select concentrations 1, 2 and 4 mg/L because they are the only ones showing both low-growth (susceptible bacteria) and high-growth curves (resistant bacteria) (SM1).

The distributions of the resistance metric for each concentration of colistin are shown in SM1. The standard deviation is 18.1 for 1 mg/L, 17.4 for 2 mg/L and 15.0 for 4 mg/L. We therefore select the resistance metric under c = 1 mg/L as measure of resistance in all samples.

As a result, out of 57 (19 × 3) samples, 31 (54.4%) are classified as resistant and 26 (45.6%) as susceptible. Among the 38 (19 × 2) samples belonging to the 2nd and 3rd sampling rounds and included in the model (see Section 2.3), 21 are classified as resistant and 17 as susceptible.

3.2 Model selection and fit

Our validation study shows that our methodology allows to successfully identify the scenario generating the simulated data (see SM5). We can therefore apply the method to the real field data.

The model presenting the lowest IC_H,Q is Model 7 (Figure 2 and SM6). In this model, parameters estimates are: $\hat \mu$ = −12.1 (95% confidence interval: [−33.3; −4.05]), $\hat \alpha$ = 9.78 [4.61; +∞[ and $\hat \beta$ = 1.73 [2.80 × 10⁻⁷; 2.90]. Therefore, the use of antimicrobials during the 1.73 weeks preceding a sampling round is positively associated with colistin resistance in the sample.

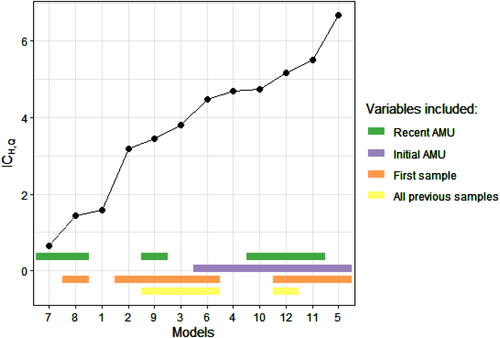
The recent use of antimicrobials is a variable included in the two models with the lowest IC_H,Q. The models including an effect of initial AMU always have a higher value of IC_H,Q than their counterpart without this effect (Figure 2 and SM6).

3.3 Local spatial clusters of the probability of external source importation

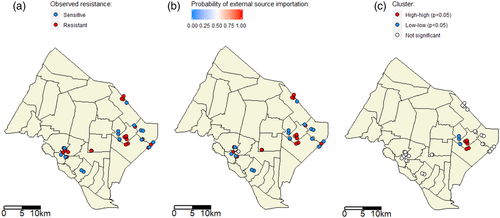
For the computation of the local Moran's I statistic, the tuning distance parameter D is set to 2.3 km. Figure 3 presents the spatial distribution of the colistin resistance metric (Figure 3(a)), and of the probability of external source importation P^inf estimated in Model 7 for each observation (sample) with the E–M algorithm (Figure 3(b)). Six (resp. four) data points show significant spatial high–high (resp. low–low) clustering (p < .05) (Figure 3(c)). This indicates that there is one local spatial cluster of high probability of external source importation, and one local spatial cluster of low probability. For all other observations, P^inf is not significantly spatially clustered.

3.4 Robustness of the results

Results are similar to the baseline analysis for all five tested values of (c; η) (see details in SM7). Indeed, in all cases, the selected model – that is, the model with the lowest IC_H,Q – is also Model 7. Estimates of parameters are similar, especially $\hat \beta$ that ranges from 1.63 to 1.69. It means the estimated antimicrobials effect, including its duration, does not depend on the assumption for (c; η). Moreover, we always detect a high–high cluster of the probability of external source importation P^inf in the same geographical area than in the baseline analysis. However, low–low spatial clustering is not always retrieved as in the baseline analysis (SM7).

4 DISCUSSION

In this study, we explore the contributions of within-farm and outside-farm factors to the phenotypic colistin resistance observed in commensal E. coli isolated from chicken farms of the Mekong delta of Vietnam. Our methodology was validated using a simulation study (SM5), allowing to have confidence in our results.

4.1 Main findings

Some studies (Nguyen et al., 2016; Poolperm et al., 2020) have suggested an association between AMU and colistin resistance of Enterobacterales isolated from food-producing animals in Southeast Asia. Here, the collection of detailed and reliable AMU data on a weekly basis allows us to account for the dynamics of the effect of AMU on AMR. We find that our measure of colistin resistance is associated with the use of antimicrobials during the 1.73 weeks preceding the sample collection, similarly to (Nhung et al., 2021). The reason may be that AMU selects for colistin resistant E. coli strains that were already present at low level or that were introduced to the farm. This suggests that mitigating the global exposure of chickens to antimicrobials – and not only the exposure to colistin – during the production cycle would help preserve the effectiveness of colistin. The effect of other antibiotic classes on colistin resistance could be explained by mechanisms of co-selection.

However, AMU in the first weeks is not found to lastingly affect colistin resistance measured later in the production cycle. This could be due to the non-persistence of the effect of AMU on colistin resistance over time, after the interruption of antimicrobials use, as was described before (Poolperm et al., 2020). Consistently, our estimate of parameter β (1.73 weeks) suggests that the effect of AMU does not last longer than 2 weeks in the chicken flocks. This might be explained by the evolutionary costs associated with resistance in bacteria (Melnyk et al., 2015). Nonetheless, these findings must be confirmed by other studies exploring the impact of AMU at different periods of the production cycle.

A second result is that, during the course of our study, most of the colistin resistance observed in chickens (17 out of 21 of resistant samples) was actually not explained by within-farm AMU, but imported from outside the flock. Although we cannot determine the nature of these events of infection, an explanation may be the introduction of colistin-resistant bacteria to the flock from other animals or humans, as it is known that antibiotic-resistant bacteria can be transmitted between species (Kawahara et al., 2019; Woolhouse et al., 2015).

The source of these unexplained external source importations may also be the environment, for example as a result of the contamination of water sources or the soil with antibiotic residues or resistance genes (Liang et al., 2020; Sun et al., 2017; Zhou et al., 2019). In our study, the presence of a local spatial cluster of high probabilities of external source importations was suggested from the computation of the local Moran's I statistic (Figure 3). It supports the hypothesis of a common environmental source of colistin resistance in this geographical area. A previous publication (Rosenkrantz et al., 2019) also found spatial drivers of AMR in food-producing animals, whereas another did not (Huber et al., 2021). More studies should be carried out to investigate the relative contribution of geographical factors to AMR, as compared with within-farm factors, for instance using genomic data to detect introductions of new E. coli clones to the flock.

The contribution of antimicrobials administered at the hatchery level to AMR in poultry production farms has been suggested (Baron et al., 2014; Okorafor et al., 2019; Seo et al., 2020; Verrette et al., 2019). However, in our analysis, the best model does not include an effect of colistin resistance carriage in day-old chicks on its carriage later in the production cycle. This does not necessarily mean that the phenomenon does not occur, but simply that in our farms it is not the predominant mechanism.

Because we use a statistical classification to distinguish susceptible from resistant strains, and not a clinical breakpoint, the percentage of resistant samples presented here should not be interpreted as a prevalence result comparable to other prevalence surveys. This said, our method has the advantage to overcome the usual difficulties of measuring susceptibility to colistin due its poor diffusion in agar (Apostolakos & Piccirillo, 2018; Kempf et al., 2016). Furthermore, our results are not affected by the exact value chosen for the parameter c used to perform the statistical classification (see Section 3.4).

4.2 Limitations

A limitation of our work is that we use only phenotypic data. Genomic data would be useful to test the hypothesis of a common environmental source of colistin resistance in different farms for instance. Such an approach is not possible with the design used, as samples are pooled. Conversely, this pooling method has the advantage to provide a representative aggregate of the colistin resistance observed in the gut flora of all chickens of the flock.

Another limitation of our model is that it does not account for the antimicrobials used in the previous production cycles of each farm, as this information was not systematically collected. In the future, it would be interesting to build model variants accounting for such data, as a previous study (Mo et al., 2019) suggested that AMR in successive broiler flocks of a same farm could be associated.

4.3 Implications for AMR study and control

Our study confirms the importance of considering the landscape scale when investigating the determinants of AMR (Singer et al., 2006; Zhao et al., 2021). Here, we could interpret our results in terms of sources and sinks of resistance. Farms in which colistin resistance can be explained by within-farm factors (such as AMU) might act as sources of colistin resistance to their environment and therefore to other farms. Inversely, farms where the resistance is only driven by events of external source importation may act as sinks of colistin resistance, exposed to environmental contamination with resistance genes. Geographical areas with high environmental exposure can be characterized as local hotspots of colistin resistance.

The detection of such local hotspots of resistance suggests that it would be more efficient to account for geographical factors in AMR mitigation interventions. Indeed, if a farm is located in a geographical hotspot of AMR, the benefits of mitigation strategies implemented in the farm (e.g., AMU reduction) might be cancelled by the influence of its neighbours (Rosenkrantz et al., 2019). Therefore, it would be interesting to compare the efficacy of interventions (e.g., raising AMR awareness or veterinary advice) implemented in a large percentage of farms of a small area, versus in a smaller percentage of farms of a larger area.

ACKNOWLEDGEMENTS

We are grateful to all participating farmers and to SDAHP staff. This study was part of the baseline phase of the ViParc Project. It was funded by the Wellcome Trust through an Intermediate Clinical Fellowship awarded to J. C.-M. (grant reference number 110085/Z/15/Z). J. B. was funded by the INCEPTION project (PIA/ANR-16-CONV-0005), and his work was supported by Fondation Pierre Ledoux Jeunesse Internationale and internal resources of Institut Pasteur, the French National Institute of Health and Medical Research (Inserm) and the University of Versailles Saint-Quentin-en-Yvelines (UVSQ). Funding was also received from the French Government ‘Investissement d'Avenir’ program Laboratoire d'Excellence ‘Integrative Biology of Emerging Infectious Diseases’ (grant ANR-10-LABX-62-IBEID). The funders had no role in study design, data collection and analysis, decision to publish or preparation of the manuscript.

CONFLICT OF INTEREST

The authors declare no conflict of interest.

ETHICS STATEMENT

The authors confirm that the ethical policies of the journal, as noted on the journal's author guidelines page, have been adhered to. The project was granted ethics approval by the Oxford Tropical Research Ethics Committee (OXTREC) (Ref. 5121/16).

Open Research

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Supporting Information

REFERENCES

Anselin, L. (1995). Local indicators of spatial association—LISA. Geographical Analysis, 27(2), 93–115. https://doi.org/10.1111/j.1538-4632.1995.tb00338.x
10.1111/j.1538-4632.1995.tb00338.x
Web of Science® Google Scholar
Apostolakos, I., & Piccirillo, A. (2018). A review on the current situation and challenges of colistin resistance in poultry production. Avian Pathology, 47(6), 546–558. https://doi.org/10.1080/03079457.2018.1524573
10.1080/03079457.2018.1524573
CAS PubMed Web of Science® Google Scholar
Baron, S., Jouy, E., Larvor, E., Eono, F., Bougeard, S., & Kempf, I. (2014). Impact of third-generation-cephalosporin administration in hatcheries on fecal Escherichia coli antimicrobial resistance in broilers and layers. Antimicrobial Agents and Chemotherapy, 58(9), 5428–5434. PubMed. https://doi.org/10.1128/AAC.03106-14
10.1128/AAC.03106?14
CAS PubMed Web of Science® Google Scholar
Bivand, R. S., & Wong, D. W. S. (2018). Comparing implementations of global and local indicators of spatial association. Test, 27(3), 716–748. https://doi.org/10.1007/s11749-018-0599-x
10.1007/s11749-018-0599-x
Web of Science® Google Scholar
Boeckel, T. P. V., Pires, J., Silvester, R., Zhao, C., Song, J., Criscuolo, N. G., Gilbert, M., Bonhoeffer, S., & Laxminarayan, R. (2019). Global trends in antimicrobial resistance in animals in low- and middle-income countries. Science, 365(6459), eaaw1944. https://doi.org/10.1126/science.aaw1944
10.1126/science.aaw1944
PubMed Web of Science® Google Scholar
Carrique-Mas, J. J., Choisy, M., Van Cuong, N., Thwaites, G., & Baker, S. (2020). An estimation of total antimicrobial usage in humans and animals in Vietnam. Antimicrobial Resistance and Infection Control, 9, 16–16. PubMed. https://doi.org/10.1186/s13756-019-0671-7
10.1186/s13756?019?0671?7
PubMed Web of Science® Google Scholar
Carrique-Mas, J. J., & Rushton, J. (2017). Integrated interventions to tackle antimicrobial usage in animal production systems: The ViParc project in Vietnam. Frontiers in Microbiology, 8, 1062. https://doi.org/10.3389/fmicb.2017.01062
10.3389/fmicb.2017.01062
PubMed Web of Science® Google Scholar
Cuong, N. V., Phu, D. H., Van, N. T. B., Dinh Truong, B., Kiet, B. T., Hien, B. V., Thu, H. T. V., Choisy, M., Padungtod, P., Thwaites, G., & Carrique-Mas, J. (2019). High-resolution monitoring of antimicrobial consumption in Vietnamese small-scale chicken farms highlights discrepancies between study metrics. Frontiers in Veterinary Science, 6, 174. https://doi.org/10.3389/fvets.2019.00174
10.3389/fvets.2019.00174
PubMed Web of Science® Google Scholar
Dempster, A. P., Laird, N. M., & Rubin, D. B. (1977). Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society. Series B (Methodological), 39(1), 1–38. JSTOR.
10.1111/j.2517-6161.1977.tb01600.x
Web of Science® Google Scholar
ECDC, EFSA, & EMA. (2017). Second joint report on the integrated analysis of the consumption of antimicrobial agents and occurrence of antimicrobial resistance in bacteria from humans and food-producing animals: Joint Interagency Antimicrobial Consumption and Resistance Analysis (JIACRA) Report. EFSA Journal, 15(7), e04872.
PubMed Web of Science® Google Scholar
EFSA & ECDC. (2021). The European Union Summary Report on Antimicrobial Resistance in zoonotic and indicator bacteria from humans, animals and food in 2018/2019. EFSA Journal, 19(4), e06490.
PubMed Web of Science® Google Scholar
Ferri, M., Ranucci, E., Romagnoli, P., & Giaccone, V. (2017). Antimicrobial resistance: A global emerging threat to public health systems. Critical Reviews in Food Science and Nutrition, 57(13), 2857–2876. https://doi.org/10.1080/10408398.2015.1077192
10.1080/10408398.2015.1077192
CAS PubMed Web of Science® Google Scholar
Huber, L., Hallenberg, G. S., Lunha, K., Leangapichart, T., Jiwakanon, J., Hickman, R. A., Magnusson, U., Sunde, M., Järhult, J. D., & Van Boeckel, T. P. (2021). Geographic drivers of antimicrobial use and resistance in pigs in Khon Kaen Province, Thailand. Frontiers in Veterinary Science, 8, 331. https://doi.org/10.3389/fvets.2021.659051
10.3389/fvets.2021.659051
Web of Science® Google Scholar
Ibrahim, J. G., Zhu, H., & Tang, N. (2008). Model selection criteria for missing-data problems using the EM algorithm. Journal of the American Statistical Association, 103(484), 1648–1658. PubMed. https://doi.org/10.1198/016214508000001057
10.1198/016214508000001057
CAS PubMed Web of Science® Google Scholar
Kawahara, R., Fujiya, Y., Yamaguchi, T., Khong, D. T., Nguyen, T. N., Tran, H. T., & Yamamoto, Y. (2019). Most domestic livestock possess colistin-resistant commensal Escherichia coli harboring mcr in a rural community in Vietnam. Antimicrobial Agents and Chemotherapy, 63(6), e00594–19. PubMed. https://doi.org/10.1128/AAC.00594-19
10.1128/AAC.00594?19
CAS PubMed Web of Science® Google Scholar
Kempf, I., Jouy, E., & Chauvin, C. (2016). Colistin use and colistin resistance in bacteria from animals. International Journal of Antimicrobial Agents, 48(6), 598–606. https://doi.org/10.1016/j.ijantimicag.2016.09.016
10.1016/j.ijantimicag.2016.09.016
CAS PubMed Web of Science® Google Scholar
Lee, S., Mir, R. A., Park, S. H., Kim, D., Kim, H. - Y., Boughton, R. K., Morris, J. G., & Jeong, K. C. (2020). Prevalence of extended-spectrum β-lactamases in the local farm environment and livestock: Challenges to mitigate antimicrobial resistance. Critical Reviews in Microbiology, 46(1), 1–14. https://doi.org/10.1080/1040841X.2020.1715339
10.1080/1040841X.2020.1715339
PubMed Web of Science® Google Scholar
Liang, X., Guan, F., Chen, B., Luo, P., Guo, C., Wu, G., Ye, Y., Zhou, Q., & Fang, H. (2020). Spatial and seasonal variations of antibiotic resistance genes and antibiotics in the surface waters of Poyang Lake in China. Ecotoxicology and Environmental Safety, 196, 110543. https://doi.org/10.1016/j.ecoenv.2020.110543
10.1016/j.ecoenv.2020.110543
CAS PubMed Web of Science® Google Scholar
Majewski, M., Łukomska, A., Wilczyński, J., Wystalska, D., Racewicz, P., Nowacka-Woszuk, J., Pszczola, M., & Anusz, K. (2020). Colistin resistance of non-pathogenic strains of Escherichia coli occurring as natural intestinal flora in broiler chickens treated and not treated with colistin sulphate. Journal of Veterinary Research, 64(3), 399–405. https://doi.org/10.2478/jvetres-2020-0060
10.2478/jvetres?2020?0060
CAS PubMed Web of Science® Google Scholar
Melnyk, A. H., Wong, A., & Kassen, R. (2015). The fitness costs of antibiotic resistance mutations. Evolutionary Applications, 8(3), 273–283. PubMed. https://doi.org/10.1111/eva.12196
10.1111/eva.12196
PubMed Web of Science® Google Scholar
Mo, S. S., Urdahl, A. M., Nesse, L. L., Slettemeås, J. S., Ramstad, S. N., Torp, M., & Norström, M. (2019). Occurrence of and risk factors for extended-spectrum cephalosporin-resistant Enterobacteriaceae determined by sampling of all Norwegian broiler flocks during a six month period. PLoS One, 14(9), e0223074–e0223074. PubMed. https://doi.org/10.1371/journal.pone.0223074
10.1371/journal.pone.0223074
CAS PubMed Web of Science® Google Scholar
Nadimpalli, M., Delarocque-Astagneau, E., Love, D. C., Price, L. B., Huynh, B. - T., Collard, J. - M., Lay, K. S., Borand, L., Ndir, A., Walsh, T. R., Guillemot, D., Borand, L., De Lauzanne, A., Kerleguer, A., Tarantola, A., Piola, P., Chon, T., Lach, S., Ngo, V., …, & Abdou, A. Y. (2018). Combating global antibiotic resistance: Emerging one health concerns in lower- and middle-income countries. Clinical Infectious Diseases, 66(6), 963–969. https://doi.org/10.1093/cid/cix879
10.1093/cid/cix879
PubMed Web of Science® Google Scholar
Nguyen, N. T., Nguyen, H. M., Nguyen, C. V., Nguyen, T. V., Nguyen, M. T., Thai, H. Q., Ho, M. H., Thwaites, G., Ngo, H. T., Baker, S., & Carrique-Mas, J. (2016). Use of colistin and other critical antimicrobials on pig and chicken farms in southern Vietnam and its association with resistance in commensal Escherichia coli bacteria. Applied and Environmental Microbiology, 82(13), 3727–3735. https://doi.org/10.1128/AEM.00337-16
10.1128/AEM.00337-16
CAS PubMed Web of Science® Google Scholar
Nhung, N. T., Yen, N. T. P., Thien, N. V. K., Cuong, N. V., Kiet, B. T., Campbell, J., Thwaites, G., Baker, S., Geskus, R. B., & Carrique-Mas, J. (2021). Method for measuring phenotypic colistin resistance in Escherichia coli populations from chicken flocks. Applied and Environmental Microbiology, 87(5), e02597–20. https://doi.org/10.1128/AEM.02597-20
10.1128/AEM.02597?20
CAS Web of Science® Google Scholar
OECD & FAO. (2020). OECD-FAO Agricultural Outlook 2020–2029. https://www.oecd-ilibrary.org/content/publication/1112c23b-en
Google Scholar
Okorafor, O. N., Anyanwu, M. U., Nwafor, E. O., Anosa, G. N., & Udegbunam, R. I. (2019). Multidrug-resistant enterobacteria colonize commercial day-old broiler chicks in Nigeria. Veterinary World, 12(3), 418–423. PubMed. https://doi.org/10.14202/vetworld.2019.418-423
10.14202/vetworld.2019.418?423
CAS PubMed Web of Science® Google Scholar
Phu, D. H., Cuong, N. V., Truong, D. B., Kiet, B. T., Hien, V. B., Thu, H. T. V., Yen, L. K., Minh, N. T. T., Padungtod, P., Setyawan, E., Thwaites, G., Rushton, J., & Carrique-Mas, J. (2021). Reducing antimicrobial usage in small-scale chicken farms in Vietnam: A 3-year intervention study. Frontiers in Veterinary Science, 7, https://www.frontiersin.org/article/10.3389/fvets.2020.612993
10.3389/fvets.2020.612993
PubMed Web of Science® Google Scholar
Poolperm, P., Tangkoskul, T., Seenama, C., Maknakhon, N., & Thamlikitkul, V. (2020). Association between the use of colistin for short-term treatment of Gram-negative bacterial infections and the emergence of colistin-resistant Enterobacteriaceae in swine from selected swine farms in Thailand. Plos One, 15(10), e0238939–e0238939. PubMed. https://doi.org/10.1371/journal.pone.0238939
10.1371/journal.pone.0238939
CAS PubMed Web of Science® Google Scholar
Puyvelde, S. V., Deborggraeve, S., & Jacobs, J. (2017). Why the antibiotic resistance crisis requires a One Health approach. The Lancet Infectious Diseases, 0(0), https://doi.org/10.1016/S1473-3099(17)30704-1
10.1016/S1473?3099(17)30704?1
Google Scholar
R Core Team. (2019). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing. https://www.R-project.org
Google Scholar
Rosenkrantz, L., Amram, O., Caudell, M. A., Schuurman, N., & Call, D. R. (2019). Spatial relationships between small-holder farms coupled with livestock management practices are correlated with the distribution of antibiotic resistant bacteria in northern Tanzania. One Health, 8, 100097. https://doi.org/10.1016/j.onehlt.2019.100097
10.1016/j.onehlt.2019.100097
PubMed Web of Science® Google Scholar
Seo, K. W., Shim, J. B., Kim, Y. B., Son, S. H., Bi Noh, E., Yoon, S., Lim, S. - K., & Ju Lee, Y. (2020). Impacts and characteristics of antimicrobial resistance of Escherichia coli isolates by administration of third-generation cephalosporins in layer hatcheries. Veterinary Microbiology, 243, 108643. https://doi.org/10.1016/j.vetmic.2020.108643
10.1016/j.vetmic.2020.108643
CAS PubMed Web of Science® Google Scholar
Singer, R. S., Ward, M. P., & Maldonado, G. (2006). Can landscape ecology untangle the complexity of antibiotic resistance? Nature Reviews Microbiology, 4(12), 943–952. https://doi.org/10.1038/nrmicro1553
10.1038/nrmicro1553
CAS PubMed Web of Science® Google Scholar
Sun, J., Zeng, Q., Tsang, D. C. W., Zhu, L. Z., & Li, X. D. (2017). Antibiotics in the agricultural soils from the Yangtze River Delta, China. Chemosphere, 189, 301–308. https://doi.org/10.1016/j.chemosphere.2017.09.040
10.1016/j.chemosphere.2017.09.040
CAS PubMed Web of Science® Google Scholar
Tadesse, D. A., Zhao, S., Tong, E., Ayers, S., Singh, A., Bartholomew, M. J., & McDermott, P. F. (2012). Antimicrobial drug resistance in Escherichia coli from humans and food animals, United States, 1950–2002. Emerging Infectious Diseases, 18(5), 741–749. PubMed. https://doi.org/10.3201/eid1805.111153
10.3201/eid1805.111153
CAS PubMed Web of Science® Google Scholar
Trung, N. V., Matamoros, S., Carrique-Mas, J. J., Nghia, N. H., Nhung, N. T., Chieu, T. T. B., Mai, H. H., van Rooijen, W., Campbell, J., Wagenaar, J. A., Hardon, A., Mai, N. T. N., Hieu, T. Q., Thwaites, G., de Jong, M. D., Schultsz, C., & Hoa, N. T. (2017). Zoonotic transmission of mcr-1 colistin resistance gene from small-scale poultry farms, Vietnam. Emerging Infectious Diseases, 23(3), 529–532. https://doi.org/10.3201/eid2303.161553
10.3201/eid2303.161553
PubMed Web of Science® Google Scholar
Truong, D. B., Cuong, N. V., Doan, P. H., Dung, N. T. T., Kiet, B. T., Rushton, J., & Carrique-Mas, J. (2021). Small-scale commercial chicken production: A risky business for farmers in the Mekong Delta of Vietnam. Preventive Veterinary Medicine, 195, 105470. https://doi.org/10.1016/j.prevetmed.2021.105470
10.1016/j.prevetmed.2021.105470
PubMed Web of Science® Google Scholar
Verrette, L., Fairbrother, J. M., & Boulianne, M. (2019). Effect of cessation of ceftiofur and substitution with lincomycin-spectinomycin on extended-spectrum-β-lactamase/AmpC genes and multidrug resistance in Escherichia coli from a Canadian Broiler Production Pyramid. Applied and Environmental Microbiology, 85(13), e00037–19. PubMed. https://doi.org/10.1128/AEM.00037-19
10.1128/AEM.00037?19
CAS PubMed Web of Science® Google Scholar
WHO. (2019). Critically Important Antimicrobials for Human Medicine, 6th Revision. World Health Organization.
Google Scholar
Woolhouse, M., Ward, M., van Bunnik, B., & Farrar, J. (2015). Antimicrobial resistance in humans, livestock and the wider environment. Philosophical Transactions of the Royal Society B: Biological Sciences, 370(1670), https://doi.org/10.1098/rstb.2014.0083
10.1098/rstb.2014.0083
PubMed Web of Science® Google Scholar
Yamaguchi, T., Kawahara, R., Harada, K., Teruya, S., Nakayama, T., Motooka, D., Nakamura, S., Nguyen, P. D., Kumeda, Y., Van Dang, C., Hirata, K., & Yamamoto, Y. (2018). The presence of colistin resistance gene mcr-1 and -3 in ESBL producing Escherichia coli isolated from food in Ho Chi Minh City, Vietnam. FEMS Microbiology Letters, 365(fny100), https://doi.org/10.1093/femsle/fny100
10.1093/femsle/fny100
Web of Science® Google Scholar
Zhao, C., Wang, Y., Tiseo, K., Pires, J., Criscuolo, N. G., & Van Boeckel, T. P. (2021). Geographically targeted surveillance of livestock could help prioritize intervention against antimicrobial resistance in China. Nature Food, 2(8), 596–602. https://doi.org/10.1038/s43016-021-00320-x
10.1038/s43016?021?00320?x
Google Scholar
Zhou, L.-J., Li, J., Zhang, Y., Kong, L., Jin, M., Yang, X., & Wu, Q. L. (2019). Trends in the occurrence and risk assessment of antibiotics in shallow lakes in the lower-middle reaches of the Yangtze River basin, China. Ecotoxicology and Environmental Safety, 183, 109511. https://doi.org/10.1016/j.ecoenv.2019.109511
10.1016/j.ecoenv.2019.109511
CAS PubMed Web of Science® Google Scholar
Zhu, G., Xiao, J., Liu, T., Zhang, B., Hao, Y., & Ma, W. (2019). Spatiotemporal analysis of the dengue outbreak in Guangdong Province, China. BMC Infectious Diseases, 19, 493. https://doi.org/10.1186/s12879-019-4015-2
10.1186/s12879?019?4015?2
PubMed Web of Science® Google Scholar

Citing Literature

All articles

Modelling the impact of antimicrobial use and external introductions on commensal E. coli colistin resistance in small-scale chicken farms of the Mekong delta of Vietnam

Abstract

1 INTRODUCTION