Problems
This section of the Journal offers readers an opportunity to exchange interesting mathematical problems and solutions. Please send them to Ted Eisenberg, Department of Mathematics, Ben-Gurion University, Beer-Sheva, Israel or fax to: 972-86-477-648. Questions concerning proposals and/or solutions can be sent via e-mail to [email protected]. Solutions to previously stated problems can be seen at http://www.ssma.org/publications.
—————————————————————————————
-
5271:
Proposed by Kenneth Korbin, New York, NY
Given convex cyclic quadrilateral ABCD with
, 
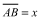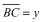, and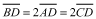 
.Express the radius of the circum-circle in terms of x and y.
-
5272:
Proposed by Tom Moore, Bridgewater State University, Bridgewater, MA
The Jacobsthal numbers begin 0, 1, 1, 3, 5, 11, 21, … with general term
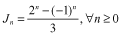. Prove that there are infinitely many Pythagorean triples like (3, 4, 5) and (13, 84, 85) that have an hypotenuse that is a Jacobsthal number. -
5273:
Proposed by Titu Zvonaru, Comănesti, Romania, and Neculai Stanciu, “George Emil Palade” General School, Buzău, Romania
Solve in the positive integers the equation abcd + abc = (a + 1)(b + 1)(c + 1).
-
5274:
Proposed by Enkel Hysnelaj, University of Technology, Sydney, Australia
Let x, y, z, α be real positive numbers. Show that if
then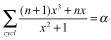
where n is a natural number.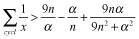
-
5275:
Proposed by José Luis Díaz-Barrero, Barcelona Tech, Barcelona, Spain
Find all real solutions to the following system of equations:
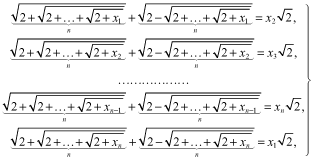
where n ≥ 2.
-
5276:
Proposed by Ovidiu Furdui, Technical University of Cluj-Napoca, Cluj-Napoca, Romania
- (a)
Let a ∈ (0, 1] be a real number. Calculate
where ⌊x⌋ denotes the integer part of x.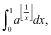
- (b)
Calculate
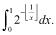
- (a)
