2.1 Plant material

French bean (Phaseolus vulgaris L.) cv. Contender, and spinach (Spinacia oleracea L.) cv. Géant d'Hiver were purchased from Vilmorin (France). Seeds were germinated in vermiculite with tap water in darkness. Seven days old seedlings were transplanted to pots (8.3 cm diameter, 11 cm height; one plant per pot) filled with sand (previously washed with tap water and sterilised in an autoclave) and grown in the greenhouse. Whole culture duration was 33 and 38 d for bean and spinach, respectively. Under our conditions (sufficient total N availability), bean plants did not form nodules. Bean plants were grown in January 2017 under natural light, with supplementary light supplied by lamps (Metal Halide Lamps, HSI-THX, 400 W, Sylvania) 10 h per day, providing a photosynthetic photon flux density (PPFD) of 140–160 μmol photons m^–2 s^–1 at plant height. Air temperature was 23 ± 2°C during the day and 17 ± 2°C at night. Humidity was 42% ± 8% during the day and 55% ± 15% at night. Spinach plants were grown in July and August 2017, with an artificial light source (200–210 μmol photons m^–2 s^–1 PPFD at plant height) only 16 h per day. Temperature and humidity were the same as for bean cultivation. Maize plants were grown at the same time to have an indirect measurement of ambient CO₂ using maize leaf organic matter. The carbon isotope composition of the ambient CO₂ in the culture rooms was about –9.5‰ (measured, Vienna-Pee Dee Belemnite as standard) and –14.1‰ (estimated, considering δ¹³C of maize) for bean and spinach, respectively. In figures below, the difference between maize leaf and bean or spinach organic matter (weighted average of root and leaf δ¹³C) is referred to as ^MaizeΔδ_TOM.

2.2 Nutrient conditions

Plants were supplied with nutrient solutions with 6 different proportions of ammonium (NH₄⁺) and nitrate (NO₃^–) as N source as follows (NH₄⁺/NO₃^– ratios): 0/100, 25/75, 50/50, 75/25, 90/10 and 100/0. In the following, N-treatments are referred to proportions of NH₄⁺ (i.e. 0%, 25%, 50%, 75%, 90% and 100%, respectively). Nutrient solutions contained 6 mmol L⁻¹ of N (total) formed with a combination of KNO₃, Ca(NO₃)₂, NH₄NO₃ or (NH₄)₂SO₄ to obtain different N-treatments. Additional components were: 1 mM CaCl₂, 0.25 mM KH₂PO₄, 1 mM MgSO₄, and trace elements (2 μM MnSO₄, 2 μM ZnSO₄, 0.5 μM CuSO₄, 25 μM B(OH)₃, 0.5 μM Na₂MoO₄, 40 μM Fe-EDTA). The pH of solutions was kept constant at 5.5. In 100% NH₄⁺ and 90% NH₄⁺ treatments, 1 mM K₂SO₄ was added to keep K concentration constant. Although the sand was sterilised by autoclaving, 1 ppm nitrification inhibitor (2-chloro-6-trichloromethylpyridine) was added to nutrient solutions for spinach, to avoid contamination by nitrifying bacteria from the environment. Nutrient solutions were used for watering the plants only after appearance of cotyledons (750 mL solution plate⁻¹ d⁻¹, with 8 pots in each plate). The amount of the solution was so that pots reached full capacity and allowed to drain to plates. During the last week before harvesting, the amount of the solution was increased to 1000–1500 mL plate⁻¹ d⁻¹ depending on plant growth rate. Chlorophyll content and Nitrogen Balance Index were measured every 3 days with a DUALEX instrument (DUALEX SCIENTIFIC + TM, ForceA, France, Orsay) to check plants were not N deficient.

2.3 Leaf gas exchange parameters

One month after planting, gas exchange and chlorophyll fluorescence were measured using a Licor 6400 with LCF chamber (LI-COR, Inc.) in the morning (9–12 h) during 3 successive days. One plant with mature leaves was selected from each treatment each day. Therefore, there were 3 replications for gas exchange measurement. Plants used for measurement were selected randomly. Before photosynthetic measurements, plants were dark-adapted for 30 min, then one mature leaf was used. Gas exchange conditions were set as follows: flow rate 300 μmol air s^–1, CO₂ mole fraction 390 μmol mol^–1 and PPFD 400 μmol m^–2 s^–1 (with 10% blue). Leaf temperature was fixed at 22°C. Leaf net CO₂ assimilation rate (A_n), stomatal conductance (g_s) and the ratio of intercellular to ambient CO₂ concentrations (C_i/C_a) data were automatically recorded every 3 min, reaching steady values after about 30 min. Three values in the steady state were recorded to get a mean value for each plant.

2.4 Carbon isotope composition of respired CO₂

To ensure that plants had enough photosynthates as (potential) respiratory substrates, they were taken from the greenhouse after at least 4 h light. They were then placed in the dark for 30 min to avoid light enhanced dark respiration (LEDR). One intact mature leaf was cut off and put into a flask (50 mL) completely covered by aluminium foil. The flask was flushed with CO₂-free air for 5 min, then sealed with a septum and left for respired CO₂ accumulation. CO₂ concentration was analysed by micro-GC (490 Micro GC, Agilent Technologies), with an injection volume of 5 μL every 3 min. When CO₂ mole fraction was above 1000 µmol mol⁻¹ (approximately after 12 min), air samples were manually collected from the flask with a syringe (0.5 to 1 mL depending on CO₂ concentration) and injected into a GC-IRMS, made of a gas chromatograph (GC HP 5890) coupled to a stable isotope ratio mass spectrometer (Optima Isochrom-µG, Fisons Instruments) to measure the carbon isotope composition of respired CO₂ (denoted as δ¹³C_R). Syringes were flushed with helium five times and then with sample air inside a given flask 10 times before each injection. Each flask was sampled and measured 3 times to ensure reproducibility of measurements. For root-respired CO₂, roots were first washed with tap water and dried with absorbing paper before incubation in flasks. Since the respiration rate and the size of roots were greater than that of leaves, bigger flasks (120 mL) were used. Measurements were made between 10:00 and 16:00 each day, and with a random selection of plants.

2.5 Sampling

Plants used for measurements of δ¹³C in respired CO₂ were harvested for biomass determination. Plants were divided into leaves, stems and roots. Samples were plunged into liquid nitrogen and then freeze-dried. Samples were then ground into a fine powder (using a Retsch MM200 mill ball, Bioblock Scientific) used for isotope measurements and extractions.

2.6 Extraction of soluble fraction

Plant powder (50 mg) was suspended in 1 mL cold distilled water and maintained on ice for 60 min with agitation with vortex every 10 min. After centrifugation (14,000 g, 5°C, 15 min), the supernatant (containing soluble sugars, organic and amino acids and soluble proteins) was separated from the pellet. The supernatant was heated at 100°C for 5 min and then kept on ice for 30 min to precipitate heat-denatured proteins. After centrifugation (14,000 g, 5°C, 15 min), the soluble fraction was collected, kept at –20°C for subsequent utilisation. Samples were referred to as water soluble organic matter (WSOM). Aliquots of 200 μL were poured into tin capsules and oven-dried at 50°C for isotope analysis.

2.7 Carbon and nitrogen isotope composition of organic material

2.8 Compound-specific isotope analysis

The δ¹³C of common organic acids (malate and citrate) and main sugars (sucrose, glucose and fructose) were determined using liquid chromatography coupled to isotope ratio mass spectrometry (IRMS) as in (Ghiasi et al., 2021). Briefly, WSOM extracts were diluted 500 times, and the pH was adjusted to 7. Then 4 mL were passed through cation exchangers (Dionex^TM OnGuard II H 1.0 cc cartridges, Thermo Scientific) and anion exchangers (Dionex^TM OnGuard II A 1.0 cc cartridges) to retain amino acids and organic acids, respectively, and collect soluble sugars. Purified soluble sugars were collected in amber silanised glass vials (Vial short tread, VWR International). Organic acids were collected in amber glass vials. The Thermo Finnigan LC-IsoLink system (Ultimate 3000, Dionex/Thermo Scientific) coupled to Delta V Advantage isotope ratio mass spectrometer (Thermo Scientific) was used for δ¹³C of individual soluble sugars and organic acids (malate and citrate). Amounts (denoted as [C]) and δ¹³C of individual sugars were used to calculate δ¹³C of total soluble sugars (δ¹³C_Sug) using mass balance, as δ¹³C_Sug (‰) = (δ¹³C_Glc · [C]_Glc + δ¹³C_Suc · [C]_Suc + δ¹³C_Fru · [C]_Fru)/([C]_Glc + [C]_Suc + [C]_Fru). Similarly, using amounts and δ¹³C of individual sugars and organic acids, we calculated the predicted δ¹³C of total water-soluble fraction to compare with measured values (δ¹³C_WSOM).

The δ¹³C of the most abundant free fatty acid (palmitic or palmiteaidic acid depending on species; simply referred to as “palmitate” thereafter), maltose and amino acids was determined on derivatised samples (methoxyamine and MSTFA in pyridine) using gas chromatography coupled to IRMS using a GC 7693 A coupled to a combustion module GC5 (filled with the GCN reactor) and precisION IRMS (Elementar), after (Domergue, Lalande, et al., 2022). Isotope standards were caffeine (IAEA-600) and nicotine (home standard, from Sigma-Aldrich/Merck) and retention time indices were obtained using an alkane mix (injected separately; Connecticut n-Hydrocarbon Mix, Supelco). Specific standards of known δ¹³C were used to determine the δ¹³C of trimethylsilyl (TMS) groups (–33.32‰) and thus correct the δ¹³C of analytes (palmitate 1 TMS, maltose 8 TMS, and TMS derivatives of amino acids) for the contribution of TMS carbons to raw isotope composition. δ¹³C was corrected for linearity to account for the fact that some metabolites were more abundant than others (in practice this correction was small, generally less than 0.2‰). The weighted-average δ¹³C of amino acids was calculated using the observed signal (mass-44) and δ¹³C of individual amino acids.

2.9 PEPC activity

Samples used for PEPC activity were periodically harvested during the daytime and conserved at –80°C. 150 mg frozen roots or leaves (without petioles and midribs) were ground in a mortar with liquid nitrogen with 100 mg sand. Then 1 mL extraction buffer (HEPES 50 mM; MgCl2 10 mM; EDTA 1 mM; EGTA 1 mM; BSA 0.025% (w/v); glycerol 10% (w/v); DTT 5 mM and protease inhibitor) was added (4°C). After agitation with a vortex for 2 s, the sample was thawed on ice and agitated again with a vortex for 5 s and centrifuged at 10,000 g, 4°C for 10 min. PEPC activity was measured using a coupled reaction assay (NADH-oxidation via malate dehydrogenase). The assay medium contained 2 mM phosphoenolpyruvate (PEP), 100 mM Tricine (pH 8.0), 10 mM NaHCO₃, 20 mM MgCl₂, 0.05% Triton, 0.5 mM NADH, 1 U mL^–1 malate dehydrogenase, 20 μL enzyme extraction solution, with 200 μL as the final volume. Two technical replicates for each sample were measured. Measurements used a 96-well plate placed in a microplate spectrophotometer (PowerWave HT, BioTek) to record NADH oxidation at 340 nm averaged across 20 min. A blank without PEP was also recorded for subtraction. An assay where PEP was replaced by H₂O was checked as a control. PEPC activity was calculated as the blank-corrected difference in NADH oxidation rate before and after the addition of PEP.

2.10 Statistics

Omics analyses were carried out on 3 to 4 samples per condition and species (i.e., 4 independent replicate). Univariate statistical analysis was conducted using an analysis of variance (one-way ANOVA) to examine differences between NH4⁺:NO₃⁻ conditions (Figures 1-4). The data were also analysed via multivariate statistics to identify features that correlate significantly with the δ¹³C in respired CO₂ conditions, using orthogonal partial least squares-discriminant analysis (OPLS) with Simca®, version 17.0.2 (Sartorius). In the OPLS, the response variable (Y variable) was δ¹³C of respired CO₂ expressed relative to δ¹³C in total organic matter (i.e., δ¹³C_R – δ¹³C_OM denoted as ^OMΔδ¹³C_R). We used ^OMΔδ¹³C_R to account for the fact that spinach and bean did not have the same range of δ¹³C due to photosynthetic fixation. Also, for statistics, it was better to express δ¹³C relative to organic matter rather than sugars (as in the model described below) to assess whether the Δδ¹³C of sugars could be a driver of respired CO₂. The performance of the OPLS was assessed with the correlation between observed and predicted Y (R²), the cross validated correlation coefficient (Q²) and the P-value of the statistical model quantifying the probability that the OPLS model was not different from a random model mean±random error (this P-value is referred to as P_CV-ANOVA). Univariate analysis was also conducted via regression and calculation of the associated P-value. Volcano plots combine results from univariate (regression) and multivariate (OPLS) analyses, showing —log(P) versus OPLS loadings (illustrated in Figure 5).

2.11 Nitrogen isotope mass balance

2.12 Modelling

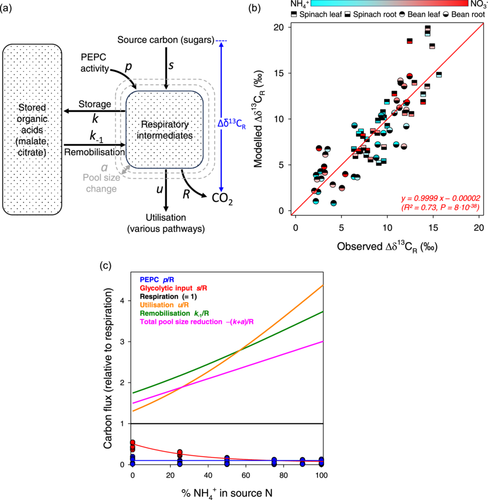
The δ¹³C of night-time respired CO₂ was modelled using a metabolic mechanistic approach illustrated in Figure 6. It was assumed that the metabolically active pool of respiratory intermediates (organic acids) was fed by both stored organic acids (remobilisation, flux k₋₁), glycolysis (s), and PEPC activity (p). This active pool is then used to produce CO₂ (respiration R), feed storage (flux k), and sustain amino acid synthesis and other metabolic pathways (utilisation u). Variation in pool size was assumed to be possible, i.e. the pool could be nonstationary. It was assumed that organic acids purified from organs mostly reflected vacuolar material and thus their δ¹³C were associated with stored organic acids. The change in pool size with time was denoted as a. Since the absolute δ¹³C is dissimilar in spinach and bean due to different CO₂ source and photosynthetic isotope fractionation, δ¹³C was expressed relative to source carbon, that is, the weighted average δ¹³C of sugars (fructose, sucrose, glucose) (i.e., δ¹³C_R – δ¹³C_sugars denoted as Δδ¹³C_R in blue in Figure 6a).

In Equation 5, p/R is known (since PEPC activity and respiration were measured) thus unknown relative metabolic fluxes are u/R, k₋₁/R and (k + a*)/R. These metabolic fluxes were not assumed to be constant and rather, supposed to vary with NH₄⁺:NO₃⁻ nutrition, using a sigmoid (u/R, k₋₁/R) or linear response (k + a*/R; a linear response was chosen in this case since a* contains a logarithm and thus an exponential component should transform to linear). Δδ_fix and Δδ_stock were known since they are the isotope difference between sugars and fixed bicarbonate, and between sugars and weighted average organic acids, respectively. Δδ_fix and Δδ_stock could thus be calculated for each sample. Solving (fitting) was performed using the Excel® solver, to optimise the match between predicted and observed Δδ¹³C_R via the minimisation of the sum of squares. The value of embedded coefficients (particular, of sigmoid and linear responses) obtained by optimisation are listed in Supporting Information S1: Table S2.

3.1 N assimilation

The utilisation of nitrogen from source N of the nutrient solution was assessed using the nitrogen isotope composition (δ¹⁵N). The δ¹⁵N of source ammonium, nitrate and total organic matter of leaves and roots is shown in Figure 1a. In both spinach and bean, leaves were slightly ¹⁵N-enriched by 1‰–2‰ compared to roots. Spinach organic matter (in both leaves and roots) tended to be more ¹⁵N-depleted than that of bean, suggesting that there was higher isotope fractionation during N assimilation in spinach. In fact, using 100% ammonium and 100% nitrate, the apparent isotope fractionation was calculated using the weighted average (biomass-weighted) of leaf and root δ¹⁵N. In bean, there was a fractionation in favour of ¹⁵N by about 4‰ during ammonium utilisation (while there was almost no fractionation in spinach) and there was a small fractionation during nitrate utilisation, i.e., about 2‰ in spinach (against ¹⁵N) and −0.5‰ (in favour of ¹⁵N) in bean (Figure 1b, inset). Accounting for these isotope fractionations, we calculated the proportion of effective ammonium utilisation (Figure 1b). Effective ammonium utilisation closely followed the proportion of ammonium in source N, although it was slightly lower in bean than in spinach, suggesting that the two species were differentially selective for nitrate and ammonium. N conditions also influenced biomass and photosynthesis (summary of results in Supporting Information S1: Figures S1 and S2). As anticipated, ammonium caused a small decline in total plant biomass and at 100% ammonium, led to a significant drop in net photosynthesis. However, there was a concurrent change in stomatal conductance so that the intercellular-to-atmospheric CO₂ ratio (C_i/C_a) did not change dramatically.

3.2 δ¹³C of organic matter and respired CO₂

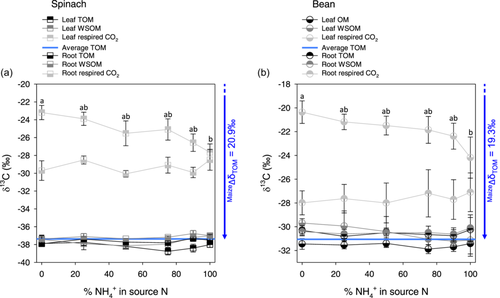
In both spinach (Figure 2a) and bean (Figure 2b), there was little change in δ¹³C of total organic matter, suggesting that the photosynthetic isotope fractionation did not vary much. The comparison with maize organic matter cultivated under the same conditions (blue arrows in Figure 2) suggests that photosynthetic fractionation was slightly higher (about 21‰) in spinach than in bean (about 19‰). The δ¹³C of water-soluble organic matter (WSOM) was relatively close to that in total organic matter and did not change considerably with NH₄⁺:NO₃⁻ nutrition. There was a relatively good agreement between the estimated isotope composition calculated with the photosynthetic isotope fractionation (Δ_i) and observed WSOM (Supporting Information S1: Figure S3). δ¹³C of leaf-respired CO₂ decreased when the proportion of ammonium increased in source N (Figure 2a,c), with a depletion of about 4‰ in 100% ammonium compared to 100% nitrate. Such a decline was likely not due to a decline in photosynthetic isotope fractionation at least in spinach, since C_i/C_a decreased under high ammonium conditions, and thus photosynthetically fixed carbon was probably slightly ¹³C-enriched (Supporting Information S1: Figures S2 and S3). The δ¹³C of root-respired CO₂ did not change much, although it tended to be higher at 100% ammonium compared to 100% nitrate, by about 1‰ (Figure 2b,d).

3.3 δ¹³C of metabolites

The δ¹³C varied considerably between metabolites (Figure 3), ranging between –40 and –25‰. There were considerable differences between sugar species, maltose being ¹³C-enriched and glucose being ¹³C-depleted. Malate was always relatively ¹³C-enriched and was isotopically close to citrate (except in spinach leaves where it was about 2‰–3‰ ¹³C-enriched compared to citrate). This suggests that malate carbon isotope composition was influenced by PEPC activity, which fixes ¹³C-enriched bicarbonate to form C₄ acids. Amino acids tended to be ¹³C-enriched with considerable variation. As expected for lipids, palmitate was generally ¹³C-depleted, in particular compared to citrate and malate.

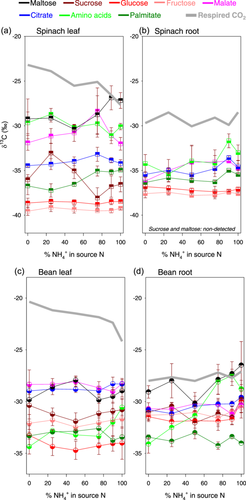
Taken as a whole, there was no consistent metabolic pattern of variation with respect to ammonium and nitrate proportions across organs and species. For example, amino acids were progressively ¹³C-enriched as the proportion of ammonium increased in bean, but it was not the case in spinach. Interestingly, there were important changes in δ¹³C of malate in spinach, with a maximum value (about −28‰) observed under 75% ammonium in leaves. Citrate tended to be enriched in ¹³C by about 1‰ as ammonium proportion increased to 100%, except in spinach leaves where it reached a maximum at 75% ammonium, like malate. It is worth noting that except for maltose at high ammonium, no metabolite was more ¹³C-enriched than respired CO₂. It suggests that CO₂ generation by respiration was either (1) fed by a ¹³C-enriched, small metabolic pool that was not well reflected by the isotope analysis of metabolites (i.e., total pools extracted from leaves and roots; Figure 3); or (2) associated with an isotope fractionation in favour of ¹³C.

3.4 Respiration, enzymatic activities and pool sizes

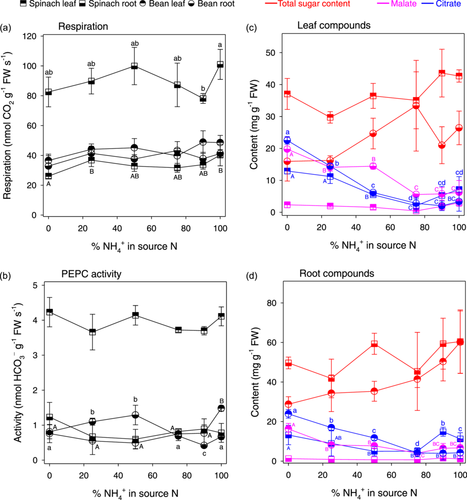
The respiration rate did not change considerably with NH₄⁺:NO₃⁻ ratio and was in the same order of magnitude (20–40 nmol g⁻¹ s⁻¹) in bean organs and spinach leaves (Figure 4a). The respiration rate of spinach roots was comparatively high (80–100 nmol g⁻¹ s⁻¹). PEPC activity tended to be higher in bean leaves when ammonium was less than 50% of source N but it was not affected by N nutrition in spinach leaves. PEPC activity in roots remained in the same order of magnitude and was only significantly affected by N nutrition in bean roots with an increase under 100% ammonium (Figure 4b). Total sugar content was quite variable in leaves with no clear pattern when N nutrition changed (Figure 4c). Leaf malate decreased significantly as ammonium proportion increased; the citrate content decreased in bean leaves but was always very low in spinach leaves. A rather similar pattern in sugars, malate and citrate was observed in roots (Figure 4d), despite a progressive (insignificant) increase on average sugar content and an increase in spinach root malate content under 90% and 100% ammonium.

3.5 Multivariate analysis of respired CO₂

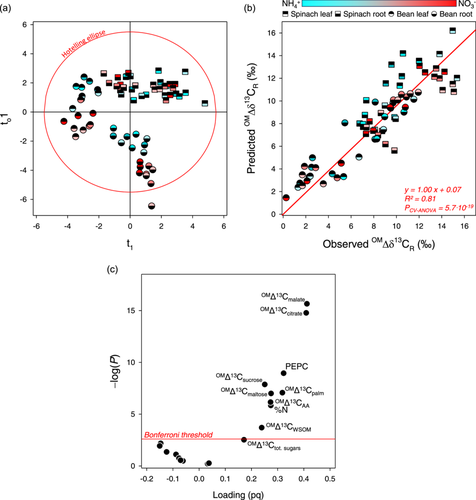
We explored best drivers of δ¹³C of respired CO₂ using a supervised multivariate method (OPLS), with ^OMΔδ¹³C_R as the response variable to be modelled. We used the full data set (i.e., all individual measurements, not average values) to assess whether it was possible to design a statistical model that was valid regardless of organs and species. Datapoints could be placed in the multivariate space according to ^OMΔδ¹³C_R along axis 1, with residual variance along axis 2 (Figure 5a). We obtained a very good statistical performance with R² of 0.81 (Figure 5b), high cross-validated coefficient Q² (0.77) and very high significance (P_CV-ANOVA = 5.7 ∙ 10⁻¹⁹). Best drivers are shown as a volcano plot combining results of univariate and multivariate statistics (Figure 5c). The isotope composition in malate and citrate were the strongest drivers, followed by PEPC activity and various other parameters. It demonstrates that respired CO₂ was determined by a combination of metabolic parameters (multivariate component) in which the isotope signature of organic acids had a relatively high weight. In other words, several metabolic fluxes and source metabolites are involved in the mechanism behind δ¹³C of respired CO₂.

3.6 Modelling

A two-pool model was designed to compute the Δδ¹³C_R as a function of source carbon, δ¹³C of stored organic acids and metabolic fluxes (Figure 6a). Although simplistic, it should in principle capture the most important metabolic features that may explain the isotope composition of respired CO₂. Two flux parameters were known: respiration (R), PEPC activity (p). The glycolytic input (s) could be deduced from other parameters. Three input parameters, namely storage/build-up (k + a*), remobilisation (k₋₁) and utilisation (u) were unknown and their response function to ammonium was determined using least squares optimisation. Taken as a whole, the model explained quite well Δδ¹³C (isotope difference between CO₂ and sugars) of respired CO₂ with a correlation coefficient (R²) of 0.73 and a very close alignment to the 1:1 line (Figure 6b). Modelled storage, remobilisation and utilisation increased with ammonium proportion while the glycolytic input decreased (Figure 6c). Interestingly, remobilisation and utilisation fluxes represented 1.5 to 4 times the respiration rate, showing that the respiratory metabolic pool was highly dynamic (high turn-over). Comparatively, the input of carbon by PEPC was small (a few percent of respiration) (see also Figure 4). There was also a predicted change in total pool size, with a more pronounced reduction in total organic acid pool as ammonium proportion increased (pink line, Figure 6c). It is worth noting that it is effectively what was observed with direct organic acid content measurements (Figure 4c,d).

4.1 Overall response of δ¹³C in respired CO₂ to N nutrition

We found that unlike in roots, the carbon isotope composition of respired CO₂ in leaves decreased as the proportion of ammonium increased in the N source (Figure 2). This pattern was remarkably similar in both species.

This effect was unlikely to be driven by N nutrition on photosynthetic isotope fractionation and thus on δ¹³C of fixed carbon. First, no similar decrease in root-respired CO₂ was found (Figure 2), suggesting that metabolic, post-photosynthetic effects are involved. Second, variations (or the lack thereof) in C_i/C_a would lead to an increase (not a decrease) in δ¹³C (Supporting Information S1: Figure S2). Similarly, (Høgh-Jensen & Schjoerring, 1997) reported that white clover plants supplied with nitrate had a lower apparent photosynthetic fractionation Δ than those supplied with ammonium. Conversely, Raven & Farquhar (1990) suggested that in nitrate-fed plants, there could be a lower C_i/C_a due to the combined effect of increased PEPC activity and higher photosynthetic capacity. Here, we found little change in δ¹³C of total organic matter (Figure 2), also suggesting minimal effect of N conditions on photosynthetic fractionation. In results obtained so far, the impact of N nutrition on δ¹³C of plant organic matter is variable, see for example (Brück & Guo, 2006; Guo et al., 2002) in bean. That said, we found here a slight ¹³C-depletion in WSOM as the proportion of ammonium increased (Figure 2). This is also visible when WSOM is compared to predicted δ¹³C of photosynthates (Supporting Information S1: Figure S3, points inside ellipses). It is more likely that under our conditions, WSOM was not properly representative of photosynthates, since the proportion of sugars and organic acids varied considerably (Figure 4) while their δ¹³C differed considerably (Figure 3). In other words, WSOM was impacted by post-photosynthetic isotope fractionations in metabolism and its metabolic composition had an impact on its δ¹³C. In fact, when we calculated the weighted average of major compounds (organic acids and sugars), we could reconstruct the isotope signature of WSOM satisfactorily (R² = 0.84; Supporting Information S1: Figure S4).

We thus argue that the change in δ¹³C of respired CO₂ as N nutrition varied was due to modifications in metabolism, leading to changes in respiratory substrates and/or in metabolic isotope fractionations. Accordingly, N nutrition had an influence on respiration, PEPC activity, sugar and organic acid content (Figure 4), the most visible effect being a decline in organic acids as the ammonium proportion increased. In bean, the sugar content changed little in leaves but increased significantly in roots under 100% NH₄⁺, while both malate and citrate contents decreased. This is consistent with previous reports (reviewed in Andrews et al., 2013; Britto & Kronzucker, 2013). It is believed that the biosynthesis of sugars and their storage in the vacuole under high NH₄⁺ supply represent a detoxification strategy (Bittsánszky et al., 2015) while lower contents in malate and citrate reflect the disappearance of their metabolic function as nitrate proportion declines in the nutrient solution. In fact, under nitrate nutrition, a proportionally higher flux of PEPC activity is generally observed, allowing the formation of negative charges, counterbalancing excess inorganic cations and ensuring pH homeostasis (Krapp et al., 2014), as opposed to what occurs under ammonium nutrition (Britto & Kronzucker, 2002, 2005; Gerendás et al., 1997). Surprisingly, there was no progressive decrease in PEPC activity as the ammonium proportion increased, under our conditions (except in bean leaves under high NH₄⁺, Figure 4b), despite the change in organic acid content. This demonstrates that N nutrition impacted various pathways and the relative flux of PEPC activity −rather than its absolute flux value− declined compared to other metabolic fluxes. This effect was visible in fitted relative flux values in Figure 6, where one can see that PEPC activity was always low under our conditions, while other flux values (such as utilisation and remobilisation) increased as ammonium proportion increased.

Interestingly, δ¹³C of CO₂ respired by roots was not as ¹³C-depleted as found previously (in practice, CO₂ was more ¹³C-enriched than total root organic matter), for example in French bean (Bathellier et al., 2009). Therefore, under our experimental conditions, roots and leaves did not compensate for each other in terms of CO₂ loss, so that δ¹³C of whole plant respired CO₂ was higher than, rather than equal to, δ¹³C of whole plant organic matter (see Introduction). Such a situation has been encountered before in woody plants and occasionally in herbaceous species (reviewed in Ghashghaie & Badeck, 2014). Presumably, the isotope composition of root-respired CO₂ is very sensitive to metabolic differences between species and growth conditions. In addition, the sampling of root-respired CO₂ may involve root manipulation (e.g., washing, transfer in vials, etc.) and this could cause differences on average δ¹³C between methods and laboratories. Effects of different methods for the preparation of roots for respiration measurements and diverse approaches for quantification of isofluxes should be scrutinised with further research.

4.2 Is δ¹³C of metabolites related to δ¹³C of respired CO₂?

Variations in δ¹³C of respired CO₂ was not simply caused by a source effect (i.e. change in respiratory substrate) and did not directly reflect changes in δ¹³C of potential respiratory substrates (such as organic acids). In fact, we measured the carbon isotope composition of various metabolites (Figure 3) and found that (i) no specific metabolite had a response to N nutrition that was comparable to that of respired CO₂; and (ii) no metabolite was always as ¹³C-enriched as respired CO₂. In particular, we observed very limited changes in the δ¹³C of soluble sugars (except for sucrose in spinach leaves) across N conditions. Interestingly, differences in carbon isotope composition between glucose, fructose and sucrose in leaves and roots were in line with previous findings: sucrose was considerably ¹³C-enriched compared to glucose and fructose (Ghashghaie et al., 2001). We also note that maltose, which derives from starch degradation, was ¹³C-enriched, in accordance with the general ¹³C-enrichment in leaf starch compared to sucrose due to chloroplast enzymes isotope effects (Tcherkez et al., 2004). It is also unsurprising to observe some ¹³C-enrichment in root sucrose (compared to glucose and fructose) too, since there is no isotope fractionation during sucrose export (Maunoury-Danger et al., 2009).

Organic acids were significantly ¹³C-enriched relative to total soluble sugars, while the ¹³C-difference between them was more pronounced in leaves than in roots. Unsurprisingly, malate exhibited a strong ¹³C-enrichment, demonstrating the impact of the carbon input by PEPC activity. In fact, when dissolved CO₂ equilibrates with bicarbonate, the equilibrium isotope effect associated with bicarbonate formation enriches in ¹³C by 9‰ (Marlier & O'Leary, 1984). Nevertheless, it should also be recognised that malate can be enriched as the result of isotope fractionations in malate degradation, leaving behind ¹³C-enriched malate molecules. For example, the malic enzyme is associated with an isotope fractionation (kinetic isotope effect) of 32‰ for CO₂ liberation (C-4 atom of malate) (Edens et al., 1997). Parenthetically, it is remarkable that palmitate, which is synthesised from acetyl-CoA, shows limited changes in δ¹³C overall (Figure 3, dark green), suggesting that metabolic modifications impacting δ¹³C of respired CO₂ were downstream of pyruvate dehydrogenation (i.e., acetyl-CoA production), that is, in organic acid pool turn-over and/or Krebs cycle metabolism.

The δ¹³C of amino acids showed a differential response in spinach and bean: while amino acids tended to be more ¹³C-enriched as the ammonium proportion increased in bean, they remained stable in spinach (Figure 3, bright green). It suggests that the metabolism of amino acids incorporated ¹³C-enriched material from carbon skeletons in bean, for example a greater proportion of ¹³C-enriched respiratory substrates. In this species, the demand for carbon skeletons to assimilate N was probably higher since the elemental % of N was higher (Supporting Information S1: Figure S5). Also, bean appeared to be slightly more selective against ammonium under intermediate ammonium nutrition (Figure 1) and therefore high ammonium conditions can be expected to have a more drastic effect on amino acids.

4.3 Metabolic origin of δ¹³C of respired CO₂

Since potential respiratory substrates were not sufficiently enriched to account for the observed ¹³C-enrichment in respired CO₂, it was necessary to address metabolic determinants of CO₂ generation by respiration. The multivariate analysis conducted with all data points and samples suggested that CO₂ could be predicted statistically via a multivariate component comprising δ¹³C of organic acids but also other variables including PEPC activity and δ¹³C in other substrates (Figure 5c). Our results show the important role of the δ¹³C in organic acids already found by Ghiasi et al. (2021) across NH4⁺:NO₃^- ratios in tobacco leaves. Nevertheless, it should be noted that δ¹³C of organic acids is always lower than that of respired CO₂. As stated above, it indicates that there is either (a) a fractionation against ¹²C during decarboxylations, or (b) utilisation of a ¹³C-enriched pool that was not reflected in our compound-specific analysis (Figure 3). Hypothesis (a) is very unlikely since enzymes responsible for CO₂ production are associated with a normal kinetic isotope effect, i.e., against ¹³C (Tcherkez et al., 2011). To our knowledge, there is only one exception, namely NADP-dependent isocitrate dehydrogenase, which has a very small kinetic isotope effect (Grissom & Cleland, 1988) and may exhibit an inverse thermodynamic isotope effect at equilibrium (Lin et al., 2008). Hypothesis (b) is much more plausible, since the consumption of organic acids by catabolism, N assimilation, malic enzyme, conversion to C₅ branched acids, etc. likely fractionates against ¹³C, leaving behind a ¹³C-enriched pool (Rayleigh effect). In addition, this effect is believed to be responsible for the general ¹³C-enrichment in -COOH groups of organic acids (see, e.g., Hobbie & Werner, 2004; Schmidt, 2003), along with the natural ¹³C-enrichment in C-atom positions C-3 and C-4 of glucose, that are at the origin of C-atoms (COOH group) decarboxylated by pyruvate dehydrogenase (Gilbert et al., 2012; Rossmann et al., 1991).

We explored the credibility of hypothesis (b) with a model that accounts for the co-occurrence of a metabolically active pool and a pool of stored organic acids (described by Equations 4 and 5 in Material and methods). In fact, the model could generate relative δ¹³C of respired CO₂ (Δδ¹³C_R) in broad agreement with observed values (R² = 0.73; Figure 6b). Interestingly, such an agreement was observed regardless of species and organs, suggesting that the metabolic mechanism explaining the δ¹³C of respired CO₂ was sufficiently generic. We recognise that there is still substantial variance (27%), due to probable species and organ effects as well as the contribution of metabolic pathways not accounted for, like OPPP. Modelling confirmed (1) the critical influence of the turn-over of the metabolically active pool, fed by remobilisation and used by respiration and other uses (with flux value that were relatively high); and (2) the fact that non-stationarity is probably important. In practice, it means that during plant development or during a diel cycle, the metabolically active organic acid pool is very dynamic and thus when respired CO₂ is sampled, this pool is probably not in the steady state. Such a non-stationarity contributes to the observed ¹³C-enrichment because organic acids are consumed by fractionating reactions, thereby exaggerating the ¹³C-enrichment in acids left behind. Our results further suggest that this effect depends on N conditions, simply because utilisation, remobilisation and variation in pool size are impacted by the NH₄⁺:NO₃^- balance (Figure 6c).

4.4 Perspectives

Taken as a whole, our results show that δ¹³C of respired CO₂ is not simply linked to a unique metabolic source but rather, is a combination of flux values and δ¹³C of different components and this could be made apparent via both multivariate and modelling approaches. We nevertheless recognise that the drivers of respired CO₂ found here may not apply to other situations, such as prolonged darkness (where the shift from sugar consumption to lipid degradation is involved) or the transition from light to dark in leaves (where light-enhanced dark respiration relates to malate degradation by the malic enzyme). Still, in all cases, emphasis should be given to non-stationarity of metabolic pools and substrates used by respiration. That is, respiratory substrates are very dynamic and their modification or their turn-over contributes to the observed ¹³C-signature of respired CO₂. Of course, we also recognise that our modelling exercise was very simplified, since it did not account for all metabolic fluxes and furthermore, disregarded intramolecular isotope compositions. As stated above, there are important δ¹³C differences between C-atom positions, including those in organic acids. Unfortunately, there is presently no method implementable routinely to analyse δ¹³C of organic acids. Typically, using quantitative ¹³C-NMR would require sample preparation to convert COOH groups to their reduced forms (-CH₂OH), break molecular symmetry (e.g., in the case of citrate) and block configuration changes and equilibria. To our knowledge, no such method has been published yet. This technical challenge will be addressed in a subsequent study so as to gain further insights into the isotope signature of CO₂ generated by plant respiration.