Optimising height-growth predicts trait responses to water availability and other environmental drivers
Abstract
Future changes in climate, together with rising atmospheric , may reorganise the functional composition of ecosystems. Without long-term historical data, predicting how traits will respond to environmental conditions—in particular, water availability—remains a challenge. While eco-evolutionary optimality theory (EEO) can provide insight into how plants adapt to their environment, EEO approaches to date have been formulated on the assumption that plants maximise carbon gain, which omits the important role of tissue construction and size in determining growth rates and fitness. Here, we show how an expanded optimisation framework, focussed on individual growth rate, enables us to explain shifts in four key traits: leaf mass per area, sapwood area to leaf area ratio (Huber value), wood density and sapwood-specific conductivity in response to soil moisture, atmospheric aridity, and light availability. In particular, we predict that as conditions become increasingly dry, height-growth optimising traits shift from resource-acquisitive strategies to resource-conservative strategies, consistent with empirical responses across current environmental gradients of rainfall. These findings can explain both the shift in traits and turnover of species along existing environmental gradients and changing future conditions and highlight the importance of both carbon assimilation and tissue construction in shaping the functional composition of vegetation across climates.
1 INTRODUCTION
The extraordinary diversity of plant species on Earth is testament to the existence of trade-offs in the ecophysiological strategies employed by plants to grow, survive, and reproduce. Biophysical constraints on plant phenotype mean that the benefits conferred by a given strategy also impose costs to fitness such that no organism is perfectly adapted to all conditions (Laughlin, 2018). As such, we expect to observe shifts in plant community composition as conditions change across space and time. Precipitation, soil types, and thus soil moisture vary widely across the globe (Fick & Hijmans, 2017), and there is ample empirical evidence that plants exhibit strong responses in their traits to water availability. These responses concern traits related to hydraulic function (such as sapwood area and conductivity), tissue construction (such as leaf mass per area and wood density), and life cycle (maximum height) (Moles et al., 2009; Niinemets, 2001; Towers et al., 2023; Wright et al., 2004). Although we understand the mechanisms underlying some of these patterns, more theory is needed to explain the selective forces causing these patterns to emerge across large spatial scales and at what temporal scales they occur.
The need for further theoretical understanding is motivated by the rapid environmental changes that Earth is experiencing. In addition to rising temperature (and thus), atmospheric dryness and carbon dioxide concentrations, climate change is expected to bring about changes in precipitation regimes across the globe (IPCC, 2023), thereby modifying the functional composition of ecosystems as populations and species adapt, migrate, or are driven extinct under new climatic conditions (Crimmins et al., 2011; Zhu et al., 2012). Indeed, there is already evidence showing an increase in the predominance of drought-affiliated species in ecosystems that are becoming drier and more seasonal and, on the other hand, the invasion of mesophilic species in locations that are becoming wetter (Fauset et al., 2012; Feeley et al., 2020, 2011). Without theoretical predictions on how these changes may determine the favourability of different plant strategies, we are unable to anticipate the direction and rate of change in the composition of future vegetation.
Eco-evolutionary optimality frameworks (EEO) offer a means to develop process-based hypotheses for how and why traits respond to the environment (Harrison et al., 2021). Under EEO, environmentally driven trait patterns are hypothesised to emerge from a selection of trait combinations that maximise fitness. Some analyses have simulated community assembly across environmental gradients by calculating the reproductive fitness of species competing for shared resources, permitting the coexistence of multiple viable strategies (Detto et al., 2022; Falster et al., 2017). However, due to the difficulty of estimating reproductive fitness under competitive dynamics, EEO-based models often maximise some other variable as a tractable proxy (Bassiouni et al., 2023) and in the absence of competition. For example, many recent implementations of EEO optimise carbon gain on an instantaneous basis or through time at the leaf, plant, or ecosystem scale to determine a single optimal strategy for each environment. These models have been shown to successfully replicate observed environmental responses for a number of traits and variables including, amongst others, the intercellular to atmospheric ratio of (Wang et al., 2017), leaf maximum photosynthetic carboxylation capacity (Dong et al., 2017) and the sapwood to leaf area ratio (Trugman et al., 2019; Xu et al., 2021). Despite success, it has been argued that optimality approaches that focus on carbon acquisition alone limit the range of traits that can be represented by EEO because traits can also affect the construction cost of and relative allocation towards different plant tissues instead of, or in addition to, carbon uptake (Bartlett et al., 2019; Dong et al., 2022; Falster et al., 2018). In such cases, an approach which explicitly considers how traits influence the translation of carbon production to growth while preserving model speed may be most appropriate for understanding how trait environment gradients emerge from selection, as has been explored in other modelling work (Falster et al., 2018; Franklin, 2007; Franklin et al., 2014; King, 1996; Potkay & Feng, 2023). The question is: Can these models adequately recreate empirical phenomena?
Trait growth theory (TGT) is a theoretical framework which integrates the effects of traits on both biomass production and plant construction costs on growth rates (Falster et al., 2011, 2018; Gibert et al., 2016; Westoby et al., 2022). This is achieved by linking both production and construction to measurable traits and the trade-offs encoded by these traits, to describe how additional biomass is allocated to different tissues as the plant grows. Thus far, TGT has been used to provide mechanistic explanations for a variety of empirical phenomena including the hump-shaped change in height-growth rate of biomass with size, the size-dependent effect of traits on growth, and effect of traits on shade tolerance (Falster et al., 2017; Westoby et al., 2022). The system of equations that make up TGT mean that, in principle, the model can be extended to include the effect of any abiotic factor on growth, so long as it influences either biomass production and/or allocation. The flexibility of TGT is particularly suited for explaining empirical patterns in the occurrence of traits along environmental gradients. To date, however, explicit representation of plant hydraulics is nonexistent and response to water availability in the TGT framework is very limited (Falster et al., 2017; Westoby et al., 2022).
Recent advances in the representation of trade-offs between photosynthetic and hydraulic functions offer a mechanistic, first-principles pathway to link stomatal response and traits to drying soil (Wolf et al., 2016). As soils dry, plants face an unavoidable trade-off between keeping their stomata open to maintain photosynthesis and closing their stomata to minimise drought-induced damaged to the water transport pathway. In contrast to empirical stomatal models, a number of optimal stomatal models assume plants to be efficient water users (Cowan & Farquhar, 1977) that actively regulate the benefits of carbon acquisition relative to the costs of water loss. Beyond their demonstrated performance in predicting observed stomatal conductance (Sabot et al., 2022), optimal stomatal models have the added advantage of being parameterised with measurable hydraulic traits, thereby mechanistically linking traits to stomatal behaviour, and thus to fitness.
Here, we integrate an optimal stomatal behaviour model into the TGT framework to generate predictions about how traits should respond to gradients in soil moisture, atmospheric vapour pressure deficit, carbon dioxide and light availability. The stomatal behaviour model is based on maximising carbon acquisition after accounting for costs associated with water acquisition. We use plant height-growth rate as a proxy for fitness, thereby integrating effects of traits on biomass production and plant construction. Our primary goal is to qualitatively capture the directions of empirically observed trait responses to changes in soil water availability as an emergent outcome of an EEO model based on height-growth rates. To evaluate the effect of processes related to tissue allocation on the predictions for each focal trait, we compare the predictions from the height-growth based model to a simpler fitness proxy based on biomass growth (i.e., carbon gain minus respiration and turnover costs). Next, we investigate whether traits are predicted to also shift with plant size, either through influencing the relative allocation of carbon to different tissues or the hydraulic transport pathway, as shifts in traits with size are also widely observed in nature (Table 1). Finally, by extending our approach to optimise across multiple trait dimensions simultaneously, we investigate our framework's ability to explain species turnover across soil moisture gradients in terms of fitness (as represented by height-growth rate).
| Phenomenon | Response of trait | |||
|---|---|---|---|---|
| Variation in trait across environments | ||||
| With soil dryness | a | a, b, c | d, e | a |
| With atmospheric vapour pressure deficit | f | g | h, i | j |
| With atmospheric carbon dioxide concentration | k, l, m | n | n, o | n |
| With light availability | m, p, q | r | s | t |
| Variation in trait within individuals | ||||
| Change with size | u | v | v, w | x |
| Co-variation among traits | ||||
| With | – | y | y | y |
| With | – | – | y | y |
| With | – | – | – | y |
- Note: Arrows show the direction of the empirical trait response. Dashes indicate cells that were intentionally left blank.
- a Towers et al. (2023)
- b Onoda et al. (2010)
- c Pickup et al. (2005)
- d Gleason et al. (2013)
- e Tavares et al. (2023)
- f Westerband et al. (2023)
- g Rocha et al. (2020)
- h Liu et al. (2021)
- i Olson et al. (2020)
- j Mencuccini and Grace (1995)
- k Hikosaka et al. (2005)
- l Pritchard et al. (1999)
- m Poorter et al. (2009)
- n Bobich et al. (2010)
- o Eguchi et al. (2008)
- p Ellsworth and Reich (1992)
- q Neyret et al. (2016)
- r Poorter et al. (2019)
- s Sellin et al. (2010)
- t de Oliveira et al. (2023)
- u Westoby et al. (2022)
- v Hietz et al. (2013)
- w Rungwattana and Hietz (2018)
- x McDowell, Barnard et al. (2002)
- y Mencuccini et al. (2019).
2 METHODS
2.1 Eco-evolutionary context
In this analysis, we simulate the growth response of individual plants parameterised with a suite of ecophysiological traits along a series of environmental gradients. In a similar manner to other trait-based optimality models, environmental conditions are fixed at each point of the gradient, and simulated plants do not explicitly experience density-dependent interactions (Dong et al., 2017, 2022; Wang et al., 2017). However, the selected environmental gradients are not assumed to be exclusively spatial and thus different points along each gradient could equally represent variation across sites or through time due to exogenous fluctuations in the environment, competition for shared resources, or position in the canopy. The question our model aims to address is: What traits would a plant ideally possess to maximise performance given a set of environment conditions? Given that our framework maximises size growth rate in plants, but does not take into account processes such as mortality and reproduction, simulated optimum strategies are presumably most representative of ‘fast’ species in the global ‘fast-slow’ trait continuum that prioritise resource acquisition at the expense of high mortality rates (Reich, 2014). Nevertheless, we propose that the mechanisms underlying simulated trait responses to the environment could be broadly applicable in explaining observable community-wide trends.
Height-growth rate, as compared to other size growth rates, was selected as our primary metric of plant performance because it is conceptually simple, has long been an indicator of relative plant success and, in light-limited environments, is an indicator of a plant's future position in the canopy under competitive scenarios. However, we note that our findings could equally be centred around other size growth rates including total canopy area which may be more relevant in water-limited systems; the critical aspect of the performance metric for our analysis is that it incorporates processes related to the costs and benefits of allocating biomass production to different plant tissues while preserving model tractability. Moreover, if canopy architecture is assumed to be invariant (Falster et al., 2018), as we do in the present study, height and leaf area growth rate are directly related, meaning that predictions emerging from our model can be viewed in light of optimisation of either size metric.
2.2 TGT
The whole-canopy rates of net photosynthesis and hydraulic cost are found by multiplying the total photosynthetic surface by the average rate of leaf-level net photosynthesis, and leaf-level hydraulic cost, , respectively, which are themselves dependent on traits, plant size, and the environment (see Section 2.3). and are described as average values, representing the central tendency of these values due to variation in light conditions throughout the canopy of an individual. Tissue-specific rates of respiration, and turnover are mass-based and are calculated by summing across the mass of each plant tissue (). and are constants being the fraction of carbon per unit of biomass and the conversion rate between and biomass, respectively (Table 2).
| Symbol | Description | Values | Units |
|---|---|---|---|
| State variables | |||
| H | Plant height | 0.5–20 | m |
| Total area of plant tissue, ia | |||
| Total mass of plant tissue, i | kg | ||
| Total mass of alive tissue | kg | ||
| B | Total plant biomass | kg | |
| Total sapwood volume | |||
| Stomatal conductance to | |||
| Stomatal conductance to | |||
| E | Transpiration per leaf area | ||
| Intercellular partial pressure | Pa | ||
| Leaf water potential | -MPa | ||
| Net photosynthetic assimilation per leaf area | |||
| Hydraulic cost per leaf area | |||
| Leaf-specific hydraulic conductance at | Derived from | ||
| Focal traits | |||
| Sapwood area to leaf area ratio | |||
| Maximum sapwood-specific conductivity | 0.01–50 | ||
| Wood density | 10–2 | ||
| Leaf mass per area | 0.01–1 | ||
| Other traits | |||
| c | Shape parameter for hydraulic vulnerability curve | 2.04b | Unitless |
| Proportional height of average leaf in canopy | 0.89c | Unitless | |
| Maximum rate of carboxylation | 50b | ||
| Maximum rate of electron transport | d | ||
| Biomass per mol carbon | 0.0245c | ||
| Fraction of assimilated converted into mass | 0.7c | ||
| at 50% conductivity lost | Derived from | -MPa | |
| b | Sensitivity parameter for curve | Derived from | -MPa |
| Maximum leaf-specific hydraulic conductance | Derived from , h | ||
| at 99% conductivity lost | Derived from b, c | -MPa | |
| Leaf nitrogen per area | Derived from e | ||
| Carbon cost per unit per second | Derived from | ||
| Turnover and respiration rates | |||
| Leaf turnover rate | Derived from | ||
| Hydraulic-independent sapwood turnover rate | 0.2c | ||
| Root turnover | 1c | ||
| Bark turnover | 0.2c | ||
| Leaf respiration | Derived from | ||
| Sapwood respiration | Derived from | ||
| Root respiration | 217c | ||
| Bark respiration | Derived from | ||
| Other parameters | |||
| Rate of hydraulically dependent sapwood loss at | 75 | ||
| Exponent for in | 1.7 | Unitless | |
| Rate of leaf turnover at | 0.457c | ||
| Exponent for in | 1.7c | Unitless | |
| at | 0.461f | ||
| Exponent for in | 0.35f | Unitless | |
| Exponent for in | 0.46f | Unitless | |
| Average | 608c | ||
| Average | 0.1978c | ||
| Average | 2f | ||
| Focal environmental variables | |||
| Soil water potential | 0.3–3 | ||
| Atmospheric | 20–80 | Pa | |
| D | Vapour pressure deficit | 0.1–3 | kPa |
| Above-canopy photon flux density | 180–1800 | ||
| Other environmental variables | |||
| Atmospheric pressure | 101.3 | kPa | |
| Atmospheric | 21 | kPa | |
| Leaf temperature | 25 | ||
| Day | Day in yearg | 20 | Days |
| T | Diurnal temperature variationg | 10 | |
| RH | Relative humidityg | 50 | % |
| Lat. | Latitudeg | 34 | S |
- Note: Values for state variables left intentionally blank as these vary dynamically.
- a Subscript refers to different plant tissues: leaves, , sapwood, , bark, , root,
- b Falster et al. (2021)
- c Falster et al. (2016)
- d Kumarathunge et al. (2019)
- e Dong et al. (2022)
- f Liu et al. (2019)
- g Used in diurnal simulation.
2.3 Stomatal behaviour model
We extended the photosynthesis submodel used in previous implementations of the plant model, by incorporating stomatal behavioural responses to the environment into the model. Specifically, inspired by the work of Bartlett et al. (2019) linking stomatal behaviour to evolutionary traits on the basis of maximising carbon acquisition relative to hydraulic costs, and following the idea that stomatal optimality should apply at any given instant (Sperry et al., 2017; Wolf et al., 2016), we propose a new extension of an instantaneous stomatal optimisation model that explicitly accounts for sapwood traits. During photosynthesis, is assimilated from the atmosphere through stomata in exchange for , which is drawn from the soil to the leaves by negative pressures along water potential gradient. Negative water potentials impose costs on the plant through a heightened risk of xylem cavitation, subsequent loss of conductivity, and cost of restoring conductivity (Choat et al., 2018). Given that plants must compromise between increasing photosynthesis and reducing hydraulic costs, the stomatal optimisation model seeks to maximise net photosynthesis at any moment by balancing these opposing forces.
We assume here that instantaneous adjustments in do not affect biomass allocation, turnover, or respiration rates beyond those captured in . Given this assumption, the that maximises Equation (4) necessarily also maximises biomass production, and the growth rate of the plant, given all other traits.
To solve Equations (4) and (5) requires values for and , which are a priori unknown. An important insight from Sperry et al. (2017) and included in subsequent stomatal optimisations is that the three variables and are all interlinked and can be solved simultaneously. All three are emergent outcomes of the stomatal optimisation. Following Sperry et al. (2017) and others(e.g. Sabot et al. 2020), we used to calculate , and then . However, note that since the equations specify a monotonic relationship between the three variables, the stomatal optimisation in Equation (4) could be performed with respect to any of them and achieve the same result.
2.3.1 Hydraulic costs
We implemented a novel representation of hydraulic costs (), extending a previous cost function that expresses costs in rates of carbon loss per unit leaf area (Bartlett et al., 2019). In this model, is assumed to account for the loss of conductivity in the xylem pathway incurred by negative . The hydraulic cost function therefore represents the absolute amount of carbon required to restore xylem conductivity.
Here, is the sapwood volume which is normalised by to define in units per leaf area and is the carbon cost of embolism per unit of sapwood volume per unit time. Importantly, this formulation implies plants will experience carbon costs even when stomata are closed, which could act as a proxy for the effect of cuticular conductance of water from the leaf to the atmosphere (Choat et al., 2018).
Here, , and , are the sensitivity and shape parameters of the Weibull distribution, respectively. Embolism damage is assumed to recover instantaneously as leaf water potential becomes less negative, with the carbon cost to repair this damage being accounted for in Equation (3).
The first part of the right-hand side of Equation (12) represents the fact that embolism would incur a greater loss of mass per unit sapwood volume for denser wood. The second part of the right-hand side of Equation (12) gives the rate of turnover, dependent on , where is the average rate of sapwood turnover rate for a fully cavitated stem when is equal to the global average, (Table 2), and defines the strength of the trade-off between and . Thus, although is assumed to increase linearly with owing to the first term on the right-hand side of Equation (12), is also assumed to decline exponentially with increasing , representing a greater resistance to embolism-inducing water potentials (Hacke et al., 2001).
2.4 Trait-based trade-offs
In order for trait-environment gradients to emerge, traits must capture trade-offs in ecological function with costs and benefits that vary with respect to the environment. These trade-offs are discussed below.
The shape parameter () might also vary with and , perhaps to capture a trade-off between the width of the hydraulic safety margin (e.g., P50–P88) and the maintenance of high conductivity under low soil moisture stress. However, as the validity of such covariation remains unclear, we instead set it as a constant value (Table 2).
Huber value, : The cross-sectional sapwood area to leaf area ratio (), influences growth rates in a number of ways. increases with by increasing the cross-sectional area of sapwood supplying a given area of leaf with water. However, declines with due to its effect on the construction cost of sapwood and bark (see Supplementary Information of Falster et al. [2016]). In addition, increases with via its effect on the sapwood volume per leaf area because a given unit of xylem damage incurs a greater absolute loss of carbon in plants with a greater amount of sapwood in our model.
Wood density, : Increasing reduces via its effect on the construction cost of sapwood and bark but also reduces the rate of sapwood damage per unit of conductivity loss as described in Equation (12).
2.5 Implementation and trait optimisation
Plant growth was simulated in the plant R package (Falster et al., 2016) using the TF24 physiological module. The TF24 physiological module adds the stomatal submodel described above into the base FF16 module. Instantaneous height-growth rates were numerically solved across gradients of soil water potential (), vapour pressure deficit (), atmospheric concentration (), and above-canopy photon flux density (), as well as at different plant heights. When simulating across environmental gradients, height-growth rates were calculated for 1 m tall plants.
For a plant of specified size, traits, and environment, we solved for the optimum using numerical methods, as no analytical solution for the that satisfies Equation (4) exists. We solved Equation (4) using the golden-section search algorithm which requires upper and lower boundary values (Kiefer, 1953). For the upper boundary value, we assumed that cannot be less negative than . For the lower boundary value, we assumed that could not be more negative than the critical point at which 95% of hydraulic conductivity is lost ().
To find the value of a traits optimising height-growth rates in a given environment, we minimised the objective function: . When considering a single trait, we used the optimise function from the stats R package. When considering multiple traits, we used generalised simulated annealing, as implemented in the GenSA R package (Xiang et al., 2013), using a maximum of 1500 iterations of the search algorithm. Finally, to compare the predicted trait–environment relationships emerging from the optimisation of height-growth rate to a simpler model based on biomass growth (and to better understand the mechanisms driving emergent patters in the height-growth optimisation), we visualised rates of height growth and net biomass growth across focal traits for 1 m tall plants and inspected how the optimum trait value for each growth rate responded to variation in the environment (Figure 4, Supporting Information S1: Figures S1–S3).
2.6 Parameterisation
In addition to any sources described above, extra parameters in the TF24 module were either obtained from existing literature or were parameterised where data was available to represent a self-supporting woody plant using the AusTraits trait database (Table 2), which is a collation of Australian plant trait data and is the single largest collation of trait data within a single continent (Falster et al., 2021). We considered our use of the AusTraits database appropriate given our focus in the present study on simulating qualitative predictions of trait–environment relationships, rather than matching site or species-specific observations. Along these lines, for parameters which relatively little is known, such as , we simply selected values which yielded realistic simulations of trait optima. Otherwise, the model was parameterised largely using the default parameters available in the base FF16 module of the plant (Falster et al., 2016).
3 RESULTS
3.1 Emergent response of stomatal behaviour to traits and environment
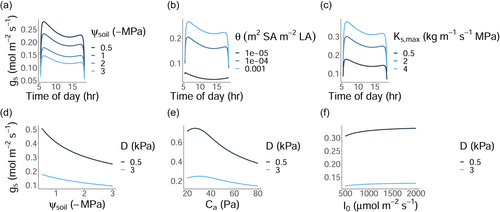
Under our optimality framework, sensitivity of stomatal conductance to the environment is an emergent property rather than the outcome of an empirical relationship.
In line with empirical observations, our stomatal optimisation model predicts a depression in (Figure 1) shortly after midday due to a peak in the atmospheric vapour pressure deficit (Koyama & Takemoto, 2014), as well as a downregulation of as soils dry (Zhou et al., 2013). Considering univariate responses of to the environment, our model predicts a decline in with decreasing soil water potential (), vapour pressure deficit (), and atmospheric concentration (), but an increase with above-canopy photon flux density (). Moreover, traits influence the response of to the environment; plants with greater and achieve a higher in a given environment, and are more water-profligate (Figure 1).
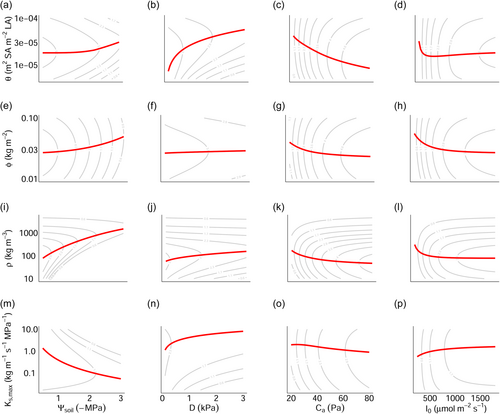
3.2 Emergent response of height-growth rate to the environment
For a given set of traits at a fixed height, absolute height-growth rates were greater in wetter soils (i.e., less negative ), lower , higher , and higher (as represented by the contour lines in Figure 2).
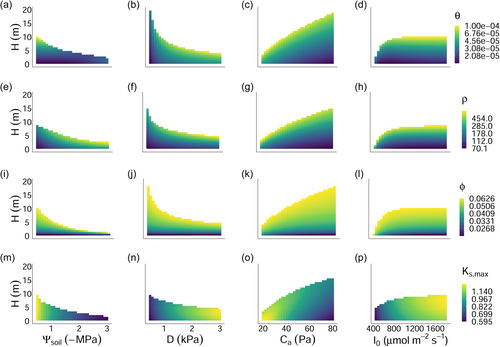
3.3 Individual trait responses to the environment
Optimal Huber value, : Increasing entails an increase in the water transport rate per leaf area at the cost of a reduced leaf area deployment. Moreover, greater leads to greater volume-based hydraulic costs and mass-based respiration and turnover rates. Thus, in general, is expected to become larger where the benefit of a greater to are more apparent relative to the combined costs of construction, respiration, and tissue turnover. Specifically, we found that the response of to was nonmonotonic (leading to the flat response in wetter soils in Figure 2a), especially at greater heights (e.g., by following the horizontal gradient towards the top of Figure 3a), and this was because the -optimising initially declined as soils dried, before increasing again in very dry soil (Figure 4a). The initial decline occurred because it was more profitable for plants to obtain water for transpiration by making more negative and saving on instantaneous costs associated with greater sapwood volume. In very dry soils, however, increased again because approached the critical xylem pressure, , such that it was more profitable to supply the transpiration stream by increasing sapwood volume (Supporting Information S1: Figure S5). also increased with and declined with (Figure 2b,c). In the former case, this increase in the atmospheric demand for water induced by (Equation 7) was compensated for by an increase in the water transport rate via increasing . In the latter case, increasing caused partial stomatal closure (i.e., lower ; Figure 1) and a reduction in which was achieved by reducing .
The nonmonotonic response of the height-growth optimising to in Figure 2 emerged despite the fact that the optimising responded monotonically positive to (Supporting Information S1: Figure S2a). This was because, under very low light, causes the height-growth optima to shift more strongly towards the value of optimising (Supporting Information S1: Figure S2a,e) than it does under high light conditions.
Optimal LMA, : increased with environmental harshness, namely increasing with soil and atmospheric aridity but declining with increasing atmospheric and light availability (Figure 2).
In our model, leaf respiration increases with while leaf turnover decreases, yielding a hump-shaped relationship between and . However, because does not mediate the response of to the environment (Figure 4), the maximising is also invariant to the environment. Nevertheless, -environment relationships emerge as changes in the height of the curve shift the balance between the relative value of biomass production and , which decreases monotonically with . Put simply, the advantageous effect of low on plant construction outweighs the combined carbon losses to respiration and turnover when is high.
Optimal wood density, : Increasing reduces the maximum rate of embolism incurred by a given proportional loss of conductivity (Equation 12) but also incurs an increasing construction cost of sapwood and bark. Thus, was predicted to be larger in more arid environments or environments with lower atmospheric (Figure 2) where more negative optimal , and thus embolism risk are encountered. Counter-intuitively, even though the optimal also becomes more negative as and increase with light availability, potentially necessitating greater resistance to embolism via higher (as indicated by the positive shift in the -optimising in Figure S2c), we found that declines with light availability. This occurred because carbon assimilation increased with increasing light availability, reducing the relative importance of maximising net biomass production and causing the optimising to shift more strongly towards lower values of which maximise the rate of leaf area deployment (i.e., ) (Supporting Information S1: Figure S2c,g).
Optimal maximum sapwood-specific conductivity, : directly traded-off with such that, all else being equal, a plant with a higher had a greater but experienced greater embolism at less negative . Importantly, because does not influence , the optimising is equivalent to the optimising (Figure 4). We observed contrasting responses of to and , with declining in the former case and increasing in the latter case (Figure 2). Contrasting responses emerged because variation in impacted the net carbon assimilation and hydraulic cost differently. In the case of , the predicted response emerged because hydraulic costs rose more rapidly as increased in drier soils, such that maximum leaf-level occurred at lower (Supporting Information S1: Figure S4). In other words, was predicted to decline to improve embolism resistance in the xylem in moisture-stressed locations. In the case of , the predicted increasing response emerged because the marginal benefit to of increasing was much greater under high atmospheric aridity than low, meaning that maximum leaf-level occurred at higher (Supporting Information S1: Figure S4). In other words, for plants experiencing dry air, more rapid water transport is more beneficial to growth, provided sufficient soil water is available to maintain the transpiration stream.
3.4 Individual trait responses to height
In our model, individuals do not experience competition and thus increasing height has no effect on the environmental conditions experienced by plants. Instead, the response of traits to ontogeny primarily emerges through the effect of height on on a per-leaf basis (i.e., the total biomass growth of the plant divided by ). As height increases, the cost of respiration and turnover in nonphotosynthetic tissues as a fraction of leaf-level assimilation also increases. Moreover, the hydraulic cost of water transport increases with the sapwood volume as height increases, all else being equal. Thus, in our model, the predicted trait responses to height reflect functional adjustments to declining leaf-level efficiency as plants grow taller.
It follows from our above analysis of trait-environment predictions, then, that for traits influencing the relative allocation and construction cost of plant tissues (i.e., ), increasing height caused the trait value optimising height-growth to move towards the construction of more expensive tissues (e.g., more dense wood; Figure 3a–l, viewing each subpanel vertically) which minimise losses to tissue turnover.
The very minor, yet positive, response of to height has a more simple explanation (Figure 3m–p). In our model, does not influence the construction cost of tissues and therefore exerts influence on height-growth rates exclusively through . As plants grow taller, declines, reflecting an increase in the length of the hydraulic pathway (Equation 13). Thus, plants are predicted to compensate for greater heights by increasing . Opposing this shift towards greater is the fact that taller plants experience greater damage to the hydraulic pathway per unit of lost conductivity (Equation 9), and must therefore balance the benefit of more rapid water transport against the need for safer xylem (i.e., a more negative ) at greater heights, explaining the low sensitivity of this trait to plant height.
3.5 Species turnover across soil moisture gradients
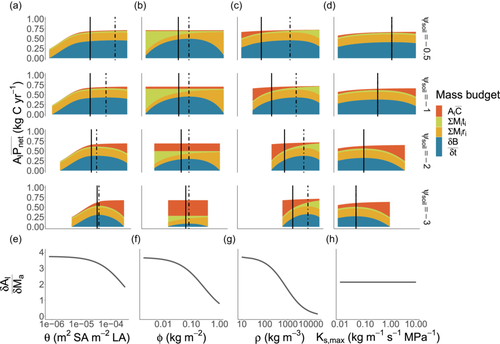
In the analyses above, we have explored how trait optima shifts across environmental gradients considering one trait at a time. However, selection operates on fitness integrated across multiple traits. Using the same framework as above, we jointly optimised height-growth rate across the four traits to evaluate whole-plant functional strategy. In general, traits responded in the same direction as when optimised in isolation, but we observed much greater sensitivity in and a much-reduced sensitivity in the remaining traits (Figure 5). Presumably, this occurred because flexibility in other traits allowed , via to more closely track presiding soil water conditions. For example, at the driest end of the gradient (−3 MPa), the optimum was slightly more negative at −3.68 MPa and at the wettest end of the gradient (−0.5 MPa), the optimum was −0.62 MPa. Considering the above predictions in terms of trait covariance, the multi-trait optimisation predicted that negatively co-varies with and , that positively co-varies with and and that positively co-varies with , consistent with a global-scale bivariate trait-trait analysis (Mencuccini et al., 2019).
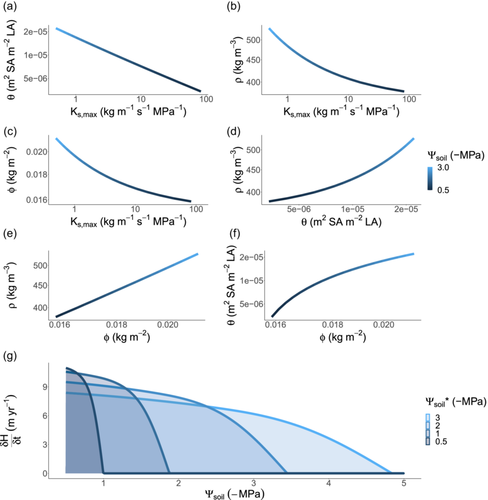
Our optimisation approach can also yield insights into how the emergent properties of plant communities respond to turnover in plant strategies across soil water availability gradients. We found that, regardless of which environment a plant is optimised to grow in, all plants grow faster when water is more plentiful (Figure 5). However, plants that are optimised to grow in wet soils achieve the highest growth rates. This is because they have traits which maximise water transport rates and minimise tissues construction costs, including high and low and . However, species with such traits are also predicted to have narrow fundamental niches (as defined by the range of conditions where they can maintain positive growth), because their growth rate declines rapidly as soils dry. In drier soils, species with low and high and are expected to dominate because they can maintain positive growth rates even under drought (i.e., have wider environmental tolerances; Figure 5).
4 DISCUSSION
Recent advances in plant optimality theory that link stomatal behaviour and gas exchange with plant hydraulics are enabling a mechanistic link between plant traits and the environment. By integrating a stomatal optimisation criterion into an existing height-growth model, we made predictions for how four key traits (LMA, SA:LA, sapwood-specific conductivity and wood density) should shift to optimise plant performance over a range of environmental gradients, including soil moisture. Broadly speaking, these predictions qualitatively match empirical trait–environment patterns (Table 1). Moreover, we predicted how these traits should shift throughout individual ontogeny. Our framework establishes the groundwork for future modelling work seeking to understand how the trait composition of vegetation, and thus, ecosystem processes, are likely to respond to future changes in water availability (Feeley & Zuleta, 2022; Harrison et al., 2021; Sakschewski et al., 2015).
4.1 Trait responses to soil moisture
We predicted an increase in wood density as soil moisture declined, in line with many (Onoda et al., 2010; Pickup et al., 2005; Sakschewski et al., 2015; Towers et al., 2023) but not all (Chave et al., 2009; Swenson & Enquist, 2007) large-scale empirical studies. This prediction emerges from our modification of the hydraulic cost function implemented in Bartlett et al. (2019), whereby we assumed that permanent damage to the xylem imposed by xylem cavitation declines with wood density, which is consistent with empirical evidence showing that denser wood has a higher resistance to xylem implosion (Hacke et al., 2001). In principle, the same outcome would emerge if wood density instead had a negative relationship with ; the critical process underlying the predicted response of wood density to soil moisture is that minimising hydraulic costs becomes more beneficial relative to minimising stem construction costs in drier conditions.
As soils dried, wood density for 1 m tall seedlings was predicted to increase 35-fold from to , approximating the smallest and largest observed values in Australia but far exceeding observed fold-changes at a community level (Figure 6; Towers et al. (2023)). Our primary goal in this article was to explore directional relationships in traits based on simplified trait trade-offs, and in this sense, we have captured empirical patterns. However, the exaggerated response of to the environment suggests that key processes which are currently missing in the model may help constrain the range of predicted values. For example, the risk of stem breakage due to wind load would put upward selective pressure on wood density (Rifai et al., 2016). Similarly, if denser wood was more resistant to stem damage inflicted by pathogen attacks and other causes, this would also cause wood density to be larger (Larjavaara & Muller-Landau, 2010 and references within). The high values of wood density that we predicted, especially for taller plants, probably relate to uncertainty regarding the parameters and , which represent the cavitation-related maximum yearly rate of sapwood loss and the trade-off slope between and wood density, respectively. Indeed, although much is known about how xylem conductance relates to stem water potential, little is known about how loss of conductivity translates into a holistic cost to the plant in absolute carbon units (Bartlett et al., 2019; Potkay & Feng, 2023), and in this case, we simply selected a value of which best captured realistic values of the four focal traits (Figure 6). Moreover, persistent exposure to the dry end of our simulated gradient (i.e., −3 MPa) represents a recurring, extreme drought which, in the absence of covariation in other focal traits such as , potentially explains the unrealistically high values of that we predicted via our single-trait optimisation (Figures 2 and 5).
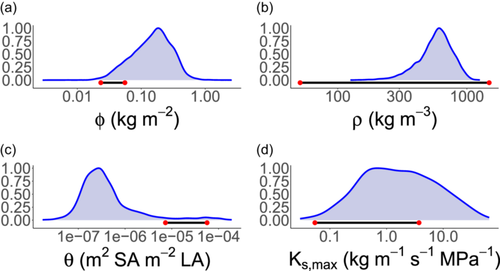
In a similar manner to wood density, our model predicted a shift towards denser, more expensive leaves (i.e., higher LMA) in drier soils. This outcome is consistent with empirical studies at a variety of spatial scales (Dwyer et al., 2014; Niinemets, 2001; Towers et al., 2023; Wright et al., 2004). Notably, the predicted response of LMA to soil moisture emerges without influencing the plant hydraulic pathway. Instead, it emerges from the well-recognised trade-off between leaf dry mass per area and the rate of leaf turnover (Wright et al., 2004). Put simply, when photosynthetic rates decline with soil moisture, plants are incentivised to invest carbon in longer-lasting tissues to avoid frequent leaf turnover, even if this leads to a more expensive upfront cost to growth. In reality, LMA could also influence plant hydraulics in addition to the above-mentioned effect, and this could help to explain the relatively low sensitivity that we predicted in this trait (Figure 6). For example, while we predicted an approximately two-fold increase in LMA for a 1ṁ tall plant along the simulated soil moisture gradient, a 10-fold shift in mean LMA has been observed across a continental rainfall gradient in Australia (Towers et al., 2023). Possible mechanisms include the involvement of LMA in maintaining leaf rigidity under dry conditions (Poorter et al., 2009), as well as determining the conductivity of the leaf hydraulic pathway (Simonin et al., 2012). Additionally, higher light in harsh environments selects for higher leaf nitrogen per area, and thus LMA (Dong et al., 2017), an effect not captured in our current model formulation.
Maximum sapwood-specific conductivity declined with a drying soil, as expected from theory and directly encoded in a model trade-off between sapwood conductivity (i.e., sapwood efficiency) and vulnerability of the xylem to cavitation (Equation 15). Evidence for the hydraulic safety-efficiency trade-off is mixed, with some studies demonstrating moderate correlations between maximum sapwood-specific conductivity and (Liu et al., 2019, 2021), whereas others demonstrate little to no correlation between these variables (Gleason et al., 2016). However, triangular distributions in empirical data demonstrates that, while species can exhibit a range of combinations of maximum sapwood-specific conductivity and , achieving both high safety and efficiency appears very uncommon, implying the presence an upper boundary for the combined value of these traits (Gleason et al., 2016; Liu et al., 2021). As for species which fall towards the lower corner of the safety-efficiency space (i.e., low safety and efficiency), emerging evidence suggests that these taxa occur more often in mesic, nonseasonal environments, because neither high maximum sapwood-specific conductivity nor low are required in these locations (Liu et al., 2021). Thus, our prediction may be more appropriate for seasonal climates where selection co-optimises these traits.
Another important consideration is that, while most analyses of the hydraulic safety-efficiency trade-off, including this analysis, focus on xylem efficiency at the sapwood-level, recent evidence suggests that the trade-off is mediated instead at the individual conduit level (Franklin et al., 2023). The implication of this is that the safety-efficiency trade-off may be weaker at the sapwood-level because maximum sapwood-specific conductivity is determined by both the conductivity of an individual conduit () and the number of conduits, which can vary independently (i.e., by moving along both the S and F axis described in Zanne et al., 2010). Conceptually, then, our model can be considered a special case of optimising when the lumen fraction is fixed. Further modelling work could investigate a link between maximum sapwood-specific conductivity and plant construction costs in addition to the vulnerability of xylem to cavitation.
Our analysis of SA:LA builds on existing work investigating the theoretical relationship between this trait and (Westoby et al., 2012). Westoby et al. (2012) predicted that SA:LA responds in a hump-shaped manner to soil water availability, because the initial benefit to plant revenue of increasing sapwood area to maintain the transpiration stream is countered by the increasing resistivity of soil as declines. Our study also reveals a nonmonotonic response of SA:LA to but for different reasons. Against our expectation, the SA:LA maximising initially declined as soils dried because plants responded by reducing sapwood area and making more negative, enlarging the sapwood area only when approached at the driest end of the moisture gradient. The reason why this occurred is that our model assumes hydraulic costs are proportional to sapwood volume. In other words, a loss of conductivity in a larger sapwood volume represents embolism in a greater absolute number of conduits. As such, the potential marginal benefit of a greater sapwood area in drier conditions is more than offset by greater hydraulic costs. The multiplication of proportional conductivity loss by sapwood volume is a chosen aspect of our representation of the hydraulic cost function in carbon units, but this implicitly assumes that hydraulic costs are associated with rebuilding the xylem (Gauthey et al., 2022). Hydraulic recovery may, however, be achieved via other mechanisms including bubble dissolution and xylem refilling (Klein et al., 2018) which, if less costly than rebuilding xylem, would potentially increase the selective advantage of higher SA:LA in drier environments, as is observed in nature (Towers et al., 2023), although we note that evidence for these mechanisms remains limited.
4.2 Trait responses to other environmental variables
A key outcome of our model is that it predicted the diverging response of maximum sapwood-specific conductivity to increasing soil dryness (i.e., declining) and atmospheric aridity (i.e., increasing) that is often observed in nature (Gleason et al., 2013; Olson et al., 2020). Increasing maximum sapwood-specific conductivity with atmospheric aridity emerged as a prediction from our model because it is more economical for plants to satisfy the additional evaporative demand for water by increasing the sapflow rate and minimising the water potential gradient between soil and the canopy. For brevity, we do not consider the interactive effect of environmental variables in this analysis. However, as hypothesised in other studies (e.g., Gleason et al., 2013), the positive response of maximum sapwood-specific conductivity to atmospheric aridity is likely the strongest when soil water is plentiful and the cost of low embolism resistance (due to a less negative ) is minimal. It is less clear how maximum sapwood-specific conductivity would respond to the combined effect of increasing soil and atmospheric dryness where the importance of embolism resistance conferred by more negative becomes more prominent. Nevertheless, given that these conditions are likely to emerge in some locations under climate change, this point is worthy of further investigation.
Although our model adequately predicted the qualitative response of LMA to soil moisture observed in nature, it yielded contrasting responses to nature for light availability (Ellsworth & Reich, 1992; Neyret et al., 2016; Poorter et al., 2009). There are number of possible reasons for this discrepancy. First, it has been suggested that declining LMA towards lower light conditions reflects a shifting allocation of leaf biomass towards a greater deployment of leaf area so as to maximise light interception (Poorter et al., 2009). In our model, however, total leaf area is fixed to plant height, and as such, there is no benefit to light interception conferred to the plant by declining LMA. Second, and perhaps more importantly, we did not consider adaptive responses in leaf photosynthetic capacity which would cause the optimum LMA to increase with light availability, as plants invest in greater photosynthetic capacity per unit area to better utilise available light (Dong et al., 2022; Poorter et al., 2009).
4.3 Comparison of height growth- and biomass growth-based outcomes
Simulating the response of traits to the environment when optimising biomass growth, as opposed to height growth, provided new insight into the potential importance of considering processes related to tissue allocation and construction costs when modelling certain traits. For example, whereas the predicted response of to the environment emerges exclusively through its effect on (and is thus independent of allocation and construction), the emergent environmental sensitivity of optimum LMA is entirely dependent on the effect of LMA on leaf area deployment efficiency (). In other words, without this latter process included in the model, we predicted no sensitivity in LMA when optimising (Figure 4, Supporting Information S1: S1–S3). For the remaining traits, the interplay of and led to occasionally contrasting responses depending on which optimality criterion was used (e.g., by comparing the positive light availability response of the biomass-growth-based optima for wood density against the negative response for the height-growth-based optima (Supporting Information S1: Figure S2c), which further demonstrates the importance of considering processes related to size-growth in future trait optimality analyses (Bartlett et al., 2019; Falster et al., 2018).
4.4 Trait responses to height
Our model accurately predicted the qualitative direction of observed trait responses to ontogenetic shifts in plant height, providing a potentially important explanation for trait variation occurring within species and independently of the environment. This work builds upon recent theoretical research developing hypotheses for how traits such as LMA should respond to increasing plant height (Falster et al., 2018; Westoby et al., 2022).
One of the key insights from our analysis is our prediction that wood density increases as plants grow taller, consistent with empirical observations based on radial wood cores (Hietz et al., 2013; Rungwattana & Hietz, 2018). The most commonly held explanation for this phenomenon is that the mechanical stability conferred by denser wood becomes more beneficial as plants grow larger and are exposed to a higher risk of mortality from wind stress (Hietz et al., 2013). Our model provides an alternative explanation based on the increasing cost of turnover and maintenance of support tissues as a fraction of net biomass production as height increases. As such, our model suggests that ontogenetic shifts in wood density may be evolutionary advantageous even for trees recruiting in the understorey where the risk of wind exposure is relatively low (Moore et al., 2018).
Surprisingly, however, we predicted only limited sensitivity in the response of maximum sapwood-specific conductivity to height, somewhat at odds with the strong empirical evidence for xylem conduit widening that is observed when comparing plants of increasing height at a fixed point along the stem (Olson et al., 2020). As described in Section 3.4, the reason that this occurred is that increasing maximum sapwood-specific conductivity also cause to become less negative, thereby limiting the extent to which the effect of greater heights on water transport rate can be offset through variation in the former trait. We note, however, that our representation of the xylem pathway is relatively simple and does not include a number of processes which could have influenced the simulated outcomes, such as tip-to-base widening of xylem conduits (Olson et al., 2021), segmentation of vulnerability along the hydraulic pathway, and the gravimetric potential of water in the water column (Choat et al., 2005; McDowell, Phillips, et al., 2002; Sperry & Love, 2015).
It is also interesting to note that while we predicted an increase in SA:LA with increasing height, in keeping with empirical data from individuals of Douglas fir (Pseudotsuga menziesii var. menziesii) (McDowell, Phillips, et al., 2002), large-scale analyses have revealed the opposite trend when regressed against maximum height (Liu et al., 2019; Mencuccini et al., 2019). This highlights an important distinction between maximum plant stature and plant ontogeny. Indeed, while our model predicts that all plants should, in general, increase their allocation to sapwood as they grow, selection for greater maximum stature in highly productive environments (e.g., non energy-limited high rainfall environments) (Moles et al., 2009) will also favour traits which maximise leaf area deployment (i.e., low SA:LA) to over-top competitors, as supported by our analysis of SA:LA in response to soil moisture (Figures 2a and 5.)
4.5 Species turnover across soil moisture gradients and implications for dynamic global vegetation models (DGVMs)
Our exploration of species turnover across a soil moisture gradient offers a useful illustrative case for the importance of adaptation in DGVMs. Specifically, in keeping with a productivity-drought tolerance trade-off from classical ecological theory (Smith & Huston, 1989), we demonstrate how the joint optimal plant strategy conferring high maximum growth rate at the wetter end of the gradient is gradually replaced by strategies favouring drought tolerance at the drier end of the gradient (i.e., the ability to maintain positive growth rates under more negative soil water potentials). Importantly, in the absence of trait optimisation along this gradient (e.g., along the height-growth rate curve for in Figure 5), we show that our growth model would underpredict the potential growth rates that could be achieved by a more optimal strategy in the wettest conditions, while simultaneously predicting nonpositive growth rates under conditions in which a more drought-tolerant species could persist. Given the link between size-growth rates and ecosystem function, height-growth simulations based on an EEO framework may be a useful tool for predicting forest growth trajectories and potential ecosystem provisioning within DGVMs, in regions where limited trait information is available (Russell et al., 2010; Senior et al., 2022; Towers & Dwyer, 2021).
4.6 Future directions and limitations
Our analysis based on height-growth rates extends upon carbon acquisition-based EEO models by directly considering the translation of acquired carbon into future ability to acquire resources and progress towards reproductive maturity. Although height growth is likely a closer approximation of plant fitness than carbon acquisition (Potkay & Feng, 2023), we note that our model omits other potentially important demographic rates which may be relevant here, including mortality risk and reproductive output. For example, taxa with greater wood density tend to have more negative lethal water potentials (Liang et al., 2021), and including this information in our model could further mediate selection towards higher wood densities in drier locations.
Perhaps the most significant opportunity for advancing the scope of the model presented here is the inclusion of a dynamic water balance and size-structured competition for water amongst individuals, akin to the light competition process that has been analysed in plant previously (Falster et al., 2017). Like many other EEO approaches (Dong et al., 2022; Trugman et al., 2019; Wang et al., 2023; Xu et al., 2021), trait optima emerged in our model for hypothetical plant individuals experiencing the environment in isolation. In reality, however, the trait optima that emerge under competition may be different due to game-theoretic interactions amongst strategies (Falster et al., 2017; Franklin et al., 2020). Importantly, including competition for water would permit coexistence amongst trait optima, thereby allowing inferences about the effect of water availability on functional diversity in the maintenance of species diversity (Harrison et al., 2021; Lindh et al., 2014).
ACKNOWLEDGEMENTS
Discussions with M. Westoby, J. Dwyer, A. Pitman, and I. Wright enhanced the scope and quality of the analysis. Isaac R. Towers was supported by a grant from Eucalypt Australia to Vesk and Falster, Andrew O'Reilly-Nugent was supported by an ARC grant to Falster & Vesk (DP200100555). Manon Sabot acknowledges support from the Australian Research Council (ARC) Centre of Excellence for Climate Extremes (CE170100023), as well as an ARC Discovery Grant (DP190101823). We thank the two reviewers of the manuscript for their insightful feedback. Open access publishing facilitated by University of New South Wales, as part of the Wiley - University of New South Wales agreement via the Council of Australian University Librarians.
CONFLICT OF INTEREST STATEMENT
The authors declare no conflict of interest.
Open Research
DATA AVAILABILITY STATEMENT
The code used to conduct the analysis is available on GitHub (https://github.com/itowers1/individual_height_growth_rate). The plant package is available on GitHub (https://github.com/traitecoevo/plant/). Data are available from AusTraits (https://zenodo.org/records/3568429) and can be accessed using the AusTraits R package.




