A method for evaluating time-resolved rheological functionalities of fluid foods
This article was published on AA publication on: 26 March 2022.
Funding information: Hayashi Rheology Memorial Foundation; Hokkaido University; Japan Society for the Promotion of Science KAKENHI, Grant/Award Number: JP19H02057
Abstract
We have developed an effective method for evaluating time-resolved rheological functionalities of swallowed foods using ultrasonic spinning rheometry (USR). USR can obtain variations over time in the rheological properties of fluids despite the fluids being in heterogeneous and nonequilibrium conditions. In addition, USR can evaluate time variations of shear-thinning property changing in a few seconds. Demonstrations were conducted with typical thickener solutions: starch, guar gum, and xanthan gum-based solutions, with alpha-amylase as a digestive enzyme. The flow curve of the starch-based solutions lowered with time, and a few minutes after addition of the amylase, the viscosity dropped to one-hundredth of the original value. In contrast, the guar gum- and xanthan gum-based solutions maintained the original viscosities as generally known. Applying the power law fitting to series of these flow curves, the time variation of the shear-thinning property is quantitatively characterized by the plots on typical K-n space, where K and n are parameters in the model, consistency index and power law exponent. The qualitative characteristics of the thickeners are successfully quantified in the K-n space, and this will be a practical tool for evaluating the time-resolved rheological properties of swallowed foods.
1 INTRODUCTION
To investigate the rheological properties that an ideal swallowed food should have to prevent aspiration, it is necessary to investigate the dynamics of the swallowed food in vivo and identify a causal relationship with the rheological properties of foods evaluated in vitro (Cutler, Morris, & Taylor, 1983; Houska et al., 1998; Hutchings & Lillford, 1988; Nakauma, Ishihara, Funami, & Nishinari, 2011; Shama & Sherman, 1973; Wood, 1968). In recent years, the development of in vivo methods of measurement has been remarkable, as represented by video fluorography (Bangyeekhan, Leelamanit, & Tekasakul, 2013; Nishinari, 2004; Palmer & Hiiemae, 1997; Qazi, Ekberg, Wiklund, Mansoor, & Stading, 2020; Takahashi et al. 2002; Zhu, Mizunuma, & Michiwaki, 2014) and ultrasonic pulse Doppler (Gao & Kohyama, 2014; Hasegawa, Nakazawa, & Kumagai, 2008; Hasegawa, Otoguro, Kumagai, & Nakazawa, 2005; Kumagai, Tashiro, Hasegawa, Kohyama, & Kumagai, 2009; Moritaka & Nakazawa, 2009; Nagatoshi et al. 2001; Qazi et al., 2020; Tashiro, Hasegawa, Kohyama, Kumagai, & Kumagai, 2010) methods, which have enabled detailed access to the behavior of the bolus in the swallowing process.
In vitro methods of measurement are technically far behind these in vivo methods. Most swallowed foods are in heterogeneous and nonequilibrium conditions, which makes it extremely difficult to evaluate the rheological properties, such as viscoelasticity and shear-rate-dependent viscosity, with the conventional torque-type rheometers widely used in academic and industrial fields (Kumagai & Kumagai, 2009; Matsumoto, 1978; Nishinari, 2003; Tashiro et al., 2010). Even though there are several practical methods for quantitatively characterizing the rheological properties (Ewoldt, Hosoi, & McKinley, 2008; Wagner, Barbati, Engmann, Burbidge, & McKinley, 2017), it should be noted that target fluids are limited only in homogenous and equilibrium states.
There are three main difficulties in in vitro evaluations caused by the heterogeneous and nonequilibrium conditions. The first problem is that wall-slip and shear-banding phenomena occur frequently in the measurements of functional swallowed foods, such as gel–sol coexistent fluids, using torque-type rheometers (Fardin et al., 2014; Fischer, Wheeler, & Fuller, 2002; Sui & McKenna, 2007). These rheometers are available in multiple geometric options, including plate–plate, cone–plate, and double cylinder types. Rheological properties, such as viscoelasticity and effective viscosity, are determined by measuring the rotational speed and the integrated axial torque, assuming that the spatial profile of the velocity is linear in the narrow gap (Irgens, 2014; Macosko, 1994). Under the wall-slip and shear-banding phenomena, the standard torque-type rheometers cannot be used to distinguish whether the evaluated rheological properties originate from the properties of the swallowed foods themselves or are superimposed phenomenon from the wall-slip and shear-banding (de Souza Mendes, Alicke, & Thompson, 2014; Saint-Michel, Gibaud, Leocmach, & Manneville, 2016). The second problem is the limited use of ordinary rheometers with heterogeneous fluids. Swallowed foods, such as porridge containing dispersions with millimeter size and yogurt, in which gel and sol states coexist, cannot fit in the narrow gap of the rheometers, and there is an increasing demand in the food and medical fields to be able to evaluate the rheology of such complex fluids. The last problem regarding the nonequilibrium conditions may be the most difficult of the three. Considering digestive enzyme in saliva decomposes the starch contained in many swallowed foods with a concomitant reduction in viscosity, the time variation of rheological properties represented by shear-rate-dependent viscosity has to be evaluated (Chen, 2009; Kumagai & Kumagai, 2009). A standard rheometer evaluates the viscosity under one fixed shear rate at a time; therefore, such temporal evaluations take an enormous amount of time and are often impossible to perform.
To meet the diverse demands for evaluating the rheological properties of swallowed foods, we have developed a new method, ultrasonic spinning rheometry (USR) (Sakurai, Tasaka, & Murai, 2013; Shiratori, Tasaka, Murai, & Takeda, 2013; Tasaka, Kimura, & Murai, 2015; Tasaka, Yoshida, Rapberger, & Murai, 2018; Yoshida, Tasaka, & Murai, 2019a). USR can be used to analyze rheological properties by substituting the flow velocity information obtained from an ultrasonic velocity profiler (UVP) (Takeda, 1986, 2012) into the equations of fluid motion. Measurements of the fluid motion itself can be obtained and the rheological properties for each radial position locally in a vessel have been evaluated. The efficacy of USR has been verified by comparing with a standard torque-type rheometer (Ohie, Yoshida, Tasaka, & Murai, 2022; Yoshida, Tasaka, & Murai, 2019a). USR has been used to investigate milli-bubble/solid particle suspensions (Sakurai et al., 2013; Tasaka et al., 2015; Yoshida, Tasaka, & Murai, 2019b), an oil–water mixture (Ohie, Yoshida, Park, Tasaka, & Murai, 2020), porridge (Tasaka et al. 2021), and gel–sol coexistent fluids (Yoshida, Tasaka, & Fischer, 2019; Yoshida, Tasaka, & Murai, 2017; Yoshida, Tasaka, Tanaka, Park, & Murai, 2018). In addition to its applicability to the analysis of complex fluids, USR can be used to evaluate the shear-rate-dependent viscosity as the shear rate is ∼(101 s−1) near the cylindrical wall of the vessel and ∼(10−1 s−1) near the central axis, which fall in the shear rate range required for evaluating the rheological properties of swallowed foods (Kumagai et al., 2009; Shama & Sherman, 1973; Tashiro et al., 2010). It is therefore possible to evaluate the effect of chemical reactions, or the time variation of multiphase states, on the shear-rate-dependent viscosity, indicating that USR may solve the third problem related to swallowed foods in the nonequilibrium condition. The time variation of the viscosity curve can theoretically be evaluated on a time scale of ∼(1 s).
Herein, we describe a method for evaluating rheological properties, especially variations over time, using USR. Aqueous solutions mixed with starch-based, guar gum-based, or xanthan gum-based thickeners were used as test fluids. These thickeners are classified as the first, second, and third-generation additives, respectively, for use in a dysphagia diet (Matsuo, Sato, Kudo, Sadzuka, & Tomita, 2020). The starch-based thickener is classified as the first generation, and it has been regarded as a problem that the viscosity decreases due to hydrolysis by amylase. The guar gum-based thickener is classified as the second generation, and the viscosity is sustained even though the amylase is mixed. The xanthan gum-based thickener classified as the third generation has further improved swallowability and flavor (Ueha et al., 2014). The time variation of the flow curves of these solutions after being mixed with alpha-amylase was evaluated by USR, and the rheological properties of the thickeners from each generation were quantitatively characterized.
2 MATERIALS AND METHODS
2.1 Materials
Three types of commercial food thickeners were used: starch-based (Tromeline, Nutri Co. Ltd, Japan), guar gum-based (Hightoromeal, Foodcare Co. Ltd, Japan), and xanthan gum-based (Softia S, Nutri Co. Ltd, Yotsukaichi). These thickeners are categorized as the first, second, and third-generation additives, respectively, and various improvements have been made with each generation (Moritaka & Nakazawa, 2009; Ueha et al., 2014; Waqas, Wiklund, Altskär, Ekberg, & Stading, 2017). Three concentrations of each thickener in pure water were used, as summarized in Table 1. The solution with the lowest concentration of the starch-based thickener was difficult in the USR measurement to capture the time variation of shear-thinning property with converting sufficient range of the shear rate due to the low viscosity. More than the specified amount was therefore added as shown in the parenthesis in Table 1. The specified amount was dissolved in 1 L of pure water with stirring with a spatula at room temperature of 25°C. Nine test solutions were degassed with a vacuum pump and then stored at room temperature for a day. As tracer particles for the UVP measurements, a small amount of styrene spherical particles (MCI GEL CHP20/P120, Mitsubishi Chemical Co. Ltd, Tokyo, Japan), with a mean diameter and density of 75–150 μm and 1.01 g/ml, were added to all the solutions. As 5 g of the tracer particles was added in 1 L of each solution, the volume fraction of the particles was φ = 0.05%. Based on the theoretical formula of the effective viscosity proposed by Einstein (1906), increase rate of the viscosity due to the volume fraction is roughly estimated by 2.5φ. In this experiment, the increase rate is estimated by 0.125%, and changes in the rheological properties can be sufficiently small to be ignored. For simplicity of notation, each solution is represented by a Greek numeral and an uppercase letter denoting the generation of the thickener and the concentration, respectively (see Table 1).
| Thickener | Concentration | ||
|---|---|---|---|
| Low (L) | Middle (M) | High (H) | |
| Starch-based (I) | 2.4 g (3.8 g) | 4.7 g | 7.1 g |
| Guar gum-based (II) | 1.5 g | 2.2 g | 2.7 g |
| Xanthan gum-based (III) | 1.0 g | 2.0 g | 3.0 g |
- Note: The solution of the starch-based thickener was so low in viscosity that it could not be measured by USR; therefore, 3.8 g was added instead of 2.4 g.
- Abbreviation: USR, ultrasonic spinning rheometry.
In the viscosity stability test, alpha-amylase (FUJIFILM Wako Pure Chemical Co. Ltd., Osaka, Japan) was used. First, 0.1 g of alpha-amylase powder was dissolved in 200 ml of pure water, then 2 ml of this amylase solution was added to 1 L of the thickened solution. The total amount of the amylase powder added was 1 ppm. This amount of amylase is almost as specified by the stability test method of thickeners determined by the Consumer Affairs Agency of Japan. The method of mixing the amylase solution and the thickened solution is specifically explained in Section 2.3.
2.2 Ultrasonic spinning rheometry
The experimental setup of USR is schematically shown in Figure 1. An acrylic cylindrical vessel (radius: R = 72.5 mm; thickness: 2 mm; and height: 60 mm) filled with a test fluid was installed in the center of a water bath for the UVP measurements and temperature control. The vessel was driven by a stepping motor as the velocity of the cylindrical wall takes a sine wave, uwall(t) = Uwall sin(2πfot), Uwall = 2πfoRΘ, where fo and Θ represent the oscillation frequency and the rotation angle of the vessel, respectively. Oscillatory shear flow is induced by the motion of the cylindrical wall, and the flow propagates toward the central axis with an accompanying phase lag. For fluids with relatively low viscosity, the fluid cannot track the motion of the cylindrical wall immediately. There is a phase lag between the fluid near the wall and that near the central axis. For relatively high viscosity fluids, such as honey, the fluid can track the motion of the wall without a considerable phase lag. These phenomena suggest that the viscosity can be evaluated by observing the movement of the fluid. The spatiotemporal distribution of the azimuthal velocity uθ (r, t) = (r/Δy)uξ was obtained using a UVP, which is also applicable for opaque fluids. Rheological properties, represented by viscoelasticity and effective viscosity, are estimated by substituting the velocity information into Navier–Stokes and constitutive equations. The theoretical background of USR has been explained in detail elsewhere (Tasaka et al., 2015; Yoshida et al., 2017).
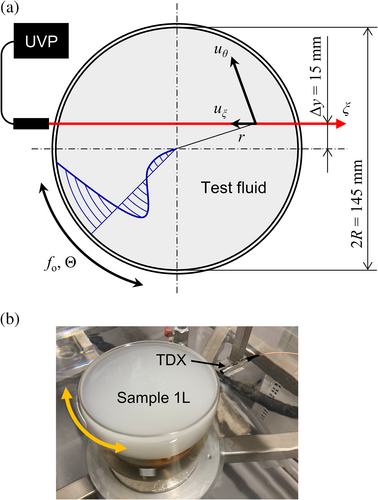
An advantage of USR is the spatially local evaluation at each radial position in the vessel. Once the vessel is driven under the parameters (fo, Θ) for more than the period of the oscillation, the spatial variations of the effective viscosity and the effective shear rate are obtained, where is ∼(101 s−1) near the cylindrical wall and ∼(10−1 s−1) near the central axis. The viscosity curve can be obtained over this shear rate range immediately. Flow curve is also obtained by the integral operation on with a boundary condition of , where τeff is the effective shear stress. In this paper, numerical integration is performed with 3 s−1, which is the minimum shear rate on the viscosity curve evaluated by USR. In this definition of differential viscosity, the power law exponent appearing in Section 3 never takes a negative value even in the limited range of the shear rate. USR can evaluate variations in the shear-rate-dependent viscosity/stress every few seconds. This local evaluation also makes it possible to evaluate the rheology of complex fluids, such as multiphase and gel–sol coexistent fluids containing dispersions with ∼(1 mm) size (Tasaka et al. 2021; Yoshida, Tasaka, & Fischer, 2019; Yoshida et al., 2017). With ordinary torque-type rheometers, these fluids cause shear-banding and wall-slip phenomena, adding bias errors to the torque measurement values, which then no longer reflect the original rheological properties.
Validation of the present USR has been conducted in studies (Ohie et al., 2022; Yoshida, Tasaka, & Murai, 2019a) with a standard torque-type rheometer (MCR 102, Anton Paar, Austria) with a plate–plate geometry. Using carboxymethyl cellulose aqueous solution, which is a representative shear-thinning fluid (Benchabane & Bekkour, 2008), Yoshida, Tasaka, and Murai (2019a) compared flow curves evaluated by USR and the torque-type rheometer. The results of both were in good agreement, indicating measurement accuracy of USR.
While USR has high applicability to complex fluids in nonequilibrium conditions, it is not always superior to torque-type rheometers in all respects. It also has a lowest limitation for viscosity evaluation, just as the limitation is specified even with a standard torque-type rheometer (Ewoldt, Johnston, & Caretta, 2015). The lowest limitation for the viscosity evaluation by USR is about 10 cSt under the experimental condition of fo = 1.0 Hz. In the theory of USR, the oscillatory flow generated by the cylindrical wall is measured by UVP, and the viscosity at each radial position is evaluated by analyzing the velocity information. The thickness of the fluid layer moving on the cylindrical wall is about δv = (ν/2πfo)1/2, where ν is the kinematic viscosity (Ohie et al., 2022; Tasaka et al. 2021). Spatial resolution of UVP in the direction of measurement line is 0.74 mm. The viscosity therefore should be higher than ν = 10 mm2·s−1 so that δv = (10 mm2/s /[2π × 1.0 Hz])1/2 = 1.3 mm is thicker than the spatial resolution of UVP.
2.3 Experimental procedures
The shear-rate-dependent rheological properties of the original solutions were investigated by USR before the addition of amylase. The cylindrical vessel was filled with each of the 1 L solutions, and the temperature of the solution was controlled at 25°C by a thermostatic chamber. The USR measurements were conducted with the oscillation parameters: fo = 1.0 Hz and Θ = π/2 rad to obtain the viscosity curves. Following the USR measurements of the original solutions, the stability after the addition of amylase was evaluated at the same temperature for the I, II-H, and III-H solutions. II and III solutions rarely react with amylase, so only the II-H and III-H solutions were evaluated as representative solutions. To allow the solution and the amylase to be mixed sufficiently, 200 ml of the solution was withdrawn from the vessel to a beaker and this solution was stirred quickly and thoroughly with 2 ml of the amylase solution with a spatula for approximately 10 s. The solution was put back in the vessel and the whole solution was similarly stirred. Immediately after that, the oscillation of the vessel and the UVP measurements were performed for the USR test in 20 min. The spatiotemporal velocity profile was extracted every 10 s, and a flow curve was obtained for each time point.
3 RESULTS AND DISCUSSION
3.1 Rheological properties of the original solutions
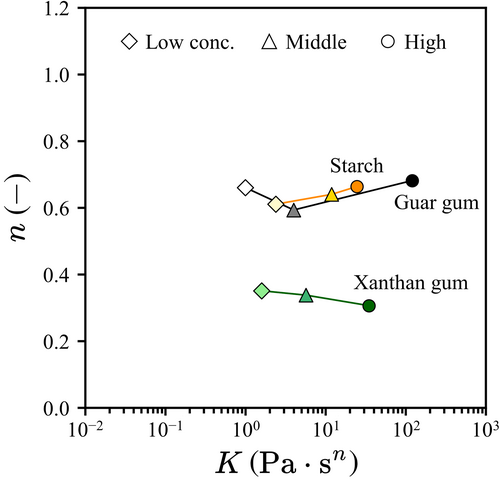
The flow curves obtained by USR before adding the amylase are shown in Figure 2, where the axes represent the effective shear rate and effective shear stress τeff in logarithmic scale. For quantitatively characterizing shear-rate-dependence of the rheological properties, power law fitting was applied to the flow curves, where K and n represent the consistency index and power law exponent, respectively. The conditions n < 1, n = 1, and 1 < n correspond to pseudoplastic, Newtonian, and dilatant fluids, respectively. The shear-thinning property becomes more dominant as the value of n decreases. The fitting based on the model was conducted against each flow curve in Figure 2 using the least square method. The fitting is in good agreement in the experimental results. The obtained parameters were plotted on the typical K-n space as shown in Figure 3, which was originally proposed for practically characterizing shear-rate-dependence of viscosity and elasticity (Wagner et al., 2017). The symbols of different concentrations are connected for better visibility. For the starch- and guar gum-based solutions, n takes almost the same value regardless of the concentration, meaning that there was little difference in the shear-thinning properties of these solutions before the addition of amylase. The guar gum-based thickener, classified as the second-generation thickener, had a better thickening effect per unit mass than the starch-based thickener, classified as the first-generation thickener, because the K value of the II-M (2.2 g per 100 ml) solution was larger than that of the I-M (4.7 g per 100 ml) solution. The plotted points for the xanthan gum solutions were located at the far lower of the graph compared with the starch and guar gum solutions. Therefore, the xanthan gum solution has remarkable shear-thinning property, which is tentatively a better condition for swallowing food (Nishinari et al., 2011; Nishinari, Turcanu, Nakauma, & Fang, 2019).
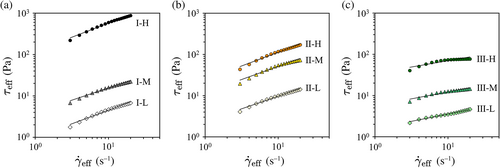
3.2 Stability of the rheological properties after addition of amylase
The temporal changes of the flow curves after being mixed with amylase are shown in Figure 4. The symbols represent the elapsed time after the addition. For the starch-based solutions, the flow curves lowered over time as shown in Figure 4a–c. Seven minutes after the addition of the amylase, the effective shear stress/viscosity of the starch-based solutions decreased to less than one hundredth of the original values. In contrast, the flow curves of the II-H and III-H solutions were maintained over 7 min, indicating that the second and third-generation thickeners were not affected by the amylase. Preliminary experiments indicated that the reaction proceeded uniformly in the vessel regardless of the radial position having a different shear rate amplitude. This is because the oscillatory shear flow in the vessel was under laminar conditions, where the stirring capacity was weaker than the turbulent conditions.
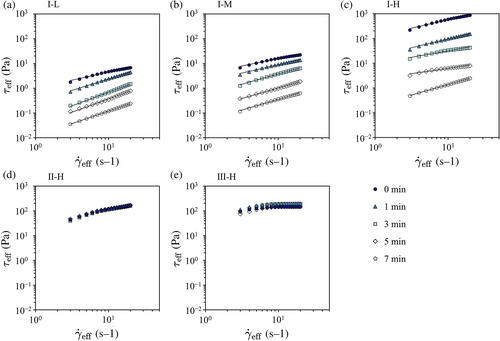
For quantitatively characterizing instantaneous shear-rate-dependence of the rheological properties, the power law fitting was applied to the flow curves, and the obtained parameters were plotted on the K-n space as shown in Figure 5. The shape of the symbols indicates the elapsed time after being mixed with the amylase, and the circles represent the time just before the addition. The symbols for different solutions with different concentrations are connected by lines for better visibility of the time variations. For the II-H and III-H solutions, the position of the plotted parameters does not change over time, indicating that mixing with amylase does not modify the rheological properties. The plot of the starch solutions (I), however, monotonically moved to the left with time elapsed. In addition, n approaches unity (Newtonian fluid) over time as an overall tendency. These indicate that the amylase changes the starch-based solutions to like pure water, increasing the risk of aspiration (Hasegawa et al., 2005; Kumagai et al., 2009; Nagatoshi et al., 2001; Tashiro et al., 2010).
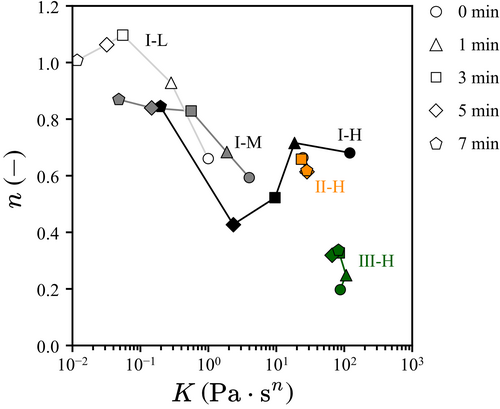
3.3 Advantages of the functional evaluation via USR
Food materials are generally in heterogeneous and exhibit markedly different properties depending on timescale, and these represent a vast majority of the real foods (Nishinari et al., 2019; Wagner et al., 2017). The evaluation method base on USR will be applied to create a database of complex fluids, such as multiphase and gel–sol coexistent fluids represented by porridge and yogurt, in which USR has a great advantage over ordinary torque-type rheometers. A data set of the time-resolved rheological properties of swallowed foods can be constructed on the K-n space. In particular, porridge, which accounts for more than half of the calories in Japanese hospital food, loses its viscosity through hydrolysis. At what time the rheological properties of porridge decrease can be evaluated using the developed method. This method can assess how long the addition of a thickener can extend the time sustaining the original properties. In addition, in vivo measurements are required in parallel with these evaluations through the K-n diagram for elucidating the area where safe swallowing food is in. The last thing to emphasize is that a food bolus is subjected to not only shear but also extensional flows during swallowing process. Elongational and yielding properties also provide important insights on the dynamics of food bolus represented by cohesiveness (Hadde & Chen, 2019; Nishinari et al., 2019; Ross, Tyler, Borgognone, & Eriksen, 2019; Tobin et al., 2020). Combining extensional viscosity and yield stress measurements in addition to the evaluation by the present USR will lead better understanding bolus dynamics of heterogeneous foods in nonequilibrium conditions.
4 CONCLUSIONS
The rheological properties of three types of thickeners after the addition of alpha-amylase were evaluated using USR, which can provide an instantaneous flow curve. In addition to evaluating the viscosity of the original solutions, the changes over time of the flow curves after mixing the solutions with amylase were subsequently obtained by USR. As expected, the guar gum-based and xanthan gum-based solutions did not decrease in the effective shear stress/viscosity over the applied shear rate range. For the starch-based solutions classified as the first-generation thickeners, the flow curves for all three concentrations decreased. The viscosity decreased to less than one hundredth of the original value, 7 min after the addition of alpha-amylase. To quantitatively characterize the time variations in this shear-rate-dependence of the effective shear stress/viscosity, which is necessary to evaluate the rheological properties of fluid foods in the swallowing process, the power law fitting was applied to series of these flow curves. The obtained parameters are plotted on the typical K-n space, where K and n are parameters in the model, consistency index and power law exponent. The rheological properties of the thickeners, which had been qualitatively characterized, were quantitatively evaluated using the diagram, indicating that this method is a practical tool for constructing a data set of the time-resolved rheological properties of swallowed food. As USR has high applicability to complex fluids, such evaluation can also be applied to porridge and yogurt with pulp, and this will be investigated in future work.
ACKNOWLEDGMENTS
This work was financially supported by Japan Society for the Promotion of Science KAKENHI (Grant Number JP19H02057) and f3 Engineering Education and Research Center, Faculty of Engineering, Hokkaido University. The authors would like to acknowledge Ms. Yoko Ikeda, Nutrition Management Center, Hokkaido University Hospital for fruitful discussions from the early stages of this project and NUTRI Co., Ltd for willingly providing their food thickeners and advice on the experimental procedures. The first author, Kohei Ohie, would like to express his deep appreciation to the scholarship from Hayashi Rheology Memorial Foundation.
AUTHOR CONTRIBUTIONS
Kohei Ohie: Conceptualization (equal); data curation; formal analysis (lead); investigation (equal); methodology (equal); project administration (supporting); software (lead); validation; visualization; writing—original draft (lead); writing—review and editing (equal). Haruko Chiba: Conceptualization (equal); investigation (equal); methodology (equal); project administration (supporting); writing—original draft (supporting); writing—review and editing (equal). Satomi Kumagai: Conceptualization (equal); investigation (equal); methodology (equal); resources; writing—original draft (supporting); writing—review and editing (equal). Taiki Yoshida: Conceptualization (equal); formal analysis (supporting); investigation (equal); methodology (equal); software (supporting); writing—original draft (supporting); writing—review and edition (equal). Yuji Tasaka: Conceptualization (equal); formal analysis (supporting); funding acquisition; investigation (equal); methodology (equal); project administration (lead); software (supporting); supervision; writing—original draft (supporting); writing—review and editing (equal).
ETHICAL STATEMENTS
Conflict of Interest: The authors declare that they do not have any conflict of interest.
Ethical Review: This study does not involve any human or animal testing.




