European Journal of Neurology
Volume 32, Issue 4 e70122
ORIGINAL ARTICLE
Open Access

The Phenotypes of Multiple Sclerosis Differ Significantly in Relative and Excess Mortality

Melinda Magyari, 

Corresponding Author

Melinda Magyari

The Danish Multiple Sclerosis Registry, Copenhagen University Hospital—Rigshospitalet, Copenhagen, Denmark

Danish Multiple Sclerosis Center, Department of Neurology, Copenhagen University Hospital—Rigshospitalet, Glostrup, Denmark

Institute for Clinical Medicine, University of Copenhagen, Copenhagen, Denmark

Correspondence:

Melinda Magyari ([email protected])

Contribution: Conceptualization, Funding acquisition, Writing - review & editing, Supervision, Resources, Project administration, Writing - original draft, Data curation

Search for more papers by this author
Frederik Elberling, 

Frederik Elberling

The Danish Multiple Sclerosis Registry, Copenhagen University Hospital—Rigshospitalet, Copenhagen, Denmark

Contribution: Methodology, Writing - review & editing

Search for more papers by this author
Nils Koch-Henriksen, 

Nils Koch-Henriksen

The Danish Multiple Sclerosis Registry, Copenhagen University Hospital—Rigshospitalet, Copenhagen, Denmark

Department of Clinical Epidemiology, Aarhus University Hospital, Aarhus, Denmark

Contribution: Conceptualization, Writing - original draft, Writing - review & editing, Formal analysis, Methodology, Data curation

Search for more papers by this author
First published: 17 April 2025
https://doi.org/10.1111/ene.70122
Citations: 1

Funding: The Danish Multiple Sclerosis Society funds the Danish Multiple Sclerosis Registry.

ABSTRACT

Background

Patients With Multiple Sclerosis (MS) Have Higher Mortality Than Matched Background Populations. We Compare Relative and Excess Mortality in MS Over the Matched Background Populations Between Primary Progressive MS (PPMS), relapsing Onset MS (ROMS), and Secondary Progressive MS (SPMS).

Methods

We included all patients from the nationwide and complete Danish MS Registry with onset 1994–2022 and compared the extra mortality of the MS phenotypes in terms of relative and excess mortality, with adjustment for sex, age at onset, disease-modifying treatment, and number of recorded relapses. We calculated the adjusted ratios of relative and excess mortalities between PPMS and ROMS and between PPMS and SPMS.

Results

The initial course was unknown in 221, leaving 1412 cases with PPMS (which includes progressive relapsing MS) and 12,449 cases with ROMS. 627 had died during follow-up by the end of 2022. After adjustment, both ratios between PPMS and ROMS came close to unity, indicating that the excess mortality is equal for PPMS and ROMS in the long run. The adjusted relative and additive mortalities were factors 6.05 (95% CI 4.42–8.27) and 1.90 (95% CI 1.65–2.18) higher in SPMS than in PPMS.

Conclusions

Compared with the matched population, the adjusted relative and excess mortalities are the same for PPMS and ROMS. However, SPMS had a higher relative and excess mortality than PPMS, probably in part owing to the burden of disease carried over from the pre-progressive phase. This underlines the need for effective treatment in this later stage of the disease and more attention to comorbidity.

1 Background

It has been known for decades that people with MS have a shorter life expectancy than the background population. Primary progressive multiple sclerosis (PPMS) is characterized by an insidious onset as opposed to relapsing onset MS (ROMS). It is a generally held opinion that PPMS is not a self-contained disease entity but a member of the MS spectrum [1-3]. PPMS has a higher age at onset and a lower female preponderance than ROMS. Life expectancy did not differ between PPMS and non-PPMS in some studies [4, 5], but in a Norwegian study, PPMS was significantly associated with a shorter survival, and the mortality was almost twice as high in PPMS as in ROMS [6]. Several studies also have shown a higher mortality from clinical onset in PPMS compared with ROMS and also a higher relative mortality in comparison with a matched background population [5-9]. In patients with ROMS, mortality correlated more with age than disease duration, but in PPMS, with its higher onset age, mortality is closely correlated with disease duration [10].

Most patients with ROMS eventually convert to secondary progressive MS (SPMS). The speed of progression seemed similar in PPMS and SPMS after the time of conversion [1, 2, 11], but some studies have found a higher progression rate in SPMS than in PPMS [4, 12], others have not [13].

Using death as an endpoint rather than disability milestones has the advantage that the endpoint is ultimate, with a known date, and complete registration is not missing. This is, however, at the expense of short-term changes in disease activity. Restricting analyses to deaths related to MS also has some uncertainties. The alternative is to record all-cause mortality and compare it with the mortality of a matched background population.

In this study, we aim to 1) compare the extra mortality in terms of relative and excess mortality hazards over the background population in PPMS and ROMS from clinical onset and from birth, and 2) to compare relative and excess mortality in PPMS and SPMS after the onset of progression and to compare SPMS with and without relapses, using the whole Danish MS population with onset since 1994. It is recommended that the term “excess mortality” is reserved for the additive hazard model, and “relative mortality” for the multiplicative hazard model [14, 15]. Where the model is not specified, we use the term “extra mortality.”

2 Methods

2.1 Study Material

We have prospectively collected data from the Danish Multiple Sclerosis Registry (DMSR) [16], established in 1956, as a nationwide and population-based registry that collects information on all Danish citizens with MS. Diagnostic and clinical management of patients with MS is carried out by 13 MS clinics in public hospitals. These are the only units authorized to prescribe and dispense disease-modifying drugs. The MS diagnosis was approved according to the current diagnostic criteria: the Poser criteria [17], and the three generations of the McDonald Criteria [18-20].

In this cohort study, we have included all patients from the DMSR with clinical onset 1994–2022 with a known initial phenotype, be it PPMS or ROMS. We have restricted the onset cohort to equalize the chance for receiving disease-modifying treatment. Patients with progressive relapsing MS were kept in the PPMS group. The endpoint was death from any cause. The patients were followed to death, the year of emigration, or the end of year 2022, whichever came first. In the first part of the study, we compare the two arms, PPMS and ROMS, in terms of relative and excess mortality with either clinical onset or birth as starting points.

In the second part of the study, we compare relative and excess mortality in SPMS with PPMS recorded from the start of progression, which in PPMS is equal to clinical onset. The endpoint is death from any cause. The time of SPMS phenotype was primarily determined by the treating physician. In cases where this information was missing, we used a validated algorithm to decide whether and when a ROMS patient had entered the SPMS phase based on worsening of EDSS not attributable to relapses [21]. Such algorithms are generally designed to identify SPMS as an endpoint rather than a starting point like in this study. Patients were assigned SPMS if EDSS in a relapse-free period had worsened with a three-stratum definition: ≥ 1.5 points from EDSS 0; ≥ 1.0 points from EDSS 1.0–5.5, and 0.5 points from EDSS 5.5, along with a 12-month confirmation of the worsening and a minimal EDSS of 3, and for this, the sensitivity was estimated at 0.97 and the specificity at 0.80.

With this relatively short confirmation period, there is a risk that patients could be classified as SPMS just because of random fluctuations of EDSS or missing registration of a relapse. In a sensitivity analysis, we used a different and more conservative customary algorithm for SPMS in which the patient should comply with the same three-stratum definition of worsening, but it should take place during at least a two-year relapse-free period. It should be confirmed throughout the rest of the observation time without a decrease in EDSS or pyramidal FS, and the minimal EDSS should be 3.0. The patients were followed to death, year of emigration, or end of follow-up, whichever came first.

2.2 Statistical Analysis

We compare mortality in patients with MS with the mortality in a closely matched background population to calculate the extra mortality caused by MS in terms of the two alternative parameters: relative mortality and excess mortality.

Mortality in the arms of the study was depicted using life-table methods with one-year steps. They were performed with both onset and birth as starting points. The life-table confidence intervals were calculated using the exponential Greenwood method [22].

We compare the observed number of deaths in the onset cohorts of ROMS, PPMS, and SPMS with the expected numbers from the population irrespective of cause of death.

The expected number of deaths in a cohort (expD) is calculated from the matched background population with sex-, age-, and calendar year-specific population mortality rates in one-year steps, published by Statistics Denmark:
exp D = ∑ i n ∑ y = start i y = end i pop M sex , y , a y . $$ \exp D=\sum \limits_i^n\sum \limits_{y= start(i)}^{y= end(i)}{\mathrm{pop}M}_{sex,y,a(y.)} $$
where n = number of patients in the cohort; start(i) and end(i) are the calendar year of diagnosis and death or censoring for the i'th patient; popM is the specific one-year survival probability in the population; y = calendar year, a(y) is age of the i'th patient in year y. Because population life tables for the onset cohorts were available only up to age 90, we right truncated at that age. Patients are “immortal” up to the year of the MS diagnosis; else they would not have been ascertained. Therefore, we only calculated the expected number of deceased from the year of diagnosis onward to the time of death or censoring for the individual patient, and for SPMS patients only from the year of change from the ROMS phenotype to the SPMS phenotype.

2.2.1 Multiplicative and Additive Hazard Ratios

The crude extra mortality from a disease can be derived in two different ways: (1) relative mortality as a multiplicative parameter like the Standardized Mortality Ratio (SMR), which is the observed number of deaths divided by the expected number and (2) excess mortality as an additive parameter like the Excess Death Rate (EDR), which in our setting is observed minus expected number of deaths per 1000 person years of observation. SMR and EDR are different: SMR is a ratio, and EDR is a difference. Confidence intervals of SMR and EDR were calculated assuming a Poisson distribution of the number of observed deaths.

Just comparing the SMR or EDR between patients of the two arms of the study would be insufficient because of a possible strong confounding by age at onset, sex, relapses, and treatment. We therefore compared the extra mortality between the two arms by expanding SMR to fit a multiplicative hazard model and EDR to fit an additive hazard model [14, 15], enabling adjustment for covariates. Both models include matched population mortality for each observation year and current age as a time-varying covariate.

In the multiplicative Cox regression, Relative Mortality Ratio (RMR) is defined as λrel(t, z) = λobs(t, z)/λ*s,a,c(t), where λobs is observed mortality, and λ*s,a,y(t) is population sex-, age-, and calendar year-specific mortality, all at time t, and z is the vector of covariates. The effects of the covariates are multiplicative. The ratio between two levels of a covariate, z, is the RMR, which is exp(β’(z1–z0)), in casu with z1 as PPMS and z0 as ROMS.

The additive hazard model is a generalized linear model, where Excess Mortality, is λexcess(t, z) = λobs(t, z)—λ*s,a,c(t). The ratio between two levels of a covariate is denoted the Excess Mortality Ratio (EMR), and because the effects of covariates also here are multiplicative, the EMR is likewise exp.(β’(z1–z0)). These methods with R-codes have been tested on end-stage renal disease and described in detail with R syntax [15]. In both models, current age is included as a time-variant covariate. With these methods, we test the effect of the covariate course (PPMS vs. ROMS), on the RMR and EMR, adjusted for sex, age at onset, DMT, and number of relapses. We applied the same methods on the comparison between SPMS and PPMS. We used SPSS v. 29, Excel Visual Basic, and R v. 4.2.2 with the packages “survival,” “timereg,” and “relsurv” for data management and analyses.

2.3 Ethics Statement

Ethical committee approval was not required because this was a registered study based on anonymized data.

3 Results

In all, 14.156 patients had onset of MS in the period 1994–2022. The initial course was unknown or could not be classified as PPMS or ROMS in 277 cases, leaving 13,861 cases to be included, 1,412 in the PPMS arm and 12,449 in the ROMS arm. In the PPMS arm, the proportion of women was lower, and the age at onset and diagnosis was higher than in the ROMS arm (Table 1). Before follow-up, 627 of the patients had died.

TABLE 1. Baseline variables.
PPMS N = 1412 ROMS N = 12,449 SPMS N = 1.461
Median observation years (IQR) 14 (9; 20) 13 (7; 20) 5 (3; 8)
Deceased 137 490 137
Women/men (%women) 804/608 (56.9) 8548/3.901 (68.7) 934/527 (63.9)
Median age at onset (IQR) 49 (42; 56) 34 (27; 42) 49 (42; 55)
Median age at diagnosis of MS (IQR) 53 (46; 60) 37 (29; 45) 39 (32; 48)
Ever treated with DMD (%) 195 (13.8) 10,625 (85.3) 773 (52.9)
Number of recorded relapses 222 29,008 414
Ever relapses (%) 193 (13.7) 9,22 (74.9) 269
  • Note: The SPMS cohort is a subset of the ROMS cohort.
  • Abbreviations: IQR, interquartile range; PPMS, primary progressive MS; ROMS, Relapsing onset MS; SPMS, Secondary progressive MS.
  • a Onset of the progressive phase.

4 PPMS vs. ROMS

4.1 Absolute Mortality

The life-table plot in Figure 1 shows higher absolute mortality in PPMS than in ROMS when calculated from clinical onset (Panel A), but when seen from birth, there was a better survival in PPMS (Panel B) and the 95% CI lines did not even overlap from about age 45. In PPMS, the 80 percentile of the cumulative survival probability and its confidence limits were intersected at age 75.5 (95% CI 74.8–77.9) and in ROMS at age 70.3 (95% CI 69.9–72.7). We compared the 80 percentiles of cumulative survival rather than the median because the cumulative survival did not go below the 50 percentile during follow-up. Some of the differences between PPMS and ROMS can be attributed to the longer immortal time (from birth to diagnosis) in PPMS. When mitigating this immortal time bias by restricting the analyses to patients with age at onset 50+, the differences between survival in PPMS and ROMS vanished (Figure 1, panel C and D).

Details are in the caption following the image
FIGURE 1
Open in figure viewerPowerPoint
Life-table plots of survival in PPMS and RMS and in the matched background population. This was calculated when observing immortality up to the year/age at diagnosis in the corresponding patients. 95% CI was calculated by the exponential Greenwood method. (A): Survival since onset; (B) Survival since age at birth. (C) Survival from onset in patients with onset before age 50. (D) Survival in patients with onset at age 50 or later. PPMS = Primary Progressive MS, ROMS = Relapsing onset multiple sclerosis.

4.2 Comparing With the Background Population Mortality

4.2.1 Univariate Analysis

When comparing with the mortality of the matched background population, the mortality in PPMS did not significantly surpass that of the matched background population as the relative mortality in terms of SMR was only 1.16 (95% CI; 0.98–1.38) as opposed to a significantly increased mortality in ROMS with a SMR of 1.56 (95% CI 1.42–1.70). The excess mortality in terms of EDR was also lower in PPMS than in ROMS. The ratios of the two mortality parameters between the two phenotypes are developed in detail below under multivariate analyses. Table 2 shows the two parameters stratified by sex and age at onset (< 50 and 50+). Particularly, in the subgroup with onset age ≥ 50, both SMR and EDR were higher in ROMS than in PPMS. This indicates that high age is more important for mortality than the initial phenotype. The same pattern was seen in both sexes.

TABLE 2. Stratified analyses of SMR and EDR in PPMS and ROMS in two classes of age at onset and separately by sex.
Age at onset < 50 Age at onset ≥ 50 Any age at onset
PPMS N = 707 ROMS N = 11,301 PPMS N = 705 ROMS N = 1148 PPMS N = 1412 ROMS N = 12,449
Both sexes
Observed deaths 58 372 79 118 137 490
Expected deaths 34.0 216.9 83.8 98.3 117.8 315.2
SMR (95% CI) 1.71 (1.30–2.21) 1.72 (1.55–1.90) 0.94 (0.75–1.18) 1.20 (0.99–1.44) 1.16 (0.98–1.38) 1.56 (1.42–1.70)
EDR (95% CI) 2.06 (0.86–3.52) 0.98 (0.74–1.23) −0.51 (−2.25–1.56) 1.51 (−0.05–3.31) 0.91 (−0.13–2.10) 1.02 (0.77–1.28)
Males
Observed deaths 31 159 41 50 72 209
Expected deaths 16.9 82.1 37.2 39.9 54.2 122.0
SMR (95% CI) 1.83 (1.25–2.60) 1.94 (1.71–2.35) 1.10 (0.79–1.50) 1.25 (0.93–1.65) 1.33 (1.04–1.68) 1.71 (1.49–1.96)
EDR (95% CI) 2.76 (0.81–5.31) 1.61 (1.11–2.17) 0.99 (−2.05–4.83) 2.27 (−0.63–5.84) 2.00 (0.24–4.10) 1.67 (1.14–2.25)
Females
Observed deaths 27 213 38 68 65 281
Expected deaths 17.1 134.8 46.6 58.4 63.6 193.1
SMR (95% CI) 1.58 (1.04–2.30) 1.58 (1.38–1.81) 0.82 (0.58–1.12) 1.17 (0.90–1.48) 1.02 (0.79–1.30) 1.46 (1.29–1.64)
EDR (95% CI) 1.52 (0.11–3.40) 0.70 (0.46–0.98) −1.52 (−3.50–1.00) 1.12 (−0.65–3.25) 0.11 (−1.11–1.58) 0.73 (0.47–1.03)
  • Abbreviations: EDR, excess death rate; PPMS, primary progressive MS; ROMS, relapsing onset MS; SMR, standardized mortality ratio.

4.2.2 Multivariate Analyses With Multiplicative Hazard Cox Models and Additive Hazard Models

To enable adjustment for the confounding effects of sex, age, treatment, and relapses, we fitted multiplicative hazard models of relative mortality ratio, the RMR, and of excess mortality ratio, the EMR, with initial phenotype as the explanatory variable. RMR is in principle comparable to the ratios between the SMRs, and EMR is comparable to the ratio between the EDRs. As seen in Table 3, column two, the PPMS/ROMS ratio of relative mortalities was, before adjustment, significantly lower than unity, again indicating lower relative mortality in PPMS than in ROMS, but after stepwise adjustment for sex, age at onset, treatment, and relapses, the statistical significance disappeared. In the additive hazard analyses, the adjusted PPMS/ROMS ratio of excess mortality in terms of EMR was not different from unity, and this did not change after adjustment for all the covariates. The tendency was the same for both sexes.

TABLE 3. Multivariate analysis of extra mortality in PPMS vs. ROMS.
Using multiplicative hazard models RMR (95% CI) Using additive hazard models EMR (95% CI)
Both sexes
Initial course 0.74 (0.61–0.90) 1.06 (0.93–1.21)
Initial course with sex 0.73 (0.60–0.88) 1.04 (0.91–1.19)
Initial course with sex and age at onset 0.82 (0.67–1.01) 0.92 (0.81–1.07)
Initial course with sex, age at onset and treatment 0.92 (0.72–119) 0.95 (0.81–1.12)
Initial course with sex, age at onset, treatment, and number of relapses 0.91 (0.71–1.17) 0.95 (0.81–1.12)
Men
Initial course 0.74 (0.57–0.97) 1.11 (0.91–1.35)
Initial course with age at onset 0.86 (0.64–1.15) 0.95 (0.77–1.18)
Initial course with age at onset and treatment 0.93 (0.64–1.34) 0.96 (0.74–1.24)
Initial course with age at onset, treatment, and number of relapses 0.91 (0.63–1.31) 0.95 (0.73–1.23)
Women
Initial course 0.71 (0.54–0.93) 0.99 (0.83–1.17)
Initial course with age at onset 0.77 (0.58–1.04) 0.90 (0.75–1.09)
Initial course with age at onset and treatment 0.90 (0.64–1.28) 0.93 (0.75–1.15)
Initial course with age at onset, treatment, and number of relapses 0.89 (0.63–1.26) 0.93 (0.75–1.15)
  • Abbreviations: EMR, excess mortality ratio; PPMS, primary progressive MS; RMR, relative mortality ratio; ROMS, relapsing onset MS.
  • a With ROMS as reference.
  • b p < 0.05.

The multiplicative and additive hazard models are indeed different, and which of them gives the most correct picture depends on the data. We arrive at the result that relative mortality and excess mortality in PPMS do not differ from that of ROMS.

5 SPMS vs. PPMS

5.1 Absolute Mortality

Among the 12,449 patients with ROMS, 1.461 had transitioned to SPMS phenotype according to the algorithm proposed by the MSBase registry [21] at a known time. The median age at conversion was 49 years (IQR: 41; 55), close to the age distribution at onset in patients with PPMS. In total, 68.7% of them were women and 145 had died between the start of SPMS and follow-up. The age distribution when entering the SP phase was close to that of PPMS. For details about the background variables, see Table 1. In SPMS, the 80 percentile of the cumulative survival probability and its confidence limits were intersected at age 64.5 (95% CI: 64.5–69.23) and in PPMS about 10 years later: 75.5 (95% CI 74.8–77.9). The life-table plots in Figure 2 show survival by time since the onset of progression and by age.

Details are in the caption following the image
FIGURE 2
Open in figure viewerPowerPoint
Life-table plot comparing PPMS and SPMS in a matched background population seen from onset and from birth. PPMS = Primary Progressive MS, SPMS = Secondary progressive MS.

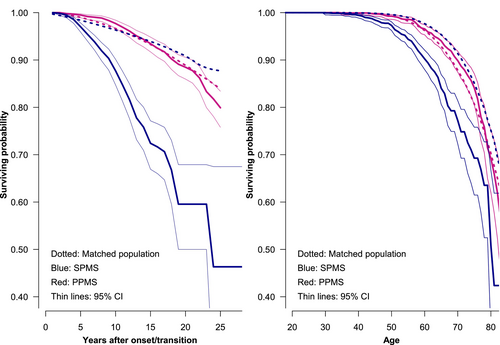
5.2 Comparing With the Background Population Mortality

5.2.1 Univariate Analysis

In the univariate analysis of mortality compared with the matched background population, the SMR from onset/transition was in SPMS 4.23 (95% CI 3.55–5.00), which is considerably higher than in PPMS, where it was 1.35 (95% CI 1.14–1.60). EDR was also higher in SPMS: 11.95 (95% CI 9.44–14.80) vs. 1.82 (95% CI 0.70–3.09).

5.2.2 Multivariate Analyses

In the multivariate analyses, the ratio between the SPMS/PPMS of relative mortality (RMR), using the multiplicative models, was 6.77 unadjusted and 6.05 when adjusted for all covariates. Using the additive models, The SPMS/PPMS ratio of excess mortality (EMR) was unadjusted 1.52 and fully adjusted 1.90. As age at onset was closer in the two cohorts, it had only a weak confounding effect; neither had treatment nor the number of relapses. The unadjusted and stepwise adjusted results are shown in Table 4 for all models, stratified by sex and with 95% CIs. There was a tendency for higher multiplicative and additive hazard ratios between SPMS and PPMS in women than in men.

TABLE 4. Multivariate analysis of extra mortality in SPMS vs. PPMS.
Using multiplicative hazard models RMR (95% CI) Using additive hazard models EMR (95% CI)
Both sexes
Course 6.77 (5.17–8.85) 1.52 (1.40–1.64)
Course with sex 6.78 (5.18–8.87) 2.03 (1.79–2.29)
Course with sex and age at onset 6.87 (5.27–8.96) 2.04 (1.81–2.31)
Course with sex, age at onset, and treatment 6.08 (4.45–8.30) 1.90 (1.66–2.19)
Course with sex, age at onset, treatment, and number of relapses 6.05 (4.42–8.27) 1.90 (1.65–2.18)
Men
Initial course 5.30 (3.61–7.88) 1.54 (1.35–1.75)
Initial course with age at onset 5.46 (3.72–8.03) 1.54 (1.36–1.75)
Initial course with age at onset and treatment 4.54 (2.87–7.17) 1.43 (1.24–1.65)
Initial course with age at onset, treatment, and number of relapses 4.48 (2.83–7.10) 1.42 (1.23–1.64)
Women
Initial course 8.52 (5.83–12.44) 3.96 (3.03–5.19)
Initial course with age at onset 8.49 (5.85–12.32) 3.97 (3.03–5.20)
Initial course with age at onset and treatment 7.96 (5.17–12.26) 3.76 (2.76–5.11)
Initial course with age at onset, treatment, and number of relapses 8.02 (5.20–12.36) 3.77 (2.77–5.13)
  • Abbreviations: EMR Excess Mortality Ratio; PPMS Primary Progressive MS; RMR Relative Mortality Ratio; Ratio; SPMS Secondary Progressive MS.
  • a With PPMS as reference.

5.3 Sensitivity Analysis

In the sensitivity analyses, we used our custom more conservative definition of SPMS, which reduced the number of approved SPMS patients from 1416 to 1104. Of these patients, 110 had died before follow-up, 62.1% were female, and the median age at onset of progression was 48 years (IQR 41; 55). Their SMR and EDR over the background population were 3.25 (95% CI; 2.67–3.92) and 8.41 (95% CI; 6.24–10.91) respectively. The adjusted SPMS/PPMS multiplicative hazard ratio and additive hazard ratios were 5.57 (95% CI; 3.9578–7.88) and 3.12 (95% CI; 2.42–4.05). Our results were largely unaffected by the difference in SPMS definitions. For both definitions of SPMS, PPMS had a strong survival advantage over SPMS.

5.4 Active vs. Non-Active SPMS

As a byproduct of the study, we compared extra mortality in the 269 patients with SPMS who had experienced relapses after the start of progression (active SPMS) with 1192 who had remained relapse-free (non-active SPMS). The 269 active SPMS patients had encountered a mean of 1.54 relapses during a mean of 7.63 years of observation. The 1192 non-active SPMS patients had zero relapses during a mean of 6.18 years of observation. Among the active patients, 68.0% were female, the median age at transition was 47 years (IQR: 40; 53), and 66.9% had received DMT in the progressive phase. Their mean observation time was 7.63 years. Among the non-active patients, 63.0% were female, the median age at transition was 49 years (IQR: 42; 56), and 49.7% had received treatment in the progressive phase. Their mean observation time was 6.18 years.

There was no statistically significant mortality difference between the two types of SPMS: With non-active patients as reference, the adjusted RMR was 1.31 (95% CI; 0.89–1.93), and the EMR was 1.11 (0.96–1.29).

6 Discussion

Patients with PPMS had higher absolute mortality from onset than patients with ROMS, but they survived to a higher age, partly because they were naturally selected to be alive at the diagnosis, and thus, could be subjected to immortal time bias up to an average of 15 years later in life owing to later clinical onset and diagnosis, and only after that time the observed and expected deaths were counted. After removing confounding by age, sex, treatment, and relapses, ROMS proved to be no more benign than PPMS in terms of survival.

Compared with the matched background population mortality, the unadjusted multiplicative hazard model showed lower relative mortality in PPMS compared with ROMS, but after adjustment for sex, age at onset, treatment, and number of relapses, the PPMS/ROMS ratio was not statistically significantly different from unity neither with nor without adjustment. Hence, PPMS and ROMS are equal in their extra mortality over the matched background population.

The most striking result of our study is that SPMS carries a substantially worse relative and excess mortality than PPMS, both in terms of RMR and EMR. This result was the same whether the approved algorithm [21] or our own more conservative algorithm was used to define SPMS.

The multiplicative hazard model is commonly used in chronic diseases, whereas the additive hazard model is often used in population-based cancer mortality studies [15]. In MS survival studies, the multiplicative hazard model has been dominating. It estimates the ratio of relative mortalities between the two arms, and the additive hazard model estimates the ratio between the excess mortalities between the two arms. The latter is linear in nature and gives, in our view, a better impression of the number of lost lives. The multiplicative hazard analysis is rather sensitive to low numbers in the dominator, and in our comparison between SPMS and PPMS gave an uninterpretable high ratio of 6.05 in contrast to the more comprehensible ratio of 1.90 of the additive hazard ratio.

A Norwegian study following onset cohorts from 1953 to 2003 used the multiplicative hazard method with adjustments, found a PPMS/RRMS relative mortality ratio of 1.55 with statistical significance [7] as opposed to 0.74 in our study. The difference may be attributed to the fact that the Norwegian study included early onset cohorts back to 1953 and a longer follow-up, but it did not adjust for possible clinical confounders. More in accordance with our study were analyses from British Columbia, with almost the same SMRs for PPMS and ROMS: 2.89 vs. 2.87 [5].

The most striking result of our study is that SPMS carries a substantially worse relative and excess mortality than PPMS, both in terms of RMR and EMR, and this applies to the validated SPMS definition [21] as well as to our own more conservative customary definition. One contributory explanation for the worse survival in SPMS compared with PPMS may be that patients with SPMS carry over a certain burden of disease from the pre-progressive phase. Nevertheless, more of the secondary progressive patients than the PPMS patients have been subjected to DMT, but patients with SPMS may also have relapses, which have been shown to contribute to permanent disability [23, 24]. However, adjustment for treatment and overlying relapses changed little, and patients with active SPMS did not have higher excess mortality than patients with non-active SPMS, which is in agreement with a recent Italian study showing similar disability progression in the two groups [25].

Are SPMS and PPMS indeed biologically different? This has been summarized in a comprehensive review [26]. In analyses of 1128 proteins in the cerebrospinal fluid from 225 patients with MS or other diseases mimicking MS, there was no difference between PPMS and SPMS [27] and no substantial differences in the MRI pattern between RRMS and PPMS [28].

The weakness of our study is that we have only followed patients for up to 27 years from onset, and significant differences may occur later in the disease course because only from 1994 was the initial phenotype systematically recorded.

The strength of our study lies in the quality of the Danish registers and the complete follow-up of death and access to sex-, age-, and calendar-year population mortality data.

In conclusion, (1) the absolute mortality from onset is higher in PPMS than in ROMS, but in a lifetime perspective, the absolute mortality is equal. Compared with matched population mortality and adjusted for sex and age at onset, the relative mortality and excess mortality are roughly the same for the two courses; (2) the relative and excess mortality from the onset of progression is substantially higher in SPMS than in PPMS irrespective of the algorithm that defines SPMS. This underlines the need for the development of effective treatments for this later stage of the disease and urges more attention to comorbidity.

Nomenclature

  • DMD
  • disease-modifying drugs
  • DMSR
  • the Danish Multiple Sclerosis Registry
  • DMT
  • disease-modifying treatment
  • EDR
  • Excess Death Rate
  • EMR
  • Excess Mortality Ratio
  • MS
  • multiple sclerosis
  • PPMS
  • Primary Progressive MS
  • RMR
  • Relative Mortality Ratio
  • ROMS
  • Relapsing onset MS
  • SMR
  • Standardized Mortality Ratio
  • SPMS
  • Secondary Progressive MS

    • Author Contributions

    Melinda Magyari: conceptualization, funding acquisition, writing – review and editing, supervision, resources, project administration, writing – original draft, data curation. Frederik Elberling: methodology, writing – review and editing. Nils Koch-Henriksen: conceptualization, writing – original draft, writing – review and editing, formal analysis, methodology, data curation.

    Acknowledgments

    We thank all our colleagues in the Danish Multiple Sclerosis Group from the 14 Danish MS Centres who systematically and currently notified the DMSR with data.

      Conflicts of Interest

      Melinda. Magyari has served on the scientific advisory board for Sanofi, Novartis, and Merck, and has received honoraria for lecturing from Biogen, Merck, Novartis, Roche, Genzyme, and Bristol Myers Squibb. Frederik Elberling has received honoraria for lecturing from Roche and Sanofi. Nils Koch-Henriksen has nothing to declare.

      Data Availability Statement

      The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.

        The full text of this article hosted at iucr.org is unavailable due to technical difficulties.