Zoning strategies for human–robot collaborative picking
Abstract
During the last decade, several retailers have started to combine traditional store deliveries with the fulfillment of online sales to consumers from omni-channel warehouses, which are increasingly being automated. A popular option is to use autonomous mobile robots (AMRs) in collaboration with human pickers. In this approach, the pickers' unproductive walking time can be reduced even further by zoning the storage system, where the pickers stay within their zone periphery and robots transport order totes between the zones. However, the robotic systems' optimal zoning strategy is unclear: few zones are particularly good for large store orders, while many zones are particularly good for small online orders. We study the effect of no zoning (NZ) and progressive zoning strategies on throughput capacity for balanced zone configurations with both fixed and dynamic order profiles. We first develop queuing network models to estimate pick throughput capacity that correspond to a given number of AMRs and picking with a fixed number of zones. We demonstrate that the throughput capacity is dependent on the chosen zoning strategy. However, the magnitude of the gains achieved is influenced by the size of the orders being processed. We also show that using a dynamic switching strategy has little effect on throughput performance. In contrast, a fixed switching strategy benefiting from changes in the order profile has the potential to increase throughput performance by 17% compared to the NZ strategy, albeit at a higher robot cost.
1 INTRODUCTION
Manual picking systems have high operational flexibility, are resilient to system failures, and can handle complex situations with intuition. However, they can also experience large demand fluctuations, particularly in e-commerce, and it is challenging to meet the required throughput and responsiveness. Moreover, there is a shortage of human pickers in many parts of the world. These challenges have encouraged companies to invest in automated picking solutions. Some companies have even opted for fully automated warehouses. About 40 fully automated warehouses are in operation in Western Europe, with many more under development (Azadeh et al., 2019). However, these systems are very expensive and inflexible with a very high setup time. These issues have given birth to robotic-based picking solutions.
In these systems, autonomous mobile robots (AMRs) work closely with order pickers to pick the orders. Note that AMRs are similar to automated guided vehicles (AGVs), however, they have more degrees of autonomy (Fragapane et al., 2021). Although AMRs are relatively cheap compared to fully automated picking systems, a large number of AMRs are required to achieve high performance, which still makes the system expensive.
Pick-support AMRs (PS-AMRs) collaborate with human pickers to perform order fulfillment jobs more efficiently and ergonomically (Azadeh et al., 2019). In this collaborative environment, the picker accompanies the AMR only for item picking, and the AMR autonomously carries out the remaining travel and drop-off functions. Because the AMRs transport items over long distances in the warehouse, the unproductive walking time of the picker reduces, and the picking efficiency improves. The PS-AMRs also have the potential to improve the well-being of human pickers. The pickers do not have to travel long distances and push heavy roll cages.
From an investment cost point of view, a PS-AMR-based system is cheaper and more easily scalable than other robotic picking systems. It can work with the existing storage racks and does not need special storage pods, like the robotic mobile fulfillment systems such as KIVA/Amazon Robotics (see Azadeh et al., 2019; Wang et al., 2022). This reduces the investment cost significantly. Also, the implementation time (and cost) is very short: it can be implemented in a running operation within a few days. Human pickers with pick carts or trucks and pickers with PS-AMRs can work side by side. As a result, companies can start manually, gradually automate their picking process, and still leave their current picking processes intact. Hence, the risks involved with automation decrease significantly. The system has picker productivity benefits compared to fully manual working because picker travel reduces significantly. Larger benefits can be reaped when operating in multiple shifts per day or in weekends. Collaborative picking systems are supplied and have been implemented by several companies, such as Fetch Robotics, Locus Robotics, Effidence, 6 River Systems, Still, Raymond, and Toyota. Such systems are implemented at several companies including Cardinal Health in Canada, DHL and Ceva Logistics in the Netherlands, Boots in the United Kingdom, alphabroder in the United States, among others. According to ABI Research (2019), there will be four million robots installed in more than 50,000 warehouses worldwide by 2025. Many of these will be PS-AMRs.
1.1 Research motivation
Our research is inspired by the implementation and the resulting operational challenges of PS-AMRs at a DHL and a CEVA Logistics warehouse, both in The Netherlands. In both warehouses worker productivity had to be increased and ramp up time for flex workers had to be expedited. According to the Innovation Lead of DHL Supply Chain Benelux, worker productivity was negatively affected due to excessive travel and manually pushing pick carts. The productivity could be enhanced using a Locus Robotics AMR solution. The pickers are no longer responsible for offloading pick carts at the depot and fetching empty pick carts for a pick tour. This is now the task of the robots and pickers can continuously engage in order picking tasks. This boosts the picker productivity substantially. Furthermore, DHL claims that worker training can be 80% faster by using PS-AMRs. In addition, due to difficulties in finding qualified labor, it is also important to improve working circumstances. PS-AMRs can bring additional comfort to the pickers as they do not spend effort pushing carts and travel less. According to a DHL press release, more than 2000 robots will be deployed in their warehouses worldwide (Deutsche Post DHL Group, 2021; Edwards, 2022; Locus Robotics, 2021).
To manage demand fluctuations, DHL typically adopts two strategies: (1) adding more robots, (2) use operational policies such as zoning to improve the pick productivity. However, DHL was not yet sure what type of zoning strategy would result in better productivity. We address this question by developing stochastic models of the human-robot collaborative system. CEVA also manages peak demand with AMRs and it is quoted that the pickers find the workflow quite intuitive, which raises pick productivity.
1.2 Research framework
The PS-AMRs and the pickers can collaborate in different ways, but the most common strategies are system-directed and swarm. In the system-directed strategy, robots and pickers are paired and pick all items on the pick list (Pasparakis et al., 2023). This strategy has two variants: (a) Robot-in-lead: the robot leads, and the picker follows the robot's instruction. A screen on top of the robot shows which item needs to be picked and where. Once all the required items are picked, the robot takes the items to the depot, and the picker is directed to another robot (e.g., by the previous robot). (b) Picker-in-lead: the picker leads, and the robot follows the picker. The picker receives all the required information using wearable technology (a terminal or headset). Once all items are picked, the picker sends the robots to the depot and starts picking with another robot. In the swarm strategy, the robots and the pickers are detached from each other. Robots receive orders and travel to pick locations. A picker, who is assigned to monitor a part of the warehouse, sees the picking task on a nearby waiting robot's screen and picks the required items. The robot then travels to the next pick location, and the picker looks for another (e.g., the closest) waiting robot. Once all items are picked, the robot takes the items to the depot (Löffler et al., 2023; Trebilcock, 2018). See Figure 1a,b for an illustration of these systems. This article focuses on the system-directed strategy, used by several companies, and leaves the investigation of the swarm strategy for a future research.
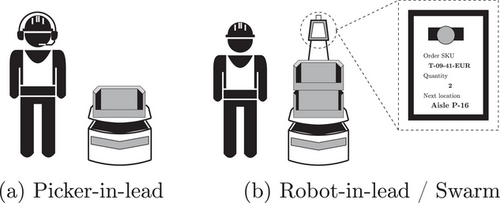
The described PS-AMRs are suitable for a shelf warehouse with piece picking and are the focus of this study. However, another type of PS-AMR, known as an autonomous order picking truck, brings similar collaboration capability to pallet warehouses with carton picking. See Appendix A in the Supporting Information for more details.
In human–robot collaborative systems, different operational policies for routing, picker, and robot allocation can be embedded in the control software. Hence, system behavior can be dynamically adjusted, which makes these systems very flexible. As a result, companies can adopt different control policies in combination with different pick strategies to improve pick performance. One of the decisions that can significantly improve the pick performance is progressive zoning (PZ). In this strategy, the warehouse is divided into zones, with a few pickers dedicated to each zone, while robots travel between the zones to collect the orders.
Almost all studies so far have investigated PZ decisions in traditional systems where zones are formed by partitioning the order pick area into groups of aisles and cross-aisles, connected by conveyors (see Section 2 for more details). Yu and de Koster (2009a) report on deciding the optimal number of zones, minimizing the order throughput time, in conveyor-based PZ. The performance of the number of zones appears to depend on the order size. While order sizes are typically small in e-commerce, they are large in store-based retail, and varied in omni-channel retail. We believe that with varying number of lines per order, different PZ strategies can be applied to potentially increase the picking operation throughput capacity. It is unclear under what situations different zoning strategies yield operational benefits in collaborative human–robot picking operations.
We investigate two strategies, the no zoning (NZ) strategy and the PZ strategy. In both strategies, a pick list is assigned to a robot, and the pick locations can be located anywhere in the warehouse. In the NZ strategy, the robot is then paired with any available picker, and together they pick all the pick list items from the whole warehouse, that is, the pickers are shared among all pick locations. Once the picking is done, the robot takes items back to the depot, and the picker becomes available for the next robot with a next pick list. In the PZ strategy, the warehouse is divided into multiple storage zones, with one or multiple pickers assigned to each zone. Pickers only pick from their dedicated zones. In every zone, the robot is paired with a picker from that zone, and together they pick all the required pick list items from that zone. If the order is incomplete, the robot progresses to another zone. Else, if all needed items are picked, it travels back to the depot, and the picker becomes available for processing the next order. The two picking operations are discussed in more detail in Section 3.
There are operational trade-offs involved in the selection of the two pick strategies. Although the robots can travel to any pick location in both strategies, the movement of the pickers is restricted, depending on the pick strategy. In the PZ strategy, the picker's travel time is reduced because her movement is restricted to the zone. In this strategy, a partially filled order is picked in the next zone by a different picker. However, due to demand variability among the zones, the robot may have to wait in a zone for an available picker. In the NZ strategy, the robot's waiting time to access an available picker is reduced because pickers may access any pick location within the warehouse. However, the picker's travel time per order can increases because she may have to visit locations throughout the warehouse.
We expect that the PZ strategy has a higher throughput performance than the NZ strategy when order sizes are small because the picker's unproductive travel time is reduced. In contrast, when order sizes are large, we expect the NZ to outperform the PZ strategy because it reduces the waiting time of the robots to access an available picker. To test these hypotheses, we need to estimate the throughput capacity of the system under different pick strategies and order sizes. We use a novel queuing network model to estimate the throughput capacity of the system under a given pick strategy and order size, and compare it for the two pick strategies. We validate our model and the underlying assumptions using a detailed and realistic simulation model that mimics the actual picking operation. We aim to answer the primary research question: How can we maximize the pick throughput performance, for a given order profile, and a given number of resources, by selecting an appropriate fixed zoning strategy in a human–robot collaborative picking system? In this study, we propose a minimization model to address a sub-research question: What combination of pickers, AMRs, and zoning strategy results in the lowest operational costs while meeting the desired throughput? We also investigate the effect of dynamic zoning in the following secondary research question: Using a dynamic zoning strategy, a given order profile, and a given number of resources, is it possible to achieve a better pick performance (throughput and cost) than with a static zoning strategy? Switching between the pick strategies (NZ and PZ) can be easily implemented in collaborative robot systems. For every pick tour, the pickers are instructed about the picks to be carried out (with which robot) through wearable technology or via the monitors mounted on top of the AMRs. We investigate two dynamic zoning policies: (1) dynamic zone switching based on real-time conditions or (2) switching at a fixed moment according to predetermined rules.
Our results demonstrate that for a fixed (small) order size typically PZ yields a higher throughput capacity than NZ, while for fixed large order sizes it is the other way around. For varying order sizes, the better strategy depends on the order mix, and the number of available robots. For the order profile of our industry partner and layout (14 aisles), zoning has the potential to improve the throughput capacity by up to 14%. In addition, we study a dynamic switching (DS) strategy, where switching between NZ and PZ occurs dynamically, for a situation with time-varying order sizes. Assuming steady state and a given zoning configuration, we use a Markov decision process (MDP) minimizing average operational cost. Our results show that using a DS strategy has little effect on throughput performance and could actually deteriorate pick performance at times. We also investigate a fixed switching (FS) strategy in which we use a different picking strategy for different demand profiles in the morning and afternoon shift. We use simulation to obtain the throughput performance of the system. Our results show that the FS strategy has the potential to increase throughput performance by 17% compared to the NZ strategy, albeit at higher robot cost.
The prime contributions of this article are as follows: (1) we are the first to develop a stochastic model for a human–robot collaborative picking system and analyze the pick performance with dynamic order profiles, (2) we develop a novel closed queuing model using the technique of two-phase queuing servers (van Doremalen, 1986) to capture the parallel movement of the picker and the robot, which is also scalable to multiple zones, and (3) we are the first to investigate the effect of zoning strategies (NZ and PZ) on throughput capacity for collaborative robot picking, and the effect of switching (fixed or dynamic) between these pick strategies, on the system performance. We also present a model to optimize the number of zones (along with the number of pickers and robots) yielding minimum operational cost.
The rest of the study is organized as follows. Section 2 reviews the related literature. In Section 3, we provide a detailed description of the human–robot collaborative zone picking strategies. We then present the queuing network models for each pick strategy in Section 4. In Section 5, we compare the performance of different fixed zoning strategies based on the queuing network models. This section also presents a model that minimizes the operational costs of a warehouse. Section 6 discusses the effect of dynamic order picking strategies on pick performance. We conclude in Section 7.
2 LITERATURE REVIEW
The operational performance of PS-AMR systems can generally be improved with better picker and robot routing policies. For example, Petersen II and Schmenner (1999) propose multiple picker routing heuristics in a volume-based storage environment and examine the interactions between routing and item storage policies. In this section, we focus our review on modeling collaborative picking systems and on the effect of zone picking decisions.
Collaborative picking systems: Azadeh et al. (2019) introduced PS-AMRs and their potential for further academic research. They state that the parallel movement of pickers and AMRs makes the modeling of these systems different from manual picking and other robotic systems. Boysen et al. (2019) provide several research opportunities for the use of PS-AMRs. For instance, they suggest that traditional storage assignments, such as full turnover and class-based storage (see, e.g., Yu et al., 2015), should be reevaluated in collaborative picking systems. The majority of these storage policies propose storing fast-moving items close to the depot. Yuan et al. (2019) investigate the performance of a Robotic Mobile Fulfilment system under a velocity-based storage policy. In this policy, popular items are stored closer to the pick stations. They use a random storage policy as the benchmark and, by using a fluid model, show that a 2- or a 3-class velocity-based storage policy reduces the travel distance by 8% and 10%, respectively. However, this might not be the best strategy in a collaborative environment, and different storage policies should be considered. Boysen et al. (2019) suggest that fast-moving products may best be stored somewhere in the middle of the storage area. Despite these research opportunities, to date, the number of research articles on PS-AMRs is still limited. Ghelichi and Kilaru (2021) proposed an analytical model to study collaborative picking systems. Particularly, they study two picking scenarios called last mile delivery (LMD) and meet in aisle (MIA). In the LMD scenario, the robot moves between dedicated workstations usually located in front of the aisles. Once a robot arrives at a workstation, a picker picks up the robot's empty cart and fills it with the required items from the aisle. Once all the items are picked the robot carries the filled cart back to the consolidation area. In the MIA scenario, the robot enters the aisles, similar to the operations that we have explained in Section 1. They show that the LMD is more suitable when a high throughput rate is needed, while MIA is preferred in facilities that have large picking areas with low picks per cycle. Meller et al. (2018) investigate the business case for collaborative picking systems. Given their assumption about the speed capabilities of the AMR and the pricing structure, they conclude that the business case for a collaborative system is limited to operations with low pick density. Löffler et al. (2022) study picker routing in a system-directed collaborative system. They develop an exact polynomial-time routing algorithm for a given order sequence and different heuristic algorithms when the order sequence is a decision variable. They show that by collaborating with an AMR, a picker can reduce the walking distance by about 20%. Lee and Murray (2019) study a system-directed collaborative system in which two AMRs collaborate to fulfill orders: a “picker” AMR that retrieves items from storage locations and a “transport” AMR, which takes picked items to the depot. They define a vehicle routing problem to minimize the required time to pick all items on a pick list. Through numerical analysis, they show the system offers the greatest improvement over the traditional manual picking system when there are more parallel storage aisles or fewer cross aisles in the warehouse. Žulj et al. (2022) propose a mathematical model to minimize the overall customers' orders tardiness through optimizing batching the orders, and then assigning the batches to AMRs in the right sequence in a zoned warehouse. AMRs do not really collaborate with the pickers: they are only responsible for transporting batches of items from predetermined handover locations in the picking area to the depot. The findings demonstrate that, in the majority of cases, increasing the robot to worker travel speed ratio has a more significant impact on reducing the average delay of customer orders compared to expanding the AMR fleet. Pugliese et al. (2022) develop a mathematical model to optimize picking operations and synchronization in a two-block warehouse where human order pickers collaborate with AMRs. The results indicate that increasing the fleet size of AMRs has a greater impact on reducing tardiness compared to increasing the speed of AMRs. Although this seems to contrast results of Žulj et al. (2022), as the studied systems differ, results are hard to compare. Löffler et al. (2023) examine the coordination problem between pickers and AMRs, by comparing the performance of the swarm strategy and the system-directed strategy (called “fixed pairing of pickers and AMRs” by the authors). The results demonstrate that the swarm strategy may outperform the system-directed strategy substantially, however, the authors indicate that, in reality, the swarm strategy is sensitive to slight delays which may propagate and distort these results. The majority of the above articles model the system in a deterministic fashion, for example, demand, travel, and picking. Furthermore, Meller et al. (2018) acknowledge that the dynamic of human–robot collaboration is complex, and further research is required.
Zone picking: Long picker travel times and congestion along the pick routes are major concerns in a warehouse (Zhang et al., 2009). Zone picking is an effective strategy to reduce congestion and improve efficiency in both manual and automated systems. Two approaches can be used for zone picking, parallel (or synchronized) zoning and sequential (or progressive) zoning (de Koster et al., 2007). In parallel (or synchronized) zone picking, a customer order is picked simultaneously in multiple zones. Once all items are picked, they are consolidated and sorted into individual customer orders. de Koster et al. (2012) study the problem of determining the right number of parallel zones for a manual picking system to minimize system throughput time (picking and consolidation process). They show that for given order size and pick list size, the throughput time is not convex in the number of zones. The problem of parallel zoning in automated parts-to-picker systems has received a bit more attention. Roy et al. (2012) investigate the effect of the number of zones in a shuttle-based storage and retrieval system. They model the matching of transactions with vehicles using a synchronization queue and the system is represented as a semi-open queuing network. Their results suggest that having multiple zones reduces system throughput time due to shorter travel time. However, as the number of zones increases, throughput time also increases due to longer waiting times for an available shuttle. Note that the additional consolidation process was not modeled in their analysis. Roy et al. (2019) investigate the robot assignment strategies for multiple storage zones in robotic mobile fulfillment systems. They model the system as a multi-class closed queuing network and show that the expected throughput time for order picking can be reduced by one-third by pooling robots among different zones. However, the average replenishment time has increased threefold. Van Gils et al. (2018) investigate the relations between different planning strategies such as storage, batching, and zone picking. Their analysis shows that an integrated approach is needed when it comes to planning decisions. Modeling and performance analysis of picker-to-parts systems with sequential (or progressive) zone picking has not received much research attention. In progressive zone picking, additional order consolidation is not required because the orders are gradually consolidated as the order tote visits each zone. De Koster (1994), Yu and de Koster (2009a), Yu and De Koster (2008), and Melacini et al. (2011) propose a queuing network model to estimate performance statistics of a conveyor-based zone picking system. In their analysis, they do not consider order tote blocking and congestion effects. However, in reality, the buffer space in each zone is limited, and therefore congestion and blocking can happen regularly in these systems. In practice, zone-picking conveyor systems often use the block-and-recirculate protocol to manage the congestion dynamically. Van der Gaast et al. (2020) develop a queuing network model and propose an approximation method based on the jump-over blocking protocol (van Dijk, 1988) to estimate the performance of a sequential zone picking system with finite buffer capacities. Also bucket brigade order picking uses progressive picking, that is, passing the work between pickers, albeit with dynamic (i.e., virtual) “zones”. These systems were introduced by Bartholdi III and Eisenstein (1996) and reviewed by Bratcu and Dolgui (2005). The system typically requires a line layout of the storage racks and a conveyor to pass the order totes between pickers. The tote is passed between the pickers at dynamic positions (see, e.g., Bartholdi III et al., 2001; Bukchin et al., 2018).
None of the mentioned literature on progressive zone picking assumes human–robot collaborative picking (see Table 1 for a comparison of studies on progressive zone picking). The effect of zoning on throughput capacity requires further study. In addition, in all literature, the zoning decision is assumed static. Once the zone picking decision is made, it does not change during the picking operation. In progressive zone picking with conveyors, it is not physically possible to change the zone sizes. However, the collaborative robot system is flexible enough to work with a more dynamic pick strategy. It is, however, not clear whether switching between different zoning strategies is beneficial. Hence, in this article, we look additionally at the effect of a switching zoning decision (switching between NZ and PZ strategies) on the performance of the cobotic system.
| Authors | System | Order profile | Resources in zone | Zoning configuration | Method |
|---|---|---|---|---|---|
| Bartholdi III and Eisenstein (1996) | Manual, Conveyor | Multi-line orders, fixed order profiles | Pickers | Dynamic (bucket brigades) | Markov chain |
| Bartholdi III et al. (2001) | Manual, Conveyor | Multi-line orders, fixed order profiles | Pickers | Dynamic (bucket brigades) | Stochastic, Fluid model |
| Bukchin et al. (2018) | Manual, Conveyor | Multi-line orders, fixed order profiles | Pickers | Dynamic (bucket brigades) | Stochastic, Markov chain |
| de Koster (1994) | Manual, Conveyor | Multi-line orders, fixed order profiles | Pickers | Conveyor based pick-and-pack zones | Open queuing network |
| de Koster and Yu (2008) | Manual, Conveyor | Multi-line orders, fixed order profiles | Pickers | Conveyor based pick-and-pack zones | Open queuing network |
| Yu and de Koster (2009b) | Manual, Conveyor | Multi-line orders, fixed order profiles | Pickers | Conveyor based pick-and-pack zones | Open queuing network |
| Melacini et al. (2011) | Manual, Conveyor | Multi-line orders, fixed order profiles | Pickers | Conveyor based pick-and-pack zones | Open queuing network |
| van der Gaast et al. (2020) | Manual, Conveyors with loops | Multi-line orders, fixed order profiles | Pickers | Conveyor based pick-and-pack zones | Open queuing network |
| This article | PS-AMR | Multi-line orders, dynamic order profile | Pickers and AMRs | Partitioning of aisles | Closed queuing network |
3 DESCRIPTION OF THE ZONING STRATEGIES
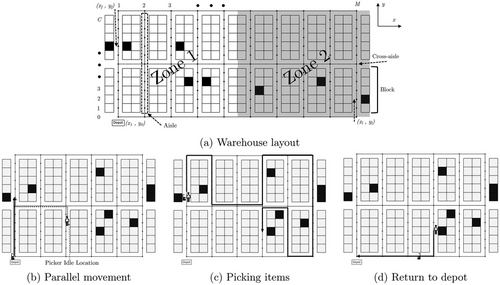
In this section, we describe the warehouse zoning strategies with reference to a layout shown in Figure 2a.
3.1 NZ strategy
When an order arrives, the corresponding pick list is generated and assigned to a robot waiting in the depot (robots dwell at the depot). The robot is then paired with an available picker and travels to the first pick location. Simultaneously, the picker also travels from her dwell position to the first pick location (pickers dwell next to the last picked item of the previous pick tour). A pick tour starts either from the leftmost aisle or the rightmost aisle from which an item needs to be picked. The choice depends on the dwell position of the picker. If the previous pick tour ended close to the left (right) side of the warehouse, the next pick tour begins at the leftmost (rightmost) aisle from which an item needs to be picked. This is a simple strategy that minimizes the picker's travel distance and improves system performance. The picking consists of three movements: (a) A parallel movement, in which the picker and the robot with an empty pick tote travel simultaneously from their dwell positions to the first pick location, as depicted in Figure 2b. (b) A picking items movement, in which the picker and the robot are paired and travel to pick all the required items on the robot's pick list, as shown in Figure 2c. (c) A return to depot movement, in which the robot transports items to the depot, and the picker becomes available to be paired with another robot, as illustrated in Figure 2d. Upon completion of the last pick, the picker receives information about the start point of the next pick tour either through wearable technology or from the monitor mounted on the previous robot.
3.2 PZ strategy
In the PZ strategy, the warehouse is divided into multiple zones (see Figure 2a). One or multiple pickers are assigned to each zone and they only pick in their dedicated zone. Similar to the NZ strategy, robots dwell at the depot, and pickers dwell next to the location of the last picked item in their zone. When an order arrives, the corresponding pick list is generated and assigned to a robot. Then the robot travels to the first zone from which an item should be picked. The robots check and if necessary visit the zones in a sequence starting from the left (right) to the right (left) of the warehouse. In this study, we assume the depot is located in front of the leftmost aisle. Therefore, the sequence of visiting the zones starts from left to right. Zones without picks are skipped.
The first two picking movements within each zone are similar to the NZ strategy, that is, parallel movement of the picker and the robot, as well as pairing and picking items within each zone. In the parallel movement, the robot travels from the last pick location in the previous zone to the first pick location in the current zone. Simultaneously, the picker also travels from her dwell position to the first pick location. A pick tour starts alternatively from either the leftmost aisle or the rightmost aisle of the zone from which an item needs to be picked. The choice depends on the dwell position of the picker in the zone. Once all items are picked from a zone, the robot travels to the next zone, and the picker pairs with another robot. The last picking movement, that is, return to the depot, occurs upon completion of picking all items on the pick list.
In this study, we are interested in estimating the throughput capacity of these two pick strategies under steady-state conditions. In the next section, we show how we use queuing network models to achieve this goal.
4 ANALYTICAL MODEL
We make the following assumptions in modeling the system:
(1) Constant velocity: We ignore acceleration and deceleration of robots and pickers. This is justified as the duration is very short. The velocity of the picker and the robot are and , respectively. (2) Picker dwell position and the start of the pick tour: In the NZ strategy, pickers dwell next to the location of the last picked item from the previous pick tour. The next pick tour starts from a location relatively close to the picker's dwell position; as with the S-shape routing strategy routes are organized from left to right and right to left in an alternating fashion. Similarly, in the PZ strategy, pickers dwell next to the last picked item location from the previous pick tour, within their dedicated zone. The next pick tour within each zone then starts from an aisle relatively close to pickers' dwell positions, from which an item needs to be picked. This is not a limiting assumption for our analytical model but rather a good operational policy that reduces the walking distance of the pickers and ultimately increases system throughput capacity. Our model can adapt to any other policy as well. (3) Selecting among multiple idle pickers: In the case of multiple idle pickers, the robot is randomly paired with one of them. (4) Pick routing: The pick tour is S-shape or traversal (Roodbergen & de Koster, 2001) for the paired picker and robot to pick items (see Figure 2c). We use the S-shape routing policy, as this policy is a simple strategy that is predominantly used in practice, near optimal if the pick density is sufficiently high, and which reduces congestion in an aisle (de Koster et al., 2007). Our model can adapt to other routing methods because they only impact the service time estimations of the queuing servers. (5) Location of the depot: The system has one depot, which is located in front of the first aisle to the left (see Figure 2a). This also mirrors the warehouse layout of our industry partner. Our model can adapt to include more than one depot at different locations. (6) Two-sided picking: Items are stored and are picked from both sides of an aisle. Goetschalckx and Ratliff (1988) have shown this is optimal in narrow aisles such as shelf racks. (7) Uniform storage: Items are uniformly stored in the warehouse, that is, the probability of any location to contain a product required on an order line is based on a uniform distribution. This storage policy is appropriate for an S-shape routing and a larger pick list. Our model can adapt to any other storage policy. (8) Sequence of checking/visiting zones: The depot is located in front of the leftmost aisle, and the sequence of visiting the zones starts from left to right. For instance, if the warehouse has three zones, the robot first checks/visits the zone on the left side of the warehouse, that is, the zone in front of the depot, then the zone in the middle, and finally the zone on the right side. Our model can adapt to any other sequence. (9) Congestion and blocking: PS-AMRs can identify obstacles in their travel path and can overtake each other. Hence, congestion and blocking effects are negligible in the system.
4.1 Throughput time expression
4.2 Queuing network model for NZ strategy
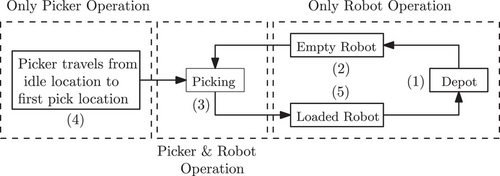
We model the system as a closed queuing network to estimate the throughput capacity of the system with robots. In the network, the recirculating jobs are the robots, and the servers are pickers. The picker's service time consists of two parts, traveling from the idle location to the first pick location ((4) in Figure 3) followed by picking items with the paired robot ((3) in Figure 3). Note that the picker and the robot travel from their idle location to the first pick location simultaneously, that is, (2) and (4) in Figure 3 are done in parallel (see Figure 2b). To capture the parallel movement of the AMR and the human picker, we use a two-phase queuing server first proposed by van Doremalen (1986) to model the picker service time. The two-phase server consists of a preparatory or setup phase, and an execution or process phase. The preparatory phase can start even when the server is idle. The execution phase can only begin when a job is waiting in the server and when the preparatory phase has been completed (van Doremalen & Wessels, 1986). We model (4) in Figure 3 as the setup phase, and (3) as the process phase. We allow the setup phase to start without any jobs in the node. The process phase starts only once there is a job in the node and when the setup phase is completed, that is, a robot is available to execute the first pick instruction jointly. We model the depot operation ((1) in Figure 3) as a one-phase single server (OPS) node. As robots can easily overtake each other and congestion and blocking effects are negligible, we model the robot travel operations, that is, (2) and (5), as infinite-server (IS) nodes. We extend the model to include more than one picker by replacing the single two-phase server node with a multi-two-phase servers (MTPS) node. Figure 4 illustrates the resulting queuing network.
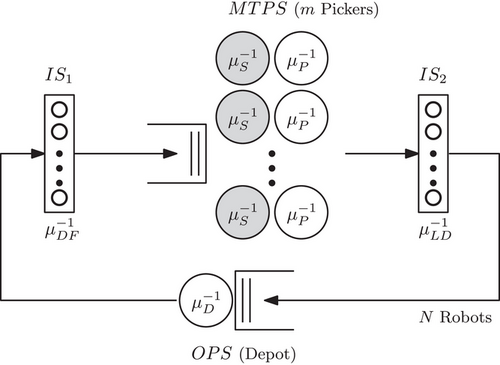
The expected service time at the depot is denoted by and depends on the processing speed of robots at the depot. The expected time for the robot to travel from the depot to the first pick location is . Similarly, is the expected time of the robot to travel from the last pick location to the depot. The expected time of the picker to travel from her dwell position to the first pick location is , and is the expected time to travel and pick all items on the pick list. The service times , , , depend on the size of the assigned order to the robot, that is, the number of items on the robot's pick list, and can be generally distributed.
4.3 Queuing network model for PZ strategy
We extend Network 1 in Figure 4 to model the PZ strategy. We focus on the PZ strategy with two, three, four, and six zones. Figure 5 illustrates the PZ strategy with two zones.
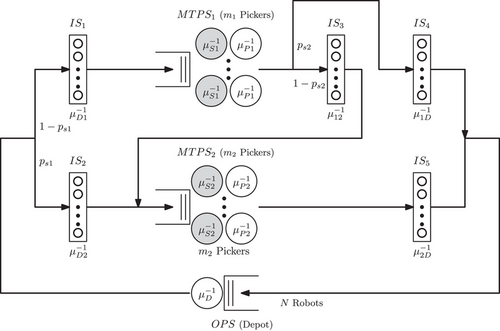
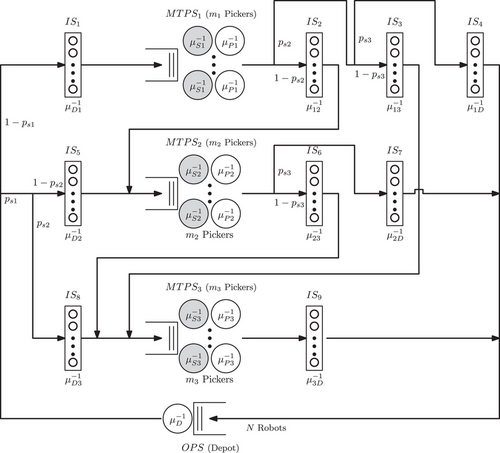
When a robot leaves the depot, it travels to the first zone with probability , or it skips the first zone and travels directly to the second zone with probability . Once the process in the first zone is completed, the robot moves to the second zone with probability , or it skips the second zone and goes to the depot with probability . We estimate and numerically based on the order profile. Note that similar to Network 1, the setup phase in and nodes (gray servers in Figure 5) can be done even without a robot in the node. The expected time for the robot to travel from the depot to the first pick location in the first (second) zone is (). The expected time for the robot to travel from the last pick location in the first zone to the first pick location in the second zone is . Note that the first pick location in the second zone can be on either side of the zone, depending on the dwell position of the picker. The expected time for the robot to travel from the last pick location in the first (second) zone to the depot is (). The expected setup time in zone one and zone two is given by and , respectively. Likewise, the process times in zone one and zone two are denoted by and , respectively. Processes are similar when there are more than two zones in the system (see Figure 6). Although we illustrate the model for up to three zones, our model is scalable to accommodate more than three zones as well. In our numerical experiments, we scale our model to four and six balanced zones as well. The routing probabilities needs to be adjusted depending on the order size distribution and the storage pick location probabilities.
4.4 Parameter estimation
We use a Monte Carlo simulation to estimate the first moment of each service time, as well as the probabilities () of skipping a zone. These parameters can also be estimated analytically (see Dijkstra & Roodbergen, 2017; Sadowsky & Ten Hompel, 2011). However, further restrictive assumptions are needed to use these analytical models while they do not contribute to gaining additional insights in answering our research question. For instance, the closed-form equations in Dijkstra and Roodbergen (2017) are for a warehouse without any middle cross-aisle. Using the Monte Carlo simulation gives us the flexibility to estimate the parameters without any further limiting assumptions.
We generate 1000 instances based on input parameters and assumptions (see the beginning of Section 4 for the list of assumptions). The parameters include: Warehouse layout: including the number of aisles, number of cross-aisles, number of storage blocks, number of storage columns per block, aisle to aisle distance, and storage location width; Resource velocity: velocity of the picker and the robot; Order profile: number of items and their pick locations in every pick tour; and Processing time: the average time to pick an item and the average time to process a robot in the depot. The warehouse layout and the order profile are based on the real-world warehouse of our industry partner, a logistics service provider in the Netherlands. The robot velocity has been obtained from an implemented PS-AMR system. The picker walking speed and pick times are based on consultation with our industry partner. For every instance, we generate a pick list and calculate the service times: (1) robot travel time from the depot to the first pick location, (2) picker travel time from her idle position to the first pick location, (3) time to pick all items, consisting of travel time and item picking time, (4) robot travel time to travel between zones in the PZ strategy, (5) robot travel time to return to depot. We then calculate the first moment of the service time for each node after running 1000 simulation instances. To calculate the skipping probabilities under the PZ strategy, we divide the number of instances that a zone is skipped by the total number of generated instances. These travel time estimates are then inserted as service times in the queuing network mode, which in turn can also estimate the waiting times.
4.5 Solution method for the queuing network models
As Networks 1, 2, and 3 include two-phase servers, they do not have a product-form solution (Baskett et al., 1975; van Doremalen & Wessels, 1986). However, the networks can still be analyzed as a continuous-time Markov chain if the state space is finite (van Doremalen & Wessels, 1986). However, solving the underlying Markov chain will be computationally intractable if the size of the state space is large. Fortunately, the size of the state space that describes the underlying continuous-time Markov chain for Network 1 is small, and we can therefore directly analyze it to estimate the performance measures. Due to curse of dimensionality, the same procedure cannot be extended to Networks 2 and 3, and hence, we use approximate methods to estimate performance measures. We use an aggregation–disaggregation (ADA) method and mean value analysis (MVA) to estimate the performance measures (see Kumawat et al., 2021), and assume that the service times of the nodes in the network are exponentially distributed. Appendix B in the Supporting Information provides the details of the solution approach. We also explain how the solution method can be extended to a network with generally distributed service times at the nodes. From the closed queuing network model, we can estimate all performance measures such as average wait time for pickers, picker utilization, throughput capacity, and average throughput time. If we estimate the throughput capacity, the average throughput time can be obtained using Little's Law. Note that the performance of zoning strategies could depend on several design parameters such as the layout of the order picking area (number of aisles), ratio of the length of the aisle to the length of the cross-aisle, and order profile (number of line items). Here, we adopt a warehouse layout from our industry partner to demonstrate the efficacy of our zoning strategies.
4.6 Model validation
To verify the performance measure estimates (in particular, maximum throughput capacity) obtained from the closed queuing network model, we developed a detailed discrete event simulation model in Python that mimics the collaborative order picking processes in detail. To simulate closed queuing networks corresponding to NZ and PZ strategies, we assume orders are always waiting in a virtual queue for picking. The picking sequence for each order is calculated based on a sorted list before the simulation, using the S-shape routing policy. However, depending on the current location of a picker, she may begin picking the items from the sorted list either from left to right or from right to left. For the NZ model, when an AMR at the depot is available, the AMR is assigned to the first order in the queue, and it travels via a shortest time path to the first pick location. Similarly and independently, when a picker is free, she heads to the first pick location of the next order. Once both the AMR and picker are present at the first pick location, they coordinate to pick the first item from the storage location and then move on to the next pick location to complete picking all items corresponding to an order. Once all items are picked, the picker becomes available to serve the next AMR, while the AMR heads back to the depot. After unloading the items, the AMR becomes available to process the next order in the queue. In the PZ model, each zone has its own dedicated pickers. Similar to the NZ model, the picking sequence for each order is determined, however now each zone has its own sorted list. A picker may begin picking the items of a zone from the sorted list either from left to right or from right to left, depending on the proximity of the picker to the first or last pick location of the sorted list. An AMR and picker collaborate to pick all the items in a zone. Then the AMR moves to the next zone (if any) and will be synced with another picker in that zone. After picking all the items of the order, the AMR heads back to the depot.
We calculate resource travel times based on the actual distance between locations and the speed of the moving agent (we use the AMR speed for modeling the AMR's movements, picker speed for modeling the picker movements, and the minimum speed between an AMR and a picker when they move jointly to pick order items). Further, the item pick time is assumed to be uniformly distributed between 7 and 13 s. The AMR unloading time at the depot is assumed to be exponentially distributed with an average of 20 s. In addition, it is assumed that stock replenishment is not performed during pick shifts. We generate 308 different instances and compare the throughput performance of the queuing networks with the simulation results. For each instance, the simulation was run 500 times, where each run represents a working day of 8 h. For each instance, 20,000 orders are generated and the sequence of these orders in the respective queue is shuffled randomly for each simulation run. To validate the analytical model, we measure the absolute error percentage, which is defined as , where and are throughput capacity estimates using analytical and simulation models, respectively. Table 2 summarizes the error terms. The details of the instances and the distribution of the error terms are presented in Appendix C in the Supporting Information.
| Statistics | Network 1 | Network 2 | Network 3 |
|---|---|---|---|
| Mean absolute error (%) | 1.186 | 4.760 | 2.268 |
| Minimum error (%) | 0.033 | 0.299 | 0.004 |
| Maximum error (%) | 2.268 | 11.595 | 11.595 |
The results show that the queueing network models can accurately capture the throughput capacity of different picking strategies.
5 STATIC ZONING STRATEGIES
Business-to-Consumer (B2C) orders, such as e-commerce orders, often consist of a single line or a relatively small number of lines per order. In contrast, Business-to-Business (B2B) orders, such as store replenishment orders, usually include many items. In an omni-channel warehouse, we have both small (B2C) and large (B2B) orders. Hence, we leverage the order profile distribution as a key parameter while evaluating the performance of the zoning strategies. In this section, we investigate static and dynamic order profiles. In a static order profile, the size of the orders is predetermined and remains constant throughout the analysis. On the other hand, in a dynamic order profile, we consider a combination of different order sizes that are present in the system, allowing for variability in the order sizes.
In the rest of this section, we first analyze the throughput of the zoning strategies using asymptotic analysis. We then perform a detailed numerical experiments with two layouts (corresponding to our industry partner warehouse layout and a similar layout with additional aisles), different order profiles, and picker/robot configurations.
5.1 Asymptotic throughput analysis
We investigate a system with pickers under an NZ strategy and under a PZ strategy with two equally sized zones, each with dedicated pickers. Furthermore, we assume that the order pick locations are uniformly spread over the warehouse, and the probability of skipping a zone in the PZ strategy is zero. Therefore, on average, half of the pick locations are located in each zone. Now, we show Proposition 1 holds (see Appendix D in the Supporting Information for the proof). The analytical expressions of picker expected travel time under NZ and PZ strategies are obtained in Appendix E in the Supporting Information.
Proposition 1.The asymptotic (in the number of robots) throughput of a system under the NZ strategy is lower than the asymptotic throughput of the same system under the PZ strategy when the order size is small. The difference between these asymptotic throughputs converges to zero as the order size increases.
5.2 Numerical experiment for fixed order profile
To conduct our experiments, we utilize a warehouse layout provided by our industry partner, which closely resembles the one depicted in Figure 2a. Their warehouse consists of 14 aisles, each of which is divided into two storage blocks. This configuration results in three cross-aisles (front, middle, back). Within each aisle and block, there are 30 picking positions on both sides, totaling to 1680 pick positions overall. The length of a pick position is 1 m, while the width of a cross-aisle is also 1 m. The distance between adjacent aisles is 4 m. The depot is positioned in front of the leftmost aisle. There are two types of resources in this system: pickers and robots. In PZ strategies, the robots are still pooled across all zones as would be the case in NZ strategy. However, pickers assist robots in their designated zones only. In our experiment we assume 12 pickers and vary the number of robots from 13 to 30. Table 3 provides an overview of all the parameters. The order data description is included in Appendix F in the Supporting Information.
| Parameter | Value | Source | Parameter | Value | Source |
|---|---|---|---|---|---|
| # Aisles | 14 | Industry partner | # Cross-aisles | 3 | Industry partner |
| # Storage columns per block | 30 | Industry partner | # Blocks | 2 | Industry partner |
| Aisle to aisle distance | 4 m | Industry partner | Storage location width | 1 m | Industry partner |
| Avg item picking time | 10 s | Authors | Avg depot processing time | 20 s | Authors |
| Robot velocity | 1.5 m/s | Industry partner | Picker velocity | 0.67 m/s | Authors |
| # Robots | 13–30 | Authors | # Pickers | 12 | Authors |
In this study, our focus is solely on configurations that demonstrate balanced zoning, ensuring an equitable allocation of aisles and dedicated pickers to each zone. Consequently, for the layout consisting of 14 aisles (our industry partner), we compare the NZ strategy with the PZ strategy consisting of two zones. Subsequently, we expand the layout to 24 aisles and examine the PZ strategy with three, four, and six zones as well.
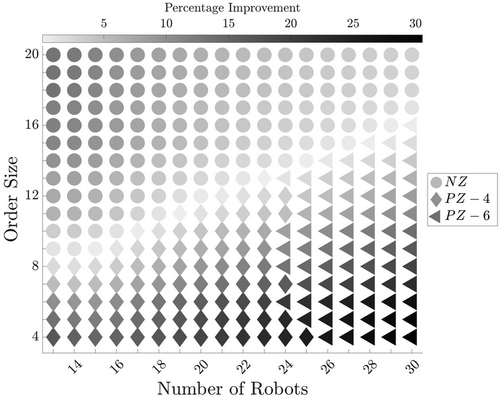
By using the closed queuing networks developed in Section 4, we calculate the throughput capacity of the system under the NZ and PZ strategies. We increase the order size from 2 to 20 items (fixed), in steps of 1. For each combination of the order size and number of robots, we then identify the pick strategy that performs better and measure the improvement percentage. Figure 7 illustrates the results.

In Figure 7, the shape of the markers visually indicates which picking strategy yields a higher throughput capacity. Additionally, the shade of the markers reflects the percentage improvement of the best of the NZ and PZ strategies over the other strategy. For example, with 15 robots and processing orders with 20 items, the NZ strategy approximately has a 14% higher throughput capacity compared to the PZ strategy. On the other hand, in a system operating with 30 robots and processing orders with four items, the PZ strategy exhibits roughly a 14% higher throughput capacity relative to the NZ strategy.
The trade-offs that we explain in the introduction can help understand the results. The throughput time to fulfill an order consists of two components: waiting time for a picker and picking time including travel. In the PZ strategy, the expected picker travel time within a zone is shorter because the robot transports the items between zones. However, the wait time to access a picker could be longer. In the NZ strategy, robot waiting time for a picker is shorter because robots can pair with any available picker. However, the picker travel time could be longer.
The picker travel time depends on the size of an order. If the order size is small enough (i.e., fewer than six order items in our experiment), the expected travel distance from one zone to another is relatively long. Therefore, by using the PZ strategy and letting the robots travel this distance, a shorter picker travel time is achieved. This time savings surpasses the wait for an available picker in a zone. Therefore, throughput time is reduced and further, a higher throughput capacity can be achieved. On the other hand, if the order size is large enough (i.e., more than 11 order items in our experiment), the benefit with respect to expected travel distance from one zone to another is relatively small. In this case, the NZ strategy has the edge over the PZ strategy because NZ reduces the robot's waiting to find an available picker in comparison to PZ strategy. In other configurations, either of the pick strategies can result in better performance, depending on the order size and the number of robots in the system.
We now extend the analysis to a warehouse with 24 aisles. We compare the throughput capacity results between NZ and the best of PZ with either two or three zones. Figure 8 illustrates the results. We observe that in the majority of cases where the PZ strategy outperforms the NZ strategy, the optimal number of zones can vary depending on the order size and the number of robots in the system. When the number of robots is large, more zones are preferable and vice versa. Appendix G in the Supporting Information explores the effect of the warehouse size on zoning decisions with more details.
We choose four order sizes (4, 10, 14, 20) for a more in depth comparison between all picking strategies. Figure 9 illustrates the results.
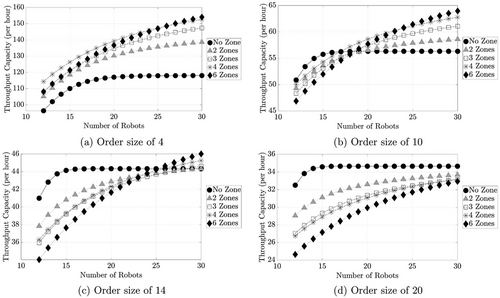
We observe that when considering small order sizes (e.g., order size of 4), PZ consistently outperforms NZ for all configurations (see Figure 9a). Conversely, for large order sizes (e.g., order size of 20), there is no throughput gain in zoning (see Figure 9d).
Figure 9b presents an interesting finding. It demonstrates that with an order size of 10, the throughput capacity of the NZ strategy cannot be increased by adding more robots beyond 18 robots in the system. In contrast, implementing the PZ strategy with additional robots enables an expansion in throughput capacity. With zoning, additional picker capacity is available due to reduced picker travel time. This extra picker capacity can be used alongside extra robots to enhance the system throughput. We see a similar trend also with an order size of 14 (see Figure 9c). However, the benefit of zoning is shown only when the number of robots exceeds 25. We also observe that we get marginal benefit in throughput with NZ when the number of robots is increased from 15 to 25, while it still dominates PZ. In addition, as depicted in Figure 9, the number of robots impacts system performance. Appendix H in the Supporting Information examines the effect of the availability of robots and pickers on throughput performance.
5.3 Numerical experiment for dynamic order profile
Up until now, we have assumed a static order profile, meaning that the size of the orders was assumed given and constant. Here, we discuss the throughput capacity of different picking strategies when the order profile is not static. The objective is to calculate the throughput capacity when we have two types of orders, small and large, simultaneously. The definition of “small” or “large” orders needs to be determined. As our analytical model assumes stationary pick time distributions, we use the detailed simulation model to determine the throughput capacity estimates of the system with variable order profile.
We classify orders into two profiles: small size (ranging from 2 to 5 items based on the order profile distribution obtained from our industry partner) and large size (ranging from 6 to 80 items based on the order profile distribution obtained from our industry partner). Additionally, we introduce a probability parameter to determine the likelihood of an order being small or large. By adjusting this probability from 0 to 1 in increments of 0.1, we explore a range of order profiles.
For our experiments, we assume 12 pickers in the system and vary the number of robots from 12 to 36. Figures 10 and 11 illustrate the results for warehouses with 14 aisles and 24 aisles, respectively.
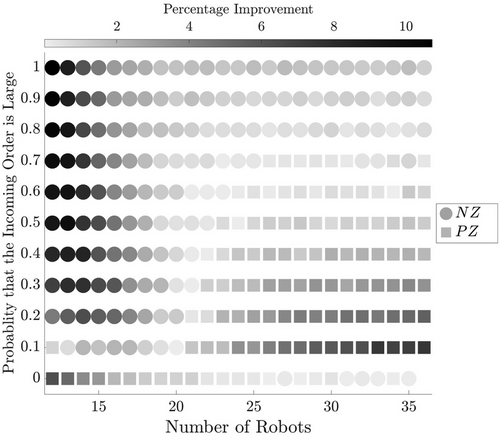
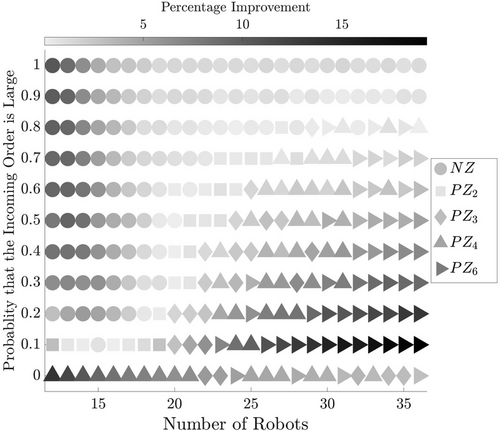
As the probability of large orders increases, the NZ strategy demonstrates greater benefits. This observation holds true for warehouse layouts with both 14 and 24 aisles. Conversely, as the probability of large orders decreases and small-sized orders become more prevalent, the PZ strategy becomes more advantageous.
With a large number of robots, the wait time for pickers to access a robot is minimized. In scenarios where the majority of orders are large, the NZ strategy outperforms PZ, particularly when the number of robots is limited. Apparently, with fewer robots, the PZ strategy experiences significant coordination delays within the zones, leading to longer wait times for pickers.
5.4 Operational costs optimization for dynamic order profile
To achieve a desired hourly order throughput, various combinations of the number of AMRs (), pickers (), and zoning strategies () can be chosen based on the specific order profile (). Each combination may incur different operational costs. In this subsection, our goal is to minimize the operational costs of the warehouse, considering the associated order profile, while ensuring a certain hourly throughput ().
Operational cost: When analyzing operational costs, we specifically focus on the pickers and robots. Many AMR providers adopt a “Robotics as a Service” (RaaS) business model, where customers can rent robots and the required infrastructure through a cloud-based subscription. This approach eliminates the need for substantial upfront investments in hardware, software, and maintenance (Biba, 2022). Hence, we assume that the company leases robots on a monthly basis (similar to the warehouses used in our study), enabling them to adjust the number of robots according to their needs.
For our calculations, we consider a picker cost of per hour and a robot cost of per hour. Let represent the hourly order throughput capacity of the warehouse, considering the order profile , AMRs, pickers, and operating under zoning strategy . Model 1 minimizes the hourly operational costs for a given target throughput capacity and order profile by finding the appropriate number of AMRs and pickers, and zoning strategy.
Model 1.
For a fixed order profile, the model can be solved using the appropriate queuing network model to estimate the throughput capacity for a given zoning strategy, number of pickers, and robots and then iterating over the number of pickers, robots and zoning strategies. As the models each can be solved rapidly, the optimal solutions are readily found. For a dynamic order profile, the detailed simulation model can be used.
Example 1.Assume a case where a decision maker should find settings that minimize the operational costs of the warehouse with 24 aisles for two different targets of throughput and order profiles when and (Forrester Research, 2019). In the first scenario, the probability of small orders equals 1, and orders/h, while in the second scenario, the probability of small orders equals 0.5 and . The orders are drawn from the distribution obtained from our industry partner. Table 4 shows some options that yield greater or equal throughput as the target. Based on Table 4 for Scenario 1 (), using 10 pickers, 14 AMRs, and PZ with two zones is the best option. The next three best options all have different zoning strategies and the number of robots equals the number of pickers. Scenario 2 () yields two different optimal solutions, one employing eight pickers and eight AMRs operating under the NZ strategy and another one with 6 pickers and 18 AMRs operating under the PZ-3 strategy. However, the NZ strategy yields a higher throughput capacity.
| Options | ||||
| 148.505 | ||||
| 147.556 | 288 | |||
| 148.867 | 288 | |||
| 148.535 | 288 | |||
| Options | ||||
| 23.103 | ||||
| 28.197 | ||||
| 29.663 | 196 | |||
| 30.069 | 200 | |||
5.5 Obtained insights
We observe that there are certain order size and number of robot combinations which are more favorable to zoning than others. In general, a smaller order size benefits more from zoning configurations. However, the number of scenarios (combination of number of robots and order size) that benefit from zoning grows with an increase in the number of aisles. As the number of aisles increases, the length of the cross-aisle increases. This increase results in a greater picker travel time along the cross-aisle that is reduced with zoning. We also notice that the benefits in throughput performance with zoning are more significant when we have a large number of robots. Note that in system-directed picking, either a robot waits for a picker or a picker waits for a robot. With zoning, the robot's wait for picker availability increases. However, with a larger number of robots, the picker's wait time for a robot decreases, which enhances the maximum throughput capacity.
In a closed system, maximum throughput capacity depends on the number of bottleneck resources (in our case either pickers or robots). Increasing the number of bottleneck resources increases throughput capacity but, beyond a certain level, the other resource will become a bottleneck, and increasing the number of none-bottleneck resources no longer helps. In our human–robot collaborative system, a manager might consider adding more robots as an immediate step to enhance capacity. However, we find that a manager can exploit the benefit of additional robots only when zoning strategies are implemented simultaneously, as a zoning strategy increases the capacity of the pickers. Further, such a strategy holds true for certain order sizes only.
Similar insights are also present for the dynamic order profile. The PZ is suitable when the majority of the orders are small. As the probability of large orders increases, the NZ strategy demonstrates greater benefits.
6 DYNAMIC ORDER PICKING STRATEGIES
The NZ strategy can achieve a higher throughput performance in warehouses that process large-sized orders and is therefore suitable for the B2B channel, for example, wholesale or the store replenishment channel. In contrast, the PZ strategy can achieve a higher throughput performance in warehouses that process small-sized orders and is more suitable for the B2C channel, such as the e-commerce channel. However, the pick strategy that maximizes the performance in an omnichannel environment with variable order size is unclear. Even single-channel warehouses employing batch picking might have to process different batch sizes. Some batches could be small due to the required short lead time for urgent orders. Therefore, many such warehouses will face a mixture of small- and large-sized order batches. When dealing with a dynamic order profile, there is a potential benefit in switching picking strategies. This switching can occur at a fixed moment according to a predetermined rule or dynamically, based on real-time conditions.
6.1 Fixed switching strategy
In a typical omnichannel warehouse, the composition of incoming orders may vary throughout the day. During the morning and early afternoon shift, the majority of orders to be processed are typically large-sized store replenishment and batched orders. However, as the day progresses and we enter the late afternoon and evening shift, the majority of incoming orders shift toward small-sized e-commerce and rush orders. Building on the insights gained from the previous sections, where we discovered that NZ is well-suited for large-sized orders and PZ is effective for small-sized orders, we now aim to explore the possibility of increasing the throughput capacity by switching picking strategies between such morning and afternoon shifts. We call this a FS strategy. We evaluate the effect on both throughput capacity and operational costs, using the simulation model.
6.2 Numerical experiment for FS strategy
We utilize the same dynamic order profile as discussed in Subsection 5.3 and assume an 8-h work day. As before, the order sizes are randomly generated. In the 4-h morning shift, the probability of an order being small is (with ), and in the 4-h afternoon shift, the probability is .
In the FS strategy, in the morning shift orders are picked using NZ, and in the afternoon shift PZ is used, by selecting a feasible balanced PZ zoning division that yields the largest throughput.
The operational cost comprises the pickers and the robots cost similar to Subsection 5.4. The picker cost is calculated, assuming 8 h per workday. The robot cost is calculated by multiplying the number of robots in the morning shift by the number of hours worked in the morning shift (4 h) and then by the cost per robot per hour. Similarly, we calculate the robot costs for the afternoon shift. The total cost is then the sum of daily picker and robot costs. For our calculations, we assume a picker cost of € 20 per hour and a robot cost of € 4 per hour (Forrester Research, 2019).
In the absence of blocking within the system, the throughput capacity increases as the number of robots is increased. However, once a certain threshold is reached, the pickers become the bottleneck and the system throughput capacity will stabilize with the addition of more robots. We define this threshold as the point at which the incremental increase in throughput capacity falls below 1% when adding an additional robot. Our objective is to determine the minimum number of robots required to reach this threshold. This helps to identify the minimum cost required to achieve the maximum achievable throughput capacity of the system, taking into account different zoning strategies.
We first focus on our industry partner warehouse, which consists of 14 aisles. As our interest lies in balanced zones, we only consider PZ with two zones. Four levels for the number of pickers are distinguished, denoted as . In each scenario, the number of robots increases from to . Subsequently, we calculate and , representing the maximum throughput capacity (orders/hour) for each picking strategy. Here, denotes the probability of incoming orders being small, while and indicate the minimum number of required robots to achieve this throughput plateau for each picking strategy, as explained earlier.
We define the order profile throughout the day as , representing the small-size orders probability in the morning and afternoon shift. Considering six different increments of from 0 to 0.5 with an increment of 0.1, the daily throughput for NZ can be calculated as , and for PZ as .
In the FS strategy, we employ the NZ policy in the morning and PZ in the afternoon shift. Hence, the daily throughput for the FS strategy is determined as .
To facilitate comparison, we normalize the throughput and costs for easier analysis. This normalization process involves dividing all values by the NZ values and then multiplying by 100 for each order profile. Figure 12 illustrates the results. The total number of robots needed for each scenario is presented in Table 5.
| Order profile | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0:1 | 0.1:0.9 | 0.2:0.8 | 0.3:0.7 | 0.4:0.6 | 0.5:0.5 | |||||||||||||
| NZ | PZ | FS | NZ | PZ | FS | NZ | PZ | FS | NZ | PZ | FS | NZ | PZ | FS | NZ | PZ | FS | |
| 6 | 17 | 25 | 22 | 16 | 27 | 23 | 15 | 27 | 23 | 15 | 27 | 22 | 15 | 25 | 20 | 14 | 26 | 20 |
| 8 | 22 | 32 | 29 | 20 | 33 | 29 | 20 | 32 | 28 | 20 | 32 | 27 | 19 | 33 | 28 | 20 | 34 | 27 |
| 10 | 29 | 40 | 36 | 25 | 39 | 35 | 24 | 39 | 34 | 24 | 41 | 34 | 24 | 38 | 32 | 24 | 38 | 31 |
| 12 | 39 | 40 | 36 | 31 | 47 | 43 | 29 | 46 | 41 | 28 | 44 | 37 | 28 | 43 | 37 | 28 | 40 | 34 |

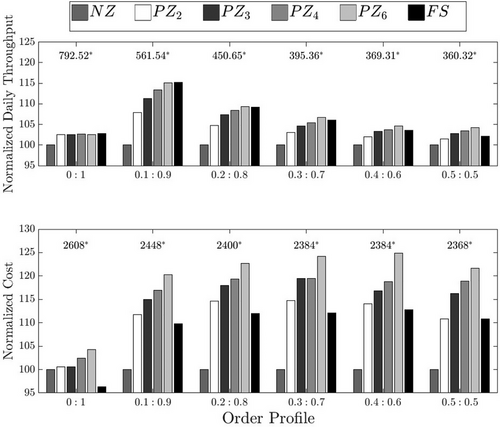
The results indicate that, in the majority of scenarios, the PZ and FS strategies achieve higher throughput compared to the NZ strategy. This is particularly evident when there is a significant imbalance in the order profiles between the morning and evening shifts. For example, in the order profile with six pickers, the FS strategy can fulfill 17% more orders compared to the NZ strategy. However, as the order profile becomes more balanced, the FS strategy does not provide significant throughput gains compared to the NZ strategy, as zoning is particularly advantageous when dealing with small-sized orders. Therefore, in scenarios with a higher proportion of small-sized orders, a higher throughput can be achieved by implementing zoning and increasing the number of robots in the system.
From a cost perspective, the NZ strategy consistently proves to be cheaper. This is because the throughput capacity of the NZ strategy reaches a plateau faster than the other two strategies. The reason is that the pickers become the bottleneck as the number of robots increases, limiting any further increase in throughput. On the other hand, both the PZ and FS strategies can achieve increased throughput by adding more robots, resulting in higher operational costs but also a higher daily throughput. We also observe that increasing the number of pickers can enhance the relative throughput performance of the NZ strategy while still maintaining lower operational costs.
The PZ and FS strategies generally yield similar daily throughput in almost all scenarios. However, the FS strategy consistently results in lower costs. This is because it uses fewer robots than the PZ strategy when fulfilling large orders. See Table 5.
We also carry out the same analysis for a warehouse with 24 aisles and 12 pickers to be able to include more zones in the analysis. We consider PZ with 2, 3, 4, and 6 zones. Figure 13 illustrates the results. The total number of robots needed for each scenario is presented in Table 6. We observe a similar pattern: FS can achieve a (nearly) similar throughput as the best PZ strategy, but at lower cost. The relative throughput difference between PZ and NZ disappears with more balanced shifts (i.e., increased value of ).
| Order profile | ||||||
|---|---|---|---|---|---|---|
| 0:1 | 0.1:0.9 | 0.2:0.8 | 0.3:0.7 | 0.4:0.6 | 0.5:0.5 | |
| 43 | 33 | 30 | 29 | 29 | 28 | |
| 44 | 51 | 52 | 51 | 50 | 44 | |
| 44 | 56 | 57 | 58 | 54 | 52 | |
| 47 | 59 | 59 | 58 | 57 | 56 | |
| 50 | 64 | 64 | 65 | 66 | 60 | |
| 37 | 48 | 48 | 47 | 48 | 44 | |
6.3 Dynamic switching strategy
In the DS strategy, the zoning strategy is dynamically adjusted based on the size of orders in the system. The primary goal is to determine whether it is possible to achieve higher pick performance with lower operational costs by dynamically switching between zoning strategies while maintaining a fixed number of resources. To identify the optimal zoning strategy that minimizes total operational costs, we develop a MDP model using input obtained from the queuing networks. More detailed information about this model can be found in Appendix I in the Supporting Information. Our analysis demonstrates that this strategy does not provide any significant benefits compared to a fixed NZ or PZ strategy.
6.4 Obtained insights
The analysis demonstrates that the FS strategy offers improvements in throughput compared to the NZ strategy, particularly when there is an imbalance in order profiles between the morning and evening shifts. It realizes (nearly) the same throughput as the best NZ strategy, but at lower cost. By increasing the number of robots and implementing zoning for small-sized orders, throughput can be enhanced, albeit at a higher cost than NZ. As an alternative, managers can also increase the throughput performance of the NZ strategy by increasing the number of pickers. In summary, there is no one-size-fits-all solution, and the choice of picking strategy should consider the composition of incoming orders, throughput requirements, and cost limitations.
7 CONCLUSIONS AND FUTURE WORK
In this research, we investigate the PS-AMR system, where robots collaborate with human pickers to fulfill the orders. This human–robot collaborative system is flexible enough to adopt different pick strategies. We investigate the effect of zoning the warehouse on the performance of the system. We focus on two pick strategies. The NZ strategy reduces robot waiting time as the pickers are pooled, whereas the PZ strategy reduces the picker travel time by using robots to transport the partially filled orders from one zone to the other. We show that the average order size affects the choice of the zoning strategy. A novel queuing network model is developed to estimate the system's performance under different pick strategies and order sizes to test our conjectures. Particularly, a two-phase queuing process is used to capture the realistic simultaneous movement of the robots and the pickers in the system. The results show that the NZ (PZ) strategy results in a higher throughput performance when the average order size is large (small). Moreover, the results indicate that in the NZ strategy the throughput capacity plateaus rapidly with an increasing number of robots. This is because the pickers become the bottleneck and more robots simply do not help. However, for a PZ strategy with the same number of robots, the pickers have more capacity and are not bottlenecks, implying we can increase throughput capacity by increasing the number of robots. The effect is contingent on the order profile. We also examine scenarios with dynamic order profiles. We categorized orders into small size (2–5 items) and large size (6–80 items) based on our industry partner data. By adjusting the probability of an order being small or large, we explore a range of dynamic order profiles. The insights obtained from these dynamic order profiles align with the findings from the static order profiles. We found that as the probability of large orders increases (decreases), the NZ (PZ) strategy offers greater benefits in terms of throughout performance. By analyzing the dynamic order profiles and considering various strategies we found that the different combinations of the number of pickers, AMRs, and zoning strategies can result in equivalent operational costs. However, the throughput capacity of the system varies for each combination, depending on the order profile. By considering such insights managers can make informed decisions to optimize the efficiency and effectiveness of their warehouse operations.
Therefore, the NZ strategy is more effective for large-sized orders in the B2B channel, while the PZ strategy performs better for small-sized orders in the B2C channel. However, determining the optimal strategy in omni-channel environments with variable order sizes is uncertain. We then study dynamic picking strategies in which we switch between NZ and PZ. This switching can occur dynamically (DS), or at a fixed moment (FS). Our results show that an FS strategy can achieve high throughput at relatively low cost compared to PZ strategies. Compared to the NZ strategy, the throughput can be significantly higher (up to 17%), especially when there is an imbalance in order profiles between morning and afternoon shifts. This is achieved by increasing the number of robots and implementing zoning for small-sized orders, which can enhance throughput but at a higher cost. Managers can also improve the performance of the NZ strategy by increasing the number of pickers. Using a DS strategy has little effect on throughput performance and could actually deteriorate pick performance at times.
The model and solution approach presented in this study can be applied to accommodate various storage policies, layouts, pick path strategies, depot locations, zone numbers and shapes, as well as order profiles. It is important to note that when these parameters deviate from the default settings used in this study, the inputs for the analytical models and simulations will vary, thereby yielding different results.
Research in collaborative AMRs is still in its early stage, and there are several potential directions for future studies. In this research, we limited ourselves to a fixed number of zones and fixed boundaries and investigated whether there is any benefit in switching picking strategies. A possible next step can be to examine the optimal dynamic zone boundaries to increase pick performance. Although RaaS has become a prevalent method for cobot deployment, rental companies play a pivotal yet often opaque role in detailed robot-to-worker assignments. Investigating the impact and capabilities of making these decisions presents an intriguing avenue for future research. Despite the provided flexibility by PS-AMRs, they also have some limitations, such as battery charging requirements. An interesting further extension would be to investigate a pick strategy considering the battery capacity of the robots. Furthermore, this collaboration calls for further study of human-machine interaction. In particular, we need more studies to address more behavioral questions. For instance, de Vries et al. (2016a) show that the picking performance in a manual warehouse is significantly impacted by the organization of the pick process, personalities of the pickers, and work incentives. A similar analysis should be done in a human–robot collaboration environment. Note that while we focus on maximizing throughput capacity (or productivity) through zoning decisions, a trade-off might exist with quality. However, such a trade-off may be contingent on many factors (including the pick tools and pickers, see, e.g., de Vries et al., 2016b) and needs further experimental research. Also, performance in the system may be influenced by the availability of resources (workers and robots), as well as inventory levels. Even though orders are typically picked when inventory is readily available, discrepancies between projected and actual inventory levels can still arise. Pickers may have to respond to this. In terms of resource availability, assuming that operational costs remain constant when a resource becomes unavailable (a picker falling ill or a robot breaking down), throughput performance may experience a decline. Consequently, conducting a more in-depth investigation into the interplay of resource availability, inventory discrepancies, and replenishment policies on system performance presents a compelling avenue for future research.
ACKNOWLEDGMENTS
Seyyed Mahdi Ghorashi Khalilabadi and René de Koster acknowledge the support of NWO (grant 439.18.452) and TKI-Dinalog in the project ‘Sharehouse: a living lab for innovating warehousing, logistics education and work’.
Biographies
Kaveh Azadeh is a research scholar at Rotterdam School of Management, Erasmus University, where he obtained a Ph.D. in Supply Chain Management. His research interests include the design, analysis, and optimization of intra-logistic systems focusing on the stochastic modeling and the performance evaluation of various robotized order picking systems. His works have been published in various international journals such as Transportation Science and European Journal of Operations Research.
Debjit Roy is a Professor in the Operations and Decision Sciences area at the Indian Institute of Management Ahmedabad, India. He holds a Ph.D. in Industrial Engineering (with a major in Decision Sciences/Operations Research and a minor in Computer Science) and an MS in Manufacturing Systems Engineering from the University of Wisconsin-Madison besides an M.Sc. (Engineering) from the Indian Institute of Science, Bangalore, India. He is also a visiting professor at the Rotterdam School of Management, Erasmus University, where he is actively involved in both teaching and research in the broad areas of operations and logistics. His research focuses on improving system performance using quantitative methods such as stochastic modeling and optimization. His specific research interests are to estimate the performance of logistical and service systems such as container terminals, automated distribution centers, vehicle rental, and restaurant systems. He has published in several leading international journals such as Operations Research, Transportation Science, Journal of Operations Management, IISE Transactions, and Interfaces.
René de Koster is a professor of Logistics and Operations Management at Rotterdam School of Management, Erasmus University since 1995. He is founder of the Material Handling Forum. He holds a Ph.D. from Eindhoven University of Technology (1988). Currently, he holds guest lecturing positions at four other universities. His research interests are warehousing, material handling, behavioral operations, city distribution, and retail operations. He is author/editor of eight books and over 140 papers in books and academic journals. He is on the editorial boards of 11 journals.
Seyyed Mahdi Ghorashi Khalilabadi is a Ph.D. researcher at the Rotterdam School of Management, Erasmus University. His research focuses on the performance analysis of intra-logistics systems, with a particular emphasis on warehouses and robotized warehousing systems. Using mathematical optimization models and queueing models, he strives to enhance the efficiency and effectiveness of these systems.




