Parameters affecting genome simulation for evaluating genomic selection method
Abstract
The present study investigated the parameter settings for obtaining a simulated genome at steady state of allele frequency (mutation–drift equilibrium) and linkage disequilibrium (LD), and evaluated the impact of whether or not the simulated genome reached steady state of allele frequency and LD on the accuracy of genomic estimated breeding values (GEBVs). After 500 to 50 000 historical generations, the base population and subsequent seven generations were generated as recent populations. The allele frequency distribution of the last generations of the historical population and LD in the base population were calculated when varying the values of five parameters: initial minor allele frequency, mutation rate, effective population size, number of markers and chromosome length. The accuracies of GEBVs in the last generation of the recent population were calculated by genomic best linear unbiased prediction. The number of historical generations required to reach mutation–drift equilibrium depended on the initial allele frequency and mutation rate. Regardless of the parameters, LD reached a steady state before allele frequency distribution reached mutation–drift equilibrium. The accuracies of GEBVs largely reflect the extent of linkage disequilibrium with the exception of varying chromosome length, although there were no associations between the accuracies of GEBVs and allele frequency distribution.
Introduction
Advances in molecular biotechnology are making genome-wide high-density single nucleotide polymorphism (SNP) marker data available for livestock species. These data combined with phenotypic data can be used to calculate genomic estimated breeding values (GEBVs). This method was termed ‘genomic selection’ by Meuwissen et al. (2001). In their method, a Bayesian model is used to estimate thousands of marker effects simultaneously under the assumption that all quantitative trait loci (QTL) are in linkage disequilibrium (LD) with at least one marker. The GEBVs of all genotyped individuals in the population can then be calculated from the sum of all estimated marker effects. The expected advantage of this method over traditional selection methods are more accurate predictive ability (Daetwyler et al. 2008) and the potential to reduce inbreeding rates (Daetwyler et al. 2007; Dekkers 2007). Another approach for evaluating individuals without explicitly estimating marker effects is to estimate genomic relationships between individuals. These genomic relationships are used in the genomic best linear unbiased prediction (GBLUP) procedure, in which genomic relationships replace pedigree-based relationships in traditional BLUP (VanRaden 2008).
Many studies aim to increase the accuracy of GEBV; most use genome data generated by computer simulation. Simulation is a useful tool for assessing the performance of new algorithms and methods in genomic selection at very low cost and allows GEBVs to be compared with true genetic values. Simulations are basically carried out in two steps: (i) a historical population is simulated to reach steady state of allele frequency (mutation–drift equilibrium) and LD; (ii) a recent population is generated mimicking the livestock population, which can have a complex pedigree structure (Sargolzaei & Schenkel 2009). In this process, a large number of historical generations were required to establish a steady state allele frequency and LD. Thus, it is important to reduce a computational requirement by determining appropriate values of parameters for historical populations, such as mutation rate, effective population size and initial allele frequency in the historical generation, in particular when there are many numbers of loci and individuals. In previous simulation studies, there are no common criteria for determining such parameters Therefore, the accuracies of GEBVs obtained in previous studies may be affected not only by the performance of prediction methods, but also by whether or not simulated genome reaches steady state of allele frequency and LD.
The present study investigated the parameters affecting the number of generations in an historical population required to simulate a genome at steady state of allele frequency and LD and evaluated the impact of whether or not simulated genome reached steady state of allele frequency and LD on the accuracy of GEBV. Understanding these relationships will help simulating efficiently and fairly genome data to investigate the accuracy of GEBV. Here, the present study focused on GBLUP as a prediction method of GEBVs because GBLUP has become a popular approach in genomic sequencing (GS) of dairy cattle (McHugh et al. 2011; Wiggans et al. 2011).
Materials and Methods
Simulation data
An historical population was simulated for five numbers of generations (NG = 500, 2000, 5000, 20 000, and 50 000) of random matings with an effective population size (Ne) of 100 (50 males and 50 females). The simulated genome consisted of one chromosome with a length (L) of 1 Morgan, containing 5000 randomly spaced SNP loci. The initial minor allele frequency (IMAF) of all SNPs was assumed to be 0, meaning all individuals were completely homozygous for the same allele in the first generation of the historical population. Mutation occured at a rate (u) of 10−4 per locus meiosis and involved the switching from one allele to another. Recombinations were sampled from a Poisson distribution with a mean of 1 per Morgan and were then randomly placed along the chromosome.
After NG generations, a base population (G0) and the following seven generations (G1 to G7) were generated as the recent population. The size of G0 increased up to 400 (200 males and 200 females). In the following generations, 40 sires were randomly selected and mated to 200 dams in each generation. Each dam had one son and one daughter; thus, each sire had five sons and five daughters.
In G0, the numbers of SNP markers (Nm) and QTL (Nq) were 1000 and 100, respectively. These markers and QTL were randomly chosen from segregating SNP loci with a minor allele frequency > 0.01. The true breeding value was simulated by summing up all true QTL genotypic values, that is,  , where m is the number of QTL; ai is the allele substation effect of the ith QTL; and Wi is 0, 1 or −1 corresponding to heterozygote, major and minor homozygote, respectively (Falconer & Mackay 1996). The allele substitution effects of QTL were drawn from a gamma distribution with a shape parameter of 0.42 and scale parameter of 1 (Meuwissen et al. 2001). The signs of allele substitution effects were drawn at random with equal chance. The total additive genetic variance (
, where m is the number of QTL; ai is the allele substation effect of the ith QTL; and Wi is 0, 1 or −1 corresponding to heterozygote, major and minor homozygote, respectively (Falconer & Mackay 1996). The allele substitution effects of QTL were drawn from a gamma distribution with a shape parameter of 0.42 and scale parameter of 1 (Meuwissen et al. 2001). The signs of allele substitution effects were drawn at random with equal chance. The total additive genetic variance (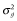 ) was calculated as the sum of variances across all QTL, that is,
) was calculated as the sum of variances across all QTL, that is, 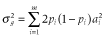 , where pi is the allele frequency at the ith QTL. Trait heritability (h2) was set to 0.3. To obtain phenotypic values, an environmental effect was added to the true breeding value, which was sampled from a normal distribution:
, where pi is the allele frequency at the ith QTL. Trait heritability (h2) was set to 0.3. To obtain phenotypic values, an environmental effect was added to the true breeding value, which was sampled from a normal distribution: 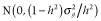 .
.
The simulation process described above was defined as the base scenario (scenario 1). An additional five scenarios (scenarios 2 to 6) were defined using various values of IMAF (0.5), u(5.0 × 10−4), Ne (500), Nm (200) and L (5), respectively (Table 1). In scenario 6, the simulated genome consisted of one chromosome with a length of 5 Morgan, and Nm and Nq were set to 5000 and 500 to obtain the same distances between markers and between QTL in scenario 1. Twenty independent simulations were run for each scenario, resulting in 20 datasets per scenario.
| Parameter | Scenario | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Initial minor allele frequency | 0 | 0.5 | 0 | 0 | 0 | 0 |
| Mutation rate | 10−4 | 10−4 | 5 × 10−4 | 10−4 | 10−4 | 10−4 |
| Effective population size | 100 | 100 | 100 | 500 | 100 | 100 |
| Number of SNP markers | 1000 | 1000 | 1000 | 1000 | 200 | 5000 |
| Chromosome length | 1 | 1 | 1 | 1 | 1 | 5 |
- SNP, single nucleotide polymorphism.
Allele frequency and extent of LD
We calculated distribution of the allele frequency of markers in the last generation of the historical population and the extent of LD in G0. The extent of LD was derived from the mean r2 value which was the pooled square of the correlation between adjacent markers. The present study investigated whether or not allele frequency and LD reached steady state when varying NG.
Model for GEBV
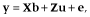
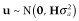 , where
, where 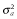 is additive genetic variance and H is the matrix that combines pedigree and genomic relationships. The inverse of H has a simple structure as follows (Aguilar et al. 2010; Christensen & Lund 2010):
is additive genetic variance and H is the matrix that combines pedigree and genomic relationships. The inverse of H has a simple structure as follows (Aguilar et al. 2010; Christensen & Lund 2010):
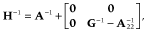

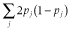 makes G analogous to A. The element of W was calculated as follows:
makes G analogous to A. The element of W was calculated as follows:
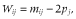
Pedigree information was available for all seven generations in the recent population, and phenotypes and genotypes were available for 1200 individuals each from G4 to G6 and G5 to G7. Thus, the reference population with both phenotypes and genotypes comprised 800 individuals from G5 to G6, and the test population with only genotypes comprised 400 individuals in G7.
Variance components were estimated with average information restricted maximum likelihood (REML) (Johnson & Thompson 1995), and the model solutions yielded GEBVs. The accuracies of the GEBVs in the test population were calculated from the correlations between GEBVs and true breeding values.
Results
Allele frequency distribution
The allele frequency distributions in the last generation of the historical population in scenarios 1 to 4 are shown in Figures 1-4, respectively. In these scenarios, when NG was larger than 20 000, the allele frequency distributions exhibited a U-shaped distribution as in Wright–Fisher mutation–drift equilibrium (Wright 1931). In scenarios 2 and 3, the population reached mutation–drift equilibrium when NG was 2000 and 5000, respectively. Under mutation–drift equilibrium, the allele frequency distributions were similar between scenarios 1 to 4, and the proportions of segregating SNP loci in scenarios 1 and 2 were about 30%, and in scenarios 3 and 4 were about 96%, respectively. For all NG values, the allele frequency distributions in scenarios 5 and 6 were similar to that in scenario 1 (results not shown).
Allele frequency distributions after random matings of 500 (◆), 2000 (■), 5000 (▲), 20 000 (◇), and 50 000 (□) generations in the historical population for scenario 1.
Allele frequency distributions after random matings of 500 (◆), 2000 (■), 5000 (▲), 20 000 (◇), and 50 000 (□) generations in the historical population for scenario 2.
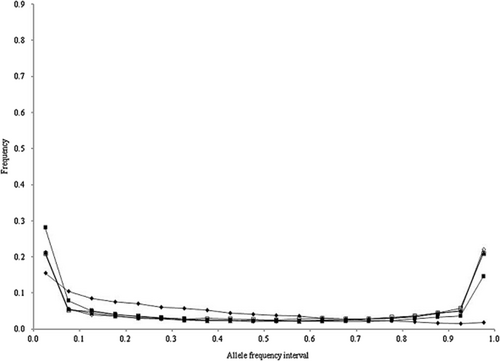
Allele frequency distributions after random matings of 500 (◆), 2000 (■), 5000 (▲), 20 000 (◇), and 50 000 (□) generations in the historical population for scenario 3.
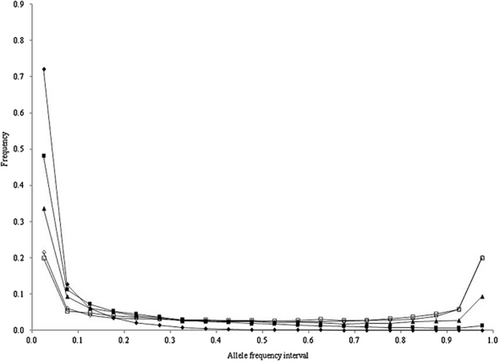
Allele frequency distributions after random matings of 500 (◆), 2000 (■), 5000 (▲), 20 000 (◇), and 50 000 (□) generations in the historical population for scenario 4.
Extent of LD
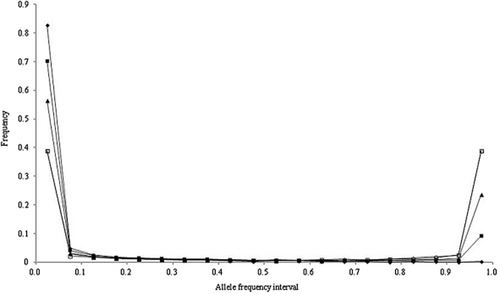
Figure 5 shows LD in the base population in scenarios 1 to 5 except when NG was 50 000. In scenario 2, the LD decreased with increasing NG, whereas the LD increased in the other scenarios. In all scenarios, when NG was 2000, the LD reached a steady state much faster than the allele frequency distributions reached mutation–drift equilibrium. The LD at steady state was approximately 0.13 in scenarios 1 to 3 and approximately 0.09 in scenarios 4 and 5. For all NG values, the LD in scenario 6 was the same as that in scenario 1 (results not shown).
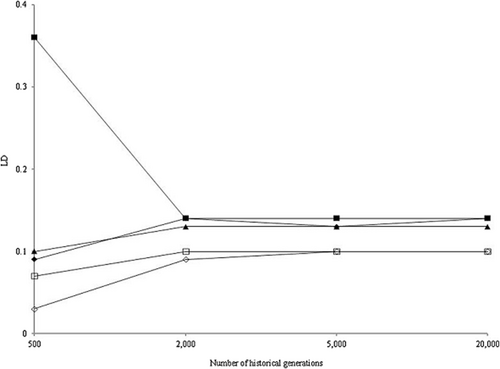
Linkage disequilibrium coefficients (LD) between adjacent marker pairs in base population for scenarios 1 (◆), 2 (■), 3 (▲), 4 (◇), and 5 (□).
GEBV accuracy
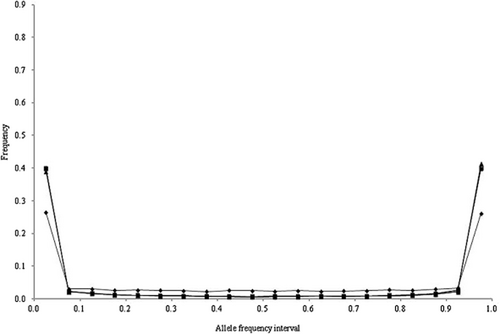
Figure 6 shows the accuracies of GEBVs in all scenarios except when NG was 50 000. In all scenarios, when NG was larger than 2000, the accuracies became constant: approximately 0.79, 0.76 and 0.70 in scenarios 1 to 3, 4 and 5, respectively. These accuracies largely reflected the extents of LD. However, scenario 6 exhibited the lowest accuracy (0.68) while the LD was the same as that in scenario 1. There were no associations between the accuracies and allele frequency distributions.
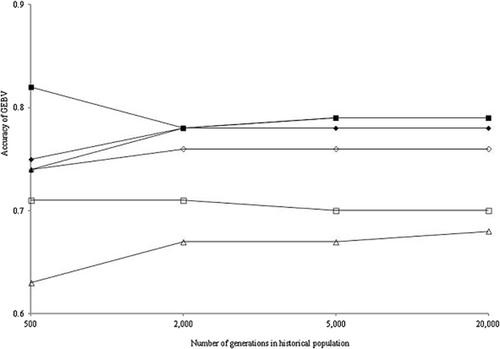
Accuracy of genomic estimated breeding values (GEBVs) in the test population for scenarios 1 (◆), 2 (■), 3 (▲), 4 (◇), 5 (□), and 6 (△).
Discussion
Allele frequency distribution
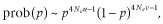
At mutation–drift equilibrium (NG = 20 000 and 50 000), the equal values of 4Neu led to the same distributions of allele frequencies in scenarios 1 and 2, and 3 and 4. However, the NG value required for the approach to mutation–drift equilibrium differed among scenarios. Comparing scenario 1 to 2 shows that when IMAF is equal to the average allele frequency at mutation–drift equilibrium (0.5) instead of fixed (0), the approach to equilibrium is much faster. Because 4Neu is the same value, the allele frequency distributions of scenarios 3 and 4 were similar. However, the allele frequency distribution in scenario 3 reached mutation–drift equilibrium faster than that in scenario 4. The rate of change in allele frequency due to mutation is equal to the total mutation rate (Wright 1949) and is much slower than that due to drift. Therefore, the NG value required for the approach to mutation–drift equilibrium is largely dependent on u.
Extent of LD
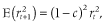
 is the squared correlation of allele frequencies between a pair of markers at time t and c is recombination rate between the markers. When IMAF was 0.5 (scenario 2), the LD decreased with increasing NG as expected according to the formula. In contrast, when IMAF was 0, the LD increased with increasing NG. This may be due to the low minor allele frequency at the small NG. In Nellore cattle data, the mean r2 values decreased with decreasing minor allele frequency under the same distance between markers (Espigolan et al. 2013). However, the relationship between allele frequency and extent of LD is little known on theoretical grounds (VanLiere & Rosenberg 2008).
is the squared correlation of allele frequencies between a pair of markers at time t and c is recombination rate between the markers. When IMAF was 0.5 (scenario 2), the LD decreased with increasing NG as expected according to the formula. In contrast, when IMAF was 0, the LD increased with increasing NG. This may be due to the low minor allele frequency at the small NG. In Nellore cattle data, the mean r2 values decreased with decreasing minor allele frequency under the same distance between markers (Espigolan et al. 2013). However, the relationship between allele frequency and extent of LD is little known on theoretical grounds (VanLiere & Rosenberg 2008).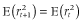 ) using the following formula:
) using the following formula:
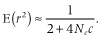
The values of Nec in scenarios 5 and 6 are equal, which led to almost the same LD as that at steady state. The LD at steady state in scenario 4 was lower than that in scenario 3 despite the same allele frequency distributions at mutation–drift equilibrium. These results demonstrate LD is affected by Ne and not u.
GEBV accuracy
LD is the key factor that drives the genomic prediction process (Solberg et al. 2008). This was confirmed by the fact that the curves of LD and accuracy in Figures 5 and 6 are very similar. Thus, using genome data in which LD reaches steady state may be sufficient for evaluating the performance of a prediction method regardless of whether the allele frequency distribution reaches mutation–drift equilibrium.
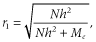
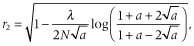
Appropriate setting of parameters
If the allele frequency and LD at steady state are the same, the computational requirements should be reduced, because simulation requires a large amount of calculations. For example, when u = v, IMAF should be 0.5 instead of 0 to quickly reach mutation–drift equilibrium. Although u and Ne equally affect the allele frequency distributions at equilibrium, u should be increased instead of Ne. The computational requirements can also be decreased by decreasing the size (L) of the genome (Hoggart et al. 2007). However, L affects only the accuracy of GEBV regardless of allele frequency and LD. Therefore, predictive methods using genome information in real livestock cannot simply be evaluated from a small simulated genome.
Effect of QTL parameter on GEBV accuracy
Setting of QTL parameters has no relation to whether or not simulated genome reaches steady state of allele frequency and LD, but it may affect GEBV accuracy. Here, the present study investigated the number of QTL, distribution of QTL effects, and location of QTL. The number of QTL was reduced to 20 (Nq = 20). The allele substitution effects of QTL were drawn from a normal distribution. The QTL were evenly spaced across the genome. The GEBV accuracies obtained in these conditions were almost the same as in scenario 1 (data not shown). Daetwyler et al. (2010) indicated that GEBV accuracy might be reduced when Nq was much lower than Me or very small QTL explained a large part of variance.
Further considerations for simulation genome data
The mode of biological action can differ from the assumption of pure additivity. Several studies report that non-additive (e.g. dominance and epistasis) genetic effects significantly contribute to phenotypic variation, especially in fitness and reproductive traits (Crnokrak & Roff 1995; Carlborg et al. 2003; Estelle et al. 2008). Furthermore, copy number variation, a structural variation including deletion, duplication and inversion, was recently identified in various organisms, including humans, yeast and cows (Seroussi et al. 2010). Copy number variation is currently thought to be a potentially major source of heritable variation in complex traits (Redon et al. 2006). The association between these factors and accuracy of GEBV should be investigated in the future.




