Impacts of genotyping strategies on long-term genetic response in genomic selection
Abstract
The present study investigated the effects of the choices of animals of reference populations on long-term responses to genomic selection. Simulated populations comprised 300 individuals and 10 generations of selection practiced for a trait with heritability of 0.1, 0.3 or 0.5. Thirty individuals were randomly selected in the first five generations and selected by estimated breeding values from best linear unbiased prediction (BLUP) and genomic BLUP in the subsequent five generations. The reference populations comprise all animals for all generations (scenario 1), all animals for 6-10 generations (scenario 2) and 2-6 generations (scenario 3), and half of the animals for all generations (scenario 4). For all heritability levels, the genetic gains in generation 10 were similar in scenarios 1 and 2. Among scenarios 2 to 4, the highest genetic gains were obtained in scenario 2, with heritabilities of 0.1 and 0.3 as well as scenario 4 with heritability of 0.5. The inbreeding coefficients in scenarios 1, 2 and 4 were lower than those in BLUP, especially within cases with low heritability. These results indicate an appropriate choice of reference population can improve genetic gain and restrict inbreeding even when the reference population size is limited.
Introduction
Genomic selection uses the associations of genome-wide dense single nucleotide polymorphism (SNP) markers with phenotypes for genomic evaluation in livestock (Meuwissen et al. 2001). The main advantage of genomic selection is the potential to greatly accelerate genetic gain. This is because genomic selection can obtain accurate genomic estimated breeding values (GEBVs) without phenotypes, thus shortening the generation interval (VanRaden et al. 2009; Hayes et al. 2009a). However, these studies focus on the first one or two cycles of selection. Thus, although genomic selection can accelerate short-term gain, such confidence cannot be extended to long-term gain. Muir (2007) and Bastiaansen et al. (2012) report the accuracies of GEBVs when applying selection based on GEBVs during cycles nine and 10 without the addition of new phenotypes to selection candidates. In these studies, the accuracies of GEBVs decreased quickly when the number of generations between the reference population and selection candidates increased. Therefore, in long-term selection, a reference population must be updated, because marker and quantitative trait loci (QTL) alleles will recombine and their frequencies will shift, changing linkage disequilibrium (LD) between them (Jannink 2010).
However, in many livestock populations and some livestock species, creating large reference populations is not very feasible for many traits (Calus 2010; Van Grevenhof et al. 2012). If large reference populations cannot be obtained, genomic selection will reach relatively low accuracies and may yield no or relatively little additional response compared to traditional selection according to estimated breeding values (EBVs) based on phenotypic and pedigree information. Therefore, choosing an appropriate design for the reference population in long-term genomic selection is important when the reference population size is limited.
In this study, we preliminarily determined the reference population size and investigated the impact of the choices of designs for reference populations on long-term responses to genomic selection.
Materials and Methods
Simulation data
A historical population was simulated to establish mutation–drift equilibrium. The simulated genome comprised one chromosome with a length of 3 Morgans containing 10 000 randomly spaced SNP markers and 1000 biallelic QTL. In the first generation of the historical population, the initial allele frequencies of all markers and QTL were assumed to be 0.5. The recurrent mutation process was applied, and the mutation rates of markers and QTL were 5.0 × 10−4 per locus per generation. Recombinations were sampled from a Poisson distribution with a mean of 1 per Morgan and then randomly placed along the chromosome. The historical population evolved over 2000 generations of random mating and random selection with a population size of 500 (250 males and 250 females) to reach mutation–drift equilibrium.
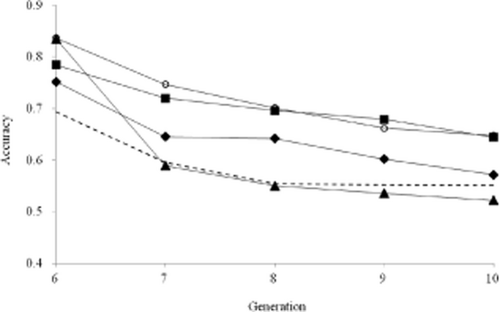
After 2000 historical generations, 30 sires and 30 dams were randomly selected as a base population (G0). In G0, 3000 markers and 150 QTL were randomly selected among the segregating markers and QTL with minor allele frequencies > 0.01, respectively. True breeding values were simulated by summing all true QTL genotypic values as follows: 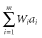 , where m is the number of QTL, ai is the allele substation effect of the ith QTL, and Wi is 0, 1,= or −1 (corresponding to heterozygote, major homozygote and minor homozygote, respectively) (Falconer & Mackay 1996). The allele substitution effects of QTL were drawn from a gamma distribution with shape and scale parameters of 0.42 and 1, respectively (Meuwissen et al. 2001). The signs of allele substitution effects were drawn at random with equal chance. The total additive genetic variance (
, where m is the number of QTL, ai is the allele substation effect of the ith QTL, and Wi is 0, 1,= or −1 (corresponding to heterozygote, major homozygote and minor homozygote, respectively) (Falconer & Mackay 1996). The allele substitution effects of QTL were drawn from a gamma distribution with shape and scale parameters of 0.42 and 1, respectively (Meuwissen et al. 2001). The signs of allele substitution effects were drawn at random with equal chance. The total additive genetic variance (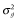 ) was calculated as the sum of variances across all QTL as follows:
) was calculated as the sum of variances across all QTL as follows: 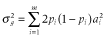 , where pi is the allele frequency at the ith QTL. The heritabilities of the trait (h2) were set to 0.1, 0.3 and 0.5. To obtain phenotypic values, an environmental effect was added to the true breeding value, which was sampled from a normal distribution as follows:
, where pi is the allele frequency at the ith QTL. The heritabilities of the trait (h2) were set to 0.1, 0.3 and 0.5. To obtain phenotypic values, an environmental effect was added to the true breeding value, which was sampled from a normal distribution as follows: 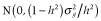 .
.
After G0, the subsequent 10 generations (i.e. G1 to G10) were generated. In G1 to G10, 30 sires and 30 dams were selected. Each sire was randomly mated to one dam with 10 offspring per mating pair. All sires and dams had five sons and five daughters.
Selection scenarios
Parents from G1 to G5 were randomly selected, whereas those from G6 to G10 were selected on the basis of EBVs. In the selection based on GEBVs, we defined four scenarios regarding the choices of designs for reference populations. In scenario 1, the reference population comprised 3000 animals from G1 to G10. In scenarios 2 to 4, the reference population size was 1500, representing a situation in which the reference population size is limited. In scenarios 2 and 3, the reference populations consisted of all animals in G6 to G10 and G2 to G6, respectively. In scenario 4, the reference population consisted of the half of the animals randomly selected from G1 to G10. The numbers of animals in reference populations are shown in Table 1. The present study assumed that selection candidates had phenotypes before selection. Thus, the reference population included all selection candidates in G6 to G10 for scenarios 1 and 2, only 300 animals in G6 for scenario 3, and half of the selection candidates in G6 to G10 for scenario 4.
| Scenario | Generation | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 |
| 2 | 0 | 0 | 0 | 0 | 0 | 300 | 300 | 300 | 300 | 300 |
| 3 | 0 | 300 | 300 | 300 | 300 | 300 | 0 | 0 | 0 | 0 |
| 4 | 150 | 150 | 150 | 150 | 150 | 150 | 150 | 150 | 150 | 150 |
We focused on the accuracies of GEBV, additive genetic variances, genetic gains, and inbreeding coefficients at the start (G6) and end (G10) of genomic selection in order to investigate the performance of long-term genomic selection. The accuracies of the GEBVs for selection candidates were calculated from the correlations between GEBVs and true breeding values. The genetic gains were calculated as the cumulative increases of the average breeding values in each generation. The inbreeding coefficients were calculated following Meuwissen and Luo (1992).
Estimation of genomic breeding values
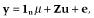
 , where
, where 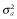 is additive genetic variance and H is the matrix that combines pedigree and genomic relationships. The inverse of H has a simple structure (Aguilar et al. 2010; Christensen & Lund 2010):
is additive genetic variance and H is the matrix that combines pedigree and genomic relationships. The inverse of H has a simple structure (Aguilar et al. 2010; Christensen & Lund 2010):
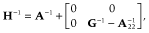
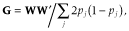
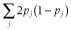 makes G analogous to A. The elements of W were calculated as follows:
makes G analogous to A. The elements of W were calculated as follows:
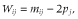
Variance components were estimated with average information restricted maximum likelihood (Johnson & Thompson 1995), and the model solutions yielded GEBVs.
Results
Accuracy of GEBVs
In G6, the accuracies of GEBVs in all scenarios were higher than those of the EBVs from BLUP for all heritability levels (Table 2). The differences in the accuracies between GEBVs and EBVs were larger with lower heritability. The accuracies in scenario 3 were higher than those in scenarios 2 and 4 because of the large reference population size. Although the reference population sizes in G6 were 300 and 900 in scenarios 2 and 4, respectively, the accuracies in scenario 4 were lower than those in scenario 2. In G10, the accuracies in scenario 2 were almost equal to those in scenario 1 and higher than those in scenarios 3 and 4 even though the reference populations were the same size. The accuracies in scenario 3 were the lowest among all scenarios in SGBLUP and lower than those in BLUP with heritabilities of 0.1 and 0.3.
| Heritability | Method | Accuracy | |
|---|---|---|---|
| G6 | G10 | ||
| 0.1 | Scenario 1 | 0.718 ± 0.058 | 0.516 ± 0.105 |
| Scenario 2 | 0.603 ± 0.103 | 0.491 ± 0.115 | |
| Scenario 3 | 0.690 ± 0.066 | 0.339 ± 0.086 | |
| Scenario 4 | 0.581 ± 0.086 | 0.380 ± 0.087 | |
| BLUP | 0.500 ± 0.099 | 0.372 ± 0.088 | |
| 0.3 | Scenario 1 | 0.841 ± 0.019 | 0.620 ± 0.089 |
| Scenario 2 | 0.785 ± 0.017 | 0.644 ± 0.096 | |
| Scenario 3 | 0.835 ± 0.023 | 0.522 ± 0.070 | |
| Scenario 4 | 0.747 ± 0.056 | 0.573 ± 0.070 | |
| BLUP | 0.694 ± 0.021 | 0.551 ± 0.079 | |
| 0.5 | Scenario 1 | 0.877 ± 0.042 | 0.707 ± 0.062 |
| Scenario 2 | 0.840 ± 0.051 | 0.716 ± 0.073 | |
| Scenario 3 | 0.875 ± 0.042 | 0.582 ± 0.064 | |
| Scenario 4 | 0.825 ± 0.056 | 0.640 ± 0.099 | |
| BLUP | 0.755 ± 0.054 | 0.556 ± 0.053 | |
- BLUP, best linear unbiased prediction.
Figure 1 shows the accuracies of GEBVs and EBVs from G6 to G10 when heritability was 0.3. In BLUP, the accuracy of EBVs decreased gradually and became almost constant after G8. The accuracies of GEBVs in all scenarios continued to decrease until G10. The accuracy in scenario 3 decreased sharply in G7, and the accuracy was lower than that in BLUP thereafter.
Accuracies of estimated breeding values (EBVs) with heritability of 0.3 for scenarios 1 (○), 2 (■), 3 (▲), and 4 (◆) and best linear unbiased prediction (BLUP) (dashed line).
Additive genetic variance
The additive genetic variances in G0 were set to 0.1, 0.3 or 0.5; these values decreased to 0.097, 0.273, and 0.434 in G6, respectively (Table 3). In G10, the reductions in additive genetic variances were larger with higher heritabilities in all scenarios. In particular, these reductions were large in scenarios 1 and 2 because of the high accuracies of GEBVs. The magnitude of reduction in scenario 4 was smallest.
| Heritability | Method | Additive genetic variance | |
|---|---|---|---|
| G6 | G10 | ||
| 0.1 | Scenario 1 | 0.097 ± 0.025 | 0.049 ± 0.009 |
| Scenario 2 | 0.049 ± 0.013 | ||
| Scenario 3 | 0.058 ± 0.013 | ||
| Scenario 4 | 0.049 ± 0.016 | ||
| BLUP | 0.061 ± 0.019 | ||
| 0.3 | Scenario 1 | 0.273 ± 0.057 | 0.099 ± 0.036 |
| Scenario 2 | 0.104 ± 0.035 | ||
| Scenario 3 | 0.141 ± 0.025 | ||
| Scenario 4 | 0.130 ± 0.055 | ||
| BLUP | 0.151 ± 0.045 | ||
| 0.5 | Scenario 1 | 0.434 ± 0.122 | 0.121 ± 0.044 |
| Scenario 2 | 0.120 ± 0.055 | ||
| Scenario 3 | 0.159 ± 0.056 | ||
| Scenario 4 | 0.186 ± 0.049 | ||
| BLUP | 0.156 ± 0.040 | ||
- BLUP, best linear unbiased prediction.
Genetic gain
In G6, the genetic gains in all scenarios were proportional to the accuracies of GEBVs (Table 4). In G10, the genetic gains in scenarios 1 and 2 were large for all heritability levels and about 30% larger than that in BLUP with heritability of 0.1. Among all scenarios in SGBLUP, the genetic gain in scenario 4 was smallest with heritability of 0.1 and largest with heritability of 0.5.
| Heritability | Method | Genetic gain | |
|---|---|---|---|
| G6 | G10 | ||
| 0.1 | Scenario 1 | 0.319 ± 0.049 | 1.056 ± 0.144 |
| Scenario 2 | 0.264 ± 0.071 | 1.055 ± 0.146 | |
| Scenario 3 | 0.288 ± 0.065 | 0.841 ± 0.131 | |
| Scenario 4 | 0.237 ± 0.075 | 0.815 ± 0.214 | |
| BLUP | 0.216 ± 0.059 | 0.808 ± 0.155 | |
| 0.3 | Scenario 1 | 0.598 ± 0.076 | 1.982 ± 0.188 |
| Scenario 2 | 0.558 ± 0.086 | 2.018 ± 0.256 | |
| Scenario 3 | 0.597 ± 0.092 | 1.812 ± 0.168 | |
| Scenario 4 | 0.550 ± 0.127 | 1.961 ± 0.297 | |
| BLUP | 0.492 ± 0.072 | 1.864 ± 0.318 | |
| 0.5 | Scenario 1 | 0.799 ± 0.142 | 2.574 ± 0.457 |
| Scenario 2 | 0.770 ± 0.138 | 2.628 ± 0.498 | |
| Scenario 3 | 0.798 ± 0.139 | 2.409 ± 0.551 | |
| Scenario 4 | 0.765 ± 0.107 | 2.664 ± 0.355 | |
| BLUP | 0.712 ± 0.149 | 2.321 ± 0.539 | |
- BLUP, best linear unbiased prediction.
Inbreeding coefficient
In G10, the inbreeding coefficients were highest in BLUP and lowest in scenario 1 for all heritability levels (Table 5). The inbreeding coefficients in all scenarios increased with decreasing heritability. The magnitudes of these increases were large in BLUP and scenario 3. In scenario 4, the inbreeding coefficient was similar to that in BLUP with heritability of 0.5 and lower than that in scenario 3 with heritability of 0.1 or 0.3.
| Heritability | Method | Inbreeding coefficient | |
|---|---|---|---|
| G6 | G10 | ||
| 0.1 | Scenario 1 | 0.037 ± 0.010 | 0.107 ± 0.013 |
| Scenario 2 | 0.123 ± 0.034 | ||
| Scenario 3 | 0.165 ± 0.035 | ||
| Scenario 4 | 0.148 ± 0.029 | ||
| BLUP | 0.217 ± 0.049 | ||
| 0.3 | Scenario 1 | 0.035 ± 0.006 | 0.105 ± 0.020 |
| Scenario 2 | 0.118 ± 0.039 | ||
| Scenario 3 | 0.142 ± 0.044 | ||
| Scenario 4 | 0.132 ± 0.018 | ||
| BLUP | 0.153 ± 0.025 | ||
| 0.5 | Scenario 1 | 0.037 ± 0.007 | 0.104 ± 0.023 |
| Scenario 2 | 0.112 ± 0.016 | ||
| Scenario 3 | 0.117 ± 0.020 | ||
| Scenario 4 | 0.126 ± 0.028 | ||
| BLUP | 0.128 ± 0.019 | ||
- BLUP, best linear unbiased prediction.
Discussion
Effect of the extent of LD between QTL on response to selection
In the present study, the total additive genetic variance was calculated as the sum of variances across all QTL. This calculation requires assumption that all QTL are at complete linkage equilibrium. If LD between QTL exists, the additive genetic variance may be underestimated and this underestimated variance may affect the selection response. Here, we investigated the effect of LD between QTL on responses to selection by varying the number of QTL (Nq). The extent of LD was derived from the mean r2 value which was the pooled square of the correlation between adjacent QTL. The Nq was varied from 150 to 30. The r2 value with Nq of 150 was 0.06 whereas that with Nq of 30 was 0.02. The responses to selection are shown in Table 6. There were no associations between the LD of QTL (or Nq) and the responses to selection.
| Item | G6 | G10 | ||
|---|---|---|---|---|
| Nq = 150 | Nq = 30 | Nq = 150 | Nq = 30 | |
| Accuracy | 0.841 ± 0.019 | 0.830 ± 0.022 | 0.620 ± 0.089 | 0.611 ± 0.098 |
| Additive genetic variance | 0.273 ± 0.057 | 0.279 ± 0.041 | 0.099 ± 0.036 | 0.090 ± 0.030 |
| Genetic gain | 0.598 ± 0.076 | 0.611 ± 0.088 | 1.982 ± 0.188 | 2.012 ± 0.194 |
| Inbreeding coefficient | 0.035 ± 0.006 | 0.036 ± 0.005 | 0.105 ± 0.020 | 0.109 ± 0.021 |
Accuracy of GEBV
In both BLUP and genomic selection, accuracies were low with small additive genetic variances or low heritabilities. In all scenarios, additive genetic variances decreased with passing generations as described below, reducing accuracy. In particular, in the early selection cycle, the reduction of accuracy was large in scenario 3; this is because the reduction of additive genetic variance was large and there was no marker information for animals after the first selection.
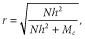
Additive genetic variance

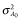 and
and  are the additive genetic variance and accuracy of GEBV before selection, respectively. According to this formula, in G10, the additive genetic variances in scenarios 1 and 2 were small because of the high accuracies of GEBVs. However, when heritability was 0.5, the additive genetic variance was larger in scenario 4 than scenario 3 despite higher accuracy. The prediction formula assumes all candidates for selection have marker information. The accuracies in scenarios 3 and 4 might not be calculable using this formula, because there were candidates without marker information.
are the additive genetic variance and accuracy of GEBV before selection, respectively. According to this formula, in G10, the additive genetic variances in scenarios 1 and 2 were small because of the high accuracies of GEBVs. However, when heritability was 0.5, the additive genetic variance was larger in scenario 4 than scenario 3 despite higher accuracy. The prediction formula assumes all candidates for selection have marker information. The accuracies in scenarios 3 and 4 might not be calculable using this formula, because there were candidates without marker information.Genetic gain
For long-term selection, it is most important to improve genetic gain at the end of selection. In G10, there were no differences in the genetic gains between scenarios 1 and 2 for all heritability levels. When heritability was 0.5, the genetic gain was highest in scenario 4. In scenario 1, the additive genetic variance decreased quickly because of the high accuracy in early selection cycles. This reduction led to the losses of genetic gains in later selection cycles. These results indicate long-term genetic gain can be improved by creating an appropriate design for the reference population that considers the degree of heritability, even if the reference population size is limited.
The present study investigated the response of genomic selection over five generations (i.e. G6 to G10). The accuracies of GEBVs and the additive genetic variances decreased with passing generations. Therefore, the advantages of genetic gains from the four scenarios will change over the course of more than five generations. When considering such long-term selection, the genetic gains from genomic selection can be predicted on the basis of the present results about patterns of accuracies and additive genetic variances.
Inbreeding coefficient
Several simulation studies show that inbreeding coefficients increase with decreasing heritabilities in long-term BLUP selection (Belonsky & Kennedy 1988; Kuhlers & Kennedy 1992; Satoh 2004). In the present study, the same results were obtained when both BLUP and genomic selection were applied. However, genomic selection led to a smaller increase in the inbreeding coefficient with lower heritability. In particular, the results of scenarios 2 to 4 indicate it is desirable to add individuals in later generations of long-term selection to the reference population.
The inbreeding coefficients used in the present study were calculated from pedigree information and describe the probability that two alleles at a randomly chosen locus were identical by descent (IBD). Although this pedigree measure of inbreeding is supposed to capture the genome-wide increase in homozygosity, it may not be the most relevant measure if genetic variance due to a few QTL or selection changes in allele frequencies at specific genome positions (Bastiaansen et al. 2012). Accordingly, Sonesson et al. (2012) recommend genome-based inbreeding coefficients be calculated from the probability of IBD based on both pedigree and marker information when applying genomic selection.
Selection strategy
The present study proposed four scenarios for choices of reference populations with five generations of genomic selection and assumed all candidates for selection were phenotyped before selection. Of course, there are several other options for constructing reference populations. Bastiaansen et al. (2012) compared two designs for reference populations consisting of one and five generations, respectively. Jannink (2010) proposes two phenotyping schemes in which all selection candidates are phenotyped before or after selection. The results of these studies and the present study will aid the selection of an optimum design for reference populations.




