In seasonal frozen soil, freezing and thawing can change the physical and mechanical properties and affect slope stability. There are complex moisture conditions in the main water transfer canal. A study of the hydrothermal evolution of canals with different initial water contents under the action of freezing and thawing is of great importance for the prevention and control of canal slope slides. Hydrothermal coupling models are the key to revealing the canal's hydrothermal evolution. As some of the modeling parameters in the current hydrothermal coupling model are based on empirical values, particularly those in the van Genuchten equation, which are not necessarily related to soil properties, they are not suitable for analyzing the hydrothermal evolution of canals. This paper determines the soil-water characteristic curve from the cumulative curve of particle gradation in the subsoil, and then determines the hydraulic parameters of the subsoil using the VG model, which then corrects the hydrothermal coupling model. The method of modifying the hydrothermal coupling model is original, which makes the model more realistically reflect drainage soil characteristics. During freezing and thawing of channel slopes with different initial water contents (21%, 25%, 29%, 33%, 37%, and 41%), temperature field, water field, and ice content distributions were investigated. Using the V-G model, the optimal parameters for canal subsoil were a = 0.06, n = 1.2, and m = 0.17, and temperature distribution trends between canals with different water contents were basically similar. Water will accumulate at the bottom as the liquid water content increases at the canal boundary.

1 INTRODUCTION

It is known that frozen soil is a special type of soil since it contains ice cement and is defined as soil with a temperature below 0°C (Xu et al., 2001). It is composed of granular skeletons of the soil, void gases, water, and other components of the multiphase system. In accordance with the amount of time spent on frozen soil, it can be divided into two types: permafrost and seasonal frozen soil. The soil that has been frozen for a longer period of time than 2 years is referred to as permafrost, and the soil that freezes during the winter months, then thaws in the summer months is referred to as seasonal frozen soil. About 70% of the global land area is covered by frozen soil, of which 14% is the permafrost and 56% is the seasonal frozen soil. There is a substantial amount of permafrost in China, with about 21.5% of the land area being permafrost, and about 53.5% being seasonal frozen soil (Xu et al., 2001). Heilongjiang Province is a typical seasonally frozen ground regions, but it is also one of the main grain-producing regions in China, the status of the grains as “ballast” is becoming increasingly apparent, and the importance of large-scale water transfer projects to irrigation farmland is becoming increasingly apparent (Gao et al., 2021; Hai et al., 2023; Ling et al., 2009; Wang, Meng, et al., 2018; Wang, Wang, et al., 2018). The Heilongjiang Province has been involved in the construction of many canal projects to accomplish this goal. Such projects include the northern part of the project, the central part of the project, the southern part of the project. As part of the first phase of the Qinglongshan Irrigation District, which irrigates a total area of more than 10,000 hectares, a 15,000 km embankment project has been built. There have been instances of large-scale freeze-thaw landslides on the slopes of the canal projects as a result of freezing and thawing in the cold zone and the complex water environment around the canals (Li et al., 2014, 2015; Wang et al., 2024).

As the canal is being frozen and thawed, the water content will become increasingly complex, and the water content is the key factor that will promote the freezing and expansion of the base soil of the canal during freezing and thawing. There are two types of water in the canal base soil: its own water and foreign water. The foreign water is affected by the rainfall, snowfall, and water table, and the degree of groundwater recharge directly affects the freezing and expansion of the canal base. As well as influencing the degree to which groundwater is recharged, the initial water content affects the degree to which the groundwater freezes and thaws to a great extent, making the study of how the initial water content influences the hydrothermal characteristics of the canal of the law of significance. It is the soil under the canal that is directly responsible for the freeze-thaw hazards found in canals. At the point when soil freezes, a temperature gradient is formed between the cold end of the soil and the warm end of the soil as the outside temperature decreases (Pei et al., 2017; Wang et al., 2022; Wen et al., 2015; Zhang et al., 2020; Zhang, Zhang, et al., 2017). It is important to note that the soil temperature continues to fall, and when it becomes colder than the freezing temperature of the water within the soil, part of the liquid water undergoes a phase change and freezes into ice, and the freezing front moves continuously forward from the cold end to the warm end of the soil. When the temperature gradient is applied to the soil, the unfrozen water will migrate, and the water will carry heat along the way as it migrates toward the freezing front, which will result in a significant change in the thermal parameters of the soil, and all of this will have a profound influence on the temperature field as a consequence (Chang et al., 2023; Fu et al., 2018; Hao et al., 2023; Tianhua & Miao, 2021; Wang, Meng, et al., 2018; Xu et al., 2022; Zhang, Pei, et al., 2017). A large temperature gradient affects the freezing and migration rates of water. As a result, if the temperature gradient is large, the water migration is fast, and therefore, the temperature field and the water field have a coupling relationship that affects each other (Guo et al., 2023; Lai et al., 2017; Liu et al., 2020; Wang et al., 2018; Yan et al., 2023). To gain a better understanding of the process of water-heat migration in frozen soil, many researchers have explored and proposed a number of coupled models for studying the movement of water and heat in frozen soil (Bai et al., 2018, 2022; Li et al., 2023; Pei et al., 2014; Sun et al., 2023). Water migration in unsaturated soils is analogous to water migration in partially frozen soils according to Harlan (1973), in which the soil-water potential is regarded as the primary driver of the migration, and a coupled equation for heat and water migration is proposed in completely frozen soils. Based on Harlan's model, Taylor and Luthin (1978) proposed a coupled equation to explain the flow of water and heat through completely frozen soils. Similarly, Sheppard et al. (1978), Jansson and Halldin (1979), and Fukuda et al. (1980) have also developed similar hydrothermal coupling models based on Harlan's model. Among the three-field coupled models developed by Zhou and Li (2012), the pore ratio of the ice lenticular body must be greater than the separation pore ratio to form ice lenticular bodies. Lai et al. (2014) conducted unilateral freezing experiments on saturated soil in an open system with unpressurized recharge, analyzed the effects of temperature gradient, overburden pressure, and cooling temperature on water migration and freezing, and proposed a coupled hydro-thermal model with temperature, porosity, and drainage as variables. Bai, Lai, et al. (2020) developed the effective strain ratio to establish a relationship between the freeze-up strains of unsaturated soils and their temperature and water fields, and proposed a simplified criterion that would help determine the effective strain ratio. Based on Richard's equation, Bai (2016) calculated the hydraulic conductivity coefficient in Harlan's model, established a new water-heat coupling model, and calculated the process of water-heat migration from a frozen soil roadbed over a period of time. According to Li et al. (2021), a coupled integrated model has been developed that describes temperature change and liquid water and water vapor redistribution in unsaturated frozen soil freezing due to thermodynamics and continuum medium mechanics. According to Lu et al. (2019), 250 published laboratory data and nearly 5 years of field observations were used to evaluate five widely used models of unfrozen water content.

A great deal of research has been carried out on coupled modeling of hydrothermal transport and has resulted in many rich results for many researchers. While the current coupled hydrothermal models are largely based on empirical values, some of the modeling parameters are mostly derived from empirical data. The parameters of the van Genuchten equation have, in particular, not been correlated with the properties of the soil. A model of the hydrothermal evolution of canals can be used to analyze the evolution of canals, but there are limitations to it as well as a need to find out a way to apply the model to an analysis that can truly reflect the evolution of canals based on the hydrothermal process. We have developed a new theory based on the Harlan model and Darcy's law, where the cumulative curve of the particle gradation in the soil and the curve of the soil-water characteristics are very similar in this paper. It is possible to determine the soil-water characteristic curve by using the cumulative curve of particles in the subsoil to determine the particle grade. As the soil-water characteristic curve is fitted to the VG model, the hydraulic characteristics of the subsoil are determined, then a modification is made to the existing hydrothermal coupling model. As part of the canal engineering process in the seasonally frozen ground regions, numerical calculations were also conducted in conjunction with the engineering of the canal to determine how the temperature field, water field, and ice content distribution laws were determined during the freezing and thawing process on the slopes of the canal with different water contents at the start of the freezing and thawing process in the seasonally frozen ground regions (21%, 25%, 29%, 33%, 37%, and 41%) during the freezing and thawing process. An innovation to this part of the study is based on the previous theoretical work, which was able to analyze the multifield interaction mechanism and dynamic coupling process of canal slopes during a freeze-thaw cycle. As a result, it is expected to serve as a reference tool for the prevention of frost damage and canal engineering design.

2 HYDROTHERMAL COUPLING MODEL FOR FROZEN SOIL

2.1 Model assumptions

It is essential to make sure that basic assumptions are established before modeling calculations are performed when dealing with coupled hydrothermal equations, which are fully coupled equations. Assumptions for making the model calculation operable as well as simplifying it while also ensuring the accuracy of the calculation results are as follows:

(1)
The soil particle size is uniform, continuous, and isotropic, and the size of the soil particle is continuous.
(2)
In water migration, water is only in a liquid state and has no other state.
(3)
Earth particles, water, and ice crystals are incompressible, ignoring the pressure thawing of ice particles.
(4)
Water migration and air movement are in accordance with Darcy's law.
(5)
Air within frozen soil is connected to the outside world.
(6)
The effect of salts and mineral ions on water migration is not considered;
(7)
The soil transfers heat through thermal conduction.

2.2 Calculation model of hydrothermal coupling field

A multifield coupling problem refers to a problem consisting of more than one physical field superimposed on each other, and it is increasingly used to solve such problems in engineering by using finite element analysis to simulate the interaction between multiple fields (Bai et al., 2021; Bai, Xu, et al., 2020; Li et al., 2019, 2024; Zhang, Zhang, et al., 2017). A coupled frozen soil water-heat model describes the spatial and temporal evolution laws of the temperature field and the water field during the freezing and thawing of soil using a set of differential equations. Basically, the model consists of three parts: the equations for the water field, the equation for the temperature field, and the equation for the linkage field. According to Fourier's law and the law of energy conservation, it is possible to establish the equation for the temperature field in accordance with the law of conservation of energy. A closed theoretical model of the frozen soil water-heat coupling can be formed by combining Darcy's law with the law of conservation of mass and giving the functional relationship between the ice content and the water content. Finally, the ice content and the temperature can be used together to construct a closed equation representing the water field.

This partial differential equation represents the mathematical model of soil temperature distribution: (Hansson et al., 2004; Harlan, 1973; Tao, 2006).

\rho C(\theta )\frac{\partial T}{\partial t}=\nabla [\lambda (\theta )\nabla T]+L\cdot {\rho }_{i}\frac{\partial {\theta }_{i}}{\partial t},

()

where T is the temperature of the soil, °C; ρ and ρ_i are the density of the soil and the density of ice, respectively, kg/m³; c is the specific heat capacity of the soil, J/(kg·°C); λ is the thermal conductivity of the soil, W/(m·°C); L is the latent heat of change of the phase of the water; θ_i is the amount of ice contained in the soil; where the value of the soil's specific heat capacity, c, and the value of the thermal conductivity of the coefficient λ, and the soil is the state of freezing or thawing related.

When the temperature drops below the freezing point temperature, the free water in the soil freezes, releasing latent heat and causing a volume expansion process in the soil. As a result of the temperature gradient within the freezing rim, water is transported from the unfrozen zone to the freezing front, resulting in a re-distribution of soil water. In light of Richard's equation, which describes the behavior of water during the freezing and thawing processes of soil, and also taking into account the blocking effect that pore ice has on the movement of unfrozen water, the equation for water transport during soil freezing and thawing is (Harlan, 1973; Lu & Likos William, 2012; Taylor & Luthin, 1978):

\frac{\partial {\theta }_{u}}{\partial t}+\frac{{\rho }_{i}}{{\rho }_{w}}\frac{\partial {\theta }_{i}}{\partial t}=\nabla [D({\theta }_{u})\nabla {\theta }_{u}+k({\theta }_{u})],

()

where θ_u is the volume content of unfrozen water in frozen soil; k(θ_u) is the permeability coefficient of soil, m/s; and D(θ_u) is the diffusivity of water in frozen soil, m²/s. The diffusivity of water in frozen soil is calculated as follows:

D({\theta }_{{\rm{u}}})=\frac{k({\theta }_{{\rm{u}}})}{c({\theta }_{{\rm{u}}})}\cdot I,

()

where I is the impedance factor (Harlan, 1973; Lu & Likos William, 2012; Taylor & Luthin, 1978), which represents the retarding effect of pore ice on unfrozen water migration and is calculated by the following equation:

I={10}^{-10{\theta }_{i}}.

()

If we define the relative saturation of frozen soil S as:

S=\frac{{\theta }_{u}-{\theta }_{r}}{{\theta }_{s}-{\theta }_{r}}.

()

Then the permeability of unsaturated soils, specific water capacity can be expressed as (Gardner, 1958; Van Genuchten, 1980):

k({\theta }_{u})={k}_{s}\cdot {S}^{l}{(1-{(1-{S}^{1/m})}^{m})}^{2},

()

c({\theta }_{u})={a}_{0}m/(1-m)\cdot ({\theta }_{s}-{\theta }_{r})\cdot {S}^{1/m}{(1-{S}^{1/m})}^{m},

()

where θ_s and θ_r represent the saturated water content and residual water content of the soil, respectively.

As we can see, Equations (1) and (2) are the two basic equations of hydrothermal coupled migration. Each equation must be solved for three unknown variables (temperature, volume of pore ice, and volume of unfrozen water). In addition, the equations do not have a unique solution, and it is necessary to introduce a linkage equation to resolve the relationship between the unfrozen water content and the temperature. There is a solid–liquid ratio used in this study (the balance between the volume of pore ice and unfrozen water in frozen soil), which is denoted as B_I (Bai, 2016).

{B}_{I}(T)=\frac{{\theta }_{i}}{{\theta }_{u}}=\left\{\begin{array}{ccc}1.1{\left(\displaystyle \frac{T}{{T}_{f}}\right)}^{B}-1.1 & T\lt {T}_{f} & \\ 0 & T\ge {T}_{f} & \end{array}\right.,

()

where T_f is the freezing temperature of the soil; B is the solid–liquid ratio coefficient.

2.3 Verification of the model

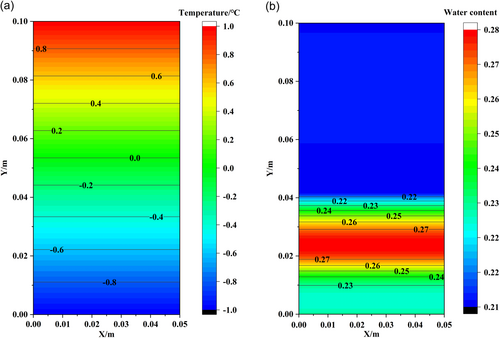
It is the purpose of this paper to examine the validity and reasonableness of the hydrothermal coupling model established above, by comparing the frozen soil column test with the numerical model under the same parameters as Xu et al. (2001), and comparing it with the experimental results of the freezing test under closed conditions. First, a two-dimensional planar soil column model is established (size: diameter of 10 cm, height of 10 cm). It is important to note that when determining the temperature field boundary for the top and bottom of the model, the same constant temperature boundary is used as that used in the test: the upper temperature is set at 1°C, while the lower temperature is set at −1°C, and both sides of the boundary are set as adiabatic boundaries, with the temperature at 1°C as the initial temperature. In connection with the boundary setting of the water field, it was determined that the boundary on each side of the moist field was set at zero flux since the test was a closed condition; the initial water content of the sample was 22.3%, and the calculation time was set to 120 h.

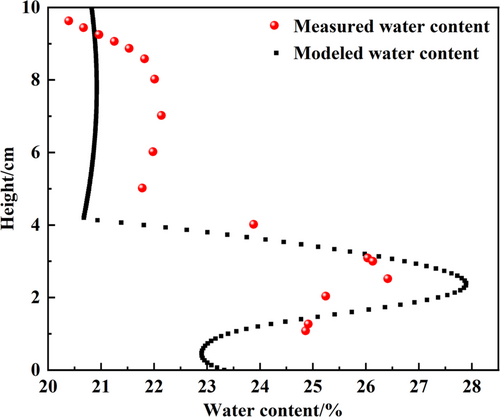
Figure 1 shows the two-dimensional cloud diagram showing the distribution of temperature and total water content along the height of the soil column after 120 h of experimentation. It was necessary to compare the data obtained from the numerical software with the data measured from the test to verify the feasibility of the model based on the data obtained from the numerical software. Figure 2 shows the variation rule of the measured and numerically simulated water content in the specimen along the height of the specimen after the one-way freezing test was performed. As can be seen from the figure, there is a gradual freezing of the whole soil body from the bottom to the top because of the cooling. Liquid water content in the freezing zone is significantly higher than that in the thawing zone, which is a result of the difference in temperature. There is a temperature gradient within the soil body, which creates a suction effect due to the presence of a gradient within the soil body. Due to the driving force of the unfrozen zone, the water from the unfrozen zone migrates towards the bottom frozen zone under the driving force. Furthermore, because of the blocking effect brought about by the ice itself, the unfrozen water, once migrating to the freezing zone, accumulates in large quantities near the freezing interface, which subsequently results in a peak of water content near the freezing peak surface, due to the blocking effect created by the ice itself. It can be concluded that the results of the simulation are largely consistent with those of the experiments, proving to be the validity of the established model of hydrothermal coupling.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Numerical calculation results. (a) Two-dimensional (2D) cloud map of temperature field after 120 h. (b) 2D cloud map of the water field after 120 h.

2.4 A physical method for predicting soil-water characteristic curves based on particle grading curves

Arya et al. proposed a physical empirical model based on particle size distribution and dry soil density of soil as a way to calculate soil-water characteristic curve based on the similarity in shape between soil-water characteristic curve and the cumulative distribution curve of soil particles (Arya & Paris, 1981). To achieve this, there are a few specific steps that need to be followed.

A cumulative particle size distribution curve of the soil was divided into n parts, and according to Equation (9), the pore volume of soil particles at individual grain levels was calculated using the cumulative particle size distribution curve:

{V}_{i}=\frac{{W}_{i}}{{\rho }_{p}}e.

()

This means that V_i if the volume of porous soil per unit of soil particle in class i is taken as the volume of porous soil per unit of soil particle in class i, ρ_p is the mass density of soil particles; W_i is the mass percent of soil particles in class i; and e is the relative porosity of the soil.

According to the following Equation (10) the pore ratio of the soil particles is converted into mass density by the following equation:

e=\frac{{\rho }_{p}-{\rho }_{d}}{{\rho }_{d}},

()

where ρ_d is the dry density of the soil.

If we assume that in this process of water filling the soil gradually fills the large pores from the small pores, Equation (11) then will show the value of the soil water content when the cumulative value of the volumetric water content is added to the soil water content once the soil voids at level i have been filled with water.

{\theta }_{i}=\frac{{\sum }_{n=1}^{n=i}{V}_{n}}{{V}_{b}},

()

where V_b is the unit volume of soil (V_b = 1/ρ_d).

It is also possible to write Equation (11) as (12):

{\theta }_{i}=\sum _{n=1}^{n=i}{V}_{n}\cdot {\rho }_{d}.

()

When soil is filled with water, there will be a water content in the soil of volume θ_i and class i.

To calculate the soil grain size and pore radius, simply follow the equation above, and the void volume water content corresponding to each soil grain level can be calculated, in accordance with the assumed three conditions:

(1)
Assume that the soil particles of all levels are equivalent to spheres, and the equivalent radius is R_i.
(2)
Assume that the voids of soil particles at all levels in the soil can be equated to the same cylindrical capillary structure, where the radius of the cylinder, r_i, is related to R_i.
(3)
Assume that there are certain voids between the soil grains at each level in the soil, which can be regarded as cylinders, and that the length of each cylinder is l_i. Each level of soil grains in the soil consists of n_i equivalent grain sizes R_i.

To calculate the soil grain volume and pore volume of soil class i using the assumptions given above, the following equation can be used.

{V}_{p}=\frac{{n}_{i}4\pi {{R}_{i}}^{3}}{3},

()

{V}_{i}=\pi {{r}_{i}}^{2}{l}_{i}=\frac{{W}_{i}}{{\rho }_{p}}e,

()

Dividing the two equations yields Equation (15):

\frac{{{r}_{i}}^{2}}{{{R}_{i}}^{3}}=\frac{4{n}_{i}e}{3{l}_{i}}.

()

The idealized soil body of level i composed of spherical particles is considered to be composed of n_i2R_i void lengths, however, an empirical parameter of greater than 1 is introduced to correct hi to get Eq for the soil particles with a shape, size, and arrangement that is more restrictive than the shape, size, and arrangement of the soil particles. It can be seen from Equation (16) that the diameter of the void is as follows:

{r}_{i}={R}_{i}{\left[\frac{4e{{n}_{i}}^{1-\alpha }}{6}\right]}^{1/2}=0.816{R}_{i}\sqrt{e{{n}_{i}}^{1-\alpha }}.

()

Substituting Equation (16) into Equation (13) yields Equation (17) for calculating the number of soil particles n_i in class i:

{n}_{i}=\frac{3{W}_{i}}{4\pi {\rho }_{p}{{R}_{i}}^{3}}.

()

A substrate suction head is calculated from Equation (18) below based on the principle of capillary action, which can be expressed as follows:

\frac{{({u}_{\alpha }-{u}_{w})}_{i}}{{\rho }_{w}g}=\frac{2{T}_{s}\,\cos \,\varphi }{{\rho }_{w}g{r}_{i}},

()

where ρ_w is the density of water, kg·m⁻³; T_s is the surface tension of 7.275 × 10⁻² kg s⁻²; φ is the contact angle, and 0 can be taken for soil drainage process.

The corresponding soil-water characteristic curves can be obtained from Equations (12) and (18).

3 ANALYTICAL MODEL OF WATER-HEAT COUPLING IN LARGE-SCALE WATER CONVEYANCE TRUNK CANALS

3.1 Physical parameter values

Taking the red flag trunk canal in the project of attracting tenderness in the northern part of Heilongjiang province as the research object, the height of the canal side slope is 3.76 m and the slope ratio is 1:3 according to the research objective. In the vicinity of the canal side slope, there is a high concentration of clay on the soil.

To avoid the influence of the boundary temperature on the model during the calculation process, 2 m of additional length is taken on each side in the length direction to avoid the influence of the boundary temperature on the model, and 5 m is expanded downward from the bottom in the height direction, as shown in Figure 3. A site plan of the canal slopes is shown in Figure 4.

It is possible to calculate the relationship between matrix suction and water content (volametric water content, saturation) by using the formula of Equations (12) and (18). To fit the soil-water characteristic curve, the V-G empirical formula was chosen by this paper and the optimal parameters for the V-G model were found to be a = 0.06, n = 1.2, and m = 0.17.

We used the literature (Wang, 2019; Xu et al., 2001) to determine the thermodynamic parameters of the soil samples for the calculation, and some of the hydrodynamic parameters were used to calculate the parameters using the literature (Wang, 2019; Xu et al., 2001). The values of these parameters are presented in Table 1 along with the corresponding values of the calculated parameters.

Table 1. Computed parameters.

Parameter	Value	Unit	Parameter	Value	Unit
${C}_{s}$	$0.84\times {10}^{3}$	${\rm{J}}/(\mathrm{kg}\cdot ^\circ {\rm{C}})$	${\rho }_{s}$	$1.8\times {10}^{3}$	$\mathrm{kg}/{{\rm{m}}}^{3}$
${C}_{w}$	$4.180\times {10}^{3}$	${\rm{J}}/(\mathrm{kg}\cdot ^\circ {\rm{C}})$	${\theta }_{s}$	$0.42$	$-$
${C}_{i}$	$2.100\times {10}^{3}$	${\rm{J}}/(\mathrm{kg}\cdot ^\circ {\rm{C}})$	${\theta }_{r}$	$0$	$-$
${\lambda }_{{\rm{s}}}$	$1.10$	${\rm{W}}/({\rm{m}}\cdot ^\circ {\rm{C}})$	${T}_{f}$	$-0.54$	$^\circ {\rm{C}}$
${\lambda }_{w}$	$0.63$	${\rm{W}}/({\rm{m}}\cdot ^\circ {\rm{C}})$	$B$	$0.56$	$-$
${\lambda }_{i}$	$2.31$	${\rm{W}}/({\rm{m}}\cdot ^\circ {\rm{C}})$	${k}_{s}$	$1\times {10}^{-7}$	${\rm{m}}/{\rm{s}}$
$L$	$3.3456\times {10}^{5}$	${\rm{J}}/\mathrm{kg}$	$l$	$0.5$	$-$
${\rho }_{i}$	$0.918\times {10}^{3}$	$\mathrm{kg}/{{\rm{m}}}^{3}$	$a$	$0.06$	$-$
${\rho }_{w}$	$1.000\times {10}^{3}$	$\mathrm{kg}/{{\rm{m}}}^{3}$	$m$	$0.17$	$-$

3.2 Boundary conditions and initial conditions

According to the local average air temperature curve, the temperature change in the study area during the period 2018–2019 is in accordance with that curve, and the change in ground temperatures can also be characterized by applying the following periodic function to the upper surface of the canal slopes using the following equation. The meteorological data for the period of 2018–2019 was fitted with Equation (19). Meteorological data was obtained from the actual monitoring data that was collected in Heilongjiang Province Hydraulic Research Institute on the ground.

T=6.03+17.6\,\sin (\frac{2\pi }{365}t+\frac{\pi }{60}).

()

There is adiabatic boundary between the left and right sides of the model, so the water content of the canal will become more complex during the freezing and thawing process. In the calculation process in this paper, the water loss resulting from external rainfall, snowmelt, and evaporation is not taken into account. The water table is fairly high at the moment, and the water is replenished during the freezing process, so the water is continuously migrating to the freezing front as the water is replenished. As part of the simulation, the water boundary conditions for the canal side slopes are set to the initial water content at the lower surface, with the rest set to zero flux. It is set for the top surface of the canal, the side slopes, and the natural ground surface of the canal to be free boundary surfaces, while the boundary on both sides of the model is set as a horizontal fixed constraint, whereas the lower boundary is set to be a vertical fixed constraint. For the calculation and analysis of the model, it was assumed that the initial temperature of 1°C would be used, and that the initial water content of the canal would be 21%, 25%, 29%, 33%, 37%, and 41% respectively.

3.3 Model verification

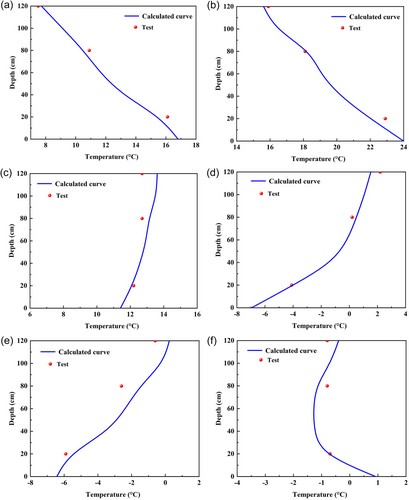
To verify the validity of the canal model, the calculated values were compared to the field monitoring results. As shown in Figure 5. The water field does not have complete measured information, and it is not yet possible to compare the calculated results with the measured results. With the help of the temperature field, the distribution pattern of the water field was indirectly verified. As a whole, the calculated results are very close to the measured results, indicating that the calculation method of the hydrothermal coupling theory can be applied to the calculations.

3.4 Analysis of hydrothermal evolution pattern of large-scale water conveyance trunk canals

3.4.1 The pattern of change in the temperature field

The starting loading time for this calculation starts from 2018 (which is set to be the initial state of the slope), and the changes in the temperature field of the canal slope over a period of 1 year are investigated. Figure 6 gives the distribution of the temperature field for 1 year when the initial water content of the canal is taken as 37%. In response to a gradual increase in the outside temperature, we can expect an increase in the upper surface of the side slope, the shallow layer of soil below 2.5 m of the side slope changes drastically, while the deeper layer is mainly affected by geothermal energy. As can be seen from the figure, the negative temperature began to appear on the 240th day, and after that the temperature continued to decrease, resulting in the soil at the canal's base gradually freezing and eventually reaching the freezing depth that is maximum when the temperature is at its utmost. A freeze-thaw cycle was triggered by a sustained rise in temperature, thawing of frozen soil, and thawing of frozen soil around the 360th day after it had been frozen for a sustained period of time. It is the deeper soil layer that has a high temperature and a gentle curve of change, is less affected by the air temperature than the surface layer, and has less fluctuations in temperature than the surface layer.

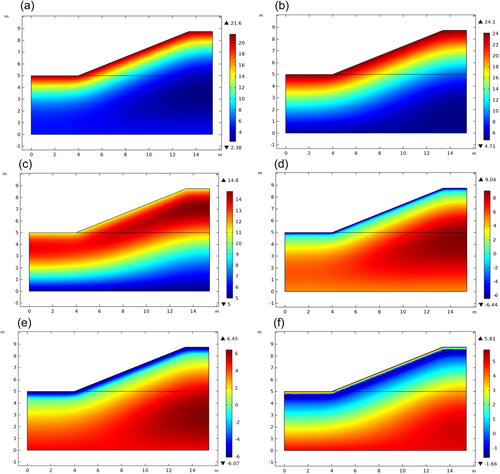
There is an important role for temperature in frost heave studies because it is the primary driving force for water to migrate within the soil and phase into ice, which is what results in frost heave. As the canal is injected with a water content of 21%, 25%, 29%, 33%, 37%, and 41%, Figure 7 shows the distribution of the temperature field for the 300th day. A number of water content canals display the same pattern of temperature distribution, and the temperature gradient of the surface layer of the canal is large, and as one progresses deeper in the canal, the temperature of the canal subsoil becomes less and less affected by the temperature. It is evident from the data that the temperature distribution trend of different water content canals is basically the same.

3.4.2 Patterns of change in the water field

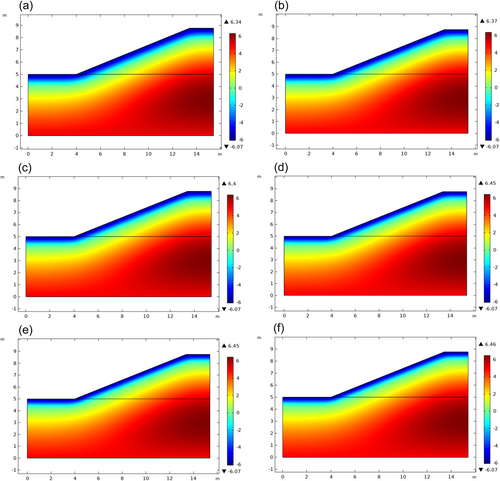
We have studied the change of water content in the slopes of a canal over a period of 1 year. Figure 8 shows the distribution of the water in the slopes of the canal along with the change in the water content over a period of 1 year assuming that the initial water content of the canal slopes was 37%. This figure illustrates that as the temperature decreases, the freezing front moves downwards, causing the water content at the freezing front to increase and increase, as well as the water content in the frozen soil section to increase and increase, so that a suction force will be formed at the freezing front, which will result in the water in the unfrozen area moving to the freezing front as a result, which will result in an increase in the water content of the frozen area. A temperature gradient and a water potential gradient determine the movement of water upward in deeper unfrozen soils. During the ablation period, the frozen layer starts to thaw successively from the upper and lower parts, the temperature rises, the upper frozen soil begins to thaw, and the water is replenished to the groundwater as a result of thawing the upper frozen soil.

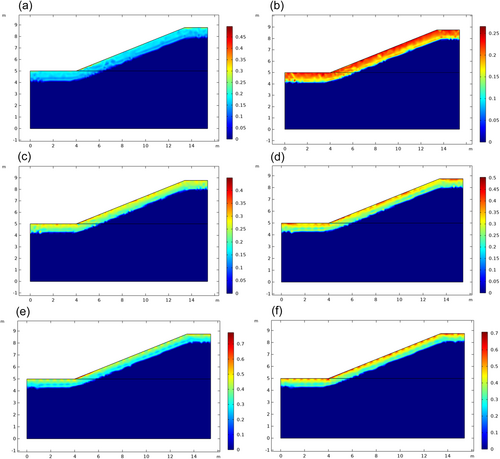
According to Figure 9, the distribution of the water field on the 300th day is shown when the canal takes the initial water content of 21%, 25%, 29%, 33%, 37%, and 41% at the beginning of the 300th day. With the increase of initial water content, it can be seen that when the boundary temperature rises to the soil thawing temperature, the water content at the canal boundary gradually increases, when the initial water content is increased. As the top layer of the frozen soil begins to thaw, the lower part of the soil remains in a frozen state, which means the water cannot seep or can only seep in a small amount, resulting in a large amount of water gathering on the surface of the canal. As the canal slope slopes down, different degrees of water accumulation will happen at the foot of the slope, which is mainly caused by the temperature difference between the slope and the surface at the bottom of the slope.

3.4.3 Canal ice content distribution

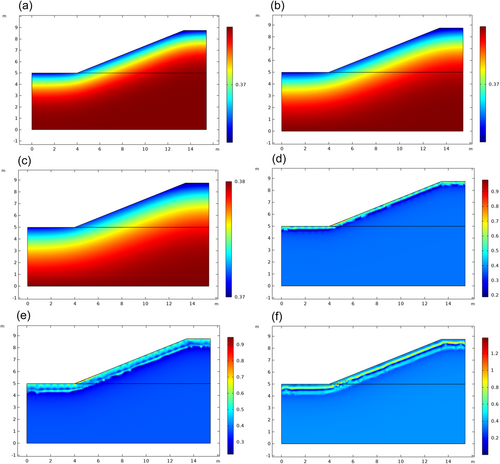
The change in ice content of the canal slopes over a period of 1 year was studied. Figure 10 shows the distribution of ice content in the canal after 1 year when 37% of water is used as the starting point. As a result of soil freezing and thawing, water and ice undergo mutual transformation, releasing and absorbing latent heat through phase change. There can be excessive ice content in the soil as a result of migration and phase change, causing it to freeze and thaw. Frozen soil ice content plays a crucial role in revealing the mechanisms of freeze-thaw damage to canal slopes in seasonally frozen ground regions, and few current studies have been reported, so this paper gives the distribution of ice content in the canal. As can be seen below, solid water does not exist in the soil in a large range below the canal base. In addition, different temperatures cause water to accumulate at the foot of slopes, which is largely due to the temperature difference between the slope and surface. At the foot of the slope, the freezing front stays longer due to the different freezing times, resulting in water migration being more pronounced, and the ice content being greater than other areas.

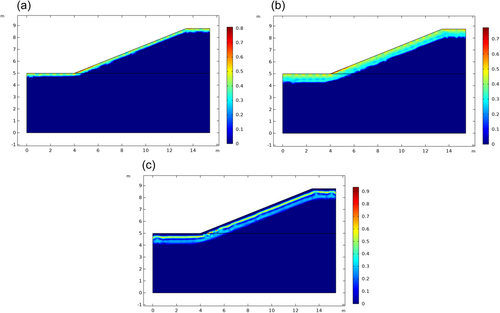
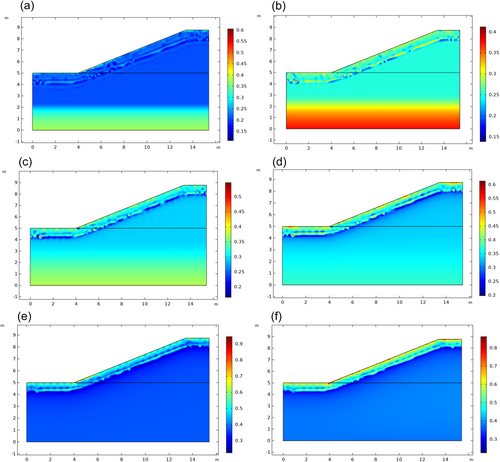
Figure 11 illustrates the distribution of the ice content on the 300th day after the canal takes in the initial water content of 21%, 25%, 29%, 33%, 37%, and 41%. With an increase in the initial water content, the water content at the canal boundary will gradually increase, as will the ice content at the canal boundary, which will also gradually increase as the water content at the canal boundary increases. At the end of the 300th day, it is still in the freezing stage of the canal slopes, and as time goes on, the cold energy within the soil continues to transfer over into ice lenses as it continues to transfer energy. A gradual increase in outside air temperature resulted in a gradual rebound of the slope's upper surface temperature, which then reached the freezing point and began thawing, leaving only a small portion of the internal existence of the ice lenticular body. Eventually, the ice lenticular body will vanish completely.

4 CONCLUSIONS

The initial water content of canals is very important for the change rule of canal hydrothermal characteristics in seasonally frozen ground regions because they will face more complex water content conditions during freezing and thawing. Using the Harlan model and Darcy's law, this paper describes hydrothermal coupling in frozen soil with phase change. A one-dimensional freezing test verifies the validity of the theoretical model. A theoretical model of hydrothermal coupling of frozen soil with phase change is established based on the similarity of the cumulative particle gradation curve to the soil-water characteristic curve of the soil at the canal base. To calculate the soil-water characteristic curve, the cumulative particle gradation curve at the canal base is used. To obtain the hydraulic characteristics parameters of the subsoil, the VG model is fitted to the soil-water characteristic curve, and then the established hydrothermal coupling model is modified to reflect the subsoil's hydrothermal evolution. On top of previous theoretical achievements, this part adds more. The distribution law of temperature field, water field, and ice content generated by phase change during freezing and thawing processes on canal slopes with different initial water contents in a seasonally frozen ground regions (21%, 25%, 29%, 33%, 37%, and 41%) is examined in conjunction with numerical calculations of canal engineering. As a reference for frost damage prevention and canal engineering design, it is expected to be helpful. Here are the main conclusions:

(1)
To derive the soil-water characteristic curve, the cumulative particle gradation curve is used. A soil-water characteristic curve is fitted with the VG model to determine the hydraulic characteristics of the canal foundation soil, and then a modified hydrothermal coupling model is used. The V-G model's optimal parameters are a = 0.06, n = 1.2, m = 0.17.
(2)
The temperature distribution trend of different water content canals is essentially the same as the main driving force for water migration and phase into ice in soil bodies. As the canal depth increases, the influence of the temperature on soil underlying the canal decreases.
(3)
As the temperature decreases, the freezing front advances downward, and water in the lower unfrozen zone continuously migrates to the freezing front as a result of the temperature gradient and various soil water potentials. When the initial water content increases, the water content at the canal boundary increases. Depending on the difference in temperature between the slope and the surface, different degrees of water accumulation will occur at the foot of the canal slope.
(4)
It shows the volumetric distribution of ice content generated by canal phase change. In the freezing stage, a partially frozen soil layer is formed in the shallow upper part of the canal slope, so the volumetric ice content gradually increases. Gradually increasing air temperature led to the gradual recovery of slope upper surface temperature, soil slope temperature reached freezing point and began thawing, only a small portion of the ice lenticular body was left, and eventually it disappeared.

ACKNOWLEDGMENTS

The authors are grateful for financial support from the Heilongjiang Provincial Key Research and Development Program Project (JD2023SJ46); Major Science and Technology Project of Ministry of Water Resources (SKS-2022095); Heilongjiang Provincial Research Institutes Scientific Research Business Fund Project (CZKYF2023-1-A009); General program of China Postdoctoral Fund (2021M690946).

ETHICS STATEMENT

None declared.

Open Research

DATA AVAILABILITY STATEMENT

All data generated or analysed during this study are included in this article.

REFERENCES

Arya, L. M., & Paris, J. F. (1981). A physicoempirical model to predict the soil moisture characteristic from particle-size distribution and bulk density data. Soil Science Society of America Journal, 45(6), 1023–1030.
10.2136/sssaj1981.03615995004500060004x
Web of Science® Google Scholar
Bai, Q. (2016). A preliminary investigation on the calibration of the parameters of the attached surface layer and the numerical simulation method of hydrothermal stability of permafrost roadbed. Beijing Jiaotong University.
Google Scholar
Bai, B., Xu, T., Nie, Q., & Li, P. (2020). Temperature-driven migration of heavy metal Pb2+ along with moisture movement in unsaturated soils. International Journal of Heat and Mass Transfer, 153, 119573.
10.1016/j.ijheatmasstransfer.2020.119573
CAS Web of Science® Google Scholar
Bai, B., Zhou, R., Cai, G., Hu, W., & Yang, G. (2021). Coupled thermo-hydro-mechanical mechanism in view of the soil particle rearrangement of granular thermodynamics. Computers and Geotechnics, 137, 104272.
10.1016/j.compgeo.2021.104272
Web of Science® Google Scholar
Bai, R., Lai, Y., Pei, W., & Zhang, M. (2020). Investigation on frost heave of saturated–unsaturated soils. Acta Geotechnica, 15, 3295–3306.
10.1007/s11440-020-00952-6
Web of Science® Google Scholar
Bai, R., Lai, Y., Pei, W., & Zhang, M. (2022). Study on the frost heave behavior of the freezing unsaturated silty clay. Cold Regions Science and Technology, 197, 103525.
10.1016/j.coldregions.2022.103525
Web of Science® Google Scholar
Bai, R., Lai, Y., Zhang, M., & Gao, J. (2018). Water-vapor-heat behavior in a freezing unsaturated coarse-grained soil with a closed top. Cold Regions Science and Technology, 155, 120–126.
10.1016/j.coldregions.2018.08.007
Web of Science® Google Scholar
Chang, D., Yan, Y., Liu, J., Xu, A., Feng, L., & Zhang, M. (2023). Micro-macroscopic mechanical behavior of frozen sand based on a large-scale direct shear test. Computers and Geotechnics, 159, 105484.
10.1016/j.compgeo.2023.105484
Web of Science® Google Scholar
Fu, Q., Hou, R., Li, T., Jiang, R., Yan, P., Ma, Z., & Zhou, Z. (2018). Effects of soil water and heat relationship under various snow cover during freezing-thawing periods in Songnen Plain, China. Scientific Reports, 8(1), 1325.
10.1038/s41598-018-19467-y
PubMed Web of Science® Google Scholar
Fukuda, M., Orhun, A., & Luthin, J. N. (1980). Experimental studies of coupled heat and moisture transfer in soils during freezing. Cold Regions Science and Technology, 3(2–3), 223–232.
10.1016/0165-232X(80)90028-2
Web of Science® Google Scholar
Gao, K., Liu, Y., Ding, L., Huang, S., Qiu, K., Wang, Z., Yang, Y., Liu, X., & Li, J. (2021). Research on the evolution law of permafrost under the influence of urbanization based on remote sensing technology. Earthquake Engineering and Engineering Vibration, 20, 1007–1019.
10.1007/s11803-021-2065-0
Web of Science® Google Scholar
Gardner, W. R. (1958). Some steady-state solutions of the unsaturated moisture flow equation with application to evaporation from a water table. Soil Science, 85(4), 228–232.
10.1097/00010694-195804000-00006
Google Scholar
Van Genuchten, M. T. (1980). A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Science Society of America Journal, 44(5), 892–898.
10.2136/sssaj1980.03615995004400050002x
Web of Science® Google Scholar
Guo, Z., Xu, X., Wang, Y., Fan, C., Sang, A., Fan, L., Hao, S., & Yan, Z. (2023). Significance analysis of the factors influencing the strength of the frozen soil-structure interface and their interactions in different phase transition zones. Case Studies in Thermal Engineering, 50, 103475.
10.1016/j.csite.2023.103475
Web of Science® Google Scholar
Hai, M., Su, A., Wang, M., Gao, S., Lu, C., Guo, Y., & Xiao, C. (2023). Large-scale freezing and thawing model experiment and analysis of water–heat coupling processes in agricultural soils in cold regions. Water, 16(1), 19.
10.3390/w16010019
Web of Science® Google Scholar
Hansson, K., Simunek, J., Mizoguchi, M., Lundin, L. C., van Genuchten, M. T., Hansson, K., Šimůnek, J., Mizoguchi, M., Lundin, L. C., & van Genuchten, M. T. (2004). Water flow and heat transport in frozen soil: Numerical solution and freeze–thaw applications. Vadose Zone Journal, 3(2), 693–704.
10.2136/vzj2004.0693
Web of Science® Google Scholar
Hao, X., Ma, W., Feng, W., Wen, Z., Zhang, L., & Chen, S. (2023). Investigation on the frost heave-induced pressure and hydro-thermal processes in freezing soil under rigid constraint and hydraulic pressure. Engineering Geology, 323, 107238.
10.1016/j.enggeo.2023.107238
Web of Science® Google Scholar
Harlan, R. L. (1973). Analysis of coupled heat-fluid transport in partially frozen soil. Water Resources Research, 9(5), 1314–1323.
10.1029/WR009i005p01314
Web of Science® Google Scholar
Jansson, P. E., & Halldin, S. (1979). Model for annual water and energy flow in a layered soil. Developments in Agricultural and Managed Forest Ecology, 9, 145–163.
10.1016/B978-0-444-41844-9.50017-2
Google Scholar
Lai, Y., Pei, W., Zhang, M., & Zhou, J. (2014). Study on theory model of hydro-thermal–mechanical interaction process in saturated freezing silty soil. International Journal of Heat and Mass Transfer, 78, 805–819.
10.1016/j.ijheatmasstransfer.2014.07.035
Web of Science® Google Scholar
Lai, Y., Wu, D., & Zhang, M. (2017). Crystallization deformation of a saline soil during freezing and thawing processes. Applied Thermal Engineering, 120, 463–473.
10.1016/j.applthermaleng.2017.04.011
Web of Science® Google Scholar
Li, S., Lai, Y., Pei, W., Zhang, S., & Zhong, H. (2014). Moisture–temperature changes and freeze–thaw hazards on a canal in seasonally frozen regions. Natural Hazards, 72, 287–308.
10.1007/s11069-013-1021-3
Web of Science® Google Scholar
Li, S., Zhang, M., Tian, Y., Pei, W., & Zhong, H. (2015). Experimental and numerical investigations on frost damage mechanism of a canal in cold regions. Cold Regions Science and Technology, 116, 1–11.
10.1016/j.coldregions.2015.03.013
Web of Science® Google Scholar
Li, X., Li, X., Liu, S., & Qi, J. (2023). Thermal-seepage coupled numerical simulation methodology for the artificial ground freezing process. Computers and Geotechnics, 156, 105246.
10.1016/j.compgeo.2023.105246
Web of Science® Google Scholar
Li, Z., Chen, J., Sugimoto, M., & Ge, H. (2019). Numerical simulation model of artificial ground freezing for tunneling under seepage flow conditions. Tunnelling and Underground Space Technology, 92, 103035.
10.1016/j.tust.2019.103035
Web of Science® Google Scholar
Li, Z., Chen, J., Tang, A., & Sugimoto, M. (2021). A novel model of heat-water-air-stress coupling in unsaturated frozen soil. International Journal of Heat and Mass Transfer, 175, 121375.
10.1016/j.ijheatmasstransfer.2021.121375
Web of Science® Google Scholar
Li, Z., Tang, A., & Chen, J. (2024). Hydrothermal interaction properties of unsaturated frozen soil studied using a modified soil freezing characteristic curve. Journal of Cold Regions Engineering, 38(1), 04023023.
10.1061/JCRGEI.CRENG-726
Web of Science® Google Scholar
Ling, X., Zhang, F., Zhu, Z., Ding, L., & Hu, Q. (2009). Field experiment of subgrade vibration induced by passing train in a seasonally frozen region of Daqing. Earthquake Engineering and Engineering Vibration, 8, 149–157.
10.1007/s11803-009-8090-z
Web of Science® Google Scholar
Liu, J., Cui, Y., Liu, X., & Chang, D. (2020). Dynamic characteristics of warm frozen soil under direct shear test-comparison with dynamic triaxial test. Soil Dynamics and Earthquake Engineering, 133, 106114.
10.1016/j.soildyn.2020.106114
Web of Science® Google Scholar
Lu, J., Pei, W., Zhang, X., Bi, J., & Zhao, T. (2019). Evaluation of calculation models for the unfrozen water content of freezing soils. Journal of Hydrology, 575, 976–985.
10.1016/j.jhydrol.2019.05.031
Web of Science® Google Scholar
Lu, N., & Likos William, J. (2012). Unsaturated soil mechanics. Higher Education Press.
Google Scholar
Pei, W., Zhang, M., Lai, Y., Jin, L., & Harbor, J. (2014). Thermal stability analysis of crushed-rock embankments on a slope in permafrost regions. Cold Regions Science and Technology, 106–107, 175–182.
10.1016/j.coldregions.2014.07.005
Web of Science® Google Scholar
Pei, W., Zhang, M., Li, S., Lai, Y., & Jin, L. (2017). Thermo-mechanical stability analysis of cooling embankment with crushed-rock interlayer on a sloping ground in permafrost regions. Applied Thermal Engineering, 125, 1200–1208.
10.1016/j.applthermaleng.2017.07.105
Web of Science® Google Scholar
Sheppard, M. I., Kay, B. D., & Loch, J. P. G. (1978). Development and testing of a computer model for heat and mass flow in freezing soils. Proceedings of the 3rd international conference on permafrost. Edmonton, Alberta.
Google Scholar
Sun, Y., Zhou, S., Meng, S., Wang, M., & Bai, H. (2023). Accumulative plastic strain of freezing–thawing subgrade clay under cyclic loading and its particle swarm optimisation–back-propagation-based prediction model. Cold Regions Science and Technology, 214, 103946.
10.1016/j.coldregions.2023.103946
Web of Science® Google Scholar
Tao, W. (2006). Heat transfer. Northwestern Polytechnical University Press.
Google Scholar
Taylor, G. S., & Luthin, J. N. (1978). A model for coupled heat and moisture transfer during soil freezing. Canadian Geotechnical Journal, 15(4), 548–555.
10.1139/t78-058
Web of Science® Google Scholar
Tianhua, L., & Miao, W. (2021). Experimental research on the development of residual strain in seasonal frozen soil under freezing-thawing and impact type traffic loads. Earthquake Engineering and Engineering Vibration, 20(2), 335–345.
10.1007/s11803-021-2001-3
Web of Science® Google Scholar
Wang, X. (2019). Research on freezing and thawing characteristics of pile-soil system in permafrost zone. Xi'an University of Science and Technology.
Google Scholar
Wang, M., Hai, M., Su, A., Meng, S., Mu, H., & Guo, Y. (2024). Experimental study on the effect of fines content on the frost swelling characteristics of coarse-grained soil in canal base under open system. Journal of Offshore Mechanics and Arctic Engineering, 146(2), 022101.
10.1115/1.4062931
Web of Science® Google Scholar
Wang, M., Meng, S., Sun, Y., & Fu, H. (2018). Shear strength of frozen clay under freezing-thawing cycles using triaxial tests. Earthquake Engineering and Engineering Vibration, 17, 761–769.
10.1007/s11803-018-0474-5
CAS Web of Science® Google Scholar
Wang, Y., Hua, W., Xu, X., Zhang, W., Wang, B., & Ma, B. (2022). Moisture migration in the Qinghai-Tibet silty clay within an added quartz sand layer under one-dimensional freezing. Cold Regions Science and Technology, 202, 103627.
10.1016/j.coldregions.2022.103627
Web of Science® Google Scholar
Wang, Y., Wang, D., Ma, W., Wen, Z., Chen, S., & Xu, X. (2018). Laboratory observation and analysis of frost heave progression in clay from the Qinghai-Tibet Plateau. Applied Thermal Engineering, 131, 381–389.
10.1016/j.applthermaleng.2017.11.052
Web of Science® Google Scholar
Wen, Z., Zhang, M., Ma, W., Wu, Q., Niu, F., Yu, Q., Fan, Z., & Sun, Z. (2015). Thermal–moisture dynamics of embankments with asphalt pavement in permafrost regions of central Tibetan Plateau. European Journal of Environmental and Civil Engineering, 19(4), 387–399.
10.1080/19648189.2014.945043
Web of Science® Google Scholar
Xu, X., Wang, J. C., & Zhang, L. X. (2001). Frozen soil physics. Science Press.
Google Scholar
Xu, X., Zhang, W., & Wang, Y. (2022). Measuring and modeling the dielectric constant of soil during freezing and thawing processes: An application on silty clay. Acta Geotechnica, 17(9), 3867–3886.
Web of Science® Google Scholar
Yan, Y., Chang, D., Liu, J., Xu, A., Zhang, M., & Xie, Y. (2023). Design and validation of a new temperature-controlled large-scale direct shear apparatus. Cold Regions Science and Technology, 216, 103992.
10.1016/j.coldregions.2023.103992
Web of Science® Google Scholar
Zhang, M., Pei, W., Li, S., Lu, J., & Jin, L. (2017). Experimental and numerical analyses of the thermo-mechanical stability of an embankment with shady and sunny slopes in a permafrost region. Applied Thermal Engineering, 127, 1478–1487.
10.1016/j.applthermaleng.2017.08.074
Web of Science® Google Scholar
Zhang, M., Zhang, X., Lai, Y., Lu, J., & Wang, C. (2020). Variations of the temperatures and volumetric unfrozen water contents of fine-grained soils during a freezing–thawing process. Acta Geotechnica, 15, 595–601.
10.1007/s11440-018-0720-z
Web of Science® Google Scholar
Zhang, M., Zhang, X., Li, S., Lu, J., & Pei, W. (2017). Effect of temperature gradients on the frost heave of a saturated silty clay with a water supply. Journal of Cold Regions Engineering, 31(4), 04017011.
10.1061/(ASCE)CR.1943-5495.0000137
Web of Science® Google Scholar
Zhou, J., & Li, D. (2012). Numerical analysis of coupled water, heat and stress in saturated freezing soil. Cold Regions Science and Technology, 72, 43–49.
10.1016/j.coldregions.2011.11.006
Web of Science® Google Scholar

Volume3, Issue2

May 2024

Pages 166-180

Study of hydrothermal characteristics of large-scale water conveyance trunk canals in seasonally frozen ground regions under the influence of different initial water contents

Abstract

1 INTRODUCTION