High valent mercury hydrides (HgH_n=1–8^0,±) are studied using DFT-B3LYP/PBE0 and CCSD(T) methods to analyze their structure, stability, bonding, electronic properties, and electrical characteristics. Molecular orbital calculations reveal a high HOMO–LUMO energy gap of ≈ 7 eV for HgH₂, HgH₄, and HgH₆, while HgH₈ shows a lower energy gap of ≈3 eV. The HgH bond capacitance (ξ^(AB)) values are 1.84, 2.03, 2.09, and 1.52 for HgH₂, HgH₄, HgH₆, and HgH₈, at the PBE0 level. These values are comparable to the CC bond capacitance range (ξ^(AB) = 1.84–2.07), providing evidence for stable high-valent HgH_n with oxidation states ranging from I to VIII. Furthermore, they show a linear response to an external static electric field up to 0.1 a.u., with a gradual decline for higher fields. These observations indicate their possible future detection through molecular beam deflection or the matter-wave interferometry technique.

1 Introduction

The relativistic mass of the electron in the Dirac-Hamiltonian perturbs the orbital energy levels of atoms through mass–velocity contraction, spin-orbit coupling, and Darwin's contract term [1-10]. Consequently, the 6s and 5d atomic orbitals in the mercury (Hg) atom undergo contraction and expansion respectively [11]. Various theoretical methods predicted the participation of 5d¹⁰ shell electrons in chemical bonding with highly electronegative atoms, such as fluorine (F) [12-17]. The involvement of 5d electrons in chemical bonding was recently confirmed in HgF_n^0/± through vibrational spectroscopy [18] and mass spectrometry [19].

The interaction between the Hg and the hydrogen (H) atom offers a unique opportunity to explore the effects of the special theory of relativity on Hg through “sd” hybridization. Quantum chemical calculations predicted the possibility of HgH₄ and HgH₆ with Hg in +IV and VI oxidation states (OS) [20]. However, other molecules in the HgH_n series like HgH₃, HgH₅, HgH₇, and HgH₈ and their corresponding ions remain unexplored. We have systematically investigated HgH_n=1–8^0± for bonding, stability, electronic properties, and electrical characteristics by quantum chemical methods to support their possible detection through molecular beam deflection or matter-wave interferometry technique.

2 Computational Methods

The molecular structure of HgH_n=1–8^0± is optimized using the density functional theory (DFT) based method at B3LYP/PBE0 hybrid electron exchange-correlation functional [21-24] and wave functional theory-based coupled cluster-single-double and perturbative triple [CCSD(T)] level [25]. Atomic natural orbital with relativistic core corrections and quadrupole-ζ plus polarization (ANO-RCC-VQZP) basis set with the following primitive/contracted sets: 25s22p16d12f4g2h/9s8p6d4f2g1h and 14s9p4d3f2g/5s4p3d2f1g is used for Hg [26] and H [27]. The scalar relativistic effects are included through one-electron integrals in ANO basis sets using the X2C (exact two-component) method [28-31]. The spin-orbit coupling (SOC) corrections are not calculated due to their negligible contribution to similar systems, HgX_n (X = F, Cl, Br, I) [32], although SO splitting of 5d orbitals in Hg is 2.052 eV at the Dirac-Fock level [4]. The resolution identity (RI) decomposed two-electron repulsion integrals are stored in Cholesky decomposition (CD) style to reduce the computation time [33, 34]. The vibrational frequency analysis is also carried out within harmonic approximation to identify the nature of minima on the potential energy surface (PES). The stability of HgH_n is determined using the atomization energy, transition state, and the energy gap between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO). The isotropic polarizability and bond capacitance are computed for a range of electric field strengths using the LoProp method. All the calculations are performed using MOLCAS 8.0 [35] and CFOUR 2.1 software [36].

3 Results and Discussion

3.1 Structure of HgH_n

Mercury has a closed shell electronic configuration [Xe] 4f¹⁴ 5d¹⁰ 6s² (¹S₀) and it does not react with molecular hydrogen (H₂; ¹∑_g⁺) in their ground state. The reaction Hg_(g) + H_2(g) → HgH_2(g) is predicted to be endothermic with a high activation energy barrier. However, HgH₂ can form via spin-orbit coupling with a triplet state that correlates to the Hg(³P₁) + H₂ asymptote, resulting in an exothermic reaction. Accordingly, by exciting Hg in its first excited electronic state, HgH and HgH₂ are produced through electronic-to-vibrational (E-V) energy transfer processes in a supersonic molecular beam [37-40]. The reaction proceeds through the following sequence:

\begin{array}{c}\kern0ex {\mathrm{Hg}}_{\left(\mathrm{g}\right)}+H{2}_{(g)}\to H\hbox{-} Hg\hbox{-} {H}_{(g)}\to Hg{H}_{(g)}+{H}_{(g)}\\ {}\kern0ex \end{array}

A stable HgH₂/HgD₂ has also been prepared by the reaction between excited Hg and H₂ gas in H₂/D₂, H₂/Ar, and H₂/N₂ matrices. The product molecules formed are detected and characterized using IR spectroscopy supported by quantum chemical calculations. Moreover, by annealing processes, (HgH₂)₂, (HgH₂)₃, and solid HgH₂ were observed in solid hydrogen in a low-temperature matrix isolation technique [40-43]. The stability of (HgH₂)_n is attributed to the closed shell Hg²⁺–Hg²⁺ mercurophilic interaction that arises from the relativistic effects and other noncovalent dispersive forces [44, 45]. Additionally, gaseous HgH₂/HgD₂ is prepared through the direct gas phase reaction of Hg vapor with H₂/D₂ in an electrical discharge. High-resolution infrared emission spectra reveal a linear covalent HHgH molecule with a HgH bond length of 1.646543 Å and Hg in a typical +II oxidation state [46, 47]. Theoretical calculations predicted a bond length of 1.615–1.713 Å with real frequency values [48-55]. In the past, HgH₄ and HgH₆ have been investigated computationally for high OS by employing DFT-B3LYP, MP2, and CCSD(T) methods [20]. However, structural and spectroscopic data for other members in the HgH_n family and their corresponding ions have not yet been reported. Table 1 lists the computed structural data, symmetry, IR frequency, ionization potential (IP), and electron affinity (EA) of HgH_n=1–8^0,± at the DFT-B3LYP/PBE0 and CCSD(T) levels.

TABLE 1. The HgH equilibrium bond lengths (Å) and symmetry of HgH_n=1–8^0/+ at DFT-B3LYP/PBE0 and CCSD(T) methods.

HgH_n=1–8^0/±	Point group	HgH bond lengths (Å) B3LYP/PBE0/{CCSD(T)}	HHgH bond angle (degree) B3LYP/PBE0/{CCSD(T)}	Harmonic vibrational frequency (cm⁻¹) B3LYP/PBE0/{CCSD(T)}	Ionization energy (eV) B3LYP/PBE0/CCSD(T)	Electron affinity (eV) B3LYP/PBE0/CCSD(T)
HgH	C_∞v	1.776/1.742/1.686		1041/1346/{1606}	8.164/8.022/7.978	1.093/0.904/0.873
HgH⁺	C_∞v	1.607 (1.610)^a/1.600/{1.560} (1.607)^a (1.596)^b {1.594}^b		1753 (1987)^a/1775/{2178} (2028)^b
HgH⁻	C_∞v	2.107/1.981/{1.890}		788/780/{1049}
HgH₂	D_∞h	1.654 (1.653)^a/1.647/{1.604} (1.645)^a {1.639}^b[1.646543]^b	180.00/180.00/{179.99}	1625, 1964, 2070/826, 1954, 2073/{872, 872, 2099, 2246} {799, 1922, 2033}^a [2164, 2023, 821]^b	10.589/10.533/10.795	−0.448/−0.491/−0.603
HgH₂⁺	C_2V	1.713/1.704/{1.667}	148.23/145.92/{179.99}	2 89,1485, 1863/3 12,1 453, 1868/{xxx}
HgH₂^−,	D_∞h	1.658/1.652/{1.609}	180.00/180.00/{179.99}	4 15,1910, 2055/4 73,1908, 2058 {529,529,2028, 2205}
HgH₃	C_2V	1.657, 1.886/1.650, 1.868/{1.671}	92.66,174.67/92.59,174.82/{119.99}	7 41,854, 927,942,1969, 2046/740,863,9 03,918,1963, 2051/{xxx}	6.243/6.213/10.512	2.226/2.357/3.250
HgH₃⁺	C_2V	1.593, 2.075/1.587, 2.025/{1.734}	21.51169.25/22.28168.86/{119.99}	532.539,683,8 64,1944, 3967/539, 569, 6 96,898,2007, 3897 /xxxx
HgH₃⁻	D_3h	1.764/1.752/{1.702}	120.00/120.00/{119.99}	i1465, 332, 637, 1400, 1449, 1540/i2564, 343,646,1478,1496, 1620 {342,342,640,1692, 1692, 1802}
HgH₄	D_4h	1.637(1.641)^a/1.628/{1.592} (1.635)^a	90.00/90.00/{90.00}	503,737,737,8 65,908,1947, 1947, 2089, 2107/677,738,7 39,877,927,1971, 1971, 2089, 2114 {869,869,874,892,921,2142, 2142, 2262, 2262} {764,759,839,884,1959, 2060, 2085}^a	9.870/9.681/11.341	−0.192/−0.236/−0.236
HgH₄⁺	D_2h	1.707/1.701/{1.627}	40.56,139.54/40.03,139.97/{90.00}	i1503, 140, 580, 819, 843,1450, 1754, 1886, 1957 /i1420, 158, 578, 861, 928, 1520, 1793, 1934, 2008 {xxx}
HgH₄⁻	D_4h	1.637/1.628/{1.592}	90.00/90.00/{90.00}	i4348, 616,718,747,792,1823, 1893, 2010, 2043 /i2144, 668,710,743,769,1913, 1915, 2045, 2075/{xxx}
HgH₅	C_4V	1.638, 2.149/1.629, 2.371/{1.616}	89.98, 90.97/90.00, 90.52/{90.00}	i301, i263, 332, 666, 726, 735, 885, 893, 1934, 1939, 2054, 2123/143, 443, 445, 714, 723, 726, 862, 900, 1969, 1970, 1993, 2097 {xxx}	6.474/10.207/9.974	2.381/2.246/2.094
HgH₅⁺	C_2V	1.563, 1.654, 1.967/1.647, 1.541/{1.594}	23.38, 82.38, 85.93/87.30, 89.97/{90.00}	426, 457, 495, 606, 800, 854,907,1148, 1973, 2010, 2183, 3630 /i1048, i1043, 718, 735, 753, 928, 929,1952, 1990, 2013, 2031, 2191/{xxx}
HgH₅⁻	C_4V	1.655, 1.908/1.645, 1.885/{1.632}	88.81, 98.28/88.74, 98.54/{90.00}	26, 586, 625, 626, 671, 686, 689, 1217, 1751, 1810, 1874, 1949/120, 566, 611, 644, 662, 735, 737, 1267, 1760, 1838, 1951, 1989 /{xxx}
HgH₆	O_h	1.632(1.636)^a/1.622/{1.592} (1.635)^a	90.00/90.00/{90.00}	i2522, i1742, 659, 697, 720, 803, 804, 808, 1909, 1941, 1943, 2032, 2065, 2354, 3126 /i3979, i1009, 691,696,698,810,813,823,1923, 1964, 1984, 1991, 2075, 2195, 4425 {757,757,757,830,830,830,2051, 2051, 2051, 2238, 2283, 2283} {695, 755, 810, 1984, 2063, 2090}^a	10.273/10.154/11.694	0.550/0.541/−0.273
HgH₆⁺	D_3d	1.665/1.655/{1.622}	70.51/69.95/{90.00}	i8574, i5921, i322, 360, 387, 608, 609, 667, 723, 1745, 1748, 1777, 1908, 6014, 8571 /i9026, i4127, i423, 320, 353, 598, 606, 671, 731, 1485, 1767, 1775, 1818, 2708, 8222/{xxx}
HgH₆⁻	D_4h	1.629, 1.787/1.637, 1.958/{1.667}	90.00/90.00/{90.00}	i1628, i1541, 513, 527, 527, 573, 720, 720, 7 507 501 395, 1397, 1490, 1849, 2042/435, 435, 574, 637, 664, 664, 677, 686, 686, 952, 1046, 1866, 1880, 1880, 1975/{xxx}
HgH₇	C_2V	1.638, 2.195, 3.613/1.629, 2.417, 3.236/{1.715}	11.79, 85.01, 90.00, 90.83/13.23, 84.93, 90.04, 90.40/{45.00}	58, 98, 105, 151, 267, 281, 292, 296, 706 714, 727, 798, 854,1940, 1940,2042, 4412, 11358/92, 94, 98, 148, 179, 206, 300, 308, 725, 726 760, 858, 875,1960, 1961, 2079, 4387, 11049/{xxx}	9.301/9.109/NC	2.375/2.226/2.353
HgH₇⁺	C₂	1.552, 1.650, 1.654, 1.952/1.547, 1.641, 1.643, 1.909/{NC}	23.64, 86.61, 86.96, 91.65/24.62, 86.01, 86.80, 90.24/{NC}	i3868, i263, i190, 389, 622, 749, 778, 840, 860, 900, 1158, 1323, 1936, 1963, 2015, 2229, 3553, 5593 /i166, i107, 163, 486, 515, 747, 756, 851, 860, 968, 1192, 1292, 1947, 1969, 1974, 2272, 3472, 5151/{NC}
HgH₇⁻	C_2V	1.656, 1.908, 4.542/1.645, 1.884, 4.307/{1.786}	9.36, 78.31, 88.78, 98.39/9.91, 77.91, 84.91, 98.61/{44.99}	i1237, i239, i180, 48, 59, 81, 542, 587, 594, 668, 674, 679, 1215, 1752, 1754, 1868, 4421, 7587/ i1030, i262, i127, i106, 58, 105, 551, 566, 583, 663, 667, 672, 1266, 1758, 1759, 1895, 4405, 7730/{xxx}
HgH₈	D_8h	1.997/1.982/{1.795}	45.00/45.00/{44.99}	i2256, i2256, i1437, i1436, i1273, i637, i634, i532, i530, i245, 623, 623, 966, 968, 1034, 1039, 1039, 1195, 1195, 1319, 1620 /i2286, i2285, i1410, i1409, i1209, i632, i633, i571, i570, i248, 712, 713, 978, 985, 1057, 1083, 1083, 1248, 1257, 1367, 1679/{xxx}	−2.944/−2.466/xxx	xx/xx/3.099
HgH₈⁺	D_2h	2.701/2.652/{1.743}	15.99, 74.01/16.37, 73.62/{44.99}	i1371, i443, i120, i108, i106, i60, i19, 43, 81, 125, 192, 239, 289, 293, 323, 703, 1124, 4252, 4258, 4258, 4278 /i3354, i468, i115, i109, i55, i45, i15, 58, 100, 124, 229, 247, 295, 317, 346, 600, 3331, 4234, 4234, 4250, 4252//{xxx}
HgH₈⁻	Cs	NC/NC/{1.843}	NC/NC/{44.99}	NC/NC/{xxx}

Abbreviations: NC, geometry not converged; xxx, not attempted.
^a Reference [20].
^b Reference [41].

3.1.1 HgH

HgH is a linear molecule with C_∞v symmetry and shows an equilibrium bond length (r_e) of 1.776/1.742/1.686 Å at B3LYP/PBE0/CCSD(T) levels. The r_e value calculated at the B3LYP level agrees with the experimental value (1.776 Å) [37] and earlier reported theoretical values (1.790, 1.796 Å) at the same level of theory [38, 44]. The HgH⁺ ion shows shortened r_e of 1.607/1.600/1.560 Å and agrees with the experimental value (1.594 Å) [42] and also the reported theoretical values (1.610/1.579/1.607 Å) [20] at the B3LYP/MP2/CCSD(T) levels with an IP of 8.164/8.022/7.978 eV. While its negative ion (HgH⁻) shows elongated r_e of 2.107/1.981/1.890 Å with a positive EA value of 1.093/0.904/0.873 eV, indicating that the anion is more stable than neutral. The molecule shows a frequency of 1041/1346/1606 cm⁻¹ with intensity of 94/113/107 km mol⁻¹. The computed zero-point vibrational energy (ZPVE) is 520/673/803 cm⁻¹. The molecule and the ions show real frequency values, indicating they are stable species.

3.1.2 HgH₂

HgH₂ is a linear molecule with D_∞h symmetry and shows r_e of 1.654/1.647/1.604 Å at B3LYP/PBE0/CCSD(T) levels and is in agreement with the earlier reported values at different levels of theory viz., 1.656/1.617/1.641 Å at B3LYP/MP2/(CCSD(T)) levels [20, 42-46]. The cation shows a bend geometry with C_2V symmetry and slightly elongated r_e of 1.713/1.704/1.667 Å and ∠HHgH = 148.23/145.92⁰ at B3LYP/PBE0 level while (CCSD(T)) shows linear structure with an angle of 180°. The anion also shows a linear structure with r_e of 1.658/1.652/1.609 Å. The linear HgH₂ shows 3N-5° of freedom and shows 4 normal modes of vibration with A₁, B₁, B₂, and A₁ irreducible notation. All the modes show real frequency and are IR active except 1A₁. Among the three IR active modes, B₂ shows a high IR frequency of 1964/1954/2099 cm⁻¹ with an intensity of 434/411/373 km mol⁻¹ and ZPVE of 2829/2427/2608 cm⁻¹. The HgH₂^0/± systems show real frequency values indicating they are stable on the PES. The molecules show an IP of 10.589/10.533/10.795 eV and an EA of −0.448/−0.491/−0.603 eV. The negative EA value indicates that the anion is less stable than the neutral molecule.

3.1.3 HgH₃

HgH₃ exhibits T-shaped trigonal planar geometry with C_2v symmetry and shows two distinct types of bonds with r_e of 1.657, 1.886/1.650, 1.868 Å along with ∠H₁HgH₂ = 174.67/174.82° and ∠H₂HgH₃ = 92.66/92.59° at the B3LYP/PBE0 level. In contrast, the CCSD(T) method shows an equal bond length of 1.671 Å with ∠HHgH = 120°. The cation shows a short HgH of r_e 1.593/1.587 Å and a long HgH of r_e of, 2.075/2.025 Å along with reduced bond angles at B3LYP/PBE0 level and it exists as HgH⁺ and H₂. The CCSD(T) method shows elongated r_e of 1.734 Å and ∠HHgH = 120° and it exists as HgH₃⁺. The anion shows slightly elongated r_e of 1.764/1.752/1.702 Å and ∠HHgH = 120° at all levels of theory. The degrees of freedom for non-linear HgH₃ are calculated using the formula 3N-6. Accordingly, HgH₃ shows 6 normal vibration modes with A′₁, A′₂, E′, A″₁, A″₂, E″ irreducible representation in the point group symmetry with IR active E′ and A″₂ modes. All the vibrational modes show a real frequency. The IR frequency for an active mode A″₂ is 1969/1963 cm⁻¹ with an intensity of 407/391 km mol⁻¹. The ZPVE is computed to be 3740/3720 cm⁻¹. The positive ion shows real frequency while the negative ion shows one imaginary frequency, indicating a stable cation and unstable anion. Both B3LYP/PBE0 levels show a low IP of 6.243/6.213 eV and EA of 2.226/2.357 eV while CCSD(T) calculations show a high IP of 10.512 eV and high EA of 3.250 eV. The relatively high EA suggests that HgH₃ is stabilized by electron capture and supports the existence of OS III in HgH₃ (5d⁹), however, it is vibrationally unstable except at the CCSD(T) level.

3.1.4 HgH₄

HgH₄ is a square planar molecule with D_4h symmetry and shows r_e of 1.637/1.628/1.592 Å at B3LYP/PBE0/CCSD(T) levels along with ∠HHgH = 90°. The r_e values agree with the reported values, 1.641/1.618/1.635 Å, and ∠HHgH = 90° at B3LYP/MP2/CCSD(T) levels [20]. The cation displays an elongated r_e of 1.707/1.701 Å and shows a decrease in bond angles and the formation of 2H₂ molecules at the B3LYP/PBE0 level, while CCSD(T) shows intact HgH₄⁺ with r_e of 1.627 Å. The anion shows the same bond lengths and bond angles as the neutral molecule. HgH₄ shows 9 normal vibration modes with 2E_u, 1A_2u, 1B_1g, 1B_1u, 2E_u, 1A_1g, 1B_2g irreducible notation in the point group symmetry. All the normal modes show real frequency but are IR inactive except the E_u modes. The IR active E_u modes show a frequency of 2089/2089/2142 cm⁻¹ with an intensity of 354/337/324 km mol⁻¹. The computed ZPVE is 5921/6051/6634 cm⁻¹, evidencing vibrationally stable HgH₄ with Hg⁴⁺(5d⁸) OS while its ions show one imaginary frequency, indicating they are not a stable minimum on the PES. An IP of 9.870/9.681/11.341 eV and an EA of −0.192/−0.236/−0.236 eV is calculated for HgH₄. The negative EA also indicates that the anion is less stable than the neutral molecule.

3.1.5 HgH₅

HgH₅ exhibits square pyramidal geometry with C_4v symmetry and displays two different types of bonds with r_e of 1.638, 2.149/1.629, 2.371 Å along with ∠H₁HgH₂ = 90.97/90.52°, ∠H₃HgH₄ = 89.98/90.00°, and ∠H₅HgH₆ = 89.98/90.00° at the B3YLP/PBE0 level. It exists as an HgH₄…H complex with a large re of 2.149/2.371 Å rather than an HgH₅ molecule. In contrast, the CCSD(T) shows an equal r_e of 1.616 Å for all bonds with ∠HHgH = 90° suggesting HgH₅ exists as a molecule. The cation shows three unequal HgH bonds with r_e of 1.563, 1.654, 1.967 Å at the B3LYP level and PBE0 shows two unequal bonds with r_e of 1.647, 1.541 while CCSD(T) shows r_e of 1.594 Å. The anion shows two unequal bonds with r_e of 1.655, 1.908/1.645, 1.885 Å at B3LYP/PBE0 levels while CCSD(T) shows r_e of 1.594 Å. The IR frequencies for the vibrational modes computed at the B3LYP level show one imaginary frequency while PBE0 shows real frequency. The positive ion shows the real frequency at the B3LYP level and an imaginary frequency at the PBE0 level. The negative ion shows real frequency at both levels of theory. An IP of 6.474/10.207/9.974 eV and an EA of 2.381/2.246/2.094 eV have been noted for HgH₅. The positive EA value indicates that the HgH₄…H complex is further stabilized through electron capture processes.

3.1.6 HgH₆

HgH₆ shows octahedral geometry with Oh symmetry and r_e of 1.632/1.622/1.592 Å along with ∠HHgH = 90° at the B3LYP/PBE0/CCSD(T) levels, which is in agreement with the reported r_e values of 1.636/1.619/1.635 Å at B3LYP/MP2/CCSD(T) levels [20]. The cation shows slightly elongated r_e of 1.665/1.655/1.622 Å while the anion shows unequal r_e of 1.629, 1.787/1.637, 1.958 Å at the B3LYP/PBE0 level and the CCSD(T) level shows equal r_e of 1.667 Å for all bonds. It has 15 normal modes, viz., 3A_1u, 3T_2u, 3T_2g, 3T_1u, 2E_g, 1A_1g irreducible representation in the point group symmetry. The 3A_1u degenerate modes show zero/imaginary vibrational frequency, while the rest of the 9 normal modes show real frequency but are IR inactive. The IR active T_1u mode shows a high IR frequency of 2032/2075/2051 cm⁻¹ with an intensity of 55/63/25 km mol⁻¹. The zero-point vibrational energy is computed to be 9602/10545/8859 cm⁻¹. Thus, it evidences a vibrationally stable HgH₆ with Hg⁶⁺(5d⁶) OS while its ions show three/two imaginary frequencies, indicating they are unstable on the PES. An IP of 10.273/10.154/11.694 eV and an EA of 0.550/0.541/−0.273 eV is computed for HgH₆. The low/negative EA evidence that the anion is marginally/less stable than the neutral.

3.1.7 HgH₇

HgH₇ exhibits capped trigonal prismatic molecular geometry with C_2V symmetry. It shows three different types of bonds with the r_e of 1.638, 2.195, 3.613/1.629, 2.417, 3.236 Å along with ∠H_1,2HgH_3,4 = 90.00/90.04°, ∠H₅HgH₆ = 90.83/90.40°, and ∠H₇HgH₈ = 11.79/13.23° at B3LYP/PBE0 level whilst CCSD(T) shows an equal r_e of 1.715 Å with ∠HHgH = 45°. The long r_e value at the B3LYP/PBE0 levels suggests that HgH₇ is a complex formed between HgH₄, H, and H₂. The cation shows unequal r_e of 1.552, 1.650, 1.654, 1.952/1.547, 1.641, 1.643, 1.909 Å at the B3LYP/PBE0 level whilst CCSD(T) shows no convergence. The anion shows an unequal r_e of 1.656, 1.908, 4.542/1.645, 1.884, 4.307 Å at the B3LYP/PBE0 level whilst CCSD(T) shows an equal r_e of 1.786 Å for all bonds. The long bond lengths at the B3LYP/PBE0 suggest that anion is also complex formed between HgH₄^0/−, H^−/0, and H₂. The HgH₇ complex shows real frequency while its ions show imaginary frequency due to their unstable nature. An IP of 9.301/9.109/X eV and an EA of 2.375/2.226/2.353 eV is computed for HgH₇. The relatively high EA indicates that the complex is stabilized more by an electron capture process similar to HgH₅.

3.1.8 HgH₈

HgH₈ exhibits dodecahedral geometry with D_8h symmetry and r_e of 1.997/1.981/1.795 Å along with ∠HHgH = 45° at the B3LYP/PBE0/CCSD(T) levels suggesting that HgH₈ is a molecule with Hg⁸⁺(5d⁴) OS. The removal of an electron results in Hg⁺…4H₂ complex with a large r_e of 2.701/2.652 Å with negative IP of −2.944/−2.466 eV at the B3LYP/PBE0 level. However, the CCSD(T) level shows a r_e of 1.743 Å for all bonds indicating it is a stable ion. The negative ion is not converged but it exists as a complex of HgH₄⁻…2H₂ moieties at the B3LYP/PBE0 level while the CCSD(T) shows a bond length of 1.843 Å and EA of 3.099 eV. It has 21 normal modes, out of which 10 out of plane angle modes show imaginary frequency and the rest display real frequency. Among the 14 irreducible representations for the D_8h symmetry point group viz., A_1g, A_2g, B_1g, B_2g, E_1g, E_2g, E_3g, A_1u, A_2u, B_1u, B_2u, E_1u, E_2u, E_3u only A_2u and E_1u are IR active. The IR active E_1u mode shows a high IR frequency of 1039/1083 cm⁻¹ with an intensity of 718/739 km mol⁻¹ and zero-point vibrational energy 5802/6082 cm⁻¹ at the B3LYP/PBE0 level.

3.2 Stability of HgH_n_=1–8

The high valent HgH_n molecules are not the global minima but are local minima with a small well depth on the PES. To evaluate their stability, the atomization and the dissociation energy for H₂ dissociation channels are calculated and are listed in Table 2.

TABLE 2. Dissociation channels and dissociation energy (eV) of HgH_n=1–8 computed at DFT-B3LYP/PBE0/CCSD(T) levels.

Molecule	Dissociation channels	Dissociation energy (eV)
Molecule	Dissociation channels	B3LYP/PBE0/CCSD(T)
HgH	Hg + H	0.553/0.543/0.955
HgH₂	Hg + 2H	3.958/3.890/5.019
	Hg + H₂	−0.958/−0.710/0.290
	HgH + H	3.404/3.347/4.065
HgH₃	Hg + 3H Hg + H₂ + H HgH + H₂ HgH₂ + H	3.984/4.045/4.466 −0.737/−0.555/−0.264 −1.290/−1.098/−1.218 0.222/0.155/−0.554
HgH₄	Hg + 4H Hg + 2H₂ HgH + H₂ + H HgH₂ + H₂ HgH₃+ H	6.919/6.726/9.047 −2.913/−2.474/−0.412 1.450/1.583/3.362 −1.954(−2.073a/−1.763/−0.702) 2.740/2.681/4.581
HgH₅	Hg + 5H Hg + 2H₂ + H HgH +2H₂ HgH₂ + H₂ + H HgH₃ + H₂ HgH₄ + H	7.035/6.792/9.375 −2.797/−2.408/−0.085 −3.351/−2.951/−1.039 −1.838/−1.700/−0.374 −2.060/−1.853/0.179 0.116/0.066/0.328
HgH₆	Hg + 6H Hg + 3H₂ HgH + 2H₂ + H HgH₂ + 2H₂ HgH₃ + H₂ + H HgH₄ + H₂ HgH₅ + H	9.338/9.020/12.595 −5.411/−4.780/−1.594 −1.048/−0.723/2.181 −4.452/−4.070/−1.884 0.242/0.375/3.399 −2.498/−2.306/1.181 2.302/2.228/3.220
HgH₇	Hg + 7H Hg + 3H₂ + H HgH + 3H₂ HgH₂ + 2H₂ + H HgH₃ + 2H₂ HgH₄ + H₂ + H HgH₅ + H₂ HgH₆ + H	11.951/11.410/4.162 −2.797/−2.390/−10.027 −3.351/−2.933/−10.981 −1.839/−1.680/−10.316 2.061/1.835/−9.763 0.116/0.084/−9.614 0.000/0.018/−9.942 2.614/2.390/−8.433
HgH₈	Hg + 8H Hg + 4H₂ HgH + 3H₂ + H HgH₂ + 3H₂ HgH₃ + 2H₂ + H HgH₄ + 2H₂ HgH₅ + H₂ + H HgH₆ + H₂	6.918/6.484/4.034 −12.747/−11.916/−14.885 −8.384/−7.859/−11.110 −11.788/−11.206/−15.175 −7.094/−6.761/−9.891 −9.834/−9.443/−14.472 −5.034/−4.908/−10.070 −5.099/−4.943/−13.291

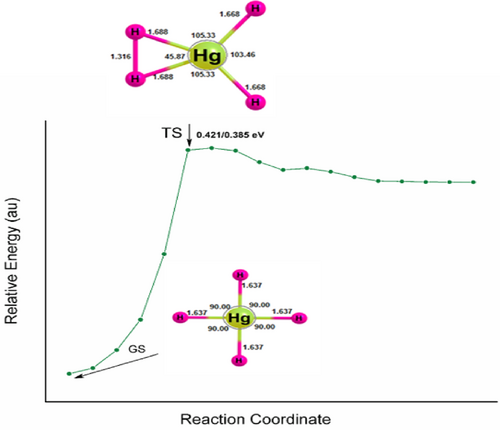
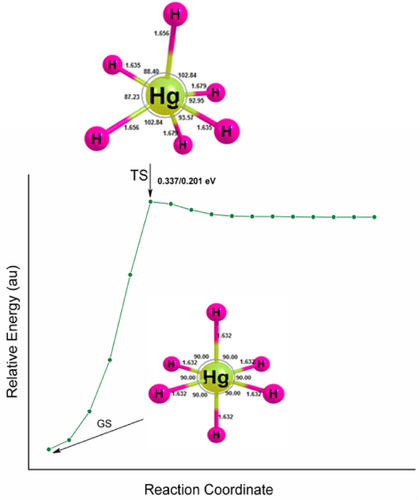
The unimolecular dissociation of hydrogen-rich mercury hydride is unstable for two-body dissociation channels, HgH₂ + nH₂. However, they are stable with positive dissociation energy for H atom reactions, and the atomization energy increases systematically and reaches a maximum for HgH₇ and drops for HgH₈. It indicates that they are meta-stable and can survive if the transition state (TS) barrier is sufficiently high on the PES for its preparation and identification by low-temperature matrix isolation or supersonic molecular beam techniques. Therefore, the TS of HgH₃, HgH₄, and HgH₆ are computed and are given in Figures 1-3. The ZPVE corrected values are 0.056/0.058, 0.421/0385, and 0.337/0.201 eV for HgH₃, HgH₄, and HgH₆ at the B3LYP/PBE0 levels. A TS with barrier heights of 0.404 and 0.311 eV for HgH₄ and HgH₆ has been reported earlier at the B3LYP level and agrees well with the values obtained here. Moreover, HgH₃ shows a high-energy isomer at 0.859/0.716 eV above the ground state. It should be noted that the HArF compound with a barrier height of 0.477 eV was synthesized and detected in a solid argon matrix at 7.5K [56-59], indicating that it may also be plausible to prepare and characterize HgH₄ and HgH₆ using the matrix isolation technique.

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

Transition state of HgH₃ computed by DFT-B3LYP/PBE0 levels.

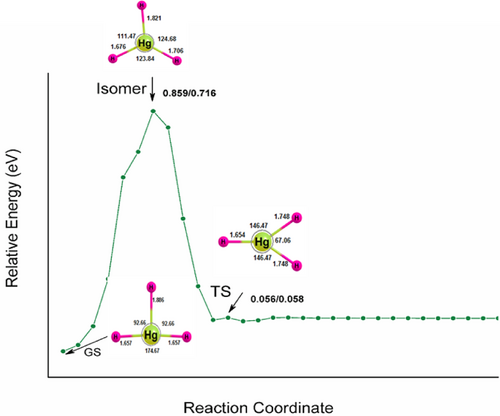
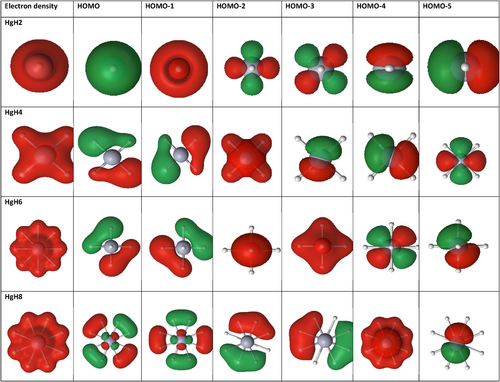
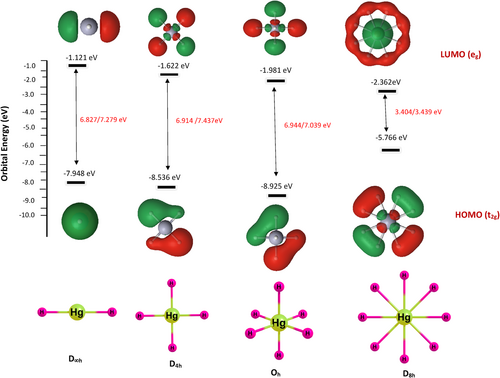
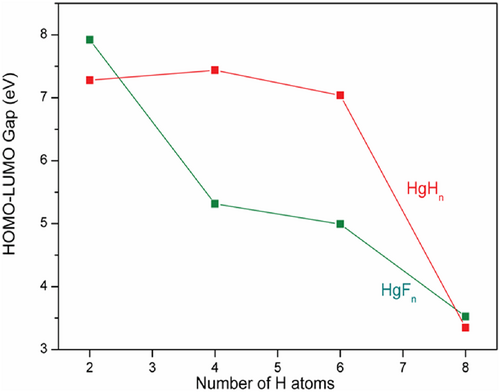
In addition to the dissociation energy and TS, the HOMO–LUMO energy gap is also computed as high HOMO–LUMO gap indicates high kinetic stability and low chemical reactivity because the addition of an electron to LUMO, and the removal of an electron from HOMO is energetically unfavorable [60-63]. Figures 4-6 show the electron density, bonding molecular orbitals, HOMO–LUMO plot, and their energy gaps for HgH₂, HgH₄, HgH₆, and HgH₈. A large HOMO–LUMO energy gap of 6.827/7.279, 6.914/7.437, 6.944/7.039 eV for HgH₂, HgH₄, HgH₆, and a relatively low 3.404/3.439 eV for HgH₈ at the B3LYP/PBE0 level. The HOMO–LUMO gap of HgH₄ and HgH₆ is higher than the energy gap of experimentally detected HgF₄ (4.556/5.317 eV) and HgF₆ (4.185/5.015 eV) [19] and supports the existence of stable high valent HgH_n.

3.3 Chemical Bonding and Population Analysis

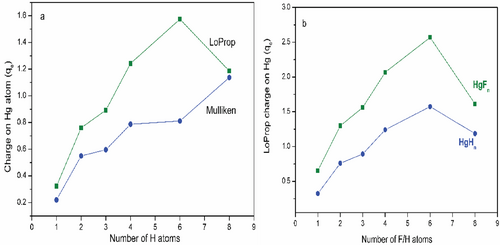
Molecules are best described by the collection of nuclei surrounded by electrons, and the electron distributions reflect the nature and strength of bonds between the atoms in molecules. The change in the electron density distribution from the simple sum of atom density provides insight into the nature and strength of bonds in molecules. Quantum chemical methods provide atomic charge redistribution in the molecular system based on the population analysis or partitioned scheme. The natural population analysis and local properties computed by the LoProp approach are less basis set dependent than the Mulliken population analysis schemes. Therefore, both schemes are employed to calculate the charge distribution characteristics of HgH_n. Table 3 lists the charge accumulation on Hg and H by Mulliken and LoProp schemes. Figure 7a shows variation in Mulliken charge on Hg for each H atom with a maximum at HgH₈ and relatively less at HgH₆. The charge accumulation trends are not in alignment with the HOMO–LUMO gap. In contrast, LoProp charge analysis shows a gradual increase in charge on Hg for each added H atom with a maximum at HgH₆ and then a decrease in HgH₈, and truly reflects the HOMO–LUMO gap of HgHn. Furthermore, LoProp charge accumulation on Hg in HgH_n and HgF_n computed with the ANO-RCC-VQZP basis set at the PBE0 level is shown in Figure 7b. It indicates that the magnitude of the charge on Hg is high in HgF_n and relatively low in HgH_n, but both systems display the same trend and truly reflect the HOMO–LUMO gap in both systems. Thus, both the charge distribution and natural bond order analysis support the existence of high OS in Hg^IVH₄ (d⁸), Hg^VIH₆(d⁶), and Hg^VIIIH₈(d⁴). However, the odd electron species shows a nonuniform charge distribution, indicating complex formation by noncovalent interaction between the precursor HgH_{n = 2,4,6} and H/H₂, respectively.

TABLE 3. Mulliken and LoProp charge distribution and natural bond order of HgH_{n = 2–8} computed at B3LYP/PBE0 levels.

	Charge	HgH₂	HgH₃	HgH₄	HgH₅	HgH₆	HgH₇	HgH₈
Mulliken	QHg	0.4274/0.5499	0.4433/0.5961	0.5640/0.7873	0.5259/0.7351	0.5578/0.8113	0.5109/0.7042	0.8694/1.1366
	qH₁	−0.2137/−0.2750	−0.1975/−0.2562	−0.1410/−0.1968	−0.1318/−0.1867	−0.0929/−0.1352	−0.1309/−0.1826	−0.1087/−0.1422
	qH₂	−0.2137/−0.2750	−0.1975/−0.2562	−0.1410/−0.1968	−0.1318/−0.1867	−0.0929/−0.1352	−0.1309/−0.1826	−0.1087/−0.1422
	qH₃		−0.0483/−0.0838	−0.1410/−0.1968	−0.1318/−0.1867	−0.0929/−0.1352	−0.1309/−0.1826	−0.1087/−0.1422
	qH₄			−0.1410/−0.1968	−0.1318/−0.1867	−0.0929/−0.1352	−0.1309/−0.1826	−0.1087/−0.1422
	qH₅				0.0015/0.0117	−0.0929/−0.1352	0.0027/0.0043	−0.1087/−0.1422
	qH₆					−0.0929/−0.1352	0.0027/0.0043	−0.1087/−0.1422
	qH₇						0.0075/0.0175	−0.1087/−0.1422
	qH₈							−0.1087/−0.1422
LoProp	QHg	0.7541/0.7607	0.8906/0.8922	1.2418/1.2421	1.2723/1.2479	1.5843/1.5744	1.2699/1.2483	1.1797/1.1866
	qH₁	−0.3770/−0.3804	−0.3699/−0.3719	−0.3104/−0.3105	−0.3074/−0.3092	−0.2640/−0.2624	−0.3076/−0.3089	−0.1475/−0.1483
	qH₂	−0.3770/−0.3804	−0.3699/−0.3719	−0.3104/−0.3105	−0.3074/−0.3092	−0.2640/−0.2624	−0.3076/−0.3089	−0.1475/−0.1483
	qH₃		−0.1509/−0.1484	−0.3104/−0.3105	−0.3074/−0.3092	−0.2640/−0.2624	−0.3076/−0.3089	−0.1475/−0.1483
	qH₄			−0.3104/−0.3105	−0.3074/−0.3092	−0.2640/−0.2624	−0.3076/−0.3089	−0.1475/−0.1483
	qH₅				−0.0426/−0.0110	−0.2640/−0.2624	−0.0016/−0.0090	−0.1475/−0.1483
	qH₆					−0.2640/−0.2624	−0.0016/−0.0090	−0.1475/−0.1483
	qH₇						−0.0363/−0.0019	−0.1475/−0.1483
	qH₈							−0.1475/−0.1483
Natural Bond Order		3.983 electrons in 2 bonds	NO HgH bond 0.920 non-bonded electrons on Hg, 1.014 non-bonded electrons on H, and the remaining 5.144 electrons are diffuse.	7.901 electrons are involved in 4 bonds.	7.872 electrons in 4 bonds and 0.963 non-bonded electrons on H₅	11.859 electrons in 6 bonds	9.976 electrons are involved in 5 bonds, and the remaining 1.214 electrons are diffuse.	11.744 electrons in 6 bonds, others did not converge.

The above structure, stability, charge redistribution, and chemical bonding data analysis indicate that HgH_n ≥ 3 is stable and can be prepared only at very low temperatures by the reaction of the Hg atom in an excited state with H₂/D₂. The reaction products can be identified and characterized using matrix isolation IR spectroscopy supported by high-level quantum chemical calculations for their spectroscopic signature, structural, and spectroscopic data. However, it is significant to note that the HgH₂ prepared by the matrix isolation technique doesn't truly reflect the formal oxidation state of Hg, as Hg is generated from the excited state (³P₁) rather than in the ground state (¹S₀) during the reaction.

Recently, HgH₂/HgD₂ were synthesized through a direct gas phase reaction between Hg vapor and H/D atoms obtained from H₂/D₂ electrical discharge. The analysis of vibration-rotation transitions in the reaction products confirms the formation of HgH₂/HgD₂ with Hg in OS II [47]. Similarly, high valent HgH_{n ≥ 3} can also be synthesized by the same technique. The vibrational-rotational spectral analysis by a high-resolution FTIR spectrometer may provide direct evidence for the existence of high valent molecules, as the HOMO–LUMO gap values of HgH₄ and HgH₆ are similar to HgH₂ and confirm the direct participation of d shell electrons in chemical bonding and the influence of the special theory of relativity in Hg. Alternatively, direct expansion of Hg vapor and the H atoms obtained from the electric discharge of H₂ in a supersonic beam source can be used for their preparation, followed by electronic spectroscopy like laser absorption/laser-induced fluorescence/photoionization/mass-selected photoelectron spectroscopy characterization. However, there is ambiguity in identifying the high-valent species by using IR frequencies computed by various theoretical methods. Therefore, alternative methods other than conventional vibrational spectroscopy signatures are sought after. Historically, the behavior of atoms and molecules in electric (Stark effect) and magnetic fields (Zeeman splitting) has been investigated to understand the quantum structure of atoms and molecules in depth. Hence, the behavior of HgH_n under the influence of an electric field has been studied to help their unambiguous detection using Stark spectroscopy/molecular beam deflection or matter-wave interferometry techniques.

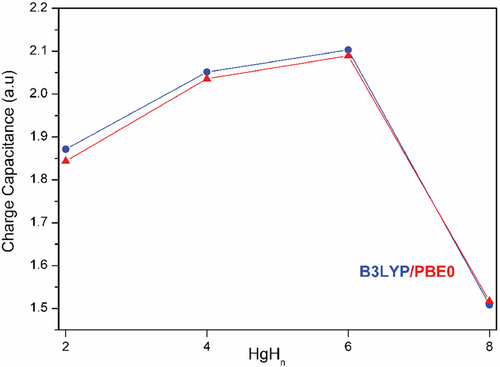
The LoProp method in MOLCAS partitions the molecular polarizability into localized polarizabilities that consist of dipole and charge mobility contributions using finite field perturbation theory (FFPT) [64, 65]. Accordingly, the change in charge due to the external electric field (EEF) is given by Δq = ΔP^(AB). ξ^(AB) where ΔP^(AB) represents the difference in the electrostatic potential and ξ^(AB) measures the ability to conduct charge in a bond for a fixed potential difference between the bonded atoms (bond/charge capacitance). The bond capacitance magnitude helps to classify different types of bonds that correlate well with bond order, polarity, conjugation, and electronegativity, and holds chemical information. Further, the bond capacitance reflects the chemical properties remarkably well in various organic molecules with different bond orders and metal-containing molecules [66, 67]. Figure 8 illustrates that the HgH bond capacitance in HgH_n gradually increases, showing a maximum for HgH₆ and declines for HgH₈ at a low field strength of 0.001 a.u. and echo the HOMO–UMO gap and LoProp charge on Hg atom. The ξ^(AB) value for the HgH bond is 1.8, 2.0, 2.1, and 1.5 for HgH₂, HgH₄, HgH₆, and HgH₈, respectively, which is comparable to the C=C bond value (ξ^(AB) = 1.923) found in benzene.

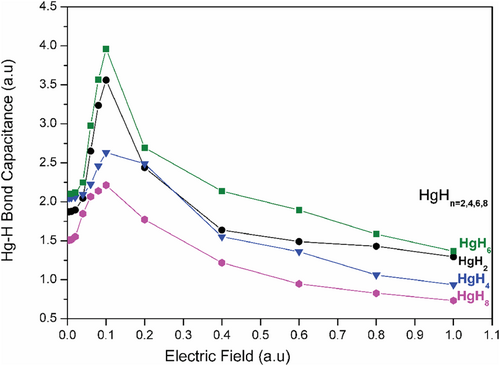
To assist their detection and identification using Stark spectroscopy/molecular beam deflection technique. We have computed the behavior of HgH bond conductance under varying applied fields. The field strength ranges from 0.001 to 1 a.u. (1a.u. = 514.225 V nm⁻¹) is shown in Figure 9. The ξ^(AB) value shows a linear dependence up to a field strength of 0.1 a.u. The values gradually decrease for increasing field strength indicating that 0.1 a.u. is the optimum field strength for their detection using molecular beam deflection or the matter wave interferometry technique [68-75]. Further details regarding the computations, as well as the HgH bond conductance and isotropic polarizability of HgH₃ and HgH₅ are given in the Supporting Information S1.

4 Conclusion

The structure, stability, bonding, electronic properties, and electrical characteristics of the HgH_n=1–8^0,± were investigated by DFT-B3LYP/PBE0 and CCSD(T) methods. The HgH₄, HgH₆, and HgH₈ molecules exhibit high HOM-LUMO gaps of 6.914/7.437 eV, 6.944/7.039 eV, and 3.404/3.439 eV with a barrier height of 0.421/0385 eV and 0.337/0201 eV for HgH₄ and HgH₆. The HgH bond capacitance (ξ^(AB)) in the HgH_n increases gradually with size and then exhibits a maximum at HgH₆ and a decline for HgH₈. The HgH bond capacitance ranges from 1.52 to 2.09 and is comparable to the C=C bond capacitance value (ξ^(AB) = 1.923) in benzene, evidencing a stable high-valent HgH_n and exhibiting high oxidation states of Hg ranging from I to VIII in HgH_n. Furthermore, the polarizability and ξ^(AB) demonstrate a linear response to external electric fields up to 0.1 a.u. for their potential detection using molecular beam deflection or matter-waver interferometry techniques.

Acknowledgments

The author would like to thank Mr. Vaibhav Kumar, kum. Duggal Vibhuti, and Mr. Kislay Bhatt from the Supercomputing Facility of Computer Division, BARC for their generous computer time allocation and support.

Conflicts of Interest

The author declares no conflicts of interest.

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Supporting Information

References

1P. A. M. Dirac, “Quantum-Mechanics of Many-Electron Systems,” Proceedings of the Royal Society of London. Series A: Mathematical and Physical Sciences 123 (1929): 714–733.
CAS Google Scholar
2I. P. Grant, “Relativistic Calculations of Atomic Structure,” Advances in Physics 19 (1970): 747–811.
10.1080/00018737000101191
CAS Google Scholar
3J. P. Desclaux, D. F. Mayers, and F. O'Brien, “Relativistic Atomic Wave Functions,” Journal of Physics B: Atomic and Molecular Physics 4 (1971): 631–642.
10.1088/0022-3700/4/5/004
CAS Google Scholar
4J. P. Desclaux, “Relativistic Dirac-Fock Expectation Values for Atoms With Z = 1 to Z = 120,” Atomic Data and Nuclear Data Tables 12 (1973): 311–406.
10.1016/0092-640X(73)90020-X
CAS Google Scholar
5S. J. Rose, I. P. Grant, and N. C. Pyper, “Direct and Indirect Effects in Relativistic Modification of Atomic Valence Orbitals,” Journal of Physics B: Atomic, Molecular and Optical Physics 11 (1978): 1171–1176.
10.1088/0022-3700/11/7/016
CAS Web of Science® Google Scholar
6P. Pyykko¨ and J.-P. Desclaux, “Relativity and the Periodic System of Elements,” Accounts of Chemical Research 12 (1979): 276–281.
10.1021/ar50140a002
CAS Web of Science® Google Scholar
7P. Pyykko¨, “Relativistic Effects in Structural Chemistry,” Chemical Reviews 88 (1988): 563–594.
10.1021/cr00085a006
CAS Web of Science® Google Scholar
8E. Kraka, D. Cremer, and M. Filatov, “Comparison of Gold Bonding With Mercury Bonding,” Croatica Chemica Acta 82 (2009): 233–243.
CAS Web of Science® Google Scholar
9P. Pyykkö, “Relativistic Effects in Chemistry: More Common Than You Thought,” Annual Review of Physical Chemistry 63 (2012): 45–64.
10.1146/annurev-physchem-032511-143755
CAS Web of Science® Google Scholar
10A. Das, U. Das, and A. K. Das, “Relativistic Effects on the Chemical Bonding Properties of the Heavier Elements and Their Compounds,” Coordination Chemistry Reviews 479 (2023): 215000.
10.1016/j.ccr.2022.215000
CAS Web of Science® Google Scholar
11D. F. Mayers, “Relativistic Self-Consistent Field Calculation for Mercury,” Proceedings of the Royal Society of London. Series A: Mathematical and Physical Sciences 241 (1957): 93–109.
CAS Google Scholar
12M. Kaupp and H. G. Von Schnering, “Gaseous Mercury (IV) Fluoride, HgF₄: An Ab Initio Study,” Angewandte Chemie, International Edition 32 (1993): 861–863, Angew. Chem. 1993, 105, 952–954.
10.1002/anie.199308611
Web of Science® Google Scholar
13M. Kaupp, M. Dolg, H. Stoll, and H. G. Von Schnering, “Oxidation State +IV in Group 12 Chemistry. Ab Initio Study of Zinc (IV), Cadmium (IV), and Mercury (IV) Fluorides,” Inorganic Chemistry 33 (1994): 2122–2131.
10.1021/ic00088a012
CAS Web of Science® Google Scholar
14S. Riedel, M. Straka, and M. Kaupp, “Validation of Density Functional Methods for Computing Structures and Energies of Mercury (IV) Complexes,” Physical Chemistry Chemical Physics 6 (2004): 1122–1127.
10.1039/b315019d
CAS Web of Science® Google Scholar
15W. Liu, R. Franke, and M. Dolg, “Relativistic Ab Initio and Density Functional Theory Calculations on the Mercury Fluorides: Is HgF₄ Thermodynamically Stable?,” Chemical Physics Letters 302 (1999): 231–239.
10.1016/S0009-2614(99)00147-5
CAS Google Scholar
16S. Riedel, M. Kaupp, and P. Pyykö, “Quantum Chemical Study of Trivalent Group 12 Fluorides,” Inorganic Chemistry 47 (2008): 3379–3383.
10.1021/ic702384y
CAS PubMed Web of Science® Google Scholar
17C. Gao, S.-X. Hu, H. Han, G. Guo, B. Suo, and W. Zou, “Exploring the Electronic Structure and Stability of HgF₆: Exact 2-Component (X2C) Relativistic DFT and NEVPT2 Studies,” Computational and Theoretical Chemistry 1160 (2019): 14–18.
10.1016/j.comptc.2019.05.007
CAS Web of Science® Google Scholar
18X. F. Wang, L. Andrews, S. Riedel, and M. Kaupp, “Mercury Is a Transition Metal: The First Experimental Evidence for HgF4,” Angewandte Chemie, International Edition 46 (2007): 8371–8375.
10.1002/anie.200703710
CAS PubMed Web of Science® Google Scholar
19T. Jayasekharan, “High Valent Mercury Fluoride Ions,” ChemPhysChem 24 (2023): e202300036.
10.1002/cphc.202300036
CAS PubMed Web of Science® Google Scholar
20P. Pyykkö, M. Straka, and M. Patzschke, “HgH₄ and HgH₆: Further Candidates for High-Valent Mercury Compounds,” Chemical Communications 16 (2002): 1728–1729.
10.1039/B203585E
Google Scholar
21A. D. Becke, “Density-Functional Exchange-Energy Approximation With Correct Asymptotic Behaviour,” Physical Review A 38 (1988): 3098–3100.
10.1103/PhysRevA.38.3098
CAS Google Scholar
22A. D. Becke, “A New Mixing of Hartree–Fock and Local Density-Functional Theories,” Journal of Chemical Physics 98 (1993): 1372–1377.
10.1063/1.464304
CAS Web of Science® Google Scholar
23C. Lee, W. Yang, and R. G. Parr, “Development of the Colle-Salvetti Correlation-Energy Formula Into a Functional of the Electron Density,” Physical Review B: Condensed Matter and Materials Physics 37 (1988): 785–789.
10.1103/PhysRevB.37.785
CAS Google Scholar
24M. Ernzerhof and G. Scuseria, “Assessment of the Perdew–Burke–Ernzerhof Exchange-Correlation Functional,” Journal of Chemical Physics 110 (1999): 5029–5036.
10.1063/1.478401
CAS Web of Science® Google Scholar
25J. F. Stanton, “Why CCSD T Works: A Different Perspective,” Chemical Physics Letters 281 (1997): 130–134.
10.1016/S0009-2614(97)01144-5
CAS Web of Science® Google Scholar
26B. O. Roos, R. Lindh, P.-A. Malmqvist, V. Veryazov, and P.-O. Widmark, “New Relativistic ANO Basis Sets for Transition Metal Atoms,” Journal of Physical Chemistry. A 109 (2005): 6575–6579.
10.1021/jp0581126
CAS PubMed Web of Science® Google Scholar
27B. O. Roos, R. Lindh, P.-A. Malmqvist, V. Veryazov, and P.-O. Widmark, “Main Group Atoms and Dimers Studied With a New Relativistic ANO Basis Set,” Journal of Physical Chemistry. A 108 (2004): 2851–2858.
10.1021/jp031064+
CAS Web of Science® Google Scholar
28W. Liu and D. Peng, “Exact Two-Component Hamiltonians Revisited,” Journal of Chemical Physics 131 (2009): 031104.
10.1063/1.3159445
PubMed Web of Science® Google Scholar
29W. Liu, “Ideas of Relativistic Quantum Chemistry,” Molecular Physics 108 (2010): 1679–1706.
10.1080/00268971003781571
CAS Web of Science® Google Scholar
30T. Saue, “Relativistic Hamiltonians for Chemistry: A Primer,” ChemPhysChem 12 (2011): 3077–3094.
10.1002/cphc.201100682
CAS PubMed Web of Science® Google Scholar
31D. Peng and M. Reiher, “Exact Decoupling of the Relativistic Fock Operator,” Theoretical Chemistry Accounts 131 (2012): 1081.
10.1007/s00214-011-1081-y
Web of Science® Google Scholar
32J. Kim, H. Ihee, and Y. P. Lee, “Spin-Orbit Density Functional and Ab Initio Study of HgXn (X=F, Cl, Br, and I; n=1, 2, and 4),” Journal of Chemical Physics 133 (2010): 144309.
10.1063/1.3497189
PubMed Web of Science® Google Scholar
33F. Aquilante, T. B. Pedersen, and R. Lindh, “Low-Cost Evaluation of the Exchange Fock Matrix From Cholesky and Density Fitting Representations of the Electron Repulsion Integrals,” Journal of Chemical Physics 126 (2007): 194106.
10.1063/1.2736701
PubMed Web of Science® Google Scholar
34F. Aquilante, L. Boman, J. Bostrom, et al., “ Cholesky Decomposition Techniques in Electronic Structure Theory,” in Linear-Scaling Techniques in Computational Chemistry and Physics. Challenges and Advances in Computational Chemistry and Physics, ed. R. Zalesny, M. Papadopoulos, P. Mezey, and J. Leszczynski (Springer, 2011), 13.
10.1007/978-90-481-2853-2_13
Google Scholar
35F. Aquilante, J. Autschbach, R. K. Carlson, et al., “Molcas 8: New Capabilities for Multiconfigurational Quantum Chemical Calculations Across the Periodic Table,” Journal of Computational Chemistry 37 (2016): 506–541.
10.1002/jcc.24221
CAS PubMed Web of Science® Google Scholar
36D. A. Matthews, L. Cheng, M. E. Harding, et al., “Coupled-Cluster Techniques for Computational Chemistry: The CFOUR Program Package,” Journal of Chemical Physics 152 (2020): 214108.
10.1063/5.0004837
CAS PubMed Web of Science® Google Scholar
37K. P. Huber and G. Herzberg, Molecular Spectra and Molecular Structure IV: Constants of Diatomic Molecules (Van Nostrand, 1979).
10.1007/978-1-4757-0961-2
Google Scholar
38W. H. Breckenridge, C. Jouvet, and B. Soep, “Orbitally Selective Chemical Reaction in Hg-H₂ Van der Waals Complexes,” Journal of Chemical Physics 84 (1986): 1443–1450.
10.1063/1.450488
CAS Google Scholar
39N. Legay-Sommaire and F. Legay, “Photochemistry in hg Doped Matrices. Infrared Spectra of Mercury Hydrides: HgH₂, HgD₂, HHgD, HgD,” Chemical Physics Letters 207 (1993): 123–128.
10.1016/0009-2614(93)87001-J
CAS Google Scholar
40N. Legay-Sommaire and F. Legay, “FTIR Study of the Photochemistry of Hg and H₂ in a Nitrogen Matrix: Formation and Dissociation of HgH₂ and HHgHgH,” Journal of Physical Chemistry 99 (1995): 16945–16952.
10.1021/j100046a021
CAS Google Scholar
41T. M. Greene, W. Brown, L. Andrews, et al., “Matrix Infrared Spectroscopic and Ab Initio Studies of ZnH₂, CdH₂, and Related Metal Hydride Species,” Journal of Physical Chemistry 99 (1995): 7925–7934.
10.1021/j100020a014
CAS Google Scholar
42X. Wang and L. Andrews, “Solid Mercury Dihydride: Mercurophilic Bonding in Molecular HgH₂ Polymers,” Inorganic Chemistry 43 (2004): 7146–7150.
10.1021/ic049100m
CAS PubMed Web of Science® Google Scholar
43X. Wang and L. Andrews, “Mercury Dihydride Forms a Covalent Molecular Solid,” Physical Chemistry Chemical Physics 7 (2005): 750–759.
10.1039/b412373e
CAS PubMed Web of Science® Google Scholar
44M. Kaupp and H. G. von Schnering, “Dominance of Linear 2-Coordination in Mercury Chemistry: Quasirelativistic and Nonrelativistic Ab Initio Pseudopotential Study of (HgX₂)₂ (X = F, Cl, Br, I, H),” Inorganic Chemistry 33 (1994): 2555–2564.
10.1021/ic00090a014
CAS Google Scholar
45P. Pyykkö and M. Straka, “Ab Initio Studies of the Dimers and Metallophilic (HgH₂)₂ (HgMe₂)₂. Metallophilic Attraction and the Van der Waals Radii of Mercury,” Physical Chemistry Chemical Physics 2 (2000): 2489–2493.
10.1039/b001171l
CAS Google Scholar
46A. Shayesteh, S. Yu, and P. F. Bernath, “Gaseous HgH₂, CdH₂, and ZnH₂,” Chemistry - A European Journal 11 (2005): 4709–4712.
10.1002/chem.200500332
CAS PubMed Web of Science® Google Scholar
47A. Shayesteh, S. Yu, and P. F. Bernath, “Infrared Emission Spectra and Equilibrium Structures of Gaseous HgH₂ and HgD₂,” Journal of Physical Chemistry. A 109 (2005): 10280–10286.
10.1021/jp0540205
CAS PubMed Web of Science® Google Scholar
48P. Pyykko, “Dirac-Fock One-Centre Calculations, Part 7.—Divalent Systems MH⁺ and MH₂, (M = Be, Mg, Ca, Sr, Ba, Ra, Zn, Cd, Hg, Yb and No),” Journal of the Chemical Society, Faraday Transactions 75 (1979): 1256–1276.
10.1039/F29797501256
CAS Google Scholar
49A. Bernier, P. Millie, and M. Pelissier, “Three-Electron Approach of HgH Using Relativistic Effects Core, Core Polarization and Spin-Orbit Operators: The Low-Lying States,” Chemical Physics 106 (1986): 195–203.
10.1016/0301-0104(86)80137-9
CAS Google Scholar
50A. Bernier and P. Millie, “The Hg-H₂ System: Potential Energy Surfaces of the Low-Lying States, Reactivity of the 6s6p States of Hg on H₂, Classical Dynamic Study of Hg (³p₁) + H₂ Half Collision,” Journal of Chemical Physics 88 (1988): 4843–4854.
10.1063/1.454695
CAS Web of Science® Google Scholar
51M. Dolg, W. Kuchle, H. Stoll, H. Preuss, and P. Schwerdtfeger, “Ab Initio Pseudopotentials for Hg to Rn II. Molecular Calculations on the Hydrides of Hg to at and the Fluorides of Rn,” Molecular Physics 74 (1991): 1265–1285.
10.1080/00268979100102951
CAS Google Scholar
52P. Schwerdtfeger, G. A. Heath, M. Dolg, and M. A. Bennett, “Low Valencies and Periodic Trends in Heavy Element Chemistry. A Theoretical Study of Relativistic Effects and Electron Correlation Effects in Group 13 and Period 6 Hydrides and Halides,” Journal of the American Chemical Society 114 (1992): 7518–7527.
10.1021/ja00045a027
CAS Web of Science® Google Scholar
53H. Xie, D. Li, and H. Guo, “A Reliable Ab Initio Potential Energy Surface and Vibrational States for the Ground Electronic State of HgH2 (X 1∑g+),” Journal of Chemical Physics 122 (2005): 144314.
10.1063/1.1876132
PubMed Google Scholar
54P. Botschwina, P. Sebald, D. Figgen, and H. Stoll, “Calculated Spectroscopic Properties of HgH₂,” Molecular Physics 105 (2007): 1193–1205.
10.1080/00268970701302532
CAS Web of Science® Google Scholar
55L. von Szentpa'ly, “Hard Bends Soft: Bond Angle and Bending Force Constant Predictions for Dihalides, Dihydrides, and Dilithides of Groups 2 and 12,” Journal of Physical Chemistry. A 106 (2002): 11945–11949.
10.1021/jp026658b
Google Scholar
56L. Khriactchev, M. Pettersson, N. Runeberg, J. Lundell, and M. Räsänen, “A Stable Argon Compound,” Nature 406 (2000): 874–876.
10.1038/35022551
PubMed Google Scholar
57L. Khriactchev, M. Pettersson, N. Runeberg, J. Lundell, and M. Räsänen, “A Theoretical Study of HArF, a Newly Observed Argon Compound,” Journal of Chemical Physics 114 (2001): 836–841.
10.1063/1.1331105
Google Scholar
58L. Khriactchev, M. Pettersson, A. Lignell, and M. Räsänen, “A More Stable Configuration of HArF in Solid Argon,” Journal of the American Chemical Society 123 (2001): 8610–8611.
10.1021/ja016197s
PubMed Google Scholar
59G. M. Chaban, J. Lundell, and R. B. Gerber, “Theoretical Study of Decomposition Pathways for HArF and HkrF,” Chemical Physics Letters 364 (2002): 628–633.
10.1016/S0009-2614(02)01411-2
CAS Web of Science® Google Scholar
60D. E. Manolopoulos, J. C. May, and S. E. Down, “Theoretical Studies of the Fullerenes: C₃₄ to C₇₀,” Chemical Physics Letters 181 (1991): 105–111.
10.1016/0009-2614(91)90340-F
CAS Web of Science® Google Scholar
61J. Aihara, “Reduced HOMO-LUMO Gap as an Index of Kinetic Stability for Polycyclic Aromatic Hydrocarbons,” Journal of Physical Chemistry. A 103 (1999): 7487–7495.
10.1021/jp990092i
CAS Web of Science® Google Scholar
62J. Aihara, “Weighted HOMO-LUMO Energy Separation as an Index of Kinetic Stability for Fullerenes,” Theoretical Chemistry Accounts 102 (1999): 134–138.
10.1007/s002140050483
CAS Web of Science® Google Scholar
63J. Aihara, “Validity of the Weighted HOMO.LUMO Energy Separation as an Index of Kinetic Stability for Fullerenes With up to 120 Carbon Atoms,” Physical Chemistry Chemical Physics 1 (1999): 227–230.
10.1039/a807917j
Web of Science® Google Scholar
64L. Gagliardi, R. Lindh, and G. Karlström, “Local Properties of Quantum Chemical Systems: The LoProp Approach,” Journal of Chemical Physics 121 (2004): 4494–4500.
10.1063/1.1778131
CAS PubMed Web of Science® Google Scholar
65P. Söderhjelm, J. W. Krogh, G. Karlström, U. Ryde, and R. Lindh, “Accuracy of Distributed Multipoles and Polarizabilities: Comparison Between the LoProp and MpProp Models,” Journal of Computational Chemistry 28 (2007): 1083–1090.
10.1002/jcc.20632
CAS PubMed Web of Science® Google Scholar
66A. Holt, G. Karlström, and R. Lindh, “The Charge Capacity of the Chemical Bond,” Chemical Physics Letters 436 (2007): 297–301.
10.1016/j.cplett.2007.01.051
CAS Web of Science® Google Scholar
67A. Holt, G. Karlström, and B. O. Roos, “The Charge Capacitance of the Chemical Bond: Application to Bonds Containing Metals,” International Journal of Quantum Chemistry 109 (2009): 618–628.
10.1002/qua.21828
CAS Web of Science® Google Scholar
68R. Antoine, P. Dugourd, D. Rayane, et al., “Direct Measurement of the Electric Polarizability of Isolated C₆₀ Molecules,” Journal of Chemical Physics 110 (1999): 9771–9772.
10.1063/1.478944
CAS Web of Science® Google Scholar
69A. Ballard, K. Bonin, and J. Louderback, “Absolute Measurement of the Optical Polarizability of C₆₀,” Journal of Chemical Physics 113 (2000): 5732–5735.
10.1063/1.1290472
CAS Web of Science® Google Scholar
70A. D. Cronin, J. Schmiedmayer, and D. E. Pritchard, “Optics and Interferometry With Atoms and Molecules,” Reviews of Modern Physics 81 (2009): 1051–1129.
10.1103/RevModPhys.81.1051
CAS Web of Science® Google Scholar
71J. S. Kienitz, K. Długołeecki, S. Trippe, and J. Küpper, “Improved Spatial Separation of Neutral Molecules,” Journal of Chemical Physics 147 (2017): 024304.
10.1063/1.4991479
PubMed Web of Science® Google Scholar
72A. Stefanov, M. Berninger, and M. Arndt, “A Novel Design for Electric Field Deflectometry on Extended Molecular Beams,” Measurement Science and Technology 19 (2008): 055801.
10.1088/0957-0233/19/5/055801
Web of Science® Google Scholar
73M. Berninger, A. Stefanov, S. Deachapunya, and M. Arndt, “Polarizability Measurements of a Molecule via a Near-Field Matter-Wave Interferometer,” Physical Review A 76 (2007): 013607.
10.1103/PhysRevA.76.013607
Web of Science® Google Scholar
74L. Hackermuller, K. Hornberger, S. Gerlich, M. Gring, H. Ulbricht, and M. Arndt, “Optical Polarizabilities of Large Molecules Measured in Near-Field Interferometry,” Applied Physics B: Lasers and Optics 89 (2007): 469–473.
10.1007/s00340-007-2873-6
Web of Science® Google Scholar
75S. Gerlich, S. Eibenberger, M. Tomandl, et al., “Quantum Interference of Large Organic Molecules,” Nature Communications 2 (2011): 263.
10.1038/ncomms1263
PubMed Web of Science® Google Scholar

Volume125, Issue14

July 15, 2025

e70073

High Valent Mercury Hydrides

ABSTRACT

1 Introduction

2 Computational Methods