The ground state of atomic two-electron systems in the independent particle model
Abstract
enScaled variational functions of the form \documentclass{article}\pagestyle{empty}\begin{document}$ \phi _{\alpha k} = e^{ - (Z - 1 + e^{ - \alpha kr})kr} $\end{document}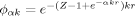
, where Z is the nuclear charge and α is a parameter, and \documentclass{article}\pagestyle{empty}\begin{document}$ \phi _{\beta \alpha k} = e^{ - (\beta + e^{ - \alpha kr})kr} $\end{document}
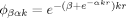, where both α and β are parameters, are used for the description of the ground state of atomic two-electron systems in the independent particle model. The scale factor k has been introduced in order to satisfy the virial theorem.
Apart from the energy, a number of one-electron expectation values have been calculated and the results are compared with those obtained from other variational functions.
The function ϕαk yields already a good approximation to the Hartree–Fock solution whereas with the function ϕβαk the Hartree–Fock results are practically reproduced.
Abstract
frL'état fondamental des systèmes atomiques à deux électrons est décrit par des fonctions variationelles “échellonnées” de type
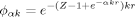
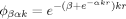
La fonction ϕαk déjà représente une bonne approximation de la solution Hartree–Fock, tandis qu'avec la fonction ϕβαk les résultats Hartree–Fock sont pratiquement reproduits.
Abstract
deVariationsfunktionen mit einem Koordinatenstreckungsfaktor k, von der Form
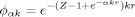
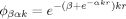
Ausser der Energie werden Mittelwerte von mehreren Einelektronoperatoren berechnet und mit entsprechenden Resultaten für andere Variationsfunktionen verglichen.
Die Funktion ϕαk schon representiert eine gute Annäherung zu der Hartree–Fock-Lösung, während mit der Funktion ϕβαk die Hartree–Fock-Resultate praktisch reproduziert werden.
