Consider a projector matrix P, representing the first order reduced density matrix in a basis of orthonormal atom-centric basis functions. A mathematical question arises, and that is, how to break P into its natural component kernel projector matrices, while preserving N-representability of 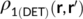. The answer relies upon 2-projector triple products, P′_jPP′_j. The triple product solutions, applicable within the quantum crystallography of large molecules, are determined by a new form of the Clinton equations, which—in their original form—have long been used to ensure N-representability of density matrices consistent with X-ray diffraction scattering factors. As such, the goal of this paper is to outline a possible pathway for the application of quantum crystallography to crystals of large molecular systems.