Characterization of Ultrathin Fully Depleted Silicon-on-Insulator Devices Using Subthreshold Slope Method
Abstract
The subthreshold current–voltage (subthreshold slope) characteristic of a fully depleted silicon-on-insulator high-k dielectric-metal gate field-effect transistor is applied for evaluation of the interface traps located at both the front and back channels. The proposed characterization method allows an estimation of averaged trap densities separately for the front and back interfaces of the channel. Performing subthreshold slope measurements at several temperatures allows the extraction of the energy distributions of the interface trap densities for both interfaces and obtaining essential characteristics of the stack.
1 Introduction
Fully depleted (FD) silicon-on-insulator (SOI) (FDSOI) high-k metal gate (HKMG) field-effect transistors (FET) are becoming a mainstream of semiconductor technology.[1, 2] Improvement in the FET characteristics depends not only on the proper design but on the elimination of defects unintentionally formed in the devices. So-called interface traps present a class of defects mostly related to structural imperfections that are formed at the semiconductor–insulator interfaces of an FET. These localized defects can trap and release mobile charge, leading to drain-current noise.[3, 4] The traps can also suppress electrostatic control of the gate over the channel.[5-7] Interface traps may be formed during device processing but can also be produced by, e.g., ionizing radiation and electrical stress. Complementary metal–oxide semiconductor (CMOS) process development, process control, and reliability assessment require an accurate estimate of the interface trap density in these devices.
The existing methods for the interface trap density (DIT) estimation are rather complicated, time-consuming, and require preliminary knowledge of many system parameters (see, e.g., ref. [5, 6] and references therein). These methods (i.e., the low-frequency (quasi-static) capacitance–voltage (CV) method, the conductance method, the high-frequency CV method, and charge pumping) require a separate back gate or body contact in the case of SOI devices. This presents a problem in SOI device configurations and requires additional processing steps.[1] In addition, the sensitivities of these methods do not allow characterization of FETs with actual, small gate areas (≪1 μm2). Moreover, in HKMG FDSOI FETs two semiconductor–insulator interfaces coexist, one at the front gate (FG) and another at the back gate (BG). None of the existing methods[5, 6] are capable of clearly distinguishing the traps located at the FG from those located at the BG and estimating their density distribution, i.e., DIF(EIT) and DIB(EIT). Here and later, we will use EIT to designate the trap-related energy level located between the EC, an energy level of the Si conduction band, and EV, its valence band.
Current–voltage characteristics of an FET in a subthreshold swing (STS) regime are widely applied for characterization of switching performance of the device.[5, 7] A sharper subthreshold slope is essential for a low-power, low-voltage CMOS: For a given threshold voltage, the off-current (IOFF, i.e., static power) is reduced or, reciprocally, at a given IOFF the threshold voltage and nominal operating voltage can be lowered.[1] For bulk devices, interface traps located at the isolator/channel interface push the value of STS (the reciprocal value of the subthreshold slope) above its thermodynamic limit (≈59.5 mV dec−1 at 300 K) due to excitation of the carriers trapped at the interfaces of the channel. Accordingly, the STS value allows estimation of the trap density at the interface.[5] For FDSOI MOSFETs, the STS value is influenced by traps present on both FG and BG interfaces.[8] Therefore, measurement of STS for such an FET may allow access to the trap densities on both channel interfaces.
First attempts to estimate DIB in MOSFET SOI devices based on the STS method was presented in ref. 9. Later this method was developed in several works for MOSFET SOI devices (see, e.g., ref. 10 and references therein), where the authors attempted estimation of DIF,IB(EIT) in Si bandgap near the FG and BG.[10] Recently appeared publications related to interface trap density estimation in Si metal–oxide–semiconductor fin FETs (SiMOS FinFET) are also based on STS measurements (see ref. 11 and references therein). New analytical expressions for the STS in FDSOI structures operated in both FG and BG modes have been proposed recently as well.[12] To the best of our knowledge, there are no publications about the application of the STS method for similar estimations in HKMG FDSOI FETs. Moreover, the authors in ref. 1 suggest that due to the small densities of the interface traps, the STS-based method can be hardly applicable for characterization of the trap density in the case of HKMG technology.
In what follows, we present an attempt to apply the STS measurement method for interface trap characterization in the case of HKMG FD SOI FETs. We show that proper modification of the measurements and parameter extraction techniques allow detection and characterization of carrier traps located at FG and BG interfaces. Moreover, depending on the actual task it is possible to apply the method for monitoring of relative changes in trap densities, obtain estimations for averaged absolute values of trap densities, or obtaining energy distributions of the trap densities.
2 Characterization Methodology
2.1 Short Review of the Previous Studies
In this section, after a brief review of the previous relevant publications, we will present our modifications to the method for characterization of interface traps in HKMG SOI FETs. The first publication reporting a possibility of application of STS measurements for estimation of interface trap densities,[13] known to the current authors, appeared in 1975. The authors[13] demonstrated that interface states, located near the channel, strongly influence the subthreshold slope of ID(VG) dependence at small drain voltages for an MOS transistor working in weak inversion. Later it was shown that for thin-film SOI MOSFETs (a laser-recrystallized Si film on oxidized Si wafer was investigated) the STS is also affected by the properties and interface states located near the back gate.[14] Introduction of bonded SOI wafers and their application in MOSFET technology intensified the research on the influence of interface traps on STS (see refs. [15-19] and references therein). In these publications, a relation of the STS to the interface traps was proved, and expressions for estimation of interface trap densities from the STS measurement results were proposed.
The buried density of interface traps (DIB) for FDSOI MOSFETs was evaluated in ref. 14. The method was based on a dual-gate (DG) voltage sweep in the subthreshold region. Namely, the STS was measured while both the FG and BG were swept with voltages changing according to a ratio k = VBG/VFG, with k = 0…10. By neglecting the DIF, i.e., the interface trap density at the FG, an average value for DIB can be derived using this approach.
Experimental results for carrier mobility and STS in HKMG SOI MOSFETs with various gate lengths obtained at various temperatures (77–300 K) were presented by Pham-Nguen et al.[20] It was shown that for short gates (LCh ≤ 100 nm), mobility is nearly independent of the temperature. The detection limit for a sum of states from both interfaces (DIF + DIB) was estimated for the direct extraction of interface state density from STS measurements as ≈1012 eV−1 cm−2.[20, 21]
Three methods for DIF,IB evaluation in HKMG SOI MOSFETs, i.e., front-channel swing, back-channel swing, and coupling effect, were compared in ref. 22. From those methods,the subthreshold swing results for the back-channel were affected by the DIF most of the others. However, the authors[22] conclude that the sensitivity of the method may not be sufficient for MOSFETs with a thin buried oxide.
The publication that triggered our interest in the STS measurement method promised extraction of DIF(EIT) and DIB(EIT) distributions for FDSOI MOSFETs.[10] The authors of ref. 10 used a similar DG operation approach to that presented in ref. 9; however, the expression for STS was applied to fit the experimental STS(ID) data measured for three different k = VBG/VFG values. Measurements for three k values were used for an iterative extraction procedure of CIF and CIB dependences on, respectively, the front- and back-surface potentials. Finally, the surface potentials were related to the energy location of the trap level in the Si bandgap responsible for DIF,IB = CIF,IB/q interface trap density (q presents an electron charge). We were unable to repeat the success of the authors[10] for two reasons. First, extraction of STS(ID) data by the expression for the swing for such a broad ID range is questionable due to the substantial impact of the regular current itself. Second, the number of unknown variable parameters substantially exceeds the possible fitting accuracy. For us, the procedure used in ref. 10 was not clearly described. Unfortunately, there were no follow-up publications related to these results.
Recently, the STS measurement method was applied for DIT (EIT) estimation in SOI FD FinFETs.[11] The results indicate that the trap density can be extracted between Eit–EV ∼ 0.65–0.90 eV. The DIT(EIT) is extracted with a minimum amount of modeling, the strongest requirement being that short-channel effects can be neglected in the device under study. The expressions presented in ref.12 provide an accurate description of the STS as a function of the main FDSOI stack parameters and interface trap density in single-gate operation mode.
In our opinion, the concept of optimal coupling (OC) in DG operation mode, used for DIB estimation in ref. 9, seemed not fully explored. For optimal coupling, such a value for the ratio in DG operation is selected experimentally that both front- and back-surface potentials increase at the same rate with the applied FG voltage. Our approach for estimation of DIF,IB(EIT) dependences from STS measurements is based mainly on the theory and calculations presented in the previous publications (see refs. [9-11, 15] and references therein). Where possible, we will refer to the previously published equations to avoid lengthy and cumbersome expressions related to the complexity of the system under consideration.
2.2 Subthreshold Swing for HKMG SOI FET
In subthreshold range, the ID(VFG), with ID as drain current and VFG FG voltage, dependence is usually represented by a plot of log(ID) versus VFG for VDS (drain-source bias) significantly exceeding thermal voltage UT = kBT/q. Such a representation is related to the expression for ID(VFG) (see, e.g., ref. 5) leading to a linear dependence with a slope of [ln(10)nUT]−1. Here, q is the electron charge, n > 1 is a nonideality factor that reflects the presence of the interface traps, kB is the Boltzmann constant, and T is temperature. By STS, we designate the reverse of the slope. The theoretical limit for this value (i.e., for n = 1) is STSTh = ln(10)UT. Therefore, for the nonideality factor, we have n = STSM/STSTh, where STSM is the experimentally measured slope.
Therefore, if the capacitances related to the oxides and Si channel are known, measurements of n and kOC using the procedure described in ref. 9 and application of the aforementioned calculations give a possibility to estimate , values and consequently DIF,IB = CIF,IB/q trap densities averaged for the measured subthreshold region.
Instant modifications in design and fabrication processes for microelectronic devices require measurements of actual FET stock parameters. The actual values for COF, COB, and CSi may differ from what is expected because of the actual fabricated thickness of layers and their real content/structure. Therefore, for getting accurate results for DIF,IB it will be advantageous to determine the stack parameters of the devices under study (DUT) experimentally. As it was noted previously, CV measurements for single FET devices with dimensions in the 10–100 nm range cannot be performed due to the low signal/noise ratio. Therefore, special structures containing hundreds of devices connected in parallel are usually applied for this purpose. A review of the measurement methods applied for the determination of the FET stack parameters can be found in ref. 1. Among others, the full-split CV (FSCV) method[23, 24] supplies all the information necessary for further application in the STS measurement procedure. This method was applied in our measurements to obtain capacitance values for the layers in the FET stack.
It also appears necessary to include a concept of “dark space”[25] in consideration of the equivalent oxide thicknesses (EOT) and, consequently, the capacitances of the stack layers in the FET. This concept was applied in the FSCV method[23] as well and reflects the fact that for nanometric oxide thicknesses the thickness associated with quantum effects (depletion of free carriers at the semiconductor surface) becomes the same order of magnitude as the measured oxide thicknesses. We used the standard value for dark-space thickness in silicon, i.e., ≈1.2 nm,[26] at both front and back Si channel interfaces. The relevant “dark-space” capacitors should be taken into account for calculations of the CIF,IB.
2.3 Temperature Dependence for STS
Measurements of the STS from an FET at a single temperature and estimation of the stack parameters by the FSCV method provide the averaged DIF,IB values (IF,IB) for an energy level in the Si channel bandgap determined by the values of temperature and bias on the gate(s). A variation of measurement temperature and the related change in the STS measurement parameters supply information about trap densities at different energy level positions in the Si bandgap. Therefore, measurements at several temperatures (multi-T measurements) will characterize density distributions of interface traps DIF,IB(EIT).
Large variation of measurement temperature is rarely used in semiconductor device characterization because it requires a special technique capable of controlling the sample temperature in a broad range and exceeds possibilities of standard probe stations. This is the reason that publications where FET characterization is studied under various temperatures (especially below 250 K) are scarce (see, e.g., ref. [20, 27-31]). On the other hand, control of the STS by temperature in combination with the gate bias is the best way of probing the energy distribution of interface traps at small-gate-bias conditions, where the current in the channel is mainly controlled by the carriers excited from the interface traps. An attempt to extract DIF,IB at various measurement temperatures for an FDSOI FET was presented in ref. 32. However, as the estimations were based on a simple model,[33] the presented results are questionable.
Determination of energy levels of traps, participating in STS, from biasing conditions and temperature also present a nontrivial task. For an “ideal” or, at least, for well-defined FET structures, the trap energy level participating in STS (i.e., the difference between the Fermi level position and energy of the Si valence band) can be obtained either using commercially available Poisson–Schrodinger equation solvers (PSESs; see, e.g., ref. 34 and references therein) or using a freely available band energy diagram program for complex multilayer dielectric devices.[35] For real devices, only approximate parameters are usually known; therefore, the application of these programs has limitations. We will use a simple approximation, which will give some scatter in energy position but still will reflect the DIF,IB(EIT) distributions semiquantitatively.
Subsequently we will present procedures necessary for obtaining interface trap density distributions for FG and BG from STS measurements in the temperature range 120–400 K. In the formalism, we will follow recent and detailed description of band structure/bias relationships for FDSOI FETs that can be found in ref. 37 and estimations used in ref. 11.
Equation (19) is valid for measurement in STS mode at temperature T and contains the unknown term . The ratio gmUT/ID is determined experimentally from ID(VFG) STS measurements at the smallest possible ID values. is calculated for a given T using the band energy diagram program for complex multilayer dielectric devices.[36] To account for the specific structure of the gate oxide of a device in the calculations,[36] we can use the EOT data estimated for the front and back oxides in FSCV measurements. The same measurement/calculation procedure may be applied for the BG ΔEBG(T) as well.
3 Experimental Section
3.1 Samples
The DUT were ultra-thin-body and BOX (UTTB) n-type FDSOI MOSFETs provided by GlobalFoundries and were produced using 22 nm node technology.[2] They were fabricated on (100) SOI wafers with highly scaled BOX and silicon channel thickness. For the characterization experiments, samples not showing top performance were chosen. The gate stack consisted of a high-k gate dielectric on top of a SiON interfacial layer, with an equivalent front oxide thickness EOT ≈ 1 nm and a TiN metal gate (SG devices). As a variation, devices with an additional thin SiO2 layer atop the channel (with equivalent front oxide thickness EOT ≈3 nm, EG devices) were also investigated. The BOX thickness in both cases was ≈20 nm. The devices applied for the STS measurements were standard FET structures with a rectangular channel and four separated contacts for the FG, BG, source (S), and drain (D). The channel length of the FETs was LCH = 100 nm and channel width WCH = 150 nm. For capacitance measurements, 144 FETs connected in parallel (three contacts: FG, BG, S + D), with dimensions LCH = WCH = 2 μm each were applied. Therefore, the total area of structures used in CV measurements was 576 μm2. The sketches of the measurement setups are shown in Figure 1a,b. The chips containing DUTs for STS and CV measurements were separated from the 8 in. wafer to be attached by thermoconductive glue on an electrically isolated sample holder.
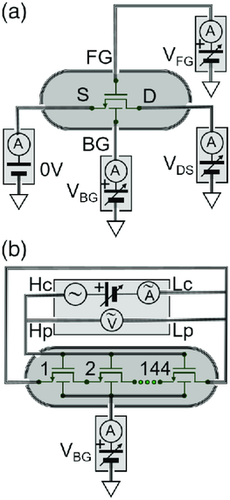
3.2 Setup
The sample holder with a sample attached was placed inside the PS-100 model probe station (Lake Shore) allowing measurement at cryogenic temperatures under vacuum conditions. A range of temperatures from 120 to 400 K was used in the measurements. Cooling of the sample stage was done by cryogenic N2 flow. Control and regulation of the temperature of the sample stage and the thermal shield, surrounding the sample stage, was performed using a “Lake Shore model 336” temperature controller with ± 0.5 K accuracy.
Electrical contact to the pins of a DUT was accomplished using four micromanipulated stages equipped with probe arms and 25 μm “continuously variable temperature probes” with tungsten tips. The whole electric circuitry was assembled using triaxial cables. A microscope (7:1 zoom), equipped with a CCD camera, light source, and monitor, was used for observation of the sample during contacting. During measurements, the sample was protected from outside illumination.
Electrical measurements were performed using a B1500A semiconductor Device Analyzer (Agilent) equipped with four 100 mA/100 V, 10 fA/0.5 μV resolution medium power source/monitor unit (SMU) modules and a multifrequency capacitance measurement unit. Measurements were performed using specially designed measurement routines written in the frame of the EasyEXPERT software installed on the B1500 setup.
4 Results and Discussion
4.1 Results for the Samples
The results of ID(VGF, k, T) measurements for EG sample are shown in Figure 2a for three temperature values (i.e., for 200, 300, and 400 K) and eight k values at each temperature (for k = 0 to 3 with step 0.5 and for kOC). The ID (VGF, kOC, T) dependencies are shown with solid lines for each T. The range of ID, where data for the IF,IB estimations are collected, is shown in Figure 2a by an arrow. Obtained STS(ID) dependencies for k = kOC values at three temperatures are shown in Figure 2b. The solid lines in Figure 2b show the fitted curves according to Equation (17). The interval between short vertical lines shows the range of ID used for DIF,IB(EIT) estimations in multi-T characterization mode.
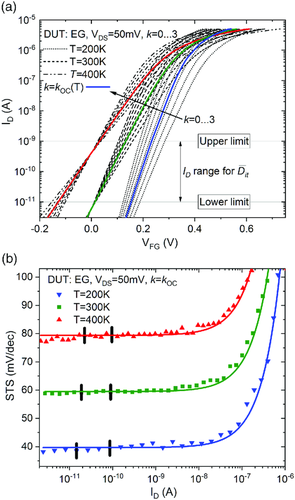
The results obtained for the SG and EG samples for FSCV + STS measurements at 300 K are included in Table 1. These results were obtained using measurement procedures similar to those described in refs. [9, 23, 37] and applying calculations presented in Section 3.1. The obtained EOT parameters of the stacks well correspond to those expected.
| Sample/parameter | SG | EG | |
|---|---|---|---|
| Front gate | FOX EOT [nm] | 1.01 | 3.1 |
|
[×1011 eV−1 cm−2] |
2.5 | 2.4 | |
| Back gate | BOX EOT [nm] | 21.8 | 20.0 |
|
[×1011 eV−1 cm−2] |
0.8 | 2.9 | |
Since the multi-T STS measurements are presented for the first time here, we will give more details on the data-processing procedures subsequently, together with the obtained results of the measurements. Because a set of the STS measurements at a single temperature and different k values is followed with the measurement at the optimal coupling conditions (kOC), where the increase in potential is equal for the BG and FG, we can apply that data for ΔEBG(T) and ΔEFG(T) estimation. Moreover, for the k = kOC conditions n = gmUT/ID ≈1 and the dependence simplifies further. For the back gate, the actual bias at k = kOC will be VBG = VFGkOC + VDS/2. It is also important to note that in Equation (19) the gm/ID ratio is contained; therefore, the actual distribution of the current in the channel, i.e., the value for α (see Section 2.2), is not essential for these energy calculations. To simplify the temperature dependence further, we can set the source–drain voltage VDS as a multiple of UT for each measurement temperature (see Equation (17)). We set VDS = 3UT in our experiments. Such a low VDS value prevents the emergence of such short-channel effects as the drain-induced barrier lowering and hot-carrier injection.
The trap density distributions are further calculated using the STS measured at optimal coupling conditions for each temperature. As before, we use data with the smallest currents from the sets here. Usually, eight to ten gm/Id values are averaged from the acceptable level of the signal-to-noise ratio in Id (VFG) measurements. These values are used in the calculation of the corresponding EIT from Equation (19) and DIF,IB(EIT) trap densities using the procedure presented in Section 2.2. The values for the can be found using a similar program to that presented in ref. 36.
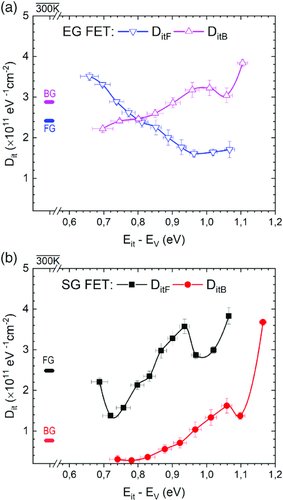
Distributions of trap densities for EG and SG samples are shown in Figure 3a,b respectively. In the same figure, the levels of average interface trap densities measured at 300 K are also shown in the left part of the figures for comparison.
4.2 Discussion
The aim of the this article is describing an updated characterization method of HKMG FDSOI FETs; therefore, we will discuss the obtained results for the FETs only briefly. Interestingly, the interface trap densities for the FG and BG in the case of EG DUT are almost equal, whereas in the case of SG DUT, this parameter for the FG is approximately three to four times larger in comparison to the BG of the same FET. It can be supposed that growth of additional silicon oxide at the FG suppresses the FG interface states, but causes an increase in the density of interface states at BOX. It should be noted that charge pumping measurements on similar samples with large gate areas also showed an increased density of interface states in the case of the EG DUT.
Comparison of DIT(EIT) dependences for FG and BG interfaces in the EG and SG samples with the averaged IF,IB levels (see Figure 3a,b and Table 1) shows the significant advantage of the multi-T measurements. Namely, for the SG DUT it appears that elevated trap density exists at ≈EV + 0.9 eV, which is suppressed in the EG DUT. Contrarily, DIT significantly increases to the center of the midgap in the case of the FG interface of the EG sample. This may correspond to the formation of Pb1-(AOD) interface states (see, e.g., ref. 40 and references therein) during the formation of the oxide near the GF in the EG sample. Interestingly, the level of defect density at the BG interface is substantially increased in the EG sample in comparison to that in the SG; however, the U-shape of the DIBG(EIT) dependence looks similar. Moreover, the peak in the DIBG(EIT) distribution between 1 and 1.1 eV also repeats in both samples.
4.3 Possible Applications of the Method and Limitations
The methodology described in Section 2.1 and 2.2 can be applied for characterization of FDSOI FET FG and BG interface trap densities in three different modes. Considering the purpose of the characterization, we can label those modes as a “monitoring,” “verification,” and “design” modes.
For relatively fast, even in-line, monitoring of product quality, the STS measurements under various k = VBG/VFG (e.g., 0–3 with step 0.5) and at a single temperature (e.g., for T = 300 K) should be performed and the value for kOC should be determined following the procedure described in ref. 9. After that, the averaged values for DIF and DIB can be determined using Equation (5)–(9). For this method, some preassumed or previously established parameters for the FET stack can be used. The limitations for this method are apparent. 1) The obtained trap densities strongly depend on the correctness of the used stack parameters. 2) The densities are averaged for a significant and generally unknown range of EIT. 3) All the stack parameters except trap densities are supposed to maintain the same values from sample to sample.
A more detailed check of the FET parameters can be accomplished, adding FSCV measurements prior to the STS monitoring mode. In this mode, first, the actual parameters of the stack are obtained using measurement procedures explained in refs. [32, 37] Further, these parameters are used for correct estimation of averaged trap density values in the monitoring mode. Therefore, intentional or unintentional process variations for samples may be tracked and analyzed. This possibility comes at the price of extended measurement time and fabrication of a particular group of structures for FSCV measurements inside every wafer or even every chip.
For the design of a newer/modified fabrication process, the detailed check may be augmented by STS measurements at several temperatures in the range 120–400 K (multi-T measurements). Such a study will provide distributions of interface trap densities at the FG and BG interfaces and will supply values for essential parameters of the stack, giving possibilities for modeling of the structure and finding possible ways for future improvements. These measurements require much longer time and, at least at present, require cutout of the chip from the wafer for effective temperature control during the test at low temperatures.
Next, we would like to formulate once more the limitations and assumptions that were used in the method. During our estimations, we assumed that carrier mobility in the channel in the applied regime and for the applied DUT dimensions is nearly independent of the measurement temperature following ref. 20. Moreover, we assumed that the fixed charges located in the front oxide are not affected by the change in temperature. It was also supposed that interface trap distributions are smooth enough in a way that for a small change in surface potential we can assume them to be nearly constant. The calculations are applicable only for the FD case when the effect of the depletion charge on the current in the channel can be ignored; i.e., the gate potential does not affect the charge and surface potential fluctuations caused by doping can be ignored. The DUTs are working out of the short-channel regime, and the VDS value significantly exceeds the thermal voltage. To avoid admixing of regular inversion channel current in the STS, only values of current slightly exceeding the noise values should be used in estimations.
The exact sensitivity limit and limitations related to the quality of an FET for the method are still to be established. From our preliminary tests, the method shows reliable results at the gate leakage under 1 mA cm−2 and for DIF and DIB levels below 5×1012 eV−1 cm−2. We should also remind the reader that for FETs with Lch > 100 nm the supposition about the independence of the carrier mobilities from the temperature will not be correct and may cause misinterpretation of the obtained STS data. It should also be noted that because expression (19) for EIT contains actual parameters of the FET (i.e., EOT, kOC, n, and ), the range of trap energies tested by measurement and the necessary energy resolution cannot be defined a priori. However, after obtaining the preliminary data (e.g., for the temperature range 120–450 K with a step 25 K), the FET can be remeasured at the specific temperatures.
5 Conclusion
Interface traps located at the front and back interfaces of the channel in HKMG FDSOI FETs were investigated using STS measured at several temperatures. The stack parameters of the FETs were characterized using the full-split CV method. The obtained results suggest that the applied methods are capable of providing essential information on the quality and properties of the devices. Namely, STS measurements of an FET at a single temperature provide averaged relative values for interface trap densities at front and back interfaces. These densities could be further specified if the FET stack parameters will be determined from the FSCV measurements for the FETs with a similar stack. Further, multi-T measurements supply information about interface trap density distribution at the front and back interfaces of the channel in a wide range of trap level energies and additional stack parameters for further performance modeling.
The studied methods can be applied in different characterization modes. The fast monitoring mode with STS measurements at a single temperature can supply relative information about device quality/compliance in-line. Combination of STS and FSCV allows obtaining specified values for averaged trap densities. Measurements in multi-T mode supply a broad range of information about stack and interface traps that will be helpful in device design.
Acknowledgements
This work was funded via subcontract from Globalfoundries Dresden Module One within the framework Important Project of Common European Interest (IPCEI) by the Federal Ministry for Economics and Energy (BMWi) and by the State of Saxony. The authors want to thank Jörg Weber (TU Dresden), Luca Pirro (Global Foundries), and Rolf Öttking (AQ Computare, Chemnitz) for thoughtful discussions and suggestions. Open access funding enabled and organized by Projekt DEAL.
Conflict of Interest
The authors declare no conflict of interest.