Viscoelastic properties and residual stresses in polyhedral oligomeric silsesquioxane-reinforced epoxy matrices
Abstract
Fiber-filled thermosetting polymer composites are extensively used in aerospace industries. One disadvantage of these materials is cure induced or thermally induced residual stresses in the matrix, which may result in deteriorated performance and premature failure. This article explores the use of epoxy/multifunctional polyhedral oligomeric silsesquioxane (POSS) nanocomposites as resins with reduced thermal stress coefficients that result in mitigated residual stresses. The effect of POSS loading on the thermal stress coefficient of the epoxy/POSS nanocomposite resins was investigated from below the β-relaxation to the α-relaxation, or glass transition temperature, (i.e., from −100 to 180 °C) by measuring the shear modulus and linear thermal expansion coefficient. The thermal stress coefficient of the epoxy/POSS nanocomposites is found to be a strong function of temperature, decreasing rapidly with decreasing temperature through the α-relaxation region, increasing in the vicinity of the β-relaxation, and then decreasing below the temperature associated with the peak in the β-relaxation. With increasing POSS content, the thermal stress coefficient is reduced compared with the neat resin in the vicinity of the α-relaxation; however, the thermal stress coefficient increases with increasing POSS content below the temperature of the β-relaxation peak. © 2008 Wiley Periodicals, Inc. J Polym Sci Part B: Polym Phys 46: 2719–2732, 2008
INTRODUCTION
Fiber-filled thermosetting resin composites are extensively used in the aerospace composite industry.1 However, these composites do not come without disadvantages. Residual stresses resulting from cure-induced or thermally induced differential volume changes between the resin and filler can lead to deteriorated performance and premature failure of these materials.2 One strategy to reduce such residual thermal stresses is to develop resins with a lower thermal stress coefficient and a lower thermal pressure coefficient by decreasing the product of the coefficient of linear thermal expansion and the Young's modulus (αE, for the thermal stress coefficient) or decreasing the product of the coefficient of thermal expansion and the bulk modulus (αK, for the thermal pressure coefficient). In fact, the aim of previous modeling work by Alcoutlabi et al.3 was to reduce residual stresses in a bismaleimide resin using a ring-opening spiro orthocarbonate monomer. In that work, isotropic residual stresses at room temperature after cure were found to depend primarily on thermal stresses and, hence, to be proportional to the glassy value of the thermal pressure coefficient, αK, which ranges from 3.5 × 10−4 to 9.5 × 10−4 GPa/K for commercial resins.3 Because of the fundamental significance of the thermal pressure coefficient, experimental measurements of αK have been carried out for rubbers,4, 5 other polymers such as poly(dimethyl siloxane),4, 6 polyoxyethylene,7 poly(vinyl methyl ether),8 polyethylene,9 and polystyrene.10 Recently, a novel technique was developed in our laboratories to measure the thermal pressure coefficient of thermosetting resins during cure and thermal cycling using an instrumented pressure vessel.11-13 In that work, we found that the thermal pressure coefficient of the liquid monomer was higher than that of the glassy polymer13 but we did not measure the property as a function of temperature or resin structure.
Here, we investigate modification of a resin system using nanoparticles to address the technological problem of residual stresses. The unique properties of nanoparticle-filled matrices generally include significant modulus improvements and a reduced linear thermal expansion coefficient, even at very low nanoparticle loadings.14-16 However, the effect on the residual thermal stress coefficients in nanoparticle-filled resins has not been well documented. In particular, we are interested in the influence of polyhedral oligomeric silsesquioxane (POSS) nanoparticles,17-19 which combine a hybrid inorganic–organic composition with nanosized cage structures. Compared with the layered silicates,20-23 POSS nanoparticles are nearly spherical and relatively soft, and because they can be functionalized, the interface can be tailored—an important issue since the interfacial properties become extremely important for polymer nanocomposites because of the large surface to volume ratio of the nanoparticles. In addition, the functionalization can facilitate dispersion. We hypothesize that the unique structures and properties of POSS nanoparticles may provide the opportunity to develop polymer/POSS nanocomposites with reduced thermal stress and pressure coefficients.
A number of studies have incorporated POSS into epoxy systems to form nanocomposites and the thermomechanical properties have been extensively investigated.24-44 It has been found that the glass transition temperature of POSS-reinforced epoxy nanocomposites either increases,24, 28, 29, 35, 38 decreases,27, 31, 38-40 stays unchanged,30, 32, 37, 39, or even disappears37 with the addition of POSS depending on the chemical structure of the functional group (R group) on the POSS and the POSS loading. In general, the glass transition temperature of the nanocomposites decreases when the R group on the POSS is long and flexible and a “soft” interface can be formed between the nanoparticle and matrix;27, 32, 40, 45 on the other hand, Tg increases if the interface is rigid and the polymer chain motions are hindered by their covalent bonding to POSS clusters. However, in some epoxy/POSS nanocomposite systems, even though the interface is expected to be rigid, a decrease in Tg is observed39 possibly due to the incomplete reaction of the functional groups on the POSS.18, 24 In addition, when the POSS loading is high (≥ 20 mol %), the glass transition of epoxy/octa(dimethylsiloxy butyl) epoxide nanocomposites disappears as measured by dynamic mechanical analysis (DMA) or differential scanning calorimetry (DSC) due to restricted segmental motion caused by the rigid POSS cage and a very high crosslink density.37
The moduli of the POSS-filled nanocomposites similarly depend on the POSS structures. The glassy modulus of the nanocomposites is found to either increase due to the nanoreinforcement of the nanoparticles27, 31, 39 or decrease;37 furthermore, the rubbery modulus also either increases presumably due to the increased crosslink density or the reinforcement of the nanoparticles28, 30, 43 or decreases due to the decreased crosslink density associated with the flexible structure of the POSS.27 One study also showed that the instantaneous modulus of the nanocomposites is not affected by the incorporation of POSS, although the physical aging process of the composites in the glassy state was found to be retarded.29
In addition to influencing the glass transition temperature and modulus, the addition of nanoparticles may influence another important property of epoxy matrices, the subglass transition β-relaxation. The β-relaxation of thermosetting materials may be important for the performance of these materials at lower temperatures; in fact, the targeted applications of the nanocomposites developed in the current study are for aerospace composites, which may be subjected to environments far below ambient temperature. For amine-cured epoxy systems, the β-relaxation occurs at temperatures from −100 to −30 °C.46 The molecular mechanisms for the β-relaxation in diglycidyl ether bisphenol A (DGEBA)-type epoxy/amine system have been attributed to the glyceryl segments, OCH2CH(OH)CH247-50 or glyceryl and diphenylpropane units, OC6H4C(CH3)2C6H4.46, 51-53 The β-relaxation peak temperature and peak intensity can be affected by curing agent structure,54 cure conditions,46, 53, 55-59 and moisture absorption in the absence of fillers.47 The β-relaxation peak temperature increases with degree of cure,53, 55-59 decreases with insufficient amount of curing agent,46, 56, 57 and is not affected by excessive amount of curing agent.56, 57 The intensity of the β-relaxation increases with degree of cure,55-59 water absorption,47 and flexibility of the curing agent,54 and it decreases with insufficient amount of curing agent.46, 56, 57 In addition, fillers of micrometer and nanometer sizes may also influence the β-relaxation in epoxy matrices. The addition of 15-μm-sized aluminum particles was found to cause a slight increase in peak temperature and depression in peak intensity of the β-relaxation.58 The effect of POSS nanoparticles on the β-relaxation of DGEBA-type epoxy matrices has been investigated by a few authors using DMA and different phenomena have been observed for various systems.31, 32, 39, 40 A shift of the peak temperature of the β-relaxation was attributed to an increased free volume introduced by the POSS cage for DGEBA/benzyldimethylamine (BDMA)/hydroxyl group-functionalized POSS with bulky and flexible organic substituents,40 DGEBA/DDM/phenyltrisilanol-POSS,31 and DGEBA/DDM/aminophenyl-POSS systems.39 In another study, the β-relaxation of epoxy matrices for a DGEBA/DDM/octa(propylglycidyl ether) POSS (OpePOSS) system split into two peaks, with the β-relaxation shifting to lower temperatures presumably because of the increased mobility due to the plasticization effect of the R group on the POSS and the β′-relaxation shifting to higher temperatures due to the rigidity of the POSS cage which restricts the polymer chain motions.32 In three of these studies, the glass transition temperature Tg decreased with POSS content;31, 39, 40 whereas the Tg of DGEBA/DDM/OpePOSS is invariant with POSS content below 30 wt % and it decreases above 30 wt % up to 40 wt %.32 The DGEBA/BDMA/hydroxyl group-functionalized POSS system showed a depressed β-relaxation peak intensity with increasing POSS content,40 whereas the other three systems did not exhibit any trend.31, 32, 39
In the current study, we investigate the effects of POSS content on the shear viscoelastic properties, the coefficient of thermal expansion (CTE), the glass transition temperature, and the β-relaxation of an epoxy resin. These properties are chosen because they impact the residual stresses that would occur in fiber-reinforced composites using an epoxy/POSS nanocomposite as matrix. The tetrafunctional aromatic diamine/DGEBA-type epoxy resin used for the study was selected because its cure kinetics60 and thermomechanical properties61, 62 have been well documented. We examine the effects of POSS loading using a multifunctional POSS, in which each nanosized cage bears 8–12 epoxide groups via a flexible carbon ether linkage. We chose this POSS because it is compatible with the epoxy resin.
EXPERIMENTAL
Materials
The epoxy resin monomer used is diglycidyl ether of bisphenol A (DGEBA) (DER332 from Dow Chemical Co.), with an epoxide equivalent weight of 171.9 g/equiv. The POSS used is a polyepoxyglycidyl silsesquioxane cage mixture (EP0409 glycidyl POSS® cage mixture, from Hybrid Plastics; lot number M022707), which according to the manufacturer includes ∼ 3 wt % octaepoxycyclohexyl POSS, 54 wt % decaepoxycyclohexyl POSS, 13 wt % dodecaepoxycyclohexyl POSS, and 30 wt % oligomers (e.g., dimers of the octa-, deca-, and dodeca-epoxycyclohexyl POSS molecules). The glycidyl POSS cage mixture has an epoxide equivalent weight of 167 g/equiv. The average functionality of the material is calculated to be 11.8 assuming that the oligomers are dimers of the octa-, deca-, and dodeca-POSS occurring with the same probability as their presence in the cage mixture [e.g., 3/0.7 = 4 wt % of the oligomer is assumed to be octaepoxycyclohexyl POSS, 77 wt % is assumed to be dimer of the deca-POSS, and 19 wt % is assumed to be dimer of the dodeca-POSS). Weight percentages ranging from 0.0 to 10.0% of POSS was incorporated into the epoxy system to form nanocomposites. The epoxy resin/POSS system was cured with a stoichiometric amount of tetrafunctional aromatic diamine, trimethylene glycol di-p-aminobenzoate, with an equivalent weight of 157 g/equiv. (Versalink 740M from Air Products). We note that the amount of epoxide groups from both epoxy resin and POSS were taken into account to determine the amount of curing agent. The molecular structures of the investigated epoxy, aromatic diamine, and POSS are shown in Figure 1.
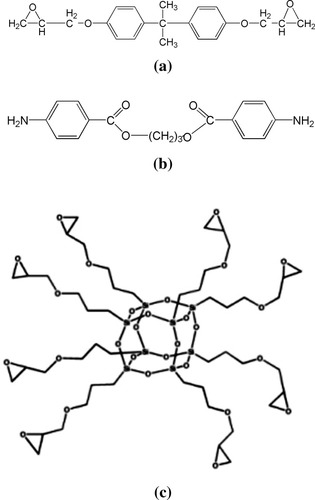
Molecular structure of resin matrix, curing agent, and nanoparticle: (a) diglycidyl ether of bisphenol A (DGEBA); (b) trimethylene glycol di-p-aminobenzoate; and (c) glycidyl POSS® cage mixture.
Curing of Epoxy/POSS Nanocomposites
Stoichiometric amounts of epoxy, aromatic diamine, and POSS were vigorously stirred in a vial at 100 °C for 30 min. The mixture was subsequently vacuum devolatilized at room temperature for 30 min and then at 100 °C until there were no visible air bubbles. The mixture was transferred into a glass tube with inner surfaces coated with silicon oil to prevent sample cracking during the cure and subsequent cooling process. Curing was performed in a temperature programmable oven. A ramp-hold-ramp-hold-ramp-hold-cool cure cycle was used with the first isothermal step performed at 100 °C for 1000 min, the second isothermal step was at 160 °C for 300 min, and the third isothermal step was at 180 °C for 48 h. The heating and cooling rates were 1 K/min, although free cooling after cure was applied below 100 °C because a cooling rate of 1 K/min could not be achieved with the oven below this temperature. The epoxy/POSS nanocomposite with 10% POSS was further postcured at Tg + 10 °C (190 °C) for 36 h to reach full conversion; a longer cure time and/or higher cure temperature has also been found in other work30 to be required for the nanocomposites to reach the same degree of crosslinking as the neat system. The samples were cured in their glass tubes under air atmosphere, but the top few centimeters of sample (that was potentially exposed to air) were not used.
Glass Transition Temperature (Tg) Measurement
The limiting fictive temperature (T′f) of the epoxy/POSS nanocomposites was measured on heating at 10 K/min after cooling at 10 K/min on a Mettler Toledo DSC (DSC823e) with a Julabo FT100 intracooler and nitrogen purge. The limiting fictive temperature approximates the glass transition temperature (Tg),63 and we refer to T′f as the glass transition temperature (Tg) in the text. The temperature of the DSC was calibrated with indium and tin on heating at 10 K/min and the heat flow of the DSC was calibrated with indium. In addition to the DSC, the glass transition temperature was also determined by rheological measurements from the peak of the loss modulus and tan δ measured at a given frequency.
Density of Epoxy/POSS Nanocomposites
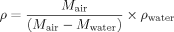 (1)
(1)Stress Relaxation and Dynamic Measurements
Stress relaxation and dynamic frequency sweep tests were performed on an Advanced Rheometric Expansion System (ARES, TA Instruments) using a cylindrical sample with a diameter of 6.35 mm and a length of 40 mm. The ARES instrument is known to be somewhat compliant and the sample geometry was chosen to minimize instrument compliance effects (less than 5%). As a result, even for the highest sample stiffness, the error in modulus due to instrument compliance was negligible.65 The strain was controlled at 0.02% to ensure the measurements are in the linear viscoelastic regime. The testing temperatures ranged from Tg − 20 °C to Tg + 20 °C. At the test temperatures below Tg + 10 °C, the sample was held at Tg + 10 °C for 30 min to erase the thermal history and then quenched to the test temperature and held isothermally for 120 min before beginning the measurement. When the test temperatures are equal or above Tg + 10 °C, the sample was held isothermally at the test temperature for 30 min before beginning the measurement. The stress relaxation measurements were carried out for 6 min and the frequency for the dynamic measurements ranges from 0.3 to 30 rad/s. The total measuring time is around 12 min, 10% of the holding time before measurement, which follows Struik's protocol.66
Dynamic temperature ramps were also performed on the ARES to investigate the effect of POSS loading on the β-relaxation of the epoxy matrices. The sample dimension is the same as that used for the stress relaxation and dynamic frequency sweep measurements. The strain was fixed at 0.01% to obtain a moderate torque which does not cause sample slip, a phenomenon that could occur during the cooling experiment because of sample contraction. The sample was first heated to 180 °C, approximately the glass transition temperature of the epoxy and epoxy/POSS nanocomposites, and was subsequently cooled to −100 °C at 1 K/min at a constant frequency of 1 Hz. Note that the thermal gradient in the sample at this cooling rate is less than 1 K. Autotension in compression mode was applied to minimize the normal force caused by sample contraction upon cooling. The storage modulus G′, loss modulus G″, and tan δ as a function of temperature were recorded. The glass transition temperature and peak temperature of the β-relaxation were determined from these measurements. In addition, the gap change was recorded as a function of temperature and this was used to determine the thermal expansion coefficient as described below.
Linear Coefficient of Thermal Expansion (CTE) Measurement
The linear coefficient of thermal expansion was determined from the temperature ramp test performed on the Advanced Rheometric Expansion System (ARES) based on the gap change as a function of temperature. The thermal expansion of the stainless steel fixtures and other parts of the ARES were calibrated using a cylinder of fused quartz (GE type 214) with a diameter of 4 mm and a length of 10 mm. The linear coefficient of thermal expansion of fused quartz is a function of temperature, and it increases from −3 × 10−7 to 8 × 10−7 K−1 as the temperature increases from −100 to 180 °C.67, 68 Two replicate runs for the quartz were performed. The actual length change with temperature of the sample is obtained by subtracting that of the fixtures and other parts of the instrument from the total length change measured. The standard deviation in the linear thermal expansion coefficient is estimated to be ±3 × 10−6 K−1 at 0 °C based on measurements made on two neat epoxy samples.
The linear coefficients of thermal expansion of the epoxy/POSS nanocomposites obtained using the ARES were compared with the data measured on a Q 400 Thermomechanical Analyzer (TMA from TA Instruments). In that measurement, a flat tipped standard expansion probe was used for the cylindrical samples having a diameter of 6.35 mm and a length of 10 mm. A force of 0.05 N was applied during the measurements. Nitrogen with a flow rate of 100 mL/min was used as purge gas. The sample was heated from 30 to 200 °C at 10 K/min and cooled using nitrogen to 40 °C, and the glassy CTE was determined in the range of 60 to 120 °C on the second heating run from 40 to 220 °C at 10 K/min. The precision of the CTE values from the Q 400 TMA are reported to be ± 2% by TA Instruments.69
RESULTS
Viscoelastic Properties of Epoxy and Epoxy/POSS Nanocomposites as a Function of Frequency
The viscoelastic properties for the fully cured neat (unfilled) epoxy as measured at temperatures ranging from 158 to 198 °C are shown in Figures 2-4. Figures 2 and 3 show the storage modulus and loss modulus as a function of frequency. Glassy behavior is observed at low temperatures and high frequencies, and rubbery behavior is observed at high temperatures and low frequencies. The loss modulus goes through a maximum as the testing temperature increases through the glass transition region. As expected, the relaxation modulus (shown in Fig. 4) decreases with increasing time and temperature with glassy behavior observed at short times and low testing temperatures and rubbery behavior observed at long times and high temperatures.
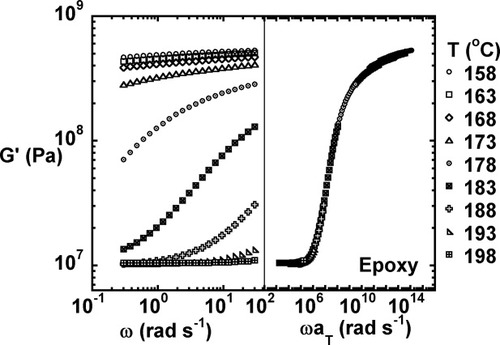
Storage modulus as a function of temperature and the master curve for the fully cured unmodified epoxy.
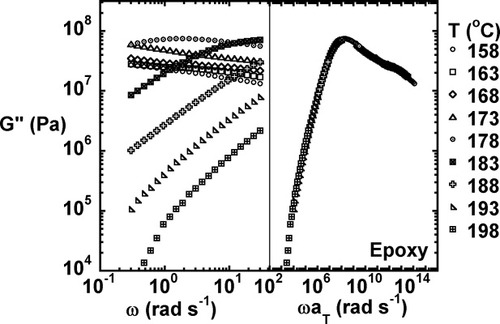
Loss modulus as a function of temperature and the master curve for the fully cured unmodified epoxy.
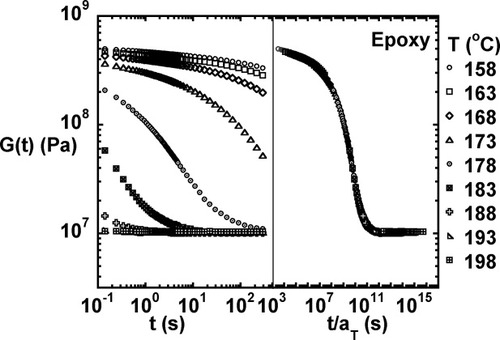
Relaxation modulus as a function of temperature and the master curve for the fully cured unmodified epoxy.
To compare the effect of the POSS content on the viscoelastic properties, we examine the time-temperature superposed master curves shown in Figures 5-8 for G′, G″, tan δ, and G(t), respectively. The reference temperature for each master curve is the Tg, as measured by DSC and reported in Table 1; we note here that the Tg values increase only a few degrees with the addition of POSS—this is discussed in more detail later. Figures 5 and 8 show that the glassy modulus just below Tg decreases slightly with increasing POSS content; a value of ∼ 530 MPa is obtained for the neat epoxy and a value ∼ 10% lower is obtained for the system containing 10% POSS. This unexpected decrease in the shear modulus may be due to the soft interface of these multifunctional POSS particles. The glassy modulus behavior at 1 Hz and at Tg − 20 K of the epoxy/POSS nanocomposites as a function of POSS content is summarized in Table 2.
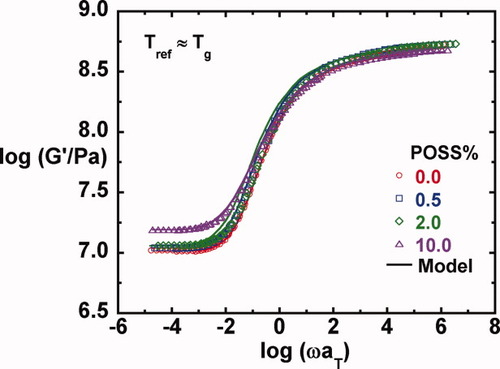
Master curves and their model fits for the storage modulus as a function of POSS loading.
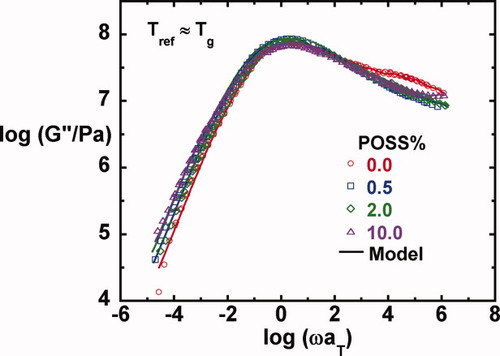
Master curves and their model fits for the loss modulus as a function of POSS loading.
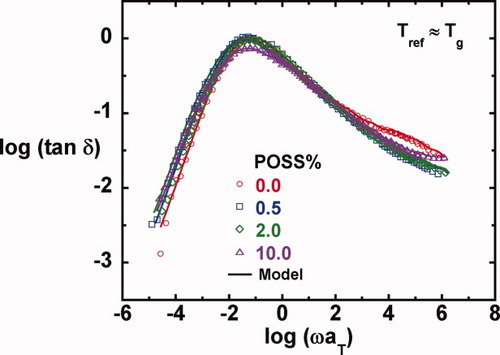
Master curves and their model fits for the loss tangent as a function of POSS loading.
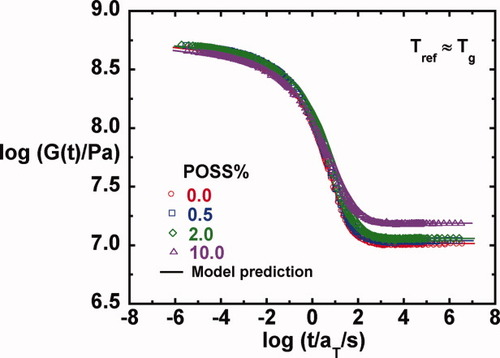
Master curves and their model predictions for the storage modulus as a function of POSS loading.
| Glycidyl POSS® Cage Mixture (wt %) | Tg,DSC (Qc = 10 K/min) (°C) | Tg,G″ (1 Hz) (°C) | Tg,tan δ (1 Hz) (°C) | Tβ,G″ (1 Hz) (°C) | Tβ,tan δ (1 Hz) (°C) |
|---|---|---|---|---|---|
| 0 | 177.6 ± 0.3 | 167.5 | 185.6 | −43.2 | −37.4 |
| 0.5 | 178.3 ± 0.04 | 173.5 | 186.1 | −53.3 | −44.6 |
| 2.0 | 178.6 ± 0.1 | 172.7 | 186.1 | −53.9 | −43.4 |
| 10.0 | 180.0 ± 0.4 | 174.4 | 187.5 | −53.4 | −44.8 |
- a The Tgs measured by DSC are obtained from at least two replicates, whereas the Tg and Tβ values from rheological measurements are obtained from one measurement only.
| Glycidyl POSS® Cage Mixture (wt %) | Gg (MPa) at Tg −20 K (Exp.) | Gg (MPa) at −80 °C (Exp.) | Gr (MPa) (Exp.) | Gr (MPa) at Tg + 20 K (Exp.) | Gr (MPa) at Tg + 20 K (Cal.) |
|---|---|---|---|---|---|
| 0 | 526 ± 4 | 1240 | 0.022 T/K ± 0.062 | 10.4 | 10.6 |
| 0.5 | 533 ± 1 | 1340 | 0.023 T/K ± 0.040 | 10.8 | 10.7 |
| 2.0 | 535 ± 2 | 1410 ± 16 | 0.025 T/K ± 0.061 | 11.3 | 11.1 |
| 10.0 | 477 ± 2 | 1330 | 0.033 T/K ± 0.034 | 15.6 | 15.6 |
- a The standard deviations for Gg at Tg – 20 K and for Gr were calculated from the scatter in the limiting high-frequency and long-time values obtained from dynamic measurements and stress relaxation measurements, respectively. The standard deviation for the shear modulus at −80 °C was calculated from two measurements on the same epoxy/POSS nanocomposite with 2.0% of POSS.
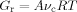 (2)
(2)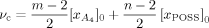 (3)
(3)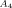 ]0 and [xPOSS]0 are the molar concentrations (mole/m3) of the diamine and POSS molecules. Values for the prefactor A and the effective functionality of the POSS (n) can be estimated by minimizing χ2 (i.e., the least square difference between the experimental and calculated rubbery moduli) for all of the epoxy/POSS nanocomposites; they are found to be 2.0 and 11.2, respectively. The calculated rubbery moduli based on eqs (2) and (3) are listed in Table 2 and they agree well with the experimental values.
]0 and [xPOSS]0 are the molar concentrations (mole/m3) of the diamine and POSS molecules. Values for the prefactor A and the effective functionality of the POSS (n) can be estimated by minimizing χ2 (i.e., the least square difference between the experimental and calculated rubbery moduli) for all of the epoxy/POSS nanocomposites; they are found to be 2.0 and 11.2, respectively. The calculated rubbery moduli based on eqs (2) and (3) are listed in Table 2 and they agree well with the experimental values.The prefactor A obtained in the current study is higher than the value of 1.36 reported by Katz and Tobolsky for a tetrafunctional amine cured epoxy system.72-74 However, the calculation of the effective concentration of chemical crosslinks from the stoichiometric amount of amine in the study by Katz and Tobolsky used a weighing factor of m/2 instead of (m − 2)/m71 for the network chains72 as suggested by Duiser and Starverman75 and Graessley.76 As a result, for a tetrafunctional amine, Katz and Tobolsky overpredicted the effective concentration of chemical crosslinks from the amine and underestimated the prefactor A.
The calculated value of 11.2 for the effective functionality of the POSS is slightly lower than the value of 11.8 expected based on the functionality and distribution of the POSS cages in the mixture. It is important to note that our calculation of n = 11.2 attributes all of the increase in the rubbery modulus to an increase in crosslink density and it assumes that the rubber density changes with nanoparticle concentration in a way similar to the change measured in the glass density (see later). In addition to ignoring any reinforcement of the resin by the nanoparticles, the calculation based on eqs 2 and 3 also ignores the possibility of ring formation prior to gelation caused by the reaction of two (or more) epoxides on a given POSS cage with aminohydrogens from a single diamine molecule; in fact, such ring formation has been observed in molecular simulations of this or similar system77, 78 and such rings would result in mechanically ineffective loops that would decrease the effective functionality of the POSS. We suggest that perhaps in this system the increase in modulus due to nanoparticle reinforcement of the resin is offset by decreases resulting from loop formation; hence, we observe that the effective functionality appears to be only slightly lower than the value expected based on the POSS molecular structure. Further work would be required to separate the relative effects.
On comparison of the master curves for the loss moduli in Figure 6 and for tan δ in Figure 7, we observe that the primary or α-relaxation broadens slightly with increasing POSS content on the low frequency side. The broadening of the α-relaxation with increasing nanoparticle concentration has been reported in the literature,28, 30, 39, 79, 80 although opposite results have also been reported,40 and in some cases, no changes or no trend is observed.28, 31, 32 In addition, the weak shoulder from the β-relaxation observed in the unmodified epoxy in the high frequency region disappears for the nanocomposites. Here, we comment that successful construction of master curves for all the shear responses as well as the loss tangent when referenced to Tg suggests that time-temperature81 and time-crosslink density superposition principles82, 83 are reasonable in the epoxy/POSS nanocomposite systems in the region of the α-relaxation; this is in part due to the wide separation between the α- and β-relaxations in this system.
The shift factors used to reduce the viscoelastic responses are plotted against T − Tg, the temperature departure from Tg, in Figure 9. The shift factors for G′, G″, and G(t) for each composite agree very well, indicating that the data are internally consistent. Upon shifting relative to the Tg, the temperature dependence of the shift factors does not vary with POSS content. At temperatures above Tg − 10 °C, WLF84 temperature dependence is observed; whereas at temperatures below Tg − 10 °C, an Arrhenius dependence is observed.
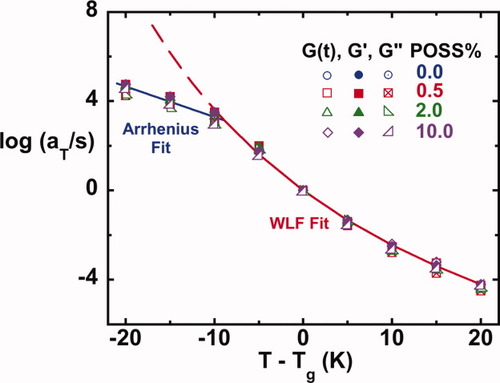
Shift factors as a function of the temperature departure from Tg for all the systems. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
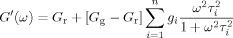 (4)
(4)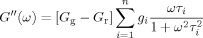 (5)
(5)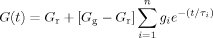 (6)
(6)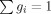 . The master curves for the storage and loss moduli, G′ and G″ were fit to such a model using the IRIS 2007 software package by Winter et al.86 to obtain the discrete relaxation spectra shown in Figure 10. The solid lines in Figures 5-7 for G′, G″, and tan δ show that the model describes the data well; in addition, the relaxation modulus G(t) predicted using the same relaxation spectra also gives a good description of that data, as shown in Figure 8.
. The master curves for the storage and loss moduli, G′ and G″ were fit to such a model using the IRIS 2007 software package by Winter et al.86 to obtain the discrete relaxation spectra shown in Figure 10. The solid lines in Figures 5-7 for G′, G″, and tan δ show that the model describes the data well; in addition, the relaxation modulus G(t) predicted using the same relaxation spectra also gives a good description of that data, as shown in Figure 8.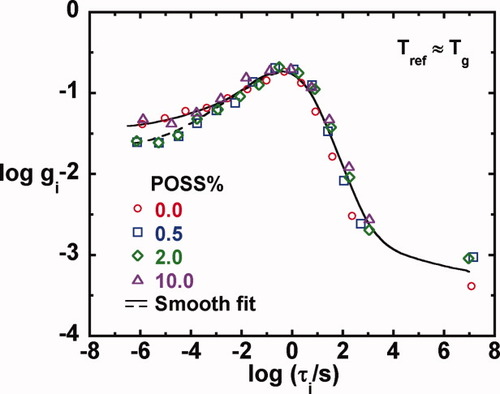
Discrete relaxation spectra as a function of POSS loading. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
Viscoelastic Properties of Epoxy/POSS Nanocomposites as a Function of Temperature
The temperature dependence of the 1 Hz storage and loss moduli for the epoxy/POSS nanocomposites having various POSS contents are shown in Figures 11(a,b), respectively. The data were obtained upon cooling at 1 K/min. Figure 11(a) shows that as the temperature decreases from the glass transition region, the storage modulus increases and reaches the glassy plateau. As shown previously, the glassy modulus just below Tg decreases slightly with increasing POSS content. A second transition, the β-relaxation, appears as the temperature decreases further. The glassy modulus below the β-relaxation (Gg,β at −80 °C) for the epoxy/POSS nanocomposites increases by ∼ 10% compared with the neat unfilled system; values of the modulus at −80 °C are listed in Table 2 for each sample.
(a) Storage modulus and (b) loss modulus as a function of temperature measured at 1 K/min on cooling for epoxy/POSS nanocomposites with various POSS loadings. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
The loss modulus as a function of temperature shown in Figure 11(b) shows two maxima, corresponding to the α-and β-relaxations. The glass transition temperature increases with increasing POSS content: for the epoxy/10% POSS nanocomposites, a 7 K increase in Tg is observed based on the G″ measurements and a 2.4 K increase is found using DSC. The magnitude of the glass transition temperature depends on measurement technique, and in this work, the value determined based on the loss modulus from rheological measurements is the lowest, the value from DSC is in the middle, and the value from tan δ is the highest. This observation is expected since different techniques weigh the distribution of relaxation times differently.87-89 The increase of the glass transition temperature with POSS content in this study is similar but slightly smaller than that found in the literature, in which a 7.7 K (based on DSC measurement) increase was reported for an DGEBA epoxy system with 10 wt % addition of monofunctional POSS.29 The glass transition temperature of epoxy/POSS nanocomposites is determined by several competing factors: (1) the POSS cages hinder the motion of the polymer chains giving rise to an increased Tg, (2) the bulky POSS cages increase the free volume of the system resulting in a lowered Tg,38 (3) the rigidity of interlayer between the POSS and the polymer matrix can cause Tg to increase or decrease, the latter of which was referred to as an internal plasticization effect,32 and (4) the multifunctionality of the POSS has the effect of increasing the effective crosslink density (increasing functionality of the junctions) and this would be expected to increase the Tg.90 As a result, an increase, no change, or decrease in the glass transition temperature of polymer/POSS nanocomposites are all possible outcomes. The glass transition temperatures measured from DSC and dynamic mechanical measurements along with the β-relaxation peak temperature of the epoxy/POSS nanocomposites are tabulated in Table 1.
The β-relaxation of the neat epoxy occurs at around −50 °C based on the peak in G″ (and at −35 °C based on the peak in tan δ); these values agree with those reported for the same epoxy by Wisanrakkit and Gillham61 as measured on cooling at 1 K/min and at 2.3 Hz using torsional braid analysis (TBA). With increasing POSS content, the β-relaxation shifts to lower temperatures. The maximum temperature shift for the epoxy nanocomposites with 10% of POSS is ∼ 10 K as shown in Figure 11(b). This finding is also consistent with the master curves of G″ obtained from isothermal dynamic measurements as shown in Figure 6, in which the neat epoxy shows the beginning of a β-relaxation in the frequency range investigated, whereas nothing is seen for the nanocomposites. The absence of the β-relaxation in the nanocomposites in the frequency range investigated could be due to the suppression of the β-relaxation or a shift to higher frequency or lower temperature. The latter is the case as confirmed by the dynamic temperature ramp study. The difference in the relaxation spectra between the neat epoxy and the nanocomposites at short times, as shown in Figure 10, also occurs because of the β-relaxation. The peak temperature depression of β-relaxation in the nanocomposites may be attributed to the increased mobility of the glyceryl segments, OCH2CH(OH) CH2, and/or diphenylpropane units, OC6H4C(CH3)2C6H4, of the epoxy matrices presumably due to the increased free volume resulting from the presence of the bulky POSS cages and/or the flexible chains on the POSS nanocages. The peak intensity of the β-relaxation seems to increase with POSS content although not systematically, in agreement with some literature reports.31, 32, 39 In addition, G″ broadens with increasing POSS content in the β-transition region; this experimental observation cannot be explained to the best of our knowledge. Despite the depressed β-relaxation peak temperature, the glass transition temperature of the current nanocomposites increases with increasing POSS content implying that the mobility of the molecular segments on the different length scales relevant to the α- and β-relaxations is influenced by the POSS molecule in different ways.
Density of Epoxy/POSS Nanocomposites
The density of the epoxy/POSS nanocomposites at room temperature increases by 9% for the system with 10% POSS loading as shown in Table 3, and in agreement with the findings for other epoxy/POSS nanocomposite systems.25, 40
| Glycidyl POSS® Cage Mixture (wt %) | Density (g/cm3) |
|---|---|
| 0 | 1.35 ± 0.02 |
| 0.5 | 1.34 ± 0.004 |
| 2.0 | 1.33 ± 0.03 |
| 10.0 | 1.47 ± 0.08 |
Thermal Stress Coefficient of Epoxy/POSS Nanocomposites
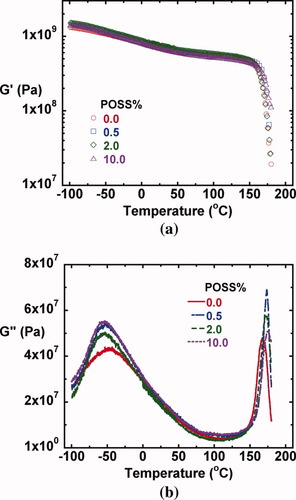
The linear coefficient of thermal expansion (CTE) as a function of temperature from below the β-relaxation to the vicinity of the glass transition temperature (−80 to 150 °C) for the epoxy/POSS nanocomposites with various POSS contents are shown in Figure 12. The data obtained using the ARES is comparable with that from TMA. The linear coefficient of thermal expansion for the epoxy/POSS nanocomposites increases with increasing temperature with a slight leveling off in the temperature range between the β and α-relaxations. The value also appears to be a weak function of POSS content. At temperatures close to the β-relaxation, the CTE does not vary with POSS content significantly, but as the temperature increases to the vicinity of the glass transition temperature, the CTE decreases with increasing POSS content, perhaps due to the constraint from the hard silicon-oxygen POSS cage similar to conventional nanoparticles such as clay or layered silicates.14-16
Linear thermal expansion coefficient as a function of temperature from −80 to 150 °C for epoxy/POSS nanocomposites with various POSS contents. The standard deviation in the linear thermal expansion coefficient is estimated to be ±2.96 × 10−6 K−1 at 0 °C based on the measurements on two neat epoxy samples. The dashed lines for epoxy/POSS nanocomposites with 0.0% and 10.0% of POSS are to guide the eyes. Solid symbols are the data obtained from ARES and open symbols are the results from TMA. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
It is important to note that the thermal expansion coefficient and Young's modulus (or shear modulus) usually change in opposite directions,14-16 i.e., one increases and the other decreases. However, the epoxy/POSS nanocomposites show decreases in both shear modulus [Fig. 11(a)] and linear thermal expansion coefficient (Fig. 12) in the vicinity of the glass transition temperature, and increases in shear modulus and no change in linear thermal expansion coefficient below the β-relaxation region. In our case, we attribute the fact that α and G do not change in opposite directions to the unique structure of the POSS and its interface which have competing influences on the CTE and modulus, and the magnitude of these effects changes with temperature. Similarly, Abdalla et al.14 found an increase in both the Young's modulus and the thermal expansion coefficient in polyimide/organically modified montmorillonite nanocomposites (OLS/PMR-15); however, in their case, they attributed the increase in CTE to the degradation of the modifier.
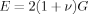 (7)
(7)The thermal stress coefficient as a function of temperature of the epoxy/POSS nanocomposites is plotted in Figure 13. The temperature and POSS content both affect the thermal stress coefficients of the epoxy/POSS nanocomposites although the effect of temperature is stronger. As the temperature increases, the thermal stress coefficient goes through two maxima, corresponding to the two relaxations. The thermal stress coefficient in the vicinity of the glass transition is higher than that in the β-relaxation region. At temperatures near to the β-relaxation, the glassy modulus of the epoxy/POSS nanocomposites increases compared with that of the neat resin as shown in Figure 11(a). The CTE in this temperature region does not vary significantly with POSS content (Fig. 12). Consequently, the product of CTE and G increases by 23% below the β-relaxation for the 10% POSS sample compared with the neat resin.
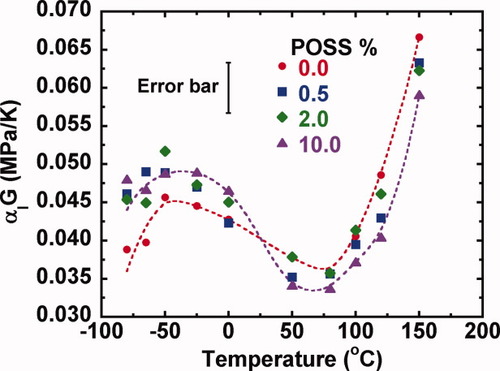
The thermal residual stress as a function of POSS content from −80 to 150 °C. The standard deviation in the thermal stress coefficient is estimated to be ± 0.0033 (MPa/K) at 0 °C based on the measurements on two neat epoxy samples. The dashed lines for epoxy/POSS nanocomposites with 0.0% and 10.0% of POSS are to guide the eyes. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
In the vicinity of the glass transition temperature, as shown previously in Figure 11(a), the glassy modulus decreases slightly with increasing POSS content, whereas the coefficient of thermal expansion decreases with increasing POSS content as shown in Figure 12; as a result, the thermal stress coefficient (as estimated by the product of CTE and G) is reduced at a 10% POSS loading, boding well for decreases in thermal residual stress in this temperature range. Although the reduction is similar to the size of the error bars, we suggest that the trend is real. Our interpretation is backed up by other recent data from our laboratory showing that the thermal pressure coefficient (the product of the volumetric coefficient of thermal expansion and the bulk modulus) decreases by 14% at 10% POSS loading in the temperature range below Tg.91 Even though the reduction in the product of the glassy linear coefficient of thermal expansion and glassy shear modulus in the vicinity of glass transition seems somewhat small, being only 13%, such a change can actually be significant for increasing material lifetime. For example, the logarithmic time to failure of polymeric resins, can be represented as a power law in the stress,92-94 and the exponent on the stress can be as strong as −19 for PMMA92 even though further experimental work is warranted to confirm the anticipated improvement in the time to failure for epoxy/POSS nanocomposites.
SUMMARY AND CONCLUSIONS
The shear viscoelastic responses and the coefficients of thermal expansion for fully cured epoxy/polyhedral oligomeric silsesquioxane (POSS) nanocomposites are reported as a function of POSS content. The viscoelastic data show time-temperature and time-crosslink density superposition in the region of the α-relaxation with only a slight broadening of the relaxation time distribution with increasing POSS content; however, the β-relaxation is shifted to higher frequencies or lower temperatures with increasing POSS content. The rubbery modulus increases with POSS concentration; the data can be fit assuming an effective functionality of 11.2 for the POSS. This value is consistent with the value of 11.8 expected based on the POSS molecular structure indicating that perhaps in this system the increase in modulus due to nanoparticle reinforcement of the resin is offset by decreases resulting from loop formation. The glassy modulus decreases with increasing POSS content in the vicinity of the α-relaxation, but it increases for a 10% POSS content in the vicinity of the β-relaxation. The coefficient of thermal expansion is found to be a strong function of temperature and a weak function of POSS concentration. The product of the CTE and the glassy modulus decreases for the sample containing 10% POSS compared with the neat resin in the vicinity of glass transition; the result is expected to lead to reduced thermal stresses in composite applications. However, the thermal stress coefficient increases in the β-relaxation region for the 10% POSS loading, which is undesirable for cryogenic applications.
Acknowledgements
Funding from National Aeronautics and Space Administration (NASA, contract number NNX07AD44A) is greatly acknowledged. The authors thank K. Mohomed from TA Instruments for measuring the coefficient of thermal expansion and S. Kohl and R. Kern for their help in facilitating the measurement.




