Dynamics of end-grafted polystyrene brushes in theta solvents
Abstract
The dynamics of the concentration fluctuations in end-grafted polystyrene brushes in a theta solvent (cyclohexane) are probed by evanescent wave dynamic light scattering at different wavevectors q and temperatures. When the solvent quality changes from marginal to poor, the relaxation function C(q, t) exhibits strong effects as compared with the smooth variation of the brush density profile. From a single exponential above 50 °C, C(q, t) becomes a two-step decay function. The fast decay is still assigned to the cooperative diffusion albeit slower than in the good solvent regime whereas the slow nonexponential and nondiffusive process might relate to microsegragated and/or chain dynamics in the present polydisperse brush. The relaxation function of the present three brushes with different grafting density reveals similarities and disparities between wet brushes and semidilute polymer solutions. © 2006 Wiley Periodicals, Inc. J Polym Sci Part B: Polym Phys 44: 3590–3597, 2006
INTRODUCTION
Endgrafting macromolecules to solid surfaces represents one of the most popular ways of modifying and functionalizing surfaces, with a breadth of applications in various fields of microsystems engineering such as biochips, microfluidics, and sensor construction.1 At high surface coverage, polymer chains grafted at one end to a planar surface in contact with good solvent are strongly stretched, forming a polymer brush.1, 2 This high stretching, a result of large excluded volume interaction between monomers, can be affected by controlling the grafting density of the latter. Upon lowering the solvent quality, the brush becomes increasingly compact and finally becomes insoluble as schematically shown in Figure 1.3 At theta conditions, where the excluded volume interactions vanish, chains adopt Gaussian statistics. Such a switching between an extended and a compact conformation of the surface-attached molecules is very interesting for sensor applications because at such a transition the sensitivity of the sensing layer is highest due to the increased analyte concentration.

Schematic representation of an end-anchored polymer chain at different solvent conditions ranging from “good” to “bad.”
Scaling concepts of polymer solutions have been applied to grafted chains and provide simple scaling laws for polymer brush (the Alexander-de Gennes model2) for both theta and good solvents. It demonstrated that the length scale governing polymer brushes is the distance between anchor points connecting the brush to the surface. The brush is represented as a linear array of blobs of that size, which generate a uniform concentration profile of the segments of the grafted chains. Within the blob the chains adopt an expanded conformation typical for a chain in good solvent and a Gaussian one in theta solvent. The predicted linear scaling for the brush height with the molecular mass of the chains has been largely confirmed. After the early work of Alexander and de Gennes,2 Milner et al.4 and Balasz and coworkers5 developed a self-consistent field theory, which took advantage of the fact that in a system in which polymers are strongly stretched, as in a brush, fluctuations around the most probable, or “classical,” paths are small, and can to the first approximation be ignored. It confirmed the Alexander-de Gennes scaling laws and leaded to a parabolic profile for monodisperse brushes in good solvents and smoother profiles for polydisperse chains. For polymer brushes, the conformation change and its consequences on concentration profile has been addressed theoretically5 and to some extent verified experimentally.6, 7 For sufficiently poor solvents, computer simulations8-10 and self-consistent field calculations5 have predicted lateral inhomogeneities leading to segregation within the grafted layer.
Although the contraction of model brushes upon lowering solvent quality and the resulting concentration profiles have received considerable attention both theoretically and experimentally, the underlying concentration fluctuations in the brush at thermal equilibrium is essentially unexplored.11 Here, we report on the collective dynamics of end-grafted polystyrene (PS) brushes in a theta solvent (i.e. cyclohexane) as studied by evanescent wave dynamic light scattering, extending the measurements of recent reports.12, 13
EXPERIMENTAL
Samples
Three polymer brushes were prepared by surface-initiated polymerization, using a glass surface as a substrate. The chains were grown via free-radical polymerization from an azo initiator previously covalently attached to the glass surface.14, 15 Molecular weight and grafting density are varied by controlling the polymerization time and the monomer concentration. The grafting density (σ) is estimated from the measured dry film thickness (d) and the average molecular weight (Mw) of the free chains generated in the polymerization process and isolated from solution. The molecular parameters of the three brushes are shown in Table 1. The polydispersity of the tethered chains is assumed from the free chains in solution to be slightly lower than Mn/Mw = 2.
| Code | Molecular Weight (g/mol) | Dry Thickness d (nm) | Grafting Density σ (nm−2) |
|---|---|---|---|
| PS-3 | 1.6 × 106 | 90 | 0.16 |
| PS-5 | 1.1 × 106 | 30 | 0.05 |
| PS-8 | 1.6 × 106 | 9 | 0.016 |
Evanescent Wave Dynamic Light Scattering
The experimental set-up allowing for the probing of the Fourier component of the concentration fluctuations cq(t) with wavevector q at thermal equilibrium by the evanescent wave with a penetration depth Ξ inside the polymer brush layer was described elsewhere.12, 13 The evanescent light was generated by total internal reflection of the laser (λ = 532 nm) at the interface of a semicylindrical lens to which the polymer chains were covalently attached using the “grafting from” technique.
The cylindrical solvent cell with a semicylindrical lens in the center was placed in a precision θ–2θ goniometer, which allows for independent rotation of the cell and a single mode optical fiber. This in turn permits to define both the angle θ1 of the goniometer and the penetration depth Ξ = λ/2πn(sin2 θ1−sin2 θc)−1/2, with θc being the critical angle and n is the refractive index of the solvent. Hence the scattering wavevector is q = kf − kev with kev and kf being the wavevectors of the evanescent and scattered light. The autocorrelation function G(q, t) of the scattered intensity was recorded over a broad time range by the ALV-5000 fast correlator under heterodyne conditions due to the strong elastic scattering from the rough glass substrate. The intermediate scattering function C(q, t) = 〈cq(t)c−q(0)〉/〈|cq|2〉 at a given q was computed from the experimental G(q, t) under heterodyne conditions that is C(q, t) = [G(q, t) − 1]/a where a is the short-time amplitude of G(q, t). The magnitude q was q ≅ (4πn/λ) sin (θ/2), where θ is the scattering angle since qΞ > 1 in the experiments. The measurements were performed at different temperatures above, below, and near the theta temperature (theta temperature Tθ is 35 °C for bulk PS/cyclohexane solutions).
RESULTS
 (1)
(1)
The normalized intermediate scattering function C(q, t) for the PS-3 brush (a), PS-5 brush (b) and PS-8 brush (c) in cyclohexane at q = 0.02 nm−1 and penetration depth Ξ = 400 nm for a range of temperatures (26 °C ≤ T ≤ 50 °C) increasing in the direction of the arrow. The solid lines denote the fit of eq 1 to the experimental functions.
The obtained relaxation times and associated intensities for the fast and slow relaxation are presented in Figure 3. For the C(q, t), the characteristics of the fast process resemble the single process of C(q, t) for the same brushes in dioxane (good solvent).13 It is therefore attributed to the cooperative diffusion Dc = Γc/q2 (breathing of the brush)18 that slows down with decreasing temperature, in analogy to the behavior of semidilute solutions of PS in cyclohexane.19 In contrast to the latter solutions, τc (= 1/Γc) does not diverge up to the lowest (20 °C) examined temperature (well below the nominal θ of the bulk PS/cyclohexane solutions). The relaxation time τs(q) is found to exhibit a stronger temperature dependence than τc(q), which nonetheless slows down upon cooling. Below 25 °C, the slow process runs out of the experimental time window.
(a) The relaxation time for the slow (τs, solid symbols) and the fast cooperative (τc, open symbols) processes in the three polystyrene brushes; PS-3 brush (○), PS-5 brush (▪) and PS-8 brush▴ in cyclohexane at q = 0.02 nm−1 plotted versus temperature. The solid lines indicate a power law fit as described in the text. (b) The intensity of the slow (Is solid symbols) and the fast (If open symbols) plotted as a function of temperature. The relaxation times and the intensities were obtained from the fit of eq 1 to the experimental C(q, t) of Figure 2. The dashed lines (for the fast process) are to guide the eye. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
The slowing down of τs with decreasing temperature can be described by power law τs ∼ (T − Tc)−x (solid lines in Fig. 3) with Tc ∼ (299 ± 1) K and x = 2.6 ± 0.2 for all three PS brushes. This value is clearly larger than the critical exponent reported for the mutual diffusion in critical polymer solutions.20, 21 Based on the intensity plot of Figure 3, the contribution of the induced slow process is evidently increased below Tθ. The increase of Is (T) with decreasing temperature in all three samples is a signature of the diminishing solvent quality for the end-grafted PS chains. In contrast to the PS/cyclohexane solutions, which phase separate below Tθ, the brush can only accommodate unfavorable thermodynamic interactions by adjusting its thickness as it looses the ability to macrophase separate. Furthermore, the total intensity (Is + If) was found to increase with grafting density of PS.
Turning to the wavevector dependence of the correlation function, Figure 4(a) shows the experimental C(q, t) for the brush with the highest grafting density, PS-3, at Ξ = 400 nm and three q's (0.01, 0.02, and 0.025 nm−1) at 32 °C. The fast decay shifts to shorter time with q whereas the slow decay of C(q, t) appears to be insensitive to the variation of q. The representation of C(q, t) by eq 1 reveals the diffusive (q2-dependent) nature of the relaxation rate of the fast process in contrast to the slow mode that is found to display no apparent q-dependence for its characteristic rate Γs. This q-dependence of C(q, t) also applies to the other two PS brushes as shown in Figure 4(b). The fast diffusion Dc (= Γf/q2) increases with grafting density as found for the same brushes in good solvents, while the slow rate Γs shows the opposite trend. The q-independent rate appears different from the diffusive slow mode of a dense brush reported in an earlier paper.12 We may attribute this discrepancy to the very broad relaxation time distribution, which results the q-dependent measurements being somewhat ambiguous and to the stronger and slower process of the brush in ref.12. In the present study, the insensitivity of Γs to q-variations was found for all three brushes.
(a) Normalized intermediate scattering functions C(q, t) of the PS-3 brush in cyclohexane at 32 °C at three different q values between 0.01 and 0.025 nm−1 increasing in the direction of the arrow. The solid lines denote the fit of eq 1 to the experimental functions. Inset: The diffusive nature of the relaxation rate Γc(q), where the solid line denotes the diffusive [Γc(q) = Dcq2, Dc = 3.7 × 10−7 cm2/s] behavior and the insensitivity of the rate Γs(q) of the slow process to the variation of q indicated by the dashed line. (b) The relaxation rate Γc(q) of the fast process in the three polystyrene brushes; PS-3 brush (○), PS-5 brush ▴, and PS-8 brush (▪) immersed in cyclohexane as a function of q2 at T = 35 °C, where the solid lines denote the diffusive [Γc(q) = Dcq2] behavior and the dashed lines indicate the insensitivity of the rate Γs(q) of the slow process to the variation of q. The solid symbols refer to the relaxation rates of the fast process of the three polystyrene brushes and the open symbols refer to the relaxation rate of the slow process. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
To examine possible surface segregation, the dynamic behavior of the three PS brushes was investigated around Tθ for a wide range of the penetration depth Ξ in the range 150–750 nm. According to the experimental C(q, t) of the PS-5 and the PS-8 brushes in Figure 5(a,b), there is no apparent penetration depth dependence. Equation 1 represents well the experimentally obtained normalized C(q, t). The total intensity I associated with both processes plotted as a function of Ξ is shown in the insets of Figure 5(a,b). In both brushes, the total intensity increases linearly with the penetration depth.
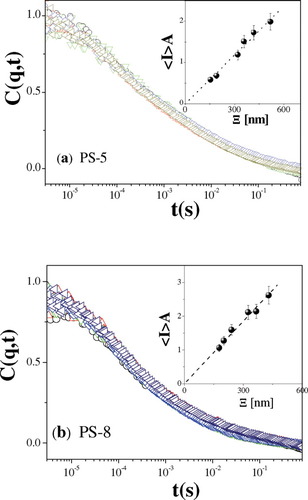
Normalized intermediate scattering functions C(q, t) for (a) PS-5 brush in cyclohexane and (b) PS-8 brush in cyclohexane at 35 °C at q = 0.02 nm−1 for a range of penetration depths (150 nm ≤ Ξ ≤ 750 nm). Insets: The intensity 〈I〉A, associated with the two processes (○) is plotted as a function of Ξ. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
Conversely, the brush PS-3 with the highest grafting density exhibits a quite different behavior as depicted in Figure 6(a). Strong penetration depth dependence of the dynamics was observed in the vicinity of Tθ, with an apparent slowing down at larger Ξ's. Fits obtained by eq 1 return a constant slow time independent of Ξ and associated intensities of the fast (solid symbols) and the slow mode (open symbols) plotted as a function of Ξ, as shown in Figure 6(b). As it can be seen in Figure 6(b), the associated intensity of the slow mode displays stronger Ξ dependence than the associated intensity of the fast mode, that is the inside part (nearer to the hard wall) relaxes proportionally less through the slow process than the outside part (closer to the brush/solvent interface), leading to the overall slowing down of the relaxation.
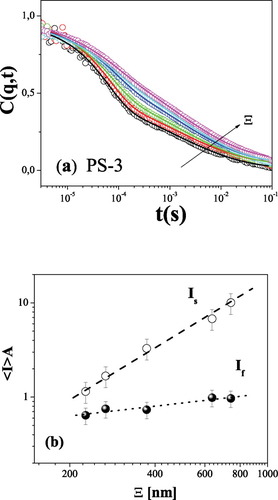
Normalized intermediate scattering functions C(q, t) for the PS-3 brush in cyclohexane at (a) 35 °C at q = 0.02 nm−1 for a range of penetration depths (150 nm ≤ Ξ ≤ 750 nm). (b) The intensity of the slow (Is○) and the fast (If ○) contributions to the experimental C(q, t) at 35 °C plotted as a function of Ξ. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
Summing up, the measured relaxation functions for the three brushes can be represented by eq 1, leading to a diffusive Γc(q) of the fast mode and a virtually q-independent Γs of the slower process. The hydrodynamic size (kT/6πηDc, with η being the solvent viscosity) is found to increase upon cooling and the characteristic rate Γs of the slower mode exhibits stronger temperature (swelling) dependence. This is the case for all three brushes with different grafting densities, which, however, appear to be distinguished in the dynamic heterogeneity toward the brush edge.
DISCUSSION
The emergence of a slow mode as solvent quality decreases is reminiscent of the dynamics of entangled polymer solutions. The issue of concentration fluctuation dynamics in semidilute solutions is not entirely understood, but there is a consensus on the overall behavior. The major modification as compared with the good solvent case is the extra length scale introduced by the viscoelasticity of the solution. This was first noticed by Brochard and de Gennes22 and soon supported by dynamic light scattering experiments.19, 20, 23-25
Brochard and de Gennes22 have developed scaling expressions for theta systems. They propose two limiting regimes: at low scattering vectors (q) (such that Dq2 < τr−1, where τr, is the characteristic disentanglement time for the chains or the terminal time from viscoelastic measurements) the restoring force for the concentration fluctuations, originating from the osmotic compressibility, leads to a cooperative diffusion coefficient that is linearly proportional to the polymer concentration. At high scattering vectors (corresponding to Dq2 > τr−1), they predict that the correlation function is bimodal. The fast mode characterizes the cooperative diffusion and the other mode, which is independent of the scattering vector, characterizes the structural relaxation of the transient network. The time autocorrelation function of the scattered field was found to be bimodal and the results concerning the slow relaxation process could be accounted for by the theoretical models describing the coupling of concentration fluctuations to the viscoelasticity.23, 24 In these reports, the correlation function was analyzed at large scattering vectors in terms of two modes as had been predicted by Brochard and de Gennes: The fastest mode was found to be diffusive and the slowest was independent of the scattering vector and close to the longest relaxation time obtained by viscoelastic measurements.
This “ideal picture” may not be observed for all systems as other works25 have reported more complex (in various theta systems) spectrum. Besides the diffusive mode they observed a number of slower modes that were independent of the scattering vector. The slowest of these modes was of the order of τr.
Keeping the simplest approach of a step-like brush that still captures qualitatively all features, the situation in theta solvents should be represented by Gaussian chains of blobs when the structure inside the blob is also Gaussian, whereas in good solvent the conformation inside the blob is extended. Dynamically, the brush may be visualized as a slice of semidilute polymer solution, where the concentration is set by the grafting density. As it now appears, the brush case may well be understood from the 3D bulk solutions in theta solvent.
The modification compared with the bulk solution case relates to the terminal relaxation time, since such a time does not exist for grafted chain. The slowest time for one chain is the “disentanglement time” and that has to be long and given the polydispersity, extremely broadly distributed. Therefore, the broad range of times may find its origin in the grafted geometry and the large polydispersity of the PS brushes. The brush specificity also lies in its ability to shrink and hence the reduced dimension in the z-direction. Based on these two distinct features some modification of the solution picture is expected. No phase separation occurs and the measurements of Dc can be extended well below Tθ as the brush adjusts its height with decreasing solvent compatibility and the increase of the characteristic length scale cannot exceed the brush thickness; part of the solid surface would be fully uncovered, which is not feasible for grafted chains. As far as the viscoelastic mode and the polydispersity concern, large distribution of relaxation time is expected from grafted structure of polydisperse entangled chains. A theoretical treatment would be needed for grafted chains, including the specificity described above.
The two brushes with lower graft density, PS-5 and PS-8, show no penetration depth dependence, which suggests similar fluctuations throughout the brush. For the denser PS-3, Is is stronger at high penetration depth [Fig. 6(b)] reflecting inhomogeneities within the brush thickness with longer fluctuations near the polymer/solvent interface. Further, these enhanced inhomogeneities might arise from the large free chain-end distribution and the high grafting density of this polydisperse brush.
CONCLUSIONS
We have extended our previous studies12, 13 to PS brushes in contact with solvents of varying solvent quality. We studied slow and broad dynamics when the solvent environment changes, from good to theta conditions. The decay of the relaxation function for the polymer density fluctuations becomes bimodal and is well described by a sum (eq 1) of one single exponential and a broad stretched exponential decay with β = 0.32. For the three brushes, the diffusive relaxation rate Γc(q) of the fast mode relates to the cooperative diffusion whereas the origin of q-independent Γs of the slower process with a q-independent rate is not certain. The brush-specific behavior concerns both the nondivergence of Γc and the heterogeneous dynamics associated with Γs Based on the current documentation of the structural behavior of brushes, their rich and complex dynamics is rather unexpected, given the smooth variation of the average density profile.6
In agreement with expectations close to theta-conditions, concentration fluctuations become stronger. Interestingly, we observe under solvent conditions around theta (even for solvent qualities slightly below the theta-point, wherein bulk solution phase separation occurs) cooperative diffusion that is a “breathing” of the brush. The results of the study show that measurements of the brush dynamics provide detailed local structural information and allow quantifying the solvent quality directly, which is not possible based on static measurements (i.e. reflectivity measurements) alone.6, 7




