Data-driven research in retail operations—A review
Meng Qi
Department of Industrial Engineering & Operations Research, University of California at Berkeley, Berkeley, California, USA
Search for more papers by this authorCorresponding Author
Ho-Yin Mak
Saïd Business School, University of Oxford, Oxford, UK
Correspondence
Ho-Yin Mak, Saïd Business School, University of Oxford, Oxford, UK.
Email: [email protected]
Search for more papers by this authorZuo-Jun Max Shen
Department of Industrial Engineering & Operations Research, University of California at Berkeley, Berkeley, California, USA
Search for more papers by this authorMeng Qi
Department of Industrial Engineering & Operations Research, University of California at Berkeley, Berkeley, California, USA
Search for more papers by this authorCorresponding Author
Ho-Yin Mak
Saïd Business School, University of Oxford, Oxford, UK
Correspondence
Ho-Yin Mak, Saïd Business School, University of Oxford, Oxford, UK.
Email: [email protected]
Search for more papers by this authorZuo-Jun Max Shen
Department of Industrial Engineering & Operations Research, University of California at Berkeley, Berkeley, California, USA
Search for more papers by this authorFunding information: National Natural Science Foundation of China, Grant/Award Number: 71991462
Abstract
We review the operations research/management science literature on data-driven methods in retail operations. This line of work has grown rapidly in recent years, thanks to the availability of high-quality data, improvements in computing hardware, and parallel developments in machine learning methodologies. We survey state-of-the-art studies in three core aspects of retail operations—assortment optimization, order fulfillment, and inventory management. We then conclude the paper by pointing out some interesting future research possibilities for our community.
1 INTRODUCTION
Modern operations management (OM) has become a major academic discipline and one of the most important business functions in corporations. Over the past decades, the academic OM literature has co-evolved closely with practice, shifting its focus from the early topics of production systems (e.g., the assembly line, factory physics) to broader supply chain concepts (e.g., Just-in-Time), to operations strategy (e.g., outsourcing, offshoring), to revenue management, to managing operations risks and disruptions. In the last decade, the most important development in business has arguably been digitalization. As more and more firms ponder how digital technology and big data may transform their operations strategies, so have OM researchers begun to investigate operations problems from a digital, data-driven lens. In this article, we shall focus on developments in OM research in retail, one of the key industries undergoing digital disruption.
As an illustration of how the focus of OM may be evolving over time, consider nomenclature trends in supply chain management, a primary study area of OM. Figure 1 shows the relative Google search frequencies of three key phrases related to supply chain management over the past 10 years (compiled from Google Trends). For decades, OM researchers and practitioners have been employing operations research (OR) techniques in optimizing their operations. In the supply chain context, a large part of this methodology is synonymous with the phrase supply chain optimization. With digitalization, data analytics has quickly become a core element of OM. Figure 1 shows that the popularity of supply chain analytics has rapidly grown, and surpassed supply chain optimization (the search frequency for which has stayed relatively flat) in around 2014 to 2015. While it can be rightfully argued that supply chain analytics is a broader concept that subsumes supply chain optimization as a subset, this observation still suggests that many (especially practitioners) now embrace data-driven (analytics) approaches as the present of OM.

As a future-proof strategy, the business world has been investing heavily in key technologies such as artificial intelligence (AI). Figure 1 shows that interest in supply chain AI has grown from practically zero a decade ago to about half the level of supply chain optimization today. This is an interesting observation regarding the future of OM. Many academics (the authors included) have had the negative experience of interacting with some practitioners about potential collaborations, just to find that they are only interested in descriptive and predictive analytics methods that inform managers in their decision making, rather than prescriptive methods that recommend decisions to managers, which is the specialty of the OR community. The headline-grabbing success of AI may be changing this mentality by instilling confidence in practitioners to trust (sometimes black-box) prescriptive methods for decision making.
Under this backdrop, interesting avenues have opened up for researchers in the operations of retail, a prime industry in the digitalization movement. Traditionally, research in retail operations has focused on model-based approaches built on theoretical assumptions on how systems work. Often, this is due to the fact that researchers did not possess the necessary data to accurately depict the operations, and thus simplifying assumptions were necessary. Although model-based approaches often provide valuable strategic insights to practitioners and tractable solution methods, the assumptions they are built upon sometimes fail to hold in real life, especially as modern retail operations become increasingly complex. With digitalization, data of unprecedented richness, volume, and accuracy has become available. For instance, now we have detailed records for every customer order in online retail, from keywords that the customer searched, the products (assortment) displayed on screen, to the resulting click-through and even social media activities of the customer, to the eventual order, on the demand side. Likewise, on the supply side, we have detailed accounts of procurement records from suppliers, shipment dates and location tracking, arrival at warehouse and storage, distribution trajectories and eventual outbound shipment to customers, for every item. Therefore, there is no lack of data for laying out every process in detail. The challenge is how to extract the necessary information for modeling, and subsequently optimizing, these complex operations.
In the last few years, researchers have focused on the development of such data-driven models and solutions for retail operations problems. Besides access to high-quality data, methodological advances in machine learning (ML) and data-driven OR techniques have been another key enabling factor behind this development. For example, statistical learning models provide parametric and nonparametric models for high-quality prediction, while recurrent neural networks (RNN) can be used to model time-series data, which is common in retail operations problems. Besides, an easier access to high-performance computing resources has also made a major impact, since data-driven methods (especially nonparametric ones) often require significant computational efforts compared with model-based methods. For example, recent developments in GPU-based training of deep neural networks, availability of analytical (especially open-source) software packages, and availability of cloud computing, all combine to provide convenient tools for researchers and practitioners to implement data-driven models.
In this article, we provide an up-to-date review by stocktaking this rapidly-growing literature. To maintain a manageable scope, we limit our attention to three main aspects of data-driven research in retail operations, loosely following the physical operations trajectory of a customer's experience with a digitalized retail supply chain. First, when a customer visits a physical or online retail store, s/he chooses the product(s) to purchase based on the assortment of products displayed/ offered. We first review the data-driven literature on assortment optimization, that is, the problem of the retailer choosing the set of products to offer (Section 2). Then, once the customer places an order in an online store, the order will be fulfilled from the retailer's fulfillment network. We review the fulfillment optimization literature associated with the data-driven design of such operations (Section 3). Finally, the fulfillment and distribution networks have to ensure high service levels and low costs through efficient inventory control. We discuss the latest works on data-driven methods for inventory management (Section 4). We conclude in Section 5 with a discussion of important issues that appear across different applications in the literature and potential future directions. The set of problems reviewed is not intended to be comprehensive. We have excluded several important problems in retail operations, such as pricing (readers may refer to Besbes and Zeevi (2009), den Boer (2015) and the reference therein), joint pricing and inventory problems (e.g., Chen & Simchi-Levi, 2004, 2012; Feng, Luo, & Zhang, 2014), as well as joint pricing and assortment optimization (e.g., Jagabathula & Rusmevichientong, 2017; Wang, 2012; Miao & Chao, 2020).
2 DATA-DRIVEN ASSORTMENT OPTIMIZATION
Assortment optimization is a core problem in retail operations and revenue management. It is of core importance to businesses, as it stands on the customer-facing end and is a direct driver of revenue and customer satisfaction. The problem involves a seller choosing an optimal set of products to offer to a group of customers to maximize revenue, whereas each customer chooses to purchase at most one of the offered products based on their preferences. This is a difficult combinatorial problem as it is typically not feasible (e.g., due to limited shelf space) or not desirable (due to cannibalization) to offer the full set of products. The assortment optimization problem arises in many different application contexts, for example, in selecting products for shelf display in retail stores or vending machines, and selecting advertisements to be displayed on a YouTube or Facebook page.
In this section, we first review parametric approaches to assortment optimization based on parametric discrete choice models and methods for parameter estimation from transaction and sales data. Then, we go over nonparametric approaches to choice modeling and assortment optimization.
2.1 Parametric approach to customer choice modeling
To analyze assortment optimization problems, it is necessary to model the customers' purchase decisions given the offer set. The classical way to model customer choice is to use parametric discrete choice models, which characterize customers' choices between two or more discrete alternatives (the offer set and the no-purchase option) as functions of the alternatives' attributes. Popular discrete choice models include the Multinomial Logit (MNL), Nested Logit (NL), and Mixed Multinomial Logit (MMNL) models. We provide a brief summary of these models below. For more detailed discussion, we refer interested readers to Ben-Akiva, Lerman, and Lerman (1985), Anderson, de Palma, and Thisse (1992), Kök, Fisher, and Vaidyanathan (2008), and the references therein.
2.1.1 Review of popular choice models
Let us consider a set of n products that the retailer can offer. For an offer set S ⊂ {1, …, n} chosen by the retailer, a parametric discrete choice model characterizes the probability that a customer chooses to purchase product i as a function of S, denoted by Pi(S). Here, product 0 denotes the no-purchase option.
• Multinomial Logit model
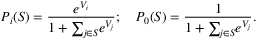
• Mixed Multinomial Logit model
Under the Mixed Multinomial Logit (MMNL) model, in addition to the random noise term, the mean utilities Vi, i = 1, …, n are also modeled as random variables. The mean utilities can follow either discrete or continuous probability distributions. The case that the utility vector V = (V1, …, Vn) follows a discrete distribution with m different values, denoted by 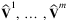 , may represent the existence of multiple customer types with
, may represent the existence of multiple customer types with 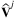 corresponding to the mean utilities of customer type j ∈ {1, …, m}. An example where V follows a continuous distribution is when there are product-independent sensitivities in the form Vi = μi + P − Bri, where μi is a deterministic constant, ri is the price of product i, and P and B are continuous random variables. The random variable B can be assumed to be positive to represent price sensitivity of the customer.
corresponding to the mean utilities of customer type j ∈ {1, …, m}. An example where V follows a continuous distribution is when there are product-independent sensitivities in the form Vi = μi + P − Bri, where μi is a deterministic constant, ri is the price of product i, and P and B are continuous random variables. The random variable B can be assumed to be positive to represent price sensitivity of the customer.
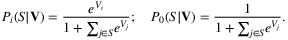
• Nested Logit model
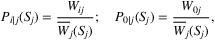
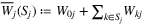 . Furthermore, each nest j is also associated with a parameter γj ≥ 0 that characterizes the degree of the dissimilarity of the products in the nest. In the NL model, the dissimilarity parameters (γ1, …, γm) are assumed to be constants and the preference weights Wij are generated by a random utility that follows a multidimensional generalized extreme value distribution with mean Vij. Then, the preference weights can be represented in a similar form as in the MNL model:
. Furthermore, each nest j is also associated with a parameter γj ≥ 0 that characterizes the degree of the dissimilarity of the products in the nest. In the NL model, the dissimilarity parameters (γ1, …, γm) are assumed to be constants and the preference weights Wij are generated by a random utility that follows a multidimensional generalized extreme value distribution with mean Vij. Then, the preference weights can be represented in a similar form as in the MNL model:
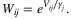
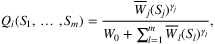
2.1.2 Learning discrete choice models from data
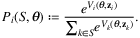
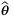 , which can be formulated as
, which can be formulated as
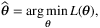

Bunch (1987) investigate the particular case where Vi(θ, zi) = θTzi, and propose an algorithm for general probabilistic choice models and show that the MLE problem can be written as a problem in generalized regression. More details about algorithms to achieve MLE and comparisons of MLE with other estimators for choice model parameters are stated in Bunch (1988), and Bunch and Batsell (1989).
However, identifying the exact explanatory variable values for each product and implementing the aforementioned independent trials is often impractical. In fact, the customer choice data collected in real-world situations are often very sparse, that is, only a small number of observations are available for each choice set and a small proportion of choice sets are observed among all possible ones. Benefited from recent advances in learning low-rank models, it is possible to learn choice models from data on comparisons and choices.
Negahban, Oh, Thekumparampil, and Xu (2018) investigate the problem of estimating MNL model parameter values that best explain the data. The authors consider different forms of available data: pairwise comparisons, that is, the customer's choice when given two options; higher-order comparisons, that is, the customer's rankings over a given subset of items; customer choices, that is, the customer's choices of the best item out of a given subset; and bundled choices, that is, the customer's choices of bundled items. For the scenario when pairwise comparisons are available, the authors propose a graph sampling method that captures sample irregularity. They also propose a convex relaxation of the MNL learning problem and show that it is minimax optimal up to a logarithmic factor. This proves that the proposed estimator cannot be improved upon other than by a logarithmic factor and identifies how the accuracy depends on the topology of sampling. The authors also extend their framework to the scenario where data includes higher-order comparisons, customer choices, and bundled purchase observations.
However, the richness of the MMNL model presents substantial difficulties for learning. In fact, Ammar, Oh, Shah, and Voloch (2014) show that for any integer k, there exist pairs of MMNL models with n = 2k + 1 items and m = 2k mixing components where the samples generated by both models with length l = 2k + 1 would be identical in distribution. Therefore, it is impossible to uniquely distinguish MMNL models in general. Oh and Shah (2014) investigate sufficient conditions under which it is possible to learn MMNL models efficiently (in both statistical and computational sense), and provide an efficient algorithm for cases with partial preference data (higher and pairwise comparisons). Given, for example, pairwise comparison observations, the goal is to learn the mixing distribution over m different MNL submodels and the parameters of each. They consider data in the following form: Each observation is generated by first selecting one of the m mixture components, and then observing comparison outcomes for l pairs of products therein. Their proposed algorithm consists of two phases. The first involves tensor decomposition to learn the pairwise marginals of mixing components. Then, the second phase makes use of these pairwise marginals to learn parameters for individual mixture components. The authors also identify conditions under which the model can be learned with sample sizes polynomial in n (number of products) and m (number of mixing components).
Chierichetti, Kumar, and Tomkins (2018) study the problem of learning a uniform mixture of two MNLs from a more realistic oracle that returns the distribution of choosing products in a given slate. In particular, the uniform 2-MNL model (a,b) assigns to item i in subset S ⊂ {1, …, n} the probability 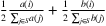 , where a(⋅) and b(⋅) denote the preference weights generated by two different MNL models. Their algorithm builds on a reconstruction oracle that returns the probabilities that each item in a given slate will be chosen. They show that slate sizes of two are insufficient for reconstruction, and thus their oracle with slate size of at most three is optimal. They propose to achieve this oracle by approximating it by sampling over choice processes. Moreover, the authors provide algorithms that makes O(n) and O(n2) queries when the oracle can be queried adaptively and non-adaptively, respectively, and show that they are optimal.
, where a(⋅) and b(⋅) denote the preference weights generated by two different MNL models. Their algorithm builds on a reconstruction oracle that returns the probabilities that each item in a given slate will be chosen. They show that slate sizes of two are insufficient for reconstruction, and thus their oracle with slate size of at most three is optimal. They propose to achieve this oracle by approximating it by sampling over choice processes. Moreover, the authors provide algorithms that makes O(n) and O(n2) queries when the oracle can be queried adaptively and non-adaptively, respectively, and show that they are optimal.
2.1.3 Assortment optimization with parametric discrete choice models
Once parameters of choice models are estimated, the optimal assortment can be determined by solving an optimization problem. A significant stream of literature deals with such optimization problems under settings with different discrete choice models and additional (e.g., capacity) constraints. The literature generally investigates assortment problems with either static or dynamic formulations. In the former case, given the choice model of purchase behavior, the decision maker decides the optimal assortment that maximizes the expected profit in one shot. In the dynamic setting, the inventory of products is taken into consideration over multiple periods.
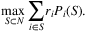
When the customer choice probabilities Pi(S) follow the MNL model with known utility parameters, the problem can be solved efficiently by considering only revenue-ordered assortments. In other words, one can start with the empty set and incrementally construct S by sequentially adding a product that results in the maximum increase in revenue at a time. This elegant result is a special case of the nested offer set property of Talluri and Van Ryzin (2004) (although this article originally investigates a more general setting). Motivated by this result, Aouad, Farias, Levi, and Segev (2018) and Berbeglia and Joret (2020) provide performance guarantees of the revenue-ordered assortments. Aouad et al. (2018) consider a general choice model where customer choices are characterized by a distribution over ranked lists of products and Berbeglia and Joret (2020) investigate customer choice models with the assumption that Pi(x) does not increase when S is enlarged.
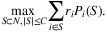
Rusmevichientong et al. (2010) develop a simple algorithm for computing a profit-maximizing assortment based on a connection between the MNL model and the geometry of lines in the two-dimensional plane, and derive structural properties of the optimal assortment. Jagabathula (2014) study the same problem and propose an easy-to-implement local search heuristic. The authors show that it efficiently finds the global optimum for the MNL model and derive performance guarantees under general choice model structures.
Rusmevichientong and Topaloglu (2012) study the robust assortment problem under the MNL model when some of the parameters of the choice model are unknown. Wang (2012) considers the problem of jointly finding an assortment of products to offer and their corresponding prices when the customers choose under the MNL model. Davis, Gallego, and Topaloglu (2013) investigate the assortment optimization problem with a set of total-unimodularity constraints when customers make purchase decisions according to the MNL model. The authors show that this problem can be formulated as a linear program. Wang (2013) considers the joint problem of assortment and price optimization with a capacity constraint and they assume that customer purchase behavior follows the MNL model with general utility functions. The author simplifies this problem to one of finding a unique fixed point of a single-dimensional function and propose an efficient solution algorithm.
Another extension of the static assortment optimization problem with the MNL model explores the consideration sets of customers. In this model, there are multiple customer types, and a particular type is interested in purchasing only a particular subset of products (the consideration set). A customer observes which of the products in her consideration set are actually included in the offered assortment and makes a choice from among only those products, according to the MNL model. Feldman and Topaloglu (2018) study capacitated assortment problems when the consideration sets are nested. The authors show that this assortment problem is NP-hard, even when there is no restrictions on the total space consumption of offered set. They also provide a fully polynomial time approximation scheme (FPTAS) for the problem. Recall that FPTAS refers to a family of algorithms that for any ϵ > 0, the algorithm is ϵ-optimal with polynomial running time with respect to the input size and 1/ϵ.
- when the utility functions include product-independent price sensitivity Vi = μi + P − Bri (where P and B are constants); or
- when customers are value conscious, where realization of V satisfies V1 ≤ V2 ≤ ⋯ ≤ Vn and
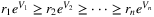 (with the products indexed such that r1 ≥ r2 ≥ ⋯ ≥ rn).
(with the products indexed such that r1 ≥ r2 ≥ ⋯ ≥ rn).
The authors also provide an approximation guarantee for the revenue-ordered assortment policy for general MMNL models. Bront, Méndez-Daz, and Vulcano (2009) show that the same problem is NP-hard and Méndez-Daz et al. (2014) develop a brand-and-cut algorithm to find the optimal assortment.
To circumvent computational difficulties, Mittal and Schulz (2013) propose a FPTAS for assortment optimization problem with MMNL model and NL model. Désir, Goyal, and Zhang (2014) consider the capacity-constrained version of the assortment optimization problem under MNL, MMNL, and NL models and provide FPTAS by exploiting connections with the knapsack problem. It is worthwhile pointing out that the running time of their algorithm depends exponentially on the number of mixture components in the MMNL model, and such exponential dependence is necessary for any (1 − ϵ)-approximation algorithm. Instead of developing approximation schemes such as FPTAS, Şen, Atamtürk, and Kaminsky (2018) reformulate the constrained assortment optimization problem under the MMNL model as a conic quadratic mixed-integer program. Making use of McCormick inequalities that exploit the capacity constraints, their formulation enables solving large instances using commercial solvers.
Davis, Gallego, and Topaloglu (2014) study the assortment optimization problem under the two-level NL model with an arbitrary number of nests. They show that the problem is polynomially solvable when the nest dissimilarity parameters (γj's in Section 2.1.1) of the NL model are less than one and customers always make a purchase within the selected nest. The problem becomes NP-hard if either assumption is relaxed. To deal with the NP-hard cases, they also develop parsimonious collections of candidate assortments with worst-case performance guarantees and formulate a convex program that provides an upper bound on the optimal expected revenue. Gallego and Topaloglu (2014) then extend the setting to accommodate constraints on the total number of products and the total shelf space used by the offered assortment.
Li, Rusmevichientong, and Topaloglu (2015) investigate the assortment optimization problem under a more general d-level NL model. In their setting, the taxonomy of the product is described by a d-level tree where each node corresponds to a set of products, and each leaf node denotes a single product. Then the customer choice probability can be formulated as a walk from the root node to one of the leaf nodes where at each of the non-leaf nodes, children nodes are chosen following probability generated by preference weights (Qis defined in Section 2.1.1). With this formulation, the authors give a recursive characterization of the optimal assortment and provide an algorithm that achieves the optimal assortment with complexity O(dnlogn). Wang and Shen (2020) also adopt the d-level NL model and investigate the assortment optimization problem with the no-purchase option in every period of the customer choice process, with cardinality constraints imposed on the lowest level. The authors show that the optimal assortment can be obtained in O(nmax{d,k}) operations (where k denotes the capacity), which is faster than the result for unconstrained case developed in Li et al. (2015). Other studies on the NL case include Mittal and Schulz (2013), who propose a FPTAS for the problem, and Désir et al. (2014), who consider the capacity constrained version of the problem and provide a FPTAS.
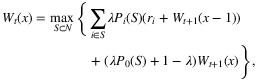
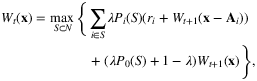 (1)
(1)Rusmevichientong and Topaloglu (2012) study the dynamic assortment optimization problem from the robust optimization perspective, where the true parameters of the choice model are assumed to be unknown and fall within an uncertainty set. In their setting, there is a limited initial inventory to be allocated over time. The authors show that offering revenue-ordered assortments in each period is still optimal. This leads to a method that computes robust optimal policies as efficiently as non-robust approaches.
Other multi-period assortment problems that differ from the aforementioned dynamic formulation include Gallego, Ratliff, and Shebalov (2015), Rusmevichientong et al. (2010), Liu, Ma, and Topaloglu (2020). Gallego et al. (2015) investigate the multi-period network revenue management problem under a more general customer choice model, known as the general attraction model, which includes the MNL model as a special case. Besides the static assortment optimization problem with capacity constraints, Rusmevichientong et al. (2010) also study an online learning version the problem. In particular, the authors consider the setting where the parameters of MNL models are initially unknown and are adaptively learned over time. The authors formulate this problem as a multiarmed bandit problem, provide a policy, and establish an O(log2T) upper bound on the regret. Liu et al. (2020) consider assortment optimization problems where the choice process of a customer takes place in multiple stages. In each stage, customer choice is captured by the MNL model, and the offered assortment is assumed not to overlap with the those offered in the previous stages. The authors prove the NP-hardness of this problem and develop a FPTAS. They also show that, if there are multiple stages, then the union of the optimal assortments to offer in each stage is nested by revenue, though there is no efficient method to determine the stage in which each product should be offered.
2.2 Nonparametric choice modeling and associated assortment optimization problems
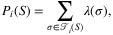
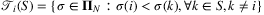 denotes the set of all customer types that would purchase product i when offered set S. The authors also assume that the data observed are given by an m-dimensional “partial information” vector y = Aλ, where λ ∈ ℝN! is the vector with components λ(σ), A ∈ {0, 1}m × N! and m ≪ N! in the case that data for only a limited number of assortments are available. Under this setting, the authors consider the problem of predicting the revenue rate (i.e., the expected revenue garnered from a random customer) for some given assortment S by solving:
denotes the set of all customer types that would purchase product i when offered set S. The authors also assume that the data observed are given by an m-dimensional “partial information” vector y = Aλ, where λ ∈ ℝN! is the vector with components λ(σ), A ∈ {0, 1}m × N! and m ≪ N! in the case that data for only a limited number of assortments are available. Under this setting, the authors consider the problem of predicting the revenue rate (i.e., the expected revenue garnered from a random customer) for some given assortment S by solving:
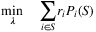
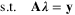

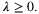
Note that it is a linear program with respect to the variables λ, so the problem is conceptually tractable. However, in practice, the number of variables is intractably (in fact, exponentially) large. The authors propose to overcome this difficulty by formulating the dual problem (with exponential number of constraints), and solving it with both constraint sampling and an efficient reformulation of the constraint set. They also examine the performance of the scheme on simulated transaction data as well as on a real-world sales prediction problem using real data.
Although Farias et al. (2013) provide the novel idea of general choice models and investigate the revenue rate of a given assortment S, optimizing the assortment that maximizes the expected revenue remains nontrivial. Aouad et al. (2018) show that the assortment problem is NP-hard even to approximate, and provide best-possible approximability. Feldman, Paul, and Topaloglu (2019) investigate the k-product nonparametric choice model in which the rankings only contain at most k products. The retailer attempts to find the revenue-maximizing assortment when customer choice is governed by the k-product nonparametric model. The authors show that this problem is strongly NP-hard even for k = 2 and develop an algorithm with an improved approximation guarantee.
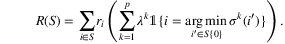
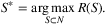
The authors reformulate this problem as a mixed-integer optimization (MIO) problem which can be relatively efficiently solved via branch-and-bound. This formulation can also be extended to incorporate additional constraints.
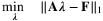

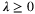
Under a data-driven environment, the availability of highly detailed purchase data enables nonparametric approaches for modeling customer choice via ranked preference, as described above. Although being more flexible with data, this approach is often computationally challenging in solving the subsequent assortment optimization problem, due to the (mixed) integer formulations and searching over permutations. Therefore, approximation algorithms and decomposition techniques such as Benders decomposition and column generation are often required.
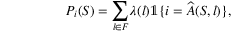
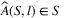 is the choice out of offer set S made by a customer according to decision tree l. This model relaxes the assumption of weak rationality, that is, that adding a product to an assortment will not increase the choice probability of another product in that assortment. Weak rationality is a common technical assumption in most choice models, but may not necessarily hold in practical scenarios where customers exhibit irrational (or boundedly rational) choice behavior. With historical observations of assortments S1, …, Sm and for each of historical assortments, the transaction data is large enough so that the probabilities Pi(Sm) can be estimated. The authors show that this model can perfectly fit such data with shallow trees and propose an efficient algorithm for estimating such models from data, based on combining randomization and optimization.
is the choice out of offer set S made by a customer according to decision tree l. This model relaxes the assumption of weak rationality, that is, that adding a product to an assortment will not increase the choice probability of another product in that assortment. Weak rationality is a common technical assumption in most choice models, but may not necessarily hold in practical scenarios where customers exhibit irrational (or boundedly rational) choice behavior. With historical observations of assortments S1, …, Sm and for each of historical assortments, the transaction data is large enough so that the probabilities Pi(Sm) can be estimated. The authors show that this model can perfectly fit such data with shallow trees and propose an efficient algorithm for estimating such models from data, based on combining randomization and optimization.Blanchet, Gallego, and Goyal (2016) propose a general semiparametric choice model known as the Markov chain choice model. The products are modeled as states in a Markov chain and substitution behavior is modeled by state transitions. Then, the choice probabilities for a given offer set can be computed as the absorption probabilities of the products in the offer set. The authors show that this model can approximate any choice model based on random utility maximization. However, estimation of this model requires data corresponding to a specific set of n + 1 assortments when there are n products.
Another interesting alternative to the data-driven nonparametric approach is to make use of the so-called persistency model in distributionally robust optimization. In this semi-parametric approach, one considers a population of heterogeneous customers each solving an instance of a linear zero-one optimization problem with random coefficients, and analyzes the aggregate behavior over the population, that is, the expected objective and the probability (known as the persistency value that a decision variable will be selected (equal to one) in the optimal solution. While these metrics are difficult to compute exactly, good approximations can be tractably obtained by evaluating the extremal (upper bound) expected objective value given only partial distributional information on the random coefficients.
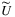 that yields the highest expected objective value out of the set Θ of all joint distributions satisfying the given distributional information (the ambiguity set). This can be computed by solving:
that yields the highest expected objective value out of the set Θ of all joint distributions satisfying the given distributional information (the ambiguity set). This can be computed by solving:
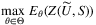
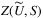 defines the optimal utility a customer may achieve
defines the optimal utility a customer may achieve
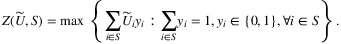
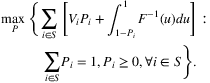
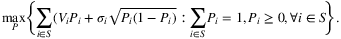
Mishra et al. (2014) show that under appropriate choice of marginals, there is a one-to-one correspondence between all choice probabilities in the simplex and the deterministic components of the utilities. The authors also study the parameter estimation problem under the MDM using the maximum log-likelihood approach. Mishra, Natarajan, Tao, and Teo (2012) also investigate a similar setting where only the mean vector and second-moment matrix of utility vectors (i.e., including covariances) are known, referred as the cross moment model (CMM). The authors show that choice probabilities under the extremal distribution can be computed by solving a semidefinite program.
3 DATA-DRIVEN ONLINE RETAIL FULFILLMENT
In online retail, once customers place orders, the next line of operations that determines customer experience concerns the order fulfillment: the physical process of satisfying an order by dispatching the purchased item from one or multiple stocking locations and shipping the products to the customer. For online retailers such as Amazon, inventory can be shipped out of a network of (75 in Amazon's case) fulfillment centers (FCs) and for omni-channel retailers such as Urban Outfitters, online orders can be fulfilled from not only dedicated FCs but also stores (Acimovic and Farias (2019)). Thus, for omni-channel retailers, fulfillment decisions not only affect shipping costs; they also provide an additional lever for the brick-and-mortar store network to maintain healthy stock levels.
3.1 Fulfillment optimization models
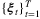 . For example, ξt can be a n-vector whose components give the quantities of each of the n products included in the order; alternatively, ξt take on an integer index value over a set of discrete demand types. Then, the fulfillment decisions can be characterized by xt,i,j, which represents the amount of demand for product i fulfilled from inventory at node j in period t. Given the order process and fulfillment decisions, the reward (profit) is denoted by R(x, ξ), which may capture revenue, shipping costs, late-delivery penalty, etc. We consider that the set J includes a dummy node with infinite inventory but low (potentially negative) reward to reflect shortage penalty. Hence, the fulfillment decisions at period t can be optimized by solving:
. For example, ξt can be a n-vector whose components give the quantities of each of the n products included in the order; alternatively, ξt take on an integer index value over a set of discrete demand types. Then, the fulfillment decisions can be characterized by xt,i,j, which represents the amount of demand for product i fulfilled from inventory at node j in period t. Given the order process and fulfillment decisions, the reward (profit) is denoted by R(x, ξ), which may capture revenue, shipping costs, late-delivery penalty, etc. We consider that the set J includes a dummy node with infinite inventory but low (potentially negative) reward to reflect shortage penalty. Hence, the fulfillment decisions at period t can be optimized by solving:
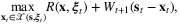 (2)
(2)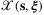 denotes the set of feasible fulfillment decisions and
denotes the set of feasible fulfillment decisions and 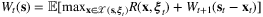 denotes the expected optimal reward starting with inventory vector s at time period t. This dynamic programming problem is difficult to solve due to the curse of dimensionality.
denotes the expected optimal reward starting with inventory vector s at time period t. This dynamic programming problem is difficult to solve due to the curse of dimensionality.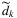 for type k orders. The reward (profit) of satisfying demand type k from node j can be written as Rj,k. Note that the index i are suppressed since the problem can be solved for each product separately. Then, given the realization of demand type ξt = k, the fulfillment decisions at time t can be approximated by:
for type k orders. The reward (profit) of satisfying demand type k from node j can be written as Rj,k. Note that the index i are suppressed since the problem can be solved for each product separately. Then, given the realization of demand type ξt = k, the fulfillment decisions at time t can be approximated by:
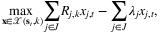 (3)
(3) (4)
(4)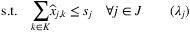
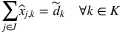
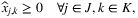
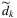 , especially for products with high sales volume, are often available by use of modern forecasting techniques. Acimovic and Graves (2015), Acimovic and Farias (2019) show that the above approximation, supported by state-of-the-art forecasting methods, achieves empirical success and has been implemented in industry.
, especially for products with high sales volume, are often available by use of modern forecasting techniques. Acimovic and Graves (2015), Acimovic and Farias (2019) show that the above approximation, supported by state-of-the-art forecasting methods, achieves empirical success and has been implemented in industry.Several other works also rely on the DLP approximation similar to one proposed in Acimovic and Graves (2015). Avrahami, Herer, and Levi (2014) consider the fulfillment problem for a two-phase distribution system with an industrial collaborator, the Yedioth Group. Using similar techniques, they also approximate the value function as a linear program and then develop an innovative stochastic gradient-based algorithm. Their proposed method has been implemented at Yedioth and has led to both reduction in production cost while maintaining the same level of sales and reduction in returns levels with total savings more than $350,000 a year.
Jasin and Sinha (2015) consider the online fulfillment problem in which customers may place orders involving multiple items. They formulate the stochastic control problem that minimizes the expected total shipping costs and approximate it with a DLP. It is worth pointing out that their DLP is constructed differently compared with Acimovic and Graves (2015). Specifically, the DLP is constructed by replacing the stochastic demand with expected values and decoupling the fulfillment decisions across items in the order. Then, the authors provide two heuristics based on the DLP solution. Their proposed approaches also require a priori demand forecasts.
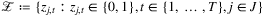 and
and 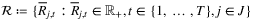 . The reward for period t is given by
. The reward for period t is given by 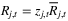 . The authors consider the values of
. The authors consider the values of 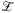 to be chosen adversarially from an uncertainty set. This adversarial model of rewards reflects uncertainty in demand, since it is possible that zj,t = 0 and thus the order is shut off. Following (3), the best fulfillment node j at time t can be chosen by solving:
to be chosen adversarially from an uncertainty set. This adversarial model of rewards reflects uncertainty in demand, since it is possible that zj,t = 0 and thus the order is shut off. Following (3), the best fulfillment node j at time t can be chosen by solving:
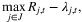
Xu, Allgor, and Graves (2009) investigate whether or not it is beneficial to reevaluate real-time order-warehouse assignment decisions during the time delay between when an order is placed and when it gets fulfilled. The real-time assignment refers to the assignment made right after a customer makes a purchase of product. This real-time assignment has to be myopic because it cannot account for any subsequent customer orders or future inventory replenishment. Starting from the myopic decision, the authors examine the benefits of periodically reevaluating these real-time assignments. Inspired by neighborhood search, they construct near-optimal heuristics for the reassignment of a large set of customer orders to minimize the total number of shipments.
3.2 Extensions
As the fulfillment optimization is highly practice-driven, the literature has extended the basic problem discussed in Section 3.2 in several directions, to capture various operations scenarios in practice. We shall review two lines of extensions, namely, on the analysis of joint problems of fulfillment and product pricing or inventory management, and on the interface with flexibility design.
3.2.1 Joint fulfillment and pricing or inventory management models
In smart retail supply chains, it is best to integrate decisions on fulfillment and pricing (which determines demand) and inventory management (which determines supply). Govindarajan, Sinha, and Uichanco (2018) investigate the joint problem of inventory management and fulfillment optimization for omni-channel retailers. They consider a multi-period, multi-location setting with no replenishment lead time. The authors provide heuristics for different fulfillment settings and show the advantages of their methods using numerical experiments on real-world data. Lim, Jiu, and Ang (2020) investigate the joint problem of inventory replenishment, allocation, and order fulfillment for online retailers. The authors formulate this problem as a multi-period stochastic optimization problem and solve it with a two-phase approach that based on robust optimization.
Lei, Jasin, and Sinha (2018) consider a similar joint pricing and order fulfillment problem for e-retailers. The authors formulate this as a stochastic control problem with random demand. They propose a tractable deterministic approximation of the problem and two practical heuristics. Lei, Jasin, Uichanco, and Vakhutinsky (2018) then move further to consider a dynamic, multi-period joint display, pricing, and fulfillment optimization problem faced by e-retailers. They provide an approximation of the stochastic control problem using its deterministic relaxation and reformulate it as a tractable linear program. They then develop a randomized heuristic policy based on the idea of hierarchical matrix decomposition and propose a novel iterative algorithm based on finding augmenting paths in a graph representation of the display assignment. Using numerical experiments with synthetic and real-world data, they show that their proposed heuristic is very close to optimal.
Harsha, Subramanian, and Uichanco (2019) examine the joint problem of pricing and order fulfillment for an omni-channel retailer instead of an e-retailer. This adds a new dimension to the problem—in the omni-channel setting, the retailer can charge different prices at different brick-and-mortar stores and online channels at the same time. Motivated by constraints encountered by retailers in practice, the authors consider the omni-channel fulfillment pattern (e.g., the proportion of online customers choosing to pick up in store) to be uncertain and exogenous and focus on optimizing the pricing strategy. The authors propose two pricing policies based on the idea of “partitions” of store inventory for online and offline demand. With partitions, inventory at a store can be used for online fulfillment as long as there is enough inventory to exceed the threshold implied by the partition. Once the inventory drops below this level, no more online orders would be fulfilled from this store. The concept is similar in spirit with the setting of booking limits of different fare classes in revenue management.
The proposed solution approach is based on controlling channel prices to adjust demand to meet the inventory partitions. The authors formulate the problem as a mixed-integer program with a tractable number of binary variables, and suggest a scheme to reduce the number of binary variables when demand follows the MNL model. Such a strategy is computationally tractable at a practical scale and the authors describe a successful implementation at their partner firm, where the partitions are implied from network-level pricing strategies.
3.2.2 Flexibility design in fulfillment optimization
Another extension of the fulfillment problem is to investigate the flexibility structure of the fulfillment network. In manufacturing, the long-chain strategy has been shown to be a very effective flexibility structure, in that a long chain with a small degree of flexibility can perform almost as well as a fully flexible system in meeting uncertain demand (Jordan and Graves (1995), Simchi-Levi and Wei (2012)). The effectiveness of this structure is also investigated by Asadpour, Wang, and Zhang (2020) in an online resource allocation problem with inventory considerations, which is closely related to online fulfillment problem. The authors show that the long-chain structure is effective in hedging against demand uncertainty and mitigating supply–demand mismatch. In their work, the performance of an allocation policy is measured by the expected total number of lost sales in the system and their work aims to provide an upper bound on 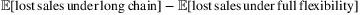 . The authors assume a total of T demand requests of n possible types will arrive, where the types of requests are stochastic with known probabilities. They propose a simple and practical policy, known as the modified greedy policy, and show that the expected lost sales under the long-chain design is finite and does not diverge as T increases. In the regime when T is significantly larger than the number of types n, the upper bound being independent of T implies that the expected lost sales as a function of total demand is very small.
. The authors assume a total of T demand requests of n possible types will arrive, where the types of requests are stochastic with known probabilities. They propose a simple and practical policy, known as the modified greedy policy, and show that the expected lost sales under the long-chain design is finite and does not diverge as T increases. In the regime when T is significantly larger than the number of types n, the upper bound being independent of T implies that the expected lost sales as a function of total demand is very small.
The authors then investigate the fulfillment optimization problem as a potential application. They consider an online retailer that operates n warehouses and customers are also segmented into n regions (demand types) according to geographic proximity. However, the long-chain concept, which would suggest that each customer region can only be fulfilled by two warehouses (in the case of a 2-chain), does not directly apply well to the online fulfillment problem. In practice, even if the preferred (chain-connected) warehouses run out of stock, the retailer would rather incur higher shipping cost from the n − 2 non-preferred warehouses than lost sale. The authors adapt their proposed policy to account for this. Under this policy, fulfillment is made from one of the chain-connected warehouses if there is stock, and from other non-connected warehouses otherwise. Then, the relevant performance metric is the total outbound shipping cost. The authors compare the performance of their method with Acimovic and Graves (2015) and Jasin and Sinha (2015). Their numerical experiments show that their method outperforms that of Jasin and Sinha (2015) in all parameter settings and outperforms Acimovic and Graves (2015) when n is small.
Xu, Zhang, Zhang, and Zhang (2018) extend the work of Asadpour et al. (2020) and investigate online resource allocation problems involving sparsely connected networks with arbitrary numbers of resources and request types, and positive generalized capacity gaps (GCGs). The GCG concept formalizes a notion of “effective chaining” and measures the effectiveness of a given flexibility structure. It is first introduced by Shi, Wei, and Zhong (2019) when discussing the process flexibility of a multi-period make-to-order system. Xu et al. (2018) show that positive GCGs are both necessary and sufficient for sparse network structures to achieve bounded performance gap compared with full-flexibility networks.
Jehl, Shi, Wu, and Shen (2020) investigate the product placement problem for a fulfillment network with the long-chain structure. Instead of investigating inventory allocation of the fulfillment problem, the authors focus on the allocation of SKUs in different warehouses to maximize the number of orders that can be fulfilled. The authors simplify the problem by assuming that an order can be fulfilled by a warehouse if all SKUs involved in the order are placed in the warehouse, and formulate the resulting product placement problem as a mixed-integer program. The authors use a Lagrangian relaxation solution approach, and show that the Lagrangian dual function can be evaluated by solving a minimum cut problem. They also conduct numerical experiments to show that the performance of the long-chain structure achieves over half of the performance of a fully flexible network.
3.3 Practice-driven research
Research on the fulfillment problem and its extensions are both practice- and data-driven in nature, and often involve performance evaluation by numerical experiments with real-world data. Often, this also involves implementation of the proposed methods by industry collaborators. Compared with data-driven frameworks for assortment optimization and inventory management, this line of work has shown strong potential of making real-world impact.
For example, Harsha et al. (2019) implemented their proposed method with their industrial partner, a large U.S. retailer, and achieved a 13.7% increase in clearance-period revenue. DeValve, Wei, Wu, and Yuan (2018) collaborated with one of China's leading e-commerce companies with over 300 million active users and tested their proposed fulfillment policy, leading to a profit improvement on the order of tens of millions in U.S. dollars. Avrahami et al. (2014) collaborated with Yedioth Group, the largest media group in Israel, and implemented fundamental changes in how Yedioth distributed print magazines and newspapers.
While real-world implementation is not always possible, several others have made contributions via pursuing a practice-driven path, focusing on empirical analysis with large-scale real data from industry. For example, Sun, Lyu, Yu, and Teo (2018) analyze data from a wedding gown e-retailer in China to analyze the impact of the fulfillment by Amazon (FBA) model compared with fulfillment by seller (FBS). They develop a risk-adjusted fulfillment model that incorporates the e-retailer's risk attitude toward FBA. They use generalized linear models to predict the expected rewards of shifting to FBA, while controlling the variability of the reward distribution. Applied on a set of real data, the numerical experiments show that their interpretable decision rule can improve the e-retailer's total rewards by more than 35%.
Glaeser, Fisher, and Su (2019) empirically study a “buy online, pickup in store” problem faced by omni-channel retailers. In their setting, online orders can be fulfilled by customers picking up their orders from trucks parked at specific convenient locations. The retailer needs to decide the location and schedule to deploy its trucks to maximize profit. In this setting, customer demand is influenced by the convenience of pickup days as well as locations. The authors first train a regression model using machine learning techniques to predict observed sales while extracting cannibalization effects. The model is built using over 200 explanatory features in three categories: demographic and economic data, business location data, and the retailer's historical sales. Then, the authors solve the spatial-temporal location problem that maximizes weekly revenue, where different from traditional location problem formulation, the objective includes not only the revenue earned, but also spatial and temporal cannibalization effect. The authors use sales data from an industry partner, together with data from the U.S. Census Bureau and OpenStreetMap, for numerical experiments. The numerical results suggest a potential revenue increase of at least 51% from the improved location configuration and schedule.
Cachon, Gallino, and Xu (2018) focus on the setting of deciding free shipping threshold, that is, the minimum order amount over which free shipping is offered. Using actual transaction and product return data, the authors provide an analytical model to assess the profitability of a retailer's current shipping threshold policy and identify the best policy. They conclude that free shipping threshold policies are profitable only under a set of restrictive conditions.
4 DATA-DRIVEN INVENTORY MANAGEMENT
Inventory management is another field where availability of data makes a revolution. In this section, we discuss emerging data-driven approaches for single- and multi-period inventory problems. The typical stochastic inventory management problem involves making decisions on ordering quantities under uncertainty in demand, either over a single selling season or an episode of multiple periods. While the traditional literature typically assumes knowledge of the probability distribution of uncertain demand, the emerging data-driven literature relaxes this by starting with a historical sample of demand. Thus, data-driven inventory management involves both modeling the uncertainty from data, as well as optimizing ordering quantities. We shall review data-driven approaches to analyzing both single- and multi-period problems, in Sections 4.1 and 4.2, respectively.
In the rapidly growing line of literature on data-driven inventory management, an important consideration is on contextual information that supplements the modeling of the key uncertainties of interest. By contextual information (also known as features, covariates, explanatory variables), we refer to exogenous variables that are observable at the point of decision making, and thus may serve as predictors of the focal uncertainty. For example, in inventory control problems where the key uncertainty is in terms of demand volume, the decision-maker may use observable side information, such as social network data, weather forecasts, seasonality, economic indicators, etc., as predictors. Such relevant information often reduces the degree of uncertainty in the model and often leads to better decisions.
4.1 Single-period problems
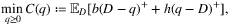 (5)
(5)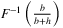 , the
, the 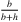 -quantile of the demand distribution.
-quantile of the demand distribution.In practice, it is not possible to directly solve (5), since the distribution of D is unknown and must be estimated from data. Consider the case where data in the form of N independent historical observations of D, 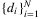 is available. The traditional way of solving this is to assume that demand falls in a family of parametric distributions, estimate the parameters based on data, and then solve the stochastic optimization problem (5). MLE and the Bayesian approach (Scarf (1959), Iglehart (1964)) are common methods for parameter estimation.
is available. The traditional way of solving this is to assume that demand falls in a family of parametric distributions, estimate the parameters based on data, and then solve the stochastic optimization problem (5). MLE and the Bayesian approach (Scarf (1959), Iglehart (1964)) are common methods for parameter estimation.
Although this sequential estimation and optimization framework is a standard and widely-adopted approach, it has intrinsic disadvantages—as the estimation stage has a different objective (e.g., maximizing log-likelihood) than the optimization stage, the “optimal” parameter values in the estimation sense may not necessarily lead to optimal solutions in the optimization stage. To tackle this issue, Liyanage and Shanthikumar (2005) then propose the operational statistics approach that integrates parameter estimation and optimization. Chu, Shanthikumar, and Shen (2008) show the connection between the optimal operational statistic and the Bayesian framework. Ramamurthy, George Shanthikumar, and Shen (2012) study the operational statistics approach when the demand distribution has an unknown shape parameter. Lu, Shanthikumar, and Shen (2015) then generalize operational statistics to the risk-averse case under the conditional value-at-risk (CVaR) criterion.
4.1.1 Models without contextual information
In the era of digitalization and e-retailing, inventory management is supported by the availability of high-quality data. Endowed with this richness of data, researchers begin to explore purely sample-based, data-driven approaches as an alternative to the conventional parametric approaches. We first consider approaches that do not make use of contextual information, that is, rely only on historical data on demand.
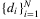 . To be more specific, they consider the problem with the following formulation:
. To be more specific, they consider the problem with the following formulation:
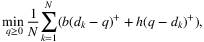
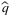 is the b/(b + h)-quantile of the random sample, which is random due to the randomness of sample. Thus, a critical issue is to quantify and guarantee the performance of the solution
is the b/(b + h)-quantile of the random sample, which is random due to the randomness of sample. Thus, a critical issue is to quantify and guarantee the performance of the solution 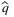 , which is a function of historical data, when applied to future decisions. In general, these out-of-sample performance guarantees, also known as generalization bounds, are often achieved by proving probability bounds on expected test-set performance of the solution. Levi, Roundy, and Shmoys (2007) introduce the concept of ϵ-optimality of a solution
, which is a function of historical data, when applied to future decisions. In general, these out-of-sample performance guarantees, also known as generalization bounds, are often achieved by proving probability bounds on expected test-set performance of the solution. Levi, Roundy, and Shmoys (2007) introduce the concept of ϵ-optimality of a solution 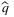 , which suggests that its relative regret, denoted by
, which suggests that its relative regret, denoted by 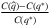 , is no more than ϵ (where q* is the true optimal solution, and C(⋅) denotes the expected cost under the true demand distribution). Using Hoeffding's inequality (see Hoeffding (1994) for a reference), they derive a bound on the probability that the SAA solution solved with a sample size N (denoted by
, is no more than ϵ (where q* is the true optimal solution, and C(⋅) denotes the expected cost under the true demand distribution). Using Hoeffding's inequality (see Hoeffding (1994) for a reference), they derive a bound on the probability that the SAA solution solved with a sample size N (denoted by 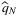 ) has one-sided derivative bounded by
) has one-sided derivative bounded by 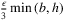 , and use this boundedness property to prove ϵ-optimality of the solution using the piece-wise linear structure of the newsvendor cost function. In particular, Theorem 2.2 of Levi et al. (2007) shows that
, and use this boundedness property to prove ϵ-optimality of the solution using the piece-wise linear structure of the newsvendor cost function. In particular, Theorem 2.2 of Levi et al. (2007) shows that 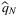 is ϵ-optimal with probability at least
is ϵ-optimal with probability at least
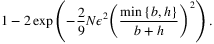
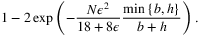 (6)
(6)The key difference between these two bounds is in the constants within the exponential terms, 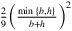 vs
vs 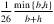 . For an illustration, to achieve an ϵ-optimal solution with probability 1 − 2δ with min{b,h}/(b + h) = 0.1, the bound provided in Levi et al. (2007) suggests a sample size of
. For an illustration, to achieve an ϵ-optimal solution with probability 1 − 2δ with min{b,h}/(b + h) = 0.1, the bound provided in Levi et al. (2007) suggests a sample size of 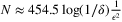 ; whereas the result of Levi et al. (2015) suggests
; whereas the result of Levi et al. (2015) suggests 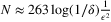 . When min{b,h}/(b + h) = 0.01, the former suggests
. When min{b,h}/(b + h) = 0.01, the former suggests  and the latter suggests
and the latter suggests 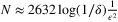 . Therefore, the latter is a significant improvement when min{b,h}/(b + h) is small, which is often the case in real-world problems. Later on, Cheung and Simchi-Levi (2019) prove a lower bound on the number of samples needed for an ϵ-optimal solution that matches the upper bound (6), which implies that the upper bound is indeed tight.
. Therefore, the latter is a significant improvement when min{b,h}/(b + h) is small, which is often the case in real-world problems. Later on, Cheung and Simchi-Levi (2019) prove a lower bound on the number of samples needed for an ϵ-optimal solution that matches the upper bound (6), which implies that the upper bound is indeed tight.
Besides the improved bound based on Bernstein's inequality, the authors also introduce a property of the demand distribution known as the weighted mean spread (WMS) and show that it is the key property of a distribution that determines the accuracy of the SAA method when solving newsvendor problems. The WMS is defined as f(q*)Δ(q*), where f(q*) is the probability density at q*, 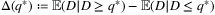 and q* is the
and q* is the 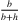 quantile of D. The authors show that, by choosing
quantile of D. The authors show that, by choosing 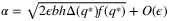 , and biasing the SAA solution to
, and biasing the SAA solution to 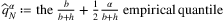 ,
, 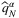 is ϵ-optimal with probability at least
is ϵ-optimal with probability at least 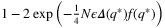 . The authors show that this bound is tighter than previously stated ones and matches the empirical accuracy of the SAA observed in many computational experiments. Although this bound is tighter, it requires extra information on the demand distribution; whereas the previously stated bound based on Bernstein's inequality only requires knowledge of the Lipschitz constant of the newsvendor cost function.
. The authors show that this bound is tighter than previously stated ones and matches the empirical accuracy of the SAA observed in many computational experiments. Although this bound is tighter, it requires extra information on the demand distribution; whereas the previously stated bound based on Bernstein's inequality only requires knowledge of the Lipschitz constant of the newsvendor cost function.
4.1.2 Models with contextual information
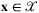 to ordering decision q ∈ ℝ+ that minimizes the conditional expected cost function with respect to the distribution of the random demand D. Therefore, problem (5) would be replaced by
to ordering decision q ∈ ℝ+ that minimizes the conditional expected cost function with respect to the distribution of the random demand D. Therefore, problem (5) would be replaced by
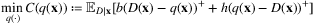 (7)
(7)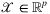 to decision space ℝ+. Available data takes the form of a historical sample of both features and demand, denoted by
to decision space ℝ+. Available data takes the form of a historical sample of both features and demand, denoted by 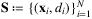 .
.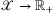 , to be learned through a learning algorithm. A natural way to obtain such hypothesis, given sample S, is through empirical risk minimization (ERM):
, to be learned through a learning algorithm. A natural way to obtain such hypothesis, given sample S, is through empirical risk minimization (ERM):
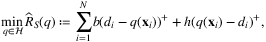 (8)
(8)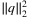 , is added to
, is added to 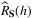 to avoid overfitting. It is interesting to note that the data-driven contextual newsvendor problem is equivalent, up to scaling, to the conditional quantile prediction problem. Therefore, multiple machine learning models, including linear regression, kernel methods as well as deep neural networks, can be applied to provide order policies (Beutel & Minner, 2012; Ban & Rudin, 2018; Cao & Shen, 2019; Huh, Levi, Rusmevichientong, & Orlin, 2011; Oroojlooyjadid, Snyder, & Takáč, 2020).
to avoid overfitting. It is interesting to note that the data-driven contextual newsvendor problem is equivalent, up to scaling, to the conditional quantile prediction problem. Therefore, multiple machine learning models, including linear regression, kernel methods as well as deep neural networks, can be applied to provide order policies (Beutel & Minner, 2012; Ban & Rudin, 2018; Cao & Shen, 2019; Huh, Levi, Rusmevichientong, & Orlin, 2011; Oroojlooyjadid, Snyder, & Takáč, 2020).Beutel and Minner (2012) propose linear programming models to deal with the case when demand is a linear combination of some exogenous variables and a random shock. Sachs (2015) extends the Beutel and Minner (2012) study to the case where demand observations are censored. In both papers, the goal is to minimize an objective of in-sample cost, following ERM.
Ban and Rudin (2018) consider a linear hypothesis class with ERM and regularization and provide performance guarantees for these methods under certain conditions. Oroojlooyjadid et al. (2020) use deep neural networks to fit the policy map and conduct numerical experiments on real-world data. Cao and Shen (2019) use a deterministic polynomial feed-forward neural network for the newsvendor problem with stationary and non-stationary time series demand.
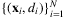 , machine learning methods can be utilized to assign weights wN,i(x) for each data point (xi, di) based on the similarity between xi and x. For instance, both Ban and Rudin (2018) and Bertsimas and Kallus (2019) investigate a method motivated by kernel regression which sets the weights as
, machine learning methods can be utilized to assign weights wN,i(x) for each data point (xi, di) based on the similarity between xi and x. For instance, both Ban and Rudin (2018) and Bertsimas and Kallus (2019) investigate a method motivated by kernel regression which sets the weights as
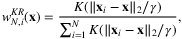
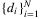 weighted by wN,i(x). Then, problem (7) can be rewritten as:
weighted by wN,i(x). Then, problem (7) can be rewritten as:
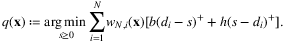 (9)
(9)Ban and Rudin (2018) investigate the out-of-sample performance guarantee for the case where weights are generated by kernel estimation. Bertsimas and Kallus (2019) propose a more general framework that is applicable to not only the newsvendor problems, but to general convex optimization problems, and provide guarantees on consistency and generalization bounds.
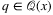 ), one simply needs to solve for
), one simply needs to solve for
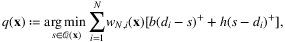
Other works that adopt similar settings include Meller and Taigel (2019), Ho and Hanasusanto (2019), Lin et al. (2020). Meller and Taigel (2019) propose to use the quantile loss function when learning the tree structure for the weights and compare the joint estimation-optimization method with traditional separated estimation and optimization methods. Ho and Hanasusanto (2019) propose a kernel-based approach with regularization and provide performance guarantees. Lin et al. (2020) investigate a risk-averse newsvendor problem subject to a value-at-risk constraint.
4.2 Multi-period problems
The goal of the stochastic, multi-period inventory management problem is to determine (dynamically) a sequence of orders over a planning horizon of multiple discrete periods, to satisfy a sequence of random demand over the planning horizon, and to minimize expected cost. The problem often adopts the following system dynamics: at the beginning of each time period t = 1, …, T, the system state is characterized by inventory level It. The planner chooses an order quantity qt, and then the uncertainty zt (e.g., demand and/or lead time) is realized, which leads an incurred cost Ct(qt, It, zt) for the period. Then, after satisfying as much demand as possible, the inventory state is updated as It + 1 = f(q:,t, It, zt), where q:,t = (q1, …, qt), since the transition of inventory state depends previous order quantities under positive lead time, current state It and the uncertainty zt. The one-period cost function Ct(qt, It, zt) may include holding cost, stockout cost, fixed and variable order costs, and so on. The goal of the multi-period inventory management problem is to find a control policy that yields qt given the current state It to minimize the total inventory cost over a finite or infinite horizon. Dynamic programming has been the most dominant approach in studying this type of problem (see Zipkin (2000) for a representative reference). This involves defining the optimization problem recursively over time periods. Unlike the single-period newsvendor model, the multi-period problem is often difficult even when the probability distribution of uncertain parameters (e.g., demand) is precisely known. One major challenge is the curse of dimensionality, where the complexity of the problem explodes exponentially in the number of periods.
4.2.1 Models without contextual observation
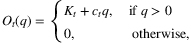
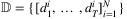 for N previous selling seasons, each with T periods. Demand in each period is assumed to fall within support
for N previous selling seasons, each with T periods. Demand in each period is assumed to fall within support 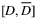 . Then, the optimal
. Then, the optimal 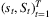 are estimated by
are estimated by 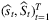 , where:
, where:
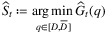
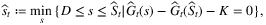
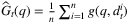 and
and
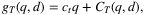
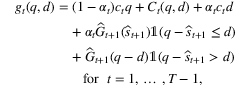
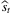 and
and 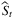 converge to the optimal values st and St as t → ∞. The author also provides confidence intervals by first proving the central limit theorem for
converge to the optimal values st and St as t → ∞. The author also provides confidence intervals by first proving the central limit theorem for 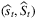 with the property of “M-estimators.” Then, confidence intervals can be constructed based on asymptotic normality. The author also extends the method to the case of censored demand.
with the property of “M-estimators.” Then, confidence intervals can be constructed based on asymptotic normality. The author also extends the method to the case of censored demand.Some other works focus on the SAA method. Levi et al. (2007) study the multiperiod extension of Newsvendor problem (i.e., without fixed ordering costs), where the optimal policy is the base-stock policy. Similar to the single-period Newsvendor setting, the authors describe a sampling-based algorithm that provides 1 + ϵ-base-stock level with any given confidence level δ. Cheung and Simchi-Levi (2019) then consider the multi-period inventory management problem with a constraint on the order quantity in each period. The authors investigate the minimum number of samples required by the SAA method to achieve a near-optimal base-stock policy with any given confidence level. In particular, it is sufficient for the SAA method to achieve near-optimal solution with polynomially many (w.r.t. T and ϵ) samples.
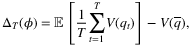
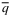 is the optimal Newsvendor quantity. By proposing gradient descent based algorithms, the authors provide a policy achieving the average expected regret
is the optimal Newsvendor quantity. By proposing gradient descent based algorithms, the authors provide a policy achieving the average expected regret 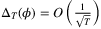 .
.Huh, Janakiraman, Muckstadt, and Rusmevichientong (2009) propose algorithms for finding the optimal order-up-to levels in lost-sales inventory systems with deterministic, positive lead time. They prove that the T-period running average expected cost under their algorithm converges to the cost of the best base-stock policy with a convergence rate 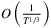 . Later, Zhang, Chao, and Shi (2020) close the gap between upper and lower bounds of the regret by providing an algorithm that achieves regret
. Later, Zhang, Chao, and Shi (2020) close the gap between upper and lower bounds of the regret by providing an algorithm that achieves regret 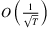 that matches the theoretical lower bound. Agrawal and Jia (2019) further provide an upper bound of the regret that depends linearly on the lead time L. This result improves the bound provided in Zhang et al. (2020) that depends exponentially on the lead time L. Huh et al. (2011) apply the Kaplan-Meier estimator to develop nonparametric adaptive data-driven policies for the multiperiod distribution-free newsvendor problem with censored demand. Later, Shi, Chen, and Duenyas (2016) propose a data-driven, stochastic gradient descent type algorithm for solving the periodic review multi-product inventory management problem over a finite horizon, under capacity constraints. They show that the average regret converges to zero at the rate of
that matches the theoretical lower bound. Agrawal and Jia (2019) further provide an upper bound of the regret that depends linearly on the lead time L. This result improves the bound provided in Zhang et al. (2020) that depends exponentially on the lead time L. Huh et al. (2011) apply the Kaplan-Meier estimator to develop nonparametric adaptive data-driven policies for the multiperiod distribution-free newsvendor problem with censored demand. Later, Shi, Chen, and Duenyas (2016) propose a data-driven, stochastic gradient descent type algorithm for solving the periodic review multi-product inventory management problem over a finite horizon, under capacity constraints. They show that the average regret converges to zero at the rate of 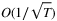 .
.
4.2.2 Models with contextual observation
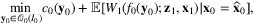 (10)
(10)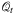 denotes the feasible region of decision variable yt in period t, which may depend on state variable It (such as the inventory level) and the realization of zt, and Wt denotes the cost-to-go function defined recursively as:
denotes the feasible region of decision variable yt in period t, which may depend on state variable It (such as the inventory level) and the realization of zt, and Wt denotes the cost-to-go function defined recursively as:
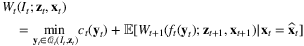
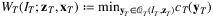 .
.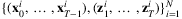 , weights
, weights  are learned and the recursion of Wt can be approximated by approximating the conditional expectation
are learned and the recursion of Wt can be approximated by approximating the conditional expectation 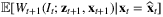 by:
by:
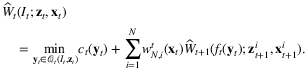
From the perspective of computational tractability, this method still requires solving a dynamic programming problem (10), which requires exact or approximate solution techniques. Note that (10) is no more difficult to solve, yet often leads to significant improvements, compared with sample average approaches that ignore covariates.
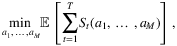 (11)
(11)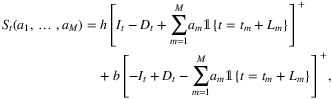
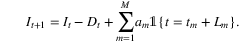
Note that the expectation is taken over the joint distribution of the demand 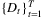 and the VLTs
and the VLTs 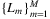 .
.
Qi et al. (2020) propose a one-step end-to-end (E2E) framework that uses deep-learning models to output replenishment quantities directly from input features without any intermediate steps. To apply deep learning methods, it is necessary to construct a training data set consisting of paired features and label values. As the available data consists of historical observations of demand, VLT, and contextual information, the label, that is, the target decision variables, are not directly known. The ideal target decision would be the optimal solution of the stochastic multi-stage optimization problem (11). However, this is not an option since the joint distribution of multi-period demand and VLTs is unknown. To overcome this difficulty, the training dataset is labeled with the optimal dynamic programming solutions 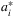 under observed trajectories.
under observed trajectories.
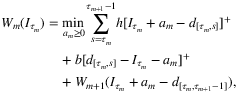
 is the optimal cost overtime interval [τm, τm + 1 − 1],
is the optimal cost overtime interval [τm, τm + 1 − 1], 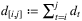 . The authors show that this problem admits a closed-form solution
. The authors show that this problem admits a closed-form solution 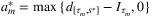 , where
, where 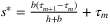 . Therefore, labeling observations with
. Therefore, labeling observations with 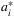 serves as an efficient method even with enormous data.
serves as an efficient method even with enormous data.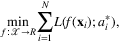
 . By conducting a series of thorough numerical experiments including a field experiment from a leading e-commerce company, the authors demonstrate the numerical advantages of the proposed framework.
. By conducting a series of thorough numerical experiments including a field experiment from a leading e-commerce company, the authors demonstrate the numerical advantages of the proposed framework.It is interesting to note that, thus far, much of the success of data-driven research in retail operations stems from the availability and clever use of demand-side data, such as contextual information that influences demand and sales. Qi et al. (2020) provide an interesting example of incorporating both demand- and supply-side data (on VLT) in an E2E framework. We believe the integrated use of data from both ends of the supply chain is a promising direction for future research.
5 DISCUSSION AND CONCLUSION
As Simchi-Levi (2014) pointed out, the emergence of data-driven research is a major paradigm shift for the operations research (OR) community, who has historically focused on problem-oriented research. Not only does this development lead to new topics for research, it also calls for rethinking of our community's core philosophy. Elaborating on this, we shall close the paper by pointing out some promising directions for future work.
Various methodologies and techniques have been employed in the reviewed literature. First, many (e.g., assortment fulfillment optimization) problems involve formulations that are hard to solve, for example, in the form of integer or mixed-integer problems. It is common to develop approximation schemes to find nearly optimal solutions in polynomial time. Second, it has become a popular in data-driven research is to apply (statistical) machine learning methods. In fulfillment optimization problems, machine learning techniques are extensively used in forecasting customer behavior. In assortment optimization problems, low-rank learning methods are used to estimate choice model parameters from data. While in many cases, machine learning techniques are mainly used for forecasting, there are successful attempts to develop learning frameworks that integrate both prediction and optimization, particularly for inventory problems. In scenarios where offline data is not available, the online learning framework has become another methodological trend that is widely adopted in assortment optimization and inventory management. Such a framework balances the trade-off between exploration and exploitation, and often provides performance guarantees in the form of regret bounds.
In Sections 2 and 4, we reviewed both parametric and nonparametric methods for assortment optimization and inventory management. Parametric methods are a natural fit with conventional OR research, which typically proceeds with a set of model assumptions to ensure tractability. While some of these assumptions (e.g., stationarity of demand distributions in multi-period problems) often play important roles in proving important structural results, the extent to which they hold in practice, and thus the generalizability of structural results, may vary substantially from one setting to another. With the rapid growth in computational power and availability of rich, high-quality data sets, nonparametric methods become both feasible and practical, although they are often less “elegant” and more reliant on numerical solution methods. This development challenges our conventional mindset of focusing on model-based structural properties. Rather than viewing this as a strict trade-off to reconcile, we believe that our community should identify synergies between these apparently divergent approaches. For example, one may investigate problem properties that translate at least qualitatively (if not in the strict technical sense) to more general and practical settings, and use these to inform the design of data-driven solution methods.
Associated with the choice between parametric and nonparametric approaches, an important direction for future research is the integration of prediction/estimation and optimization. Many of the works reviewed in this article adopt the sequential estimation/optimization paradigm. Although separating estimation and optimization is intuitive and common in practice, it may lead to sub-optimal solutions as we discussed in Section 4. To address this, there is an active stream in the machine learning (ML) and OR literature focusing on integrating the prediction and optimization stages. It remains to be studied how these concepts can be extended to the wide range of supply chain problems.
Another important direction where one can marry OR and ML methods is in tackling dynamic, multi-period problems, which arise in different applications in supply chain management. Traditionally, the OR community has focused on developing structural properties of optimal policies to reduce the search space in optimization, often in idealized settings. To extend these to practical settings where various simplifying assumptions are relaxed, researchers often employ approximate dynamic programming (ADP) techniques. In parallel, the ML community has focused on the development of reinforcement learning (RL) methods, which enable (virtual) agents are trained to learn the best actions for solving a Markov decision problem in virtual/simulated environments. As pointed out by prominent researchers in this area (e.g., Bertsekas (2019)), the key concepts of ADP and RL overlap substantially. Building on recent advances in deep learning, RL has achieved great success in solving many difficult problems. We believe that one promising future research direction is to leverage (deep) RL techniques to develop practical solution frameworks for complex supply chain management problems. While direct applications of existing RL techniques may already lead to interesting findings, we believe that the most interesting avenue will involve leveraging the wealth of structural insights of our community (e.g., on optimal inventory policies) to steer the design of RL algorithms, such as the design of special-purpose neural net architectures.
As our community continues to adopt ideas from ML in developing supply chain solutions, we believe that it is critical to blend these ideas with our domain knowledge about supply chain management and expertise in optimization techniques so that the methods can best exploit domain-specific problem (and/or data) characteristics in the supply chain context. For instance, Qi et al. (2020) provide an example of using domain knowledge to develop a better deep learning solution in a scenario where it is not apparent how a supervised learning framework can be applied. Besides, as pointed out by Mišić and Perakis (2020), it is an important future direction to develop interpretable data-driven models. Black-box machine learning models, although they may achieve favorable numerical performance, often fail to provide intuitive insight that helps real-world practitioners to understand this model. Therefore, the lack of interpretability may hold back the implementation of practical data-driven solutions. Although interpretability already becomes a major research area in ML (we refer to Murdoch, Singh, Kumbier, Abbasi-Asl, and Yu (2019) and Rudin (2019) for comprehensive reviews), there have been few works that address this issue in our community until very recently (e.g., Bertsimas, Dunn, and Mundru (2019)). We believe this is also an issue that our domain knowledge will play an important role.
Finally, our community may take inspiration from our ML counterparts in the development of standard benchmark datasets for testing new models. Not only would this improve transparency and reproducibility of our data-driven research, but this would also aid dissemination of our research outputs. Imagine if a set of online courses on our methods, complemented by open-source code and benchmark datasets, are made widely available for the general audience, just like similar courses on ML and artificial intelligence. We believe this has not yet happened, in part, due to our community's focus on problems and data that companies consider proprietary. Yet, there has been promising recent development toward this direction, as in the publication of interesting, real datasets (e.g., Acimovic, Erize, Hu, Thomas, & Mieghem, 2019; Shen, Tang, Wu, Yuan, & Zhou, 2019; Zhao, Li, & Shen, 2020) in leading journals. While these datasets are intentionally chosen to be rich and practical to encourage the exploration of new problems, we believe that extracting benchmark datasets for several common problem themes (such as those reviewed in Sections 2, 4) can be extremely valuable for our community.
ACKNOWLEDGMENTS
The authors gratefully acknowledge feedback from Professor Ming Hu (Editor-in-Chief), the Associate Editor, and two anonymous referees, which have helped improve this article. This research is partially supported by the National Natural Science Foundation of China (NSFC) Grant 71991462 (Zuo-Jun Max Shen).
REFERENCES
- Acimovic, J., Erize, F., Hu, K., Thomas, D. J., & Mieghem, J. A. V. (2019). Product life cycle data set: Raw and cleaned data of weekly orders for personal computers. Manufacturing & Service Operations Management, 21(1), 171–176.
- Acimovic, J., & Farias, V. F. (2019). The fulfillment-optimization problem. In Operations Research & Management Science in the age of analytics (pp. 218–237). Catonsville, MD: INFORMS.
- Acimovic, J., & Graves, S. C. (2015). Making better fulfillment decisions on the fly in an online retail environment. Manufacturing & Service Operations Management, 17(1), 34–51.
- Agrawal, S., & Jia, R. (2019). Learning in structured mdps with convex cost functions: Improved regret bounds for inventory management. Proceedings of the 2019 ACM Conference on Economics and Computation. pp. 743–744.
- Ammar, A., Oh, S., Shah, D., & Voloch, L. F. (2014). What's your choice? Learning the mixed multi-nomial. In: Proceedings of the 2014 ACM International Conference on Measurement and Modeling of Computer Systems, pp. 565–566.
- Anderson, S. P., de Palma, A., & Thisse, J.-F. (1992). Discrete choice theory of product differentiation. Cambridge, MA: MIT Press.
10.7551/mitpress/2450.001.0001 Google Scholar
- Andrews, J. M., Farias, V. F., Khojandi, A. I., & Yan, C. M. (2019). Primal–dual algorithms for order fulfillment at urban outfitters, inc. Interfaces, 49(5), 355–370.
- Aouad, A., Farias, V., Levi, R., & Segev, D. (2018). The approximability of assortment optimization under ranking preferences. Operations Research, 66(6), 1661–1669.
- Asadpour, A., Wang, X., & Zhang, J. (2020). Online resource allocation with limited flexibility. Management Science, 66(2), 642–666.
- Avrahami, A., Herer, Y. T., & Levi, R. (2014). Matching supply and demand: Delayed two-phase distribution at yedioth group—Models, algorithms, and information technology. Interfaces, 44(5), 445–460.
- Ban, G.-Y. (2020). Confidence intervals for data-driven inventory policies with demand censoring. Operations Research, 68(2), 309–326.
- Ban, G.-Y., & Rudin, C. (2018). The big data newsvendor: Practical insights from machine learning. Operations Research, 67(1), 90–108.
- Ben-Akiva, M. E., Lerman, S. R., & Lerman, S. R. (1985). Discrete choice analysis: Theory and application to travel demand (Vol. 9). Cambridge, MA: MIT Press.
- Berbeglia, G., & Joret, G. (2020). Assortment optimisation under a general discrete choice model: A tight analysis of revenue-ordered assortments. Algorithmica, 82(4), 681–720.
10.1007/s00453-019-00610-8 Google Scholar
- Bertsekas, D. P. (2019). Reinforcement learning and optimal control. Belmont, MA: Athena Scientific.
- Bertsimas, D., Dunn, J., & Mundru, N. (2019). Optimal prescriptive trees. INFORMS Journal on Optimization, 1(2), 164–183.
10.1287/ijoo.2018.0005 Google Scholar
- Bertsimas, D., & Kallus, N. (2019). From predictive to prescriptive analytics. Management Science, 66(3), 1025–1044.
- Bertsimas, D., & McCord, C. (2019). From predictions to prescriptions in multistage optimization problems. arXiv Preprint arXiv:1904.11637.
- Bertsimas, D., & Mišic, V. V. (2015). Data-driven assortment optimization. Cambridge, MA: Operations Research Center, MIT.
- Bertsimas, D., & Mišić, V. V. (2019). Exact first-choice product line optimization. Operations Research, 67(3), 651–670.
- Besbes, O., & Zeevi, A. (2009). Dynamic pricing without knowing the demand function: Risk bounds and near-optimal algorithms. Operations Research, 57(6), 1407–1420.
- Beutel, A.-L., & Minner, S. (2012). Safety stock planning under causal demand forecasting. International Journal of Production Economics, 140(2), 637–645.
- Blanchet, J., Gallego, G., & Goyal, V. (2016). A markov chain approximation to choice modeling. Operations Research, 64(4), 886–905.
- Bront, J. J. M., Méndez-Daz, I., & Vulcano, G. (2009). A column generation algorithm for choice-based network revenue management. Operations Research, 57(3), 769–784.
- Bunch, D. S. (1987). Maximum likelihood estimation of probabilistic choice models. SIAM Journal on Scientific and Statistical Computing, 8(1), 56–70.
- Bunch, D. S. (1988). A comparison of algorithms for maximum likelihood estimation of choice models. Journal of Econometrics, 38(1–2), 145–167.
- Bunch, D. S., & Batsell, R. R. (1989). A Monte Carlo comparison of estimators for the multinomial logit model. Journal of Marketing Research, 26(1), 56–68.
- Cachon, G. P., Gallino, S., & Xu, J. (2018). Free shipping is not free: A data-driven model to design free-shipping threshold policies. Available at SSRN, 3250971.
- Cao, Y., & Shen, Z.-J. M. (2019). Quantile forecasting and data-driven inventory management under nonstationary demand. Operations Research Letters, 47(6), 465–472.
- Chen, X., & Simchi-Levi, D. (2004). Coordinating inventory control and pricing strategies with random demand and fixed ordering cost: The finite horizon case. Operations Research, 52(6), 887–896.
- Chen, X., & Simchi-Levi, D. (2012). Pricing and inventory management. The Oxford Handbook of Pricing Management, 1, 784–824.
- Chen, Y.-C., & Mišić, V. V. (2019). Decision forest: A nonparametric approach to modeling irrational choice. arXiv Preprint arXiv:1904.11532.
- Cheung, W. C., & Simchi-Levi, D. (2019). Sampling-based approximation schemes for capacitated stochastic inventory control models. Mathematics of Operations Research, 44(2), 668–692.
- Chierichetti, F., Kumar, R., & Tomkins, A. (2018). Learning a mixture of two multinomial logits. Proceedings of the International Conference on Machine Learning, pp. 961–969.
- Chu, L. Y., Shanthikumar, J. G., & Shen, Z.-J. M. (2008). Solving operational statistics via a bayesian analysis. Operations Research Letters, 36(1), 110–116.
- Davis, J., Gallego, G., & Topaloglu, H. (2013). Assortment planning under the multinomial logit model with totally unimodular constraint structures. Work in Progress.
- Davis, J. M., Gallego, G., & Topaloglu, H. (2014). Assortment optimization under variants of the nested logit model. Operations Research, 62(2), 250–273.
- den Boer, A. V. (2015). Dynamic pricing and learning: Historical origins, current research, and new directions. Surveys in Operations Research and Management Science, 20(1), 1–18.
10.1016/j.sorms.2015.03.001 Google Scholar
- Désir, A., Goyal, V., & Zhang, J. (2014). Near-optimal algorithms for capacity constrained assortment optimization. Available at SSRN 2543309.
- DeValve, L., Wei, Y., Wu, D., & Yuan, R. (2018). Understanding the value of fulfillment flexibility in an online retailing environment. Available at SSRN 3265838.
- Farias, V. F., Jagabathula, S., & Shah, D. (2013). A nonparametric approach to modeling choice with limited data. Management Science, 59(2), 305–322.
- Feldman, J., Paul, A., & Topaloglu, H. (2019). Assortment optimization with small consideration sets. Operations Research, 67(5), 1283–1299.
- Feldman, J., & Topaloglu, H. (2018). Capacitated assortment optimization under the multinomial logit model with nested consideration sets. Operations Research, 66(2), 380–391.
- Feng, Q., Luo, S., & Zhang, D. (2014). Dynamic inventory–pricing control under backorder: Demand estimation and policy optimization. Manufacturing & Service Operations Management, 16(1), 149–160.
- Gallego, G., Ratliff, R., & Shebalov, S. (2015). A general attraction model and sales-based linear program for network revenue management under customer choice. Operations Research, 63(1), 212–232.
- Gallego, G., & Topaloglu, H. (2014). Constrained assortment optimization for the nested logit model. Management Science, 60(10), 2583–2601.
- Glaeser, C. K., Fisher, M., & Su, X. (2019). Optimal retail location: Empirical methodology and application to practice: Finalist–2017 m&som practice-based research competition. Manufacturing & Service Operations Management, 21(1), 86–102.
- Govindarajan, A., Sinha, A., & Uichanco, J. (2018). Joint inventory and ful fillment decisions for omnichannel retail networks. Ross School of Business Paper 1341, Ann Arbor, MI.
- Harsha, P., Subramanian, S., & Uichanco, J. (2019). Dynamic pricing of omnichannel inventories: Honorable mention–2017 m&som practice-based research competition. Manufacturing & Service Operations Management, 21(1), 47–65.
- Ho, C. P., & Hanasusanto, G. A. (2019). On data-driven prescriptive analytics with side information: A regularized nadaraya-watson approach. Technical report, March.
- Hoeffding, W. (1994). Probability inequalities for sums of bounded random variables. In N. I. Fisher & P. K. Sen (Eds.), The Collected Works of Wassily Hoeffding (pp. 409–426). New York, NY: Springer.
10.1007/978-1-4612-0865-5_26 Google Scholar
- Huh, W. T., Janakiraman, G., Muckstadt, J. A., & Rusmevichientong, P. (2009). An adaptive algorithm for finding the optimal base-stock policy in lost sales inventory systems with censored demand. Mathematics of Operations Research, 34(2), 397–416.
- Huh, W. T., Levi, R., Rusmevichientong, P., & Orlin, J. B. (2011). Adaptive data-driven inventory control with censored demand based on Kaplan-meier estimator. Operations Research, 59(4), 929–941.
- Huh, W. T., & Rusmevichientong, P. (2009). A nonparametric asymptotic analysis of inventory planning with censored demand. Mathematics of Operations Research, 34(1), 103–123.
- Iglehart, D. L. (1964). The dynamic inventory problem with unknown demand distribution. Management Science, 10(3), 429–440.
- Jagabathula, S. (2014). Assortment optimization under general choice. Available at SSRN 2512831.
- Jagabathula, S., & Rusmevichientong, P. (2017). A nonparametric joint assortment and price choice model. Management Science, 63(9), 3128–3145.
- Jasin, S., & Sinha, A. (2015). An LP-based correlated rounding scheme for multi-item ecommerce order fulfillment. Operations Research, 63(6), 1336–1351.
- Jehl, T., Shi, Y., Wu, D., & Shen, Z.-J. M. (2020). Warehouse assortment planning with fulfillment flexibility. Working Paper.
- Jordan, W. C., & Graves, S. C. (1995). Principles on the benefits of manufacturing process flexibility. Management Science, 41(4), 577–594.
- Kök, A. G., Fisher, M. L., & Vaidyanathan, R. (2008). Assortment planning: Review of literature and industry practice. In N. Agrawal & S. Smith (Eds.), Retail Supply Chain Management. International Series in Operations Research & Management Science (Vol. 122, pp. 99–153). Boston, MA: Springer.
- Kunnumkal, S., & Topaloglu, H. (2008). Using stochastic approximation methods to compute optimal base-stock levels in inventory control problems. Operations Research, 56(3), 646–664.
- Lei, Y., Jasin, S., & Sinha, A. (2018). Joint dynamic pricing and order fulfillment for e-commerce retailers. Manufacturing & Service Operations Management, 20(2), 269–284.
- Lei, Y. M., Jasin, S., Uichanco, J., & Vakhutinsky, A. (2018). Randomized product display (framing), pricing, and order fulfillment for e-commerce retailers.
- Levi, R., Perakis, G., & Uichanco, J. (2015). The data-driven newsvendor problem: New bounds and insights. Operations Research, 63(6), 1294–1306.
- Levi, R., Roundy, R. O., & Shmoys, D. B. (2007). Provably near-optimal sampling-based policies for stochastic inventory control models. Mathematics of Operations Research, 32(4), 821–839.
- Li, G., Rusmevichientong, P., & Topaloglu, H. (2015). The d-level nested logit model: Assortment and price optimization problems. Operations Research, 63(2), 325–342.
- Lim, Y. F., Jiu, S., & Ang, M. (2020). Integrating anticipative replenishment-allocation with reactive fulfillment for online retailing using robust optimization. Manufacturing and Service Operations Management.
- Lin, S., Chen, F., Li, Y., & Shen, Z.-J. M. (2020). Procurement of new products: Data-driven newsvendor with profit risk. Available at SSRN 3540448.
- Liu, N., Ma, Y., & Topaloglu, H. (2020). Assortment optimization under the multinomial logit model with sequential offerings. INFORMS Journal on Computing, 32, 835–853.
- Liu, Q., & van Ryzin, G. (2008). On the choice-based linear programming model for network revenue management. Manufacturing & Service Operations Management, 10(2), 288–310.
- Liyanage, L. H., & Shanthikumar, J. G. (2005). A practical inventory control policy using operational statistics. Operations Research Letters, 33(4), 341–348.
- Lu, M., Shanthikumar, J. G., & Shen, Z.-J. M. (2015). Technical note–operational statistics: Properties and the risk-averse case. Naval Research Logistics (NRL), 62(3), 206–214.
- Meller, J., & Taigel, F. (2019). Machine learning for inventory management: Analyzing two concepts to get from data to decisions. Available at SSRN 3256643.
- Méndez-Daz, I., Miranda-Bront, J. J., Vulcano, G., & Zabala, P. (2014). A branch-and-cut algorithm for the latent-class logit assortment problem. Discrete Applied Mathematics, 164, 246–263.
- Miao, S., & Chao, X. (2020). Dynamic joint assortment and pricing optimization with demand learning. Manufacturing and Service Operations Management.
- Mishra, V. K., Natarajan, K., Padmanabhan, D., Teo, C.-P., & Li, X. (2014). On theoretical and empirical aspects of marginal distribution choice models. Management Science, 60(6), 1511–1531.
- Mishra, V. K., Natarajan, K., Tao, H., & Teo, C.-P. (2012). Choice prediction with semidefinite optimization when utilities are correlated. IEEE Transactions on Automatic Control, 57(10), 2450–2463.
- Mišić, V. V., & Perakis, G. (2020). Data analytics in operations management: A review. Manufacturing & Service Operations Management, 22(1), 158–169.
- Mittal, S., & Schulz, A. S. (2013). A general framework for designing approximation schemes for combinatorial optimization problems with many objectives combined into one. Operations Research, 61(2), 386–397.
- Murdoch, W. J., Singh, C., Kumbier, K., Abbasi-Asl, R., & Yu, B. (2019). Definitions, methods, and applications in interpretable machine learning. Proceedings of the National Academy of Sciences of United States of America, 116(44), 22071–22080.
- Natarajan, K., Song, M., & Teo, C.-P. (2009). Persistency model and its applications in choice modeling. Management Science, 55(3), 453–469.
- Negahban, S., Oh, S., Thekumparampil, K. K., & Xu, J. (2018). Learning from comparisons and choices. The Journal of Machine Learning Research, 19(1), 1478–1572.
- Oh, S., & Shah, D. (2014). Learning mixed multinomial logit model from ordinal data. In M. I. Jordan, Y. LeCun, & S. A. Solla (Eds.), Advances in Neural Information Processing Systems (pp. 595–603). Cambridge, MA: MIT Press.
- Oroojlooyjadid, A., Snyder, L. V., & Takáč, M. (2020). Applying deep learning to the newsvendor problem. IISE Transactions, 52(4), 444–463.
- Qi, M., Shi, Y., Qi, Y., Ma, C., Yuan, R., Wu, D., & Shen, Z.-J. M. (2020). A practical end-to-end inventory management model with deep learning. Working paper. Berkeley, CA: University of California.
- Ramamurthy, V., George Shanthikumar, J., & Shen, Z.-J. M. (2012). Inventory policy with parametric demand: Operational statistics, linear correction, and regression. Production and Operations Management, 21(2), 291–308.
- Rudin, C. (2019). Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nature Machine Intelligence, 1(5), 206–215.
- Rusmevichientong, P., Shen, Z.-J. M., & Shmoys, D. B. (2010). Dynamic assortment optimization with a multinomial logit choice model and capacity constraint. Operations Research, 58(6), 1666–1680.
- Rusmevichientong, P., Shmoys, D., Tong, C., & Topaloglu, H. (2014). Assortment optimization under the multinomial logit model with random choice parameters. Production and Operations Management, 23(11), 2023–2039.
- Rusmevichientong, P., & Topaloglu, H. (2012). Robust assortment optimization in revenue management under the multinomial logit choice model. Operations Research, 60(4), 865–882.
- Sachs, A.-L. (2015). The data-driven newsvendor with censored demand observations. In Retail analytics (pp. 35–56). Cham: Springer.
- Scarf, H. (1959). Bayes solutions of the statistical inventory problem. The Annals of Mathematical Statistics, 30(2), 490–508.
- Şen, A., Atamtürk, A., & Kaminsky, P. (2018). A conic integer optimization approach to the constrained assortment problem under the mixed multinomial logit model. Operations Research, 66(4), 994–1003.
- Shen, Z.-J. M., Tang, C. S., Wu, D., Yuan, R., & Zhou, W. (2019). Jd. com: Transaction level data for the 2020 msom data driven research challenge. Available at SSRN 3511861.
- Shi, C., Chen, W., & Duenyas, I. (2016). Nonparametric data-driven algorithms for multiproduct inventory systems with censored demand. Operations Research, 64(2), 362–370.
- Shi, C., Wei, Y., & Zhong, Y. (2019). Process flexibility for multiperiod production systems. Operations Research, 67(5), 1300–1320.
- Simchi-Levi, D. (2014). OM forum–OM research: From problem-driven to data-driven research. Manufacturing & Service Operations Management, 16(1), 2–10.
- Simchi-Levi, D., & Wei, Y. (2012). Understanding the performance of the long chain and sparse designs in process flexibility. Operations Research, 60(5), 1125–1141.
- Snyder, L. V., & Shen, Z.-J. M. (2011). Fundamentals of supply chain theory. Hoboken, NJ: Wiley Online Library.
- Sun, L., Lyu, G., Yu, Y., & Teo, C.-P. (2018). Fulfillment by amazon versus fulfillment by seller: An interpretable risk-adjusted fulfillment model. Available at SSRN 3256746.
- Talluri, K., & Van Ryzin, G. (2004). Revenue management under a general discrete choice model of consumer behavior. Management Science, 50(1), 15–33.
- Wang, R. (2012). Capacitated assortment and price optimization under the multinomial logit model. Operations Research Letters, 40(6), 492–497.
- Wang, R. (2013). Assortment management under the generalized attraction model with a capacity constraint. Journal of Revenue and Pricing Management, 12(3), 254–270.
10.1057/rpm.2012.40 Google Scholar
- Wang, Y., & Shen, Z.-J. M. (2020). Constrained assortment optimization problem under the multilevel nested logit model. Working paper.
- Xu, P. J., Allgor, R., & Graves, S. C. (2009). Benefits of reevaluating real-time order fulfillment decisions. Manufacturing & Service Operations Management, 11(2), 340–355.
- Xu, Z., Zhang, H., Zhang, J., & Zhang, R. (2018). Online demand fulfillment under limited flexibility. Available at SSRN 3201734.
- Zhang, D., & Adelman, D. (2009). An approximate dynamic programming approach to network revenue management with customer choice. Transportation Science, 43(3), 381–394.
- Zhang, H., Chao, X., & Shi, C. (2020). Closing the gap: A learning algorithm for lost-sales inventory systems with lead times. Management Science, 66(5), 1962–1980.
- Zhao, L., Li, L., & Shen, Z.-J. M. (2020). Transactional and in-store display data of a large supermarket for data-driven decision-making. Naval Research Logistics.
- Zipkin, P. H. (2000). Foundations of inventory management. London: McGraw-Hill.




