Magnetic Resonance in Medicine
Volume 88, Issue 4 pp. 1575-1591
RESEARCH ARTICLE
Open Access

Free-breathing motion-informed locally low-rank quantitative 3D myocardial perfusion imaging

Tobias Hoh, 

Tobias Hoh

Institute for Biomedical Engineering, University and ETH Zurich, Zurich, Switzerland

Search for more papers by this author
Valery Vishnevskiy, 

Valery Vishnevskiy

Institute for Biomedical Engineering, University and ETH Zurich, Zurich, Switzerland

Search for more papers by this author
Malgorzata Polacin, 

Malgorzata Polacin

Institute for Biomedical Engineering, University and ETH Zurich, Zurich, Switzerland

Institute of Diagnostic and Interventional Radiology, University Hospital Zurich, University of Zurich, Zurich, Switzerland

Search for more papers by this author
Robert Manka, 

Robert Manka

Institute for Biomedical Engineering, University and ETH Zurich, Zurich, Switzerland

Institute of Diagnostic and Interventional Radiology, University Hospital Zurich, University of Zurich, Zurich, Switzerland

Department of Cardiology, University Heart Center, University Hospital Zurich, University of Zurich, Zurich, Switzerland

Search for more papers by this author
Maximilian Fuetterer, 

Maximilian Fuetterer

Institute for Biomedical Engineering, University and ETH Zurich, Zurich, Switzerland

Search for more papers by this author
Sebastian Kozerke, 

Corresponding Author

Sebastian Kozerke

Institute for Biomedical Engineering, University and ETH Zurich, Zurich, Switzerland

Correspondence

Sebastian Kozerke, Institute for Biomedical Engineering, University and ETH Zurich, Gloriastrasse 35, Zurich 8092, Switzerland.

Email: [email protected]

Search for more papers by this author
First published: 17 June 2022
https://doi.org/10.1002/mrm.29295
Citations: 2

Funding information: Innosuisse - Schweizerische Agentur für Innovationsförderung, Grant/Award Number: 31010.1

Click here for author-reader discussions

Abstract

Purpose

To propose respiratory motion-informed locally low-rank reconstruction (MI-LLR) for robust free-breathing single-bolus quantitative 3D myocardial perfusion CMR imaging. Simulation and in-vivo results are compared to locally low-rank (LLR) and compressed sensing reconstructions (CS) for reference.

Methods

Data were acquired using a 3D Cartesian pseudo-spiral in-out k-t undersampling scheme (R = 10) and reconstructed using MI-LLR, which encompasses two stages. In the first stage, approximate displacement fields are derived from an initial LLR reconstruction to feed a motion-compensated reference system to a second reconstruction stage, which reduces the rank of the inverse problem. For comparison, data were also reconstructed with LLR and frame-by-frame CS using wavelets as sparsifying transform ( ℓ 1 $$ {\ell}_1 $$ -wavelet).

Reconstruction accuracy relative to ground truth was assessed using synthetic data for realistic ranges of breathing motion, heart rates, and SNRs. In-vivo experiments were conducted in healthy subjects at rest and during adenosine stress. Myocardial blood flow (MBF) maps were derived using a Fermi model.

Results

Improved uniformity of MBF maps with reduced local variations was achieved with MI-LLR. For rest and stress, intra-volunteer variation of absolute and relative MBF was lower in MI-LLR (±0.17 mL/g/min [26%] and ±1.07 mL/g/min [33%]) versus LLR (±0.19 mL/g/min [28%] and ±1.22 mL/g/min [36%]) and versus ℓ 1 $$ {\ell}_1 $$ -wavelet (±1.17 mL/g/min [113%] and ±6.87 mL/g/min [115%]). At rest, intra-subject MBF variation was reduced significantly with MI-LLR.

Conclusion

The combination of pseudo-spiral Cartesian undersampling and dual-stage MI-LLR reconstruction improves free-breathing quantitative 3D myocardial perfusion CMR imaging under rest and stress condition.

1 INTRODUCTION

The clinical utility and value of dynamic contrast-enhanced myocardial first-pass perfusion imaging has been demonstrated in a number of landmark trials.1-3 While in today's clinical use, image data are mostly assessed visually or semi-quantitatively to identify ischemia, quantitative approaches4 have gained momentum with recent technical advances in data acquisition, reconstruction, and processing.5-8

In contrast to conventional dynamic multi-slice 2D imaging sequences, 3D approaches with whole-heart coverage allow data acquisition in a single time window per cardiac cycle.9 The potential clinical value of robust 3D myocardial perfusion imaging relates, in particular, to the ability to quantify the relative ischemic myocardial volume.10, 11 In view of the increasing utilization of ischemic burden as a marker for decision making for revascularization in stable coronary artery disease,12 added value has been indicated. Moreover, the importance of quantification of myocardial blood flow (MBF) and related parameters has been emphasized in the context of triple vessel coronary artery disease,13, 14 microvascular disease,15, 16 and other conditions.17

Dynamic 3D perfusion methods require substantial scan acceleration in order to accommodate data sampling into a sufficiently short acquisition window per cardiac cycle. To this end, k-t undersampling in conjunction with k-t BLAST, k-t SENSE,18-20 and k-t PCA21, 22 has initially been deployed and demonstrated in the clinical setting for various applications and compared against reference standards in single10, 11, 23-25 and multi-center trials.26, 27 Dedicated advances to improve the reconstruction accuracy from undersampled multi-slice 2D or 3D Cartesian,28-30 radial31-36 and spiral37-40 k-space trajectories have been proposed. Work on 3D Cartesian,22 radial stack-of-stars,41, 42 and spirals43 has demonstrated improvements with impact on quantitative perfusion parameters. The ramification of spatiotemporal fidelity on quantitative perfusion indices has been investigated and quantified.44

A challenge with k-t reconstruction, however, relates to the requirement to ensure sufficient spatiotemporal data correlations. Therefore, data acquisition is typically conducted in a breathhold, which has been limiting, in particular, during adenosine-induced stress. In order to increase patient comfort and compliance, initial research has been directed to enable free-breathing 3D data acquisition based on Cartesian30 and stack-of-stars undersampling.35

To address respiratory motion of free-breathing data acquisition, approaches applying global or local registration in the image domain have been described. To address challenges due to the dynamic contrast enhancement, image signal separation into low-rank and sparse components followed by model-based registration has been proposed.45 It is noted, however, that 2D registration-based methods can inherently only correct for in-plane and not continuous through-slice motion.

In addition to image-domain registrations, radial self-gating and respiratory motion binning have been used42, 46-48 to restrict or sort data to different respiratory states. However, retrospective binning of spokes into breathing and heart phases is only applicable for moderate undersampling or continuous acquisition schemes.42, 49

In general, nonrigid motion, corrupting the data, can be corrected for using an approximate solution given an estimated motion field.50 If rigid motion is assumed, it can be compensated for by application of linear phase shifts in k-space as demonstrated for perfusion imaging.51

Motion correction has become an important step to improve the conditioning of iterative image reconstruction methods.30, 52, 53 Block low-rank sparsity tracking (BLOSM) has proved beneficial,53 and has been extended to reconstruct from continuously acquired radial, simultaneous multi-slice, heart-phase resolved data.42 Similar methods have also been used in computed tomography perfusion imaging54 and in other MR applications such as MR parameter mapping55 and MR fingerprinting.56

For quantification of perfusion data, a dual-sequence, single-bolus approach is desirable.28, 41, 57 The arterial input function (AIF) is preferably recorded in the ascending aorta in an interleaved fashion.58

The present study proposes and validates a 3D motion correction approach for locally low-rank (LLR) image reconstruction of Cartesian pseudo-spiral in-out k-t undersampled single-bolus first-pass perfusion data. The method is referred to as respiratory motion-informed locally low-rank reconstruction (MI-LLR). It is shown that, by incorporating a transformation displacement field for each dynamic frame, MI-LLR is able to correct for non-rigid in- and through-plane organ motion during rest and stress. Numerical simulations and phantom experiments are used to demonstrate the robustness of the MI-LLR approach with respect to cardiac and breathing motion in comparison to LLR55 and frame-by-frame compressed sensing (CS) using wavelets as sparsifying transform ( ℓ 1 $$ {\ell}_1 $$ -wavelet)59, 60 reconstructions. In-vivo feasibility of the proposed method is assessed in subjects during rest and stress condition.

2 METHODS

2.1 Image acquisition

A dynamically interleaved 2D/3D dual-sequence, single-bolus scheme was implemented on a clinical 1.5T MR system based on an electrocardiogram (ECG) -triggered saturation-recovery spoiled gradient echo sequences with T1- and B1-insensitive saturation preparation pulses62 as described previously.28

As shown in Figure 1A, the 3D perfusion scan is triggered to end systole. The 2D AIF images are acquired in the ascending aorta during diastole. A pseudo-spiral Cartesian undersampling pattern was implemented as illustrated in Figure 1B,C. The sampling distribution was defined by a variable density function63 with an elliptical k-space shutter as depicted in Figure 1B. For each dynamic imaging frame, k-space profiles were chosen according to the density distribution while avoiding profile duplication. At the k-space center, a 2 × 4 kz-ky area was fully sampled. The temporal order of profiles was according to a spiral-in—spiral-out scheme, placing the k-space center and the nominal saturation delay at half the acquisition time (Figure 1C). Imaging parameters were: TR/TE = 2.0/1.0 ms, spatial resolution: 2.5 × 2.5 × 10 mm3, FOV: 300 × 300 × 100 mm3, covering the full ventricle from apex to base, flip angle: 15°, acquisition window: 240 ms, saturation delay: 135 ms, undersampling factor R = 10.

Details are in the caption following the image
FIGURE 1
Open in figure viewerPowerPoint
Data acquisition. A, Dual-sequence diagram with corresponding ECG trace and typical planning of the 3D and 2D stacks. The 3D perfusion scan is triggered to end systole, the 2D arterial input function (AIF) images to diastole. The 3D volume is sampled by the proposed undersampled pseudo-spiral in-out Cartesian trajectory, while linear center-out Cartesian sampling is used for the 2D AIF slice. B, The 3D data acquisition scheme. Data are sampled using a volumetric pseudo-spiral Cartesian sampling pattern. Undersampling density function (top), idealised spiral-in-out trajectory (middle), exemplary 10-fold undersampling pattern (bottom). C, Resulting ky-kz sampling pattern after 10 dynamics. The yellow rectangle highlights the densely sampled k-space center

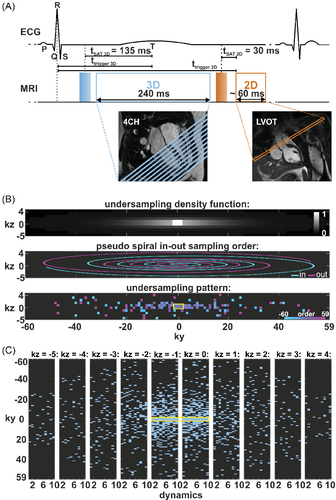
For the interleaved acquisition of the AIF, a fully sampled center-out Cartesian pattern was used with spatial resolution: 10 × 10 mm2, slice thickness: 15 mm, flip angle: 15°, acquisition window: 56–64 ms, saturation delay: 30 ms. TR and TE were set equal to the corresponding 3D sequence to avoid different T1 and T2* weightings.

All images were acquired on a 1.5T Philips Achieva MR system (Philips Healthcare, Best) using a five-element cardiac receive coil array. Gadobutrol (Gadovist, Bayer Schering Pharma) was used as contrast agent (CA).

2.2 Image reconstruction and motion compensation

Conventional LLR reconstruction55 leverages spatio-temporal correlation of imaging data by penalizing the nuclear norms of patch matrices stacked along time. For zero-filled k-space data S ∈ ℂ N s N c × T $$ \mathbf{S}\in {\mathbb{C}}^{{\mathrm{N}}_{\mathrm{s}}{\mathrm{N}}_{\mathrm{c}}\times \mathrm{T}} $$ with T $$ \mathrm{T} $$ dynamics, N c $$ {\mathrm{N}}_{\mathrm{c}} $$ coils, containing N s $$ {\mathrm{N}}_{\mathrm{s}} $$ k-space samples each, LLR reconstructed image data I LLR ∈ ℂ N v × T $$ {\mathbf{I}}_{\mathrm{LLR}}\in {\mathbb{C}}^{{\mathrm{N}}_{\mathrm{v}}\times \mathrm{T}} $$ of N v $$ {\mathrm{N}}_{\mathrm{v}} $$ voxels is achieved by solving the following convex optimization problem55:
I LLR = argmin I ‖ Ω F CI − S ‖ 2 2 + λ LLR ∑ b ∈ U P b I * $$ {\mathbf{I}}_{\mathrm{LLR}}=\underset{\mathbf{I}}{\mathrm{argmin}}{\left\Vert \boldsymbol{\Omega}\ \mathbf{\mathcal{F}}\mathbf{CI}-\mathbf{S}\right\Vert}_2^2+{\lambda}_{\mathrm{LLR}}{\sum}_{b\in \mathrm{U}}{\left\Vert {\mathbf{P}}_b\mathbf{I}\right\Vert}_{\ast } $$ (1)
with the undersampling operator Ω ∈ { 0 , 1 } N s N c × N s N c $$ \boldsymbol{\Omega} \mathbf{\in}{\left\{0,1\right\}}^{{\mathrm{N}}_{\mathrm{s}}{\mathrm{N}}_{\mathrm{c}}\times {\mathrm{N}}_{\mathrm{s}}{\mathrm{N}}_{\mathrm{c}}} $$ , Fourier transform F ∈ ℂ N s N c × N v N c $$ \mathbf{\mathcal{F}}\boldsymbol{\in}{\mathbb{C}}^{{\mathrm{N}}_{\mathrm{s}}{\mathrm{N}}_{\mathrm{c}}\times {\mathrm{N}}_{\mathrm{v}}{\mathrm{N}}_c} $$ , coil sensitivities C ∈ ℂ N c N v × N v $$ \mathbf{C}\mathbf{\in }{\mathbb{C}}^{{\mathrm{N}}_{\mathrm{c}}{\mathrm{N}}_{\mathrm{v}}\times {\mathrm{N}}_{\mathrm{v}}} $$ and regularization weight λ LLR $$ {\uplambda}_{\mathrm{LLR}} $$ . The patch extraction operator P b ∈ { 0 , 1 } n x n y n z × N v $$ {\mathbf{P}}_{\mathrm{b}}\in {\left\{0,1\right\}}^{n_x{n}_y{n}_z\times {\mathrm{N}}_{\mathrm{v}}} $$ refers to the b-th patch, where U $$ \mathrm{U} $$ is a set of patch indices, with patch size of n x × n y × n z $$ {n}_x\times {n}_y\times {n}_z $$ voxels. In each iteration, patches are selected randomly to avoid blocking artefacts. The optimization problem (Equation 1) is posed in the synthesis form64 and, therefore, solved with Nesterov-accelerated proximal gradient descent.65
For the first stage of MI-LLR reconstruction, approximate displacement fields are derived to feed a motion-compensated reference system to a second reconstruction stage, allowing to reduce the rank of the inverse problem. Therefore, the initial reconstruction I LLR = i 1 , … , i T $$ {\mathbf{I}}_{\mathrm{LLR}}=\left[{\mathbf{i}}_1,\dots, {\mathbf{i}}_T\right] $$ is then registered across T $$ T $$ dynamics using the pTV registration toolbox.66 Group-wise image registration is achieved by minimizing the nuclear image dissimilarity metric of warped images i t ∘ d t $$ {\mathbf{i}}_t\circ {\mathbf{d}}_t $$ stacked over time ‖ i 1 ∘ d 1 , … , i T ∘ d T ‖ * , $$ {\left\Vert {\mathbf{i}}_1\circ {\mathbf{d}}_1,\dots, {\mathbf{i}}_T\circ {\mathbf{d}}_T\right\Vert}_{\ast }, $$ 67 where displacement fields d t = d t d t ′ $$ {\mathbf{d}}_t={\mathbf{d}}_t\left({\mathbf{d}}_t^{\prime}\right) $$ are parametrized by first-order B-spline coefficients d t ′ $$ {\mathbf{d}}_t^{\prime } $$ with a cell width of five voxels in each spatial dimension:
d 1 ′ , … , d T ′ = argmin d 1 ′ , … , d T ′ ‖ i 1 ∘ d 1 , … , i T ∘ d T ‖ * + λ VTV ∑ pt ∑ jk ∇ k d j ′ pt 2 . $$ {\displaystyle \begin{array}{cc}& \left[{\mathbf{d}}_1^{\prime },\dots, {\mathbf{d}}_T^{\prime}\right]=\underset{\left[{\mathbf{d}}_1^{\prime },\dots, {\mathbf{d}}_T^{\prime}\right]}{\mathrm{argmin}}{\left\Vert {\mathbf{i}}_1\circ {\mathbf{d}}_1,\dots, {\mathbf{i}}_T\circ {\mathbf{d}}_T\right\Vert}_{\ast}\\ {}& \kern1em +{\lambda}_{\mathrm{VTV}}{\sum}_{pt}\sqrt{\sum_{jk}{\left({\nabla}_k{\mathrm{d}}_j^{\prime}\right)}_{pt}^2}.\end{array}} $$ (2)
The regularization weight λ VTV $$ {\lambda}_{\mathrm{VTV}} $$ penalizes the vectorial total variation (VTV),68 which imposes group sparsity over displacement component j $$ j $$ in direction k $$ k $$ for each spatio-temporal voxel location ( p , t ) $$ \left(p,t\right) $$ .
Displacements fields d j $$ {\mathbf{d}}_j $$ , estimated by image registration, map acquired images into a common reference frame. To pose the second stage of the MI-LLR reconstruction problem in the synthesis form,64 the displacement fields are inverted using linear interpolation: q t ≈ d t − 1 $$ {\mathbf{q}}_t\approx {\mathbf{d}}_t^{-1} $$ . Hence, corresponding linear operators Q t i t = Q t q t i t = i t ∘ q t $$ {\mathbf{Q}}_t{\mathbf{i}}_t={\mathbf{Q}}_t\left({\mathbf{q}}_t\right){\mathbf{i}}_t={\mathbf{i}}_t\circ {\mathbf{q}}_t $$ were used to map a fixed reference frame to the target configuration t $$ t $$ :
I MI − LLR = argmin I Ω F C Q 1 i 1 , … , Q T i T − S 2 2 + λ MI − LLR ∑ b ∈ U P b I * . $$ {\displaystyle \begin{array}{cc}& {\mathbf{I}}_{\mathrm{MI}-\mathrm{LLR}}=\underset{\mathbf{I}}{\mathrm{argmin}}{\left\Vert \boldsymbol{\Omega}\ \mathbf{\mathcal{F}}\mathbf{C}\ \left[{\mathbf{Q}}_1{\mathbf{i}}_1,\dots, {\mathbf{Q}}_T{\mathbf{i}}_T\right]-\mathbf{S}\right\Vert}_2^2\\ {}& \kern1em +{\lambda}_{\mathrm{MI}-\mathrm{LLR}}{\sum}_{b\in \mathrm{U}}{\left\Vert {\mathbf{P}}_b\mathbf{I}\right\Vert}_{\ast }.\end{array}} $$ (3)
Here, λ MI − LLR $$ {\lambda}_{\mathrm{MI}-\mathrm{LLR}} $$ weights LLR regularization in the motion-compensated configuration, while Q t i t $$ {\mathbf{Q}}_t{\mathbf{i}}_t $$ for t = 1 , … , T $$ t=1,\dots, T $$ represents the original image sequence defined by the k-spaces S $$ \mathbf{S} $$ . Since image warping operators Q t $$ {\mathbf{Q}}_t $$ are applied in the data term, this optimization problem is convex and formulated in the synthesis form allowing to use the Nesterov-accelerated proximal gradient descent.65 The algorithm was implemented in Matlab (Mathworks) on GPUs.

Sensitivity maps for coil calibration were estimated from reference scans using the ESPIRiT method.69 Imaging data from the scanner were extracted and pre-processed using MRecon (Gyro Tools LLC).

The entire framework is schematically outlined in Figure 2A–E. At first, data are acquired using the Cartesian pseudo spiral acquisition and put into the MI-LLR reconstruction, which encompasses two stages. In the first stage (Figure 2B), images are reconstructed using LLR (Equation 1) with a patch size of n x = n y = n z = 12 $$ {n}_x={n}_y={n}_z=12 $$ and underregularization to capture spatiotemporal image variations ( λ LLR = 0.05 $$ {\lambda}_{\mathrm{LLR}}=0.05 $$ ). While the images show residual undersampling artefacts, motion patterns are not suppressed and visible. These images are registered using Equation (2) with regularization weight λ VTV = 0.001 $$ {\lambda}_{\mathrm{VTV}}=0.001 $$ on the displacements to suppress the impact of residual aliasing artefacts in the initial LLR reconstruction. Thereafter, estimated displacement fields are used to perform the second stage of the MI-LLR reconstruction according to Equation (3), thereby allowing to reduce the regularization weight. The MI-LLR pipeline is illustrated for a representative case in Supporting Information Figure S1, which is available online.

Details are in the caption following the image
FIGURE 2
Open in figure viewerPowerPoint
The 3D data acquisition and reconstruction steps. A, Data acquisition using the Cartesian 10-fold accelerated spiral-in—spiral-out acquisition pattern. B, The motion-informed locally low-rank reconstruction (MI-LLR) pipeline: Patch-based initial LLR reconstruction followed by full FOV registration. Resulting deformation field allows to regularize over motion states for MI-LLR. C, Alternative image reconstructions using LLR and a frame by frame ℓ 1 $$ {\ell}_1 $$ -wavelet (wavelet) reconstruction. After step B and D, 3D image series still contain motion as indicated by the intensity-time profiles and require registration in the reduced FOV around the heart (D) in order to perform myocardial blood flow (MBF) quantification (E). Please note: The MI-LLR reconstruction pipeline is also further detailed in Supporting Information Figure S1
For alternative reconstructions (Figure 2C), LLR and ℓ 1 $$ {\ell}_1 $$ -wavelet (wavelet), referring to CS reconstruction using wavelets as sparsifying transform and sensitivity encoding (i.e., SPARSE-SENSE),59, 60, 63, 70, 71 were used. Image data I wavelet ∈ ℂ N v xT $$ {\mathbf{I}}_{\mathrm{wavelet}}\in {\mathbb{C}}^{{\mathrm{N}}_{\mathrm{v}}\mathrm{xT}} $$ of N v $$ {\mathrm{N}}_{\mathrm{v}} $$ voxels was obtained by solving:
I wavelet = argmin I ‖ Ω F CI − S ‖ 2 2 + λ wavelet ‖ D I ‖ 1 $$ {\mathbf{I}}_{\mathrm{wavelet}}=\underset{\mathbf{I}}{\mathrm{argmin}}{\left\Vert \boldsymbol{\Omega}\ \mathbf{\mathcal{F}}\mathbf{CI}-\mathbf{S}\right\Vert}_2^2+{\lambda}_{\mathrm{wavelet}}{\left\Vert \mathbf{D}\ \mathbf{I}\right\Vert}_1 $$ (4)
where D is the discrete Daubechies wavelet transform. Equation (4) was solved using the Berkeley advanced reconstruction toolbox (BART).72

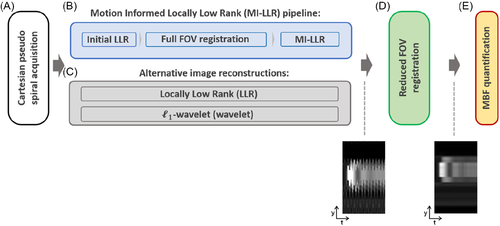
For in-vivo image reconstructions, the minimum values of the regularization parameters λ MI − LLR $$ {\lambda}_{\mathrm{MI}-\mathrm{LLR}} $$ and λ LLR $$ {\lambda}_{\mathrm{LLR}} $$ , which suppress background signal variation to 0.05% of the maximum image intensity, were chosen using a grid search approach and were λ MI − LLR ∼ 0.30 $$ {\lambda}_{\mathrm{MI}-\mathrm{LLR}}\sim 0.30 $$ and λ LLR ∼ 0.40 $$ {\lambda}_{\mathrm{LLR}}\sim 0.40 $$ . The regularization parameter of the ℓ 1 $$ {\ell}_1 $$ -wavelet reconstruction λ wavelet $$ {\lambda}_{\mathrm{wavelet}} $$ was set to 0.01. For synthetic experiments, optimal regularization parameters, yielding the lowest reconstruction error, were found using a grid search and were λ MI − LLR ∼ 0.25 , $$ {\lambda}_{\mathrm{MI}-\mathrm{LLR}}\sim 0.25, $$ λ LLR ∼ 0.30 , $$ {\lambda}_{\mathrm{LLR}}\sim 0.30, $$ and λ wavelet ∼ 0.01 $$ {\lambda}_{\mathrm{wavelet}}\sim 0.01 $$ .

2.3 Postprocessing and MBF quantification

Reconstructed 3D data were zero-filled to 1.25 × 1.25 × 5 mm3 and 2D-AIF images were zero-filled to 2.5 × 2.5 mm2. All image series were registered to compensate for residual motion prior to signal post-processing. Signal post-processing and perfusion quantification were conducted in Matlab (Mathworks). For local myocardial perfusion mapping, the images were convolved using the following kernel: 1 5 [ 0 , 1 , 0 ; 1 , 1 , 1 ; 0 , 1 , 0 ] $$ \frac{1}{5}\left[0,1,0;1,1,1;0,1,0\right] $$ to reduce noise at the cost of resolution.

The myocardium was segmented across the 10 slices and divided into six circumferential sectors per slice. Local and sector-wise myocardial signal time curves were derived along with the AIF.

Given the signal model of the saturation recovery Cartesian sequence, T 1 ( t ) $$ {\mathrm{T}}_1\left(\mathrm{t}\right) $$ translates to signal I ( t ) $$ \mathrm{I}\left(\mathrm{t}\right) $$ as73, 74:
I ( t ) = I 0 ⋅ 1 − exp − T sat T 1 ( t ) ⋅ a ( t ) n − 1 + 1 − exp − TR T 1 ( t ) ⋅ 1 − a ( t ) n − 1 1 − a ( t ) $$ {\displaystyle \begin{array}{cc}& \mathrm{I}\left(\mathrm{t}\right)={\mathrm{I}}_0\cdot \left[\left(1-\exp \left(-\frac{{\mathrm{T}}_{\mathrm{sat}}}{{\mathrm{T}}_1\left(\mathrm{t}\right)}\right)\right)\cdot \mathrm{a}{\left(\mathrm{t}\right)}^{\mathrm{n}-1}\right.\\ {}& \kern2em \left.+\left(1-\exp \left(-\frac{\mathrm{T}\mathrm{R}}{{\mathrm{T}}_1\left(\mathrm{t}\right)}\right)\right)\cdot \frac{1-\mathrm{a}{\left(\mathrm{t}\right)}^{\mathrm{n}-1}}{1-\mathrm{a}\left(\mathrm{t}\right)}\right]\end{array}} $$
with
a ( t ) = exp − TR T 1 ( t ) cos α $$ \mathrm{a}\left(\mathrm{t}\right)=\exp \left(-\frac{\mathrm{T}\mathrm{R}}{{\mathrm{T}}_1\left(\mathrm{t}\right)}\right)\ \cos\ \upalpha $$ (5)
with the baseline signal for fully relaxed magnetization I 0 $$ {\mathrm{I}}_0 $$ , saturation delay T sat $$ {\mathrm{T}}_{\mathrm{sat}} $$ , repetition time TR $$ \mathrm{TR} $$ , flip angle α $$ \upalpha $$ , the number of profiles sampled until k-space center n $$ \mathrm{n} $$ . Accordingly, T 1 ( t ) $$ {\mathrm{T}}_1\left(\mathrm{t}\right) $$ was calculated for every dynamic t $$ \mathrm{t} $$ for the myocardium as well as in the ascending aorta. Concentration-time curves c ( t ) $$ \mathrm{c}\left(\mathrm{t}\right) $$ were derived using:
c ( t ) = T 1 , 0 − T 1 ( t ) T 1 ( t ) ⋅ T 1 , 0 ⋅ r $$ \mathrm{c}(t)=\frac{{\mathrm{T}}_{1,0}-{\mathrm{T}}_1\left(\mathrm{t}\right)}{{\mathrm{T}}_1\left(\mathrm{t}\right)\cdot {\mathrm{T}}_{1,0}\cdot \mathrm{r}} $$ (6)
where T 1 , 0 $$ {\mathrm{T}}_{1,0} $$ refers to the native T1 relaxation time and r $$ r $$ to the specific CA relaxivity (gadobutrol: r = 5.2 L / mmol ⋅ s $$ r=5.2\ \mathrm{L}/\mathrm{mmol}\cdot \mathrm{s} $$ ). Accordingly, MBF was quantified using c MYO ( t ) $$ {\mathrm{c}}_{\mathrm{MYO}}\left(\mathrm{t}\right) $$ and c AIF ( t ) $$ {\mathrm{c}}_{\mathrm{AIF}}\left(\mathrm{t}\right) $$ based on a Fermi model74:
c MYO ( t ) = IRF Fermi ( t ) * c AIF ( t ) , $$ {\mathrm{c}}_{\mathrm{MYO}}\left(\mathrm{t}\right)={\mathrm{IRF}}_{\mathrm{Fermi}}\left(\mathrm{t}\right)\ast {\mathrm{c}}_{\mathrm{AIF}}\left(\mathrm{t}\right), $$
with
IRF Fermi ( t ) = MBF ⋅ 1 − ν 1 − ν ⋅ exp ( − μt ) ⋅ Θ t − t shift $$ {\mathrm{IRF}}_{\mathrm{Fermi}}\left(\mathrm{t}\right)=\mathrm{MBF}\cdot \frac{1-\upnu}{1-\upnu \cdot \exp \left(-\upmu \mathrm{t}\right)}\cdot \Theta \left(\mathrm{t}-{\mathrm{t}}_{\mathrm{shift}}\right) $$ (7)
with fitting parameters ν $$ \upnu $$ , μ $$ \upmu $$ that entail no physiological meaning and the Heaviside step function Θ, with the time difference between AIF and myocardial signal given by t shift $$ {\mathrm{t}}_{\mathrm{shift}} $$ . The parameters of interest were fitted in the least square sense. To determine the global myocardial and blood T 1 , 0 $$ {\mathrm{T}}_{1,0} $$ a MOLLI scan75 was used. Further details of the implementation of the deconvolution and estimation process are outlined in.28

2.4 Simulation studies

Numerical simulations were performed to validate the MI-LLR framework. A fully sampled free-breathing 3D perfusion numerical phantom was created using the signal model given in Equation (5) based on the MRXCAT simulation framework.76 Spatial resolution of the ground truth (GT) phantom was 1.25 × 1.25 mm2, slice thickness: 5 mm, 20 slices. To introduce partial volume effects, the GT object was subsequently downsampled to yield the final phantom parameters: 2.5 × 2.5 × 10 mm3, 10 slices, TR/TE: 2.0/1.0 ms, flip angle: 15°, CA dose: 0.075 mmol/kg body weight (b.w.), five receive coils, MBF: 3.5 mL/g/min, 70 simulated heart beats, R = 10. The numerical phantom was further modified to include cardiac and respiratory motion during readout to investigate the effects of motion on reconstruction and MBF estimation. Heart rates between 60 and 120 bpm and respiratory motion based on in-vivo navigator data with maximum amplitudes of 25 and 40 mm as provided in the supporting material (Supporting Information Figure S2) were simulated.

In order to analyze the simulation results, the normalized RMS error (nRMSE) of reconstructed magnitude images with respect to GT images in the masked myocardial region of interest (respective masks are indicated in Figure 3A) were calculated according to:
nRMSE = ∑ p ˜ ϵ mask I ( p ˜ ) − I GT ( p ˜ ) 2 N mask * max I GT ( p ˜ ) 2 $$ \mathrm{nRMSE}=\sqrt{\frac{\sum \limits_{\tilde{\mathrm{p}}\ \epsilon\ \mathrm{mask}}{\left|\mathbf{I}\left(\tilde{\mathrm{p}}\right)-{\mathbf{I}}_{\mathrm{GT}}\left(\tilde{\mathrm{p}}\right)\right|}^2}{{\mathrm{N}}_{\mathrm{mask}}\ast \max \left({\mathbf{I}}_{\mathrm{GT}}{\left(\tilde{\mathrm{p}}\right)}^2\right)}} $$ (8)
where N mask $$ {\mathrm{N}}_{\mathrm{mask}} $$ corresponds to the number of pixels p ˜ $$ \tilde{\mathrm{p}} $$ in the myocardial mask.
Details are in the caption following the image
FIGURE 3
Open in figure viewerPowerPoint
Simulation results for synthetic stress data at a heartrate of 60 bpm and 25 mm respiratory amplitude. GT (A) and the proposed motion-informed locally low-rank reconstruction (MI-LLR) (B), LLR (C), and ℓ 1 $$ {\ell}_1 $$ -wavelet (wavelet) (D). The panels show (horizontal order), for a midventricular slice, reconstruction results and errors (nRMSEs) at peak LV and peak myocardial signal in the myocardial region as indicated by white dashed masks, intensity-time profiles upon motion correction with displacement fields obtained from registration of GT image series (for reference, GT profiles are shown for the registered and the free-breathing case), concentration-time curves, for all slices, myocardial blood flow (MBF) maps, and regional means with MBF ± SD, respectively
MBF data derived from reconstructed images were compared to MBF values from GT. Reconstructed image data were registered using the displacement fields obtained from registration of the GT image series to avoid confounding effects of the final registration step on MBF accuracy. Quantification errors were evaluated as mean absolute error (MAE) ± 1 SD of the absolute error over all myocardial pixels from 10 slices of the 3D volume, calculated according to:
MAE = ∑ p ˜ ϵ mask ∣ MBF ( p ˜ ) − MBF GT ( p ˜ ) ∣ N mask $$ \mathrm{MAE}=\frac{\sum \limits_{\tilde{\mathrm{p}}\ \epsilon\ \mathrm{mask}}\mid \mathbf{MBF}\left(\tilde{\mathrm{p}}\right)-{\mathbf{MBF}}_{\mathbf{GT}}\left(\tilde{\mathrm{p}}\right)\mid }{{\mathrm{N}}_{\mathrm{mask}}} $$ (9)
where N mask $$ {\mathrm{N}}_{\mathrm{mask}} $$ corresponds to the number of myocardial pixels p ˜ $$ \tilde{\mathrm{p}} $$ in the masked 3D volume. To investigate the effects of SNR on MBF quantification accuracy, different noise levels were added to simulated data at resting heart-rate, i.e., 60 bpm, and 25 mm respiratory motion amplitude.

Statistical differences were assessed using the two tailed paired Student's t-test; p < 0.05 was considered significant.

2.5 Phantom studies

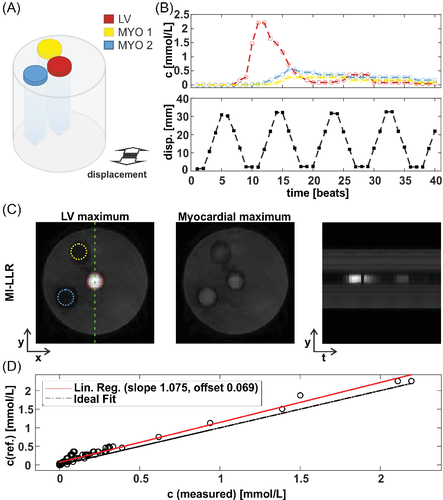
To verify the signal to concentration conversion after image acquisition and reconstruction, tubes were filled with purified water and doped with different concentrations of gadobutrol (from 0 to 2.25 mmol/L). The detailed setup of the phantom validation is summarized in Figure 5. The tubes were inserted into a cylindrical Agar phantom. Concentrations were sequentially varied to mimic the CA dynamics in the left ventricle and in myocardium by manually replacing tubes in between subsequent measurements. Concurrently, the phantom was displaced laterally to four positions with a maximum displacement of 30 mm to mimic in-vivo breathing motion dynamics.

2.6 In-vivo experiments

Twelve healthy volunteers (7 male) with an average age 25.2 ± 2.4 y underwent first-pass rest perfusion examinations; 7 underwent a rest and stress protocol. All volunteers were scanned upon written informed consent according to local ethics regulations. Two contrast-enhanced dual-sequence imaging experiments were run using CA boluses at doses of 0.075 mmol/kg b.w. to compare imaging at rest and stress. CA was injected at 4 mL/s and followed by a 30 mL saline flush at the same rate using a power injector (Medrad). Fifteen minutes were allowed for CA washout in-between the two bolus injections; stress imaging was always performed first. Adenosine (Kantonsapotheke, University Hospital Zurich) was injected for at least 3 min at doses of 140 μg/kg b.w./min under continuous monitoring of heart rate and blood pressure in accordance with standard clinical practice. Image acquisition covered 80 heartbeats during free breathing of the subject.

MI-LLR images, intensity-time profiles, concentration-time curves and resulting MBF maps were compared to LLR and ℓ 1 $$ {\ell}_1 $$ -wavelet reconstructions for reference.

3 RESULTS

3.1 Simulation studies

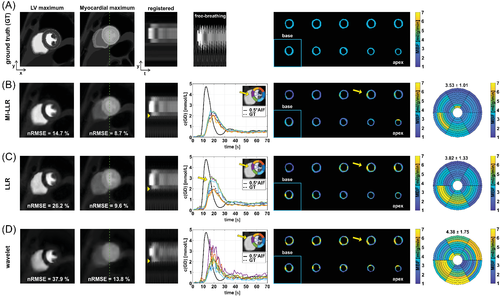
Comparing MI-LLR to LLR and ℓ 1 $$ {\ell}_1 $$ -wavelet reconstructions, image error was found to be reduced as shown by images at left-ventricular (LV) and myocardial (Myo) peak signal (Figure 3) with reconstruction nRMSEs for MI-LLR of 14.7% (LV) and 8.7% (Myo) versus LLR (26.2% and 9.6%) and ℓ 1 $$ {\ell}_1 $$ -wavelet (37.9% and 13.8%). Intensity-time profiles indicate improved motion compensation with ML-LLR relative to LLR as indicated by yellow markers (Figure 3B,C). Concentration-time curves of the six sectors reflect improved motion compensation of the myocardium. In particular, septal sectors show reduced signal variance with MI-LLR when compared to LLR and ℓ 1 $$ {\ell}_1 $$ -wavelet. For MI-LLR, local and sector-wise MBF maps reveal more uniform values of 3.53 ± 1.01 mL/g/min with MI-LLR when compared to 3.82 ± 1.33 mL/g/min with LLR and 4.38 ± 1.75 mL/g/min with ℓ 1 $$ {\ell}_1 $$ -wavelet. MBF maps generally show MBF overestimation which is, however, reduced with MI-LLR when compared to LLR and ℓ 1 $$ {\ell}_1 $$ -wavelet.

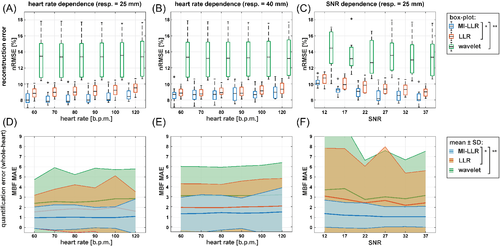
In Figure 4 reconstruction nRMSE and mean absolute error (MAE) of MBF as a function of heart rate, respiratory amplitude, and SNR are reduced with MI-LLR when compared to LLR and ℓ 1 $$ {\ell}_1 $$ -wavelet. Heart rate dependencies for 25 and 44 mm peak respiratory amplitude show reduced reconstruction nRMSEs and MBF MAEs of MI-LLR when compared to LLR (Figure 4A,B,D,E). With a peak respiratory amplitude of 25 mm, median reconstruction nRMSEs for MI-LLR varied from 7.9% to 8.5%, while LLR shows higher median reconstruction nRMSEs (8.8%–9.5%), as does ℓ 1 $$ {\ell}_1 $$ -wavelet (13.5%–13.4%). Reduced MBF MAEs resulted with MI-LLR (1.25–1.44) as compared to LLR (1.55–1.61) and ℓ 1 $$ {\ell}_1 $$ -wavelet (2.39–2.86) up to a heart rate of 120 bpm. As summarized in Table 1, regional MBF showed significantly reduced variation with MI-LLR (±30%) as compared to LLR (±38%) and ℓ 1 $$ {\ell}_1 $$ -wavelet (±45%). With a peak respiratory amplitude of 40 mm, MI-LLR yielded reduced median nRMSEs of 8.7%–8.9% when compared to 8.8%–9.3% for LLR and 13.1%–13.2% for ℓ 1 $$ {\ell}_1 $$ -wavelet; reduced MBF MAEs are seen with MI-LLR (1.25–1.44) when compared to LLR (1.89–2.03) and ℓ 1 $$ {\ell}_1 $$ -wavelet (3.05–3.14). Regional MBF showed significantly reduced variation for MI-LLR (±38%) when compared to LLR (±44%) and ℓ 1 $$ {\ell}_1 $$ -wavelet (±44%). The SNR dependence demonstrates improved performance of MI-LLR when compared to LLR; median reconstruction nRMSEs decreased from 10.1% to 8.1% for MI-LLR when compared to 10.8%–9.0% for LLR, and 14.5%–13.4% for ℓ 1 $$ {\ell}_1 $$ -wavelet when increasing SNR from 12 to 37 (Figure 4C); likewise reduced MBF MAE is seen with MI-LLR (1.38–1.07) when compared to LLR (3.11–2.44) and ℓ 1 $$ {\ell}_1 $$ -wavelet (3.73–3.17) with reduced regional MBF variation for MI-LLR (± 34%) as compared to LLR (± 53%) and ℓ 1 $$ {\ell}_1 $$ -wavelet (± 52%).

Details are in the caption following the image
FIGURE 4
Open in figure viewerPowerPoint
Simulation results comparing reconstruction nRMSE (A–C) and myocardial blood flow (MBF) MAE (D, E) for motion-informed locally low-rank (MI-LLR) versus LLR and ℓ 1 $$ {\ell}_1 $$ -wavelet (wavelet) for heart rates from 60 to 120 bpm for respiration amplitudes of 25 mm (A, D) and 40 mm (B, E), and as a function of SNR (C, F). The boxplots summarize reconstruction nRMSE over 10 slices at myocardial peak signal. Shaded areas in (D–F) indicate 1 SD (SD) of MBF over all pixels from all 10 slices. To enhance representation, shaded areas are not shown for MAE <0.5. Significant differences (p < 0.05) are marked by asterisks: * Refers to significant reduction when MI-LLR is compared relative to LLR. ** refers to significant reduction when MI-LLR or LLR are compared relative to ℓ 1 $$ {\ell}_1 $$ -wavelet (wavelet). For amplitudes of 25 mm, 40 mm, and SNR, all *p < 0.001, **p < 0.001
TABLE 1. Myocardial blood flow (MBF) quantification metrics for simulation and in-vivo data
MBF quantification metrics Motion-informed locally low-rank (MI-LLR) Locally low rank (LLR) ℓ 1 $$ {\ell}_1 $$ -wavelet (wavelet)
Simulation mean MBF ± SD [ml/g/min] (SD [%]) (ground truth = 3.5 ml/g/min) Resp. amplitude: 25 mm, HR: 60–120 bpm 3.44 ± 1.03 (30%)*, ** 3.77 ± 1.43 (38%)*, ** 4.04 ± 1.82 (45%)
Resp. amplitude: 40 mm, HR: 60–120 bpm 3.74 ± 1.42 (38%)*, ** 3.67 ± 1.62 (44%)*, ** 4.59 ± 2.02 (44%)
Resp. amplitude: 25 mm, SNR: 12–37 3.43 ± 1.17 (34%)*, ** 3.96 ± 2.10 (53%)*, ** 4.44 ± 2.31 (52%)
In-vivo Stress: ± mean intra-volunteer SD [ml/g/min] (SD [%]) Mean resp. amplitude ± SD: 24.9 ± 7.4 mmMean HR ± SD: 87 ± 9 bpm ±1.07 (33%)** ±1.22 (36%)** ±6.87 (115%)
Rest: ± mean intra-volunteer SD [ml/g/min] (SD [%]) Mean resp. amplitude ± STD: 16.3 ± 9.3 mmMean HR ± SD: 67 ± 7 bpm ±0.17 (26%)*, ** ±0.19 (28%)*, ** ±1.17 (113%)
  • Note: Significant differences (p < 0.05) of absolute and relative MBF SD (SD [%]) are marked by asterisks:
  • * Refers to significant differences when MBF SDs of motion-informed locally low-rank (MI-LLR) are compared relative to LLR.
  • ** Refers to significant differences when MBF SDs of MI-LLR or LLR are compared relative to ℓ 1 $$ {\ell}_1 $$ -wavelet (wavelet). In-vivo SDs were normalized by the means (SD [%]).

The average motion accuracy after the final registration step was 1.96 and 2.18 mm for 25 and 40 mm breathing amplitude, respectively. After registration, differences in motion accuracy between MI-LLR and LLR were insignificant.

3.2 Phantom studies

Reconstruction results for the proposed method are shown in Figure 5. Exact signal to concentration conversion is examined by comparison of reference to measured concentration with a linear regression model. Figure 5D shows the CA concentrations derived from T1 values measured with the proposed 3D acquisition and reconstruction. Data are in agreement up to gadolinium concentrations of 2.4 mmol/L as indicated by the slope of linear regression of 1.08 (offset = 0.07).

Details are in the caption following the image
FIGURE 5
Open in figure viewerPowerPoint
Phantom sequence validation. A, Agar phantom holds three sites for falcon tubes filled with saline, doped with various concentrations of gadobutrol. B, The respective concentrations are varied concomitant with a displacement of the phantom, measured with a navigator, in order to reflect the perfusion and breathing dynamics, respectively. C, Resulting motion-informed locally low-rank reconstructions (MI-LLR) at concentrations corresponding to LV and myocardial maximum with respective temporal intensity profile plot. D, Comparison of reference gadolinium concentrations, verified by T1 mapping, and the measured concentrations obtained with the 3D acquisition scheme

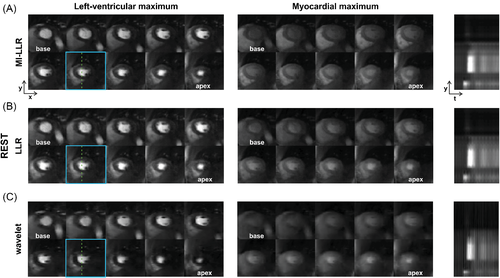
3.3 In-vivo studies

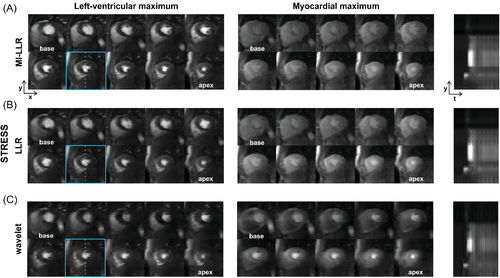
In Figures 6 and 7, example reconstruction results for rest and stress acquisitions of a healthy male volunteer (average heart rate 70 bpm [rest] and 81 bpm [stress], navigator displacement 20 mm [rest] and 24 mm [stress]) are reported at peak LV and myocardial contrast maximum, and intensity profiles (videos are included as Supporting Information Videos S1 and S2). At rest, MI-LLR images appear less blurred than LLR at myocardial intensity maximum. Intensity profiles indicate sharper borders between myocardium and blood pool for MI-LLR when compared to LLR. At stress, MI-LLR images appear less blurred than LLR; ℓ 1 $$ {\ell}_1 $$ -wavelet images show pronounced artefacts. Intensity profiles indicate sharper borders between myocardium and blood pool for MI-LLR as compared to LLR images, with more residual motion seen in the LLR profile, while ℓ 1 $$ {\ell}_1 $$ -wavelet intensity profiles are dominated by pronounced signal intensity artefacts.

Details are in the caption following the image
FIGURE 6
Open in figure viewerPowerPoint
In-vivo results for motion-informed locally low-rank (MI-LLR) (A), LLR (B), and ℓ 1 $$ {\ell}_1 $$ -wavelet (wavelet) (C) during rest condition. Imaging results are shown (horizontal order) over 10 slices at LV, myocardial signal maximum, and as a temporal intensity profile at a midventricular slice, indicated by blue frame and dashed line. Average heart rate and maximum displacement were 70 bpm and 20 mm, respectively
Details are in the caption following the image
FIGURE 7
Open in figure viewerPowerPoint
In-vivo results for motion-informed locally low-rank (MI-LLR) (A), LLR (B) and ℓ 1 $$ {\ell}_1 $$ -wavelet (wavelet) (C) during stress condition. Imaging results are shown (horizontal order) over 10 slices at LV, myocardial signal maximum, and as a temporal intensity profile at a midventricular slice, indicated by blue frame and dashed line. Average stress heart rate and maximum displacement were 81 bpm and 24 mm, respectively

In Figures 8 and 9, corresponding quantifications are summarized at rest and stress, respectively. At rest, concentration-time curves show residual artefacts for both MI-LLR and LLR. Concentration time curves exhibit reduced fluctuations over time for MI-LLR (signal maximum at 0.47 mmol/L with 0.30 ± 0.06 mmol/L) when compared to LLR (signal maximum at 0.58 mmol/L with 0.32 ± 0.08 mmol/L). Concentration time curves from ℓ 1 $$ {\ell}_1 $$ -wavelet reconstructions are corrupted by artefacts. Rest maps show uniform MBF values but signal spilling in the basal slices. Apical locations show reduced local MBFs as compared to basal locations. MBF variation are reduced using MI-LLR (±0.11 mL/g/min) vs. LLR (±0.13 mL/g/min) versus ℓ 1 $$ {\ell}_1 $$ -wavelet (±0.27 mL/g/min).

Details are in the caption following the image
FIGURE 8
Open in figure viewerPowerPoint
Quantification of in-vivo results during rest resulting from motion-informed locally low-rank (MI-LLR) (A), LLR (B) and ℓ 1 $$ {\ell}_1 $$ -wavelet (wavelet) (C) data of the volunteer presented in Figure 6. The results in panels show (horizontal order) mean concentration time curves over myocardial sectors from midventricular slice (indicated by blue frame in Figure 6) with the 2D arterial input function (AIF), myocardial blood flow (MBF) maps, and regional means with MBF ± SD. Average resting heart rate and maximum displacements were 70 bpm and 20 mm, respectively

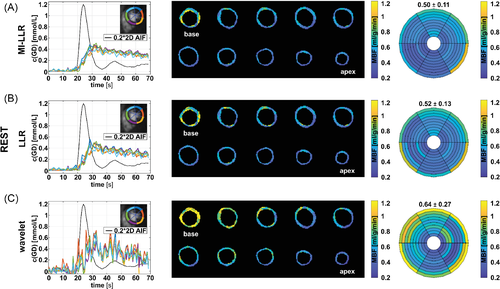
At stress (Figure 9), concentration-time curves show residual artefacts induced by motion for both MI-LLR and LLR. Signal maxima are lower for MI-LLR (at 0.69 mmol/L with 0.65 ± 0.05 mmol/L) as compared to LLR (at 0.80 mmol/L with 0.69 ± 0.08 mmol/L). MBF maps show uniform MBF values but signal spilling in the basal slices. Apical locations show reduced local MBFs as compared to basal locations. Bulls eye plots indicate that regional means are compromised less with MI-LLR; MBF variation is seen to be significantly reduced (p < 0.05) using MI-LLR (±0.70 mL/g/min) vs. LLR (±0.79 mL/g/min) versus ℓ 1 $$ {\ell}_1 $$ -wavelet (±3.36 ml/g/min).

Details are in the caption following the image
FIGURE 9
Open in figure viewerPowerPoint
Quantification of in-vivo results during stress resulting from motion-informed locally low-rank (MI-LLR) (A), LLR (B), and ℓ 1 $$ {\ell}_1 $$ -wavelet (wavelet) (C) data of the volunteer presented in Figure 7. The results in panels show (horizontal order) mean concentration time curves over myocardial sectors from midventricular slice (indicated by blue frame in Figure 7) with the 2D arterial input function (AIF), myocardial blood flow (MBF) maps, and regional means with MBF ± SD. Average stress heart rate and maximum displacements were 81 bpm at 24 mm, respectively

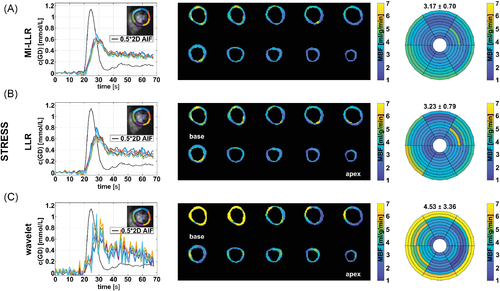
Spatial variation of CA concentration across the myocardium at peak myocardial enhancement for all volunteers is compared in Supporting Information Table S1. MBF quantification results for all subjects are summarized in Table 1 and Supporting Information Figure S3. One subject showed a high response to adenosine stress resulting in heart rates exceeding 130 bpm. Failing ECG gating resulted in triggering of only every second heartbeat. The stress scan was thus excluded from analysis. For MI-LLR reconstruction, at an average resting heart rate of 67 ± 7 bpm, the average inter-volunteer MBF was 0.65 ± 0.22 mL/g/min, while, under stress and an average stress heart rate of 87 ± 9 bpm, the average MBF was 3.23 ± 0.61 mL/g/min compared to 0.68 ± 0.23 mL/g/min (rest) and 3.39 ± 0.34 mL/g/min (stress) for LLR versus 1.03 ± 0.75 mL/g/min (rest) and 5.94 ± 3.98 mL/g/min (stress) for ℓ 1 $$ {\ell}_1 $$ -wavelet. Intra-volunteer variation of absolute and relative MBF was lower in MI-LLR (±0.17 mL/g/min [26%] and ±1.07 mL/g/min [33%]) versus LLR (± 0.19 mL/g/min [28%] and ± 1.22 mL/g/min [36%]) and versus ℓ 1 $$ {\ell}_1 $$ -wavelet (±1.17 mL/g/min [113%] and ±6.87 mL/g/min [115%]), for rest and stress, combined. At rest, the reduction in regional MBF variation between MI-LLR and LLR was significant (p = 0.0073); at stress it was insignificant. SDs of MBF values derived from MI-LLR and LLR were significantly reduced when compared to ℓ 1 $$ {\ell}_1 $$ -wavelet at rest and stress.

4 DISCUSSION

In this study, a 3D motion-informed locally low-rank image reconstruction framework, combined with Cartesian pseudo-spiral k-t undersampling, was developed and the suitability for robust free-breathing whole-heart quantitative perfusion imaging has been demonstrated under rest and stress conditions in volunteers.

The proposed MI-LLR approach yields qualitative and quantitative improvement compared to LLR reconstruction for free-breathing imaging. In-vivo MBF values derived from both 3D MI-LLR and LLR agree with the range of values reported for quantitative 2D perfusion CMR methods.17 Reduced variation of regional MBF values was found for MI-LLR when compared to LLR and ℓ 1 $$ {\ell}_1 $$ -wavelet in simulation and for in-vivo data at rest. Average rest and stress values and their variations compare well to data from other 3D studies.28, 42, 44 Differences between MI-LLR and LLR depend on individual subjects' breathing pattern and heart rates (example cases shown in Supporting Information Figures S5–S8; Supporting Information Videos S3 and S4).

Especially in simulation, MI-LLR reduces signal elevations in the septal region as caused by high contrast signal from the right-ventricular and LV blood pools. The visually apparent trend for underestimation in the infero-lateral regions is relative to the sites of increased signal which are observed predominantly in basal slices.

In order to relate MI-LLR and LLR to methods commercially available on clinical MR systems, frame-by-frame ℓ 1 $$ {\ell}_1 $$ compressed sensing with wavelets as sparsifying transform and coil encoding was used, which resulted in significant image distortions and erroneous MBF quantification. The Cartesian pseudo spiral in-out sampling pattern used in the present work ensured that the central k-space was always covered halfway during the acquisition window. This differs from other work that promotes motion robustness by means of radial sampling strategies,41, 42, 77 where the central k-space is traversed by every profile and as such is susceptible to variations in motion state throughout the acquisition, unless this is accounted for by, for example, retrospective binning. Of note, 3D stack-of-stars acquisition schemes inherently demand higher undersampling factors, i.e., pi/2 more data is required in order to fulfil the Nyquist criterion when compared to Cartesian sampling.9, 41 Possible reduction of the acquisition window by means of partial echo and partial Fourier sampling as used in other studies28, 41 was avoided as the approximated Hermitian symmetry is potentially violated by the local modulation of signal phase due to the CA.78 However, cardiac motion during the acquisition could have contributed to Gibbs ringing, i.e., dark-rim artefacts,79 which were observed in some cases in this study (e.g. Supporting Information Video S2).

Conversion of signal intensities to concentrations requires a signal model. Phantom validation (Figure 5) of MI-LLR signal intensity to concentration conversion showed good agreement within precision of experiment in the range of expected myocardial gadobutrol concentrations from 0.1 to 2.3 mmol/L and motion amplitudes of 30 mm.

Simulation studies using the MRXCAT framework confirmed sufficient robustness of MI-LLR at higher heart rates and breathing amplitudes and was shown to outperform LLR and ℓ 1 $$ {\ell}_1 $$ -wavelet over a realistic SNR range. MBF quantification from MI-LLR reconstruction showed reduced variability in apical and basal sectors, as well as reduced overestimation of midventricular, infero- and anteroseptal regions. The investigated respiratory amplitudes of 25 and 40 mm in feet-head direction were taken from recorded in-vivo respiratory motion amplitudes as shown in Supporting Information Figure S2; other work only considered amplitudes of 1.7 and ∼8 mm.30, 42 In the simulation studies, sinusoidal breathing patterns of 4.5 s cycle duration were assumed; especially under stress, more irregular and abrupt breathing patterns might occur. In these cases, the exact implications of sudden motion on quantification accuracy remain to be quantified.

It is noted that the perfusion model (Equation 7) fitting problem is reasonably well posed, i.e., three model parameters are fitted considering approximately 40 time points per pixel (the exact value depends on the time span of the first pass and thus the shape of the curve). Therefore, no clear trend in MBF accuracy vs. heartrate or SNR could be detected, contrary to reconstruction nRMSEs (Figure 4A–C). However, systematic bias is intrinsic to each of the considered methods; therefore, a significant improvement of MI-LLR compared to LLR in terms of MBF accuracy was seen in the simulation studies. In the future, a blood tissue exchange model (BTEX) with four free parameters modelled as partial differential equations should be tried as proposed in other work.80, 81 In that case, superiority of MI-LLR motion compensation is expected to improve quantification robustness more profoundly than shown for the Fermi-based fitting.

In image reconstruction, the patch size as well as the range of regularization parameters λ $$ \lambda $$ were determined empirically and found to be generalizable to all datasets. A reference ground truth image could alternatively be used to optimize λ $$ \lambda $$ s, 82 the acquisition of which is, however, hampered by the residual CA in the tissue and the resulting change in contrast. The effects of regularization and image registration used on net spatiotemporal resolution are yet to be determined. Although simulation and in-vivo results show motion robustness of the proposed reconstruction, maximum scan acceleration factors to reduce the influence of intra-shot cardiac motion contributions remain to be investigated. Previous work exploiting motion information for 3D perfusion imaging utilized uniform Cartesian k-t undersampling30 in conjunction with ℓ 2 $$ {\ell}_2 $$ based regularization, as opposed to non-uniform k-t undersampling and nuclear norm regularization used here. As a result of ℓ 2 $$ {\ell}_2 $$ -regularization, temporal blurring was observed compromising MBF quantification.30 A comparison of different quantitative free-breathing perfusion approaches (i.e., data acquisition, reconstruction and MBF quantification) for uniform Cartesian, random Cartesian, radial, and spiral undersampling based on synthetic data could be beneficial and will be subject of future work.

Relating to previous work that uses motion correction with LLR, the BLOSM approach is similar to the proposed MI-LLR strategy but was only applied in the context of 2D data53; through-plane motion from true 3D acquisitions was not investigated. Continuous Radial Interleaved simultaneous Multi-slice acquisition at sPoiled steady-state (CRIMP) achieves whole-heart coverage combining self-gating and patch tracking in a continuous multiband acquisition, which uses dual bolus injections for MBF quantification.42

Computation times for the entire reconstruction were on the order of ∼15 min per scan using a hybrid CPU-GPU implementation. Processing times are mainly determined by the cost of the 3D image registration steps. Furthermore, currently a five-channel coil is used. For larger numbers of receiver channels, the proposed method could be adapted using coil compression methods.83

A limitation of our study is the small number of subjects included. In order to allow for more generalizable statistical results, future studies should enroll larger numbers of subjects without and with suspected coronary artery disease. Diagnostic accuracy should then be addressed in simulation and the in-vivo evaluation. Reader assessment regarding image quality should be investigated. The method was implemented at 1.5T but is applicable to other field strengths.

5 CONCLUSIONS

The combination of 3D Cartesian pseudo-spiral in-out undersampling in conjunction with motion-informed low-rank reconstruction improves single-bolus free-breathing quantitative 3D myocardial perfusion imaging under rest and stress condition.

ENDNOTE

  • * Part of the work has been published in the Proceedings of the 30th Annual Meeting of the ISMRM.61

      • The full text of this article hosted at iucr.org is unavailable due to technical difficulties.