Progress in partial least squares structural equation modeling use in marketing research in the last decade
Abstract
Partial least squares structural equation modeling (PLS-SEM) is an essential element of marketing researchers' methodological toolbox. During the last decade, the PLS-SEM field has undergone massive developments, raising the question of whether the method's users are following the most recent best practice guidelines. Extending prior research in the field, this paper presents the results of a new analysis of PLS-SEM use in marketing research, focusing on articles published between 2011 and 2020 in the top 30 marketing journals. While researchers were more aware of the when's and how's of PLS-SEM use during the period studied, we find that there continues to be some delay in the adoption of model evaluation's best practices. Based on our review results, we provide recommendations for future PLS-SEM use, offer guidelines for the method's application, and identify areas of further research interest.
1 INTRODUCTION
For many years, estimating models with complex inter-relationships between observed concepts and their latent variables was equivalent to executing factor-based structural equation modeling (SEM). Recent research, however, demonstrates the rise of partial least squares (PLS) as a composite-based alternative (Jöreskog & Wold, 1982). PLS-SEM applications have grown exponentially in the past decade (Hair et al., 2022), especially in the social sciences (e.g., Ali et al., 2018; Ringle et al., 2020; Willaby et al., 2015), but also in other fields of scientific inquiry, such as agricultural science, engineering, environmental science, and medicine (e.g., Durdyev et al., 2018; Menni et al., 2018; Svensson et al., 2018). The availability of comprehensive software programs with an intuitive graphical user interface (Sarstedt & Cheah, 2019), application guideline articles (e.g., Chin, 1998; Hair et al., 2011; Henseler et al., 2009), and textbooks (e.g., Hair et al., 2022; Ramayah et al., 2018; Wong, 2019), all of which have made the method available for nontechnical use, have shaped the field significantly and contributed to PLS-SEM's dissemination.
An article by Hair et al. (2012) has had a lasting impact on the marketing and consumer behavior disciplines—as evidenced by its massive citation count. In this paper, the authors review more than 200 studies using PLS-SEM and published in top 30 ranked marketing journals between 1981 and 2010. Based on their evaluation of PLS-SEM applications according to a wide range of criteria pertaining to, for example, model characteristics and assessment practices, Hair et al. (2012, p. 428) identify “misapplications of the technique, even in top-tier marketing journals,” noting that “researchers do not fully capitalize on the criteria available for model assessment and sometimes even misapply measures.” The authors also derive comprehensive guidelines for algorithmic settings, measurement and structural model evaluation criteria, as well as complementary analyses, which have become an anchor for the method's follow-up extensions and applications.
It has been a decade since the publication of Hair et al.'s (2012) article. During these years, the PLS-SEM field has undergone extensive methodological developments (Hwang et al., 2020; Khan et al., 2019). Research has shaped the method's understanding (e.g., Rigdon, 2012), introduced new metrics (e.g., Liengaard et al., 2021), and clarified aspects related to model specification and data considerations (e.g., Rigdon, 2012; Sarstedt et al., 2016), all of which are relevant for PLS-SEM users. Some of these extensions emerged from controversies about PLS-SEM's general efficacy (Evermann & Rönkkö, 2021), such as guidelines for identifying and treating endogeneity (Hult et al., 2018), methods for estimating common factor models (Bentler & Huang, 2014; Dijkstra & Henseler, 2015; Kock, 2019), and novel means of assessing discriminant validity (Henseler et al., 2015). In addition, best practices, for example, with regard to measurement and structural model assessment (Hair et al., 2020b), have solidified in recent years as part of the PLS-SEM field's further maturation. But has PLS-SEM use truly been understood and accepted in the marketing research field? Have researchers taken the most recent best practice guidelines on board? Are there still cases of misapplications as previously pointed out by Hair et al. (2012).
This paper addresses these questions by presenting the results of a new review of PLS-SEM use in marketing research, focusing on articles published between 2011 and 2020 in the top 30 marketing journals. By applying the same coding scheme as Hair et al. (2012), our analysis facilitates drawing conclusions about developments in PLS-SEM use over time and identifying potential points of concern. In addition, our review covers recent developments in the field, such as improved metrics for assessing internal consistency reliability (Dijkstra & Henseler, 2015), discriminant validity (Henseler et al., 2015), and predictive power (Shmueli et al., 2016) to explore whether researchers follow the latest advances in the field. Based on our review results, we spell out recommendations for future PLS-SEM use, offer guidelines for the method's application, and identify areas of further research interest. Our overarching aim is to improve the rigor of the PLS-SEM method's application.
2 REVIEW OF PLS-SEM RESEARCH PUBLISHED BETWEEN 2011 AND 2020
To ensure comparability with Hair et al.'s (2012) article, we reviewed PLS-SEM applications in the top 30 marketing journals according to Hult et al. (2009) journal rankings. Since Hair et al. (2012) examined the period from 1981 to 2010, we focused our review on the following 10 years (i.e., 2011–2020) to identify possible developments and provide an overview of PLS-SEM use in recent marketing studies. We also used the keywords “partial least squares” and “PLS” to conduct a full-text search in the Clarivate Analytics' Web of Science, EBSCO Information Services, and Elsevier's Scopus databases. We ensured that we would retrieve the complete set of relevant articles by using the same search terms to search the journals' websites. The search was completed on January 12, 2021.
We excluded all articles matching our keyword list, but not related to PLS-SEM (e.g., private labels, PLs). We also excluded articles applying PLS regression or only mentioning PLS-SEM, but not applying the method. Following these adjustments, we conducted a detailed review of all the articles published in journals with interdisciplinary content (Journal of Business Research, Journal of International Business Studies, Journal of Product Innovation Management, and Management Science) to identify those in marketing. Finally, we excluded all articles introducing methodological advancements of the method (e.g., Shmueli et al., 2016) or including simulation studies comparing PLS-SEM with other methods (e.g., Hair et al., 2017b).
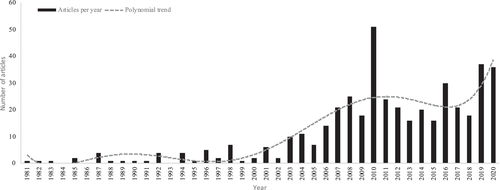
The search produced a total of 239 articles applying PLS-SEM in the last 10 years (Table 1), which is a steep increase compared to the previous period's 204 articles (Hair et al., 2012). A breakdown of the number of articles by year (Figure 1) shows that PLS-SEM use surged substantially in 2019 and 2020, with 37 and 36 articles, respectively—only 2010 saw a higher number of PLS-SEM articles. These results clearly indicate an enduring upward trend in PLS-SEM use since the early 2000s.
| Advances in Consumer Research* | Wauters, Brengman, and Janssens 2011 |
| European Journal of Marketing | Akman, Plewa, and Conduit 2019 |
| Aspara and Tikkanen 2011 | |
| Carlson, Gudergan, Gelhard, and Rahman 2019 | |
| Chen, Peng, and Hung 2015 | |
| Coelho and Henseler 2012 | |
| Davari, Iyer, and Guzmán 2017 | |
| Dessart, Aldás-Manzano, and Veloutsou 2019 | |
| Françoise and Andrews 2015 | |
| Gaston-Breton, and Duque 2015 | |
| Huang and Tsai 2013 | |
| Krishen, Leenders, Muthaly, Ziółkowska, and LaTour 2019 | |
| Mo, Yu, and Ruyter 2020 | |
| Nath 2020 | |
| Olbrich and Schultz 2014 | |
| Ormrod and Henneberg 2011 | |
| Piehler, King, Burmann, and Xiong 2016 | |
| Šerić 2017 | |
| Singh and Söderlund 2020 | |
| Vidal 2014 | |
| Wijayaratne, Reid, Westberg, Worsley, and Mavondo 2018 | |
| Willems, Brengman, and Kerrebroeck 2019 | |
| Yu, Ruyter, Patterson, and Chen 2018 | |
| Industrial Marketing Management | Ali, Ali, Salam, Bhatti, Arain, and Burhan 2020 |
| Berghman, Matthyssens, and Vandenbempt 2012 | |
| Camisón and Villar-López 2011 | |
| Faroughian, Kalafatis, Ledden, Samouel, and Tsogas 2012 | |
| Ferreras-Méndez, Newell, Fernández-Mesa, and Alegre 2015 | |
| Genc, Dayan, and Genc 2019 | |
| Gupta, Drave, Dwivedi, Baabdullah, and Ismagilova 2020 | |
| Harmancioglu, Sääksjärvi, and Hultink 2020 | |
| Hazen, Overstreet, Hall, Huscroft, and Hanna 2015 | |
| Heirati, O'Cass, Schoefer, and Siahtiri 2016 | |
| Hossain, Akter, Kattiyapornpong, and Dwivedi 2020 | |
| Inigo, Ritala, and Albareda 2020 | |
| Jain, Khalil, Johnston, and Cheng 2014 | |
| Joachim, Spieth, and Heidenreich 2018 | |
| Lopes de Sousa Jabbour, Vazquez-Brust, Chiappetta Jabbour, and Latan 2017 | |
| Mahlamäki, Rintamäki, and Rajah 2019 | |
| Mahlamäki, Storbacka, Pylkkönen, and Ojala 2020 | |
| Nagati and Rebolledo 2013 | |
| Nenonen, Storbacka, and Frethey-Bentham 2019 | |
| Ng, Ding, and Yip 2013 | |
| Niu, Deng, and Hao 2020 | |
| Poucke, Matthyssens, Weele, and Bockhaven 2019 | |
| Pulles, Schiele, Veldman, and Hüttinger 2016 | |
| Ritter and Geersbro 2011 | |
| Rollins, Bellenger, and Johnston 2012 | |
| Shahzad, Ali, Takala, Helo, and Zaefarian 2018 | |
| Sluyts, Matthyssens, Martens, and Streukens 2011 | |
| Stekelorum, Laguir, and Elbaz 2020 | |
| Teller, Alexander, and Floh 2016 | |
| Vries, Schepers, Weele, and Valk 2014 | |
| Yeniaras, Kaya, and Dayan 2020 | |
| International Journal of Research in Marketing | Miao and Evans 2012 |
| International Marketing Review | Andéhn and L'Espoir Decosta 2016 |
| Freeman and Styles 2014 | |
| Griffith, Lee, Yeo, and Calantone 2014 | |
| Jean, Wang, Zhao, and Sinkovics 2016 | |
| Kumar, Singh, Pereira, and Leonidou 2020 | |
| Moon and Oh 2017 | |
| Oliveira Duarte and Silva 2020 | |
| Pinho and Thompson 2017 | |
| Rahman, Uddin, and Lodorfos 2017 | |
| Rippé, Weisfeld-Spolter, Yurova, and Sussan 2015 | |
| Singh and Duque 2020 | |
| Sinkovics, Sinkovics, and Jean 2013 | |
| Journal of Advertising | Coleman, Royne, and Pounders 2020 |
| José-Cabezudo and Camarero-Izquierdo 2012 | |
| Journal of Advertising Research | Archer-Brown, Kampani, Marder, Bal, and Kietzmann 2017 |
| Dennis and Gray 2013 | |
| Miltgen, Cases, and Russell 2019 | |
| Robinson and Kalafatis 2020 | |
| Singh, Crisafulli, and La Quamina 2020 | |
| Journal of Business Research | Ahrholdt, Gudergan, and Ringle 2019 |
| Albert, Merunka, and Valette-Florence 2013 | |
| Ali, Ali, Grigore, Molesworth, and Jin 2020 | |
| Ballestar, Grau-Carles, and Sainz 2016 | |
| Banik, Gao, and Rabbanee 2019 | |
| Barhorst, Wilson, and Brooks 2020 | |
| Blocker 2011 | |
| Borges-Tiago, Tiago, and Cosme 2019 | |
| Caputo, Mazzoleni, Pellicelli, and Muller 2020 | |
| Cenamor, Parida, and Wincent 2019 | |
| Cervera-Taulet, Pérez-Cabañero, and Schlesinger 2019 | |
| Chang, Shen, and Liu 2016 | |
| Del Sánchez de Pablo González Campo, Peña García Pardo, and Hernández-Perlines 2014 | |
| Ferrell, Harrison, Ferrell, and Hair 2019 | |
| Flecha-Ortíz, Santos-Corrada, Dones-González, López-González, and Vega 2019 | |
| Galindo-Martín, Castaño-Martínez, and Méndez-Picazo 2019 | |
| Gelhard and Delft 2016 | |
| Gudergan, Devinney, and Ellis 2016 | |
| Hernández-Perlines 2016 | |
| Hsieh 2020 | |
| Iglesias, Markovic, and Rialp 2019 | |
| Japutra and Molinillo 2019 | |
| Japutra, Ekinci, and Simkin 2019 | |
| Kapferer and Valette-Florence 2019 | |
| Kühn, Lichters, and Krey 2020 | |
| Leischnig, Henneberg, and Thornton 2016 | |
| Leong, Hew, Ooi, and Chong 2020 | |
| Martins, Costa, Oliveira, Gonçalves, and Branco 2019 | |
| McColl-Kennedy, Hogan, Witell, and Snyder 2017 | |
| Méndez-Suárez and Monfort 2020 | |
| Merz, Zarantonello, and Grappi 2018 | |
| Mourad and Valette-Florence 2016 | |
| Navarro-García, Arenas-Gaitán, Javier Rondán-Cataluña, and Rey- Moreno 2016 | |
| Navarro-García, Sánchez-Franco, and Rey-Moreno 2016 | |
| Ohiomah, Andreev, Benyoucef, and Hood 2019 | |
| Oliveira Duarte and Pinho 2019 | |
| Padgett, Hopkins, and Williams 2020 | |
| Palos-Sanchez, Saura, and Martin-Velicia 2019 | |
| Peterson 2020 | |
| Picón, Castro, and Roldán 2014 | |
| Reguera-Alvarado, Blanco-Oliver, and Martín-Ruiz 2016 | |
| Rippé, Smith, and Dubinsky 2018 | |
| Roy, Balaji, Soutar, Lassar, and Roy 2018 | |
| Saleh Al-Omoush, Orero-Blat, and Ribeiro-Soriano 2020 | |
| Schubring, Lorscheid, Meyer, and Ringle 2016 | |
| Segarra-Moliner and Moliner-Tena 2016 | |
| Sener, Barut, Oztekin, Avcilar, and Yildirim 2019 | |
| Sharma and Jha 2017 | |
| Skarmeas, Saridakis, and Leonidou 2018 | |
| Suhartanto, Dean, Nansuri, and Triyuni 2018 | |
| Tajvidi, Richard, Wang, and Hajli 2020 | |
| Takata 2016 | |
| Thakur and Hale 2013 | |
| Tran, Lin, Baalbaki, and Guzmán 2020 | |
| Valette-Florence, Guizani, and Merunka 2011 | |
| Wu, Raab, Chang, and Krishen 2016 | |
| Zhang, He, Zhou, and Gorp 2019 | |
| Zollo, Filieri, Rialti, and Yoon 2020 | |
| Journal of Interactive Marketing | Buzeta, Pelsmacker, and Dens 2020 |
| Divakaran, Palmer, Søndergaard, and Matkovskyy 2017 | |
| Journal of International Business Studies | Lam, Ahearne, and Schillewaert 2012 |
| Lew, Sinkovics, Yamin, and Khan 2016 | |
| Journal of International Marketing | Johnston, Khalil, Jain, and Cheng 2012 |
| Journal of Marketing | Köhler, Rohm, Ruyter, and Wetzels 2011 |
| Journal of Marketing Management | Ashill and Jobber 2014 |
| Balaji and Roy 2017 | |
| Barnes and Mattsson 2011 | |
| Bennett 2011 | |
| Bennett 2018 | |
| Bennett and Kottasz 2011 | |
| Brettel, Engelen, and Müller 2011 | |
| Brill, Munoz, and Miller 2019 | |
| Carlson, Rahman, Rosenberger, and Holzmüller 2016 | |
| Carlson, Rosenberger, and Rahman 2015 | |
| Chiang, Wei, Parker, and Davey 2017 | |
| Dall'Olmo Riley, Pina, and Bravo 2015 | |
| Falkenreck and Wagner 2011 | |
| Fernandes and Castro 2020 | |
| Finch, Hillenbrand, O'Reilly, and Varella 2015 | |
| Hankinson 2012 | |
| Helme-Guizon and Magnoni 2019 | |
| Iriana, Buttle, and Ang 2013 | |
| Jack and Powers 2013 | |
| King, Grace, and Weaven 2013 | |
| Ledden, Kalafatis, and Mathioudakis 2011 | |
| Mouri, Bindroo, and Ganesh 2015 | |
| Ngo and O'Cass 2012 | |
| Papagiannidis, Pantano, See-To, and Bourlakis 2013 | |
| Richard and Zhang 2012 | |
| Ross and Grace 2012 | |
| Roy, Balaji, and Nguyen 2020 | |
| Roy, Singh, Hope, Nguyen, and Harrigan 2019 | |
| Stocchi, Michaelidou, Pourazad, and Micevski 2018 | |
| Tabeau, Gemser, Hultink, and Wijnberg 2017 | |
| Tafesse and Wien 2018 | |
| Taheri, Gori, O'Gorman, Hogg, and Farrington 2016 | |
| Teller, Gittenberger, and Schnedlitz 2013 | |
| Wu, Jayawardhena, and Hamilton 2014 | |
| Wyllie, Carlson, and Rosenberger 2014 | |
| Journal of Product Innovation Management | Beuk, Malter, Spanjol, and Cocco 2014 |
| Borgh and Schepers 2014 | |
| Brettel, Heinemann, Engelen, and Neubauer 2011 | |
| Calantone and Rubera 2012 | |
| Carbonell and Rodríguez-Escudero 2016 | |
| Carbonell and Rodríguez-Escudero 2019 | |
| Dubiel, Durmuşoğlu, and Gloeckner 2016 | |
| Ernst, Kahle, Dubiel, Prabhu, and Subramaniam 2015 | |
| Feurer, Schuhmacher, and Kuester 2019 | |
| Hammedi, Riel, and Sasovova 2011 | |
| Heidenreich and Handrich 2015 | |
| Heidenreich, Spieth, and Petschnig 2017 | |
| Jean, Sinkovics, and Hiebaum 2014 | |
| Kock, Gemünden, Salomo, and Schultz 2011 | |
| Kuester, Homburg, and Hess 2012 | |
| Langley, Bijmolt, Ortt, and Pals 2012 | |
| Lee and Tang 2018 | |
| Mahr, Lievens, and Blazevic 2014 | |
| Matsuno, Zhu, and Rice 2014 | |
| Mauerhoefer, Strese, and Brettel 2017 | |
| McNally, Akdeniz, and Calantone 2011 | |
| McNally, Durmuşoğlu, and Calantone 2013 | |
| Ngo and O'Cass 2012 | |
| Nijssen, Hillebrand, Jong, and Kemp 2012 | |
| Pitkänen, Parvinen, and Töytäri 2014 | |
| Schuster and Holtbrügge 2014 | |
| Siahtiri 2018 | |
| Spanjol, Mühlmeier, and Tomczak 2012 | |
| Spanjol, Qualls, and Rosa 2011 | |
| Zobel 2017 | |
| Journal of Public Policy and Marketing | Hasan, Lowe, and Petrovici 2019 |
| Journal of Retailing | Pelser, Ruyter, Wetzels, Grewal, Cox, and Beuningen 2015 |
| Journal of Service Research | Boisvert 2012 |
| Mullins, Agnihotri, and Hall 2020 | |
| Journal of the Academy of Marketing Science | DeLeon and Chatterjee 2017 |
| Ernst, Hoyer, Krafft, and Krieger 2011 | |
| Fombelle, Bone, and Lemon 2016 | |
| Hansen, McDonald, and Mitchell 2013 | |
| Heidenreich, Wittkowski, Handrich, and Falk 2015 | |
| Heijden, Schepers, Nijssen, and Ordanini 2013 | |
| Hillebrand, Nijholt, and Nijssen 2011 | |
| Houston, Kupfer, Hennig-Thurau, and Spann 2018 | |
| Hult, Morgeson, Morgan, Mithas, and Fornell 2017 | |
| Leroi-Werelds, Streukens, Brady, and Swinnen 2014 | |
| Martin, Johnson, and French 2011 | |
| Miao and Evans 2013 | |
| Nakata, Zhu, and Izberk-Bilgin 2011 | |
| Ranjan and Read 2016 | |
| Santos-Vijande, López-Sánchez, and Rudd 2016 | |
| Steinhoff and Palmatier 2016 | |
| Weerawardena, Mort, Salunke, Knight, and Liesch 2015 | |
| Wilden and Gudergan 2015 | |
| Wolter and Cronin 2016 | |
| Marketing Letters | Dugan, Rouziou, and Hochstein 2019 |
| Psychology and Marketing | Barnes and Pressey 2012 |
| Borges-Tiago, Tiago, Silva, Guaita Martínez, and Botella-Carrubi 2020 | |
| Devece, Llopis-Albert, and Palacios-Marqués 2017 | |
| Evers, Gruner, Sneddon, and Lee 2018 | |
| Fatima, Mascio, and Johns 2018 | |
| Gong and Yi 2018 | |
| Hernández-Perlines, Moreno-García, and Yáñez-Araque 2017 | |
| Jain, Malhotra, and Guan 2012 | |
| Revilla-Camacho, Vega-Vázquez, and Cossío-Silva 2017 | |
| Sheng, Simpson, and Siguaw 2019 | |
| Verhagen, Dolen, and Merikivi 2019 | |
| Zhang and Zhang 2014 |
- Note: California Management Review, Harvard Business Review, Journal of Consumer Psychology, Journal of Consumer Research, Journal of Marketing Research, Management Science, Marketing Science, Quantitative Marketing and Economics, and Sloan Management Review did not produce any relevant articles.
- Journal of Business ceased publication of the journal at the end of 2006.
- Abbreviation: PLS-SEM, partial least squares structural equation modeling.
- * We excluded five studies by Caemmerer and Mogos Descotes (2011), Chen et al. (2011), Kidwell et al. (2012), Luo et al. (2015), and Rippé et al. (2019) published in Advances in Consumer Research as these were only published as extended abstracts.
The 239 articles were published in 20 journals, with Journal of Business Research (58 articles; 24.27%), Journal of Marketing Management (35 articles, 14.64%), and Industrial Marketing Management (31 articles, 12.97%) being the top three most used publishing outlets. Compared to the previous period, PLS-SEM was applied far more frequently in Journal of Product Innovation Management, Journal of the Academy of Marketing Science, and International Marketing Review. In contrast, European Journal of Marketing and Journal of Marketing published fewer articles using PLS-SEM. Table 2 documents these results with respect to all journals that published more than one PLS-SEM article between 2011 and 2020, also showing the previous period's corresponding frequencies.
| Publications | ||||
|---|---|---|---|---|
| Journals | 1981–2010 (n = 204) | Proportion (%) | 2011–2020 (n = 239) | Proportion (%) |
| Journal of Business Research | 15 | 7.35 | 58 | 24.27 |
| Journal of Marketing Management | 6 | 2.94 | 35 | 14.64 |
| Industrial Marketing Management | 23 | 11.27 | 31 | 12.97 |
| Journal of Product Innovation Management | 11 | 5.39 | 30 | 12.55 |
| European Journal of Marketing | 30 | 14.71 | 22 | 9.21 |
| Journal of the Academy of Marketing Science | 13 | 6.37 | 19 | 7.95 |
| International Marketing Review | 3 | 1.47 | 12 | 5.02 |
| Psychology and Marketing | 9 | 4.41 | 12 | 5.02 |
| Journal of Advertising Research | 4 | 1.96 | 5 | 2.09 |
| Journal of Advertising | 3 | 1.47 | 2 | 0.84 |
| Journal of Interactive Marketing | 2 | 0.98 | 2 | 0.84 |
| Journal of International Business Studies | 2 | 0.98 | 2 | 0.84 |
| Journal of Service Research | 7 | 3.43 | 2 | 0.84 |
Of the 239 articles, 93 (38.91%) report two or more alternative models or different datasets (e.g., collected in different years, countries, target groups, or resulting from a segmentation), yielding a total number of 486 analyzed PLS path models. In the following, we use the term “studies” to refer to the 239 journal articles and “models” to refer to the 486 PLS path models analyzed in these articles. Compared to the previous period, the average number of PLS path models analyzed per article increased from approximately 1.5 to 2 in more recent years, showing a shift to multistudy designs that have become the norm in marketing and consumer research (McShane & Böckenholt, 2017).
3 REVIEW OF PLS-SEM RESEARCH: 2011–2020
We evaluated the 239 articles and the models included therein in terms of the following criteria, which Hair et al. (2012), follow-up reviews, and conceptual articles (e.g., Hair et al., 2020b, 2019b, 2019c) identified as relevant for PLS-SEM use: (1) reasons for using PLS-SEM, (2) data characteristics, (3) model characteristics, (4) measurement model evaluation, (5) structural model evaluation, (6) advanced modeling and analysis techniques, and (7) reporting. Addressing these seven critical issues, we provide an update of PLS-SEM applications in marketing and compare our findings with those of Hair et al. (2012). Where applicable, we discuss major shifts in PLS-SEM use between the two periods under consideration (i.e., 1981–2010 and 2011–2020).
3.1 Reasons for using PLS-SEM
Our review shows that 196 (82.01%) of the 239 studies provide a rationale for using PLS-SEM instead of factor-based SEM or sum scores regression (Table 3). The five most frequently mentioned reasons are: small sample size (114 studies, 47.70%), nonnormal data (76 studies, 31.80%), theory development and exploratory research (73 studies, 30.54%), high model complexity (70 studies, 29.29%), predictive study focus (61 studies, 25.52%), and formative measures (56 studies, 23.43%).
| 1981–2010 | 2011–2020 | |||
|---|---|---|---|---|
| Number of studies (n = 204) | Proportion (%) | Number of studies (n = 239) | Proportion (%) | |
| Nonnormal data | 102 | 50.00 | 76 | 31.80 |
| Small sample size | 94 | 46.08 | 114 | 47.70 |
| Formative measures | 67 | 32.84 | 56 | 23.43 |
| Explain variance in the endogenous constructs | 57 | 27.94 | – | – |
| Theory development and exploratory research | 35 | 17.16 | 73 | 30.54 |
| High model complexity | 27 | 13.24 | 70 | 29.29 |
| Categorical variables | 26 | 12.75 | 5 | 2.09 |
| Theory testing | 25 | 12.25 | 11 | 4.60 |
| Predictive study focus | – | – | 61 | 25.52 |
| PLS-SEM's popularity and standard use in the field | – | – | 14 | 5.86 |
| Moderation effects | – | – | 12 | 5.02 |
| Higher-order constructs | – | – | 8 | 3.35 |
| Simultaneous use of multi- and single-items constructs | – | – | 6 | 2.51 |
| Latent variable scores availability | – | – | 5 | 2.09 |
| Mediation effects | – | – | 3 | 1.26 |
| Other reasons (e.g., small number of indicators per construct, model comparison assessment, higher statistical power than factor-based SEM) | – | – | 19 | 7.95 |
- Abbreviation: PLS-SEM, partial least squares structural equation modeling.
The two main reasons mentioned in our study are similar to those reported by Hair et al. (2012) a decade ago. Given the increasing calls to move beyond data characteristics to motivate the use of PLS-SEM and, instead, emphasize the research objective (e.g., Hair et al., 2019b; 2019c; Sarstedt et al., 2021), this finding raises concerns. While PLS-SEM performs well in terms of statistical power (Sarstedt et al., 2016) and convergence compared to other methods when the sample size is small (Henseler et al., 2014; Reinartz et al., 2009), it is undeniable and axiomatic that small samples adversely affect all statistical techniques, including PLS-SEM (Benitez et al., 2020). In fact, more than two decades ago, Chin (1998, p. 305) warned researchers that “the stability of the estimates can be affected contingent on the sample size.” Cassel et al. (1999) also noted that PLS-SEM analyses should draw on sufficiently large sample sizes to warrant small standard errors. Numerous others, such as Marcoulides and Saunders (2006), Hair et al. (2013), and Rigdon (2016), have clearly advised against relying on the logic of using PLS-SEM to derive results from small samples—unless the nature of the population can justify such a step (e.g., a small population size as commonly encountered in B2B research; Benitez et al., 2020; Hair et al., 2019c). In fact, critics such as Evermann and Rönkkö (2021), Rönkkö and Evermann (2013), and Rönkkö et al. (2016) have repeatedly used PLS-SEM's misapplication as a “strawman” argument to criticize the technique itself, rather than the weak research designs (Petter & Hadavi, 2021; Petter, 2018). Similarly, simulation studies have shown that PLS-SEM does not offer substantial advantages over other SEM methods in terms of parameter accuracy when the data depart somewhat from normality (Goodhue et al., 2012; Reinartz et al., 2009). Reflecting this evidence, guideline articles have emphasized that it is not sufficient to motivate the choice of PLS-SEM over alternative methods primarily on the basis of nonnormality alone (e.g., Hair et al., 2019b, 2019c, 2020b).
Despite their strong emphasis on the data characteristics, our results also attest to marketing researchers' higher maturity in terms of motivating their method choice. For example, compared to the previous period, an increasing number of researchers emphasize model complexity and their study's predictive focus. Both are valid arguments, as PLS-SEM can handle highly complex models with many indicators, constructs, and model relations without identification concerns (Akter et al., 2017). When estimating these models, PLS-SEM follows a causal-predictive paradigm aimed at testing the predictive power of a model developed carefully on the basis of theory and logic (Liengaard et al., 2021). The underlying theoretical rationale, also referred to as explanation and prediction-oriented (EP) theory, “corresponds to commonly held views of theory in both the natural and social sciences” (Gregor, 2006, p. 626). Numerous standard models, such as the various customer satisfaction index (e.g., Eklöf & Westlund, 2002; Fornell et al., 1996) or technology acceptance models (e.g., Davis, 1989; Venkatesh et al., 2003), follow an EP-theoretic approach by aiming to explain the cause-effect mechanisms the model postulates, while also generating predictions that underline its practical usefulness (Sarstedt & Danks, 2021). PLS-SEM's ability to strike a balance between machine learning methods, which are fully predictive but atheoretical by nature (Hair & Sarstedt, 2021), and factor-based SEM, which is purely concerned with theory confirmation (Hair, et al., 2021b), makes PLS-SEM a particularly valuable method for applied research disciplines like marketing.
Researchers' increased focus on predictive purposes is no coincidence. Seminal articles by Evermann and Tate (2016) as well as Shmueli et al. (2016) on the method's predictive performance have opened a new chapter in PLS-SEM-based methodological research. For example, Sharma et al. (2021c) introduced prediction-oriented model comparison to the field by identifying metrics that excel at selecting the model with the highest predictive power and adequate fit from a set of competing models. Liengaard et al.'s (2021) cross-validated predictive ability test and its recent extension (Sharma et al., 2021a) enable researchers to test a model's predictive power relative to that of competing models and on a standalone basis. Other studies have extended prior research by comparing PLS-SEM's predictive power with that of Hwang and Takane's (2004) generalized structured component analysis, identifying situations that favor each method's use from a prediction point of view (Cho et al., 2021). Guideline articles that make these techniques accessible to a broader audience have accompanied these methodological extensions (Chin et al., 2020; Hair, 2021; Shmueli et al., 2019). Our review of the reasons given for the choice of PLS-SEM reflects some of these developments, but we expect a further shift toward emphasizing the method's causal-predictive focus in the future.
Finally, and unlike in the previous period, researchers also suggest additional reasons, such as PLS-SEM's popularity and standard use in the field (14 studies, 5.86%), the estimation of moderation effects (12 studies, 5.02%), mediation effects (3 studies, 1.26%) and higher-order constructs (8 studies, 3.35%). Indeed, recent research emphasizes the method's efficacy regarding estimating conditional process models combining mediating and moderating effects in a single analysis (Cheah et al., 2021; Sarstedt et al., 2020a), and clarifies the specification, estimating, and evaluation of higher-order constructs by means of PLS-SEM (Sarstedt et al., 2019). At the same time, fewer studies motivate their choice of PLS-SEM on the grounds of formative measurement—a finding that the studies' model characteristics, which we discuss later, also mirror.
3.2 Data characteristics
Of the 486 models, 476 report the sample size (97.94%). The average sample size (5% trimmed mean = 279.19) and the median (199) of the models in our review are higher than those that Hair et al. (2012) reported for the 1981–2010 period (5% trimmed mean = 211.29; median = 159). Four studies in our review were conspicuous due to their very large sample sizes of between n = 8876 and n = 26,576. At the same time, 85 of the 476 models (17.86%) rely on sample sizes of less than 100 (i.e., the smallest sample size was n = 29). Only 17 of the 476 models (3.57%) fail to meet the ten times rule (Barclay et al., 1995), which is a very rough guideline for determining the minimum sample size required to achieve an adequate level of statistical power (for details and alternatives, see Hair et al., 2022, Chap. 1). Those models that do not meet the ten times rule draw on sample sizes that are, on average, only 10.98% below the recommended level (Table 4).
| 1981–2010 | 2011–2020 | |||
|---|---|---|---|---|
| Models (n = 311) | Proportion (%) | Models (n = 486) | Proportion (%) | |
| Sample size: no. of models reporting | 311 | 100% | 476 | 97.94 |
| 5% trimmed mean | 211.29 | – | 279.19 | – |
| Median sample size | 159 | – | 199 | – |
| Sample size below 100 | 76 of 311 | 24.44 | 85 of 476 | 17.86 |
| Ten times rule of thumb not met | 28 of 311 | 9.00 | 17 of 476 | 3.57 |
| Average deviation from the recommended sample size | 45.18% | 10.98% | ||
| Number of studies (n = 204) | Proportion (%) | Number of studies (n = 239) | Proportion (%) | |
| Missing values: No. of studies reporting | – | – | 41 | 17.15 |
| Casewise deletion | – | – | 39 of 41 | 95.12 |
| Mean replacement | – | – | 2 of 41 | 4.88 |
| Outliers: No. of studies reporting | – | – | 7 | 2.93 |
| Nonnormal data: No. of studies reporting | 19 | 9.31 | 24 | 10.04 |
| Degree of nonnormality reported | – | – | 5 of 24 | 20.83 |
| Use of discrete variables: No. of studies reporting | 57 | 27.94 | 24 | 10.04 |
| Binary variables | 43 of 57 | 75.44 | 15 of 24 | 62.50 |
| Categorical variables | 14 of 57 | 12.28 | 9 of 24 | 37.50 |
These results are encouraging compared to those in Hair et al. (2012), who reported a greater share of models estimated with less than 100 observations (24.44%), more models that failed the ten times rule (9.00%), and a higher relative deviation from the recommended sample size (45.18%). Marketing researchers—despite their reporting of PLS-SEM's efficacy regarding estimating models with small sample sizes as motivating their method choice—seem to be more concerned about sample size issues than previously. Critical accounts of the method (Goodhue et al., 2012; Rönkkö & Evermann, 2013) and conceptual discussions (Hair et al., 2019c; Rigdon, 2016) have certainly contributed to this increased awareness. Nevertheless, empirical research almost never discusses the statistical power arising from a concrete analysis, despite the available tutorials on power analyses in a PLS-SEM context (Aguirre-Urreta & Rönkkö, 2015). For sample size determination, researchers can also draw on Kock and Hadaya's (2018) inverse square root method, which is relatively easy to apply and offers a more accurate picture of minimum sample size requirements than the ten times rule does.
Missing values are a primary concern in the data collection and processing phases. Nevertheless, only 41 studies (17.15%) acknowledge missing values in their data, while almost all of them (39 of 41 studies, 95.12%) used casewise deletion to treat them (Table 4). Grimm and Wagner (2020) have recently shown that PLS-SEM estimates are very stable when using casewise deletion on datasets with up to 9% missing values. However, when doing so researchers need to ensure the missing value patterns are not systematic, and that the final model estimation yields sufficient levels of statistical power. None of the relevant studies in our review offer such information. While casewise deletion seems to be the default setting for researchers using PLS-SEM, extant guidelines recommend using mean replacement when less than 5% values are missing per indicator or applying more complex procedures, such as maximum likelihood and multiple imputation (Hair et al., 2022). However, while the efficacy of more complex imputation procedures has been tested in a factor-based SEM context (Graham & Coffman, 2012; Lee & Shi, 2021), their impact on PLS-SEM's parameter accuracy and predictive performance remains a blind spot in methodological research.
Even though outliers influence the ordinary least squares regressions in PLS-SEM, only seven studies (2.93%) explicitly considered them. In one of these studies, the authors did not try to identify outliers but used an interval smoothing approach to mitigate the effect of corresponding observations. Of the remaining six studies that considered outliers, three did not mention the specific method used to detect outliers, whereas the remaining three studies included brief descriptions of the approaches: univariate and multivariate outlier detection, inconsistent or overly consistent response patterns, and univariate outlier detection using boxplots followed by detecting incongruence in response patterns. Most of these studies (5 out of 6) removed outliers from their dataset; the other study did not identify any outliers. While the presence of outliers might influence results substantially (Sarstedt & Mooi, 2019), our findings indicate that applied PLS-SEM research generally disregards outlier detection and treatment.
Nonnormal data is the second most frequently mentioned reason for using PLS-SEM. Nevertheless, only 24 studies (10.04%) acknowledge the nonnormal distribution of their data with few studies quantifying the degree of nonnormality by means of, for example, kurtosis and skewness (5 studies; Table 4). This is generally unproblematic, since PLS-SEM is a nonparametric method and, as such, robust in terms of processing nonnormal data (Hair et al., 2017b; Reinartz et al., 2009). While Hair et al. (2022, Chap. 2) note that highly nonnormal data may inflate standard errors derived from bootstrapping, Hair et al.'s (2017b) simulation study results suggest that such data do not impact Type I or II errors negatively.
Using discrete variables (i.e., binary and categorical variables) when measuring models is a final area of concern in PLS-SEM applications. Of the 239 studies, only 24 (10.04%) use binary or categorical variables as elements in measurement models (i.e., not as a grouping variable to split the dataset as part of a multigroup analysis), which is considerably less than what Hair et al. (2012) reported (27.94%). In line with Hair et al.'s (2012) recommendations, which raised concerns regarding their general applicability, especially when used as binary single-item indicators of endogenous constructs (e.g., to represent a choice situation), recent studies primarily use binary and categorical variables to perform multigroup analyses. However, research on the handling of discrete variables in PLS-SEM has progressed since 2012. For example, Hair et al. (2019a) document how to process data from discrete choice experiments where binary indicators representing a choice situation (e.g., buy/not buy) measure the constructs. Similarly, Cantaluppi and Boari (2016) extended the original PLS-SEM algorithm to accommodate ordinal variables when researchers cannot assume equidistance between the scale categories (see also Schuberth et al., 2018b). Given these developments, we expect the use of discrete variables in PLS path models, such as when estimating data from choice experiments, to gain traction in the future.
To summarize, while our results point to improvements in researchers' awareness of sample size issues in PLS-SEM use, they devote too little effort toward quantifying the degree of statistical power associated with the model estimation. Missing data are not routinely discussed, and their treatment in PLS-SEM is still an area of potential concern, which methodological research should address. Researchers should also be aware of recent extensions that facilitate the inclusion of discrete variables in PLS path models.
3.3 Model characteristics
The number of constructs and indicator variables that define model complexity and the use of formative measurement models are the key reasons for PLS-SEM's attractiveness (Hair et al., 2022, Chap. 1). Table 5 offers an overview of these and other model characteristics, contrasting our results with those of Hair et al.'s (2012) review of the 1981–2010 period.
| 1981–2010 | 2011–2020 | |||
|---|---|---|---|---|
| Criterion | Results (n = 311) | Proportion (%) | Results (n = 486) | Proportion (%) |
| Number of latent variables | ||||
| Mean | 7.94 | – | 7.39 | – |
| Median | 7.00 | 7.00 | ||
| Range | (2; 29) | (2; 24) | ||
| Number of structural model relations | ||||
| Mean | 10.56 | – | 11.90 | – |
| Median | 8.00 | 10.00 | ||
| Range | (1; 38) | (1; 70) | ||
| Model typea | ||||
| Focused | 109 | 35.05 | 161 | 33.13 |
| Unfocused | 85 | 27.33 | 149 | 30.66 |
| Balanced | 117 | 37.62 | 176 | 36.21 |
| Measurement modelb | ||||
| Only reflective | 131 | 42.12 | 374 | 76.95 |
| Only formative | 20 | 6.43 | 7 | 1.44 |
| Reflective and formative | 123 | 39.55 | 105 | 21.60 |
| Not specified | 37 | 11.90 | 233 | 47.94 |
| Number of indicators per reflective construct | ||||
| Mean | 3.99 | – | 3.85 | – |
| Median | 3.50 | 3.00 | ||
| Range | (1; 27) | (2; 30) | ||
| Number of indicators per formative construct | ||||
| Mean | 4.62 | – | 4.28 | – |
| Median | 4.00 | 3.00 | ||
| Range | (1; 20) | (2; 38) | ||
| Total number of indicators in models | ||||
| Mean | 29.55 | – | 29.39 | – |
| Median | 24.00 | 24.00 | ||
| Range | (4; 131) | (3; 222) | ||
| Number of models with single-item constructs | 144 | 46.30 | 177 | 36.42 |
- a Focused model: number of exogenous constructs at least twice as high as the number of endogenous constructs in the model; unfocused model: number of endogenous constructs at least twice as high as the number of exogenous constructs in the model; balanced model: all remaining models.
- b This paper's authors classified models with missing information about the measurement mode ex post.
The average number of latent variables in the path models is 7.39, which is only slightly lower than in the previous period (7.94). Similarly, the average number of indicators per model is similar in both periods (1981–2010: 29.39; 2011–2020: 29.55), suggesting there has been no change in the model complexity over the years. The average number of structural model relationships, which increased only slightly from 10.56 to 11.90 from the initial period to the most recent, also supports this finding. In addition, we do not observe any substantial changes in the model types considered in the studies; that is, whether the models are focused versus unfocused by comprising a higher versus lower share of exogenous constructs than endogenous constructs. Specifically, the share of focused, unfocused, and balanced models is almost the same and very similar to those reported in Hair et al. (2012). We therefore repeat Hair et al.'s (2012) call to consider focused and balanced models, also because these model types should meet PLS-SEM's prediction goal better.
PLS path models, depending on their measurement model specifications, can be classified as either only reflective, only formative, or a combination of both.1 We find the majority of the 486 models' constructs (374 models, 76.95%) are only reflectively measured, followed by models with both reflective and formative measures (105 models, 21.60%)—a much higher share of reflective measures compared to Hair et al. (2012). Only 7 of the 486 models' constructs (1.44%) are purely formatively specified. Somewhat surprisingly, a large percentage of the models (233 models; 47.94%) lack a description of the constructs' measurement modes, which is much higher than in Hair et al.'s (2012) review (11.90%). Classifying these models ex post by means of Jarvis et al. (2003) guidelines suggests the overwhelming majority (227 models; 97.42%) should be considered as only comprising reflectively specified constructs. While this result suggests that researchers consider reflective measures the default option, the consequences of measurement model misspecification should not be taken lightly. The impact of misspecifications on downstream estimates are generally not pronounced (Aguirre-Urreta et al., 2016), but the primary problem of such misspecifications arises from content validity concerns, since both measurement types rely on fundamentally different sets of indicators (Diamantopoulos & Siguaw, 2006). In line with Hair et al. (2012), researchers should ensure the measurement model specification is explicit to preempt criticism arising from potential misspecification claims. The confirmatory tetrad analysis for PLS-SEM (Gudergan et al., 2008; CTA-PLS; Hair et al., 2018, Chap. 3) provides a statistical test to confirm the choice of measurement model. However, only six studies (2.51%) used this approach to assess the adequacy of their measurement model specification.
The average number of indicators for reflectively measured constructs is 3.85 and 4.28 for formatively measured ones, which is similar to those in the previous period (Table 5). Contrary to their reflective counterparts, formative measurement models need to cover a much broader content bandwidth, as they are not conceived as interchangeable (i.e., highly correlated) measures of the same theoretical concept (Diamantopoulos & Winklhofer, 2001). Consequently, formative measurement models should have more indicators than reflective models do. Our review supports this notion, but the comparably small, albeit significant (t = 2.037, p = 0.044) difference in the average number of indicators is surprising, suggesting that future studies should devote more attention to content validity concerns in formative measurement.
We also find the share of single-item constructs decreased from 46.30% to 36.42% from one period to the next. On the one hand, this finding is encouraging, as it suggests researchers have become aware of single-item measures' limitations in terms of explanatory power. Specifically, Diamantopoulos et al. (2012) show that, due to the absence of multiple indicators of the same concept, the lack of measurement error correction deflates the model estimates, potentially triggering Type II errors in the model estimates (Sarstedt et al., 2016). On the other hand, single items are still too prevalent in PLS path models, which is particularly problematic when measuring endogenous target constructs. Researchers should generally refrain from using single items unless they measure observable characteristics, such as is commonly done in the form of control variables (e.g., income, sales, and number of employees).
To summarize, we observe a clear shift toward reflective measurement in PLS-SEM studies. The various controversies about formative measures' use (Howell et al., 2007; Rhemtulla et al., 2015; Wilcox et al., 2008) probably triggered this development, prompting researchers to “take the safe route” and rely on standard reflective measures. By following this mantra, researchers forego the opportunity to offer marketing practice differentiated recommendations. Contrary to their reflective counterparts, formative measures offer practitioners concrete guidance on how to “improve” certain target constructs—an important consideration in light of the growing concerns about marketing research's relevance for business practice (Homburg et al., 2015; Jaworski, 2011; Kohli & Haenlein, 2021; Kumar, 2017). At the same time, we see some improvement in the model specification practices, with researchers relying less on single-item measures. Nevertheless, the percentage of studies using single items is still high, providing an opportunity for improvement.
3.4 Model evaluation
Since Hair et al.'s (2012) review, research has proposed various improvements in the model evaluation metrics for both measurement and structural models. In the following, we assess whether researchers consider best practices, while acknowledging that some of these improvements have only recently been introduced. We distinguish between reflective and formative measurement models, since their validation—as extensively documented in the literature—relies on totally different sets of criteria (Hair et al., 2021a, 2022; Ramayah et al., 2018; Wong, 2019).
3.4.1 Reflective measurement models
A total of 479 of the 486 models (98.56%) included at least one reflectively measured construct (Table 5). Of these 479 models, 390 models (81.42%) reported the indicator loadings and 386 models (80.59%) reported at least one measure of the internal consistency reliability (Table 6). The majority of the models reported composite reliability ρC in conjunction with Cronbach's alpha (190 models, 39.67%). Composite reliability ρC was the only reliability metric reported in 132 models (27.56%), and Cronbach's alpha was the only reliability metric in 49 of the 479 models (10.23%). While these reporting practices reflect previous recommendations in the literature (Hair et al., 2017a), more recent guidelines call for using ρA (Dijkstra & Henseler, 2015) as an additional appropriate measure of internal consistency reliability. However, only 15 models rely on this criterion, either exclusively (3 models; 0.63%) or in conjunction with one or more other metrics (12 models, 2.51%). Compared to the previous period, a larger percentage of researchers consider both the indicator reliability and internal consistency reliability (Table 6). The internal consistency reliability assessment more frequently relies on Cronbach's alpha, whose use in the PLS-SEM context is criticized due to the metric assuming a common factor model (Rönkkö et al., 2021). When used in composite models, however, Cronbach's alpha underestimates internal consistency reliability, making it a conservative reliability measure. Consequently, when Cronbach's alpha does not raise concerns in a PLS-SEM analysis, the construct measurement can a fortiori be expected to exhibit sufficient levels of internal consistency reliability.
| Panel A: Reflective measurement models | |||||
|---|---|---|---|---|---|
| 1981–2010 | 2011–2020 | ||||
| Empirical test criterion in PLS-SEM | Number of models reporting (n = 254) | Proportion reporting (%) | Number of models reporting (n = 479) | Proportion reporting (%) | |
| Indicator reliability | Indicator loadingsa | 157 | 61.81 | 390 | 81.42 |
| Internal consistency reliability | Only Cronbach's alpha | 35 | 13.78 | 49 | 10.23 |
| Only ρc | 73 | 28.74 | 132 | 27.56 | |
| Only ρA | – | – | 3 | 0.63 | |
| Cronbach's alpha & ρc | 69 | 27.17 | 190 | 39.67 | |
| Cronbach's alpha & ρA | – | – | 1 | 0.21 | |
| ρc & ρA | – | – | 2 | 0.42 | |
| All three | – | – | 9 | 1.88 | |
| Convergent validity | AVE | 146 | 57.48 | 371 | 77.45 |
| Other | 7 | 2.76 | 16 | 3.34 | |
| Discriminant validityb | Only Fornell-Larcker (FL) criterion | 111 | 43.70 | 176 | 36.74 |
| Only cross-loadings | 12 | 4.72 | 8 | 1.67 | |
| Only HTMT | – | – | 25 | 5.22 | |
| FL criterion & cross-loadings | 31 | 12.20 | 81 | 16.91 | |
| FL criterion & HTMT | – | – | 38 | 7.93 | |
| Cross-loadings & HTMT | – | – | 3 | 0.63 | |
| All three | – | – | 12 | 2.51 | |
| Panel B: Formative measurement models | |||||
|---|---|---|---|---|---|
| 1981–2010 | 2011–2020 | ||||
| Empirical test criterion in PLS-SEM | Number of models reporting (n = 143) | Proportion reporting (%) | Number of models reporting (n = 112) | Proportion reporting (%) | |
| Reflective criteria used to evaluate formative constructs | 33 | 23.08 | 10 | 8.93 | |
| Collinearity | Only VIF/tolerance | 17 | 11.89 | 43 | 38.39 |
| Only condition index | 1 | 0.70 | 1 | 0.89 | |
| Both | 4 | 2.80 | 9 | 8.04 | |
| Convergent validity | Redundancy analysis | – | – | 6 | 5.36 |
| Indicator's relative contribution to the construct | Indicator weights | 33 | 23.08 | 74 | 66.07 |
| Significance of weights | Standard errors, significance levels, t values/p values | 25 | 17.48 | 36 | 32.14 |
| Only confidence intervals | – | – | 0 | 0.00 | |
| Both | – | – | 2 | 1.79 | |
- Abbreviation: PLS-SEM, partial least squares structural equation modeling.
- a Single item constructs were excluded in 1981–2010 and 2011–2020.
- b Proportion reporting (%) for 2011–2020 uses all 479 models as the base even though the HTMT criterion has only been proposed in 2015.
Of the 479 models, 371 (77.45%) assessed the convergent validity correctly by using the average variance extracted. The remaining models either established convergent validity incorrectly by using criteria such as cross-loadings and composite reliability (16 models, 3.34%) or did not comment on this aspect of model evaluation (92 models, 19.21%).
Discriminant validity is arguably the most important aspect of validity assessment in reflective measurement models (Farrell, 2010), because it ensures each construct is empirically unique and captures a phenomenon that other constructs in the PLS path model do not represent (Franke & Sarstedt, 2019). Against this background, it is surprising that only 343 of the 479 models (71.61%) assessed their discriminant validity. The most frequently used metric is the well-known Fornell-Larcker criterion (Fornell & Larcker, 1981), either as a standalone metric (176 models, 36.74%), or in conjunction with other criteria (131 models, 27.35%). The second most used criterion is an analysis of the indicator cross-loadings, which 104 of the 479 models (21.71%) report. Recent research has shown, however, that both criteria are largely unsuitable on conceptual and empirical grounds to assess discriminant validity. Henseler et al. (2015) propose the heterotrait-monotrait (HTMT) ratio of correlations as an alternative metric to assess discriminant validity, and a series of follow-up studies have confirmed its robustness (Franke & Sarstedt, 2019; Radomir & Moisescu, 2020; Voorhees et al., 2016). We find that 78 models of the 326 (23.93%) models that have been published since the publication of Henseler et al. (2015) draw on this criterion, either exclusively (25 models, 7.67%) or jointly with at least one other criterion (53 models, 16.26%). Of the 78 models applying the HTMT, 47 (60.26%) compare its values with a fixed cutoff value, two models (2.56%) rely on inference testing based on bootstrapping confidence intervals, and 23 models (29.49%) apply both approaches.
While our findings demonstrate some improvements in the reflective measurement model assessment compared to the previous period, concerns about the discriminant validity assessment remain. Given methodological innovations' diffusion latency in applied research, the strong reliance on the Fornell-Larcker criterion and cross-loadings seems understandable. However, future studies should only draw on the HTMT criterion and use bootstrapping to assess whether its values deviate significantly from a predetermined threshold. This threshold depends, however, on the conceptual similarity of the constructs under consideration. For example, a higher HTMT threshold, such as 0.9, can be assumed for conceptually similar constructs, whereas the analysis of conceptually distinct constructs should rely on a lower threshold, such as 0.85 (Franke & Sarstedt, 2019; Hair et al., 2022). Roemer et al. (2021) recently proposed the HTMT2, which relaxes the original criterion's assumption of equal population indicator loadings. Their simulation study shows that the HTMT2 produces a marginally smaller bias in the construct correlation estimates when the indicator loading patterns are very heterogeneous; that is, when some loadings are 0.55 or lower while others are close to 1. The small differences between the values of HTMT and HTMT2 are, however, extremely unlikely to translate into different conclusions when using the criterion for inference-based discriminant validity testing—as recommended in the extant literature (Franke & Sarstedt, 2019). For common loading patterns, where loadings vary between 0.6 and 0.8, the regular HTMT actually performs better than the HTMT2, unless one assumes extremely high construct correlations that would violate discriminant validity, regardless which criterion is being used. Hence, while the notion of an “improved criterion for assessing discriminant validity” appears appealing, the HTMT2 does not offer any improvement over the original metric.
3.4.2 Formative measurement models
The assessment of formative measurement models draws on different criteria than those used in the context of reflective measurement due to the conceptual differences between the two approaches. Specifically, while reflective measurement treats the indicators as error-prone manifestations of the underlying construct, formative measurement assumes that indicators represent different aspects of a construct that jointly define its meaning (Diamantopoulos et al., 2008).
Overall, 112 of the 486 models (23.05%) include at least one formatively measured construct (Table 5). In 10 of these 112 models (8.93%), the researchers use reflective measurement model criteria to evaluate formative measures (Table 6). This practice is very problematic, however, because formatively measured constructs' indicators do not necessarily correlate highly, which renders standard convergent and internal consistency reliability metrics meaningless (Diamantopoulos & Winklhofer, 2001)—even though corresponding metrics may occasionally reach satisfactory values, since strong indicator correlations may also occur in formative measurement models (Nitzl & Chin, 2017). Instead, researchers need to (1) run a redundancy analysis to assess the formative construct's convergent validity, (2) ensure the formative measurement model is not subject to collinearity, and (3) evaluate the formative indicator weights. Table 6 shows the results of this aspect of our review.
In only 6 of the 112 models (5.36%) with formative measures, the authors reported the results of a redundancy analysis. This analysis establishes a formative measure's convergent validity by showing that it correlates highly with a reflective multi-item or single-item measure of the same concept (Cheah et al., 2018). Chin (1998) introduced the redundancy analysis in a PLS-SEM context more than 20 years ago, but extant guidelines only adopted this method more recently (Hair et al., 2022; Ramayah et al., 2018), which could explain its limited use.
Conversely, collinearity assessment is much more prevalent in formative measurement model evaluation, with about half of the models (53 models, 47.32%) assessed in this regard. The variance inflation factor is the primary criterion for collinearity assessment and applied in most studies (Table 6).
Formative measurement model assessment's main focus is interpreting the indicator weights, which represent each indicator's relative contribution to forming the construct's (Cenfetelli & Bassellier, 2009). Slightly less than two-thirds of the models in our review (74 models, 66.07%) report the formative indicator weights, and researchers also assess the indicators' statistical significance in 44 of the 74 models (59.46%). In six of these 44 models (13.63%), researchers only comment on the weights' significance, whereas they report inference statistics in 38 models (86.26%). A detailed analysis shows that 21 of the 44 models (47.73%) include nonsignificant weights. Rather than deleting corresponding indicators, extant guidelines suggest analyzing the formative indicators' loadings, which represent their absolute contribution to the construct (Hair et al., 2019b, 2022). Only five of the 21 models (23.81%) follow this recommendation.
Overall, our results regarding formative measurement model evaluation are encouraging, as they suggest researchers have become more concerned about applying criteria dedicated to this measurement mode. In comparison, in the previous period, less than one-third of all models analyzed the formative indicator weights and far fewer tested for potential collinearity issues. Nevertheless, in absolute terms our results offer room for improvement. There is virtually no redundancy analysis in PLS-SEM research, which is problematic, since it offers an empirical validation that the formative measure is similar to established measures of the same concept. In addition, many of the models still do not report collinearity statistics. This finding is surprising, since collinearity assessment has long been acknowledged as an integral element of formative measurement model assessment (Cenfetelli & Bassellier, 2009; Diamantopoulos & Winklhofer, 2001; Petter et al., 2007). Researchers should consider these aspects carefully before focusing on indicator weight assessment.
3.4.3 Structural model
Once the measures' reliability and validity have been established, the next step is to assess the structural model's explanatory and predictive power, as well as the path coefficients' significance and relevance (Hair et al., 2020b). Table 7 documents our review's corresponding results.
| 1981–2010 | 2011–2020 | ||||
|---|---|---|---|---|---|
| Criterion | Empirical test criterion in PLS-SEM | Number of models reporting (n = 311) | Proportion reporting (%) | Number of models reporting (n = 486) | Proportion reporting (%) |
| Path coefficients | Values | 298 | 95.82 | 480 | 98.77 |
| Significance of path coefficients | Standard errors, significance levels, t values/p values | 287 | 92.28 | 419 | 86.21 |
| Confidence intervals | 0 | 0.00 | 11 | 2.26 | |
| Both | 0 | 0.00 | 43 | 8.85 | |
| Effect size | f2 | 16 | 5.14 | 86 | 17.70 |
| Explanatory power | R2 | 275 | 88.42 | 430 | 88.48 |
| Predictive power | PLSpredicta | – | – | 23 | 4.73 |
| Predictive relevance (blindfolding) | Q2 | 51 | 16.40 | 162 | 33.33 |
| q2 | 0 | 0.00 | 15 | 3.09 | |
| Model fit | GoF | 16 | 5.14 | 60 | 12.35 |
| SRMR | – | – | 40 | 8.23 | |
| dULS | – | – | 1 | 0.21 | |
| dG | – | – | 1 | 0.21 | |
| RMStheta | – | – | 1 | 0.21 | |
| 1981–2010 | 2011–2020 | ||||
|---|---|---|---|---|---|
| Criterion | Empirical test criterion in PLS-SEM | Number of studies reporting (n = 204) | Proportion reporting (%) | Number of studies reporting (n = 239) | Proportion reporting (%) |
| Observed heterogeneity | Categorical moderator | 47 | 23.04 | 57 | 23.85 |
| Continuous moderator | 15 | 7.35 | 58 | 24.27 | |
| Unobserved heterogeneity | Latent class techniques (e.g., FIMIX-PLS) | 0 | 0.00 | 10 | 4.18 |
- a Proportion reporting (%) for 2011–2020 uses all 486 models as the base even though PLSpredict has only been proposed in 2016.
In a first step, researchers need to ensure that potential collinearity between sets of predictor constructs in the model does not negatively impact the structural model estimates. Our review results show that marketing researchers generally omit this step, as only 100 of the 486 models (20.58%) mention inspecting collinearity in the structural model.
Not surprisingly, almost all the models (480 models, 98.77%) report path coefficients and their significance (473 models, 97.33%). Inference testing relies primarily on t tests with standard errors derived from bootstrapping (419 models, 86.12%). In keeping with recommendations in the more recent literature (Streukens & Leroi-Werelds, 2016), 54 models (11.11%) report bootstrapping confidence intervals either alone (11 models, 2.26%) or together with t values (43 models, 8.85%). Aguierre-Urreta and Rönkkö's (2018) simulation study suggests that researchers should primarily draw on percentile confidence intervals or, alternatively, on bias-corrected and accelerated confidence intervals. Both approaches perform very similarly, but the bias-corrected confidence intervals achieve slightly better results when the bootstrap distributions are highly skewed. Researchers seem to have internalized these recommendations, since 39 of 54 models (72.22%) rely on the percentile method, while 15 models (27.78%) apply the bias-corrected and accelerated confidence intervals. Supplementing the path coefficient reporting, 86 of 486 models (17.70%) also express the structural model effects in terms of the f2 effect size, which provides evidence of an exogenous construct's relative impact on an endogenous construct in terms of R2 changes. While earlier guidelines called for the routine reporting of the f2 (Chin, 1998), more recent research emphasizes that this statistic is redundant in terms of path coefficients, and concluding that reporting it should be optional (Hair et al., 2022).
The majority of the models report the R2 (430 models, 88.48%) to support the structural model's quality, which is almost identical to what occurred in the previous period (88.42%). During our review, we noticed that some authors view the R2 as a measure of their models' predictive power. However, the R2's computation draws on the entire dataset and, as such, indicates a model's explanatory power (Shmueli, 2010). Assessing the PLS path model's predictive power requires estimating the parameters by means of a subset of observations, and using these estimates to predict the omitted observations' case values (Sarstedt & Danks, 2021; Shmueli & Koppius, 2011). Our review shows that only 11 of the 239 studies (4.60%) use holdout samples to validate their results, possibly because research has only recently offered clear guidelines on how to run a holdout sample validation in a PLS-SEM context (Cepeda Carrión et al., 2016). Alternatively, researchers could draw on Shmueli et al.'s (2016) PLSpredict procedure, which implements k-fold cross-validation to generate case-level predictions on an indicator level. The procedure partitions the data into k subsets and uses k-1 subsets to predict the indicator values of a specific target constructs in the remaining data subset (i.e., the holdout sample). This process is repeated k times such that each subset once serves as a holdout sample.
PLSpredict is a relatively new procedure and research has only recently offered guidelines for its use (Shmueli et al., 2019). It is therefore not surprising that only 23 of the 295 models (7.80%) that have been published after Shmueli et al.'s (2016) introduction of PLSpredict apply the procedure. Instead, many researchers (162 of the 486 models, 33.33%) rely on the blindfolding-based Q2 statistic, which scholars had long considered a suitable means of assessing predictive power (Sarstedt et al., 2014)—a far greater percentage than in the previous period, when only 16.40% of all models included this assessment. However, recent research casts doubt on this interpretation, noting that this statistic confuses explanatory and predictive power assessment (Shmueli et al., 2016). We, therefore, advise against its use and that of the q2, which is a Q2-based equivalent of the f2 effect size that 15 of the 486 models (3.09%) report.
A controversial and repeatedly raised issue in research is whether model fit—as understood in a factor-based SEM context—is a meaningful evaluation dimension in PLS path models. While some researchers strongly advocate the use of model fit metrics (e.g., Schuberth & Henseler, 2021; Schuberth et al., 2018a), others point to the available metrics' conceptual deficiencies and question their performance in the context of PLS-SEM (e.g., Hair et al., 2019c; Hair et al., 2022; Lohmöller, 1989). Our review shows that model fit assessment does not feature prominently in recent PLS-SEM applications as researchers report model fit metrics for only 103 of the 486 models (21.19%). Most researchers rely on Tenenhaus et al. (2004) GoF metric (60 models, 12.35%), which Henseler and Sarstedt (2013) debunked as ineffective for separating well-fitting models from misspecified ones. Some researchers (additionally) report SRMR (40 models, 8.23%), relying on thresholds proposed by Henseler et al. (2014). The reporting of distance-based measures dULS and dG as well as the RMStheta is practically nonexistent in PLS-SEM research (1 model each, 0.21%). Scholars have conceptually discussed (Schuberth & Henseler, 2021) and empirically tested (Schuberth et al., 2018a) the SRMR, which lend this metric some authority. However, given SRMR's performance in research settings commonly encountered in applied research, Hair et al. (2022, Chap. 6) comment critically on its practical utility. Specifically, in PLS path models with three constructs, the SRMR requires sample sizes of approximately 500 to detect misspecifications reliably. Our review shows that the vast majority of PLS path models are far more complex (Table 5) and rely on much smaller sample sizes, therefore supporting the raised concerns. The same holds for the bootstrap-based test for exact model fit, whose use recent research advocates (Benitez et al., 2020; Henseler et al., 2016a; Schuberth & Henseler, 2021), but which none of the studies in our review applies.
To summarize, we observe some improvements in PLS-SEM-based structural model assessment, with more researchers seeming to be concerned about predictive power evaluations. In this respect, researchers have made increasing use of the Q2 statistic, which is, however, not a reliable indicator of a model's predictive power. The latter practice is not surprising, since concerns regarding Q2's suitability have only been raised in rather recent research (e.g., Shmueli et al., 2016). Researchers should therefore follow the most recent recommendations and apply k-fold cross-validation by using PLSpredict or drawing on holdout samples. Researchers should also be aware of the controversies surrounding the efficacy of extant model fit metrics in PLS-SEM, and carefully check whether their model and data constellations favor their use. Judging by Schuberth et al.'s (2018a) findings, the SRMR and exact fit test will exhibit very weak performance on the average model identified in our review with seven constructs and 280 observations.
3.5 Advanced modeling and analysis techniques
With the PLS-SEM field's increasing maturation (Hwang et al., 2020; Khan et al., 2019), researchers can draw on a greater repertoire of advanced modeling and analysis techniques to support their conclusions' validity and to identify more complex relationships patterns (Hair et al., 2020a).
For example, many researchers use PLS-SEM because of its ability to accommodate higher-order constructs without identification concerns. Analyzing the prevalence and application of higher-order constructs, we find that 71 of the 239 studies (29.71%) included at least one such construct. The majority of these studies considered second-order constructs (65 studies), while the remaining studies included third-order constructs (5 studies) or both (1 study). Analyzing the measurement model specification of the second-order constructs (Wetzels et al., 2009), we find that most of the studies employ Type I (reflective-reflective; 30 studies), Type II (reflective-formative; 26 studies), or both (4 studies). Only five studies employ Type IV (formative-formative), while no study draws on a Type III (formative-reflective) measurement specification. Analyzing the specification, estimation, and evaluation of the higher-order constructs in greater detail, gives rise to concern in two respects. First, 47 of the studies that employed higher-order constructs do not make the specification and estimation transparent.2 Those that do, either draw on the repeated indicators approach (15 studies) or the two-stage approach (9 studies). This practice is problematic as endogenous Type II and IV higher-order constructs cannot be reliably estimated using the standard repeated indicators approach (Becker et al., 2012). Second and more importantly, only eight studies correctly evaluate the higher-order constructs using criteria documented in the extant literature (e.g., Sarstedt et al., 2019). The majority of the 71 studies do not evaluate the higher-order constructs at all (30 studies) or incompletely apply the relevant criteria (21 studies), typically disregarding discriminant validity assessment in reflective (i.e., Type I) and the redundancy analysis in formative higher-order constructs (i.e., Types II and IV). Finally, 12 studies misapply the evaluation criteria by erroneously interpreting the relationships between lower- and higher-order components as structural model relationships. Overall, our findings suggest that researchers need to provide much more care in their handling of higher-order constructs by considering the most recent guidelines (Sarstedt et al., 2019).
The identification and treatment of observed and unobserved heterogeneity is another aspect that has attracted considerable attention in methodological research (Memon et al., 2019; Rigdon et al., 2010; Sarstedt et al., 2022). Our review shows that researchers' use of PLS-SEM also mirrors this development. A total of 115 studies (48.12%) in our review took observed heterogeneity into account by either considering continuous (58 studies 24.27%) or categorical (57 studies 23.85%) moderating variables. The strong increase in the percentage of studies using continuous moderating variables compared to the previous period, when only 7.35% undertook corresponding moderation analyses, demonstrates the growing interest in more complex model constellations. Although a total of 57 studies investigated the categorical moderators' impact by means of multigroup analysis (Sarstedt et al., 2011), only 12 address the issue of measurement invariance by using the MICOM procedure (Henseler et al., 2016b). This practice is problematic as establishing measurement invariance is a requirement for any multigroup analysis. By establishing (partial) measurement invariance, researchers are assured that the group differences in the model estimates are not the result of, for example, group-specific response styles (Hult et al., 2008).
While the consideration of moderators facilitates the identification and treatment of observed heterogeneity, group-specific effects can also result from unobserved heterogeneity. Since failure to consider such unobserved heterogeneity can be a severe threat to PLS-SEM results' validity (Becker et al., 2013), researchers call for the routine use of latent class procedures. Recent guidelines recommend the tandem use of finite mixture PLS (FIMIX-PLS; Hahn et al., 2002) and more powerful latent class techniques, such as PLS prediction-oriented segmentation (PLS-POS; Becker et al., 2013), PLS genetic algorithm segmentation (PLS-GAS; Ringle et al., 2014), and PLS iterative reweighted regressions segmentation (PLS-IRRS; Schlittgen et al., 2016). While FIMIX-PLS allows researchers to reliably determine the segments to extract from data (Sarstedt et al., 2011), techniques such as PLS-POS reproduce the actual segment structure more effectively. Recent research calls for the routine application of latent class techniques to ensure that heterogeneity does not impact the aggregate level results adversely (Sarstedt et al., 2020b). Despite these calls, only 10 of the 239 studies in our review (4.18%) conduct a latent class analysis. All these studies apply FIMIX-PLS, which, while detecting heterogeneity issues well, clearly lags behind in terms of treating the heterogeneity.
Researchers have long noted the need to explore alternative explanations for the phenomena under investigation by considering different model configurations. Such explanations will allow researchers to compare the emerging models by using well-known regression literature metrics (Burnham & Anderson, 2002) to select the best-fitting model in the set. Only 10 of our review studies (4.18%) compare alternative models by using the same data set. By disregarding alternative theoretically plausible model configurations, researchers could fall prey to confirmation biases, since they only look for configurations that support “their” model (Nuzzo, 2015), and miss out on opportunities to fully understand the mechanisms at work (Sharma et al., 2019). Further, very few studies compare multiple models by drawing on a large set of criteria, therefore, applying between one and nine different criteria. However, none of the studies applies the Bayesian Information Criterion (Schwarz, 1978) or the Geweke and Meese (1981) criterion, which prior research identified as superior in PLS-SEM-based model comparisons (Danks et al., 2020; Sharma et al., 2019; Sharma et al., 2021c). With further recent developments in these directions (e.g., based on the cross-validated predictive ability test, CVPAT), we expect the popularity and relevance of the predictive model assessment (Sharma et al., 2021a) and model comparison (Liengaard et al., 2021) to increase.
While our review results point to some progress in terms of applying advanced analysis techniques, there is still ample room for improvement. First, researchers need pay greater attention to the specification, estimation and particularly the validation of higher-order constructs. Second, measurement invariance assessment should precede any multigroup analysis (Henseler et al., 2016b), since failure to establish at least partial measurement invariance renders any multigroup analysis meaningless. Third, researchers should routinely apply latent class analyses to check their aggregate level results' robustness. Failure to do so may result in misleading interpretations when unobserved heterogeneity affects the model estimates. Finally, researchers should more often compare theoretically plausible alternatives to the model under consideration. Considering alternative explanations is a crucial step before making any attempt to falsify a theory (Popper, 1959).
3.6 Reporting
Hair et al.'s (2012) review emphasized that the algorithm settings used in the analysis needed to be transparent to facilitate its replicability. Our review shows some improvements compared to the previous period, most notably with regard to documenting the software used for the analysis. Whereas less than half of all the studies in the previous period report the software (49.02%), the percentage is much higher in recent PLS-SEM research (193 studies, 80.75%). Most PLS-SEM studies (166 studies, 69.46%) apply SmartPLS, with PLS-Graph following far behind (18 studies, 7.53%). Other rarely used software programs include XLSTAT (4 studies, 1.67%), WarpPLS (3 studies, 1.26%) and ADANCO (2 studies, 0.84%). In addition, two studies (0.82%) use the plspm package of the R software.
Only five studies (2.09%) mention the parameter or algorithm settings, seven studies (2.93%) the computational options (e.g., weighting schemes), and 12 studies (5.02%) the maximum number of iterations. Although making these algorithm settings transparent is certainly useful, different algorithm settings do not normally induce significant deviations in the estimation results. This, however, differs in bootstrapping settings; Rönkkö et al. (2015), for example, show that the use of sign change options can trigger considerable Type I errors, whereas Streukens and Leroi-Werelds (2016) emphasize the need to draw many bootstrap samples (i.e., at least 10,000) from the original data. In this regard, it is encouraging that 175 studies (73.22%) mention the use of bootstrapping, 141 of which provided additional details of the algorithmic settings, such as the number of bootstrap samples used. None of the studies use jackknifing as an alternative means of deriving standard errors, which is likely due to this method only being implemented in the early PLS-Graph software that only a few researchers still use.
Research has produced various variants of the original PLS-SEM algorithm (Becker & Ismail, 2016). One prominent research stream deals with the original PLS-SEM's extensions, to estimate common factor models. While researchers have introduced various such extensions (Bentler & Huang, 2014; Kock, 2019), consistent PLS-SEM (PLSc-SEM) has become the primary technique in this stream (Dijkstra & Henseler, 2015). The use of PLSc-SEM has triggered discussions with certain researchers, who call for its routine application (Benitez et al., 2020; Evermann & Rönkkö, 2021; Henseler et al., 2016a), while others conclude the method “adds very little to existing knowledge of SEM” (Hair et al., 2019c, p. 570). PLS-SEM users seem to share this skepticism as only five studies (2.09%) apply PLSc-SEM.
Finally, we see no increase in the share of studies reporting indicator covariance or correlation matrices. This practice is problematic, because it hinders the results' replicability and checking whether model evaluation metrics, such as the HTMT, are adequate. On the contrary, studies routinely report construct-level correlation matrices (180 studies, 75.31%), largely due to their relevance for Fornell-Larcker-based discriminant validity assessment.
To summarize, reporting practices regarding the software and algorithm settings used have improved since Hair et al.'s (2012) review. Nevertheless, more studies need to make the software and, particularly, the bootstrap settings transparent. Furthermore, SmartPLS (Ringle et al., 2015) is currently the most widely applied software, likely due to its user friendliness (Sarstedt & Cheah, 2019), features, and functionalities (Memon et al., 2021). However, with new software packages, such as cSEM (Rademaker & Schuberth, 2021) and SEMinR (Ray et al., 2021), as well as the detailed documentation on them (Hair et al., 2021a; Henseler, 2021), we expect the use of R packages to gain traction. Finally, in light of the growing concerns about social science research's replicability (Rigdon et al., 2020), reporting indicator and construct-level correlation matrices should become mandatory.
4 CONCLUSION
The substantial increase in the number of articles applying PLS-SEM during the last decade shows that PLS-SEM has become an essential element in marketing researchers' methodological toolbox. Our review covers 239 articles published in the top 30 marketing journals between 2011 and 2020—a significant increase compared to those in Hair et al.'s (2012) study, which covered 204 articles published in the same journals between 1981 and 2010.
We find that researchers are currently more aware of the stumbling blocks of PLS-SEM use. Recent research uses PLS-SEM to estimate models with similar average complexity as in the previous period, but drawing on larger datasets, which favors the analyses' statistical power. Our results also suggest that researchers have become more aware of single-item measures' limitations (Diamantopoulos et al., 2012) and of more complex modeling options, like higher-order constructs (Sarstedt et al., 2019) and moderation (Memon et al., 2019). Similarly, researchers have started accommodating recently introduced model evaluation metrics, like the ρA, to assess internal consistency reliability (Dijkstra & Henseler, 2015), the HTMT to assess discriminant validity (Henseler et al., 2015), and Shmueli et al.'s (2016) PLSpredict procedure to evaluate a model's predictive power.
At the same time, we also observe a certain degree of latency in other areas of PLS-SEM use. For example, researchers still rely strongly on the Fornell-Larcker criterion (Fornell & Larcker, 1981) and on cross-loadings to assess discriminant validity; they also hardly use a redundancy analysis to establish formative measures' convergent validity. The use of more advanced analyses, such as latent class techniques, is still lacking in applied PLS-SEM research despite persistent calls for their routine use to ensure the results' validity (Becker et al., 2013; Sarstedt & Danks, 2021a; Sarstedt et al., 2017, 2022). Reporting practices in terms of, for example, the software used and the bootstrapping algorithm settings, are still inadequate. The latency with which methodological innovations diffuse in applied research might explain some of these findings, but certainly not all of them. Researchers, reviewers, and editors should pay greater attention to current developments and the latest best practices in PLS-SEM use (e.g., Hair et al., 2022). Table 8 summarizes these best practices in keeping with the aspects covered in our review and serves as a checklist for future applications of PLS-SEM. We also offer common rules of thumb, which offer initial guidance for estimating and assessing models, and provide supporting references for further reading. Figure 2 visualizes the specific aspects that researchers need to consider in their application of PLS-SEM, focusing on the illustration of the model evaluation and all relevant metrics.
| Aspect | Recommendation/rules of thumb | Suggested references |
|---|---|---|
| General | ||
| Motivate the use of PLS-EM | Motivating the use of PLS-SEM on the grounds of “small sample size” should be done with caution, as small samples affect the method adversely. Do not motivate PLS-SEM use on the grounds of nonnormal data alone. | Hair et al. (2019b); Rigdon (2016) |
| Emphasize the causal-predictive nature of the analysis, model complexity, the estimation of conditional process models, and the use of formative measures. | Hair et al. (2019b); Sarstedt et al. (2020a); Sarstedt et al. (2016) | |
| Data characteristics | ||
| Sample size | Run power analyses to determine the required sample size prior to the analysis or, alternatively, apply the inverse square root method. The ten times rule offers only very rough guidance regarding the minimum sample size requirements and should not be used as a justification. | Aguirre-Urreta and Rönkkö (2015); Kock and Hadaya (2018) |
| Missing values | Report missing values and the use of imputation procedures. | Hair et al. (2022) |
| Outliers | Detect outliers using univariate or multivariate methods. Delete outliers if necessary or treat them as a separate segment. | Sarstedt and Mooi (2019) |
| Use of discrete variables | Discrete variables may be used as grouping variables in multigroup analyses or be included as dummy variables. PLS-SEM can process discrete choice modeling data. | Hair et al. (2019a); Hair et al. (2019b) |
| Model characteristics | ||
| Model type | Specify funnel-like models where the number of predictor constructs in the model's partial regressions are larger than the endogenous constructs. Avoid chain-like models. Use CB-SEM for unfocused models. | Hair et al. (2012); Hair et al. (2021b) |
| Description of the measurement models | Provide a detailed list of indicators in the appendix; distinguish between reflective and formative measurement. | Hair et al. (2022) |
| Single items | Generally, refrain from using single items unless measuring observable characteristics, which is commonly done in the form of control variables (e.g., income, sales, number of employees, etc.). | Cheah et al. (2018); Diamantopoulos et al. (2012) |
| Measurement model evaluation: reflective | ||
| Internal consistency reliability Cronbach's alpha, composite reliability ρc and ρA | Consider Cronbach's alpha as the lower and ρC as the upper boundary of internal consistency reliability. ρA should be considered the best point estimate of internal consistency reliability. | Dijkstra and Henseler (2015); Hair et al. (2022) |
| Thresholds of all reliability measures: 0.70-0.90 (0.60 in exploratory research, max. 0.95 to avoid indicator redundancy). | ||
| Convergent validity | Interpret the average variance extracted (AVE). | Sarstedt et al. (2021) |
| Threshold: | ||
| AVE ≥0.50 | ||
| Discriminant validity | Do not use the Fornell-Laker criterion or cross-loadings, but the HTMT. | Franke and Sarstedt (2019); Henseler et al. (2015) |
| Thresholds: | ||
| HTMT <0.90 for conceptually similar constructs | ||
| HTMT <0.85 for conceptually different constructs | ||
| In addition, test whether the HTMT is significantly lower than the threshold value. | ||
| Measurement model evaluation: formative | ||
| Convergent validity (redundancy analysis) | Use the redundancy analysis to assess the convergent validity; a global single- item or a reflectively measured multi-item scale can be used as an alternative measurement. The construct correlation should be ≥0.70 | Cheah et al. (2018); Chin (1998) |
| Collinearity | Use the variance inflation factor (VIF) to assess collinearity in all sets of formative indicators. | Hair et al. (2019b) |
| Thresholds: | ||
| VIF≤3: no collinearity issues | ||
| VIF 3–5: possible collinearity issues | ||
| VIF ≥5: critical collinearity issues | ||
| Indicator weights | Report the indicator weight estimates and information regarding their significance. | Aguirre-Urreta and Rönkkö (2018); Hair et al. (2022) |
| For inference testing, report the t values, p values with standard errors or, preferably, the bootstrapping confidence intervals. Use the percentile method to construct confidence intervals; use the bias-corrected and accelerated bootstrap method for highly asymmetric bootstrap distributions. | ||
| Consider the indicator loadings of nonsignificant weights. Indicators with nonsignificant and low loadings (<0.5) should be removed from the measurement model. | ||
| Structural model evaluation | ||
| Collinearity | Use the variance inflation factor (VIF) for the collinearity assessment of all sets of predictor constructs in the structural model. | |
| Thresholds: | ||
| VIF≤3: no collinearity issues | ||
| VIF 3–5: possible collinearity issues | ||
| VIF ≥5: critical collinearity issues | ||
| Path coefficients | Report the path coefficient estimates and information on their significance. | Aguirre-Urreta and Rönkkö (2018); Hair et al. (2022) |
| For inference testing, report t values, p values with standard errors or, preferably, the bootstrapping confidence intervals. Use the percentile method to construct confidence intervals; if the bootstrap distributions are highly asymmetric, use the bias-corrected and accelerated (BCa) bootstrap method. | ||
| Explanatory power | Report the R2, but do not consider the metric as indicative of predictive power. | Hair (2021); Hair et al. (2019b); Shmueli and Koppius (2011) |
| The R2 values depend on the model complexity and the phenomena under research. Note that very high R2 values such as 0.90 are usually indicative of model overfit when measuring theoretical concepts. | Hair et al. (2019b) | |
| Predictive power | Use PLSpredict to compare the predictions generated by the PLS path model with those of a naïve linear benchmark model. | Shmueli et al. (2016); Shmueli et al. (2019) |
| Model fit | Do not use the GoF index. Apply the SRMR or the bootstrap-based test for an exact model fit, but only if the model complexity and sample size support this step. | Hair et al. (2022); Schuberth and Henseler (2021); Schuberth et al. (2018b) |
| Advanced modeling and analysis techniques | ||
| Higher-order constructs | The specification, estimation, and evaluation of higher-order constructs require particular scrutiny. Follow the most recent guidelines. | Sarstedt et al. (2019) |
| Observed heterogeneity | Consider recent guidelines on moderator, multigroup, and conditional process model analyses. | Klesel et al. (2019); Memon et al. (2019); Sarstedt et al. (2020a) |
| Unobserved heterogeneity | Use latent class analyses as a robustness check to ascertain that unobserved heterogeneity does not adversely impact the aggregate level results. | Becker et al. (2013); Sarstedt et al. (2022); Sarstedt et al. (2020b), |
| Use finite mixture PLS in combination with more advanced latent class procedures, such as PLS prediction-oriented segmentation. | ||
| Measurement Invariance | Use the MICOM procedure to at least establish partial measurement invariance as a necessary condition for any multigroup analysis. | Henseler et al. (2016b) |
| Model comparisons | Consider different model configurations as representations of alternative explanations of the phenomena under consideration. | Liengaard et al. (2021); Sharma et al. (2019); Sharma et al. (2021b) |
| Use the Bayesian information criterion (BIC) to select the best model. | ||
| Consider using BIC-based Akaike weights to quantify each model's relative suitability. Alternatively use the cross-validated predictive ability test (CVPAT). | ||
| Reporting | ||
| Software | Mention the software applied and correctly cite its use, especially if required by the license agreement. | Hair et al. (2012) |
| Algorithm settings | Report, at least, the following bootstrapping settings: the number of bootstrap samples used (recommendation: 10,000) and the type of bootstrapping confidence interval. | |
| Do not use sign change options. | ||
| Correlation matrix | Report the indicator and construct correlation matrices. | Hair et al. (2012) |
- Abbreviation: PLS-SEM, partial least squares structural equation modeling.
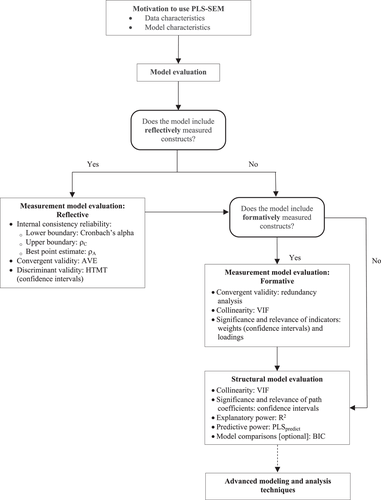
As evidenced by PLS-SEM's numerous extensions (e.g., Liengaard et al., 2021; Rasoolimanesh et al., 2021; Richter et al., 2020) and by controversial debates (Hair et al., 2021b; Rönkkö et al., 2021), research in the field is highly dynamic (Hwang et al., 2020; Khan et al., 2019). This rapid progress makes it difficult for researchers to keep up with the latest developments and to make up their minds regarding which research stream to follow. For example, our review points to some confusion in terms of model fit assessment. Some researchers seem to be tempted to report a model fit metric, which has become the sine qua non in factor-based SEM research, adopting the GoF index prematurely which, however, cannot separate correctly specified models from misspecified ones (Henseler & Sarstedt, 2013). Very few researchers apply metrics, like the SRMR, which have been tested in simulation studies (Schuberth et al., 2018a), but whose users seem to disregard their quite weak performance in typical model and data constellations. Future research should, therefore, develop better model fit metrics that detect model misspecifications reliably in standard data and model settings, which reflect those of the various customer satisfaction indices (e.g., Fornell et al., 2020) and technology acceptance models (e.g., Venkatesh et al., 2012).
Recent research also presents various developments that could soon play very important roles in the PLS-SEM field. Hwang and Cho (2020) recently addressed a criticism of the PLS-SEM algorithm by introducing a variant that draws on a single optimization criterion. This extension has the potential to solve various criticisms of the original PLS-SEM method in terms of its modeling options (e.g., introducing model constraints) and model fit assessment. Future studies should further explore this global PLS-SEM method's efficacy for applied research.
Researchers should also advance recently proposed methodological extensions, which we document in Table 9. For example, Richter et al. (2020) subject the PLS-SEM-produced construct scores to a necessary condition analysis (NCA). By following a necessity logic, NCA implies that an outcome—or a certain level of an outcome—can only be achieved if the necessary cause is in place, or is at a certain level (see also Rasoolimanesh et al., 2021). PLS-SEM-based construct scores have also been used in other contexts, such as in the identification and treatment of endogeneity (Hult et al., 2018). Other advances in PLS-SEM address nonlinear effects estimation (Basco et al., 2021) and ensuring the validity of results by uncovering unobserved heterogeneity (Becker et al., 2013; Sarstedt & Danks, 2021). Future research should build on these initial efforts to develop more comprehensive methods that consider the necessity logic and endogeneity before initially computing the construct scores. Such efforts would further enhance PLS-SEM's capabilities and lead to its even more accelerated use in the decade to come.
| Procedure | Description | Suggested references |
|---|---|---|
| Agent-based simulation | The combination with agent-based simulation (ABS) makes PLS-SEM results dynamic and extends their predictive range. The PLS-SEM agent uses a static path model and PLS-SEM results to determine the ABS settings at the agent level. Then, the dynamic ABS modeling method extends PLS-SEM's predictive capabilities from the individual level to the population level by modeling the diffusion process in a network (e.g., consumers). | Schubring et al. (2016) |
| Endogeneity | Methods for identifying and treating endogeneity, which occurs when a predictor construct is correlated with the error term of the dependent construct to which it is related. | Hult et al. (2018) |
| Fuzzy-set qualitative comparative analysis (fsQCA) and necessary condition analysis (NCA) and | In fsQCA, both the independent and dependent variables are calibrated into set membership scores in order to identify (calibrated) independent variables that are sufficient but not necessary for an outcome of the dependent variable. This approach has been transferred to PLS-SEM to analyze necessary conditions in the structural model. Different from the fsQCA, the NCA does not rely on binary necessity statements and therefore considers that an outcome or a certain level of an outcome can only be achieved if the necessary cause is in place or is at a certain level. | Leischnig et al. (2016), Rasoolimanesh et al. (2021), Richter et al. (2020) |
| Importance-performance map analysis | Allows researchers to gain more insights from the PLS-SEM analysis by contrasting constructs' total effects with their (rescaled) average scores. | Ringle and Sarstedt (2016) |
| Latent class analysis techniques to identify segments with distinct construct scores | Partial least squares k-means facilitates identifying groups of data that maximize score differences while at the same time accounting for structural and measurement model heterogeneity. | Fordellone and Vichi (2020) |
| Latent class techniques to identify segments with distinct model relations | Response-based segmentation techniques that identify distinct segments that differ in terms of structural or measurement model relations (e.g., FIMIX-PLS, PLS-IRRS, PLS-POS). | Becker et al. (2013), Sarstedt et al. (2021a), Schlittgen et al. (2016) |
| Model comparisons | Empirically compare a set of theoretically plausible models. | Danks et al. (2020), Liengaard et al. (2021), Sharma et al. (2019) |
| Moderated mediation and conditional process analysis | This approach combines the moderator analysis and mediator analysis into a moderated mediation and conditional process analysis in PLS-SEM. | Cheah et al. (2021), Sarstedt et al. (2020a; 2020b) |
| Nonlinear effects estimation | PLS-SEM assumes linear relationships. In some instances, however, this assumption does not hold in that relationships may be nonlinear and require nonlinear estimations of coefficients in PLS-SEM. | Basco et al. (2021), Sarstedt et al. ( 2020b) |
| Weighted PLS-SEM (WPLS) | The WPLS algorithm is a modified version of the original PLS-SEM algorithm that incorporates sampling weights. | Becker and Ismail (2016), Cheah et al. (2021) |
- Abbreviation: PLS-SEM, partial least squares structural equation modeling.
5 ACKNOWLEDGMENT
Open Access funding enabled and organized by Projekt DEAL.
CONFLICT OF INTERESTS
The authors declare that there are no conflict of interests.
Open Research
DATA AVAILABILITY STATEMENT
The data that support the findings of this study are available from the corresponding author upon reasonable request.
REFERENCES
- 1 Note that this distinction refers to the measurement-theoretic perspective. To estimate formative measurement models, PLS-SEM uses composite indicators that define the construct in full. The method does not allow for estimating a formative construct's error term using causal indicators (Cho et al., 2021; Sarstedt et al., 2016).
- 2 In most cases, the descriptions suggest that the authors averaged the items of the lower-order components to generate indicators of the higher-order construct. This practice is, however, problematic as it ignores the biasing effect of measurement error that PLS-SEM's differential indicator weighting accounts for.




