Macromolecular Bioscience
Volume 23, Issue 5 2200563
Research Article
Open Access

Chain Sliding versus β-Sheet Formation upon Shearing Single α-Helical Coiled Coils

Anna-Maria Tsirigoni, 

Anna-Maria Tsirigoni

Max Planck Institute of Colloids and Interfaces, Mechano(bio)chemistry, Am Mühlenberg 1, 14476 Potsdam, Germany

Max Planck Institute of Colloids and Interfaces, Department of Biomaterials, Am Mühlenberg 1, 14476 Potsdam, Germany

Search for more papers by this author
Melis Goktas, 

Melis Goktas

Max Planck Institute of Colloids and Interfaces, Mechano(bio)chemistry, Am Mühlenberg 1, 14476 Potsdam, Germany

Search for more papers by this author
Zeynep Atris, 

Zeynep Atris

Max Planck Institute of Colloids and Interfaces, Mechano(bio)chemistry, Am Mühlenberg 1, 14476 Potsdam, Germany

Max Planck Institute of Colloids and Interfaces, Department of Biomaterials, Am Mühlenberg 1, 14476 Potsdam, Germany

Search for more papers by this author
Angelo Valleriani, 

Angelo Valleriani

Max Planck Institute of Colloids and Interfaces, Department of Biomaterials, Am Mühlenberg 1, 14476 Potsdam, Germany

Search for more papers by this author
Ana Vila Verde, 

Corresponding Author

Ana Vila Verde

University of Duisburg-Essen, Faculty of Physics, Lotharstrasse 1, 47057 Duisburg, Germany

E-mail: [email protected]; [email protected]

Search for more papers by this author
Kerstin G. Blank, 

Corresponding Author

Kerstin G. Blank

Max Planck Institute of Colloids and Interfaces, Mechano(bio)chemistry, Am Mühlenberg 1, 14476 Potsdam, Germany

Johannes Kepler University Linz, Institute of Experimental Physics, Department of Biomolecular & Selforganizing Matter, Altenberger Strasse 69, Linz, 4040 Austria

E-mail: [email protected]; [email protected]

Search for more papers by this author
First published: 01 March 2023
https://doi.org/10.1002/mabi.202200563

Abstract

Coiled coils (CCs) are key building blocks of biogenic materials and determine their mechanical response to large deformations. Of particular interest is the observation that CC-based materials display a force-induced transition from α-helices to mechanically stronger β-sheets (αβT). Steered molecular dynamics simulations predict that this αβT requires a minimum, pulling speed-dependent CC length. Here, de novo designed CCs with a length between four to seven heptads are utilized to probe if the transition found in natural CCs can be mimicked with synthetic sequences. Using single-molecule force spectroscopy and molecular dynamics simulations, these CCs are mechanically loaded in shear geometry and their rupture forces and structural responses to the applied load are determined. Simulations at the highest pulling speed (0.01 nm ns−1) show the appearance of β-sheet structures for the five- and six-heptad CCs and a concomitant increase in mechanical strength. The αβT is less probable at a lower pulling speed of 0.001 nm ns−1 and is not observed in force spectroscopy experiments. For CCs loaded in shear geometry, the formation of β-sheets competes with interchain sliding. β-sheet formation is only possible in higher-order CC assemblies or in tensile-loading geometries where chain sliding and dissociation are prohibited.

1 Introduction

Coiled coils (CCs) are self-assembled structures, consisting of two to seven α-helices that intertwine to form a supercoil conformation.[1] CCs are characterized by a repetitive amino acid sequence, (abcdefg)n, named heptad. Self-assembly occurs when hydrophobic amino acids are placed in positions a and d of each heptad. This arrangement aligns all hydrophobic amino acids on one face of each helix, allowing the formation of a well-organized hydrophobic core. Positions e and g are typically occupied by charged amino acids that form interhelical ionic interactions. While contributing to CC stability, the pattern of charged amino acids also determines if the CC folds into a homo- or heteromeric assembly. Positions b, c, and f, which are exposed to solvent, mainly affect the helicity of the individual chains.[2] A minimum of three heptads is necessary to form a stable dimeric CC supercoil at room temperature.[3] While synthetic CCs usually possess a length between three and five heptads,[3, 4] much longer CCs are observed in natural CC-containing proteins, e.g., in myosin, intermediate filaments, and fibrin.[5]

Nature exploits CC structures in ≈10% of all eukaryotic proteins.[6] They are found in proteins that participate in biological processes as diverse as signal transduction, gene regulation, and membrane fusion.[1, 7] In the mammalian cytoskeleton and the extracellular matrix, CCs contribute to the mechanical function of these structures.[5, 8] CCs further serve as structural and mechanical building blocks in biogenic materials, e.g., hagfish slime,[9] whelk egg capsules,[10] and insect silk.[11] The mechanical properties of natural CCs have motivated multiple experimental studies[5, 9-12] and steered molecular dynamics (SMD) simulations.[12, 13] At small tensile or shear loads, CCs extend like an elastic rod and the force increases almost linearly with extension. Once a critical value is reached, the α-helices begin to unfold and the structure elongates at a nearly constant force. During this phase, intrachain hydrogen bonds may be replaced with interchain hydrogen bonds, resulting in a β-sheet structure.[5, 9, 10, 12-14] As β-sheets are mechanically stronger,[15] this α-β transition (αβT) protects the material from further deformation.[5]

The structure–function relationships of CCs are not only of interest for their critical importance in biological systems.[1, 7] Engineered or de novo designed CCs also find a wide range of biotechnological and biomedical applications, e.g., as oligomerization domains,[16] purification, immobilization, and labeling tags,[17] artificial scaffolds for catalytic reactions,[18] biomineralization templates[19] and building blocks for biomimetic materials.[20] CCs have further been programmed to serve as molecular switches.[21] For example, the protonation state of the charged e and g residues has been utilized to realize pH-induced switching between α-helical and β-sheet conformations.[22] Other possible triggers of αβT in engineered and designed CCs are variations in ionic strength,[22] or temperature[23] as well as metal ion coordination.[24]

Here, we aim to design, synthesize and utilize de novo CC sequences with a length of four to seven heptads. Our goal is to probe their mechanical response to shear loads as a function of CC length and to investigate if the force-induced αβT can be mimicked with synthetic sequences. Shear loading is particularly relevant for labeling, purification, and self-assembly applications of CCs, where the CC is used to establish a reversible link between two molecules of interest. Synthetic sequences that are able to undergo a force-induced αβT are expected to strengthen under load (i.e., act as catch bonds[25]) and are thus of high interest for the synthesis of self-reinforcing materials.

Shearing of different CCs in SMD simulations revealed that the probability of observing a force-induced αβT increases for longer CCs and slow rates of force application (i.e., loading rates, dF/dt).[13] To test this prediction, we utilize de novo designed heterodimeric CCs with lengths ranging from four to seven heptads.[4, 12, 26] We probe their response to shear forces, using atomic force microscope (AFM)-based single-molecule force spectroscopy (SMFS) and SMD simulations. An αβT is expected to cause a visible increase in the forces required for chain dissociation, both in experiments and simulations. The simulations further provide mechanistic insight into the structural response to the applied force. Our simulations confirm that the αβT is more likely for longer sequences; however, they suggest that the αβT is more probable at higher loading rates. The αβT appears to compete with uncoiling-assisted chain sliding,[12] which appears to be more probable at lower loading rates. Our SMFS experiments do not show any evidence for a force-induced αβT, suggesting that chain sliding also happens in experiments and that the chains dissociate before interchain hydrogen bonds can form. Earlier experimental observations of αβT involved higher-order CC assemblies, e.g. in keratin or vimentin intermediate filaments,[5, 9, 12] where chain sliding is probably hindered as a result of interactions with neighboring CCs.

2 Results

2.1 Design and Synthesis of Coiled Coils with Different Lengths

With the goal of mimicking the αβT in synthetic sequences, we designed a series of heterodimeric CCs with lengths ranging from four to seven heptads (Figure 1A). The four-heptad CC (A4N3B4N3) has already been characterized in shear loading geometry in our earlier SMFS experiments and SMD simulations.[2, 12, 30] A4N3B4N3 contains one asparagine (Asn, N) in the third heptad of each chain. The resulting polar pairing in the hydrophobic core prevents chain misalignment and thus aids folding into a unique four-heptad CC structure.[4, 27] The subscripts in the CC name indicate the positions of the Asn residues.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Setup for single-molecule force spectroscopy experiments and molecular dynamics simulations. A) Amino acid sequences of the four- to seven-heptad CCs. The cysteine (Cys, C) residues were used for site-specific immobilization and represent the force application points in the experiments. B) Experimental setup for SMFS experiments. The A-peptides were immobilized onto a glass surface while the B-peptides were coupled to the AFM cantilever. Both peptides were covalently attached via a maleimide-terminated PEG linker. The CC forms when approaching the cantilever to the surface, while subsequent retraction leads to chain separation. C) Setup for pulling and restrained equilibrium simulations. The force was applied via virtual harmonic springs with a spring constant k = 100 kJ mol−1 nm−2 = 0.166 N m−1, acting in three dimensions. The springs were attached to the α-carbon atom (points A and B) of the N-terminus of the A-peptide and the C-terminus of the B-peptide. The terminal Cys residues were not included in the simulations.

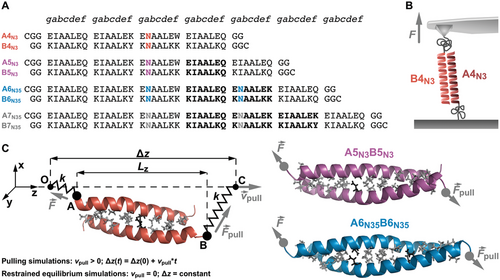
For the probed pulling geometry (N-terminal force application point on A4N3 and C-terminal force application point on B4N3; Figure 1B,C), no αβT was observed in either experiments or simulations.[2, 12] We thus followed the above-mentioned prediction[13] and increased the length of this CC stepwise by one heptad and up to seven heptads, i.e., lengths that can still be produced synthetically with solid-phase peptide synthesis. The rationale for the design of the elongated peptides was based on the following three criteria. First, additional heptads were inserted in front of the C- terminal heptad (Figure 1A). This ensures that the heptad sequences at both force application points remain unaltered. Second, earlier work has shown that CC-forming peptides with lysine (Lys, K) in the e and g positions have a tendency to form homodimers.[28] It is expected that thermodynamically more stable homodimers form when the CCs are longer. For the planned SMFS experiments, the probability of homodimer formation needs to be minimized to ensure a high probability of heterodimer formation during the short contact time of the cantilever on the surface (Figure 1B). Third, our aim was to reduce the number of possible misaligned structures (Figures S1 and S2, Supporting Information).

To achieve all of the above, the polar Asn residue in the third heptad of A4N3B4N3 was maintained in all elongated sequences. One polar pairing in the third heptad is sufficient to prevent misaligned structures for the resulting five-heptad CC A5N3B5N3 (Figure S1, Supporting Information). For the six- and seven-heptad CCs, one additional Asn was introduced in the fifth heptad (A6N35B6N35, A7N35B7N35). While a misaligned structure with four-heptad overlap can form for this design (Figure S2, Supporting Information), the Asn clearly reduces the helix propensity of the individual peptides (Figure S3, Supporting Information). We prioritized the minimization of homodimers, as these are detrimental for SMFS and included a control experiment to probe the stability and contribution of a possible misaligned A6N35B6N35 structure (Figure S2, Supporting Information). This overlapping CC structure may appear in the SMFS experiments as a four-heptad folding or unfolding intermediate and was synthesized (A6IB6I) and characterized in our experiments.

2.2 Coiled-Coil Structure and Thermodynamic Stability

All CC-forming peptides (Figure 1, Figures S4–S8, Supporting Information) and the respective heterodimeric CCs were first characterized with circular dichroism (CD) spectroscopy to determine their secondary structure and thermodynamic stability. For the individual peptides, the CD spectra of A4N3 and A5N3 show a random coil conformation (Figure S9A, Supporting Information). The A-peptides A6N35 and A7N35 and all B-peptides show an α-helical conformation, indicating homodimer formation (Figure S9, Supporting Information). At the same time, the melting temperatures, Tm, of the homodimer structures tend to increase with peptide length. Importantly, the Tm of B6N35 is lower than for B5N3. This supports our design strategy of introducing a second Asn into the six- and seven-heptad CCs to reduce homodimer stability. For all homodimers (except B7N35), the Tm values are below 60 °C (Figure S10, Supporting Information). We consider the homodimer structures as sufficiently dynamic to not interfere with heterodimer formation in SMFS experiments.

The CD spectra of the CC heterodimers (Figure 2A) show the characteristic minima at 208 and 222 nm for the four- to six-heptad sequences. The ratio of the mean residue molar ellipticity [Θ]MRE at 222 and 208 nm, [Θ]MRE_222/[Θ]MRE_208, is larger than 1, indicating folding into a stable CC structure on the time scale of the experiment.[29] The seven-heptad-long peptides do not assemble into a heterodimeric CC structure under the same experimental conditions. An equilibrated CC structure is only obtained after overnight incubation. This result suggests that the longest A7N35B7N35 sequence folds into the desired heterodimers very slowly, most likely because formation of a fully aligned heterodimeric structure competes with the formation of homodimers and misaligned intermediates.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Structural and thermodynamic characterization of coiled-coil (CC) heterodimers. A) Circular dichroism (CD) spectra of the heterodimeric CCs, measured at a temperature of 23 ± 2 °C. The CC-forming peptides were mixed, and incubated for 10 min before the measurement. For A7N35B7N35, an additional measurement was performed where the sample was incubated overnight (ON). The spectra show the average of three independent experiments, each measured as three technical replicates. B) CD thermal denaturation, measured in PBS (+500 µm TCEP). One typical denaturation curve, recorded at 222 nm, is shown. C) CD thermal denaturation, measured in PBS + 1.5 m GuHCl (+500 µm TCEP). One typical denaturation curve, recorded at 222 nm, is shown.

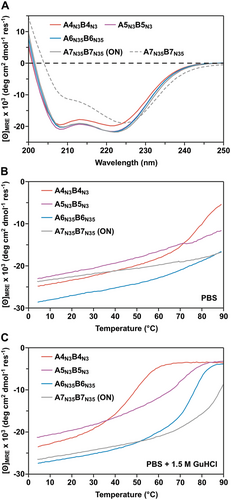
To determine the thermodynamic stability of the fully folded CC heterodimers, thermal denaturation experiments were performed. Initial measurements under native conditions (Figure 2B) confirmed that the Tm of A4N3B4N3 (79.1 °C; Table 1) is similar to published values.[2, 4, 12, 26] For the longer five- to seven-heptad CCs, no unfolding transition was observed up to 90 °C. To qualitatively determine how CC elongation affects thermodynamic stability, thermal denaturation was also measured in the presence of guanidine hydrochloride (GuHCl; 1.5 m) as a denaturant (Figure 2C). These measurements highlight that each additional heptad increases Tm and, therefore, the thermodynamic stability (Table 1, Table S2, Supporting Information). While these results cannot be quantitatively extrapolated to native conditions, they support our design strategy to utilize a second Asn pair for A6N35B6N35 and A7N35B7N35. Clearly, this additional Asn pair destabilizes homodimer structures while heterodimer stability increases as intended.

Table 1. Summary of structural, thermodynamic and kinetic coiled coil properties, obtained from circular dichroism spectroscopy and single-molecule force spectroscopy
Coiled coil Θ222nm/Θ208nm Tm_native [°C] Tm_GdnHCl [°C] koff [s−1] Δx [nm]
A4N3B4N3 1.01 79.1 ± 1.1 45.2 ± 0.3 2.6 x 10-6 2.17
A5N3B5N3 1.03 >95 66.9 ± 0.6 4.1 x 10-6 2.50
A6N35B6N35 1.07 >95 75.1 ± 0.9 8.5 x 10-8 4.75
A6IB6I 0.96 75.1 ± 0.8 n.d 9.8 x 10-9 5.36
A7N35B7N35 1.09 >95 83.6 ± 1.6 n.d. n.d.
  • a) Determined at room temperature;
  • b) Measured after overnight equilibration at room temperature;
  • n.d., not determined.

Considering the slow folding kinetics of A7N35B7N35, this CC was not included in subsequent SMFS experiments as folding of the fully aligned structure is highly unlikely during the short contact time of the cantilever on the surface. To obtain more detailed insight into the folding kinetics of the second longest CC A6N35B6N35 in comparison to A7N35B7N35, both CCs were subjected to two rounds of subsequent heating and cooling cycles, performed at a rate of 1 °C min−1. While the data for A7N35B7N35 may show a small hysteresis, good overlap is observed during the heating and cooling cycles of A6N35B6N35 (Figure S11, Supporting Information). This motivated us to include A6N35B6N35 in the SMFS experiments even though it cannot be excluded that misaligned structures are formed. To estimate a possible contribution of the most probable A6IB6I structure, which is formed with almost four-heptad overlap (Figure S2, Supporting Information), its thermodynamic properties were characterized (Figure S12, Supporting Information). A6IB6I forms a stable CC (Tm = 75.1 °C) so that it was necessary to include this CC as a control sequence for the SMFS experiments of A6N35B6N35.

2.3 Coiled Coil Shearing with Single-Molecule Force Spectroscopy

The CCs A4N3B4N3, A5N3B5N3, A6N35B6N35, and A6IB6I were mechanically characterized with dynamic SMFS to determine the rupture forces as well as the energy landscape parameters of the CC interaction. In particular, the rupture forces are expected to increase significantly if a parallel β-sheet should form.[5, 13] The A-peptide was immobilized onto a glass surface, making use of an N-terminal Cys residue, while the B-peptide was coupled to the AFM cantilever at its C-terminus (Figure 1B). CC formation occurs when the cantilever approaches the surface, while subsequent cantilever retraction leads to chain separation. Each CC was measured at six different retract speeds between 50 and 5000 nm s-1 as chain separation in shear geometry is a loading rate-dependent process.[2, 12]

The obtained force-extension curves (Figure 3A, Figure S13, Supporting Information) and the resulting rupture force histograms (Figure 3B; Figures S14–S16 and Table S3, Supporting Information) do not yield any force values higher than what was measured previously for A4N3B4N3.[2, 12] Most interestingly, A5N3B5N3 is mechanically less strong than A4N3B4N3 over the entire range of retract speeds (Figure 3C). For A6N35B6N35, the rupture forces are even lower and approach the limit of what can be resolved with the cantilever used. The data points for A6N35B6N35 and the misaligned A6IB6I intermediate overlap. It is thus not possible to conclude if A6N35B6N35 displays even lower rupture forces than A5N3B5N3 or if only the misaligned structure A6IB6I is measured as an intermediate on the folding or rupture pathway.

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Single-molecule force spectroscopy of the coiled coils A4N3B4N3, A5N3B5N3, A6N35B6N35, and the control sequence A6IB6I. A) Characteristic force-extension curves, measured at a retract speed of 400 nm s−1. B) Example rupture force histograms for the four- to six-heptad long CCs, obtained at a retract speed of 400 nm s−1. C) Dynamic SMFS plot, showing the most probable rupture force values plotted against the most probable loading rates. The different symbols correspond to three independent experiments, performed with different cantilevers and surfaces. The lines are fits to the data using the Bell-Evans model (equation shown as inset). The data for A4N3B4N3 have been reanalyzed and replotted.[12, 30]

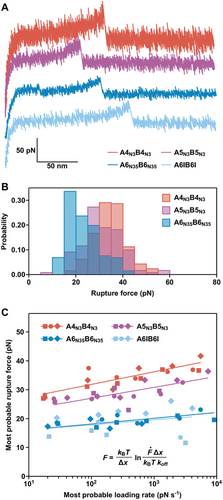
To gain more insight into the energy landscape of CC shearing, the most probable rupture forces and loading rates were determined from Gaussian fits to the respective histograms (Figures S14–S17 and Table S3, Supporting Information). Fitting the data with the Bell–Evans model[31] yielded the dissociation rate at zero force, koff, and the distance to the transition state, Δx (Figure 3C, Table 1). Focusing on A4N3B4N3 and A5N3B5N3, an increase in Δx is observed for the longer CC while koff is similar. The increase in Δx is consistent with earlier results of CC shearing, which have suggested that longer CCs tolerate the unfolding of larger amounts of helical structure before rupture.[12] Structures with larger Δx values are characterized by a smaller slope in the Bell-Evans plot. Larger Δx values can thus result in lower rupture forces at high loading rates, as we observe here when comparing A4N3B4N3 and A5N3B5N3. Assuming that the CCs maintain a helical conformation upon shearing, this suggests that an increase in CC length and thermodynamic stability does not necessarily increase the rupture forces measured in the loading rate range accessible in AFM-based SMFS.

2.4 Coiled Coil Shearing with Molecular Dynamics Simulations

The absence of an αβT in SMFS experiments opens up the question if the αβT is sequence-specific and does not occur for the synthetic sequences used in our experiments, which have been optimized for high helix propensity.[4] To answer this question, we switched to SMD simulations, which have detected αβT for a range of different CC sequences.[13] We performed simulations for A4N3B4N3, A5N3B5N3, and A6N35B6N35, using an all-atom force field for the CCs and the GBSA implicit solvent model, as implemented in the Gromacs simulation package.[32] Our prior work has shown that simulations with this implicit solvent model result in force-extension curves similar to those obtained with an explicit solvent model, at a fraction of the computational cost.[12] We used this advantage to perform simulations with the lowest pulling speeds that are currently computationally accessible with atomic resolution. The SMD simulations are nevertheless still orders of magnitude faster than the highest pulling speed accessible in our SMFS experiments. We show below that, despite this limitation, simulations and experiments probe forces of comparable magnitude, indicating that our simulations yield insight into molecular mechanisms that occur in the experiment.

The setup geometry (Figure 1C) mimicked the geometry used in SMFS experiments. We first investigated the response of the CCs using vpull = 0.01 nm ns−1, which is the lowest pulling speed where simulations can be performed until chain separation occurs. Figure 4 shows force-extension curves of individual realizations at this speed for the CCs A4N3B4N3, A5N3B5N3, and A6N35B6N35. The CC extension is defined as Δz(t) – 〈L0〉, where 〈L0〉 is the average length of the unrestrained CC at equilibrium, obtained when averaging the distance between the termini (points A and B in Figure 1C) in unrestrained simulations with a duration of 100 ns. The pulling force initially rises approximately linearly with extension. For all realizations of A4N3B4N3, the initial rise phase is followed by a plateau phase where the pulling force oscillates around an approximately constant value until the two chains separate. This behavior is consistent with our earlier simulations, which used a similar simulation procedure but applied virtual springs one order of magnitude stiffer.[12] For the two longer CCs, this type of response is not always observed. Some realizations show a dramatic increase in the pulling force (up to 800 pN) at large extensions, which is the typical signature of an αβT in simulations.[13]

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Force-extension (Δz(t) – 〈L0〉) curves from SMD simulations obtained at vpull = 0.01 nm ns−1. Shown are several independent realizations of A) A4N3B4N3, B) A5N3B5N3, and C) A6N35B6N35. Each curve consists of a rolling average over 100 points for ease of viewing.

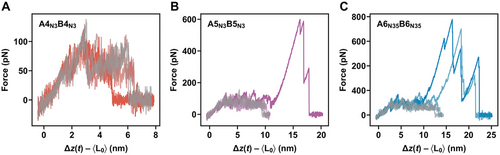
To understand the origin of these large forces, we characterized the response of individual realizations in detail, focusing on the evolution of secondary structure, hydrogen bonds, and interchain contacts (Figure 5). The criteria used to quantify each observable are described in the Experimental Section and in the Supporting Information (Section S4.1. and Figure S18, Supporting Information). For A5N3B5N3 pulled at vpull = 0.01 nm ns-1, two realizations were chosen. In one realization, an increase in the pulling force up to 600 pN was observed. In the second realization, chain separation occurred during the plateau phase. These realizations were further compared to a realization obtained from simulations at a pulling speed of vpull = 0.001 nm ns−1, which is the lowest pulling speed accessible with atomistic models.

Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Mechanical and structural response of A5N3B5N3 to shear pulling as a function of extension (Δz(t) − 〈L0〉) for two different realization at vpull = 0.01 nm ns−1 (A, B) and one realization at vpull = 0.001 nm ns−1 (C). Shown are i) illustrative CC structures at the indicated points marked in ii) the individual force traces, iii) the number of hydrogen bonds within each chain (intraA and intraB) and between chains (inter), iv) the number of interchain contacts, and v) the secondary structure calculated using STRIDE as implemented in VMD (T, turn; E, extended conformation; B, isolated bridge; H, α-helix; G, 310-helix; I, π-helix; and C, coil).

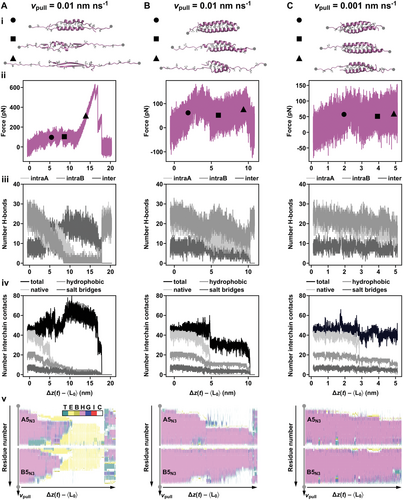
In all three realizations, the initial rise phase stops near 2 nm. During this phase, the number of hydrogen bonds (both intrachain and interchain) and of the different types of contacts stays constant (Figure 5). After the initial rise phase, the average force remains approximately constant (between 50 and 100 pN). In the realization where the pulling force rises to 600 pN (Figure 5A), this force plateau ranges from 2 to 11 nm. In the plateau phase, a large number of interchain hydrogen bonds form and, as a result, the total number of contacts increases dramatically. In parallel, native contacts disappear and the number of hydrophobic contacts and salt bridges decreases. The helical structure entirely vanishes and with it all intrachain hydrogen bonds. Beyond an extension of 11 nm, the structure can no longer deform because all amino acids are either in β-sheet configuration, forming interchain hydrogen bonds, or are in an extended coil configuration. As the large number of interchain hydrogen bonds prevents interchain sliding, the pulling force must increase monotonically until it is large enough to break multiple hydrogen bonds. Realizations of A6N35B6N35 that show high force peaks (Figure S19 Supporting Information) display the same type of structural response. The observed high force peaks reflect an αβT, highlighting that our synthetic CC sequences can show a similar response to shear forces when compared to other CCs investigated in SMD simulations.[13]

For a realization where the chains separate without a large force peak, very different structural changes occur in the plateau region even though the average plateau force is similar (between 50 and 100 pN). The similarity of plateau forces in the two cases is not surprising. Plateaus occur during a structural transition from a closed (or shorter) to an open (or longer) configuration,[5, 33] e.g., upon uncoiling of α-helices into more extended β-sheet or random coil conformations. Figure 5B shows a realization obtained at vpull = 0.01 nm ns-1 where the pulling force always remained below 200 pN. In the plateau region, the number of interchain hydrogen bonds decreased slowly with an increasing extension until it reached zero when the chains separate. The number of intrachain hydrogen bonds never approached zero and the helical structure was partially preserved until chain separation. The number of native contacts sharply decreased to almost zero at an extension of 5 nm, and the number of hydrophobic and total contacts showed a step decrease. This sharp decrease signals sliding of the two chains relative to each other, facilitated by transient uncoiling followed by helix reformation. Further deformation proceeds via a transition from α-helix to an open coil configuration at the pulled and restrained termini, which are no longer in contact with the neighboring chain. Chain separation occurs through another sliding event. This response is also present for the shorter four-heptad CC (Figure S20, Supporting Information) and was also observed in our earlier work.[12]

At the lower pulling speed of vpull = 0.001 nm ns-1, the simulation was only run until an extension of 5 nm (Figure 5C). Compared to vpull = 0.01 nm ns-1, the force-extension curves are qualitatively similar with lower average forces beyond the initial rise phase. The CC responds to the extension with sliding and no increase in the number of interchain hydrogen bonds is observed, as would be required for an αβT. These results at lower vpull suggest that A5N3B5N3 will not experience αβT at experimentally relevant loading rates. Pulling realizations at higher vpull that display an αβT show a very characteristic structural response already at extensions below 5 nm, i.e., long before the onset of the actual αβT. The number of intrachain hydrogen bonds continuously decreases while the number of interchain hydrogen bonds and of total interchain contacts concomitantly increases. This type of structural response is not observed in any of the five A5N3B5N3 realizations (Figure 5C and Figure S21, Supporting Information), obtained at lower vpull. All realizations show stepwise sliding, leading to CC conformations with significantly lower thermodynamic and kinetic stability (Figure S1, Supporting Information). Most probably slid configurations quickly dissociate in experiments and do not extend any further. This scenario is supported by the absence of clear force plateaus in our SMFS experiments. In contrast, force plateaus have been observed in SMFS experiments of myosin,[5] vimentin,[5] and spectrin.[34] The length of the myosin and vimentin CCs as well as the helix-loop-helix architecture of spectrin allow for a longer plateau region that is more clearly observed in experiments. At present, investigating if and how chain sliding and αβT compete on the chain separation pathway is not possible in simulations with atomistic resolution, as discussed in detail in Supporting Information Section S4.3.

2.5 Molecular Mechanism of Interchain Sliding

Assuming that chain sliding dominates over an αβT in SMFS experiments, the question remains which structural parameters determine the onset and progression of chain sliding. Quantifying the structural response of the CCs with amino acid resolution can identify weak points where deformation starts and thus suggest strategies for tuning the mechanical strength of CCs to shear forces. We quantified the loss of helical structure as a function of extension through the fraction of time, fic, that each residue i spends in a configuration of type c (e.g., α-helix, turn, coil) for a given extension Δz. The fraction is calculated for each extension as
f i c = δ i c $$\begin{equation}{f_{i{\rm{c}}}} = \left\langle {{\delta _i}\left( {\rm{c}} \right)} \right\rangle \end{equation}$$ ()
where δ is the delta function. The delta function takes the value one when the amino acid is in configuration of type c, and takes the value of zero otherwise. The angle brackets indicate an average, which in this work was done over multiple SMD simulations and, for improved sampling, over 10 ns for each extension in each simulation. Within this small time interval, the extension varies only by 0.0001 nm. The fraction fic varies between 0 and 1, with 1 indicating that the residue was always in configuration c at the indicated extension in all the simulation runs, and 0 indicating that it never assumed configuration c in any of the simulation runs.

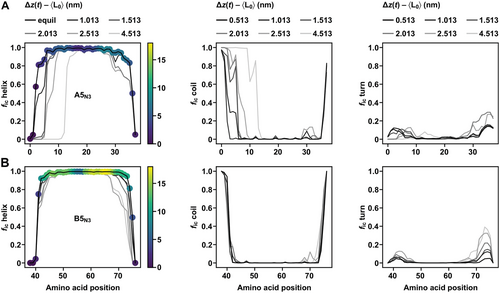
Figure 6 shows the structural evolution of A5N3B5N3 at the lowest pulling speed, quantified by the fraction fic that each amino acid spends in helical, turn, or random coil configuration; analogous results for A6N35B6N35 are shown in Figure S23 (Supporting Information). Initially, the applied shear force causes a loss of helical structure at the pulled termini (Figure 6). Once the helical structure disappeared, the interchain contacts were reduced, lowering the stability of the opposing helical chain. The C-terminus of chain A quickly lost its helical structure, consistent with its low helical propensity as assessed by AGADIR.[35] In contrast, the N-terminus of chain B has a high helical propensity. Consistent with this fact, the N-terminus remained largely helical for extensions up to 5 nm. Helical structure was primarily converted to extended coil, with a small fraction being converted to turn configuration. β-sheet formation was residual in A5N3B5N3 at the lowest pulling speed (Figure 6), but occurred in A6N35B6N35 for some realizations (Figure S23, Supporting Information). These SMD simulation results are consistent with experimental results that have shown that local stabilization of the pulled termini increases the mechanical strength of A4N3B4N3-derived CCs.[36] Considering the current and these earlier results, engineering local helix propensity may thus be a more powerful approach towards tuning CC mechanical strength than modifications of CC length.

Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
Fraction of time (fic) that each residue of A5N3B5N3 spends in α-helical, coil, or turn configurations for the indicated extensions (Δz(t) – 〈L0〉). The analysis was performed for the SMD simulations at vpull = 0.001 nm ns−1. The CC-forming peptides A5N3 (A) and B5N3 (B) are shown separately, but with continuous amino acid numbering. Each curve is the average of five simulations. The fraction of time that each residue spends in α-helical configuration at equilibrium is also shown (equil). This curve was calculated from an unrestrained simulation with a duration of 100 ns. It is superimposed on the helical propensity calculated using AGADIR.[35] The helix propensity is shown using a color scale from dark blue (low helix propensity) to yellow (high helix propensity).

3 Discussion

Earlier work on de novo designed three- to four-heptad CCs suggested that elongating CCs increases their thermodynamic stability and their mechanical strength to shear forces.[12] Here, we designed a series of CCs to explore if this trend continues for CCs with a length between five and seven heptads. This was motivated by the need for CCs with increased mechanical strength for applications as molecular force sensors[37] and hydrogel crosslinks.[20] Increasing CC length beyond five heptads, however, comes with a number of challenges. With increased length, the thermodynamic stability of homodimers increases along with the number of possible misaligned configurations. We attempted to address this problem by introducing a second polar Asn pair in the hydrophobic core. This strategy reduced the stability of six- and seven-heptad homodimers but did not fully eliminate misaligned intermediates. As a result, the folding rate to reach the fully aligned CCs is reduced and misaligned structures possibly dominated the SMFS experiment of A6N35B6N35. With extending CC length, we further aimed to establish a synthetic CC model system that mimics the transition from α-helices to β-sheets (αβT), frequently observed in natural CC-based materials.[5, 9-12] For the five-heptad CC, which is the longest CC that still forms a unique heterodimeric structure, we did not observe any evidence of an αβT. Our simulations indicate that chain sliding dominates over an αβT in the loading rate range accessible in SMFS experiments.

Our simulation studies shed light on the structural response of CCs to shear forces. Performing simulations at pulling speeds 10 to 100 times slower than those used in earlier atomistic studies,[13] we show a key contribution of interchain sliding. For the four-heptad CC, chain sliding is facilitated by a limited number of localized, reversible uncoiling events as well as permanent uncoiling at the helix termini.[12] Sliding of helices has been observed in molecular dynamics studies,[13, 38] but the details of the sliding mechanism were not discussed. Our work clarifies that sliding occurs in a sharply stepwise manner and that chain separation happens after only a few sliding events (2 to 4 in our simulations of A4N3B4N3).

The simulations at vpull = 0.01 nm ns -1 show that the longer five- and six-heptad CCs may respond to shear forces in two different ways. The most frequent response is again stepwise sliding, i.e., local uncoiling and refolding events combined with permanent unfolding at the termini. Less frequently, however, these longer CCs show an αβT whereby multiple interchain hydrogen bonds form, similar to what is observed when CCs are pulled in tension.[13, 39] Once these hydrogen bonds are in place, and all other amino acids are in an extended configuration, the pulling force rises up to values of 600 to 800 pN. Once the pulling force is large enough to break multiple interchain hydrogen bonds simultaneously, the two chains in β-sheet configuration slide and the force decreases sharply. The subsequent reformation of a smaller number of interchain hydrogen bonds is followed by another increase in the pulling force until the hydrogen bonds simultaneously break again. A sequence of multiple such sliding events causes a sawtooth-like pattern in the force-extension curves until the chains finally separate. This was also observed when shearing a long myosin CC fragment (2x126 amino acids) at a pulling speed of 100 nm ns-1.[13]

First signs of the αβT become already visible at small extensions, much before the force peak occurs. These signs include early uncoiling of the restrained and pulled termini and subsequent formation of a small number of interchain hydrogen bonds, which reduce the probability of chain sliding. Our simulations at the lowest pulling speed, vpull = 0.001 nm ns-1, suggest that this response becomes less likely at lower pulling speeds while the competing sliding process appears to be facilitated. These early structural changes, indicating the occurrence of the αβT, are more frequent for the six-heptad CC when compared to the shorter CCs. Also, early interchain sliding is less sharp for A6N35B6N35 than for A5N3B5N3. In combination, these results suggest that the αβT becomes more likely for longer CCs and at faster pulling speeds.

Other studies of CC shearing have proposed that the minimum CC length for the onset of the αβT becomes smaller at lower pulling speeds.[13, 38] Our present results hint that the opposite should be true. The minimum CC length for the onset of the αβT becomes larger for lower pulling speeds. Slow pulling speeds increase the occurrence of the competing sliding process where the chains maintain a helical configuration. It is thus not likely that we detect the αβT in the range of experimentally accessible loading rates. The experimental results are consistent with a scenario where the CCs dissociate at small extensions, possibly after assuming a thermodynamically and kinetically unstable conformation after the first sliding event.

When comparing our results with the experimentally observed αβT for a number of different natural CCs,[5, 9-12] it appears likely that sliding events must be minimized in these structures. Natural CCs, such as intermediate filaments,[5, 9, 12] frequently assemble into higher-order structures so that each CC is interacting with a number of neighbors. The CCs and thus also the individual chains are locked in place by additional stabilizing interactions so that sliding is prevented. Our results are thus not in discrepancy with other shear or tensile experiments of CCs. They rather highlight that natural, self-assembled CC bundles have evolved mechanisms to balance local unfolding and refolding, interchain sliding, and structural transitions.[12, 34]

4 Conclusion

In conclusion, we have shown that extending the length of synthetic CCs up to seven heptads increases their thermodynamic stability but not their mechanical strength against shear forces. Overall, our results show that length is not a good parameter to engineer CC mechanics. From a practical point of view, the optimum CC length for mechanical experiments is in the range of four to five heptads. In this range, CCs show good thermodynamic, kinetic, and mechanical properties, lack stable homodimers, and show a low occurrence of misaligned conformations. To improve the resistance of CCs to shear forces, we propose strategies that stabilize the helices against uncoiling. Placing covalent and dynamic staples in regions with low helix propensity or at the force application points increases the energy barrier for uncoiling[36] and is one possible strategy to achieve this goal.

Our combined experiment and simulation approach further shows that isolated CC heterodimers do not undergo a transition from α-helices to β-sheets when mechanically loaded in shear geometry. Chain separation initiates with helix uncoiling at the pulled termini but does not proceed via a β-sheet conformation. Instead, helix uncoiling and recoiling facilitate interchain sliding, which yields kinetically unstable intermediates that dissociate quickly. In the future, it will be interesting to experimentally investigate higher-order oligomers[13] where the presence of additional chains is expected to alter the probabilities for interchain hydrogen bond formation versus helix recoiling and interchain sliding.

5 Experimental Section

Peptide Synthesis

The CC-forming peptides were obtained via solid-phase peptide synthesis, following standard Fmoc-based protocols. The peptides were obtained from commercial suppliers (Centic Biotec, Heidelberg, Germany; Proteogenix, Schiltigheim, France) or produced in house. For in-house synthesis, two different protocols and synthesizers were used to obtain peptides with an N-terminal acetyl group and C-terminal amidation. Method 1 was performed with a Tribute peptide synthesizer (Gyros Protein Technologies Inc., Tucson, AZ, USA) while a MultiPep RS synthesizer was used for method 2 (Intavis AG, Koeln, Germany). A full list of all peptides and their source is provided in Table S1 (Supporting Information).

For method 1, H-rink amide ChemMatrix resin (Merck Millipore, Darmstadt, Germany) was used. Fmoc protected amino acids (5× excess), coupling agent 2-(6-chloro-1-H-benzotriazole-1-yl)-1,1,3,3-tetramethylaminium hexafluorophosphate (HCTU; 5× excess) and N,N-diisopropylethylamine (DIPEA; 2.5× excess) were used for the automated synthesis reaction with double coupling. The N-terminus was acetylated using a mixture of 1:1:3 acetic anhydride/pyridine/dimethylformamide (DMF). All peptides were cleaved from the resin using a mixture of trifluoroacetic acid (TFA)/triisopropylsilane/ethandithiol/water (92.5:2.5:2.5:2.5). Crude peptides were precipitated with ice-cold diethyl ether and obtained after centrifugation at 5000 × g for 15 min at 4 °C. They were dried under nitrogen flow.

For purification, the dried peptides were dissolved in 10 to 20% acetonitrile (ACN) in water. Purification was performed with reverse-phase HPLC (LC-20A Prominence, Shimadzu Corporation, Duisburg, Germany) on a semi-preparative C18-column (Macherery Nagel, Dueren, Germany). A linear gradient of solution A (water + 0.1% TFA) and solution B (ACN + 0.1% TFA) was used. The gradient ranged from 10 to 90 % solution B in 30 min. The flow rate was 25 mL min-1. Collection of the eluted fractions was based on the absorbance at 220 nm. The purity of each fraction was analyzed using MALDI-TOF (Autoflex Speed, Bruker, Bremen, Germany). The measurement was performed in positive reflector mode (80 to 100% laser intensity, 700 to 5000 m/z), using 2,5-dihydrobenzoic acid (DHB) as matrix.

For method 2, TentaGel S RAM (Iris Biotech, Marktredwitz, Germany) was used as the resin. Fmoc-protected amino acids were used in 5× excess. Synthesis was performed as single couplings in DMF, using HCTU (5× excess) as coupling reagent and N-methylmorpholine (NMM; 10× excess) as base. For side chain deprotection and cleavage from the resin, a mixture of TFA/triisopropylsilane/phenole/water (92.5:2.5:2.5:2.5) was used. The crude peptides were purified using reverse-phase HPLC (Gilson, Limburg, Germany), equipped with a semi-preparative PLRP-S column (300 × 25 mm, 8 µm; Agilent Technologies, Santa Clara, CA, USA). The mobile phases were solution A (water + 0.1% TFA) and solution B (ACN + 0.1% TFA). Samples were eluted with a linear gradient from 5% to 95% solution B over 90 min. The peptides were characterized with MALDI-TOF (Microflex LT, Bruker) in positive reflector mode, using α-cyano-4-hydroxycinnamic acid (HCCA) as the matrix.

Circular Dichroism Spectroscopy (CD)

CD spectroscopy was employed to determine the secondary structure and thermodynamic stability of the individual CC-forming peptides and the resulting CCs. The individual peptides were measured at a concentration of 50 µm in phosphate-buffered saline (PBS; 10 mm Na2HPO4/2 mm KH2PO4, pH 7.4, 137 mm NaCl, 2.7 mm KCl). To prevent possible disulfide bond formation, 500 µm tris(2-carboxyethyl)phosphine (TCEP; 10× excess) was added. For CC formation in native conditions, the A- and B-peptides were each added in a concentration of 50 µm. This yields a CC concentration of 50 µm and a total peptide concentration of 100 µm. The TCEP concentration was again 500 µm (5× excess over the total concentration of thiols). For experiments with the denaturant GuHCl, measurements were performed in PBS + 1.5 m GuHCl (10 mm Na2HPO4/2 mm KH2PO4, pH 7.4, 137 mm NaCl, 2.7 mm KCl, 500 µm TCEP, 1.5 m GuHCl).

All spectra were recorded with a Chirascan CD spectrometer (Applied Photophysics, Leatherhead, Surrey, UK), equipped with a Peltier temperature controller. A quartz cuvette with 1 mm path length (Hellma, Muellheim, Germany) was used. All spectra were measured at 23 ± 2 °C and over a wavelength range from 200 to 250 nm with 1 nm step size, 1 nm bandwidth, and 0.7 s time-per-point. The measured ellipticity was converted into the mean residue molar ellipticity, [Θ]MRE, using Equation 2:
Θ M R E d e g c m 2 , d m o l − 1 , r e s − 1 = θ / 10 × d × c × n $$\begin{equation}{\left[ \Theta \right]_{MRE}}\left( {deg\;c{m^2},dmo{l^{ - 1}},re{s^{ - 1}}} \right) = \theta /\left( {10 \times d \times c \times n} \right)\end{equation}$$ ()
where θ is the measured ellipticity in mdeg, d the path length in cm, c the total peptide concentration in m, and n the number of amino acid residues. For all CCs, the spectra were recorded as three technical repeats for three independent measurements.

Functionalization of AFM Cantilevers and Glass Surfaces for SMFS

For the site-specific immobilization of the CC-forming peptides to AFM cantilevers and glass surfaces, all A-peptides carry an N-terminal Cys residue and all B-peptides contain Cys at the C-terminus. The A-peptides were immobilized onto a round glass coverslip (diameter 24 mm; Gerhard Menzel GmbH, Braunschweig, Germany), and the B-peptides to the AFM cantilever (MLCT, Bruker, Camarillo, CA, USA). Functionalization of glass coverslips and AFM cantilevers with Cys-containing biomolecules was performed following a modified version of a previously established protocol.[40] The coverslips were cleaned in isopropanol and ultrapure water, using a sonicator. After drying under nitrogen flow, they were first treated in a UV-ozone cleaner for 10 min and then silanized with an amino-functionalized silane. For silanization, they were incubated in an ethanolic solution of 1 % (v/v) 3-aminopropyl dimethyl ethoxysilane (ABCR GmbH, Karlsruhe, Germany) for 30 min under gentle agitation. After washing in isopropanol and ultrapure water, they were baked for 1 h at 80 °C. MLCT cantilevers were also UV-ozone treated for 10 min and then immersed in neat 3-aminopropyl dimethyl ethoxysilane for 2 min. Each cantilever was washed with isopropanol and ultrapure water, followed by baking at 80 °C for 30 min. Coverslips and cantilevers were then incubated in a solution of NHS-PEG-maleimide (10 kDa, Rapp Polymere, Tuebingen, Germany) dissolved in sodium borate (50 mm, pH 8.5) in a concentration of 50 mm. After 1 h of incubation, coverslips and cantilevers were washed in ultrapure water to remove unbound PEG and dried under a stream of nitrogen. All peptides were dissolved in 50 mm sodium phosphate, 50 mm NaCl, 10 mm EDTA (pH 7.2 at 4 °C) in a concentration of 0.6 to 2 mm (depending on the CC used). For the A-peptides, 50 µL of the peptide solution was incubated on the AFM cantilever for 1 h at 4 °C and 50 µL of the B-peptide solution was used for the coverslip. After rinsing in cold PBS, the functionalized glass coverslips and cantilevers were stored in PBS at 4 °C until the start of the measurement.

Single-Molecule Force Spectroscopy

SMFS experiments were performed using a JPK ForceRobot300 (Bruker Nano, Berlin, Germany). All measurements were performed at room temperature in PBS, using MLCT cantilever C with a nominal spring constant of 0.01 N m−1. Several thousand approach-retract cycles were performed at six different retract speeds, ranging from 50 to 5000 nm s-1. For all measurements at the different retract speeds, the cantilever was moved on an 8 × 8 grid, covering an area of 10 × 10 µm2. The cantilever spring constants were determined at the end of each measurement, using the thermal noise method.[41] A correction factor of 0.769 was applied for V-shaped cantilevers.[42] The determined spring constants ranged from 0.007 to 0.025 N m−1. For each CC, three independent experiments were performed, each with a different coverslip and cantilever.

Data Analysis

The data were analyzed using JPK Data Processing Software (version 6.1.41). The raw data were converted into force-extension curves and corrected for drift, offset, and cantilever bending. Force-extension curves that displayed a single rupture event were manually selected and fitted with the worm-like chain (WLC) model (Equation 3):
f z = k B T L P 1 4 1 − z L C − 2 − 1 4 + z L C $$\begin{equation}f\left( z \right) = \frac{{{k_B}T}}{{{L_P}}}\left[ {\frac{1}{4}{{\left( {1 - \frac{z}{{{L_C}}}} \right)}^{ - 2}} - \frac{1}{4} + \frac{z}{{{L_C}}}} \right]\end{equation}$$ ()
where kB is the Boltzmann constant, T is the absolute temperature. LC is the contour length of the PEG chain, and LP the persistence length, while f stands for the force acting on the polymer and z for the end-to-end distance. Only force-extension curves that could be fitted with the WLC model and displayed LC ≥ 105 nm and LP ≥ 0.3 nm were used for further analysis. Considering that one 10 kDa PEG chain in its helical conformation is 60–65 nm long,[43] this ensures that only rupture events that include the stretching of two PEG chains are considered (i.e., one coupled to the surface and one to the cantilever). For each retract speed, the obtained rupture forces and loading rates were plotted into histograms and the most probable rupture force F and most probable loading rate r were obtained from Gaussian fits. The most probable values were subsequently fitted with the Bell-Evans model to obtain the dissociation rate at zero force (koff) and the potential width (Δx) (Equation 4):
F r = k B T Δ x × l n r × Δ x k o f f × k B T $$\begin{equation}F\left( r \right) = \frac{{{k_B}T}}{{\Delta x}} \times ln\left( {\frac{{r\; \times \;\Delta x}}{{{k_{off}}\; \times \;{k_B}T}}} \right)\end{equation}$$ ()

Molecular Dynamics Simulations

All simulations used the AMBER99SB-ILDN force field for proteins.[44] This force field includes an improved description of the side chain torsion potentials for isoleucine, leucine, aspartic acid, and asparagine, which are abundant in the amino acid sequences investigated here. The solvent was modeled implicitly using the Generalized Born and accessible surface area formalism, to approximate a 0.137 mol dm-3 solution of a 1:1 salt dissolved in water. The dielectric constant was set to 80. The Born radii were calculated using the Still approximation[45] at every time step. The cutoff for the calculation of the Born radii was 1 nm and the distance for the dielectric offset was 0.009 nm. The non-polar contribution was calculated using the ACE approximation introduced by Schaefer.[46] Simulations were performed in non-periodic simulation boxes without pressure coupling. Lennard-Jones and Coulomb interactions were calculated for maximum interparticle separations of 1 and 5 nm, respectively.

The initial configurations of the CCs were produced with CCBuilder 2.0,[47] as they have not been resolved experimentally. Equilibration simulations were performed with the molecular dynamics package Gromacs-5.1.1,[48] using a leap-frog algorithm with a 1 fs time step. The temperature was controlled with a velocity rescaling thermostat applied every 1 ps. The thermostat includes a stochastic term[49] which ensures that the canonical ensemble is sampled. Each CC was equilibrated for 0.5 ns, using a simulated annealing procedure that linearly increased the temperature from 10 K up to the target 300 K during the first 0.4 ns of simulation time. Bond lengths were kept fixed using the LINCS algorithm[50] with fourth-order matrix expansion and one corrective iteration.

SMD and restrained equilibrium simulations were performed using the geometry illustrated in Figure 1C, using Gromacs-4.6.4.[32] In both types of simulations, the α-carbon atoms of the N-terminus of chain A and of the C-terminus of chain B (points A and B in Figure 1) were attached to virtual harmonic springs of spring constant k = 100 kJ mol−1 nm−2 = 0.166 N m−1, acting in three dimensions. The N-terminus of helix A was restrained with a virtual harmonic spring tethered to a fixed point (point O in Figure 1C). In the pulling simulations, the C-terminus of helix B was restrained with a virtual harmonic spring attached at point C that moved along the OZ axis with a constant speed vpull. The time average of the pulling force along OX and OY was zero in the SMD simulations; however, force fluctuations in these directions substantially impact the mechanical response of the CC. These forces facilitate changes in the configuration that reduce the average force along OZ relative to a simulation setup where pulling on the virtual spring acts only along the pulling direction.[13] In each restrained equilibrium simulation, both virtual attachment points (O and C) were kept fixed at a predetermined distance, Δz. Multiple restrained equilibrium simulations were performed, each for a different value of Δz. Restrained equilibrium simulations approximate the limit of infinitely slow pulling speeds and allow insight into the response of the CCs to pulling speeds smaller than those directly accessible with SMD. Bond lengths were kept fixed using the LINCS algorithm with parameters identical to those used during the equilibration phase, with the exception that three corrective iterations were used, for better temperature control. The equations of motion were integrated using a leap-frog stochastic dynamics integrator with a 2 fs time step, a reference temperature of 300 K, and an inverse friction constant of 2 ps. With this friction constant, friction is lower than the internal friction of water while still ensuring the necessary temperature control. At vpull = 0.001 nm ns-1, simulations of A4N3B4N3 required ≈35 days until chain separation, when running four threads on an Intel Xeon Gold 6226R CPU @ 2.90 GHz.

Criteria for Structural Characterization

Hydrogen bonds exist when the distance between the oxygen atoms of the donor and acceptor groups is below 3 Å and the OH…O angle is larger than 140°. This set of criteria identifies both strong and weak hydrogen bonds. Hydrophobic contacts are present when the distance between the β-carbons of any pair of hydrophobic residues is below 7.5 Å. Salt bridges exist if the distance between the δ-carbon of the acidic amino acid and the ε-carbon of the lysine are within 6 Å of each other. The native contacts of each CC were initially identified from an unrestrained equilibrium simulation. A native contact exists if the average distance between the β-carbons of any pair of amino acids is below 7.5 Å. Native contacts were considered broken in the SMD simulations when the distance between the β-carbons of the amino acids became larger than 7.5 Å. The distance cutoffs used to identify contacts were selected as indicated in Section S4.1. in the Supporting Information. The secondary structure was calculated using the STRIDE algorithm[51] as implemented in VMD.[52]

Acknowledgements

The authors thank Dr. Sven Rothemund (Core Unit Peptide Technologies, University of Leipzig) for providing the peptides A6N53, B6N35, A7N35 and B7N35 and A4* as well as Margit Rößner (Max Planck Institute of Colloids and Interfaces) for synthesizing peptides A4N3, B4N3, A5N3 and B5N3. This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – project number 189853844 (SFB-TRR 102, project B17, K.G.B.). A.V.V. further acknowledges funding from the Deutsche Forschungsgemeinschaft under Germany's Excellence Strategy - EXC 2033 - 390677874 - RESOLV. Z.A. thanks the International Max Planck Research School (IMPRS) on Multiscale Bio-Systems for a Ph.D. scholarship.

Open access funding enabled and organized by Projekt DEAL.

    Conflict of Interest

    The authors declare no conflict of interest.

    Data Availability Statement

    All experimental data (CD and SMFS) are openly available at 10.5281/zenodo.7682233. All input and output files for the SMD simulations and all post-processing scripts can be found at 10.5281/zenodo.7663738.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.