Estimation of grain yield in wheat using source–sink datasets derived from RGB and thermal infrared imaging
Abstract
Timely and efficient monitoring of crop aboveground biomass (AGB) and grain yield (GY) forecasting before harvesting are critical for improving crop yields and ensuring food security in precision agriculture. The purpose of this study is to explore the potential of fusing source–sink-level color, texture, and temperature values extracted from RGB images and thermal images based on proximal sensing technology to improve grain yield prediction. High-quality images of wheat from flowering to maturity under different treatments of nitrogen application were collected using proximal sensing technology over a 2-year trial. Numerous variables based on source and sink organs were extracted from the acquired subsample images, including 30 color features, 10 texture features, and two temperature values. The principal component analysis (PCA), least absolute shrinkage and selection operator (LASSO), and recursive feature elimination (RFE) were used to screen variables. Support vector regression (SVR) and random forest (RF) were applied to establish AGB estimation models, and the GY prediction models were built by RF. The source dataset and sink dataset performed differently on AGB and GY estimation, but the combined source–sink dataset performed best for estimating both AGB and GY. Based on the source–sink dataset, the LASSO-RF model was the best combination for predicting AGB and GY, with the coefficient of determination (R2) of 0.85 and 0.86, root mean square error (RMSE) of 1179.09 and 609.61 kg ha−1, and the ratio of performance to deviation (RPD) of 2.10 and 2.45, respectively. This study demonstrates that the multivariate eigenvalues of both source and sink organs have the potential to predict wheat yield and that the combination of machine learning models and variable selection methods can significantly affect the accuracy of yield prediction models and achieve effective monitoring of crop growth at late reproductive stages.
1 INTRODUCTION
Winter wheat is an important cereal crop in the world. The sustainable production of wheat plays a crucial role in ensuring food security in the context of rapid global population growth (Fu et al., 2021; Lv et al., 2021). The external environment and genotype together determine the grain yield (GY) potential of wheat. The effect of genetic improvement on wheat yield under the same cultivation conditions was up to 47.1% (Novoselović et al., 2000). Source–sink interactions regulate carbon assimilation, translocation, allocation, and storage throughout the wheat and exert a major influence on the productivity of harvestable organs. Crop yield also depends on the source–sink relationship, which is affected by environmental changes (Yu et al., 2015). The essence of wheat variety improvement is the modification of source–sink traits, that is, by coordinating the relationship between source and sink, to increase source and sink, thereby enhancing wheat yield (Tian et al., 2011).
The communication between source organs and sink organs modulates carbohydrate assimilation and distribution during the growth of wheat (Yu et al., 2015). Plant productivity is advanced by source activity and sink strength. With continuous photosynthesis, source organs (mainly from leaves) can provide sufficient photosynthetic assimilates (sucrose) to sink organs (grains; Yu et al., 2015). The two components of sink strength, sink size and sink activity are recognized for their potential to accumulate starch mainly by increasing the activity of sucrose to starch-converting enzymes (Dai et al., 2009). The sustainable supply of sucrose from source organs (mainly from leaves) to sink organs (spikes) has comprehensively accelerated the sink strength (Yu et al., 2015). Therefore, it is crucial to maintain source activity and sink strength for the sustainable production of wheat during the reproductive and grain-filling periods (Serrago et al., 2013). As a result, selecting appropriate source–sink indices is a method that can provide strategies to develop crop productivity. Aboveground biomass (AGB) plays a leading role in the formation of dry matter and the utilization of light energy, and it is an essential basis for yield formation (Araus & Cairns, 2014; Jin et al., 2019). Therefore, effective monitoring of wheat AGB at the field source–sink level can support timely management interventions (such as fertilization and pesticide application), which is vital to enhance crop yield and preserve food security in precision agriculture (Chen et al., 2018; Dong et al., 2017). Routine measurement of crop AGB mainly involves an enormous investment in labor and destructive sampling in the field (Hansen & Schjoerring, 2003). The traditional sampling approach is time-consuming and unsuitable for large-scale crop monitoring, as most agronomic parameters exhibit high spatial variability at the field scale (Jin et al., 2021). Hence, it is pivotal to develop modern and efficient methods to obtain crop biomass information in a prompt and cost-effective manner during the growing season.
In recent years, remote sensing technology has been gradually considered as a timely and effective tool to estimate crop biomass and characterize its spatial and temporal variability (Breunig et al., 2020; Fu et al., 2021). However, the use of satellite or airborne remote sensing for precision agriculture often faces several limitations involving insufficient revisit frequency and cloud interference, resulting in suboptimal spatial and temporal resolution (Weiss et al., 2020). Proximal sensing techniques, with centimeter-level spatial resolution and flexible field data collection, have been applied to monitor crop growth (Lv et al., 2021; Riihimäki et al., 2019; Zeng et al., 2021). In particular, short-range-based optical remote sensing (such as RGB, thermal, multispectral, and hyperspectral cameras) has been employed competently to estimate the AGB of many crops including wheat, corn, and soybean (Maimaitijiang et al., 2017; Weiss et al., 2020; Yue et al., 2019). Statistical models are commonly used to establish empirical relationships between vegetation indices (VIs) and ground-measured biomass to estimate crop AGB (Marino & Alvino, 2020; Zheng et al., 2019). Compared with satellite-based sensors, short-range-based optical remote sensing remains an attractive option for acquiring crop biomass data because of its relative economic and the availability of optical sensors with good temporal and spatial resolution. To achieve higher accuracy of AGB estimation, many efforts have been made to search for suitable indices and modeling methods, which greatly contributes to the development of remote sensing monitoring technology (Xu et al., 2020). For purposes, the AGB of corn, rice, and wheat were estimated by using relevant vegetation indexes (VIs such as normalized difference vegetation index (NDVI), modified soil adjusted vegetation index (MSAVI), and green optimal soil adjusted vegetation index (GOASVI) and so on), and satisfactory results were achieved in the prediction results (Qi et al., 1994; Weiss et al., 2020; Yue et al., 2019; Zha et al., 2020; Zhu et al., 2019). However, in addition to canopy structure differences, other factors such as the interference of soil background, the saturation of high-density vegetation, and the emergence of reproductive organs (e.g., wheat spikes) also could have significant impacts on the performances of VIs throughout the growth cycle of crops (Li et al., 2021; Zha et al., 2020). Crop AGB is the collection of aboveground dry weight of different plant organs, but there are notable differences in structural and optical traits between plant organs, affecting the canopy reflectance essentially (Xu et al., 2022). For example, compared with pendulous leaves, rice stems in the straight position have less chlorophyll concentration but more weight in the same volume content (Li et al., 2021). Furthermore, the properties of crop organs are distinct to plant species and have dynamical variations in the growth stages (Dandrifosse et al., 2022). In the vegetative growth stage, wheat is mainly composed of stems and leaves. At this stage, with the expansion of canopy coverage, leaves gradually become the dominant organ in the collection of AGB. However, during the reproductive growth stage, the canopy structure changes with the emergence of panicles and grain filling, and the photosynthetic products are constantly transferred from leaves to panicles, finally resulting in the reflectance of wheat canopy (Makanza et al., 2018; Wang et al., 2019). In addition to the effect of canopy differences, previous studies have shown that saturation problems with optical remote sensing may affect the performance of models in estimating crop biophysical parameters (e.g., AGB) on high-density vegetation (Cai et al., 2019; Maimaitijiang et al., 2017).
Several studies have demonstrated that multisource remote sensing fusion, which combines the advantages of optical, structural, and thermal properties, can solve the saturation issue inherent in remote sensing applications (Maimaitijiang et al., 2017; Maimaitijiang, Sagan, Sidike, Hartling, et al., 2020; Tilly et al., 2015). For the thermal images, plant canopy temperature (CT) reflects the photosynthesis and transpiration intensity, which is beneficial for monitoring crop growth (Gonzalez-Dugo et al., 2015; Matese & Di Gennaro, 2018). Specifically, plant CT was used as a valid indicator to observe crop pigment concentration, yield, and leaf area index (LAI; Elarab et al., 2015; Guo et al., 2016; Neinavaz et al., 2016). To enhance the accuracy of crop phenotype monitoring, researchers have constructed a great number of phenotype estimation models based on the fusion of multiple remote sensing data (Lv et al., 2021; Xu et al., 2020, 2022).
For example, using thermal and multispectral data fusion (Maimaitijiang et al., 2017) discovered that it was beneficial for gaining better modeling results for soybean chlorophyll and nitrogen content compared with using thermal or multispectral data only. (Geipel et al., 2014) found that combining optical RGB-VIs with plant height could increase the accuracy of maize yield prediction. (Maimaitijiang, Sagan, Sidike, Hartling, et al., 2020) integrated RGB, multispectral and thermal data for soybean yield estimation under the framework of a deep neural network (DNN), and the results demonstrated that multisource data fusion improved the accuracy of the soybean yield estimation. The fusion of spectral and texture information made better results of monitoring potassium accumulation in rice based on the unmanned aerial vehicle (UAV) remote sensing technology (Lu et al., 2021). Consequently, the fusion of multisource data provides a new developmental outlet for the study of crop phenotypes (Comba et al., 2020; Matese & Di Gennaro, 2018; Meng et al., 2019; Yang et al., 2020). High-dimensional data usually mean that the dataset contains many redundant and irrelevant features, which can lead to discrepancies between high-dimensional data and redundant or irrelevant features (Inoue & Sakaiya, 2013). One of the prime reasons is that the number of inherent features of high-dimensional data is not high (Inoue et al., 2014), and the prediction result of the restricted training set reduces as more features are involved, which is related to the attribute of dimensionality (Rossi & Erten, 2015). Another reason is that extracting and adopting more proper values in modeling analysis would lead to a time-consuming processing (Erten et al., 2015). Therefore, the redundancy inherent in high-dimensional data may impair the performance of a learning model (Bouvet et al., 2009). In short, it makes sense to investigate whether feature or dimension reduction helps to search for the most important features and whether the reduced feature set can achieve the same or higher classification accuracy than the original feature set (Lopez-Sanchez et al., 2011). To achieve this goal, feature selection methods are often employed to exclude highly correlated and redundant features from regression analysis by identifying a subset of the original features to maintain meaningful information (Küçük et al., 2015).
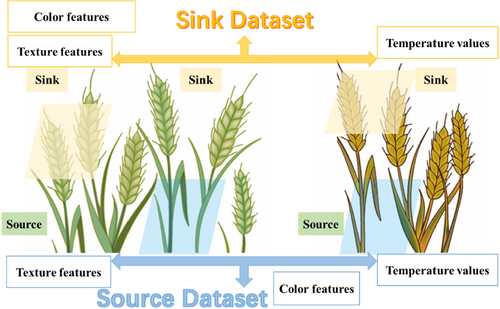
Many studies have indicated that the utilization of appropriate VIs can effectively predict yield. However, the success of using traditional VIs to assess wheat yield has been limited. The main reason is that the correlation between VIs and agronomic traits is various at different reproductive periods. As an example, NDVI is relevant to agronomic traits during the nutritional growth period, but tends to lose sensitivity during the reproductive growth period, which is not beneficial to developing robust yield prediction models in the late growth period (Sulik & Long, 2016; Yue et al., 2019). Therefore, this paper investigates the potential of integrating color, texture, and temperature information at the source–sink level (leaf-spike) to improve wheat yield prediction (Figure 1). Statistical modeling methods are required to develop yield prediction models based on indices deriving from proximal images. Although various models using image data have been constructed to estimate crop yields, these data-driven empirical models differ from the plant variety, climatic region, and the planting location (Gong et al., 2018; Kira & Rendell, 1992; Peng et al., 2019). In this study, we used proximal sensors including RGB and thermal sensors to extract relevant indices such as color, texture, and temperature information for different organs (leaves and spikes) (Figure 1), filtered the features according to different weights, and then utilized machine learning algorithms to predict AGB and grain yield from flowering to mid-late grain filling. The approach of extracting image information of wheat leaves and spikes, respectively, can ensure the difference of source–sink level indices to the greatest extent. As far as we know, this is the first time to propose the AGB and grain yield estimation models developed at the source–sink level in the later growth stage of wheat. Consequently, the main purpose of this study is to explore the potential of using color, texture, and temperature information at the source–sink level to predict wheat yield. The specific objectives of this study are as follows: (1) to evaluate the potential of multisource data (color, texture, and temperature information) based on the source–sink level for wheat later growth monitoring; (2) to compare the performance of various feature selection algorithms in estimating wheat grain yield; (3) to investigate the feasibility of improving grain yield prediction based on source–sink level data fusion and verify the robustness of the prediction models.
2 MATERIALS AND METHODS
2.1 Field experimental design
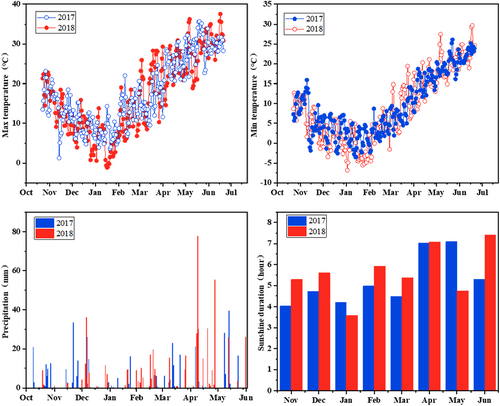
Three field trials were conducted over a 2-year period in Yangzhou, Jiangsu, China (32°30′N, 119°28′E), which is located in the middle and lower reaches of the Yangtze River plain, with an average altitude of 21 m above sea level, an average annual temperature of 15.8°C, and average annual precipitation of 1020 mm. The soil in the fields is classified as sandy loam with an organic content of 23.88–30.13 mg kg−1, total nitrogen content of 1.33–1.43 g kg−1, and an available nitrogen/phosphorus/potassium content of 91.31–94.11 mg kg−1/38.22–41.12 mg kg−1/89.97–104.09 mg kg−1 at top 20 cm soil layer, respectively. This experimental station is a transition zone from a subtropical monsoonal humid climate to a temperate monsoonal climate, and the profile of the meteorological parameters during the wheat-growing season in 2016–2018 is shown in Figure 2.
The field trials were conducted in experimental fields and considered three variables included different nitrogen (N) application levels, planting densities, and wheat cultivars (Table 1). The experiments were designed using a three-factor randomized block design, and the experiment 1 (Exp.1) followed this design included two replications of two cultivars (Yangmai 23 and Ningmai 13), four N application levels (N0, N1, N2, and N3), and three planting densities (M1, M2, and M3). In Exp.1, 48 sampling plots were divided into each covering area of 10.5 m2 (3 × 3.5 m). These two experiments (Exp.2 and Exp.3) had 48 and 24 sampling plots, separately. The area of each plot in Exp.2 was approximately 16.5 m2 (3 × 5.5 m), and the plot area was approximately 18 m2 (3 × 6 m) in Exp.3. In addition, Exp.1 and Exp.3 were located in a rained agroecosystem with a wheat-rice rotation, while the field of Exp.2 was located in a rained agroecosystem with a wheat-corn rotation. The nitrogen application strategy was to apply urea at a ratio of 5:1:2:2 at four stages: presowing, four-leaf stage, jointing stage, and booting stage. For all treatments, approximately120 kg ha−1 P2O5 (as Ca(H2PO4)2) and 120 kg ha−1 K2O (as KCl) were split equally into applications at the base and jointing stages. Field management and irrigation followed local practice.
| Growing season | Cultivar | Sowing date | Harvest date | Treatments | Sampling period |
|---|---|---|---|---|---|
| Exp.1: 2016–2017 | Yangmai 23, Ningmai 13 | 15 November | 2 June |
N level (kg ha−1): 0, 180, 240, 300 Density (million individual plants ha−1): 1.5, 2.25, 3.00 |
29 April, flowering; 14 May, filling |
| Exp.2: 2017–2018 | Yangmai 23, Ningmai 13 | 6 November | 30 May |
N level (kg ha−1): 0, 180, 240, 300 Density (million individual plants ha−1): 1.5, 2.25, 3.00 |
19 April, flowering; 26 April, early filling; 3 May, middle-late filling |
| Exp.3: 2017–2018 | Ningmai 13 | 2 November | 26 May |
N level (kg ha−1):CK,180,240,300 Density (million individual plants ha−1):1.5, 2.25, 3.00 |
28 April, flowering; 11 May, filling |
2.2 Image data collection
2.2.1 Temperature
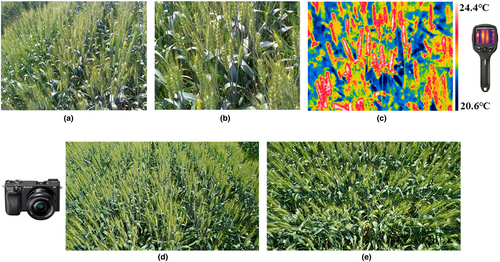
A handheld FLIR® E40 thermal imaging camera (FLIR Systems, Inc.) was used to obtain thermal infrared postflowering images of wheat. The FLIR® E40 handheld thermal infrared instrument was the main piece of equipment used for canopy-scale thermal image acquisition. The size of the thermal imager is 246 × 97 × 184 mm; it has a resolution of 160 × 120 pixels, a temperature measurement range of −20°C to 650°C, a thermal sensitivity of <0.07°C at 30°C, a field of view of 25° × 19°, and a minimum focal length of 0.4 m. The instrument is small in size, easy to carry, easy to operate, and has automatic positioning and full-frame focus control; its data acquisition is fast and efficient. During the process of thermal infrared image acquisition, the handheld camera was positioned at a height of approximately 1 m, and the emissivity was 0.95. The thermal images were captured 4–5 times from the heading stage to the dough stage, at the time interval of 2 h from 8:00 to 20:00 on both clear and cloudy day without extremity weather (i.e., windy, rainfall). At the same time, the air temperature was recorded using a thermometer. In this study, about 420 thermal images were collected at the wheat canopy level by handheld thermal imager in each period. Later, the FLIR Tools software (version 6.4; FLIR Systems, Inc.) was used to obtain wheat plant temperature data (leaf and spike) under the different treatments.
2.2.2 RGB
Two different image acquisition devices were used, including a handheld FLIR® E40 thermal imaging camera (FLIR Systems, Inc.) and a Sony camera (Sony Corporation). The thermal imaging camera has visible light and thermal infrared sensors, and the image size is 320 × 240 pixels (Figure 3b,c), with a lens of 1.0 m from the wheat canopy. Moreover, FLIR Tools software can also be used to extract complete RGB images with a resolution of 2048 × 1536 pixels (Figure 3a). The other device was the Sony Alpha 6300 digital camera with an image sensor of 23.5 × 15.6 mm Exmor CMOS, 24.2 effective megapixels, and the lens of E PZ 16-50 mm f 3.5–5.6. The frame of the acquired image was 6000 × 3376 pixels in JPG 24-bit depth (Figure 3d,e). The digital camera was set at an aperture of f/5, a fixed ISO value of 100, and a 1/200s exposure time with the flash turned off. In this mode, the color balance was set to the white balance for daylight conditions. For image segmentation and target recognition, about 10 images of different orientations were generally obtained between 9:00 and 12:00 for each plot, and the total images of the wheat canopy in each period were approximately 480 RGB pictures.
2.3 AGB and GY
The period from flowering to grain filling is an important period of grain development in wheat. Field sampling and image acquisition were carried out successively (specific sampling times as shown in Table 1) to provide real ground data. In each plot of fertilization test (Exp.1–3), the destructive sampling of 30 plants was randomly performed with two replications of each treatment. The samples were cleaned and divided into three categories according to plant organs: leaves, stems, and spikes, and then these organs were dried in an oven at 105°C for 30 min and dried at 80°C to constant weight (about 48 h). Afterward, the dry matter weight (DW) of plant samples under each period was measured, and the aboveground biomass (AGB) of the sample plot was calculated based on the planting density and DW of the sampled plants. The effective sample size of AGB in each period of Exp.1 and Exp.2 was 48, and the number in Exp.3 was 24. A total of 228 valid AGB samples were collected in the three experiments.
Yield measurement was carried out on 1 × 1 m2 quadrat from each plot at the maturity stage of wheat, and it was repeated three times. The number of plants, the grains per spike, and the spikes (more than five grains per spike as 1 spike) were counted separately for each measurement plot. The wheat kernels were threshed and dried; then, 1000 kernels were randomly selected to calculate the thousand kernel weight (TKW) according to the 13% kernel moisture content with three replications of each treatment. Grain yield (GY) and theoretical yield calculations were performed based on 3 × 1 m2 sampling plots harvested.
2.4 Image processing and extraction of feature values
Prior to extracting informative features from proximal-based RGB and thermal images, image preprocessing must be performed with the main procedures including denoising, smoothing, and cropping. The color and texture of visual RGB images were extracted by MATLAB (V2019a; MathWorks). Thermal infrared images were read by using FLIR Tools (version 6.4; FLIR Systems, Inc.), and the plant temperatures (including leaf temperatures and spike temperatures) were exported to MATLAB for data analysis. Image segmentation was performed on the RGB images to obtain subsample images with a size of 40 × 40 pixels. Before estimating wheat yield, image processing must be given to obtain a set of image datasets containing source and sink datasets, including corresponding color features, texture features, and plant temperature values, as shown in Figure 4.
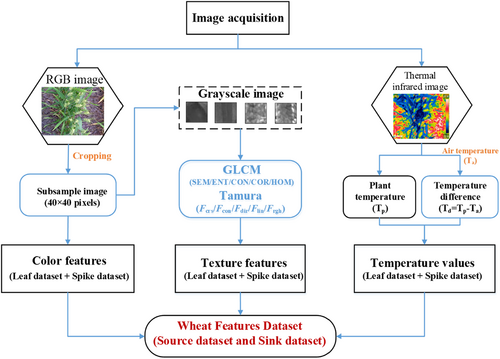
2.4.1 Color features extraction
Various color features extracted from RGB images have been used to evaluate the growth state of wheat. Twenty-seven color features, as shown in Table 2, were calculated from RGB images, which possess the capacity to estimate yield. The calculated color feature values were averages of the RGB image subsamples.
| Index | Abbreviation | Equation | Reference |
|---|---|---|---|
| Normalized Red Index | r | Guo et al. (2020); Meyer and Neto (2008) | |
| Normalized Green Index | g | Guo et al. (2020); Meyer and Neto (2008) | |
| Normalized Blue Index | b | Guo et al. (2020); Meyer and Neto (2008) | |
| Green Blue Difference Index | GBDI | Kawashima and Nakatani (1998) | |
| Excess Green Vegetation Index | EGVI | Meyer and Neto (2008) | |
| Excess Red Vegetation Index | ERVI | Meyer and Neto (2008) | |
| Gray | Gray | Kazmi et al. (2015) | |
| Red Green Ratio Index | RGRI | Saberioon et al. (2014) | |
| Excess Red Index | ExR | Meyer and Neto (2008) | |
| Excess Green Index | ExG | Woebbecke et al. (1995) | |
| Excess Blue Index | ExB | Woebbecke et al. (1995) | |
| Excess Green Minus Excess Red | ExGR | Camargo Neto (2004) | |
| Normalized Green Blue Difference Index | NGBDI | Sulik and Long (2016); Verrelst et al. (2008) | |
| Woebbecke Index | WI | Woebbecke et al. (1995) | |
| Normalized Pigment Chlorophyll Ratio Index | NPCI | Peñuelas et al. (1994) | |
| Normalized Green Red Difference Index | NGRDI | Tucker (1979) | |
| Visible Atmospherically Resistance Index | VARVI | Gitelson et al. (2002) | |
| Green Leaf Index | GLI | Guijarro et al. (2011) | |
| Hue Index | HI | Gholizadeh et al. (2020) | |
| True Color Vegetation Index | TCVI | Jiang et al. (2019) | |
| Color Index Of Vegetation | CIVE | Kataoka et al. (2003) | |
| Red Green Blue Vegetation Index | RGBVI | Bendig et al. (2015) | |
| Modified Green Blue Vegetation Index | MGBVI | Guo et al. (2021) | |
| Modified Green Blue Vegetation Index | MGRVI | Bendig et al. (2015) | |
| Redness Index | RI | Barron and Torrent (1986) | |
| Brightness Index | BI | Gholizadeh et al. (2020) | |
| Visible Atmospherically Resistant Index | VARI | Gitelson et al. (2002) |
- Note: R, G, and B are the reflectance of red, blue, and green channels, respectively.
2.4.2 Texture features extraction
Texture features are dominant indicators for object detection and image classification, and they are widely applied to the yield estimation (Hall-Beyer, 2017; Khatami et al., 2016; Peña-Barragán et al., 2011; Zhang et al., 2007). The gray-level co-occurrence matrix (GLCM) was first proposed by Haralick et al. (1973), and this algorithm creates the corresponding grayscale co-occurrence matrix through the relative position between two pixels of an image, so as to express the spatial grayscale dependence between image pixels, and then achieve the relevant texture information of the image (Hall-Beyer, 2017; Singh et al., 2017). By contrast, the Tamura texture feature is more intuitive and more consistent with human visual perception than the texture feature obtained by the gray-level co-occurrence matrix. Therefore, this study selected GLCM and Tamura algorithms to extract texture features of wheat plants (source and sink organs).
2.4.3 Temperature feature calculation
2.5 Data analysis and model development
Not all predictor variables are equally important for machine learning models, and redundant variables can significantly degrade model performance (Nadafzadeh & Abdanan Mehdizadeh, 2019; Son et al., 2015). Appropriate feature selection can improve the performance of predictive models (Nadafzadeh & Abdanan Mehdizadeh, 2019). To optimize the model, this study used three algorithms, principal component analysis (PCA), least absolute shrinkage and selection operator (LASSO), and recursive feature elimination (RFE), to select proper features and remove insignificant to improve the prediction accuracy.
Principal component analysis is one of the most commonly used dimensionality reduction methods, which mainly regroups variables that were originally correlated to some extent and transforms them into new comprehensive variables that are uncorrelated with each other, reflecting most of the information provided by the original variables (Fischer, 2019). PCA was implemented through MATLAB 2019a.
LASSO was originally developed by (Kumar et al., 2019; Tibshirani, 1996) in 1996. LASSO is an embedded feature selection method, which is another feature selection algorithm suitable for the data in this study. LASSO is a regression method for variable selection and regularization to improve the statistical models (Kumar et al., 2019; Shafiee et al., 2021). Data values shrink toward the center point, and the algorithm facilitates variable selection and parameter elimination. LASSO fits models with high multicollinearity. By adding a penalty equal to the absolute value of the coefficient size, the algorithm makes some coefficients become zero, resulting in variable elimination, so it can also be used as variable screening (Dai et al., 2021; Dutta et al., 2020; Yang et al., 2018). The LASSO feature selection used the “lars” package in R (version 4.1.3).
Recursive feature elimination is the third variable selection algorithm selected in this study. RFE is a well-known filter feature selection method (Chen et al., 2022; Han et al., 2019; Wang et al., 2021). It designs a “correlation statistic” to measure the importance of features: firstly searching a subset of variables from all variables in the training dataset, each corresponding to an initial feature, removing the least important variables according to the variable ranking, and then fitting the base model with the remaining subset of features (Wang et al., 2021). The “mlbench” and “caret” packages in R language were implemented for RFE feature selection.
Considering the possible nonlinear relationships between features and GY, two regression models (i.e., random forests (RF) and support vector regression (SVR)) were applied to estimate the grain yield for wheat with different parameter combinations. Random forest (RF) is a parallel learner based on the decision tree (Hoa et al., 2019). RF algorithm can reduce the overfitting phenomenon to a certain extent (Dang et al., 2019). The main steps include building a training set, using set to generate a regression model, and then making predictions. Support vector machine is a machine learning algorithm specialized at data classification and regression (Vapnik, 1999), which creates hyperplanes to maximize the margins between different classes by reducing the cost function for high prediction performance (Chen et al., 2022). In this study, we used epsilon-support vector regression (SVR) (Chang & Lin, 2011) to develop models and set tolerance of termination criterion (default 0.001). In addition, this study used the method of SVM kernel function (i.e., SVM with radial basis kernel function [RBF]) with the cross-validation 10-fold for classification to explore the variability of different types of eigenvalues at the source–sink level. The advantages, disadvantages, and application scenarios of two regression models are shown in Table 3.
| Algorithm | Advantages | Disadvantages | Application scenario | Reference |
|---|---|---|---|---|
| RF | Fast training | RF tends to fall into overfitting with noisier sample sets. | Crop Yield | Dong et al. (2020) |
| High accuracy rates | Lodging Detection | Zhang et al. (2020) | ||
| Generalizability | Plant N Content | Pereira et al. (2022) | ||
| Handling high-dimensional data | Aboveground Biomass | Maimaitijiang, Sagan, Sidike, Daloye, et al. (2020); Pereira et al. (2022); Zha et al. (2020) | ||
| Easy to make parallel methods | Nutritional Nitrogen Index | Pereira et al. (2022); Zha et al. (2020) | ||
| Plant N Uptake | Zha et al. (2020) | |||
| Canopy Nitrogen Weight | Lee et al. (2020b); Yu et al. (2022) | |||
| Total Nitrogen Content | López-Calderón et al. (2020) | |||
| CO2 Emission | Singh et al. (2022) | |||
| Moisture Content | Azmi et al. (2021) | |||
| Field Soil Moisture | Acharya et al. (2021) | |||
| Crop Coefficient Kc | Shao et al. (2021) | |||
| Leaf Area Index | Maimaitijiang, Sagan, Sidike, Daloye, et al. (2020) | |||
| SVR | Generalizability | Not suitable for large datasets. | Crop Yield | Dong et al. (2020) |
| Lodging Detection | Zhang et al. (2020) | |||
| Robustness | Plant N Content | Maimaitijiang, Sagan, Sidike, Daloye, et al. (2020) | ||
| Plant N Uptake | Zha et al. (2020) | |||
| Validity | Aboveground Biomass | Maimaitijiang, Sagan, Sidike, Daloye, et al. (2020); Zha et al. (2020) | ||
| Nutritional Nitrogen Index | Zha et al. (2020) | |||
| Computational simplicity | Poor prediction when the dataset has more noise. | Canopy Nitrogen Weight | Lee et al. (2020b); Yu et al. (2022) | |
| Groundwater Level Prediction | Guzmán et al. (2018) | |||
| CO2 Emission | Singh et al. (2022) | |||
| Moisture Content | Abdollahpour et al. (2020); Azmi et al. (2021) | |||
| Field Soil Moisture | Acharya et al. (2021) | |||
| Leaf Area Index | Maimaitijiang, Sagan, Sidike, Daloye, et al. (2020) |
Based on RGB images and thermal images, these features were generated using the equations as shown in Table 2 and Formulas 1-11. The average values of features for each plot (source and sink) were calculated to represent the average growth condition. Then, all variables were screened using feature selection algorithms (PCA, LASSO, and RFE). Regression analyses were performed based on the results of feature selection applying machine learning algorithms (SVR and RF) to explore the feasibility of these features for estimating wheat biomass and yield, respectively.
3 RESULTS
3.1 Correlation analysis of ground data
The minimum, maximum, mean, and standard deviation of the AGB and GY of the training set and validation set of this study are shown in Table 4. The range of AGB for the dataset was 5274–21,682 kg ha−1, and the mean value of AGB for the calibration set was 13,130 kg ha−1 with a standard deviation of 3415 kg ha−1; the mean value for the validation set was 10,760 kg ha−1 with a standard deviation of 2885 kg ha−1. The range of GY was 3218–8822 kg ha−1, and the mean value of GY for the calibration set was 6757 kg ha−1 with a standard deviation of 1663 kg ha−1; the mean of the calibration set was 6610 kg ha−1, and the standard deviation was 1709 kg ha−1. The large range of data ensured the robustness of the machine learning models derived from the data.
| Parameters | Calibration | Validation | ||||||
|---|---|---|---|---|---|---|---|---|
| Min | Max | Mean | SD | Min | Max | Mean | SD | |
| AGB (kg ha−1) | 6765 | 21,682 | 13,130 | 3415 | 5274 | 16,016 | 10,760 | 2885 |
| GY (kg ha−1) | 3414 | 8819 | 6757 | 1663 | 3218 | 8822 | 6610 | 1709 |
The corresponding variables of the source organs (leaf) and the sink organs (spike) were quite different, but they behaved differently under different nitrogen applications and planting density treatments. Figure 5a–c shows the differences of r, g, b in the wheat source and sink, and it can be seen that there are some differences in the RGB channels at the source–sink level, with overlaps in all three channels. This indicated that the color features of the source–sink based on RGB channels also overlap to a certain extent, and it is difficult to use color features to identify the source and sink. It might have limitations to using the color variable to estimate the yield. The GLCM texture features of the source and sink were distinctly different (Figure 5e,f), which would greatly improve the accuracy of identifying the source and sink. Previous studies had shown that the canopy temperature of wheat decreases with increasing N fertilizer level within a certain range, and there is a negative correlation between canopy temperature and grain yield during the filling period (Elbashier et al., 2012). Preliminary continuous temperature measurement was carried out on the wheat varieties after flowering, and the results showed that the average temperature of the sink was 26.26°C, and the average temperature of the source was 23.46°C. There was also a certain crossover area between the Tp of the source and sink (Figure 5d), but there were obvious differences between the average temperatures of the source and sink, and this inherent temperature difference between the source and sink did not change with the variety and treatment. Due to this difference, the thermal infrared device could easily identify the source–sink target and obtain the corresponding temperature in the later stage of wheat growth. Figure 6 shows the variation of Tp and Td from the flowering stage to the filling stage. The Tp of both source and sink organs decreased with the increase in nitrogen application. During the flowering stage, the Td between the source organs and the atmosphere was positively correlated with nitrogen application, and there was a negative correlation between the Td of the sink and nitrogen application. The Td of both the source and sink organs showed a negative correlation variation with the level of nitrogen application during the filling stage. This result suggested that the Tp and Td of the source and sink organs can be used as valid indicators for wheat yield estimation.
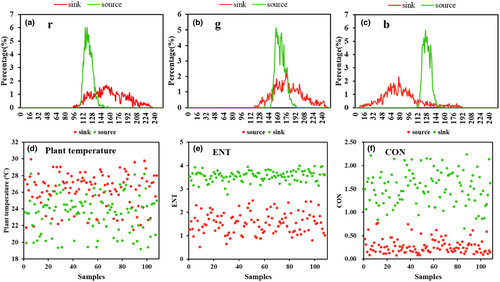

Correlation coefficients between source–sink eigenvalues and wheat AGB (Figure 7a) were calculated. The sensitivity of the source–sink eigenvalues differed from AGB and GY (Figure 7b). In the dataset containing only source eigenvalues, the parameters with significant correlation with AGB were SEM, ENR, Fcrs, Fdir, R, ERVI, RGRI, and other 16 variables (including four GLCM texture features, two Tamura texture features, nine color features, and one temperature value). The parameters for which the correlation between the source eigenvalues and the AGB reached a highly significant level were Fcon, Frgh, r, and ExR. In addition, there was a significant correlation between the relevant parameters of sink organs and AGB, including Fcon, Frgh, r, ExR, and spike temperature values. In summary, Fcon, Frgh, r, ExR, and Tp of source and sink organs were significantly correlated with AGB. The results demonstrated that the eigenvalues of the source–sink organs have a good correlation with AGB, and it is feasible to use the source–sink multivariate eigenvalues to predict the AGB in the later stage of wheat growth.
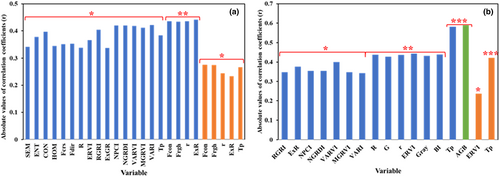
Figure 7b shows the correlation coefficient between wheat GY and source–sink eigenvalues. Among them, the source organ values with good correlations with GY include seven color values such as RGRI, ExR, and NPCI. The source variables that correlated with GY at highly significant levels were the six color values of R, G, r, ERVI, and the Tp of the source organs, and the temperature values of the sink organs also correlated well with GY. This indicated that there is a significant relationship between multivariate eigenvalues such as color value and temperature value of source–sink organs and GY, and this potential relationship can be used to predict wheat grain yield.
3.2 Feature selection
Before analyzing the raw data, it was necessary to standardize the data and then used the standardized data for data analysis. Therefore, this study used “Z-score normalization,” a standardization method based on the mean and standard deviation of the original data, to standardize the data. The principal component analysis was then performed on the variables, and PCA was performed on the feature matrix to check the potential grouping of the sample and identify possible feature outliers for the final purpose of dimensionality reduction. The principal component analysis results are shown in Figure 8 and Table 5. The cumulative contribution rate of the first nine principal components exceeded 95%, and PC1-PC9 explained most of the information in the original data.

| Principal component | Eigenvalue | Variance | Contribution rate (%) | Cumulative contribution rate (%) |
|---|---|---|---|---|
| PC1 | 16.76 | 6.16 | 39.90 | 39.90 |
| PC2 | 10.56 | 6.18 | 25.22 | 65.12 |
| PC3 | 4.41 | 0.89 | 10.51 | 75.63 |
| PC4 | 3.52 | 2.06 | 8.39 | 84.02 |
| PC5 | 1.46 | 0.35 | 3.48 | 87.50 |
| PC6 | 1.11 | 0.24 | 2.65 | 90.15 |
| PC7 | 0.88 | 0.09 | 2.09 | 92.24 |
| PC8 | 0.78 | 0.11 | 1.87 | 94.10 |
| PC9 | 0.67 | 0.06 | 1.60 | 95.70 |
| PC10 | 0.61 | 0.20 | 1.44 | 97.14 |
- Note: PC1-PC10 represent the first ten principal components of PCA.
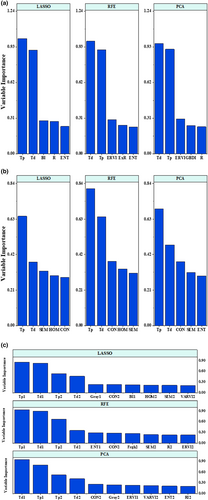
It was important to use appropriate variable selection methods to identify variables before modeling. An optimal variable selection algorithm can select the smallest and most efficient subset of features from the original dataset to improve model accuracy and speed up model runtime. The features selected by the three variable screening algorithms applied in this study are shown in Table 6. Among all the variables, including 42 indices such as GLCM texture features, Tamura texture features, color features, and temperature values, the PCA algorithm selected 35 indices, LASSO selected 35 indices, and 33 variables were selected by the RFE algorithm. Random forest (RF) is not only a regression algorithm, but also a commonly used method for variable selection. Therefore, this paper used RF to calculate and rank the importance of each variable in the models, and the top 5 variables of importance for each selected dataset are shown in Figure 9. The results in Figure 9 indicated that the models applying the source dataset mainly selected the variables related to temperature values and color features, and the models applying the sink dataset mainly selected the variables such as temperature values and GLCM texture features. In the machine learning models using the source–sink dataset, the important metrics included temperature values, GLCM features, and color values. By analyzing the importance of variables in the models, it was found that overall temperature indicators and GLCM texture indicators were more valuable for AGB and yield estimation in late reproduction and that temperature values (including Tp and Td) had high importance of variables in each model.
| Variable | PCA | LASSO | RFE |
|---|---|---|---|
| SEM | ✓ | ✓ | ✓ |
| ENT | ✓ | ✓ | ✓ |
| CON | ✓ | ✓ | ✓ |
| COR | ✓ | ✓ | |
| HOM | ✓ | ✓ | ✓ |
| Fcrs | ✓ | ✓ | |
| Fcon | ✓ | ✓ | |
| Fdir | ✓ | ✓ | |
| Flin | ✓ | ✓ | |
| Frgh | ✓ | ✓ | ✓ |
| R | ✓ | ✓ | ✓ |
| G | ✓ | ✓ | ✓ |
| B | ✓ | ✓ | ✓ |
| r | ✓ | ✓ | ✓ |
| g | ✓ | ✓ | |
| b | ✓ | ||
| GBDI | ✓ | ✓ | ✓ |
| EGVI | ✓ | ✓ | ✓ |
| ERVI | ✓ | ✓ | ✓ |
| Gray | ✓ | ✓ | ✓ |
| RGRI | ✓ | ✓ | ✓ |
| ExR | ✓ | ✓ | |
| ExG | ✓ | ||
| ExB | ✓ | ✓ | ✓ |
| ExGR | ✓ | ✓ | |
| NGBDI | |||
| WI | ✓ | ✓ | |
| NPCI | ✓ | ✓ | |
| NGRDI | ✓ | ✓ | |
| VARVI | ✓ | ✓ | ✓ |
| GLI | ✓ | ✓ | ✓ |
| HI | ✓ | ✓ | |
| TCVI | ✓ | ✓ | ✓ |
| CIVE | ✓ | ✓ | |
| RGBVI | ✓ | ✓ | |
| MGBVI | ✓ | ✓ | |
| MGRVI | ✓ | ✓ | ✓ |
| RI | ✓ | ✓ | ✓ |
| BI | ✓ | ✓ | |
| VARI | ✓ | ✓ | ✓ |
| Tp | ✓ | ✓ | ✓ |
| Td | ✓ | ✓ | ✓ |
3.3 AGB estimation models
Table 7 shows the model comparison between the SVR models and the RF models for estimating AGB using different datasets. In terms of the utilized datasets, the models constructed by combining the source and sink datasets performed better (LASSO-SVR: R2 = 0.76, RMSE = 1493.45 kg ha−1, SD = 2785.13 kg ha−1, RPD = 1.86; LASSO-RF: R2 = 0.85, RMSE = 1179.09 kg ha−1, SD = 2474.25 kg ha−1, RPD = 2.10), and this result indicated that the source–sink features achieve better accuracy of estimating AGB. Comparing the performance of two machine learning models, RF outperformed the SVR models, and RF models generally had higher R2, smaller RMSE and SD. To further analyze the model performance, Figure 10 presents the scatterplots of the estimated AGB against the measured AGB of the SVR models and the RF models using the three variable selection algorithms and using the source–sink dataset. For all six models, the data points were evenly distributed along with the 1:1 relationship, showing a good agreement between the measured and estimated values of AGB using the source–sink dataset. Comparing the three variable selection algorithms in this study, it can be found that the SVR models and RF models constructed by the LASSO algorithm achieve the highest estimation accuracy (LASSO-SVR: = 0.75, RMSEcal = 1711.14 kg ha−1, RPDcal = 1.90; = 0.76, RMSEval = 1493.45 kg ha−1, RPDval = 1.86; LASSO-RF: = 0.92, RMSEcal = 1489.67 kg ha−1, RPDcal = 1.92; = 0.85, RMSEval = 1179.09 kg ha−1, RPDval = 2.10), and the RF models were again superior to the SVR models.
| Method | Dataset | SVR | RF | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R 2 | RMSE (kg ha−1) | SD (kg ha−1) | RPD | R 2 | RMSE (kg ha−1) | SD (kg ha−1) | RPD | ||
| PCA | Source | 0.68 | 1717.91 | 2839.29 | 1.65 | 0.80 | 1258.94 | 2512.47 | 2.00 |
| Sink | 0.70 | 1645.77 | 2795.55 | 1.70 | 0.82 | 1421.47 | 2343.24 | 1.65 | |
| Source–Sink | 0.75 | 1499.06 | 2789.71 | 1.86 | 0.85 | 1176.95 | 2461.05 | 2.09 | |
| LASSO | Source | 0.68 | 1715.33 | 2838.91 | 1.66 | 0.81 | 1237.03 | 2511.13 | 2.03 |
| Sink | 0.69 | 1680.69 | 2795.12 | 1.66 | 0.79 | 1442.55 | 2345.58 | 1.63 | |
| Source–Sink | 0.76 | 1493.45 | 2785.13 | 1.86 | 0.85 | 1179.09 | 2474.25 | 2.10 | |
| RFE | Source | 0.66 | 1761.53 | 2796.62 | 1.59 | 0.79 | 1310.73 | 2498.04 | 1.91 |
| Sink | 0.67 | 1714.51 | 2792.39 | 1.63 | 0.76 | 1514.07 | 2326.03 | 1.54 | |
| Source–Sink | 0.68 | 1717.91 | 2785.84 | 1.81 | 0.80 | 1258.94 | 2470.75 | 2.09 | |
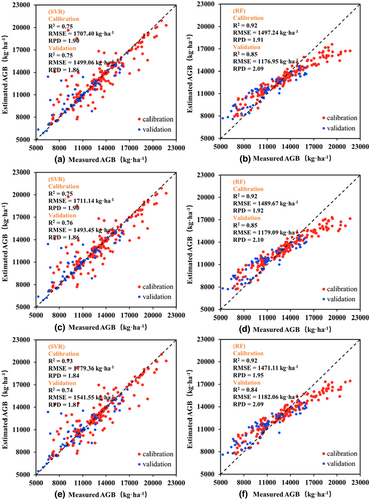
In general, higher R2 values and lower RMSE and SD values indicate better model performance. Therefore, the AGB estimation model built by the LASSO algorithm and RF machine learning model has the best performance and 2.0 ≤ RPD <2.5, which can be expressed as a very good estimation model (Bruning et al., 2019).
3.4 GY estimation models
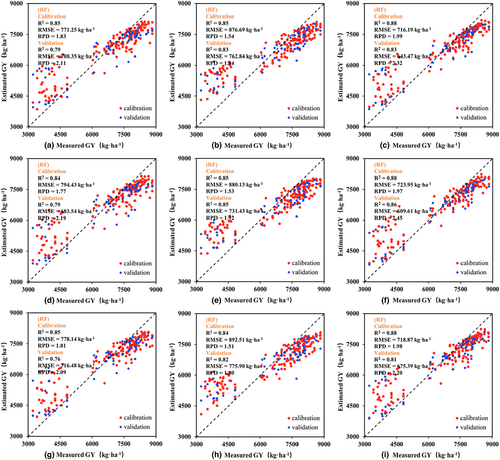
To evaluate the performance of yield estimation for different datasets, R2, RMSE, SD, and RPD were calculated to assess the performance of the RF model (Table 8). The results of the validation dataset showed that the RF estimation yield models built by the three variable selection algorithms (PCA-RF: RPD = 2.32; LASSO-RF: RPD = 2.45; RFE-RF: RPD = 2.20) could all be expressed as good models (2.0 ≤ RPD < 2.5). Among the three variable selection algorithms, the RF yield estimation accuracy based on LASSO screening variables reached the highest, which was consistent with the comparative results of the AGB estimation model. Further model analysis results demonstrated that among the three RF yield estimation models with the same variable selection algorithm, the wheat yield estimation models constructed based on the source dataset and sink dataset were comparable. With the model performance of the source dataset outperformed that of the sink dataset, and the model that fused the source and sink features had the best performance (Figure 11). Taking the LASSO-RF model as an example, the RMSE of the LASSO-RF model using the source–sink dataset was reduced by 10.82% and 16.66%, respectively, compared with the yield estimation model that only used the source dataset and the sink dataset. According to the model classification of previous studies on RPD (Bruning et al., 2019), RF estimation models using the source dataset can be defined as good/very good models (2.50 > RPD ≥ 1.80); RF models based on the sink dataset have fair performance, while the models combining source and sink features have the best performance (the validation set: R2 > 0.81, RMSE: 609.61–675.39 kg ha−1, RPD ≥ 2.20). These findings demonstrated the feasibility of using RF regression models with eigenvalues of sink organs for grain yield prediction, and the combination of sink eigenvalues can increase the accuracy of wheat yield estimation.
| Method | Dataset | Calibration | Validation | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R 2 | RMSE (kg ha−1) | SD (kg ha−1) | RPD | R 2 | RMSE (kg ha−1) | SD (kg ha−1) | RPD | ||
| PCA | Source | 0.85 | 771.25 | 1411.70 | 1.83 | 0.79 | 700.35 | 1481.14 | 2.11 |
| Sink | 0.85 | 876.69 | 1349.42 | 1.54 | 0.83 | 762.84 | 1399.85 | 1.84 | |
| Source–Sink | 0.88 | 716.19 | 1422.33 | 1.99 | 0.83 | 643.47 | 1490.56 | 2.32 | |
| LASSO | Source | 0.84 | 794.43 | 1408.16 | 1.77 | 0.79 | 683.54 | 1496.88 | 2.19 |
| Sink | 0.85 | 880.13 | 1349.90 | 1.53 | 0.85 | 731.43 | 1407.28 | 1.92 | |
| Source–Sink | 0.88 | 723.95 | 1423.44 | 1.97 | 0.86 | 609.61 | 1496.36 | 2.45 | |
| RFE | Source | 0.85 | 778.14 | 1407.55 | 1.81 | 0.76 | 716.48 | 1496.20 | 2.09 |
| Sink | 0.84 | 892.51 | 1349.40 | 1.51 | 0.82 | 775.90 | 1394.11 | 1.80 | |
| Source–Sink | 0.88 | 718.87 | 1424.20 | 1.98 | 0.81 | 675.39 | 1486.03 | 2.20 | |
4 DISCUSSION
4.1 Comparison of source features and sink features
Both source and sink in wheat are important organs for photosynthetic function. Source–sink interactions regulate carbon assimilation, translocation, allocation, and storage throughout the wheat and exert a major influence on the productivity of harvestable organs. The entire life cycle of wheat is accompanied by the conversions of source and sink, and yields depend on the source–sink relationships influenced by environmental changes (Yu et al., 2015).
The vegetation indices calculated based on RGB images showed the potential of wheat yield prediction, but the yield estimation results in the later growth period need to be improved. This is mainly due to the fact that the main body of the plant structure changes gradually as the wheat spikes begin to grow in the late growth stage, and the vegetation indices lose sensitivity at this stage. In addition, under the treatment of high density and high nitrogen, the vegetation characters are also prone to saturation (Li et al., 2021; Serrago et al., 2013; Xu et al., 2022; Zha et al., 2020). Therefore, this study proposed to integrate the multivariate eigenvalues of the source and sink organs to overcome the saturation problem of the conventional vegetation indices. The feature selection algorithm and machine learning algorithm were used to realize the AGB and GY estimation of wheat in the later stage of growth, so as to improve the robustness of the prediction models.
In this study, due to the differences in the eigenvalues of the source and sink organs, the differences between the two were not consistent. This revealed that the original sample space does not have a hyperplane that can correctly divide the two types of samples from the source and the sink organs, and this binary classification problem is nonlinear. Therefore, we used the method of SVM kernel function (i.e., the SVM of the RBF kernel function) for classification. The classification results are displayed in Table 9, and the recognition accuracy was low only by using color features. The Tamura texture values were used to identify the source–sink organs, and the recognition results were also unsatisfactory, which indicated that there are more overlapping areas between the color values and the texture values of the source organs and the sink organs without significant differences. GLCM is a representation of the grayscale correlation of adjacent pixels using conditional probability to reflect texture distribution, and GLCM can reflect the comprehensive information of image grayscale regarding direction, adjacent interval, and change magnitude (Haralick et al., 1973; Khatami et al., 2016; Peña-Barragán et al., 2011; Zhang et al., 2007). As a result, GLCM texture features reflect the variation of statistical features between neighboring pixels in grayscale images (Hall-Beyer, 2017). Tamura texture feature is a theory proposed based on the psychological study of human visual perception of texture (Tamura et al., 1978). Using only Tamura texture for the source–sink classification in this paper had little application value, but combining it with color values can increase the classification accuracy. The classification accuracies were ranked in the following order: G + A + T, C + G + A + T, C + G + A, G + A, G + T, and C + G, and the classification accuracy of these datasets was higher than 97% (Table 9). This result demonstrated that the GLCM and temperature values of the source–sink organs are more different, and these features are favorable for target identification, while the Tamura texture and color values have more overlapping regions, which affects the target classification accuracy.
| Dataset | 10-fold cross-validation | |
|---|---|---|
| 80%train | 20%test | |
| C | 54.12% | 41.30% |
| G | 96.70% | 98.91% |
| A | 56.31% | 57.60% |
| T | 95.05% | 92.39% |
| C + G | 97.25% | 97.82% |
| C + A | 84.34% | 48.91% |
| C + T | 90.65% | 80.43% |
| G + A | 98.90% | 97.82% |
| G + T | 98.90% | 98.91% |
| A + T | 94.50% | 83.69% |
| C + G + A | 99.45% | 98.91% |
| C + G + T | 98.62% | 93.47% |
| C + A + T | 93.13% | 73.91% |
| G + A + T | 99.72% | 98.91% |
| C + G + A + T | 99.45% | 98.91% |
- Note: “C” refers to the color features, “G” refers to the GLCM texture features, “A” refers to the Tamura texture features, and T refers to the temperature values, respectively.
Based on the above studies, we constructed 18 AGB estimation models and 9 GY estimation models using three datasets, respectively. Comparing SVR models of AGB estimation with RF models of that, it is found that even the worst AGB estimation model based on the source–sink dataset (RFE-SVR: R2 = 0.74, RMSE = 1541.55 kg ha−1, RPD = 1.81) can also produce better AGB estimated values (the validation dataset: R2 > 0.70 and RPD > 1.80). The nine RF models of GY estimation were compared, revealing that the GY estimation model based on the source–sink dataset showed excellent performance to predict GY values (the validation set: R2 > 0.80 and RPD >2.00). Therefore, a comprehensive evaluation of the model performance of the three datasets (Tables 7 and 8) indicated that the models established by the source–sink dataset have the best performance, followed by the models based on the source dataset (AGB estimation model: source outperforms the sink) or the models using the sink dataset (GY-estimated model: sink outperforms source). Ultimately, the integration of multivariate eigenvalues of source–sink organs improved the accuracy and robustness of yield prediction models.
4.2 Optimal models for wheat yield estimation
The flowering stage to the maturity stage was the key period to determine the wheat yield, and the source and sink organs played an important role in the yield accumulation. This study involved two wheat varieties, four N fertilizer applications, and three plant densities in three field planting trials over a 2-year period. The results showed that there was a very complex relationship between the multivariate eigenvalues of source–sink organs and wheat AGB and GY. Therefore, this study used two machine learning models, SVR and RF, to explore the feasibility of estimating AGB and GY using the phenotypic characteristics of source–sink organs from flowering to maturity.
For the AGB estimation models, we developed a total of 18 models including nine SVR models and nine RF models (Table 7). Among the 18 models, the combined LASSO variable selection method and the RF model based on the source–sink dataset had the best performance (the calibration set: R2 = 0.76, RMSE = 1493.45 kg ha−1, RPD = 1.86; the validation set: R2 = 0.85, RMSE = 1179.09 kg ha−1, RPD = 2.10). The RF regression model can handle multiple variables, and the generalization performance and training efficiency of the model are good (Cen et al., 2010; Sun et al., 2017). Considering the possible nonlinear relationship between multivariate variables and GY, RF prediction models that can identify collinear and nonlinear relationships between parameters are proposed (Lee et al., 2020a; Zha et al., 2020). Moreover, compared with the SVR models, the RF models in this study showed a more stable performance in estimating AGB, which is consistent with the conclusion of previous studies (Cen et al., 2019). Therefore, the RF algorithm based on three datasets combined with three variable selection methods was selected for the GY prediction (Table 8, Figure 11). For all nine models, the LASSO-RF model based on the source–sink dataset was the best and had the highest accuracy (the calibration set: R2 = 0.88, RMSE = 723.95 kg ha−1, RPD = 1.97; the validation set: R2 = 0.86, RMSE = 609.61 kg ha−1, RPD = 2.45). As with previous findings (Bruning et al., 2019), LASSO-RF (RPD = 2.45) model using the source–sink dataset achieved good GY estimation. Although the GY estimation model only applied the RF model, the other eight estimation models also had good predictions with R2 > 0.80 and RPD > 2.0 for the validation set.
In summary, the AGB and GY prediction models consist of multiple proximity sensor-based variables for source and sink organs, and the estimation results of both the SVR and RF models, which were machine learning models based on multivariate fusion, were more reasonable. To compare with the performance of the two machine learning models, it can be found that the RF models show stable performance in estimating both AGB and GY and outperforms the SVR models in this study.
4.3 Influence of feature selection methods on the performance of estimation models
Studies using variable selection methods to estimate plant AGB and GY in machine learning models have limitations (Xu et al., 2022; Zhu et al., 2019). The optimal combination of variable screening techniques and machine learning algorithms can produce more accurate estimates of AGB and GY in this study. Among various combinations of AGB estimation models with three variable selection methods and two machine learning algorithms, the combination of LASSO and RF exhibited the best AGB estimation, while the worst model accuracy was provided by the combination of RFE and SVR (Table 7). For all nine combinations of GY estimation models with three variable selection methods and three datasets, the LASSO-RF model using the source–sink dataset showed the best GY estimation, while the combination of RFE and RF showed poor GY estimation (Table 8). Coincidentally, the combination of LASSO and RF showed the best estimation power in both the AGB estimation and GY estimation models.
Furthermore, a comparison in terms of the optimal number of variables selected revealed that PCA selected 35 variables, LASSO selected 35 variables, and RFE selected 31 variables (Table 6). The number of optimal variables selected using RFE is relatively small, which is consistent with the research of (Wang et al., 2021), but the smallest number of variables selected does not represent the best performance of model estimation. Additional studies should be conducted to assess the association between the number of variable choices and model estimation performance. Using LASSO to select the best variables resulted in more accurate estimates of AGB and GY than adopting the RFE and PCA variable selection algorithms (Tables 7 and 8). However, the differences caused by using different variable selection methods were not as large as those caused by using different machine learning models. As shown in Table 7, the RMSE and SD values produced by the three variable selection methods are not significantly different, while there were significant differences in the RMSE and SD values generated using the SVR and RF models. The importance rank of the variables is shown in Figure 9, and the most important ones are Tp, Td, ENT, SEM, HOM, CON, HI, ERVI, and other variables. The above eight variables, including 2 temperature values, four GLCM texture values, and two color values, were particularly important for the accurate estimation of wheat AGB and GY. These findings indicated that the temperature and GLCM texture values contribute the most to the performance of the wheat yield estimation model, followed by the color values and finally the Tamura texture values.
4.4 Limitations and further research
This preliminary study provided a promising method for AGB and GY monitoring, but there were some limitations. Considering that the spikes started to grow in the late reproductive stage and the main body of the plant structure gradually changed, the vegetation index lost its sensitivity at this stage, and it was also prone to saturation under the high density and high N treatment (Dandrifosse et al., 2022; Dang et al., 2019; Li et al., 2021; Xu et al., 2022). This study can improve this saturation phenomenon, and the comprehensive utilization of color, texture, and temperature eigenvalues based on source and sink performs better in estimating wheat AGB and GY under different nitrogen application rates. With regard to the multiple combinations of the AGB estimation models, the model performance using the source dataset outperformed the model using the sink dataset alone. Among the GY estimation models, the accuracy of the RF model using only the sink dataset was higher than that of the model using only the source dataset. However, spectral information was not discussed in the eigenvalues of the source–sink organs involved in this study, and spectral features can be added in future studies to expand the characteristic differences of source–sink organs (Araus & Cairns, 2014; Bendig et al., 2015; Fu et al., 2021). In addition, the AGB model and GY model we developed still need to be evaluated for the suitability of other agronomic traits for this study, especially high-throughput plant phenotypes (Lee et al., 2020a; Xu et al., 2022; Yu et al., 2022; Zhu et al., 2019). Specifically, to further evaluate the effects of source and bank organs on the AGB estimation model and the GY estimation model, experiments with multiple wheat genotypes as well as other crop types under different environmental conditions are also needed (Geipel et al., 2014; Gong et al., 2018; Peng et al., 2019; Wan et al., 2020). On the contrary, due to the limitations of proximity sensors, UAV technology is becoming more and more commonly used for crop phenotype monitoring (Wan et al., 2020; Wang et al., 2021; Xu et al., 2021; Yu et al., 2022; Zhu et al., 2019), so in the next research, UAV technology and proximity sensors can be combined to obtain ultra-high-resolution images in multiple directions for more accurate crop yield estimation.
5 CONCLUSIONS
The images used in this study are based on RGB images and thermal images acquired by proximity sensors, and for the source–sink organs, the relevant variables such as color values, GLCM texture values, Tamura texture values, and temperature values were extracted. This study demonstrated the potential of multivariate eigenvalues of both source and sink organs to predict wheat yield, where the source and sink organs datasets differed in their performance on AGB estimation and GY estimation, and the combined dataset of source and sink features performed best for estimating AGB and GY. Combining machine learning models and variable selection methods can significantly affect the accuracy of the estimated models. The machine learning models made more difference for yield prediction than the variable selection algorithms. The best model based on the source–sink dataset, variable selection methods, and machine learning algorithms can produce more accurate AGB and GY estimates.
This study showed that the combination of data at the source–sink level improved the accuracy of yield prediction. The potential application of proximal sensing technology in wheat yield prediction was demonstrated. Compared with low-altitude UAV technology, proximal sensing technology obtains richer information about the source–sink information and higher image resolution, which is a significant advantage that proximity sensing technology possesses. Nowadays, with the rapid development of high-throughput phenotyping technology, the use of the newly developed LASSO-RF model to monitor the AGB of wheat in the late growth stage and predict wheat yield is of great significance for improving crop management and ensuring food security.
AUTHOR CONTRIBUTIONS
Rui Li involved in conceptualization, investigation, formal analysis, and writing—original draft. Dunliang Wang involved in investigation. Bo Zhu involved in investigation. Tao Liu involved in conceptualization. Chengming Sun involved in conceptualization, writing—review and editing, supervision, and project administration. Zujian Zhang involved in conceptualization, supervision, and project administration.
ACKNOWLEDGMENTS
This work was supported by the National Natural Science Foundation of China (31671615, 31701355, 31872852, and 32071945), the National Key Research and Development Program of China (2018YFD0300805), and the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD).
FUNDING INFORMATION
The National Natural Science Foundation of China (31671615, 31701355, 31872852 and 32071945), the National Key Research and Development Program of China (2018YFD0300805), and the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD).
CONFLICT OF INTEREST
The authors have stated explicitly that there are no conflicts of interest in connection with this article.
Open Research
DATA AVAILABILITY STATEMENT
The data that support the findings of this study are available from the corresponding author upon reasonable request.




