Layered metal halide perovskite solar cells: A review from structure-properties perspective towards maximization of their performance and stability
[Correction added on 4 August 2021, after first online publication: Reference 105 has been added and subsequent references have been renumbered. The in-text citations have also been corrected.]
Funding information: Conselho Nacional de Desenvolvimento Científico e Tecnológico, Grant/Award Numbers: 435260/2018-9, 465423/2014-0; Coordenação de Aperfeiçoamento de Pessoal de Nível Superior, Grant/Award Number: 88887.477439/2020-00; Fundação de Amparo à Pesquisa do Estado de São Paulo, Grant/Award Numbers: 2017/11986-5, 2019/25765-6
Abstract
Perovskite solar cells (PSCs) technology is now reaching its full potential in terms of power conversion efficiency, but still presenting problems related to long-term stability under operating conditions. One of the most promising alternatives to PSCs is the layered PSCs (2D-PSCs). Layered perovskites present a huge compositional variety, which can be used to directly tune photophysical characteristics that influence the operational mechanisms of the devices. This review addresses the structural organization of both the organic and inorganic sublattices, focusing on how the structure influences the quantum and dielectric confinement, phonons and charge carriers' dynamics, charge mobility, and structural defects. We discuss the relation between the structure-properties of layered perovskites with the performance of solar cells. We, then, offer insights into how these characteristics have been controlled in the assembly of 2D-PSCs to improve their efficiency and stability. We conclude by giving a perspective of future developments and open areas of exploration that might impact the progress of this rapidly growing technology.
1 INTRODUCTION
Solar cell technologies started to be developed in the 1950s based on highly pure, bulky, monocrystalline silicon for application in aerospace exploration. Later, polycrystalline and amorphous silicon devices, which also demand purification methods that result in a very high production cost, were also developed. Monocrystalline and polycrystalline materials such as Si or GaAs used in the manufacturing of photovoltaic devices are commonly known as first-generation solar cells.1, 2 Focusing on the reduction of production cost, the second generation of solar cells established the use of amorphous materials and their thin-films, which decreases the amount of material necessary to build devices and allows the usage of different raw materials such as cadmium telluride (CdTe) and copper indium gallium selenide (CIGS).3 The use of these materials, however, leads to more intrinsic structural defects than observed in the first generation devices, resulting in a lower power conversion efficiency (PCE).4 The so-called third-generation solar cells focus on new materials, different operation mechanisms, alternative architectures, and a variety of distinct and cheaper preparation methods.4, 5
Among them, perovskite solar cells (PSCs), in which hybrid organic–inorganic or purely inorganic halide perovskites are applied as the active layer, have emerged as a prominent alternative with rapid deployment compared to other emerging technologies. In a little more than a decade, these devices achieved an unprecedented rise in PCE, from 3.8% in 2009, when Kojima first used this material as a sensitizer in dye-sensitized solar cells, to the certified record of 25.5%.6 The efficiency6, 7 record achieved by PSCs is getting closer to other highly efficient photovoltaic technologies: 26.1% for single crystal silicon devices and 27.8% for single-crystal GaAs devices.7 Among the advantages of PSCs technology, perhaps the most appealing one is the relatively lower production cost due to the ease of processing with wet routes at low temperatures. However, for a practical solar cell, a stable PCE at operational conditions is expected; that is, one sun at moderate temperatures, environmental moisture, and in the presence of oxygen. Yet, in these conditions, PSCs have not delivered acceptable PCE for long periods due to both structural and environmental instability.8-10
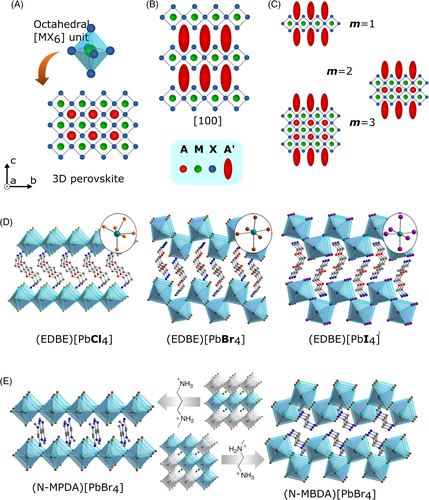
As an alternative to achieve greater operational stability, 2D and quasi-2D layered perovskite structures have received increasing attention in the last years. For clarity, 2D perovskite refers to the family of layered metal halides with a single inorganic slab (i.e., a two-dimensional plaque of [PbX6]4− octahedrons – m = 1, where m is the number of slabs), whereas quasi-2D perovskite denotes structures with 2 or more slabs (m > 1). Whenever we intend to refer to these materials in a more general form (i.e., 2D and quasi-2D perovskites together), we will use the term layered metal halides or simply layered perovskites. In this review, we opt to use m to refer to the number of slabs in the inorganic sublattice, and we use n to denote the principal quantum number when discussing their electronic structure. These layered structures are known to be more resistant to moisture than their 3D counterparts (Figure 1A–C illustrates their crystal structure).11, 12 This class of materials is formed by the insertion of an organic cation in the bulk structure, which acts as a separator of the octahedron slabs. This organic layer is responsible for the improved moisture stability of layered metal halides due to the hydrophobic characteristics of the chains, which is the main reason for the growing interest in the application of 2D perovskite in solar cells.
By controlling the stoichiometry of the components in the precursor solution, 2D structures, or randomly quasi-2D perovskites can be formed.13-19 In addition, an organic cation solution can be coated over the 3D perovskite films, allowing the formation of layered metal halides within the bulk grains and/or surface; however, in this situation, most of the properties of the layered material can be masked by the bulk.20 The optical behavior of these layered structures is associated with the thickness of the inorganic framework; while the 2D perovskites present remarkable excitonic dynamics, the quasi-2D counterparts vary from a quantum-well-like (up to m ≈ 5) to a bulky-like behavior (m > 5).
Layered metal halides have been studied for decades and present a wide variety of compositions. Besides the inorganic precursors (i.e., metal halides), a wide set of organic separators can be applied for the synthesis of these layered structures.21-23 This compositional variability allows for an equally rich variety of physical and optical properties for these semiconductors. As such, these materials find applications in many optoelectronic devices such as LEDs, photodetectors, solar cells, and spintronics.23-25 In this manner, the comprehension of their structure–property relationship will direct the development of efficient and durable devices.
In this review, we first introduce the main characteristics of layered perovskites with respect to the inorganic and organic structures. Then, we discuss their optoelectronic properties, establishing a relationship with their structural features. We carry on the discussion exploring the influence of these characteristics in the performance of these materials in devices, focusing on layered PSCs (2D-PSCs). The modification of 3D PSCs with layered metal halides, known as 2D/3D PSCs, is not covered in this review, although some works are eventually mentioned to emphasize a specific property of layered metal halides in these systems. Lastly, we present the current development of the field and the milestones in the efficiency and stability of 2D-PSCs devices. To conclude, a perspective of future developments and challenges is given.
2 MATERIAL STRUCTURE
M-X-M bond lengths and angles are a consequence of the M and X ions sizes and the nature of their chemical bonds. In addition, A-site cations may influence the bond lengths and angles due to the steric effect.36 Due to the strong ionic character, metal halide perovskites present a “soft” structure, meaning that distortions in the bond angles may easily occur, which directly influence their optical and structural properties.36, 37 These distortions are more evident in layered metal halides, as reduction of dimensionality on a given direction releases the structural tension in the inorganic network, allowing greater distortions in the lattice. Thus, distortions on the M-B-M and B-M-B angles in the framework are closely linked with electrostatic interactions between organic separator.38-40
2.1 The inorganic framework
Layered perovskites are separated by a (bi)layer of organic cations which are formed by “slicing” their 3D analogs in specific crystallographic directions <hkl> (Figure 1B). The resulting inorganic framework consists of octahedrons connected by the vertices and, in the case of quasi-2D perovskites, two cations are necessary for charge neutrality: the cation A and the separating cation (A')—Figure 1C. The condition for layered perovskites formation can be rationalized as a break in the Goldschmidt tolerance factor, where the organic cations, A', have dimensions larger than the limit for the A site. The optical properties of these slabs are connected to the slicing direction, as it defines how the octahedrons are arranged in the inorganic framework. In the <100> − oriented, which is the most common crystal structure of layered perovskites, the octahedrons are linearly arranged in the plane perpendicular to the [100] direction. The number of inorganic slabs varies from m = 1 to m = ∞ (which is equivalent to a 3D perovskite). The <110> − oriented present zigzag patterns according to specific characteristics of the organic cations and specific compositions (Figure 1D,E).41-43 The <111> orientation, only observed in structures where the M site is occupied by a M3+ or by a mixture of MI2+-MII3+ cations, is rarely observed and, due to the distinct composition, significant differences in their electronic structure and charge carriers' dynamics, compared to the <100> and < 110> phases, are observed.44, 45
Layered perovskites oriented in the direction <100> are formed when alkylammonium or alkyl-diammonium are used as organic cations. Multiple slabs with both cage structures containing A and the separator molecules A' can be prepared using different molar ratios of the cations, originating 2D and quasi-2D perovskites.46-49 The formation energy of these materials increases with the reduction in the number of slabs (m = 1, 2, 3, …).13 Experimentally, thermal treatment may be necessary to assist the formation of layered perovskites, and polycrystalline materials are almost always comprised of a mixture of phases with different values of m.20, 49, 50 An important characteristic of layered perovskites regarding the value of m is the occurrence of quantum and dielectric confinement when m is ≤5, approximately.51
The morphology of these structures is also dependent on the size compatibility between the A' cation and the inorganic framework. Since the size of the cavity is determined by the dimensions of the octahedrons, the same A' cation may lead to <100> orientation in [PbCl6]4−, while, for [PbBr6]4− or [PbI6]4−, the <110> − oriented phase is formed instead (Figure 1D).41, 52 However, it is noteworthy that distortions observed in the octahedrons are also related to the ns lone-pair electrons present in metals of the group 14, and, according to the dimensions and orbital overlapping with the X anion, this effect can be more or less pronounced. As a consequence of this interplay between M and X, the expression of the ns electron pair in the coordination environment around the group 14 metals varies from static trigonal or tetragonal distortions (mainly in 4s2 of Ge2+ halides) to dynamic distortions (more evident in 6s2 Pb2+ compounds).53-55 Different octahedral distortions also occur with different lengths of the A' cations, since their organization within the organic bilayer is affected by their size. Similarly, small changes in the size of the organic separator can be decisive for the morphology, as exemplified in Figure 1E.56, 57
For applications in photovoltaic devices, the <100> phase is more appropriate than the <110> phase, as the formation of electronic states that allow for different recombination paths and non-radiative recombination in <110> − oriented phases is detrimental.41, 58-61 In general, the quasi-2D perovskites are preferred for 2D-PSCs because the bandgap energy (Eg) decreases as m increases, which widens the absorption window of the solar spectrum. In addition, the resistivity of these materials to charge transport decreases with an increase in the number of slabs.60 In this review we directed the discussion to the <100> − oriented phase layered perovskites.
The inorganic framework is responsible for the band structure and, in many cases, for the photon absorption and formation of free carriers, as will be further discussed herein. However, the organic framework strongly influences the dynamics of the carriers, as fundamental aspects of the material behavior, like phonon scattering, charge mobility, and recombination, depend on the organic part. The next section is dedicated to the organic framework and its influence on the layered metal halides properties.
2.2 The organic framework
The organic cation can be separated into two regions: one interacting with the inorganic framework (I), and the other separating two adjacent inorganic slabs (II, Figure 2A). The interaction between the organic cation and the inorganic framework influences the structural and, consequently, the electronic properties of layered perovskites because the M-X-M bond angles (θ) are influenced by steric effects related to the dimensions of A' (Figure 2B).37 Primary ammonium cations cause lower bond tension on the M-X-M bonds (with 140° < θ < 160°, Figure 2C left), while larger molecules such as 2,2′-biaziridinium, 2,2′-biimidazolium, and 4.4′-bipyridinium lead to greater tension (θ ~ 187°) in tin iodide slabs with m = 1 (Figure 2C right).58, 62 Thus, the characteristics of the A' cation may be critical to the performance of the 2D-PSC.
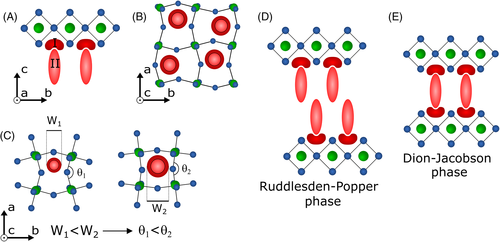
The <100> − oriented perovskites can also be classified into two groups based on the charge of cation A'; that is, the number of interacting sites with the inorganic framework presented by this cation. If it presents charge 1+ (aryl/alkylammonium), the structure formed consists of a bilayer of organic cations separating two adjacent inorganic frameworks (Figure 2D) with the general formula (A')2Am-1MmX3m + 1, where m is the number of slabs. The resulting crystalline structure is named Ruddlesden-Popper (RP) phase.23, 63, 64 When the organic cation presents two ammonium groups (charge 2+), a monolayer separates two adjacent inorganic slabs (Figure 2E), presenting the general formula A'Am-1MmX3m + 1. This structure is labeled as the Dion-Jacobson (DJ) phase.65-68 Differences between RP and DJ phases are not only on the charge of the organic cations, but also in the way these cations interact with each other. On the DJ phases, there is a chemical connection between the two perovskite inorganic slabs. On the other hand, interactions between adjacent slabs in the RP phases are strongly dependent on the organic cation structure. Aspects like chain length, chain volume, the character of the interactions between the chains, donor, or withdrawing groups on the molecules, and so forth, are strongly related to the structural arrangement and charge separation in these layered materials.22, 48, 69 In the case of linear aliphatic saturated organic cations applied as separators on RP phases, the poorly interacting chains will lead to the formation of a region called the van der Waals gap between adjacent slabs.69 As a consequence, the interaction between the inorganic portions is poor. Increasing the interactions between the organic cations is a method to overcome this van der Waals gap, and new molecules are being engineered to boost or quench these effects, depending on the application intended for them.22, 48, 70
As a manner to increase the interaction in the organic sublattice, aromatic ammonium cations might also be applied as organic spacers. Aromatic cations can interact with each other by π-staking, and the planarity of the system allows a more effective organization (i.e., less statistical disorder of the aryl chains) in the self-assembled layered metal halides. Molecules containing multiple aromatic rings are capable to increase even more the interaction by the π-staking.17, 22, 71-73 In small aromatic cations, such as phenylethylammonium (PEA), interaction with other molecules is weak due to the low orientation among the organic rings. Fluorination on a specific position of the ring induces a higher organization of the system, improving π-π interaction and increasing the hydrophobicity.74-76 Other forms of interaction were also applied as strategies to reduce the van der Waals gap. Molecules containing sulfur, focusing on disulfide bridges, or conjugated molecules with sulfur atoms, like (poly)thiophene groups, have been applied with this purpose.22, 72, 77, 78 It is important to point out that, as the strength of the interactions between the organic chains increases, the insulating character related to long unsaturated organic chains is expected to be diminished.
3 ELECTRONIC STRUCTURE AND CHARGE CARRIER DYNAMICS
3.1 Electronic structure
To begin our discussion about the electronic structure of layered perovskites, we start by reviewing the electronic properties of their 3D perovskite analogs. Given the main characteristics of the 3D perovskites, we can set a parallel analysis of their electronic properties with those of the layered metal halides, emphasizing their similarities, and then we highlight the main differences in the optoelectronic properties, especially concerning quantum- and dielectric-confinement.
Numerous theoretical studies on the density of states (DOS) of 3D perovskites were performed using computer simulations based on density functional theory (DFT) to correlate the composition of the bands with the DOS. It is well-accepted that the valence band is formed by the ns orbitals of the M-site cation and by the np orbitals of the X-site anions, while the conduction band is formed by np orbitals from the M cation and X anions.79-81 Also, it is well-understood that the valence band maximum (VBM) and conduction band minimum (CBM) have antibonding character, resulting from the orbital overlap of the filled ns of M and np of X.79, 82 As the composition varies from I to Cl, the ionic character of the bonds increases, and a higher Eg is observed due to the wider energy spacing between ns and np halogen atomic orbitals (Figure 3A, bottom). The influence of A-site cations in the 3D perovskites band structure is mostly indirect, and it is related to the angle formed between X-M-X; that is, depending on the size and structure of the cation, the bond lengths and octahedral distortions are affected, influencing directly on the orbital overlap between M and X. As mentioned before, the dimensionality reduction relives the movement restriction of the inorganic framework; therefore, these effects are even more pronounced in 2D and quasi-2D perovskites with few slabs.
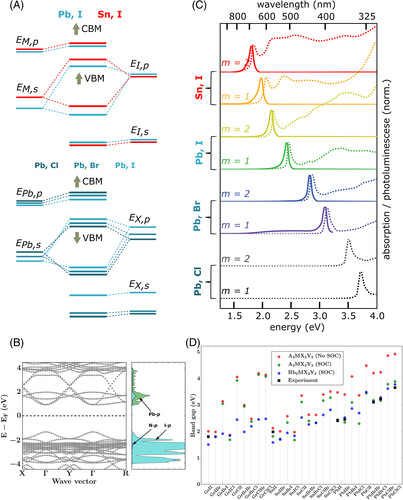
The effect of the M metals on the band structure is less obvious (Figure 3A). Phenomena such as the ns2 lone pairs, relativistic stabilization of the 6s2 level in Pb2+, and the nature of M-X bonds (degree of covalence) all influence the final band structure. Considering all these features, it is possible to finely tune the Eg of these materials by simply changing compositions or forming alloys. Besides, perovskites present a direct bandgap, which increases the probability of electronic transitions by allowing them to occur independently of electron–phonon coupling. In materials with direct bandgap, the VBM and CBM are aligned in relation to the crystal momentum of the electron (vector k), a vector associated with a quantized wave motion of the electron in a periodic crystalline lattice described by its reciprocal space.83, 84
The basic concepts of the electronic properties of 3D perovskites set the basis for the understanding of layered perovskites, which is the aim of our discussion hereafter. Essentially, 2D-perovskites semiconductors present direct bandgap at the center of Brillouin zone (Γ) with the same band composition as their 3D counterparts; that is, band edges composed by M ns/np, and X np orbitals (Figure 3B).85 The VBM is antibonding in character, and the CBM retains characteristics of bonding and antibonding interactions, mainly from M np orbitals.86 Figure 3C presents the trends in the optical properties of layered perovskites nanocrystals with different compositions and values of m (m = 1 and m = 2). As the thickness of the inorganic layer decreases, the bandgap increases until the higher limit with m = 1. Figure 3D shows a more general trend in the change of the Eg for 2D-perovskites with different compositions. As expected, the changes in the Eg in these semiconductors follow a similar trend as the 3D perovskites. Figure 3D also shows the clear influence of spin-orbit coupling (SOC) in the Eg when M = Pb. Having in mind this rich composition and structural tunability, it is worth mentioning that the selection of the semiconductor in a solar cell always considers the most appropriate Eg for light-harvesting (1.5 eV),87, 88 which limits the direct application of some thicknesses (m) and compositions of layered perovskites.
3.2 Excitons
Carrier dynamics in 3D perovskites are almost exclusively related to band-to-band transition, while, in layered perovskites, part of the excited electron population will not occupy states in the conduction band due to electrostatic interaction between electrons and holes.46, 89-91 Instead, electron–hole pairs are bonded together by coulombic interactions to form a quasi-particle called excitons. The energy difference between the excitonic state and the CBM is the exciton binding energy (Eb); that is, the energy necessary to break the electrostatic interaction between the electron and hole. Figure 4A schematically represents the bands and electronic/excitonic states presented by the layered perovskites. Hence, electrons that reach the conduction band minimum present two possible paths: band-to-band radiative recombination, or thermal decay to the excitonic state. Once the exciton is formed, depending on the Eb, excitonic recombination or excitonic ionization (thermal excitation back to the CBM) is observed. The exciton binding energy of the material is related to the dimensions and composition of the inorganic framework (quantum confinement) and also on the organic layer, represented by the position of the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO).92-94 Aliphatic alkylammonium chains, for instance, normally form type I heterojunctions (Figure 4B, left) with the inorganic framework in the RP phase; that is, the HOMO and the LUMO are positioned above and below the VBM and the CBM, respectively.22 In this condition, due to the high-energy difference between the frontier orbitals, an insulating barrier is created between two adjacent inorganic layers, further confining electrons, and holes in the quantum well, creating the so-called dielectric confinement. In addition, it is possible the situation where the HOMO and LUMO are positioned between the bands in which both charge carriers tend to be transferred to the organic sublattice. Due to the characteristics of interaction between the organic separator molecules, the charge extraction is often compromised, and charge recombination increases. The selection/engineering of the organic separator allows the formation of type II heterojunction (Figure 4B, right), where electrons and holes can be separated into different sublattices (organic/inorganic framework) on the material.22 The separation of free carriers in different layers reduces the rate of recombination in the material, increasing the lifetime of the charged species.95
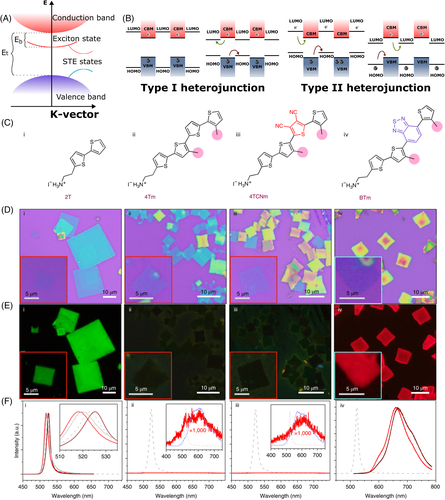
As a remarkable example of organic separator engineering, Gao et al. performed a series of synthesis to prepare different asymmetric conjugated ammonium species, in which each step of the synthesis was designed to tune a specific property on the molecule.22 The studies started with the bithiophene (2T) unit as the base structure. The terthiophene (4T) was synthesized to extend the conjugation and to reduce the bandgap and then methyl groups were inserted to suppress intermolecular self-aggregation forming the new ligand 4Tm. In addition, the authors performed the insertion of cyano groups, which is electron-withdrawing, and a 2,1,3-benzothiadiazole unit, with a small HOMO-LUMO gap, forming the new molecules 4TCNm and BTm, to finely tune the electronic properties by the position of the frontier orbitals. The structures of 2T, 4Tm, 4TCNm, and BTm are presented in Figure 4C. Crystals of these layered perovskites, Figure 4D, present excitonic behavior: (2T)2PbI4 presents a sharp emission around 520 nm, and (BTm)2PbI4 presents a broad emission centered around 660 nm. Very low-intensity signals were registered for the (4Tm)2PbI4 and (4TCNm)2PbI4 layered materials (Figure 4E,F). This is a consequence of the type of heterojunction that occurs between the organic and inorganic sublattices, as the synthetic strategies were designed to change the position of the HOMO and LUMO of the organic molecules. While in the (2T)2PbI4 and (BTm)2PbI4, type I heterojunction restricts charge separation, boosting excitonic recombination, type II heterojunction formed in (2T)2PbI4 and (BTm)2PbI4 structures leads to charge separation between the sublattices causing the suppression of the luminescence in these materials.
Experimental data on the optical behavior of these materials present some tendencies. In the absorption edge, it is possible to notice a strong peak before the band-to-band transition due to the strong excitonic resonance upon optical excitations (Figure 5A). The strong exciton Eb in layered metal halides and the high oscillator strength of the transitions are the two main factors that account for the room-temperature stability of excitons.48, 98, 100 However, the emission profile of these materials may present much more complex features than the absorption: beyond the free-exciton recombination, layered perovskites present several interesting phenomena, all related to the excitonic dynamics. For instance, exciton-phonon coupling, polaronic effects, self-trapping states, broadband emission, and dark excitonic states have been reported in recent studies.101, 102
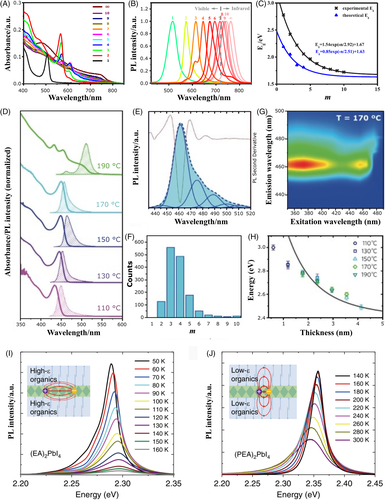
The α parameter of the material is related to the number of slabs on Equation (1). A material with a single slab presents α = 2, and for 1 < m < ∞, α will assume values between 2 and 3. The effects on the reduction of the dimensionality on quantum and dielectric confinement in layered metal halides can be noticed when m ≤ 5.99 Also, by controlling the composition of the inorganic framework, it is possible to tune the absorption/emission of the material from UV to infrared in the same manner that is possible to control the Eg and position of the bands on a 3D perovskite. To illustrate the trend in the energy of the excitonic emission as a function of m, the photoluminescence spectra of several 2D perovskites with general composition (OA)2(MA)m-1PbmI3m + 1 (where OA = n-octylammonium) are represented in Figure 5B.48, 98, 103 It is possible to notice that the emission peak shifts from higher wavelengths, with emission around 760 nm, to smaller, with emission at around 515 nm in layered perovskites. In addition, it is possible to expect exponential growth in the emission energy and the bandgap of these materials as the m value decreases (Figure 5C).
During the synthesis of quasi-2D perovskites, it is quite common the formation of structures with different numbers of slabs, as materials with higher values of m present smaller formation energy.20, 49 Consequently, the optical spectrum is composed of the energy transitions occurring on a highly heterogeneous material as layers with different m values are formed.12, 20, 49, 103 In our group, Bonato et al. prepared a series of samples of perovskite nanoplatelets prepared at different temperatures (Figure 5D). The contribution on the emission of each thickness subfamily in this complex layered perovskite matrix was identified combining a thickness distribution histogram, built with careful counting of hundreds of nanoplatelets from images acquired with High-Angle Annular Dark-Field-Scanning Transmission Electron Microscopy (HAADF-STEM), with the second derivative of the PL spectrum (Figure 5E,F).105 The absorption band edges of these samples were also monitored by mapping the excitation versus PL spectra of the sample (Figure 5G), allowing the discrimination of each population of nanoplatelets with a different thickness by the position of their excitonic resonance. Figure 5H shows the absorption peak position for each nanoplatelet thickness according to the excitation versus PL maps acquired for each sample in Figure 5D.
Considering the excitonic influence in solar cells, as the free hot carriers relax to the band edges, they may fall into the excitonic states.110 The higher the Eb, the more likely is the exciton formation. The charge extraction in a 2D-PSCs must, therefore, occur during the relaxation time.111 As the excitons are formed, radiative recombination processes start to take place, which hinders the charge separation and device performance. Nonetheless, opposing the negative effect of excitonic recombination in layered perovskites with large Eb, photon recycling, and energy transfer process have been demonstrated to be beneficial. This effect was demonstrated in 2D/3D-PSCs, in which a thin film of quasi-2D perovskite forms an interface with a film of 3D perovskite.112 Energy transfer occurs from the phases with wider to those with narrower optical bandgap, and this phenomenon contributes to charge carriers generation in the device.112, 113 Therefore, the rapid excitonic recombination in highly confined layered perovskites may be beneficial in 2D-PSCs if conditions for photon recycling and energy transfer are optimized/improved. For instance, controlling the deposition process in ways to stack layers of different values of m (a layered perovskite tandem architecture) can improve charge extraction and photon recycling in the device. Indeed, this beneficial alignment effect has been demonstrated by some authors, with two of them assembling efficient 2D-PSCs.114-116
3.3 Phonons
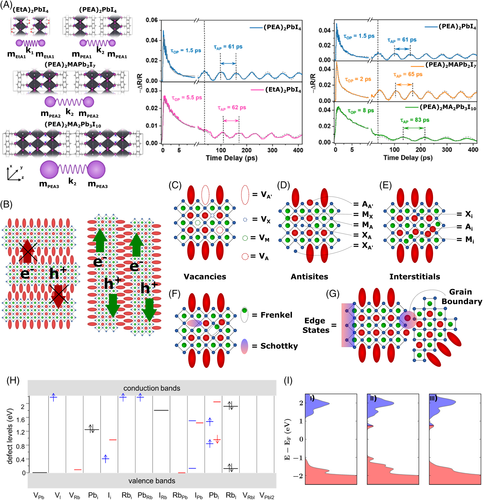
The reduced dimension allows in- and out-of-plane octahedral tilting, and, the higher is the tilting angle (θtilt), the higher will be the momentum transfer between the free carriers and excitons in the lattice (phonon emission).117 Depending on the nature of the organic spacer, the interaction between organic and inorganic sublattices can be stronger, making the structure more rigid and less susceptible to θtilt distortions. The most significant phonon modes related to the cooling process in layered lead halides are the longitudinal acoustic phonons and longitudinal optical phonons through the 2D lattice.46 In acoustic phonons, the atoms in the crystal vibrates in-phase, while in optical phonons the vibration in the lattice is out-of-phase. In addition, acoustic phonons last longer than optical phonons and present lower activation energy. The decay time and velocity of propagation of these phonon modes tend to increase with the augment of the dielectric constant on the organic sublattice.46, 111 The increase in the number of slabs (m) leads to a gain in mass on the inorganic sublattice, altering the oscillation dynamics and boosting the lifetime of the longitudinal phonons.46, 111, 118-120 Therefore, the hot carriers' relaxation tends to be slower when Eb decreases; that is, with thicker inorganic slabs and organic components presenting a higher dielectric constant. Figure 6A left shows a schematic illustration of how the mass of the inorganic layers and dielectric constants influence the frequency of longitudinal phonons, measured directly from photo-induced absorption spectroscopy (Figure 6A right panels).
Hot electrons/holes travel through the crystal lattice and, by doing so, they dissipate energy transferring momentum to the crystal lattice via phonon scattering, the so-called electron–phonon interaction. Phonons not only influence the hot carriers' relaxation but also influence carriers' recombination mechanisms.121, 122 For instance, excitonic states may be split into an exciton-phonon replica before radiative recombination.122-124 Besides, the transfer of momentum from the carriers to the crystal lattice reduces the maximum power output as part of the incident photon energy is dissipated as heat (i.e., carriers-phonon coupling are non-adiabatic processes). Besides this energy loss, phonons may also interfere with the charge carrier's mobility.
The organic layers in layered lead halides influence further the carrier-phonon coupling if compared to 3D metal halides. For instance, the statistical disorder of the alkyl chains in microcrystals increases the lattice strain, augmenting the exciton-phonon coupling in these systems.125, 126 Although this phenomenon is absent in thin films, it exemplifies the influence of the organic cations in the emission dynamics of these materials.122, 125, 126 The thickness-dependent electron–phonon coupling is believed to be due to an ineffective screening of the van der Waals gap to phonon confinement in RP 2D lead halides.127 Indeed, increasing the distance between inorganic slabs, by either intercalating molecules within the van der Waals gap or increasing the chain length of organic molecules, causes a reversible transition between a dual-band (phonon replica) and single-band excitonic emission.128 Recently, our group highlighted that coupled vibrational modes between the ammonium polar heads (R-NH3+) and the inorganic sublattice are the origin of this strong exciton-phonon coupling in microcrystalline 2D lead iodide, originating this dual-band emission profile.122 Also, some vibrational modes in the organic layers of 2D lead iodide influence the phase transition of these materials, revealing a soft-mode characteristic of these vibrations upon temperature variations.122, 127
As far as 2D-PSCs are concerned, phonons may hinder the charge separation during the operation of the device. Since the 2D lattice is “softer” than the 3D analog, the frequency distribution of each phonon mode tends to be broader. In other words, the vibrational wave functions are more diffuse. It means that electronic and vibrational wave functions are more likely to overlap.121 Therefore, both the relaxation and recombination processes of hot carriers are facilitated by carriers-phonon coupling. In this manner, the application of A' cations with rigid planar structures that can result in stronger intermolecular interactions and even facilitate charge extraction is advantageous.
3.4 Charge mobility
There is a significant difference when comparing the charge mobility in the RP and DJ phases. The spacer with two ligand groups removes the Van der Waals gap present on the RP phase, leading to the partial suppression of the structural dynamics of the inorganic framework, especially regarding equatorial distortions. In this situation, the thermally active structural fluctuations become less intense. Differently from what is observed in the RP phase, where the nonradioactive recombination channels are frequently thermally accessed due to the effects of instantaneous charge localization, in the DJ phase the electron–phonon coupling is less intense, which leads to a greater charge delocalization in the structure, a reduction in non-adiabatic dissipation, and an enhancement of the carrier's lifetime.129
The dimensionality reduction in one direction, associated with the presence of the organic layer, is responsible for anisotropic charge mobility in these layered metal halides, meaning that growth control over the orientation of the slabs highly contributes to the mobility of the charge on layered perovskite films. Two different transport mechanisms may take place in these materials: carriers' diffusion and photon recycling.130, 131 The first mechanism as the name suggests, concerns the diffusion of the charge carriers through the crystal lattice. The second is related to the reabsorption of photons emitted during the recombination process. Naturally, if the absorption cross-section of the absorber and the photoluminescence quantum yield of the emitter are high, photon recycling is more likely to occur. Therefore, both diffusion and photon recycling mechanisms are important in 2D and quasi-2D perovskites.130-132
The growth of oriented layered perovskites can increase the carrier diffusion and increase the performance of the solar cells. The obtention of these highly organized systems, however, is tricky and demands high control of the crystallization process. When the nucleation of the films starts within the solution, the layers on the crystallites will be randomly organized, which is the most common situation.133, 134 Due to the anisotropic characteristics of the perovskite layers, the organization of the slabs parallel to the substrate (horizontally oriented) strongly increases the series resistance (Figure 6B left). With the randomly organized slabs, a parcel of the grown slabs will be horizontally oriented, thus, reducing the charge mobility through the films. When the nucleation occurs on the solid–liquid interface, the films are expected to grow horizontally and even smaller charge mobility is expected.133, 134 The most interesting strategy to increase the charge mobility on layered perovskites, however, is to organize the inorganic slabs perpendicularly to the substrate. This orientation takes direct advantage of the anisotropic charge transport of these materials, allowing charge carriers to move easily in the direction of the transport layers of the device (Figure 6B right).13, 28, 60, 77, 135 The growth mechanism is still not fully clarified, but studies indicate that the vertical growth of the layers happens when the crystallization occurs slowly and starts at the air-liquid interface between the precursor solution and the substrate.133, 134 To achieve this vertical alignment, several methods have been developed: the most common is the hot-cast, in which the substrate is heated during the rotation to increase the temperature of the solution and allow the solvent evaporation.13, 109, 134 Another approach is to decrease the rotation period, creating a liquid thin film, and follow with thermal treatment, making the crystallization occur in the last step.133, 134 It is also possible to use additives that induce the orientation during the crystalization.67
It is also important to point out the role of the heterojunction created between the organic and inorganic sublattices within the material. As the exciton is split into free carriers in the junction, the probability of excitonic recombination reduces if a proper band alignment is achieved. As mentioned before, type II heterojunction between the organic and inorganic sublattices can be interesting, as charge carriers follow different ways, and, in this way, can diffuse for longer paths. The selection and the engineering of the A' organic cations are, therefore, very important to achieve the best performance. Conjugated organic cations may present better alignment of the frontier orbitals, and also increase the interaction between adjacent inorganic layers.66, 136-138 Electron withdrawing groups positioned in the middle of the organic sublattice (i.e., in terminal regions in mono-ammonium or central regions in diammonium cations) also help in the repositioning of the frontier orbitals.48, 139-142 Synthetic approaches may consider these characteristics as ways to build new organic structures that might improve charge separation and extraction in the device or even electronically connect adjacent inorganic slabs. It can be speculated that the association of vertically oriented layers and type II heterojunctions can boost the performance to record levels.
The photon recycling process is highly relevant in charge transport since it can increase the density of free charge carriers. Considering the situation in which an interface is formed by a layered metal halide and a 3D perovskite; the energy of the photons emitted by excitonic recombination on the layered perovskite must be higher or equals to the Eg of the 3D perovskite for reabsorption to occur.112 This process, however, can also occur within the layered perovskite when a distribution of the thicknesses of the inorganic sublattice is present. In this case, thinner layers, which present a higher Eg, emit the photon and the thicker layers reabsorb the radiation. Photon recycling studies within layered quasi-2D perovskites, however, are yet scarce in the literature, and careful experiments showing these phenomena still need to be carried out. It is possible to predict, though, that photon recycling must be influenced by the m distribution in these films and the orientation of the layers. Despite the photon recycling effect, the random mixture of slabs with different thicknesses generates an irregular energy landscape that also hinders charge mobility.50 Carriers' mobility is also heavily influenced by the presence of lattice defects, which is the topic of the next section.
3.5 Structural defects and traps
A perfect crystal structure is formed when atoms are periodically ordered and with chemical bonds homogeneously distributed in a lattice. Real crystals, however, have their periodicity disrupted by the so-called punctual defects, occurring at/or around a single lattice point during crystallization and/or posttreatment processes. A particularly intriguing defect present in crystals is the dislocation: defects formed when the linearity of a crystal plane is disturbed abruptly, forcing the layers of a crystal plane to slip over each other. Studies about dislocation in perovskites still missing, but it was recently shown that, by reducing its concentration in one order of magnitude, the carrier's lifetime can be increased by around four times.143
The formation of punctual defects is thermodynamically favorable and is heavily influenced by the temperature in which layered metal halides and 3D perovskites are prepared. Their concentration in a crystal is, therefore, related to the growth conditions and concentration of each precursor species (chemical potential). Point defects are classified according to the origin of the disruption in the lattice and can be denoted using Kröger–Vink notation, whereby an MS label identifies the defective species and the lattice site of the species relative to the site that it occupies. In this notation, M stands for the defective species, and it can be an atom, an anti-site, or a vacancy (V), for example. The atom/ion that should be occupying the site is represented by S, which may also indicate the presence of an M species in an interstice (i).144
Considering a quasi-2D perovskite, there are several types of intrinsic (or native) point defects such as VA, VB, VX (vacancies); Ai, Bi, Xi (interstitials); AB, AX, BA, BX, XA, AA’, BA’, XB (anti-sites); and so forth. (Figure 6C–E). Besides, some defect associations may be observed, and they have special names. A pair formed by a vacancy and an interstitial defect is called a Frenkel defect, and vicinal vacancies in the cation and anion sites are called Schottky defects (Figure 6F). Intrinsic point defects caused by impurities/dopants may also be observed.144 Defects of higher-order and unsaturated surface bonds (mostly present on the crystal surface or grain boundaries in polycrystalline structures), or even precipitates, voids, and different crystal phases within the material may also be present in a real crystal.49 Figure 6G shows two examples of higher-order defects. Figure 6H presents the position of trap states compared with the in Rb2PbI4 layered systems, calculated through DFT simulations using the Vienna Ab-initio Simulation Package (VASP) with Projector Augmented Wave (PAW) pseudopotentials performed by Liu et al.145 The authors used Rb+ to represent the organic cation A' to reduce computational costs. Although the authors consider that the difference in size between Rb+ and A' cations leads to differences in lattice parameters, they argue that it does not affect the dominance of M and X cations on the valence and conduction bands due to states related to Rb+ cation. The discussion on the effect of Rb+ addition for the calculations is deepened in the work of Pandey et al., corroborating the previous conclusion and adding new insights to this approach.85
The presence of crystal defects leads to the formation of localized states, and, when a charge carrier reaches these states, they will be trapped. Its relaxation dynamics will depend on the position of the localized level within the bandgap (see Figure 6H for examples). Three situations are observed regarding the formation of these localized energy levels: (a) defect states happening above or below the CBM or VBM, respectively; (b) levels occurring between bands, but close to the band edges; and (c) energy levels existing between bands and far from the band edges. In the first case, the defect states are considered harmless. The second situation is called shallow defects and some extra energy, from optical or thermal excitation, is sufficient to detrap the charge carriers. However, shallow traps can reduce charge mobility in devices and are detrimental to efficient charge extraction. Finally, the last condition is called a deep-trap level. Although both shallow and deep defects cause energy loss, deep defects are more detrimental to the carrier's mobility and device performance.35
Layered perovskites present similar tolerance to defects as their 3D counterparts regarding vacancy and Schottky defects.85, 146 As for 3D perovskites, these defects in layered metal halides add shallow gap states near the CBM, as depicted in Figure 6H,I, the latter showing the DOS plots of pristine (I), axial halide vacancy (II), and equatorial halide vacancy (III) for A'2PbI4 (A = butylammonium).85, 145 The calculations to generate the DOS plots in Figure 6I were performed using DFT with the GLLB-SC functional.85, 147, 148 Despite this tolerance to defects, deep traps in layered perovskites (e.g., Ii and Pbi) seem to have an energy level even deeper within the bandgap of these materials compared to 3D perovskites, as discussed in a recent report.149 Therefore, beyond the complexity regarding exciton and phonons, defects are also an important (if not critical) parameter to control when fabricating 2D-PSCs.
To exemplify how defects may form and influence the behavior of layered perovskites, we discuss the anti-site and interstitial iodide defects (Ii, IA, and IPb, respectively). A recent report has pointed that, in synthetic conditions where the chemical potential of I (μI) is high, IA, IPb, and Ii are more likely to form.145 These deep-trap states within the bandgap lead to (non)radiative recombination pathways (Figure 6H). These deactivation channels are harmful to the performance of 2D-PSCs since they may extinguish the charge carriers. Also, Ii has been pointed out as the reason for broad-band emissions with large Stokes shift in single crystals of 2D perovskites of the type A'2PbI4, further supporting the potentially detrimental effect of these interstitial defects in the performance of 2D-PSCs.150, 151 Other interstitial defects such as PbI and Pbi are also predicted to generate deep-trap states within the bandgap.145
In addition to these point defects, the so-called excited-state defects, or self-trapped excitons (STEs), may also play a role in the performance of layered metal halides devices. When an exciton is formed, the surrounding lattice of the crystal responds to its electric field with local distortions. Depending on the extension of the lattice distortion and the exciton-lattice coupling, local energy minima may be created, and these states can trap excitons. STEs are very common in metal halide materials.152, 153 Also, the energy barrier for self-trapping decreases with the dimensionality of the system; in the case of halide perovskites, the likelihood of STEs to occur increases from the 3D family to the 1D counterparts.154 Thus, the 2D perovskites falls within these two extremes (α = 2, Equation (2)), and quasi-2D perovskites are an intermediate between 3D and 2D systems (2 < α < 3, Equation (2)). The formation of these STEs crates more recombination channels, allowing the carriers to populate other states than the conduction band and causing energy loss. Therefore, the formation of STEs also contributes for the inferior energy conversion in devices assembled with layered perovskites with small m values when compared with high m values and their 3D counterparts. These STE states are responsible for the extra recombination paths present in <110> phase mentioned before, although it might be also formed on the <100> phases. In addition, it is important to note that there exist two types of self-trapping mechanism: intrinsic- and extrinsic-self-trapping. While the first occurs without the assistance of defects (solely exciton-lattice coupling), in the latter, defects influence directly in their formation. In other words, the distortions caused by defects in the lattice facilitate the exciton-lattice coupling, generating an STE with a different energy depth than an intrinsic STEs.110, 155
Despite the open discussion on STEs in 2D-perovskites, especially on the iodide-based ones, this effect may also act as a disruptive channel for charge carriers in 2D-PSCs, decreasing the performance.150, 155 Considering the quasi-2D perovskites with m > 5, which are the ones of interest for 2D-PSCs, STEs may not be so frequent. However, they should not be disregarded in any case, especially because a distribution of m values is obtained during the preparation of quasi-2D perovskites thin films. Therefore, the presence of defects and other m-phases may increase the likelihood of self-trapping even in the quasi-2D perovskites with m > 5. As such, self-trapping is another parameter that may pose an additional challenge in achieving high-performance 2D-PSCs.
3.6 Practical remarks on layered PSCs
Despite the promising advantages of layered perovskites regarding moisture and photostability compared to their 3D counterparts, the achievement of high-efficiency 2D-PSCs tends to be complex and challenging. The factors behind these challenges are many. For instance, for layered perovskites, special care has to be taken during the deposition of the active layer to guarantee that the slabs are oriented perpendicularly to the substrate; otherwise, as mentioned before, a poor charge extraction is obtained due to the strong anisotropic charge mobility characteristics of these materials.64, 156 Also, higher m-phases (preferably m > 5) are required for efficient light harvesting, which is a parameter difficult to control during the preparation of the films.50, 157 Besides, for m ≤ 5, the exciton binding energy is more relevant, and the optical dynamics might be predominantly excitonic, leading to an increase in radiative recombination and a consequent decrease in the charge carrier density.28, 158 Finally, the defects in layered metal halides, which have received little attention to date, also influence the device's performance. Therefore, controlling the types of defects and defect density are critical parameters that must be accounted for in 2D-PSCs.
To avoid the drawbacks that originated from the defects, STEs, and excitonic recombination, few strategies may be adopted. Deep-trap states in layered perovskites may be avoided by simply controlling synthetic and deposition conditions such as the μI.145 Also, similar passivating agents commonly used in perovskites (e.g., fluorinated alkylammonium halides or alkali metal salts) may also be applied to passivate the surface of layered perovskites. By controlling defects and guaranteeing a narrow distribution over the number of layers, keeping its mean value around 5, STEs can be drastically reduced or even extinguished. Finally, to avoid strong excitonic recombination, the randomly oriented phases with m ≤ 5 should be suppressed during the formation of the films, and this control is also achieved by optimizing the concentration of the precursors and deposition techniques, especially the ratios between A' and A cations. However, if the layered materials are properly overlapped in a tandem architecture, photon recycling may be more beneficial than exciton recombination. Therefore, this balance must be accounted for when engineering 2D-PSCs. In addition, choosing the right organic separator, or even intercalating polarizable molecules between the inorganic slabs, can reduce drastically the Eb, decreasing the excitonic recombination rate.159, 160
The development of 2D-PSCs is yet in the early stages and, to date, the PCE remains under 20%.161, 162 The development of the hot-casting technique to fabricate high-quality RP metal halide films with a preferential vertical orientation by Tsai et al. resulted in a PCE of 12.5%.64 Recently, with the introduction of additives, and engineering of deposition methods, including vacuum poling, antisolvent-assisted crystal growth, and preferred orientation method, the efficiency values were improved to about 18%.163-165 Tailoring the organic spacer has been proposed to be one of the most efficient strategies to improve the photovoltaic efficiency of 2D-PSCs. Different organic spacers, such as phenyltrimethylammonium,166 2-thiophenemethylammonium,165 3-bromobenzylammonium,13 and 2-(methylthio)ethylamine,77 have been developed to continuously improve the performance of 2D-PSCs. For example, by replacing PEA with 4-fluoro-phenethylammonium (4FPEA) cation on a PEA, MA, Pb, I with m = 5 layered structure, Shi et al. increased the efficiency of the solar cells from 11.1% to 17.3%. According to the authors, this was possible by ensuring a better interaction between the organic cations due to improved π-staking and vertically oriented layers.109 Thiophene unit has been widely used in organic electronic materials and has shown promising properties. Lai et al. have successfully developed a layered RP perovskite with m = 6 using 2-thiophenemethylammonium as spacer cation with MACl additive to assist in growth control of the films.165 This approach led to a nanorod-like morphology and high photovoltaic performance (15.4%). Dong et al. presented for the first time the synthesis of a formamidinium derivative, 2-thiopheneformamidinium, based 2D-PSC.167 The results showed that this approach produced a layered perovskite film with increased grain size, reduced grain boundaries, decreased trap density, and preferential vertical growth orientation, leading to enlarged carrier lifetime and suppressed nonradiative recombination loss. The optimized device exhibited a champion PCE of 16.7% with negligible hysteresis. Zangh et al. introduced the vacuum poling method where treatment of immediately after spun layered perovskite solution films on the vacuum.163 This methodology allowed a uniform arrangement of different-m-value nanoplates (PEA)2MAm-1PbmI3m + 1 because of the enforcement of the nucleation during the crystallization after thermal annealing. After careful mechanical peeling of the perovskite film top layer, devices presented PCE up to 18%. Table 1 summarizes some of the approaches used to incorporate layered perovskites on photovoltaic devices.
| Year | Composition | m | PCE (%) | Observations |
| 2015 | BA, MA, Pb, I | 4 | 2.34 | n-i-p mesoporous architecture. Randomly oriented quasi-2D structures.162 |
| 2016 | BA, MA, Pb, I | 4 | 12.52 | p-i-n planar architecture. Vertically oriented 2D structures by hot casting methodology.64 |
| 2016 | CA, MA, Pb, I | 1 | 15.12 | p-i-n planar architecture. Small rigid separator.211 |
| 2016 | PEA, MA, Pb, I | 40 | 15.3 | n-i-p planar architecture. Randomly oriented and thick quasi-2D structures.12 |
| 2017 | PEA, MA, Pb, Br | 50 | 8.5 | n-i-p mesoporous architecture, Randomly oriented and thick quasi-2D structures.212 |
| 2017 | BA, MA, FA, Pb, I | 4 | 12.81 | p-i-n planar architecture. The growth kinetics and orientation were controlled by the addition of FA.116 |
| 2018 | ThMA, MA, Pb, I | 3 | 15.42 | p-i-n planar architecture. Application of MACl for increase control over crystallization, morphology, and vertical orientation.165 |
| 2018 | PDA, MA, Pb, I | 4 | 13 | Planar p-i-n structure. Dion-Jacobson phase.213 |
| 2019 | BA, MA, Pb, I | 4 | 14.42 | Planar p-i-n structure on a “Homo-tandem” device.114 |
| 2019 | BA, Cs, MA, FA, Pb, I | 5 | 14.23 | Planar n-i-p structure. Engineering of the inorganic framework.214 |
| 2019 | 4FPEA, MA, Pb, I | 5 | 17.34 | Planar p-i-n structure. Vertically oriented layers. Insertion of fluorine groups to increase the organization and interaction of the organic chains of the separator.109 |
| 2019 | PEA, MA, Pb, I | Multiple | 18.04 | Planar p-i-n structure. Vacuum pooling treatment leading to arranging different-m-value nanoplates.163 |
| 2020 | ThDMA, MA, Pb, I | 5 | 15.75 | Planar p-i-n structure. Vertically oriented layers by DMSO assisted film growth.106 |
| 2020 | ThFA, MA, Pb, I | 3 | 16.72 | Planar p-i-n structure. Vertically oriented layers. A deposition methodology in which a diluted solution of ThFAI, MAI, and MACl in isopropanol is spin-coated over the layered perovskite film leads to better control over crystallization, morphology, and vertical orientation.167 |
4 STABILITY
The ongoing advancements of PSCs are remarkable, considering both the advances of new materials and the recent advances toward an in-depth understanding of the device's working principles. Despite the incredible increase in performance, the commercial potential of PSCs has recently been questioned, owing to their relatively poor stability under real operational conditions.19, 20, 168-171 Current products on the market typically have a warranty of 20–25 years, and the solar panels retain 80% of its initial output after this period, corresponding to a system loss of <1%/year.172 The instability of the PSCs comes mostly from the degradation of the perovskite materials, as well as extrinsic factors that degrade the device as a whole. The four key factors causing degradation of the perovskite films are oxygen, moisture, UV light, and thermal effects.170, 173-176 In this scenario, layered-perovskites have attracted considerable attention due to their higher environmental stability.167, 177, 178
Among different factors, moisture has been considered one of the biggest challenges.172 The exact processes governing the degradation mechanism caused by the relative humidity (RH), the combined effect of humidity and illumination, and the role of crystal surface terminations are still open to debate in the perovskite research community.179, 180 In addition to inducing degradation, humidity can be used to improve the crystal growth of perovskite materials under certain conditions, which makes the effect of water even more complicated to elucidate.181, 182 The highly hydrophilic properties of the inorganic sublattice lead to the absorption of water from the surrounding environment and induce the formation of hydrate products.183 This greater moisture stability in layered metal halides is mainly related to the hydrophobic nature of the spacer cation, as well as the highly oriented structure and dense packing, which reduces the superficial area and prevents direct contact of adventitious water.23, 40
The stability facing UV-light and temperature are related to the controlled structural dynamics of the inorganic sublattice, previously discussed, which effectively prevent phase transitions to optically inactive phases. The layered structure also avoids UV and thermal-induced ion migration within the inorganic framework, and, as this effect leads to induced structural defects that weaken the perovskite skeleton, the degradation is retarded.184-186 Besides, the encapsulation of the perovskite slabs by the organic separator can stop the thermal evaporation of the A cations, which is speculated as one of the main degradation mechanisms for bulk perovskites, especially in compositions presenting a high proportion MA.187
Despite this high stability, layered metal halides present limited charge transport and a large bandgap for solar cell applications.182 To overcome the charge transport properties Liang et al., developed solar cells with phase-pure (m = 1 to 5) layered perovskite vertically oriented (Figure 7A).188 They prepared the films using a liquid butylammonium acetate precursor, resulting in a fine control over the QW thickness of the layered perovskites. This approach led to a champion device (m = 4) with a PCE of 16.25% and VOC of 1.31 V, with robust environmental, thermal, and illumination stability. Li et al. reported a formamidinium-based 2D perovskite, using bifunction aromatic spacers to improve the stability and performance of 2D-PSCs.66 Although the reported PCE was 7%, the 2D-PSCs presented >60% retention of the efficiency after 500 h, at 60°C, under accelerated aging conditions. Ahmad et al. showed that, by eradicating the van der Waals gaps incorporating diammonium cations into MAPbI3, Dion-Jacobson layered PSCs with 13.3% PCE and high stability are achievable.69 The unencapsulated devices retained 95% of their initial PCE after 4000 h of exposure to ambient atmosphere (40%–70% RH), 168 h of heat stress (85°C and 85% RH), and 3000 h of illumination. As aforementioned, the large bandgap, poor charge transportation, and large exciton binding energies limit the PCE values.184 These issues can be resolved by mixing 2D with the conventional 3D lead halide perovskites, where the establishment of 2D/3D structure, not only ensures the long-term stability, but also increases the performance of PCSs.185 Wang et al. reported the introduction of a 2D perovskite into γ-CsPbI3 film to overcome its thermodynamic instability.189 Carefully controlling the amount of PEA+ groups in γ-CsPbI3 resulted in a changed dimensionality, forming a quasi-2D structure. Interestingly, the formation of this structure promoted an improvement in crystal orientation, surface morphology, and water resistance. The sum of these factors resulted in a device with enhanced stability in ambient conditions with a high PCE of 13.65%.
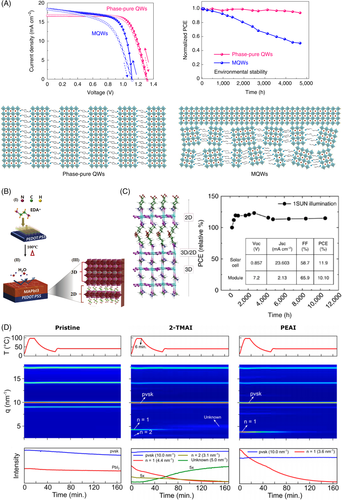
Regarding the 2D/3D interfaces, recent studies have demonstrated the advantage of layered perovskites in increasing the tolerance toward moisture and even the increase of PCE. In a remarkable work published by Grancini et al. the authors assembled solar cells using an interfacial mixture of 2D/3D perovskites leading to a module with the stability of over 10 000 h (Figure 7C).168 The 2D layer constitutes a barrier towards electron recombination without acting as a barrier to electron injection to TiO2. The combination of the 2D layer acting as a protective window against moisture leads to the achievement of high efficiency and stable devices. The in situ approach for the formation of 2D structures over 3D polycrystalline CH3NH3PbI3 reported by Holanda et al. promoted the increase of 17% of the assembled devices' lifetime under ambient humidity conditions.20 Hangoma et al. demonstrated the growth of 2D/3D perovskite films using a layered perovskite seeding layer positioned underneath a 3D perovskite film, in a device with n-i-p architecture (Figure 7B).190 They introduced ethylenediamine (EDA) cations on the top of the hole transport layer in the device. The EDA cations readily reacted with the perovskite precursor during the spin-coating, resulting in a growth of a thin layered perovskite film. This thin film induced an ordered growth of the 3D perovskite during the annealing, causing grain boundaries to merge, reducing site defects that could act as trap centers, and maintaining a robust and stable perovskite framework. This structure yielded high-efficiency devices fabricated in ambient conditions, with enhanced moisture stability.190
Another important factor influencing the stability of PSCs is UV light exposure. As for multiple solar cell technologies, illumination becomes the reason for degradation in PSCs.174, 191 Ahmad et al. studied 2D/3D hybrid PSCs using electric field induced second harmonic generation and impedance spectroscopy.192 They showed that these are powerful techniques to study the soaking conditions in PSCs and that, under the same experimental soaking conditions, the 2D/3D PSCs showed better performance compared to their 3D counterparts. The formation of 2D perovskite platelets, interspersed between highly orientated 3D perovskite grains, reported by Snaith et al., promoted a great enhancement in crystallinity and evidence for reduced defects responsible for nonradiative recombination. With this approach, they achieved not only a high efficiency device, but also greater stability under simulated sunlight illumination.193 The light stability of PSCs can be enhanced by the formation of a large-grain 2D/3D hybrid film. Teng et al. presented a posttreatment with diethylammonium bromide (DABr) to fabricate high quality 2D/3D perovskite films.194 The introduction of DABr induced the formation of large crystals and also the formation of a layered perovskite capping layer on 3D perovskite films. The large grain size leads to preferable interfacial contact between the TiO2 and the perovskite layer, which eliminates the light soaking effect, enhancing light stability.194
The thermal stability of PSCs also raises a serious concern about solar modules. These devices are subjected to elevated temperatures during operation, causing their degradation.158 The solar cell must require thermal stability up to 85°C, which corresponds to 0.093 eV.176 It is a well-known fact that temperature has a great effect on the crystal structure and phase of perovskite.195-197 Layered perovskites have already demonstrated over 1000 h device thermal stability.198, 199 With encapsulation, the device shows a constant value under the combined effect of illumination, temperature, and humidity for more than 2000 h.200 Zhou et al. demonstrated that the thermal photoinduced degradation can be largely suppressed by a postdeposition treatment of the perovskite films with benzylamine.201 Figure 7D shows in situ grazing-incidence wide-angle X-ray scattering (GIWAXS) approach, which, combined with steady-state, and time-resolved photoluminescence, revealed a slow dynamical variation of the 2D/3D interface under thermal cycles.202 It leads to a structural modification of the 2D perovskite and, when the 3D perovskite is protected by the 2D layer, the 3D bulk is unperturbed. 202 The presence of a structurally robust 2D layer is very important to control the device stability, that is, the purity of the layered 2D structure and its robustness against ion movement and infiltration has a crucial impact on the long-term device stability.14, 202
5 PERSPECTIVES
As the global clean energy demand is constantly increasing, new photovoltaic technologies are key to achieving this demand while assuring a positive environmental impact. Perovskites are a breakthrough in this field and hold promise in contributing to a greener energetic source worldwide. The main reasons for this great potential lie in the low manufacturing cost and high efficiency of perovskite-based solar cells, despite the current concerns involving the use of lead because of its toxicity in living organisms and in the environment and stability issues.
With the advance in PSCs and the concern regarding their operational instability, layered perovskites naturally stood out as a versatile alternative to carry the technology further. 2D-PSCs are yet in the early stages of development and much improvement is still necessary; for instance, the charge mobility in both organic and inorganic sublattices, fine crystalline phase control, and the orientation of these phases regarding the substrate and charge transport layers. The further optimization of such parameters is critical to provide more operational stable 2D-PSCs (or 2D/3D-PSCs) with efficiency values comparable to current technologies and state-of-the-art 3D-PSCs.
From a practical perspective, the great versatility of layered perovskites also brings unprecedented challenges, especially to what concerns the interface of the inorganic and organic sublattices. The work of Gao et al. offers a promising avenue when it comes to engineering of the organic separators and positioning of the frontier orbitals (HOMO and LUMO) regarding the VBM and CBM of the perovskite sublattice.22 Another interesting approach to developing further the class of organic separators is the modification of formamidinium cation: the hydrogen bonded to the carbon in this cation can be easily substituted by other groups, which opens the door for innumerous possibilities. Examples of this strategy in the literature are given by a pioneer work of Mitzi et al.60 in 1995 and the recent work Dong et al.167; the latter achieving highly efficient 2D-PSCs.
Although several works focusing on the orientation of layered perovskite films have been reported, there still much to accomplish and to understand in this complex puzzle.203 All the approaches cited above such as hot-casting, vacuum-poling, or the use of additives to favor preferential orientation have their pros and cons, and the nucleation and growth mechanisms of these fabrication methods are complex and not fully elucidated. Therefore, more research on the existing approaches, as well as the development of new ones, are still highly desirable for the community of 2D-PSCs. An alternative field of exploration, in this sense, is the solvent-vapor post-annealing method: the hot-solvent vapor plasticizes the layered perovskite films and induce their reorganization/reorientation.204, 205 In this broad avenue of post-annealing methods, we speculate that hot-air annealing, recently demonstrated to improve the crystallinity and film quality of 3D perovskites,206, 207 may also be a promising option to explore in 2D-PSCs.
Another aspect of interest that presents an open field of development to improve the performance of 2D-PSCs is defect passivation. Exploring different passivation agents such as the previously mentioned alkylammonium salts will certainly lead to a reduction in the concentration of surface defects, resulting in a potential increase in devices' performance. Nonetheless, other approaches are yet to be explored. For instance, the application of groups that can coordinate with the M cation on the surface of the layer, such as alkylthiols and thiocyanates, to passivate M2+ dangling bonds. Alkali metal cations might also be explored to assist in the passivation of defects in both A and A' sites. Our group developed a post-synthetic method of passivation that might be suitable to passivate 2D-PSCs: the use of rubidium butyrate as a passivating agent may effectively passivate both cation vacancies (VA and VA’) and surface halide vacancies (VX).208 Another advantage in using this passivation method is that the organic acylate can be chosen to match the aryl/alkylammonium backbone of the separators (e.g., butyrate/butylammonium), so that its introduction when passivating halides vacancies would be less disturbing to the crystal structure.
At last, improving the long-term stability of PSCs is critical to the deployment of this technology. As it is not viable to test a device in the field for decades (20–25 years), accelerated tests are typically used to determine long-term stability. For PSCs, a testing standard that has been adopted is the internationally recognized IEC 61646.170, 190, 209 To pass this test, the device performance must decrease by no more than 20% after 1000 h of aging at 85°C and 1 sun illumination. Despite the great emphasis on stability-related investigations, publications lack consistency in experimental procedures and parameters reported. It is therefore challenging to reproduce and compare results and, thereby, develop a deep understanding of degradation mechanisms. In this way, a new paper published this year, that is a collaboration of many of the most outstanding names in the field of PSCs, reported a consensus between researchers in the field on procedures for testing perovskite solar cell stability, which are based on the International Summit on Organic Photovoltaic Stability (ISOS) protocols.210 These protocols are not intended as a replacement of the existing qualification standards, but rather they aim to unify the stability assessment and to understand failure modes. Therefore, for the development of 2D-PSCs, it is equally fundamental that such standards are met to avoid misleading conclusions and accelerate the deployment of 2D-PSCs technology as well.
ACKNOWLEDGMENT
This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - Brasil (CAPES). Paulo E. Marchezi and Ana Flávia Nogueira gratefully acknowledge the support from the FAPESP (Grant 2017/11986-5) and Shell and the strategic importance of the support given by ANP (Brazil's National Oil, Natural Gas, and Biofuels Agency) through the R&D levy regulation. Raphael F. Moral gratefully acknowledges the support from FAPESP (process number: 2019/25765-6). We would also like to thank the publishing companies Springer Nature, American Chemical Society (ACS) and John Wiley and Sons for allowing the usage of images from their journals.
CONFLICT OF INTEREST
The authors declare no conflict of interest.
Biographies

Matheus S. de Holanda, born in 1988, is currently a postdoctoral researcher in the “Gleb Wataghin” Institute of Physics at the University of Campinas. He obtained his Bachelor's (2012) and Master's (2014) degrees in Chemistry from the University of Brasilia, working on the synthesis of material for application on photocatalysis, and his PhD in Chemistry from the University of Campinas (2020), focusing on the in situ formation of 2D structures with bulk perovskites. His research focuses in the formation and stability layered perovskites films and application in perovskites solar cells.

Raphael F. Moral is a chemist who received his BS degree from University of Sao Paulo (USP). During his undergraduate course, he worked mainly with organic and inorganic synthesis as a junior scientist. Then, he received his MS degree from University of Campinas (UNICAMP), where he worked with perovskite nanocrystals and 2D perovskites. He is currently taking his PhD degree, and his work is focused on the understanding of the growth dynamics of perovskites (nano)materials probing in situ reactions, their fundamental optical properties, and their application in optoelectronic devices. His current research project is being developed in collaboration with the new Brazilian synchrotron light source, Sirius, using x-ray scattering and diffraction as means to probe nucleation and growth of solution-process materials.

Paulo E. Marchezi is a postdoctoral researcher in Chemistry Institute at University of Campinas (UNICAMP). He received his BS degree in chemistry from Federal University of Santa Maria (UFSM). Then, he received his MS degree from University of Campinas (UNICAMP), where his polymer electrolytes for dye sensitized solar cells. He received PhD degree from University of Campinas (UNICAMP), where he studied the degradation mechanisms of mixed perovskites and its modifications with reduced graphene oxide. His current research project consists in the studying of the 2D/3D perovskites interfaces and its effects on the stability of perovskite solar cells.

Francisco das Chagas Marques is a full professor at the “Gleb Wataghin” Institute of Physics, University of Campinas (UNICAMP), from where he received PhD degree in physics in 1989. He was a postdoctoral fellow at Harvard University, visiting professor at the University of Utah and visiting researcher at SCIRO, Melbourne. He has published over 100 research papers and some patents and books. He works in the development and study of optoelectronic, structural, and thermomechanical properties of amorphous, microcrystalline, and nanostructured materials and in the manufacture of photovoltaic devices.

Ana Flavia Nogueira obtained her Bachelor's degree in Chemistry from the University of São Paulo (1996) and Master (1998) and PhD degrees in Chemistry from the University of Campinas (2001). She worked as a postdoctorate fellow at the Imperial College, UK, in 2001–2002 and as visiting researcher at Stanford University in 2017–2018. At the moment, Ana Flavia is Professor in the Institute of Chemistry at UNICAMP and Director of the Center for Innovation on New Energies (CINE). Prof. Nogueira's research focuses on the development of functional (nano)materials and their application in solar energy conversion. She has experience in the field of perovskite solar cells, perovskite quantum materials, and dense energy carriers.